Immersed Boundary Methods for Simulations of Biological Flows in Swimming and Flying Bio-Locomotion: A Review

Abstract

Biological flows in swimming and flying bio-locomotion usually involve intricate flexible or rigid structures that undergo large deformations and displacements, as well as rich mechanisms of bio-fluid interactions. Immersed boundary methods (IBMs) have gained increasing prevalence in numerical investigations of such biological flow problems due to their simplicity and capability for simulating these problems on a Cartesian mesh, which does not require tedious grid-regeneration or mesh deformation processes. In recent years, the vigorous development of IBM variants has enriched numerical techniques for bionic simulations. This review focuses on the development of the IBM and its applications in the field of biological aerodynamics and hydrodynamics, including both diffuse and sharp interface IBMs. The fundamentals of the former are introduced in detail, and the hybrid Cartesian-IBM is briefly presented as one representative method of the latter. In particular, the velocity correction IBM is highlighted in the diffuse interface IBM due to its superiority in accurately satisfying no-slip boundary conditions. To shed light on the dynamic characteristics of flying and swimming behaviors with predefined or passive motion and deformation, some recent results from IBM applications are also presented. Finally, this review discusses some challenges and promising techniques in the research of bio-inspired motions based on the IBM.

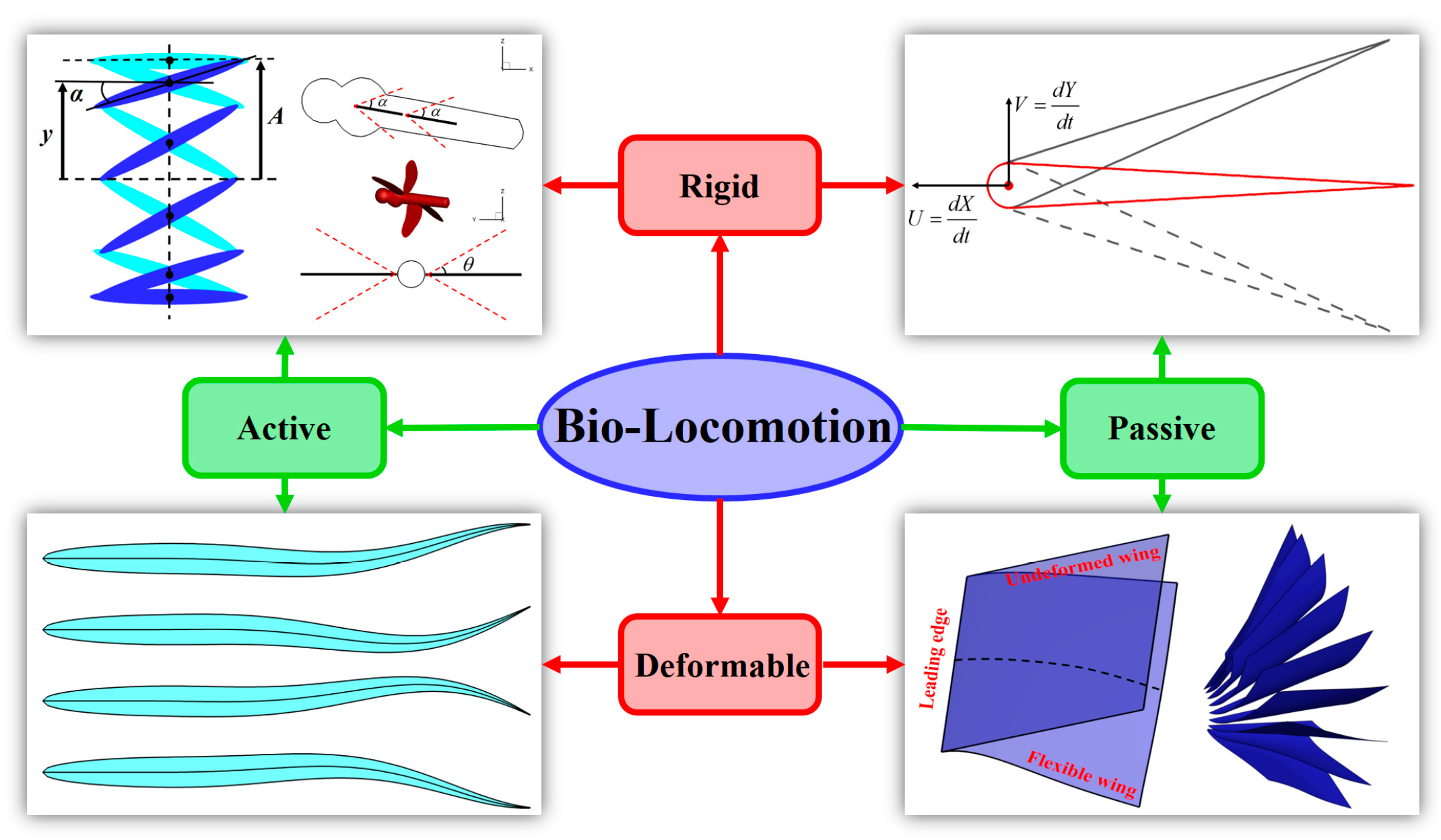
1. Introduction

Bio-inspired motions are ubiquitous in nature and commonly encountered in bionic designs involving flying insects/birds, swimming fishes, micro air vehicles, and underwater robots. Learning from nature has been a constant throughout human progress. Since the last century, interest in the mechanisms of bio-locomotion has erupted with the rise of biomimetics [1,2,3]. The purpose of designing robotic flyers and swimmers with biological features has sparked a number of studies on living animals with relatively tiny sizes [4,5]. Now it is commonly recognized that the major attributes of bio-inspired motions are autonomous motion, low Reynolds number, incompressible flow, and high unsteadiness [2,4,5,6]. Numerous scholars have put efforts into this field over the years to explore the mechanisms of bio-fluid dynamics through both experiments and numerical simulations and gained fruitful achievements.

Numerical methodologies have two primary types based on the mesh for spatial discretization. The body-fitted arbitrary Lagrangian–Eulerian (ALE) method is the one with the mesh conforming to the solid-fluid interface [7]. For bio-locomotion problems, the interface is changeable at every time step. The mesh needs re-generation simultaneously to match the moving structures, which causes a high computational cost. The immersed boundary method (IBM) is a representative approach for the other [8]. It adopts a non-conformal mesh, which is fixed during the whole simulation regardless of the moving and deforming interface, without any re-meshing process. The frequently used Cartesian mesh is easier to code and generate than body-fitted mesh and is even unaffected by the surface complexity, demonstrating its enormous potential in simulating sophisticated biological flows.

The IBM was initially proposed by Peskin for blood flow in the heart [8]. To solve more problems, the original IBM has been improved, producing a series of variants. They have been successfully applied to simulate flow problems involving flexible or rigid bodies over the past few decades due to their simplicity and practicality. In the IBM, the fluid and solid domains are discretized by independent meshes and are described by Eulerian and Lagrangian coordinates, respectively. Therefore, the fluid field and solid motion/deformation can be solved by their own governing equations. Then, the IBM is applied to deal with the boundary conditions at their mutual interface through a so-called forcing term. The different treatments of this term motivate various IBMs. In the original IBM [8,9,10], the forcing term is computed by the elastic law of flexible structures, which restricts its application to rigid bodies. By introducing some free parameters to model the forcing term, different versions of the penalty forcing IBM are developed [11,12,13,14,15]. However, the values of the user-defined free parameters are hard to choose for different problems, and the rigidity restriction has not been completely overcome. A variety of direct forcing IBMs have been developed in the following years, aiming to solve the rigid particle-laden flows [16,17,18,19,20,21,22]. Since then, the limitations of IBMs in problems with rigid bodies have been lifted. Due to separate solvers for fluid and solid, IBMs can combine with most of the prevalent fluid solvers, such as Navier–Stokes solvers [8,10,23,24] and the lattice Boltzmann method (LBM) [16,25,26]. More details will be discussed later. Among the developed IBMs, to our knowledge, a momentum exchange-based IBM is unique for LBM solvers [27,28]. Most of the above-mentioned methods have pre-computed forcing terms, causing the streamlined penetration at the solid surface, which indicates that the no-slip boundary condition is not accurately satisfied [29]. To solve this drawback, the multi-direct forcing IBM [18] or extra iterations [30] are applied. On the contrary, a velocity correction IBM is developed without the pre-determined forcing term, which is an implicit method [31,32,33,34,35]. The forcing term is replaced with the velocity correction, which can accurately enforce the boundary condition imposed on the solid surface. This method is highlighted in this review due to its vigorous applications in simulations of biological flows, which are being continuously improved and developed. All of the aforementioned IBMs need a Dirac delta function to realize information transfer between fluid–solid domains. This function often spans over several grids near the interface, which neglects the sharpness of the interface. These methods belong to the diffuse interface IBM. To eliminate the numerically undesirable feature, a series of sharp interface IBMs has been developed, to name a few, the cut-cell method [36,37,38], immersed interface method [39,40,41], and the hybrid Cartesian-IBM [42,43,44,45]. Among these methods, the hybrid Cartesian-IBM has been widely applied to the simulations of bio-locomotion. Due to this, only the hybrid Cartesian-IBM [43] is introduced in this review. Some published reviews can assist readers in fully comprehending IBM [46,47,48,49,50,51]. Consequently, the flourishing development of the IBM has made it full of potential in the field of bio-fluid dynamics.

IBM has become an efficient tool for bionic simulations. Rich species that live in fluid environments have sophisticated motions and deformations. Researchers have created various mathematical models to determine the bionic dynamics for different study purposes. These models usually include active/passive motions and deformations involving both rigid and flexible structures. The inherent simplicity of the IBM to couple with these models has promoted the wide applications of bionic simulations. This review is organized as follows: Section 2 presents the governing equations of bio-fluid dynamics, including the incompressible viscous NS equations for fluids and some typical descriptions for active/passive motions and deformations of bionic structures. Section 3 introduces the development of the IBM, where more attention is paid to the diffuse interface IBM. The sharp interface IBM is briefly introduced, as well as some flow solvers combined with the IBM. Section 4 presents applications of the IBM for bio-locomotion involving both flying and swimming behaviors. Section 5 discusses some future issues of IBMs in the area of bio-fluid dynamics. Conclusions for this review are given in Section 6.

2. Governing Equations

The bio-inspired motions often occur in the incompressible viscous flow according to the summarized characteristics above; the flow field is governed by the Navier–Stokes equations:

$$\nabla ·\mathit{u}=0,$$

(1)

$$\frac{\partial \mathit{u}}{\partial t}+\nabla ·\left(\mathit{u}\mathit{u}\right)=-\nabla ·\left(p\mathit{I}\right)+\nabla ·\left[\nu \left(\nabla \mathit{u}+{\left(\nabla \mathit{u}\right)}^T\right)\right]+\mathit{f},$$

(2)

where $\rho$, $\mathit{u}$, and $p$ represent the density, velocity, and pressure in the flow field, respectively. $\nu$ is the kinematic viscosity of the fluid. $\mathit{f}$ is the forcing term representing the mutual interaction between immersed objects and fluids. It will be handled in different forms in various IBMs.

In the bionic simulations, there is a variety of governing equations to characterize the movement and deformation of bodies. Without loss of generality, we present some typical descriptions involving prescribed motion/deformation and passive ones that are affected by ambient fluids. We illustrate these four types of bio-locomotion in Figure 1, where the rigid and deformable properties are relative to the geometrical shapes in simulations, and active and passive characteristics determine the interaction between the structures and fluids. Active motion and deformation are prescribed without consideration of the hydrodynamical forces, while passive ones are affected by the ambient fluids.

For rigid structures, the prescribed motion is often adopted in simulations of insect/bird flight relying on flapping wings. As shown in Figure 1, for a two-dimensional (2D) flapping foil with heaving and pitching motions, or a three-dimensional (3D) dragonfly flight with pitching or rolling motions, a series of harmonic functions are commonly used to describe these types of flapping motions [52,53,54]:

$$\theta ={\theta }_0\sin \left(2\pi ft+\phi \right),$$

(3)

where $\theta$ is the attitude angle for pitching or rolling motions. ${\theta }_0$ is the amplitude of harmonic motion with frequency $f$ and phase difference $\phi$. In the 2D heaving and pitching motions, the translation displacement and pitching angle are also prescribed in the form of Equation (3). Some other governing equations for prescribed motions can be found in the literature [55,56]. In biological motion research, the passive motion of a rigid body is mainly reflected in self-propulsion by thrust, as shown in Figure 1. The propelling motion is governed by Newton’s second law [54,57,58]:

$$m\frac{d^2\mathit{X}}{d{t}^2}=\mathit{F},$$

(4)

where $\mathit{X}$ is the position vector, $m$ is the mass of the swimming body, and $\mathit{F}$ is the hydrodynamic force. Note that this passive motion is usually driven by harmonic pitching in the form of Equation (3) around a pivot point.

For deformable bodies, as shown in the lower part of Figure 1, the prescribed deformation of a swimming fish is often encountered in recent studies [6,59,60,61,62,63,64]. Some mathematical models are used to characterize the deformation of the swimming body periodically. Here we present one of them to elucidate the prescribed deformation [59], where the shape is determined by geometric parameters, and the backbone waveform is controlled by

$$y\left(x,t\right)=\left(c_{1}x+c_2{x}^2\right)\sin \left(k_{w}x-\omega t+\phi \right),$$

(5)

where $y\left(x,t\right)$ is the waveform along the backbone, $k_w$ is the wavenumber, $\omega$ is the circular frequency, the two coefficients $c_1$ and $c_2$ determine the amplitude envelope of straight-line swimming, $\phi$ is the phase difference in multibody problems. In Figure 1, we present some deformations governed by Equation (5), where the basic geometric shape is NACA0006 airfoil, and the parameters of the waveform are referred to [59]. This type of deformation is independent of the hydrodynamic forces exerted on the structures, called the active or prescribed deformation. The passive deformation is related to flexible structures and is deformed by hydrodynamic forces, which can be found in elastic wings or swimmers [58,65,66]. The 3D flexible flag is the basic structure, including stretching, shearing, bending, and twisting deformations [65]. It can also be simplified to a 2D filament in some applications [58,66]. Then it can be treated as the thin flapping wing of insects or the elastic fin of fishes, where the flexible property is maintained. The 3D governing equation can be written as

$${\rho }_s\frac{{\partial }^2\mathit{X}}{\partial t^2}={\displaystyle \sum _{i,j=1}^2\left[\frac{\partial }{\partial s_i}\left({\sigma }_{ij}\frac{\partial \mathit{X}}{\partial s_j}\right)-\frac{{\partial }^2}{\partial s_i\partial s_j}\left({\gamma }_{ij}\frac{{\partial }^2\mathit{X}}{\partial s_i\partial s_j}\right)\right]}+\mathit{F},$$

(6)

where ${\rho }_s$ is the area density, ${\sigma }_{ij}$ is the stretching and shearing stress, ${\gamma }_{ij}$ is the bending and twisting stress. $\mathit{X}$ is the position vector of the discrete points on the surface. $\mathit{F}$ is the force density generated by the ambient fluids. A deformed flapping wing governed by Equation (6) is shown in Figure 1. Moreover, the absolute nodal coordinate formula (ANCF) is another prevalent method to model flexible thin structures [67]. Due to the great variety of biological species in nature, the above-mentioned governing equations of motion and deformation, Equations (3) to (6), are limited but sufficient for discussions on the IBM in this review.

3. Immersed Boundary Method

3.1. Diffuse Interface IBM

Since the immersed boundary method was proposed by Peskin [8], it is famous for its simple generation of meshes. There are two sets of discrete points called the Eulerian points and Lagrangian points, as shown in Figure 2, where the former represents the fluid domain, and the latter is for the surface of an immersed object. The two meshes are separate. The immersed object can move independently, corresponding to the coordinate updating of Lagrangian points. Using IBM, the relationship between the solid and fluid domains can be established. The boundary condition at the phase interface is dealt with using the IBM simultaneously. Central to the entire process of the IBM is the handling of the body force $\mathit{f}$ of the fluid domain in Equation (2) and obtaining an accurate fluid velocity $\mathit{u}$ near the immersed boundaries. Based on these goals, various IBMs have been proposed in succession. Some typical methods will be presented hereafter in 3D form.

3.1.1. Classic IBM

The original IBM was developed for simulations of heart blood flows with elastic boundaries [8,9,10]. The coupled equations can be written as:

$$\mathit{f}\left(\mathit{x},t\right)={\displaystyle {\int }_{\Gamma }\mathit{F}\left(s,t\right)}D\left(\mathit{x}-\mathit{X}\left(s,t\right)\right)ds,$$

(7)

$$\frac{\partial \mathit{X}\left(s,t\right)}{\partial t}=\mathit{u}\left(\mathit{X}\left(s,t\right),t\right)={\displaystyle {\int }_{\Omega }\mathit{u}\left(\mathit{x},t\right)}D\left(\mathit{x}-\mathit{X}\left(s,t\right)\right)d\mathit{x},$$

(8)

$$\mathit{F}\left(s,t\right)=S\left(\mathit{X}\left(s,t\right),t\right),$$

(9)

where $\mathit{f}\left(\mathit{x},t\right)$ is the body force in Equation (2) of the fluid domain at the position $\mathit{x}$ and time $t$, and $\mathit{u}$ is the fluid velocity. $\mathit{F}\left(s,t\right)$ is the boundary force at the position $s$ in the Lagrangian system $\Gamma$. $\mathit{X}\left(s,t\right)$ is the corresponding coordinate on the Cartesian mesh $\Omega$. Equation (7) is the distribution relationship between the boundary force and fluid body force, from Lagrangian points to Eulerian points. Equation (8) is the interpolation of fluid velocity from Eulerian points to Lagrangian points. Equation (9) is applied to compute boundary force, where the function $S$ can be simplified to Hooke’s law for the elastic boundary. This original IBM is naturally suitable for elastic bodies due to the inherent rigid limit.

An important Dirac delta function $D\left(\mathit{x}-\mathit{X}\right)$ runs through the development of the diffuse interface IBM. It is a distribution function related to the distance $\mathit{r}$ and can be computed using

$$D\left(\mathit{r}\right)=\varphi \left(r_x\right)\varphi \left(r_y\right)\varphi \left(r_z\right),$$

(10)

where $\varphi$ is the kernel function with many practicable expressions. Figure 3 presents four typical ones. For specific expressions, please refer to [68], where Yang and his co-workers develop more smoothed functions for IBMs. By the way, the study on the distribution function for the IBM attracts many researchers, aiming to improve the calculation stability and accuracy. Amiri et al. [69] constructed a new kernel function using Lagrangian velocity interpolation. The moving-least-squares approach has been developed to improve the interpolation for IBMs [24,70,71].

3.1.2. Penalty Forcing IBM

The classic IBM computes the boundary force $\mathit{F}\left(s,t\right)$ by Equation (9) for elastic structures, where the function $S\left(\mathit{X}\left(s,t\right),t\right)$ is determined by a certain problem. The feedback scheme proposed by Goldstein et al. [11] established a unified model for boundary force, which inspired a new IBM, the so-called penalty forcing IBM. Dimensional constants $\alpha$ and $\beta$ are introduced in the feedback loop:

$$\mathit{F}\left(s,t\right)=\alpha {\displaystyle {\int }_0^t\mathit{u}\left(s,t^{\prime }\right){dt}^{\prime }}+\beta \mathit{u}\left(s,t\right),$$

(11)

where $\mathit{u}$ is the fluid velocity at the boundary surface. To satisfy the no-slip boundary condition, the constants $\alpha$ and $\beta$ are set negative and large enough that then $\mathit{u}$ will approximately converge to zero for stationary objects. Inspired by this, the penalty forcing IBM has been widely studied and applied from then on [12,13,15]. However, it is difficult to select appropriate values with physical meaning for the two constants. For different flow problems, the optimal values may be different. Therefore, several penalty forcing IBMs are developed using particular cases of Equation (11). By choosing $\alpha =0$ and $\beta =\mu /K$ [72,73], the external force becomes $\mathit{F}=\mu \mathit{u}/K$. This treatment is suitable for flows with a porous medium with permeability $K$. So far, the porous medium is rarely introduced in biological motion simulations, but it may be useful in more detailed simulations of the feather or fin in the future. By setting $\beta =0$ [13], the boundary force can be rewritten as:

$$\mathit{F}\left(s,t\right)=-\kappa \left(\mathit{X}\left(s,t\right)-{\mathit{X}}^e\left(s,t\right)\right),$$

(12)

where the position of boundary points $\mathit{X}\left(s,t\right)$ is connected to the corresponding equilibrium points ${\mathit{X}}^e\left(s,t\right)$ with a spring stiffness constant $\kappa$. For the rigid boundary, ${\mathit{X}}^e\left(s,t\right)$ is the desired position, and the spring model is defined with large stiffness $\kappa \gg 1$. The movement of the boundary points can be constrained to some degree. A famous application of the penalty forcing IBM for rigid bodies is the simulations of particle-laden flows. Feng and Michaelides [14] define a displacement $\xi \left(s,t\right)=\mathit{X}\left(s,t\right)-{\mathit{X}}^r\left(s,t\right)$ for each Lagrangian point, where ${\mathit{X}}^r$ is the reference boundary point position that can be computed using the position of mass center ${\mathit{X}}_c$ and the instantaneous rigid rotational matrix $R$:

$${\mathit{X}}^r\left(s,t\right)={\mathit{X}}_c\left(t\right)+R\left(t\right)\left({\mathit{X}}^r\left(s,0\right)-{\mathit{X}}_c\left(0\right)\right).$$

(13)

The restoration force $\mathit{F}\left(s,t\right)$ is needed to restore the boundary point back to its prescribed position from $\mathit{X}$ to ${\mathit{X}}^r$. The expressions of $\mathit{F}\left(s,t\right)$ is given by

$$\mathit{F}\left(s,t\right)=-\kappa \xi \left(s,t\right),$$

(14)

which is a linear spring relationship and similar to Equation (12). Another piecewise expression is written as

$$\mathit{F}\left(s,t\right)=\left\{\begin{array}{cc}0,& ‖\xi \left(s,t\right)‖=0\\ -\frac{c_f}{{\epsilon }_d}\frac{\xi \left(s,t\right)}{‖\xi \left(s,t\right)‖},& ‖\xi \left(s,t\right)‖>0\end{array}\right.,$$

(15)

where the coefficients $c_f$ and ${\epsilon }_d$ are scale factors, corresponding to force and stiffness, respectively.

Compared with the original IBM, this spring-like model for the solid boundary can behave well in simulating elastic structures [13,23] and preliminarily apply to rigid body simulations. However, the key issue for the rigid boundary is choosing the value of stiffness $\kappa$. Although a large value can maintain the rigidity of an immersed body, it leads to severe time-step limitations [13]. Conversely, a small value mitigates the rigidity of the boundary by the spurious elastic effects.

3.1.3. Direct Forcing IBM

All the penalty forcing methods cannot completely solve the rigid body problems. Another way to construct the boundary force was initially proposed by Mohd-Yusof and his co-workers [74,75], called the direct forcing method. There is no free user-defined constant. The basic point of view is that the boundary force can be directly evaluated from the governing equations of fluid with the boundary velocity. Equation (2) can be rewritten in a simplified form for incompressible flows:

$$\frac{\partial \mathit{u}}{\partial t}=\mathit{r}\mathit{h}\mathit{s}+\mathit{f},$$

(16)

where the term $\mathit{r}\mathit{h}\mathit{s}$ includes the convective, viscous, and pressure gradient terms. Equation (16) is valid in the whole fluid domain. Hence the properties of the fluid at the same positions of Lagrangian points can also be computed using Equation (16). If the flow properties for the time step $n$ is already known, the explicit expression of the force term at Lagrangian points at $\mathit{X}\left(s,t\right)$ in a forward finite difference form reads

$${\mathit{f}}^{n+1}=\frac{{\mathit{u}}^{n+1}-{\mathit{u}}^n}{\Delta t}-{\mathit{r}\mathit{h}\mathit{s}}^n,$$

(17)

which is generally adopted in the direct forcing IBM [16,18,22]; the spatial accuracy depends on the computation of ${\mathit{r}\mathit{h}\mathit{s}}^n$. Theoretically, other time-advanced strategies can be applied in Equation (17), such as the central difference method. It is an intermediate expression for satisfying the no-slip boundary condition, where the fluid velocity ${\mathit{u}}^{n+1}\left(\mathit{X}\left(s,t\right)\right)$ is set equal to the boundary velocity ${\mathit{U}}^{n+1}\left(s,t\right)$. ${\mathit{U}}^{n+1}$ can be obtained by rigid motion using $\mathit{U}\left(s,t\right)={\mathit{U}}_c+\omega \times \left(\mathit{X}\left(s,t\right)-{\mathit{X}}_c\right)$. Hence ${\mathit{f}}^{n+1}\left(\mathit{X}\left(s,t\right)\right)$ can be computed. Note that in the original method by Mohd-Yusof [74] and Fadlun et al. [75], the Lagrangian points are not introduced to represent the solid boundary. The boundary velocity at the intersection of the grid line and the solid interface is computed using interpolation from neighboring grid points, which is hard to trace the position of the intersection for a moving boundary, and their works are the origin of the sharp interface IBM. Feng and Michaelides [16] develop a direct forcing IBM for rigid moving particles using a series of Lagrangian points for the solid boundary and give the relationship between the fluid body force $\mathit{f}\left(\mathit{X}\left(s,t\right)\right)$ and boundary force $\mathit{F}\left(s,t\right)$:

$${\displaystyle {\int }_{{\Gamma }_{\epsilon }}\mathit{F}\left(s,t\right)ds}\approx \mathit{f}\left(\mathit{X}\left(s,t\right)\right){\delta }_A,$$

(18)

where ${\Gamma }_{\epsilon }$ is the boundary element and ${\delta }_A$ is the area of influence. In this method, the body force is explicitly expressed. The relationship of Equation (7) for distributing boundary force to neighboring grids is not considered. Uhlmann [17] incorporates the process of transferring quantities between Lagrangian and Eulerian locations in the direct forcing IBM, including the force transfer from $\mathit{F}\left(s,t\right)$ to $\mathit{f}\left(\mathit{x},t\right)$.

It is worth mentioning that the body force $\mathit{f}\left(\mathit{x},t\right)$ can also be obtained using a fractional method [18,22]. An intermediate fluid velocity ${\mathit{u}}^{*}$ is determined and computed with $\partial \mathit{u}/\partial t=\mathit{r}\mathit{h}\mathit{s}$, where the body force is firstly treated as $\mathit{f}=0$. Then the fluid velocity ${\mathit{u}}^{*}\left(\mathit{x},t\right)$ at the Eulerian points is obtained using

$${\mathit{u}}^{*}={\mathit{u}}^n+{\mathit{r}\mathit{h}\mathit{s}}^n\Delta t,$$

(19)

where ${\mathit{u}}^{*}\left(\mathit{x},t\right)$ can be used to compute the fluid velocity at Lagrangian points ${\mathit{u}}^{*}\left(\mathit{X}\left(s,t\right)\right)$ by Equation (8) in a discrete form:

$${\mathit{u}}^{*}\left(\mathit{X}\left(s,t\right)\right)={\displaystyle \sum _{\mathit{x}\in \Omega }{\mathit{u}}^{*}\left(\mathit{x},t\right)D\left(\mathit{x}-\mathit{X}\left(s,t\right)\right)h^3},$$

(20)

where $h=\Delta x=\Delta y=\Delta z$ is the grid space. The no-slip boundary condition is modeled by the intermediate velocity ${\mathit{u}}^{*}\left(\mathit{X}\left(s,t\right)\right)$ and boundary velocity $\mathit{U}\left(s,t\right)$, which also gives the expression of boundary force $\mathit{F}\left(s,t\right)$:

$$\mathit{F}\left(s,t\right)=\frac{\mathit{U}\left(s,t\right)-{\mathit{u}}^{*}\left(\mathit{X}\left(s,t\right)\right)}{\Delta t}.$$

(21)

Then $\mathit{F}\left(s,t\right)$ at Lagrangian points is distributed to Eulerian points to obtain the body force $\mathit{f}\left(\mathit{x},t\right)$ using Equation (7), and the velocity fields for the next time step are:

$${\mathit{u}}^{n+1}\left(\mathit{x},t\right)={\mathit{u}}^{*}\left(\mathit{x},t\right)+\mathit{f}\left(\mathit{x},t\right)\Delta t.$$

(22)

In this section, only the explicit direct forcing scheme is presented. Some other powerful direct forcing IBMs are developed to solve certain problems. Luo and his co-workers [18,19] proposed the multi-direct forcing scheme to satisfy the no-slip boundary condition accurately through iterations, where Equations (19)–(22) are the basic procedures in the iterative loop. This multi-direct forcing scheme can also contribute to improving the accuracy of the IBM [20], which reaches second-order spatial accuracy. Implicit direct forcing IBMs [25,76] provide a new treatment for the force terms, which couples the velocity interpolation and force distribution between Lagrangian and Eulerian points. Since the direct forcing IBM is initially developed to simulate particulate flows [16,17], it has made significant contributions in this area along with its development [19,20,21,22,77,78]. Due to its flexibility and adaptability to different problems, it can be conveniently extended to simulate fluid-structure interaction problems, including both rigid [79,80] and elastic [25,26] bodies. Obviously, this method is a promising tool for simulating biological flows.

3.1.4. Velocity Correction IBM

Most of the above-mentioned IBMs have a common characteristic that the boundary force is needed to be obtained during the calculation process. The boundary force $\mathit{F}\left(s,t\right)$ is then distributed to neighboring grids to obtain the body force of the fluid field $\mathit{f}\left(\mathit{x},t\right)$. Although $\mathit{F}\left(s,t\right)$ is modeled by the no-slip boundary condition, such as Equation (21), the final velocity field is computed with $\mathit{f}\left(\mathit{x},t\right)$ using Equation (22). The distribution procedure of Equation (7) leads to the failure to satisfy the no-slip boundary condition. The physical phenomenon is streamlined penetration. Shu et al. [29] point out that it is due to pre-determined body force $\mathit{f}\left(\mathit{x},t\right)$. To remove this drawback, an iterative procedure [18,30] or a priori correction [81] is often introduced. Wu and Shu [31,32] proposed a velocity correction IBM that can accurately satisfy the no-slip boundary condition without the iterative procedure. In this method, the computation of body force $\mathit{f}\left(\mathit{x},t\right)$ is replaced by the velocity correction because adding a body force to Equation (2) is equivalent to making a velocity correction in the flow field [29]. Using this method, the body force $\mathit{f}\left(\mathit{x},t\right)$ can be seen as a post-determination.

A fractional technique is used in this method. Similar to the direct forcing IBM in [22], the body force is neglected initially, and the intermediate fluid velocity ${\mathit{u}}^{*}\left(\mathit{x},t\right)$ is also computed using $\partial \mathit{u}/\partial t=\mathit{r}\mathit{h}\mathit{s}$ first. Then an unknown velocity correction of the fluid field $\Delta \mathit{u}\left(\mathit{x},t\right)$ is assumed to obtain the expression of corrected fluid velocity $\mathit{u}\left(\mathit{x},t\right)$:

$$\mathit{u}={\mathit{u}}^{*}+\Delta \mathit{u}.$$

(23)

Corresponding to the distribution of boundary force $\mathit{F}\left(s,t\right)$ to the body force in the fluid $\mathit{f}\left(\mathit{x},t\right)$ as Equation (7), a boundary velocity correction $\Delta \mathit{U}\left(s,t\right)$ is set at the Lagrangian point. It can also be distributed to the Eulerian points using

$$\Delta \mathit{u}\left(\mathit{x},t\right)={\displaystyle {\int }_{\Gamma }\Delta \mathit{U}\left(s,t\right)}D\left(\mathit{x}-\mathit{X}\left(s,t\right)\right)ds,$$

(24)

$$\Delta \mathit{u}\left(\mathit{x},t\right)={\displaystyle \sum _{s\in \Gamma }\Delta \mathit{U}\left(s,t\right)D\left(\mathit{x}-\mathit{X}\left(s,t\right)\right)\Delta s},$$

(25)

where Equation (25) is the discrete form, $\Delta s$ is the arc length of the boundary element. In the intermediate velocity field, the fluid velocity ${\mathit{u}}^{*}\left(\mathit{X}\left(s,t\right)\right)$ can be computed with Equation (20). The corrected velocity $\mathit{u}\left(\mathit{X}\left(s,t\right)\right)$ at the same position of the Lagrangian point can be computed in the same way. It should equal the boundary velocity $\mathit{U}\left(s,t\right)$ according to the no-slip boundary condition. Then the relationship reads:

$$\mathit{U}\left(s,t\right)=\mathit{u}\left(\mathit{X}\left(s,t\right)\right)={\displaystyle \sum _{\mathit{x}\in \Omega }\mathit{u}\left(\mathit{x},t\right)D\left(\mathit{x}-\mathit{X}\left(s,t\right)\right)h^3},$$

(26)

Substituting Equations (20) and (23) into Equation (26), the following equation system is obtained:

$$\mathit{U}\left(s,t\right)={\mathit{u}}^{*}\left(\mathit{X}\left(s,t\right)\right)+{\displaystyle \sum _{\mathit{x}\in \Omega }{\displaystyle \sum _{s\in \Gamma }\Delta \mathit{U}\left(s,t\right)\Delta sD\left(\mathit{x}-\mathit{X}\left(s,t\right)\right)}D\left(\mathit{x}-\mathit{X}\left(s,t\right)\right)h^3}.$$

(27)

This equation system can be rewritten in the form of matrix

$$A\mathit{X}=\mathit{B},$$

(28)

where $\mathit{B}=\mathit{U}\left(s,t\right)-{\mathit{u}}^{*}\left(\mathit{X}\left(s,t\right)\right)$, $\mathit{X}$ is the unknow variable to be solved, $A$ is a matrix. Here, we present the solution process proposed by Wang et al. [33,34,35,82], due to its simplicity. The term $\Delta \mathit{U}\Delta s$ is taken as the primary unknowns at the Lagrangian points, which can avoid the calculation of the arc length of a boundary element $\Delta s$. The matrix $A$ is of dimension $N\times N$, where $N$ is the number of Lagrangian points. Every element of $A$ can be computed with $D\left(\mathit{x}-\mathit{X}\left(s,t\right)\right)$:

$$A_{lk}={\displaystyle \sum _j^M{D}_{lj}{D}_{jk}}{h}^3,$$

(29)

where $l,k=1,\cdots ,N$, $j=1,\cdots ,M$, $M$ is the number of Eulerian points. By solving $\mathit{X}=A^{-1}\mathit{B}$, $\Delta \mathit{U}\Delta s$ can be obtained. However, the coefficient matrix $A$ is introduced in this method. In the original velocity correction IBM, the procedure for solving $A^{-1}$ is required. In this way, Equation (28) is difficult to be solved efficiently if the number of Lagrangian points is excessive, especially for 3D problems. This has been considered a drawback of this method. Recently, Zhao et al. [83] proposed an explicit technique to handle the matrix $A$. Using this method, Equation (28) can be solved efficiently. Matrix $A$ is simplified to a diagonal matrix, where the diagonal elements are computed using

$${\lambda }_l={\displaystyle \sum _k^N{A}_{lk}},$$

(30)

where $l$ represents the row of matrix $A$. In this way, Equations (27) and (28) can be simplified to each Lagrangian point:

$$\lambda \left(s,t\right)·\Delta \mathit{U}\Delta s=\mathit{U}\left(s,t\right)-{\mathit{u}}^{*}\left(\mathit{X}\left(s,t\right)\right).$$

(31)

After obtaining the terms $\Delta \mathit{U}\Delta s$, substituting them into Equation (25), the velocity correction $\Delta \mathit{u}\left(\mathit{x},t\right)$ is obtained. Finally, Equation (23) can be applied to solve the corrected velocity $\mathit{u}\left(\mathit{x},t\right)$ at Eulerian points. Through this procedure, the fluid velocity is enforced to equal the boundary velocity. The no-slip boundary condition can be accurately satisfied, which avoids streamline penetration. This feature is validated by Wu and Shu [31], as shown in Figure 4, where the streamlines penetrate the solid boundary in Figure 4a obtained by the direct forcing IBM [16] while the no-slip boundary condition is satisfied in Figure 4b using velocity correction IBM [31]. In this method, the velocity correction procedure replaces the calculation of the boundary force $\mathit{F}\left(s,t\right)$ and fluid body force $\mathit{f}\left(\mathit{x},t\right)$. The iterative process for the boundary condition in other IBMs [18,30] is also removed. Obviously, this method is powerful for simulations with both rigid and flexible structures and has successful applications [54,67,84,85,86].

Some diffuse interface IBMs are presented above. The pros and cons of these methods are also mentioned. For instance, the classic IBM and penalty forcing IBM both have difficulties in simulating problems involving rigid bodies. They are early IBMs. The direct forcing IBM and velocity correction IBM are more prevalent recently. The basic framework of the former is efficient but cannot accurately satisfy the no-slip boundary condition at the solid surface. To overcome this drawback, a multi-direct forcing scheme is proposed. The velocity correction IBM can satisfy the conditions at the immersed boundaries conveniently but introduces a complex matrix in the computations. Some efforts have been put into the aspect of eliminating the complexity. By focusing on the CPU time with different numbers of Lagrangian points, some improved methods for solving Equation (28) are tested in [87], such as the Gaussian elimination method, Cholesky factorization method, and generalized minimal residual (GMRES) method, where the multi-direct forcing IBM is also incorporated into the comparison. The comparison in [87] indicates that with the help of efficient methods for solving the linear equation system, such as the GMRES method, the inefficiency of the velocity correction IBM can be overcome and is more efficient than the direct forcing IBM. Additionally, Zhao et al. [83] have compared the computational complexity of these IBMs, which indicates that the computational complexity of the multi-direct forcing IBM is lower than the original velocity correction IBM, and with an explicit technique for handling the matrix $A$, the improved velocity correction IBM with Equations (30) and (31) has the lowest computational complexity. By comparing the average CPU time, the case of flow past a transversely oscillating circular cylinder is simulated for the test of efficiency in [83], and the results are shown in Figure 5, where four IBMs are included. In these methods, the boundary condition-enforced IBM is the same as the original velocity correction IBM in this Section, and the explicit IBM is the improved one. The conjugate gradient IBM is also an improved scheme of the velocity correction IBM. For this scheme, readers can refer to [83]. Consequently, with improved schemes and the velocity correction IBM has superiority in simulations of biological flows. Moreover, this method and its variants also support improving computational efficiency by reducing the number of grids while ensuring computational accuracy [88,89].

3.2. Sharp Interface IBM

The boundaries in all the above diffuse interface IBMs are smeared across several grid cells, which depends on the choice of the Dirac delta function in Figure 3. A series of sharp interface IBMs is developed to eliminate the diffuse feature. The hybrid Cartesian-IBM proposed by Mittal et al. [43] is a representative sharp interface IBM and has been widely applied in the simulations of bio-inspired motions. This method removes the momentum forcing term from the computational process, which means that the governing equations of fluid flow are the same as Equations (1) and (2) but with the term $\mathit{f}=0$ in Equation (2). In this method, the fluid field is solved by a well-developed Navier-Stokes solver.

Different from the above-mentioned diffuse interface methods, Lagrangian points are not required to represent the boundary surface, which is inspired by Mohd-Yusof [74] and Fadlun et al. [75]. The ghost-cell methodology is the key step to finding three types of points, as shown in Figure 6, where the ghost cells (GC) are defined as the ones that locate inside the solid body and have at least one neighboring node in the fluid domain, every ghost-cell has a symmetric point, called the image point (IP), and the intersection on the immersed boundary is the boundary intercept (BI). To satisfy the boundary condition on the interface in the vicinity of each ghost cell, it is required to determine the flow properties at the ghost cells using appropriate interpolation schemes.

Note that there are four neighboring cell points in 2D cases, such as the four corners of the shadow square in Figure 6, and eight points in 3D cases. Here, we present the method in 3D form. For a flow property $\phi$ (denoting velocity $\mathit{u}$ and pressure $p$), a trilinear interpolant is given as:

$$\phi \left(x,y,z\right)=C_{1}xyz+C_{2}xy+C_{3}yz+C_{4}zx+C_{5}x+C_{6}y+C_{7}z+C_8,$$

(32)

where the coefficients $C_i$ are determined by the value of $\phi$ at the eight points. If the ghost-cell is included in these points surrounding the image point, it should be replaced by the boundary intercept. Then the values at the image points can be computed using

$${\phi }_{IP}={\displaystyle \sum _{i=1}^8{\beta }_i{\phi }_i},$$

(33)

where ${\beta }_i$ is computed by the coefficients $C_i$ as well as ${\left(x,y,z\right)}_{IP}$ according to Equation (32). Then the Dirichlet boundary condition is applied for the velocity

$${\phi }_{GC}+{\phi }_{IP}=2{\phi }_{BI}.$$

(34)

The Neumann boundary condition is applied for the pressure

$${\phi }_{GC}-{\phi }_{IP}=-\Delta l{\left(\frac{\delta \phi }{\delta n}\right)}_{BI},$$

(35)

where $\delta \phi /\delta n$ is the second-order central difference, $\Delta l$ is the gradient distance from GC to IP.

Mittal et al. [43] validated the second-order global and local accuracy by simulating the case of flow past a circular cylinder. The results are shown in Figure 7, where the error norms show nearly second-order convergence and indicate the hybrid Cartesian-IBM is globally and locally second-order accurate.

This method is improved by Luo et al. [44] and Tian et al. [45], aiming to suppress the numerical oscillations caused by the motion of the immersed boundary. These methods reserve the sharp characteristics of interfaces and improve local accuracy. For bio-inspired motions, they are developed to simulate the flight of the dragonfly [43], hummingbird [44], and cicada [45]. Later, these series of sharp interface IBMs are extended to study more bio-fluid problems [90,91,92,93,94,95,96,97,98].

Here, we summarize the numerical characteristics of the above-mentioned IBMs in

Table 1. Numerical characteristics of the above-mentioned IBMs.

Methods	Applicability to Structures	Interface Accuracy	Spurious Oscillation	Time Step Restriction	Complexity or Cost
Classic IBM	Elastic	Low	Small	Moderate	Determination of boundary force
Penalty forcing IBM	Elastic/rigid	Low	Small	Severe	Selection of stiffness
Direct forcing IBM	Elastic/rigid	Low	Small	Moderate	Streamline penetration
Multi-direct forcing IBM	Elastic/rigid	Moderate	Small	Moderate	Additional iterations
Velocity correction IBM	Elastic/rigid	Moderate	Small	Moderate	Treatment of the matrix
Hybrid Cartesian-IBM	Elastic/rigid	High	Severe	Moderate	Search for ghost-cells

. With the development of the IBM, the applicability to rigid structures has been completely achieved. Due to the inherent features of diffuse and sharp interface IBMs, the interface accuracy of the hybrid Cartesian-IBM is high. In the diffuse interface IBMs, the velocity correction IBM has an advantage in interface accuracy. The spurious oscillation and time step restriction are discussed in [50]. It is reported that the spurious oscillation is mainly due to the moving interface for the sharp interface IBMs, and the time step restriction in the penalty forcing IBM with a feedback approach [11] is more severe than other methods. The typical complexity and cost of the methods are also briefly listed in Table 1, associated with some special procedures or drawbacks of these methods.

3.3. Flow Solver for IBM

The IBM is a tool for dealing with boundary conditions at the solid-fluid interface. With the development of the IBM, the flow solvers matching them have also been widely developed. An excellent flow solver can improve overall efficiency. This subsection will briefly summarize some prevalent and recent combinations of IBMs and flow solvers. Navier–Stokes (NS) equation solver, as a classic method in fluid mechanics, is first combined with IBM and is well developed later [8,10,23,24]. The NS solver based on direct discretization of the Navier–Stokes equations is at the macroscopic level with physical conservation laws for fluid flow. In the sharp interface IBM, the NS solver is frequently applied [43,44,45]. However, the velocity–pressure coupling in the governing equations brings computational difficulties to the Poisson pressure equation. Such drawbacks of flow solvers will remain in the coupled scheme of IB-NS. With the development of kinetic methods at the mesoscopic level, the computational efficiency of flow solvers is increased due to their distinctive merits [99,100], such as the famous lattice Boltzmann method (LBM) [101] and gas kinetic scheme (GKS) [102]. In recent years, the family of flow solvers based on kinetic methods has grown considerably [103,104,105,106,107,108]. To our knowledge, only a few efforts have been put into the combinations of IB-GKS [109,110,111]. Note that IB-GKS is successfully applied for simulations of bio-inspired motions [6,54,57,112,113,114]. However, in the last two decades, IB-LBM has been rapidly developed due to its promising potential to improve computational efficiency [14,16,27,31,32,115,116,117]. The constraints between the time step and mesh spacing in LBM inherently remained in the coupling scheme. This drawback is circumvented in the lattice Boltzmann flux solver (LBFS) proposed and developed by Shu and his co-workers [118,119,120], using the framework of the finite volume method. Wang et al. [33,34,35,82,121] developed the IB-LBFS for rigid bodies. The work of Liu et al. [67] indicates that it is also practicable for flexible structures. A more recent coupling scheme of the IBM and reconstructed LBFS (IB-RLBFS) is proposed by Wu et al. [89], which simulates biological flows involving both rigid and flexible bodies.

4. Applications of IBM for Biological Flows

The research on bio-fluid dynamics has significant meanings for designing bio-inspired robots and exploring nature mechanisms. This section mainly focuses on the applications of the IBM for solving bio-inspired motions, including the flying/swimming behaviors of animals and some parts of their structures. Sotiropoulos and Yang [49] reviewed the insect flying and aquatic swimming simulated by IBMs until about ten years ago. We will present some recent research in the last decade.

4.1. Flying Behaviors

The simulations of the entire body and the flapping wing are the two most prevalent aspects. A dragonfly consists of a main body and four wings. The flow field has complex structures due to the fluid-body-wing interaction. It abstracts a large number of researchers to reveal its aerodynamic mechanism. Figure 8 presents the 3D vortical structures of the forward flying dragonfly with the prescribed motion of the four wings, using the same simplified model in [52], where Figure 8a,b give the time evolution diagrams, Figure 8c shows the vortical structure at a certain moment with multi-direction views. Equation (3) is used to govern the motions of pitching and rolling. The physical parameters for controlling the harmonic motion of the wing are referred to [52], and the Reynolds number is 500. Figure 9 gives the quantitative results of force coefficients for the forewings and hindwings, respectively, where the force coefficients of the two forewings (hindwings) are the same in the x-, and z-directions, while they undergo anti-phase evolution in the y-direction due to the symmetry. The results of Wu and Shu [52] and Yang et al. [109] are included in Figure 9. Inamuro and his co-workers [122,123] simulated the free flight at different physical angles of a dragonfly-like body to reach various moving states. Bode-Oke et al. [124] constructed a more detailed model of a dragonfly to study the aerodynamics of backward free flight. They observed the revolution of the leading edge vortex (LEV), trailing edge vortex (TEV), and tip vortex (TV), affected by the backward-flying dragonfly.

With the aid of the IBM, the simulations involving the whole body of other flying insects/birds have been successfully performed, such as the cicada [91,94], hummingbird [93,97], fruit fly [98], and butterfly-like body [125,126]. The fluid-wing-body interaction can lead to lift enhancement, Wang et al. [97] and Liu et al. [91] studied this phenomenon using both wing-body and wing-only models for the hummingbird and cicada, respectively. The results of their works are presented in Figure 10.

In addition to the simulations of entire flying bodies, some basic structures of insects/birds are also worth investigating, such as the wing. The single drosophila wing with prescribed motion is simulated with several different IBMs [55,56,83]. Lee et al. [56] compared the vortex structures around the drosophila and cicada wings. Shahzad et al. [95,96] revealed the aerodynamic performance of a hawkmoth-like wing, considering the effects of wing shape, aspect ratio, deviation angle, and flexibility. Due to the flexibility of the wing, it will have passive deformations, which are studied by Dai et al. [65] using an elastic rectangular wing under hovering flapping states. Figure 11 presents the results of Dai et al. [65], as well as our recent simulations of forward flight states with pitching and rolling motions, where the governing equation of the deformation is Equation (6) in our simulations.

4.2. Swimming Behaviors

It is meaningful for biomimetics to investigate swimming behaviors, which can give inspiration in underwater swimmer designs [127,128,129]. Both sharp interface and diffuse interface IBMs have been tested for aquatic animal locomotion [52,55]. Different species of underwater animals have their own shapes and swimming mechanisms, such as a mackerel-like body [52,55,63,128,130], oblate body [6,131], anguilliform body [132,133], and jellyfish [134,135,136]. Figure 12 presents the numerical results of two types of fishes with significantly different shapes, where Zhang et al. [6] revealed the role of vortices in the force enhancement mechanism in aquatic swimming using the derivative-moment transformation (DMT) theory, and Fang et al. [63] investigated the flow patterns and analyzed the periodic effects caused by tail paddling using dynamic mode decomposition (DMD). Both fishes undergo prescribed deformation, where the batoid fish deforms corresponding to different wavenumbers and longitudinal amplitudes while the tuna is governed by Equation (5).

Underwater animals often have rich swimming mechanisms, such as self-propulsion [54,57,58] and power extraction [66,113]. Figure 13 shows the self-propulsion process of an underwater swimmer, which is simulated by our in-house code of IB-LBFS. The geometry of the swimmer is the same as that in Figure 1 for the passive motion of rigid bodies, and relative physical parameters can refer to [54]. According to Lin et al. [54], an unconstrained swimmer has two degrees of freedom to move, which are governed by Equation (4). A harmonic pitching motion, Equation (3), can drive its self-propelled motion. The reversed Karmann vortex is well-known for generating thrust in self-propulsion. The propulsion velocities are shown in Figure 13a, as well as the results from the work of Lin et al. [54] and Wu et al. [58], where the U velocity is always positive. Wu et al. [58] proved that with a flexible fin clamped at the swimmer’s tail, the propulsion performance can be improved. The flexible fin also takes on the role of power extraction from the ambient fluids, which is sensitive to the flexibility of the tail [66]. When it comes to multibody, the collective locomotion [112,113,114] and wake-body interaction [62,64,137] appear and are worth studying. Due to the self-propelled motion, the collective locomotion appears as a stable system with multiple swimmers in forward swimming together [113], as shown in Figure 14.

It is attractive to explore the fishes with flexible bodies governed by Equation (5) in special underwater environments. Shao and Li [60] investigated the fish swimming in oblique flows and reported that the amplitude of undulation was dominant in thrust generation. Xie et al. [61] considered the wall effects in their study on the power extraction efficiency of a fish with carangiform swimming in a narrow channel. Moreover, a group of these undulating fishes has complex wake-body interactions. High-density fish school is studied by Pan and Dong [62,137], where the fishes have various phase differences that improve the thrust efficiency of the fish school. Many representative characteristics of fish swimming are included in a recent work by Wei et al. [64], such as deformable body, fish school, self-propulsion, and collective behaviors. Two main stable configurations are found in this work, rectangular and diamond configurations and each of them has in-phase and anti-phase formulations. The vorticity contours are shown in Figure 15.

5. Future Issues of IBM in Biological Flows

In some recent reviews of the IBM [50,51], the authors concluded two main future challenges of the IBM: numerical stability in issues of low fluid-solid mass ratio and computation complexity in cases with a high Reynolds number. In this section, we discuss five future issues of the IBM in biological flows, computational efficiency, high-order accuracy, numerical stability, high Reynolds number, and complex multiphase interaction, which may be helpful and inspirational for researchers to make progress in future developments in the field of simulating biological flows using IBMs.

Computational efficiency is a representative performance of a numerical method. IBM is efficient due to its Cartesian property in mesh generation. It has superior parallelism when it combines with LBM-based flow solvers. Most codes of IB-LBM, to our knowledge, are paralleled based on the CPU. The efficiency is commonly lower than GPU-based parallelism. The GPU acceleration technique is introduced into the IBM [138,139], which reaches high-efficiency enhancement. This is also suitable for simulations of biological flows using an IBM. Additionally, the conventional IBMs adopt the fixed Cartesian mesh, where the region of the fine mesh should cover all the trajectories of immersed objects. In this aspect, the fine mesh zone will be large if the immersed object has large movement or deformation, such as self-propelled motions, which leads to a huge number of grids due to the unchangeable background mesh, especially for 3D problems. The same is indeed true for multibody problems. In this regard, continuous changeable regions of fine mesh covering the bodies can reduce the grid number. Compared with a huge number of grids for simulations, the cost of a simple re-meshing process is well worth it. The adaptive mesh refinement [140,141,142] and overset mesh [88] techniques have been tried with the IBM recently. These re-meshing techniques can be applied to bio-inspired motions with large movement/deformation or multibody [64].

Computational accuracy is another representative performance of a numerical method. High-order accuracy has been a goal of the IBM since its inception [13,143]. For biological flows associated with more detailed structures, the requirement for high-order accuracy will increase in the future. A common thought is that the accuracy of the sharp interface IBM is better than the diffuse one due to the sharpness. Therefore, many methods for improving accuracy are based on the sharp interface IBM [144,145,146]. However, for the diffuse interface IBM, efforts may be put into the Dirac delta function, such as constructing the kernel function using Lagrangian interpolation [69] and the moving-least-square method [24,70,71]. Some multi-step schemes can also improve accuracy [19,147]. High-order flux reconstruction is considered in a penalty forcing scheme by Kou et al. [148] to reach high accuracy. We expect more contributions to accuracy improvement for the IBM in the near future, which is the foundation of high-fidelity simulations of biological flows.

Numerical stability is one of the most important factors in guaranteeing an accurate numerical simulation. The instability in the issue of low fluid-solid mass ratio is commonly encountered in all numerical methods, not the proprietary IBM. There indeed exist some structures of ratio in the bio-system and biomimetics, such as the thin wing of an insect, the fin of a fish, and the long whisker of jellyfish. Huang and Tian [51] summarized that instability mainly comes from the numerical rigidity between fluid and structure dynamics and the large acceleration of structure. In some cases of flexible structures, the numerical instability is equivalent to the time step restriction [117]. Many efforts have been put into this aspect of the IBM [117,143,149,150,151,152]. Their methods can give inspiration for the numerical stability of the IBM in bio-inspired motions. However, numerical instability is still an open issue.

Due to the characteristics of most bio-inspired motions, the high Reynolds number has not been a key issue until now. However, as the scope of research expands, this will become an increasingly important factor in the future due to the high flow velocity or large size. As reviewed in [2,3], the Reynolds number of small fishes and insects is found to fall in a range of ${10}^2–{10}^4$, while it is larger than ${10}^5$ for birds and reaches ${10}^8$ for whales with large size. Therefore, it is unavoidable in future research on bio-fluid dynamics. At a high Reynolds number, the flow transition from laminar to turbulent is a crucial phenomenon occurring in a thin layer. Most IBMs fail to resolve the boundary layer. Aiming to overcome this drawback, locally refined mesh and velocity reconstruction techniques are introduced into IBMs, where the locally refined mesh is applied to trace the thin boundary layer [153,154], and the velocity reconstruction is used to impose a wall model-based velocity profile near the solid surface [155,156]. Lee and Yang [157] used both techniques to simulate turbulent flow past a circular cylinder for Reynolds numbers up to 252,000. Most flow solvers combined with IBM for turbulent flows at high Reynolds numbers are large eddy simulations (LESs) [155,156,157,158,159,160]. Xu et al. [161] developed an IB-LBM to simulate flow problems at moderate and high Reynolds numbers, using large eddy simulation models to model turbulent flows. The above-mentioned techniques and coupling schemes may be helpful for future simulations of biological flows at high Reynolds numbers.

As for complex multiphase interactions [162], the realistic, complex environment for bio-locomotion should be taken into consideration to meet special needs, such as flying affected by the wind and rain, swimming around the water-air interface, and locomotion in a non-Newtonian fluid. It is possible to simulate these sophisticated problems with the help of some special flow solvers involving binary fluid components [163,164,165,166,167], more fluid phases [168], and non-Newtonian fluid [169,170]. Coupling with these flow solvers can enhance the capability of the IBM to simulate intricate biological flows with multiphase interactions. Some preliminary IBMs have been proposed recently. Chen et al. [171] and Yan et al. [172] coupled the IBM with multiphase flow solvers and studied the interactions between the solid and two-phase fluid. Cartwright and Du [173] studied the swimming behaviors near the multi-fluid interface. Ma et al. [174] developed an IB-LBM involving viscoelastic fluids and complex geometries. To our knowledge, these methods have not been extended to bio-inspired motions. In future research, these methods will play a role in exploring nature and engineering design.

6. Conclusions

This paper focuses on immersed boundary methods (IBMs) for biological flows in swimming and flying bio-locomotion, reviewing their development and applications. First, we introduce the fundamentals of the IBM, including both diffuse and sharp interface methods, as well as some flow solvers combined with the IBM. More attention is paid to the diffuse interface IBM. We introduce the classic IBM, penalty forcing IBM, and direct forcing IBM successively and highlight the velocity correction IBM due to its advantages. For the sharp interface IBM, we only introduce the hybrid Cartesian-IBM, which is widely used in bio-locomotion. We then present recent research on flying and swimming behaviors, indicating that IBM is a powerful tool for studying bio-fluid dynamics. Finally, we discuss several promising issues of the IBM in this area, including computational efficiency, high-order accuracy, numerical stability, high Reynolds number, and complex multiphase interaction.

Although IBMs have been widely and successfully applied in the field of bio-locomotion and biomimetics, existing methods still need to be improved to meet more challenging and realistic requirements in the future. As mentioned in the promising future issues, the techniques for improving computational accuracy and efficiency can be integrated into well-developed IBMs for biological flows, which are expected to be realized in the near future. However, the biological structure itself with a low-density ratio will continue to be an open issue in numerical instability. The Reynolds number for biological flows cannot always be limited to a low or moderate scale. The general fluid-structure interaction of fluid and solid phases may need to be extended to the gas–liquid–solid interaction of binary fluid and solid phases to meet a more complex environment for bio-locomotion. We expect more achievements of IBMs that can contribute to numerical research of biological flows.