A Novel MPPT Controller Based on Mud Ring Optimization Algorithm for Centralized Thermoelectric Generator under Dynamic Thermal Gradients
Abstract
:1. Introduction
1.1. Literature
- A novel mud-ring-optimizer-based MPPT control technique is implemented and tested on dynamic non-uniform thermal gradients.
- The proposed MRA-based MPPT technique can track the GMPP under non-uniform temperature distribution with 99.96% efficiency within 220 ms.
- The comparison of the MRA-based technique is performed with WOA-, GWO-, and PSO-based state-of-the-art MPPT techniques.
- The MRA-based technique has a strong capability to differentiate between the LMPP and GMPP.
- The proposed technique is also tested using an experimental setup by implementing the proposed technique on a low-cost microcontroller.
- During the experimental verification, the proposed technique achieved a higher efficiency and required less time to track the GMPP.
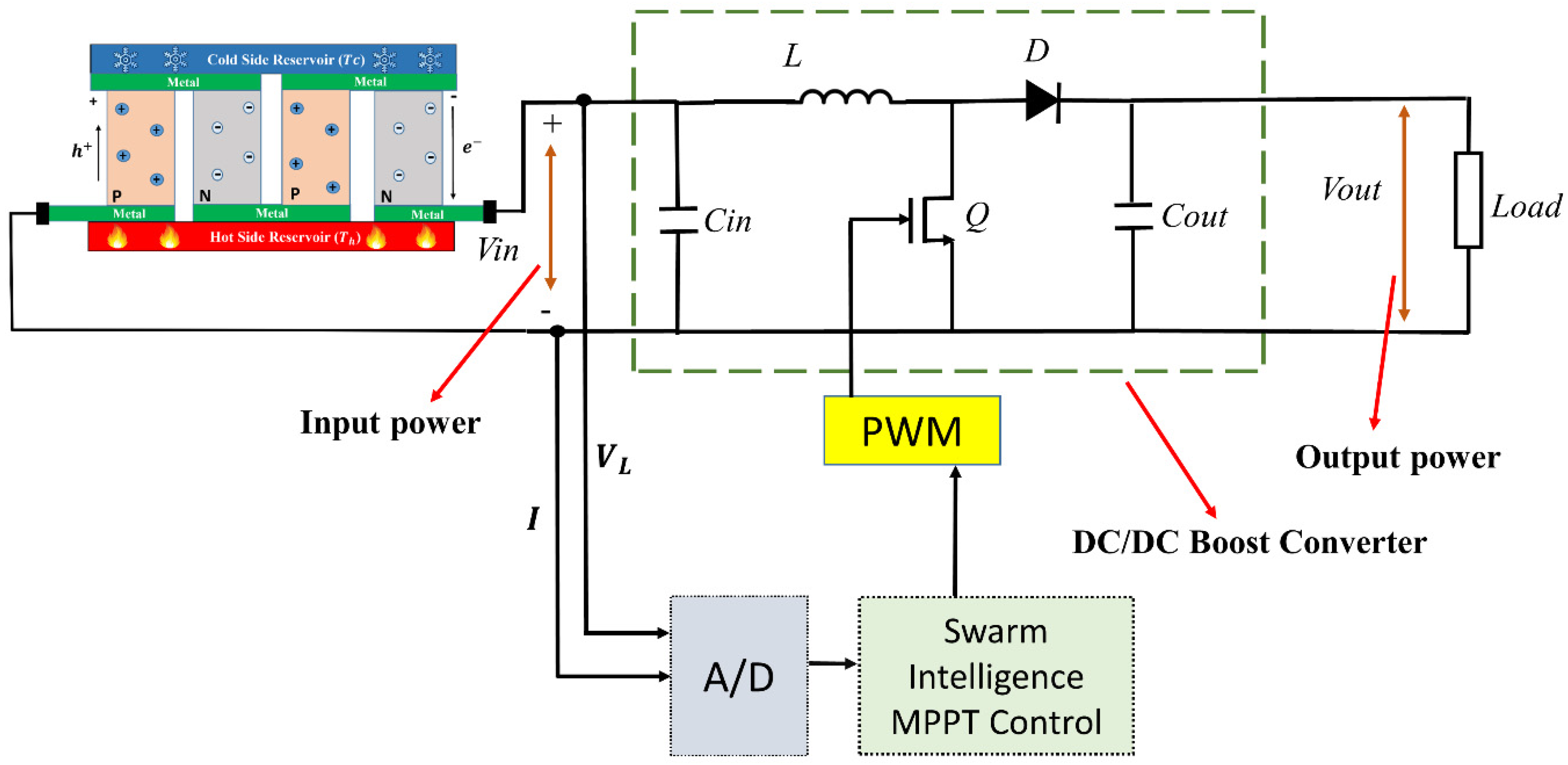
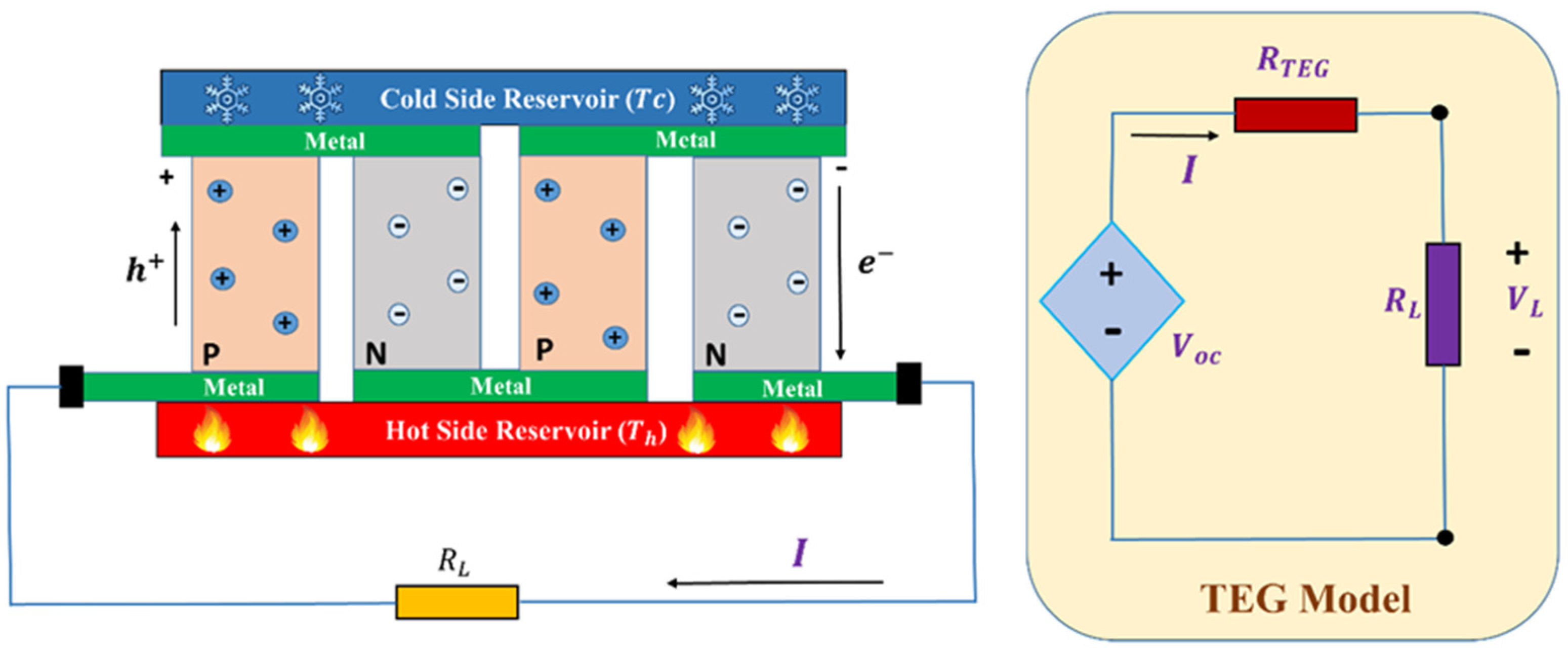
1.2. TEG Modeling
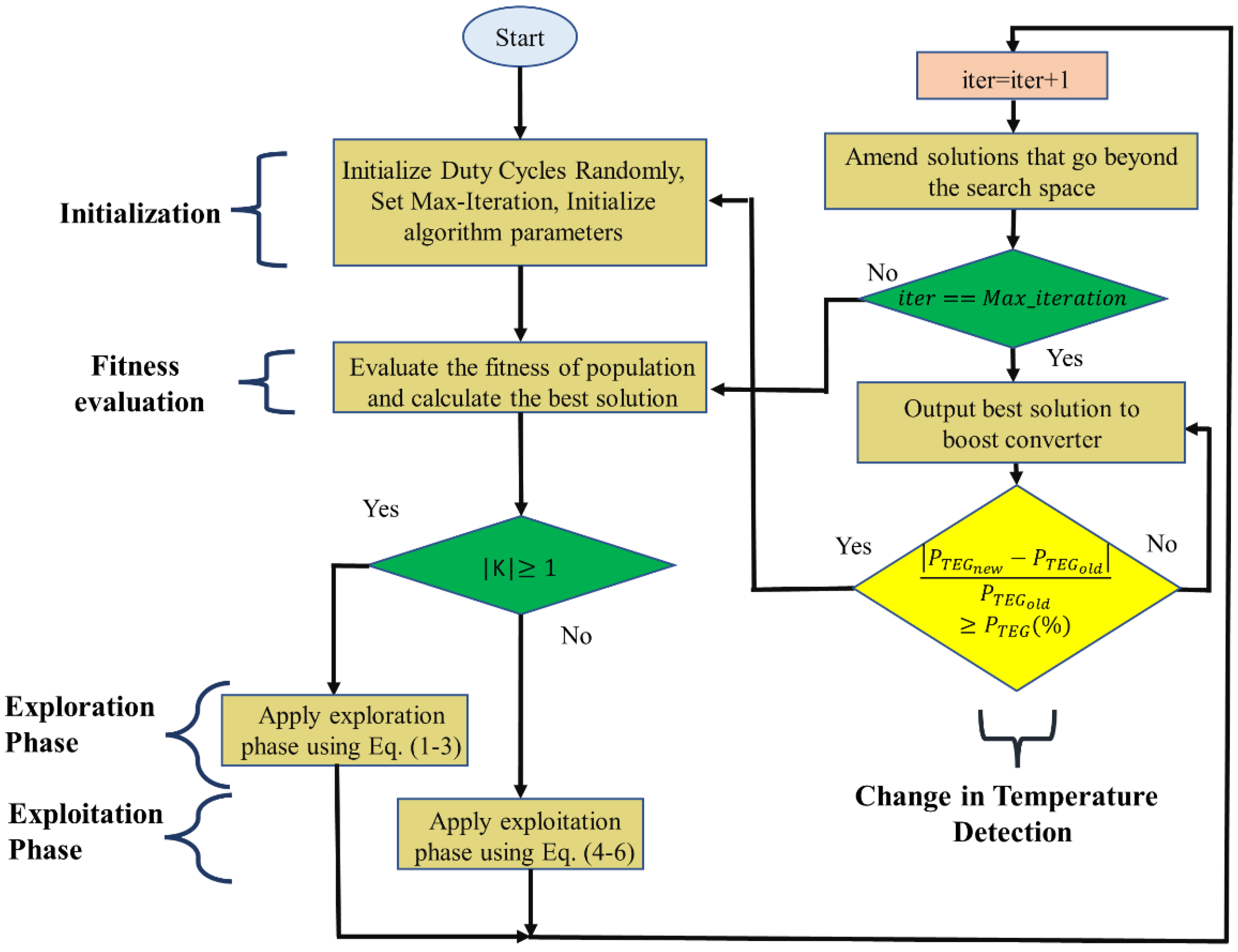
2. Mud Ring Optimization Algorithm
2.1. Mathematical Model
2.1.1. Foraging—Exploration Phase: Echolocation
2.1.2. Mud Ring Feed—Phase: Exploitation
2.2. MRA-Based MPPT Technique
2.3. Tracking Mechanism
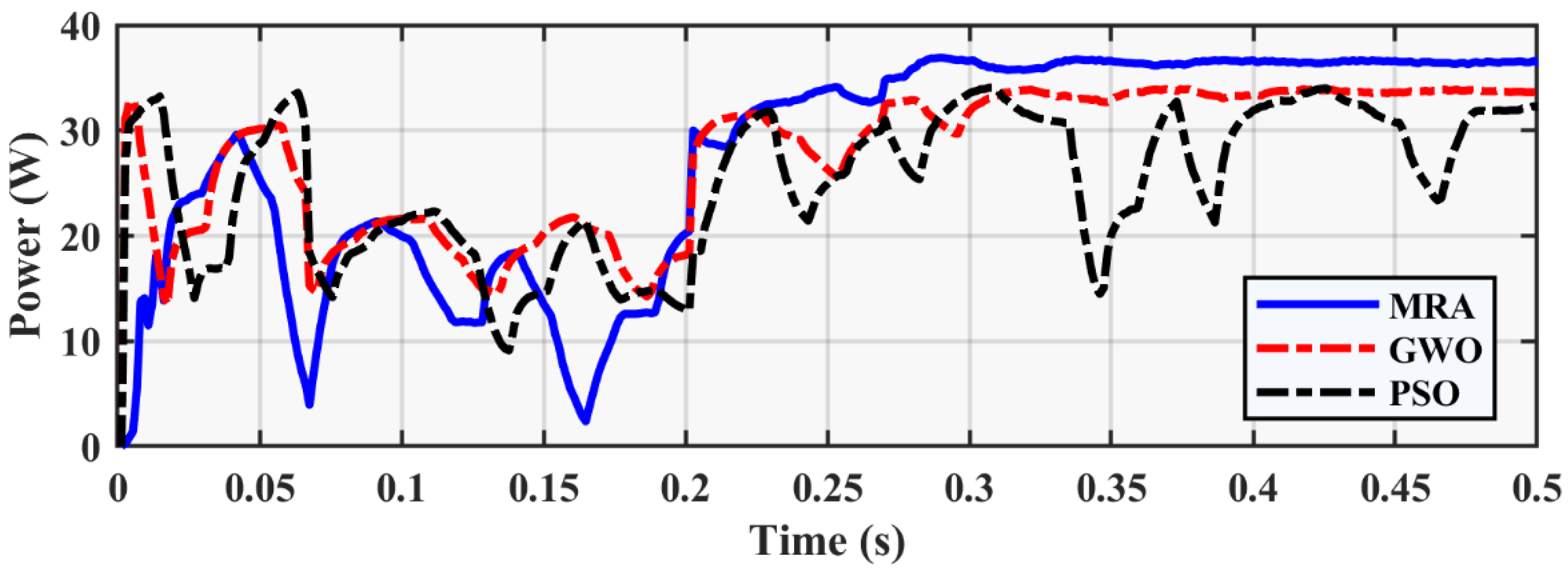
3. Results and Discussion
3.1. Start-Up Test:
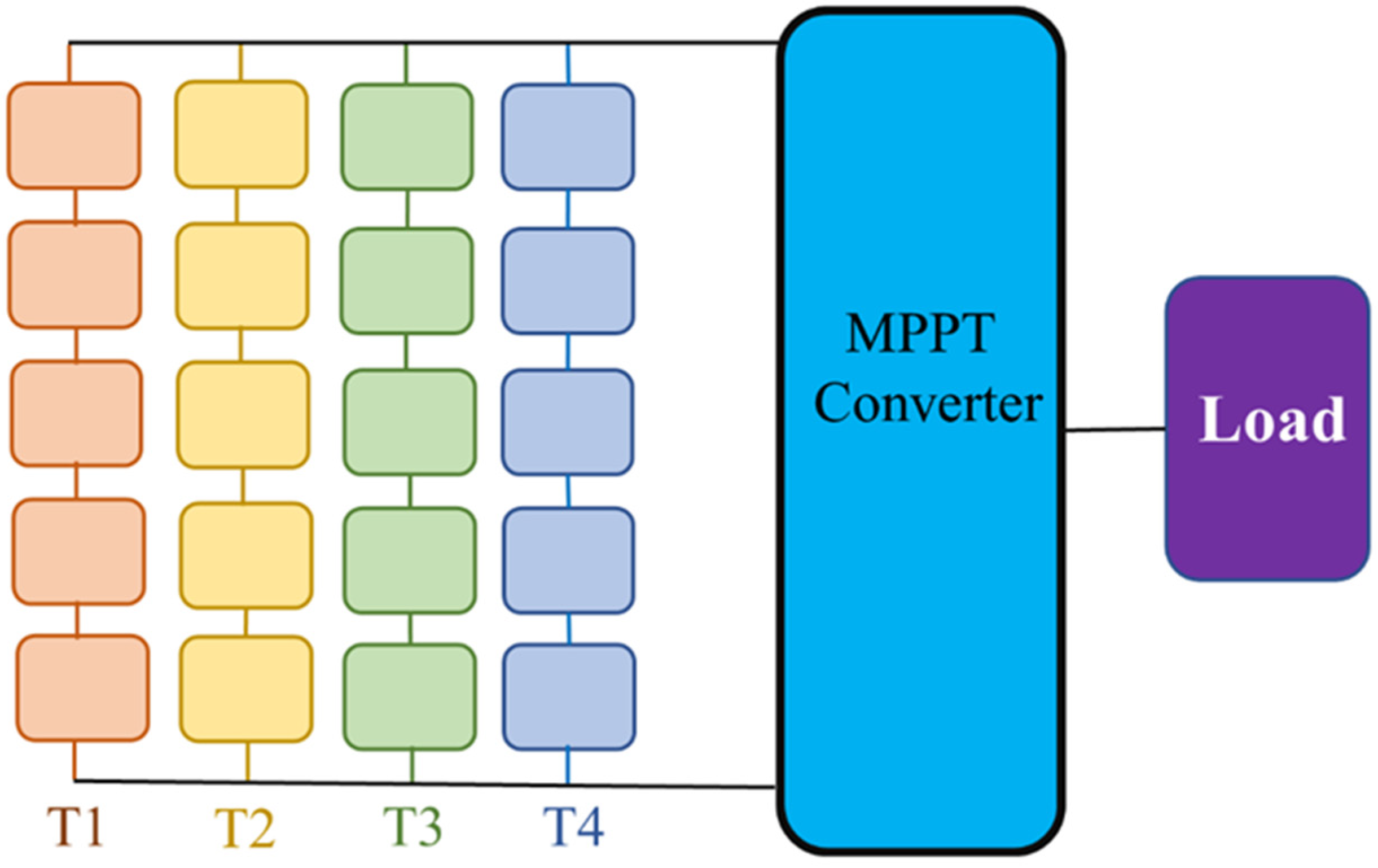
3.2. Varying Temperature
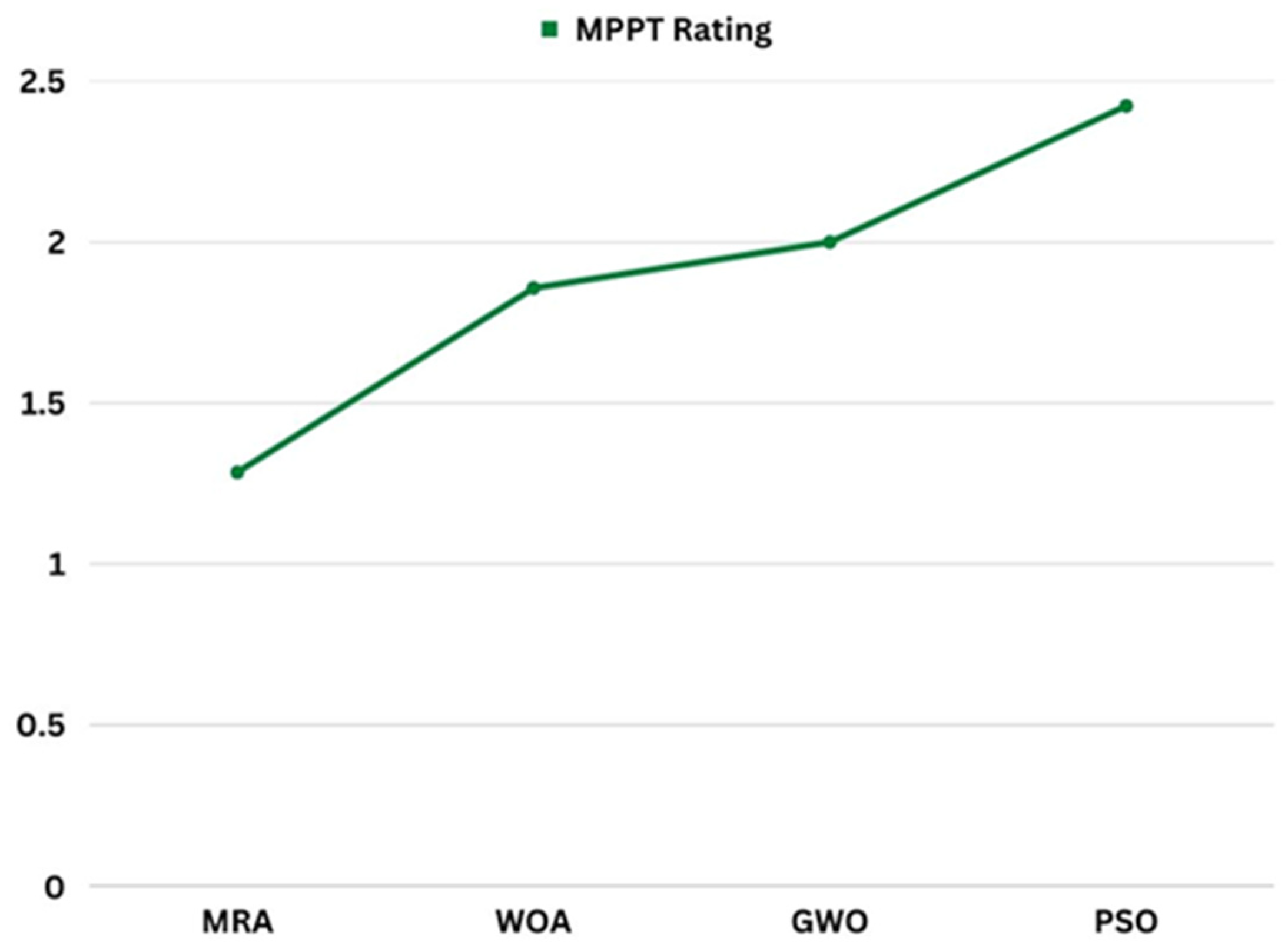
3.3. MPPT Rating
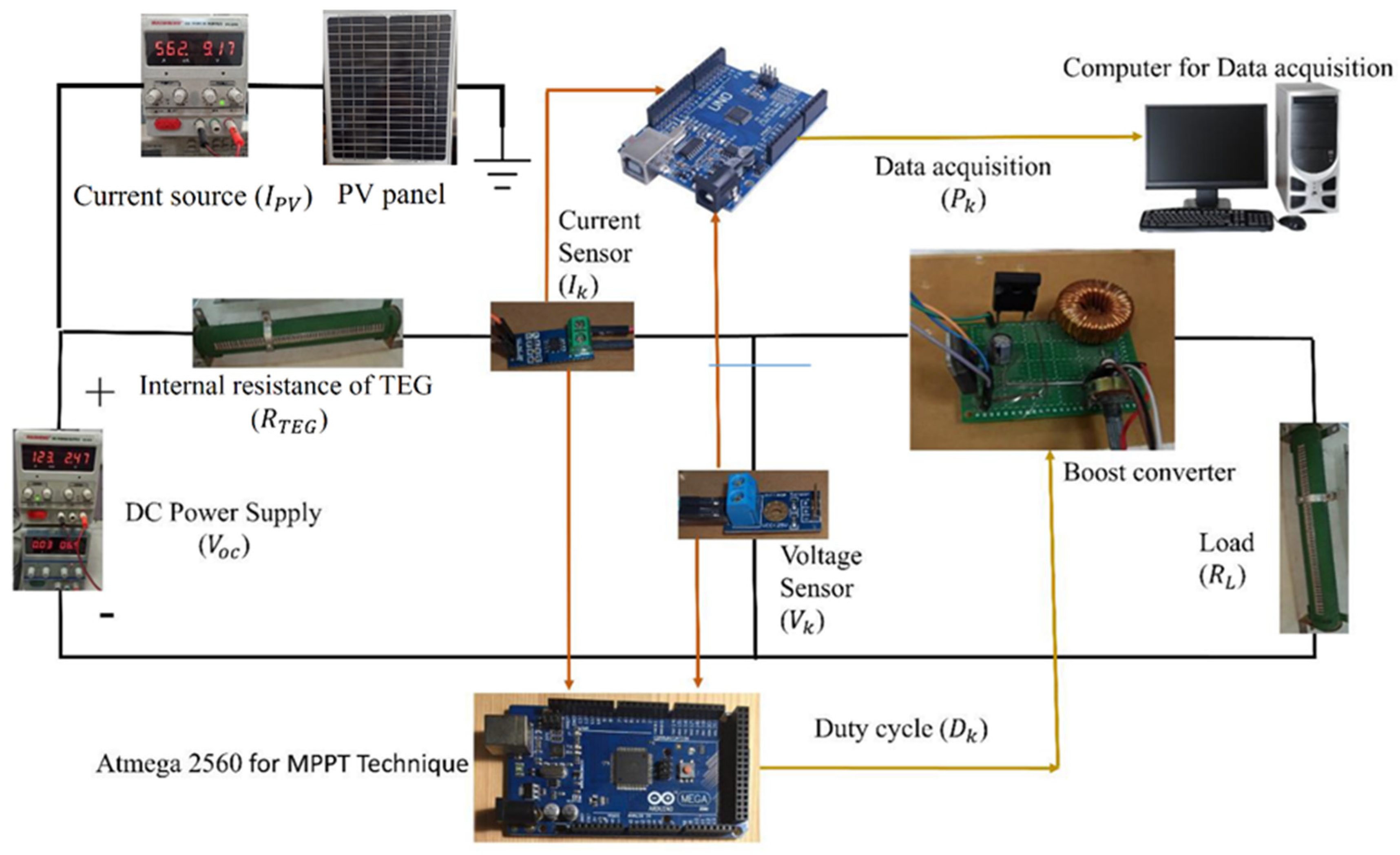
3.4. Experimental Results
4. Conclusions
- The MRA-based MPPT technique tracks the GMPP under NUTD with 99.96% efficiency within 220 ms.
- The strong capability to differentiate between the LMPP and GMPP with an improvement of up to 70% lesser tracking time.
- The experimental verification is achieved on a low-cost microcontroller, thus facilitating large-scale adoption in existing and new MPPT applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TEG | Thermoelectric Generator; |
| MPPT | Maximum Power Point Tracking; |
| P&O | Perturb and Observe; |
| IC | Incremental Conductance; |
| MRA | Mud Ring Optimizer; |
| GWO | Grey Wolf Optimizer; |
| GM | Global Maxima; |
| PSO | Particle Swarm Optimization; |
| WOA | Whale Optimization Algorithm; |
| GMPP | Global Maximum Power Point; |
| LMPP | Local Maximum Power Point. |
References
- Khan, M.K.; Zafar, M.H.; Mansoor, M.; Mirza, A.F.; Khan, U.A.; Khan, N.M. Green energy extraction for sustainable development: A novel MPPT technique for hybrid PV-TEG system. Sustain. Energy Technol. Assess. 2022, 53, 102388. [Google Scholar]
- Zafar, M.H.; Khan, N.M.; Mirza, A.F.; Mansoor, M.; Akhtar, N.; Qadir, M.U.; Khan, N.A.; Moosavi, S.K.R. A novel meta-heuristic optimization algorithm based MPPT control technique for PV systems under complex partial shading condition. Sustain. Energy Technol. Assess. 2021, 47, 101367. [Google Scholar]
- Bollipo, R.B.; Mikkili, S.; Bonthagorla, P. Critical Review on PV MPPT Techniques: Classical, Intelligent and Optimisation. IET Renew. Power Gener. 2020, 14, 1433–1452. [Google Scholar] [CrossRef]
- Aoughlis, C.; Belkaid, A.; Colak, I.; Guenounou, O.; Kacimi, M.A. Automatic and Self Adaptive P&O MPPT Based PID Controller and PSO Algorithm. In Proceedings of the 2021 10th International Conference on Renewable Energy Research and Application (ICRERA), Istanbul, Turkey, 26–29 September 2021. [Google Scholar]
- Renaudineau, H.; Donatantonio, F.; Fontchastagner, J.; Petrone, G.; Spagnuolo, G.; Martin, J.-P.; Pierfederici, S. A PSO-based global MPPT technique for distributed PV power generation. IEEE Trans. Ind. Electron. 2014, 62, 1047–1058. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Amjad, M.; Mekhilef, S. An improved particle swarm optimization (PSO)–based MPPT for PV with reduced steady-state oscillation. IEEE Trans. Power Electron. 2012, 27, 3627–3638. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P. A new MPPT design using grey wolf optimization technique for photovoltaic system under partial shading conditions. IEEE Trans. Sustain. Energy 2015, 7, 181–188. [Google Scholar] [CrossRef]
- Mansoor, M.; Mirza, A.; Ling, Q. Harris hawk optimization-based MPPT control for PV Systems under Partial Shading Conditions. J. Clean. Prod. 2020, 274, 122857. [Google Scholar] [CrossRef]
- Mansoor, M.; Mirza, A.F.; Ling, Q.; Javed, M.Y. Novel Grass Hopper optimization based MPPT of PV systems for complex partial shading conditions. Sol. Energy 2020, 198, 499–518. [Google Scholar] [CrossRef]
- Jiang, L.L.; Maskell, D.; Patra, J. A novel ant colony optimization-based maximum power point tracking for photovoltaic systems under partially shaded conditions. Energy Build. 2013, 58, 227–236. [Google Scholar] [CrossRef]
- Kinattingal, S.; Simon, S.; Nayak, P. MPPT in PV systems using ant colony optimisation with dwindling population. IET Renew. Power Gener. 2020, 14, 1105–1112. [Google Scholar]
- Lyden, S.; Haque, M. A simulated annealing global maximum power point tracking approach for PV modules under partial shading conditions. IEEE Trans. Power Electron. 2015, 31, 4171–4181. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- Ma, J.; Ting, T.O.; Man, K.L.; Zhang, N.; Guan, S.-U.; Wong, P.W.H. Parameter estimation of photovoltaic models via cuckoo search. J. Appl. Math. 2013, 2013, 362619. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Yang, D.; Su, W.; Lu, J.; Yu, X. An overall distribution particle swarm optimization MPPT algorithm for photovoltaic system under partial shading. IEEE Trans. Ind. Electron. 2018, 66, 265–275. [Google Scholar] [CrossRef]
- Mirza, A.F.; Ling, Q.; Javed, M.Y.; Mansoor, M. Novel MPPT techniques for photovoltaic systems under uniform irradiance and Partial shading. Sol. Energy 2019, 184, 628–648. [Google Scholar] [CrossRef]
- Agwa, A.M.; El-Fergany, A.; Maksoud, H. Electrical characterization of photovoltaic modules using farmland fertility optimizer. Energy Convers. Manag. 2020, 217, 112990. [Google Scholar] [CrossRef]
- Huang, C.; Wang, L.; Yeung, R.S.-C.; Zhang, Z.; Chung, H.S.-H.; Bensoussan, A. A prediction model-guided Jaya algorithm for the PV system maximum power point tracking. IEEE Trans. Sustain. Energy 2017, 9, 45–55. [Google Scholar] [CrossRef]
- Mirza, A.F.; Mansoor, M.; Ling, Q.; Yin, B.; Javed, M.Y. A Salp-Swarm Optimization based MPPT technique for harvesting maximum energy from PV systems under partial shading conditions. Energy Convers. Manag. 2020, 209, 112625. [Google Scholar] [CrossRef]
- Fathy, A. Butterfly optimization algorithm based methodology for enhancing the shaded photovoltaic array extracted power via reconfiguration process. Energy Convers. Manag. 2020, 220, 113115. [Google Scholar] [CrossRef]
- Soufyane Benyoucef, A.; Chouder, A.; Kara, K.; Silvestre, S.; Sahed, O.A. Artificial bee colony based algorithm for maximum power point tracking (MPPT) for PV systems operating under partial shaded conditions. Appl. Soft Comput. 2015, 32, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Cheng, R.; Yan, B.; Zhang, J.; Zhang, Z.; Zhang, M.; Lai, L.L. A dynamic particles MPPT method for photovoltaic systems under partial shading conditions. Energy Convers. Manag. 2020, 220, 113070. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, B.; Chen, N. Arithmetic optimization algorithm based MPPT technique for centralized TEG systems under different temperature gradients. Energy Rep. 2022, 8, 2424–2433. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Ramachandaramurthy, V.; Padmanaban, S.; Azam, F. An ant colony optimized MPPT for standalone hybrid PV-wind power system with single Cuk converter. Energies 2019, 12, 167. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, J.M.; Ahmed, T. Fitness dependent optimizer: Inspired by the bee swarming reproductive process. IEEE Access 2019, 7, 43473–43486. [Google Scholar] [CrossRef]
- Mansoor, M.; Mirza, A.F.; Long, F.; Ling, Q. An Intelligent Tunicate Swarm Algorithm Based MPPT Control Strategy for Multiple Configurations of PV Systems Under Partial Shading Conditions. Adv. Theory Simul. 2021, 4, 2100246. [Google Scholar] [CrossRef]
- Maher, R.A.; Abdelsalam, A.K.; Dessouky, Y.G.; Nouman, A. High performance state-flow based MPPT technique for micro WECS. IET Renew. Power Gener. 2019, 13, 3009–3021. [Google Scholar] [CrossRef]
- Tatabhatla, V.M.R.; Agarwal, A.; Kanumuri, T. Improved power generation by dispersing the uniform and non-uniform partial shades in solar photovoltaic array. Energy Convers. Manag. 2019, 197, 111825. [Google Scholar] [CrossRef]
- Lasheen, M.; Rahman, A.K.A.; Abdel-Salam, M.; Ookawara, S. Adaptive reference voltage-based MPPT technique for PV applications. IET Renew. Power Gener. 2017, 11, 715–722. [Google Scholar] [CrossRef]





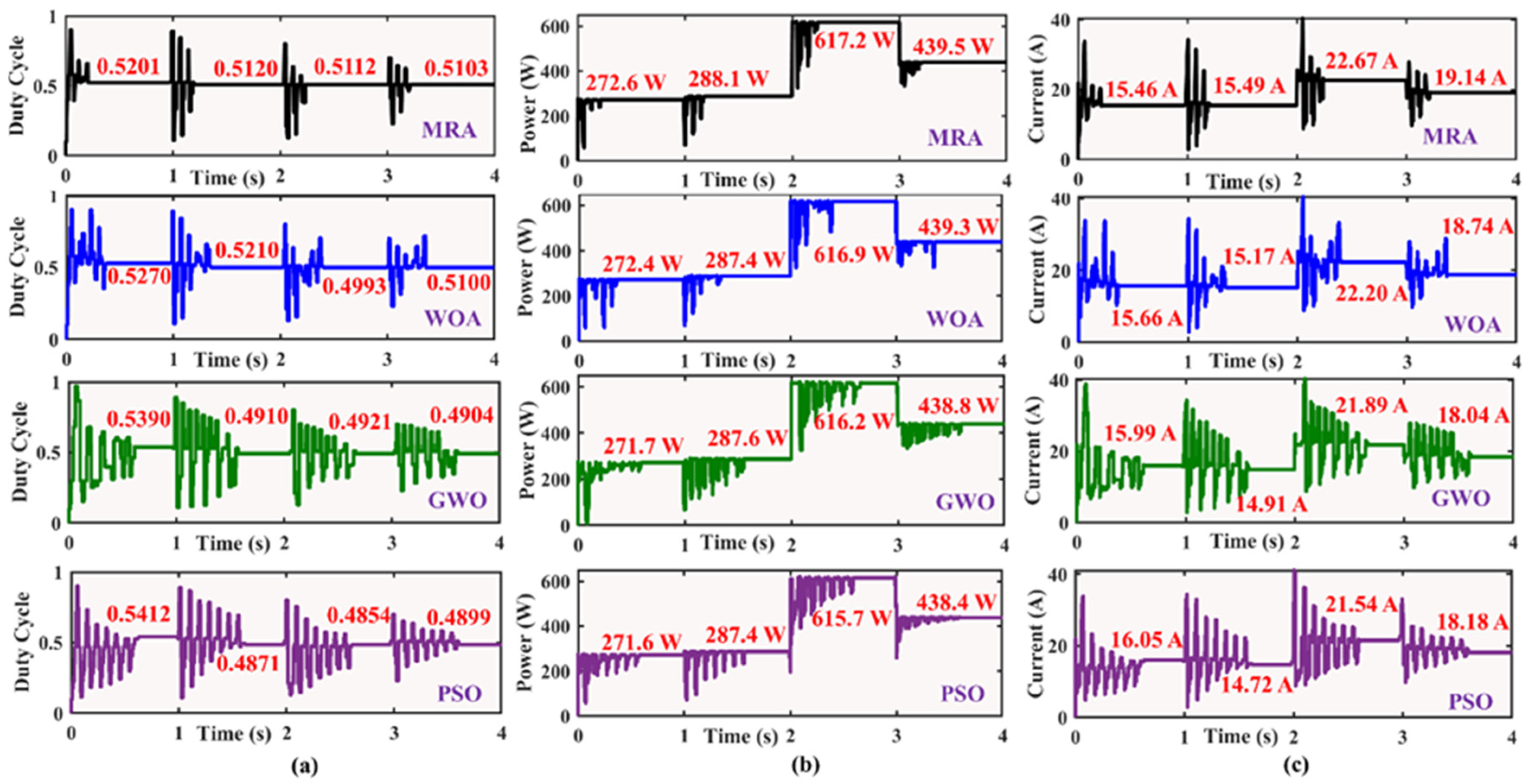
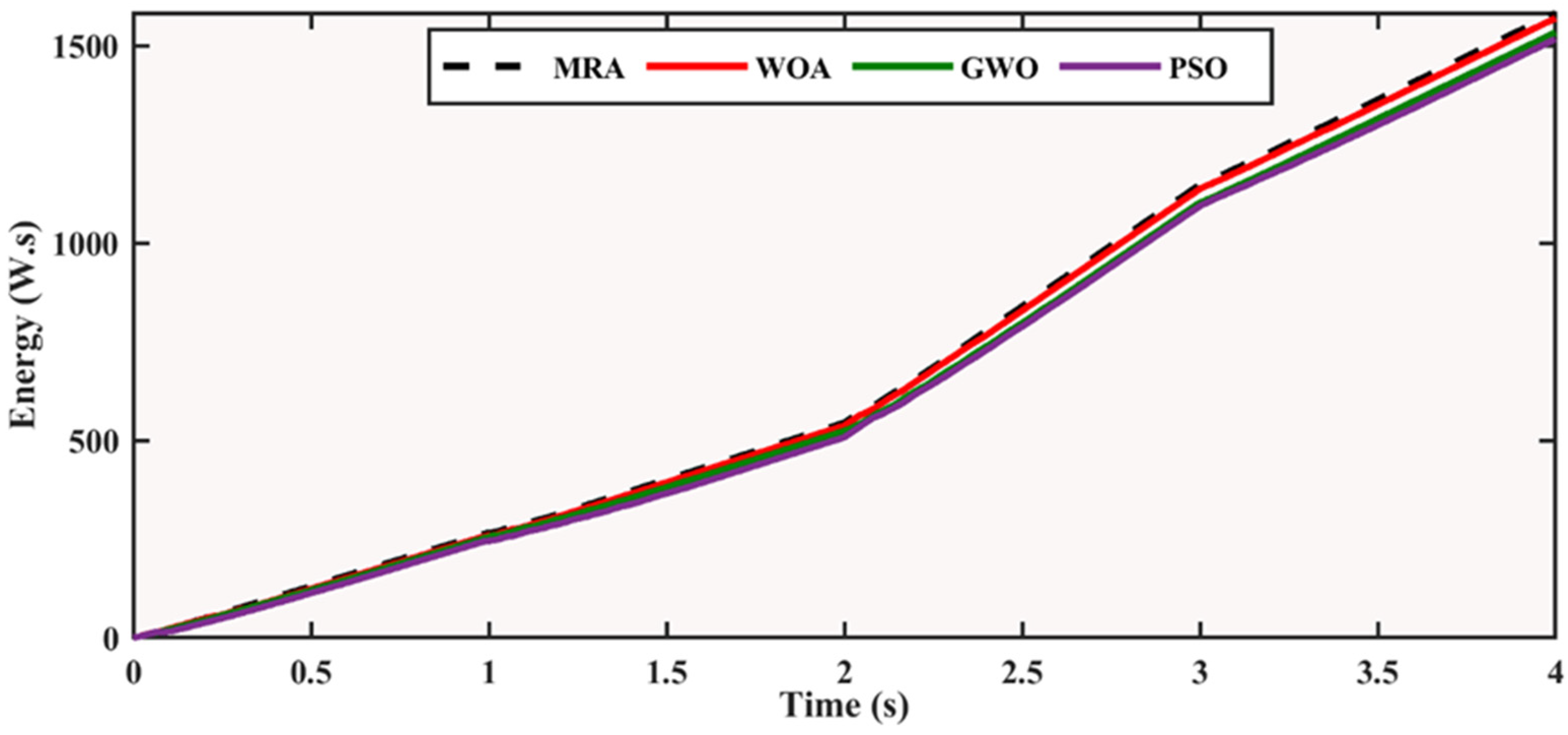

| Tech. | Power Achieved (W) | Actual Global Power (W) | Efficiency (%) | Energy (W.s) | Tracking Time (s) |
|---|---|---|---|---|---|
| MRA | 691.8 | 692 | 99.97 | 673.7 | 0.22 |
| WOA | 691.1 | 692 | 99.86 | 669.1 | 0.34 |
| GWO | 688.9 | 692 | 99.55 | 622.3 | 0.49 |
| PSO | 686.1 | 692 | 99.14 | 608.3 | 0.58 |
| Tech. | Power Achieved (W) | Actual Global Power (W) | Efficiency (%) | Energy (W.s) | Tracking Time (s) |
|---|---|---|---|---|---|
| MRA | 404.35 | 404.5 | 99.96 | 1583 | 0.24 |
| WOA | 404 | 404.5 | 99.87 | 1570 | 0.36 |
| GWO | 403.45 | 404.5 | 99.74 | 1517 | 0.50 |
| PSO | 403.35 | 404.5 | 99.71 | 1513 | 0.61 |
| Tech. Name | Tuning Parameter Number | Rand. No. | Termination Criteria Achieved? | Avg. TT (s) | Avg. Effic. (%) | Hardware Modification | Response Time in Variation (s) | Rating Score |
|---|---|---|---|---|---|---|---|---|
| MRA | 1 (1) | 2 (2) | No (1) | 0.23 (1) | 99.96 (1) | No (1) | Fast (2) | 1.285 |
| WOA | 3 (3) | 1 (1) | Yes (2) | 0.35 (1) | 99.86 (1) | Yes (2) | Slow (3) | 1.857 |
| GWO | 2 (2) | 2 (3) | Yes (2) | 0.49 (1) | 99.65 (1) | No (1) | Very slow (4) | 2.000 |
| PSO | 3 (3) | 2 (3) | Yes (2) | 0.60 (2) | 99.42 (2) | No (1) | Very slow (4) | 2.423 |
| Component | Magnitude |
|---|---|
| Current at MPP | 1.0702 A |
| Ideality factor | 1.0037 |
| Maximum power | 20.1 W |
| Peak efficiency | 19.3% |
| Open circuit voltage | 22.7 V |
| Series resistance | 1.0547 |
| Short circuit current | 1.17 A |
| Shunt resistance | 405.96 |
| Temperature coefficient of | 0.043%/K |
| Temperature coefficient of | −0.35%/K |
| Voltage at MPP | 18.76 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zafar, M.H.; Abou Houran, M.; Mansoor, M.; Khan, N.M.; Moosavi, S.K.R.; Khan, M.K.; Akhtar, N. A Novel MPPT Controller Based on Mud Ring Optimization Algorithm for Centralized Thermoelectric Generator under Dynamic Thermal Gradients. Appl. Sci. 2023, 13, 4213. https://doi.org/10.3390/app13074213
Zafar MH, Abou Houran M, Mansoor M, Khan NM, Moosavi SKR, Khan MK, Akhtar N. A Novel MPPT Controller Based on Mud Ring Optimization Algorithm for Centralized Thermoelectric Generator under Dynamic Thermal Gradients. Applied Sciences. 2023; 13(7):4213. https://doi.org/10.3390/app13074213
Chicago/Turabian StyleZafar, Muhammad Hamza, Mohamad Abou Houran, Majad Mansoor, Noman Mujeeb Khan, Syed Kumayl Raza Moosavi, Muhammad Kamran Khan, and Naureen Akhtar. 2023. "A Novel MPPT Controller Based on Mud Ring Optimization Algorithm for Centralized Thermoelectric Generator under Dynamic Thermal Gradients" Applied Sciences 13, no. 7: 4213. https://doi.org/10.3390/app13074213






