Predictive Modeling and Analysis of Material Removal Characteristics for Robotic Belt Grinding of Complex Blade
Abstract
:1. Introduction
2. Preliminary
2.1. Belt Grinding
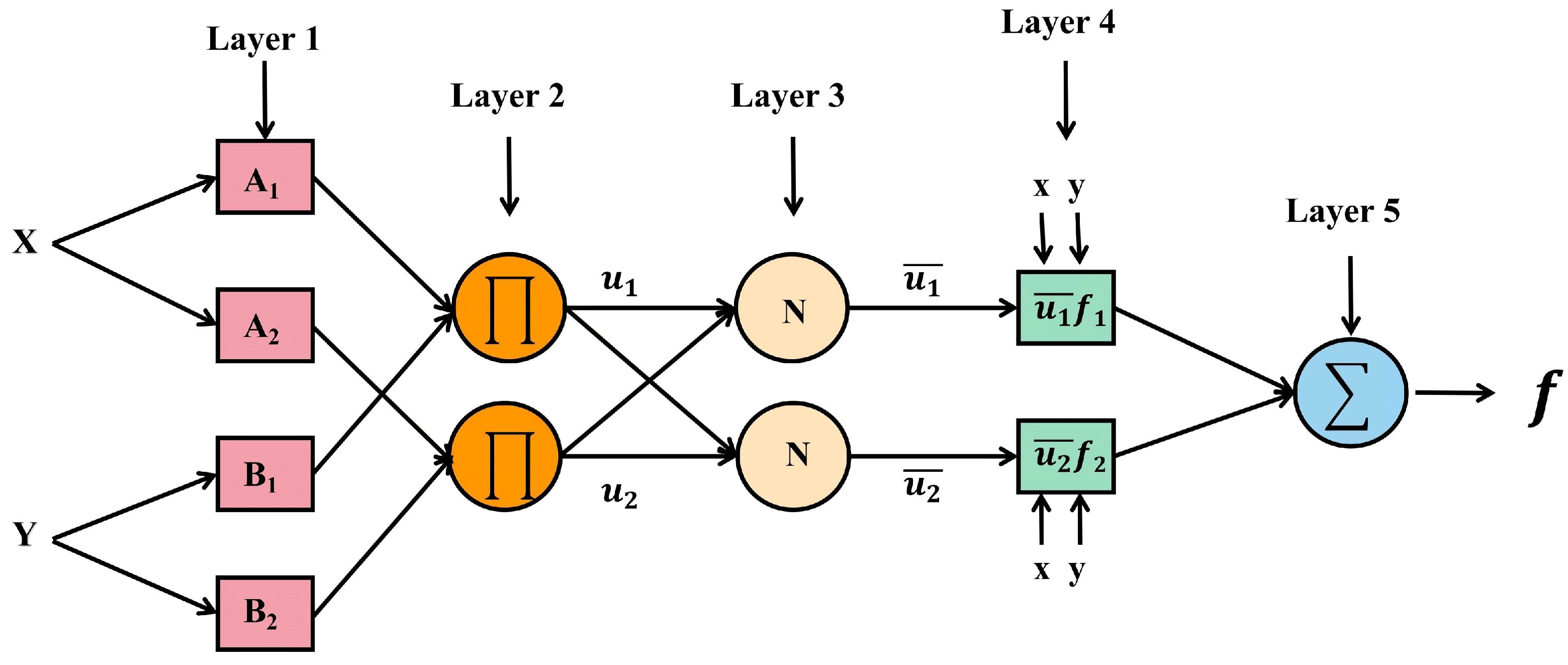
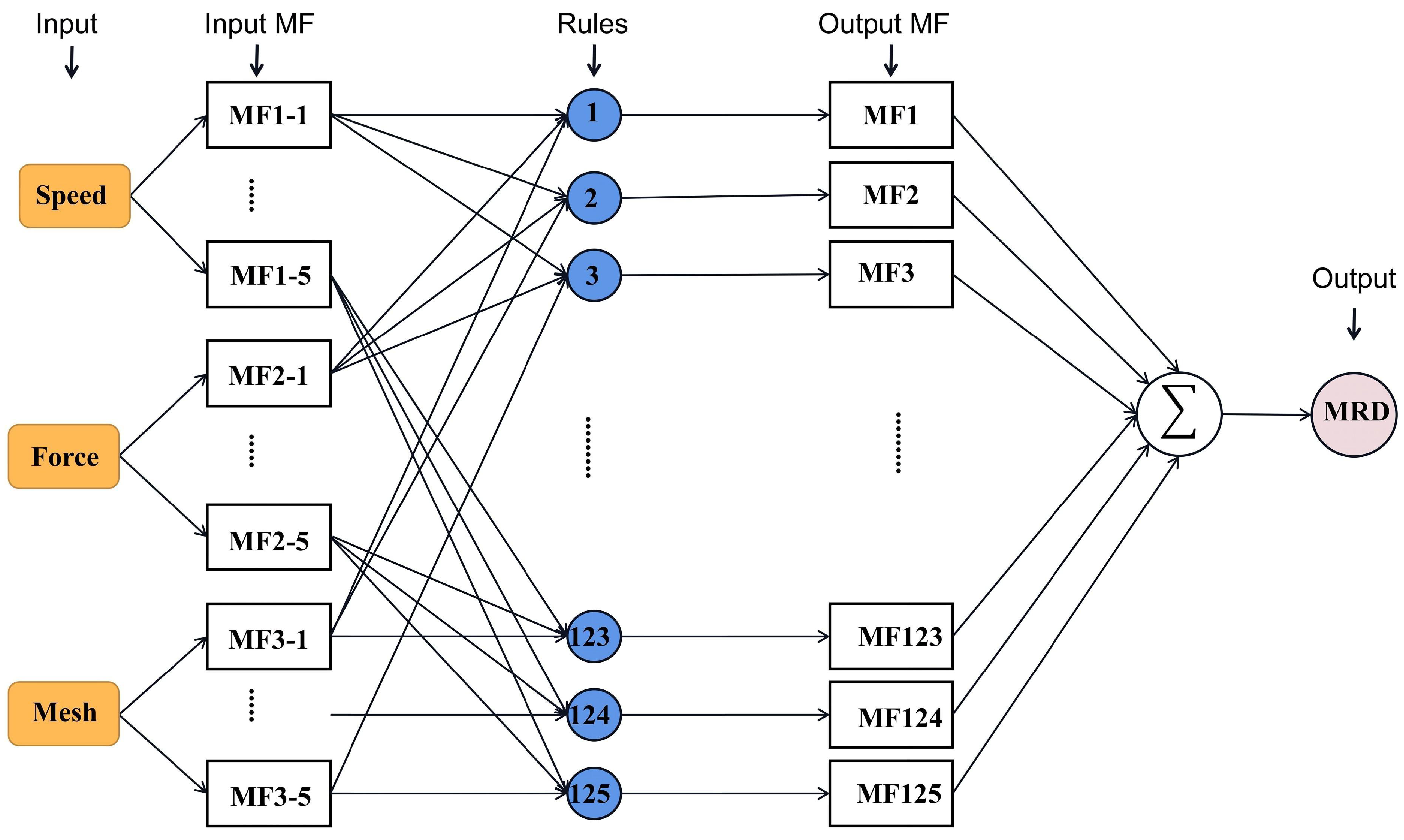
2.2. ANFIS Architecture
3. Main Results
3.1. Experimental Procedures
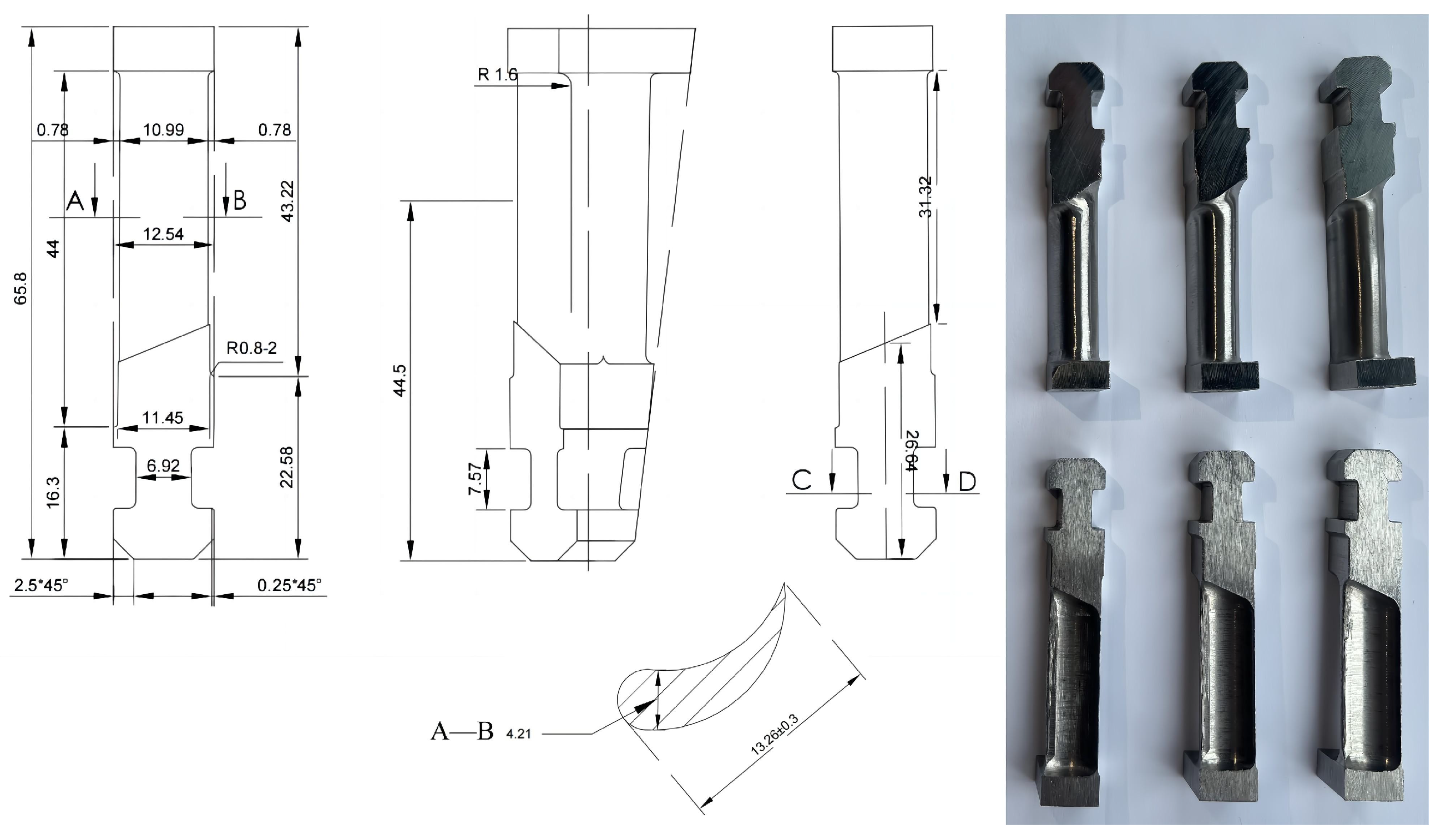
3.1.1. Materials
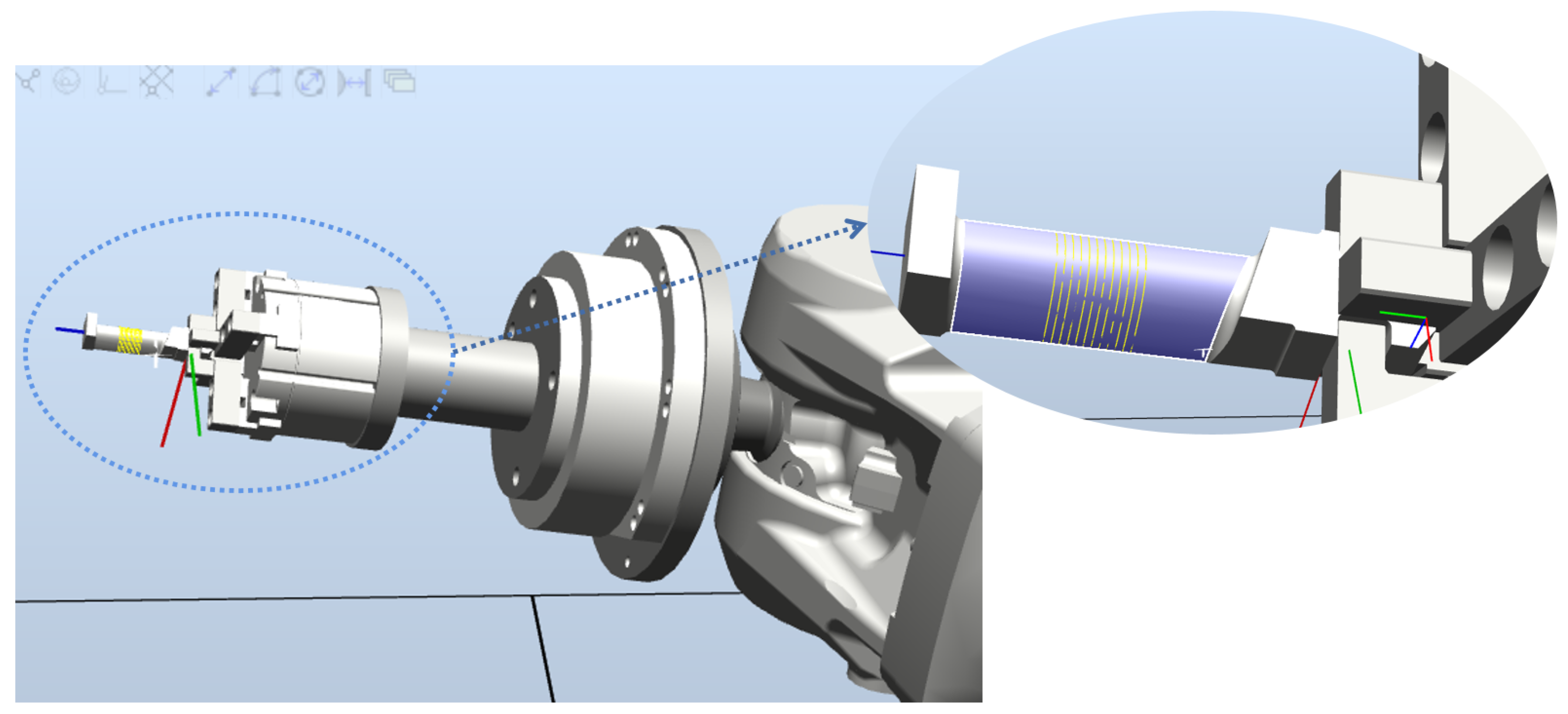
3.1.2. Experimental Setup
3.1.3. Grinding Trajectory
3.1.4. Taguchi Experimental Design
3.2. Experimental Conditions
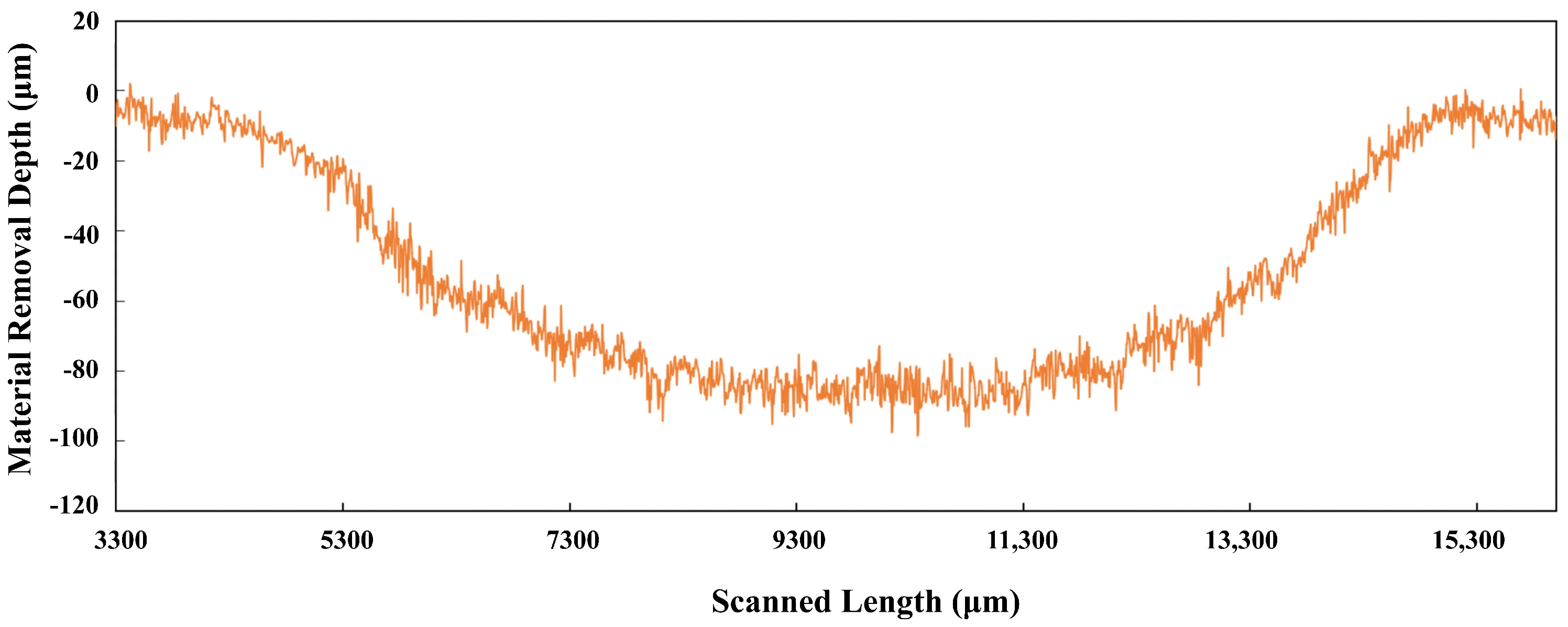
3.3. Data Acquisition for Grinding Depth
4. Results and Discussion
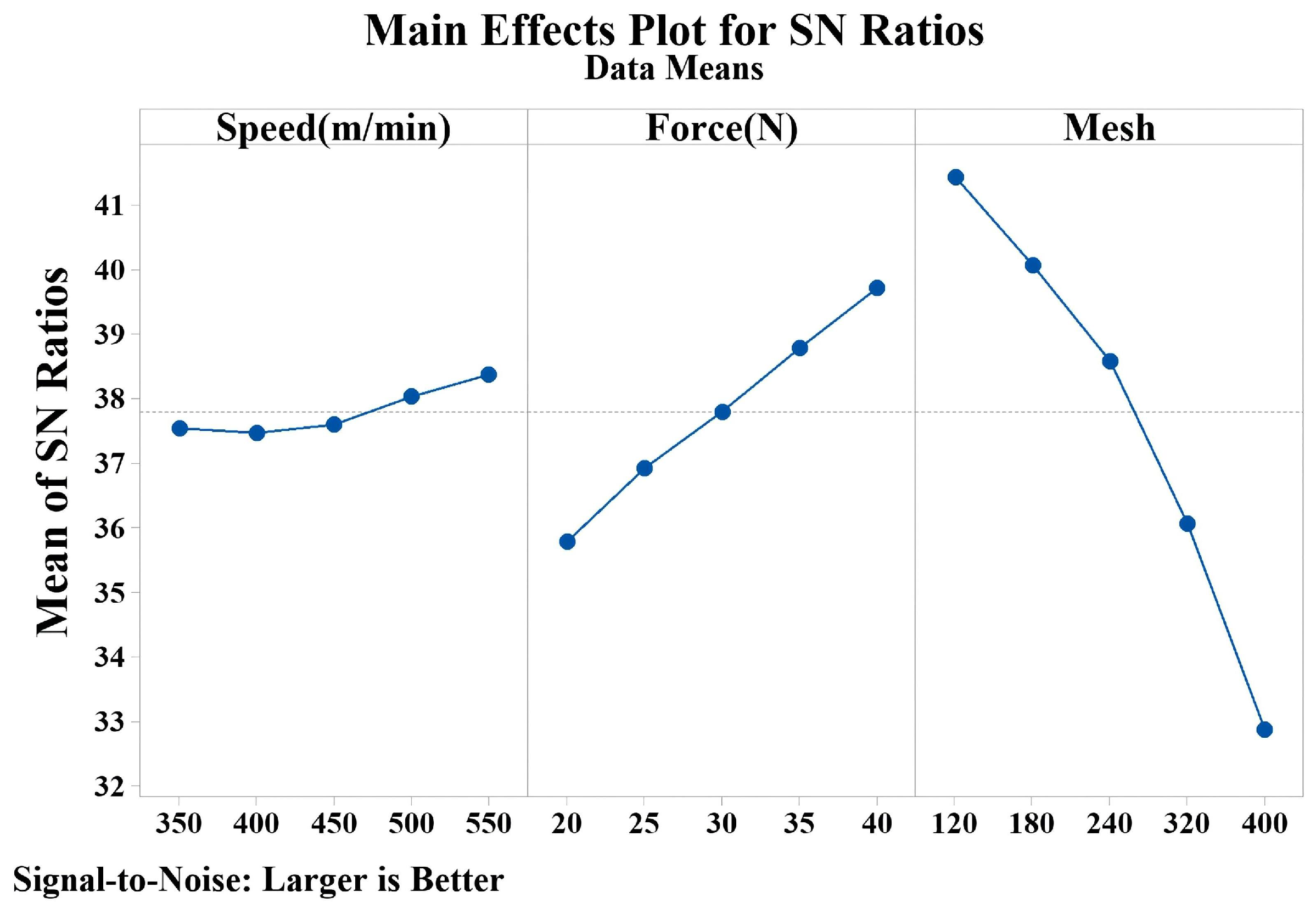
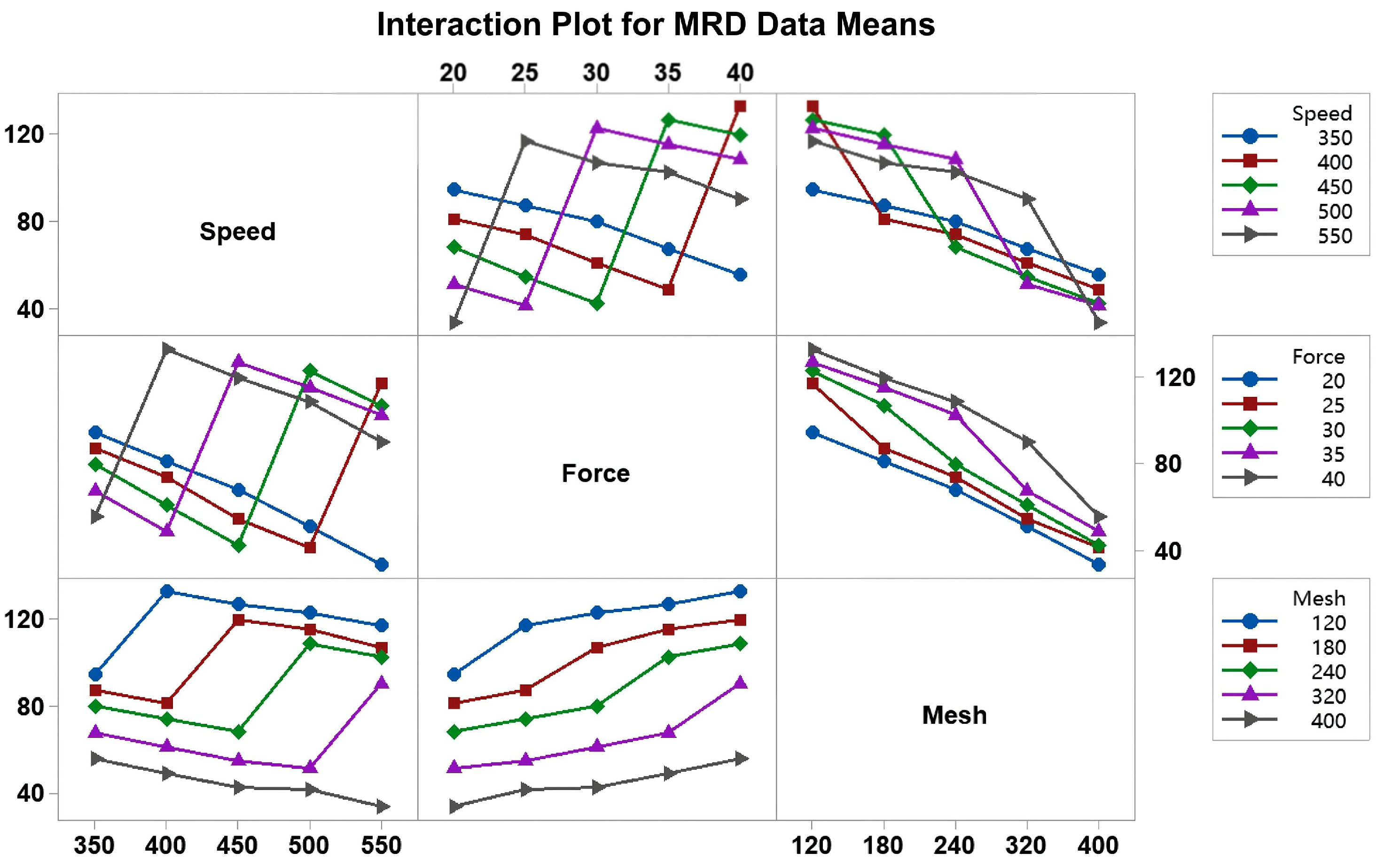
4.1. Analysis of Variance
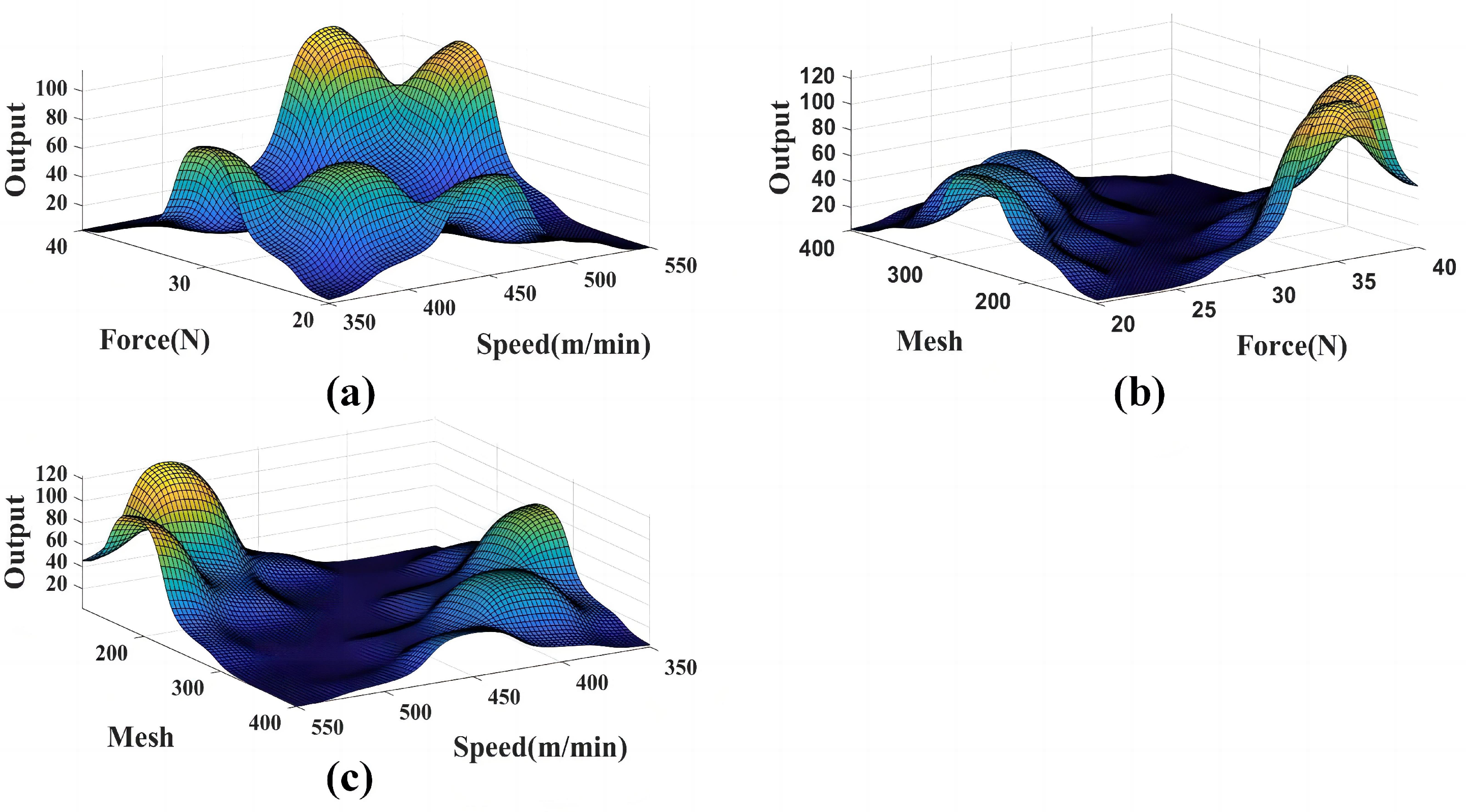
4.2. ANFIS in Predicting MRD
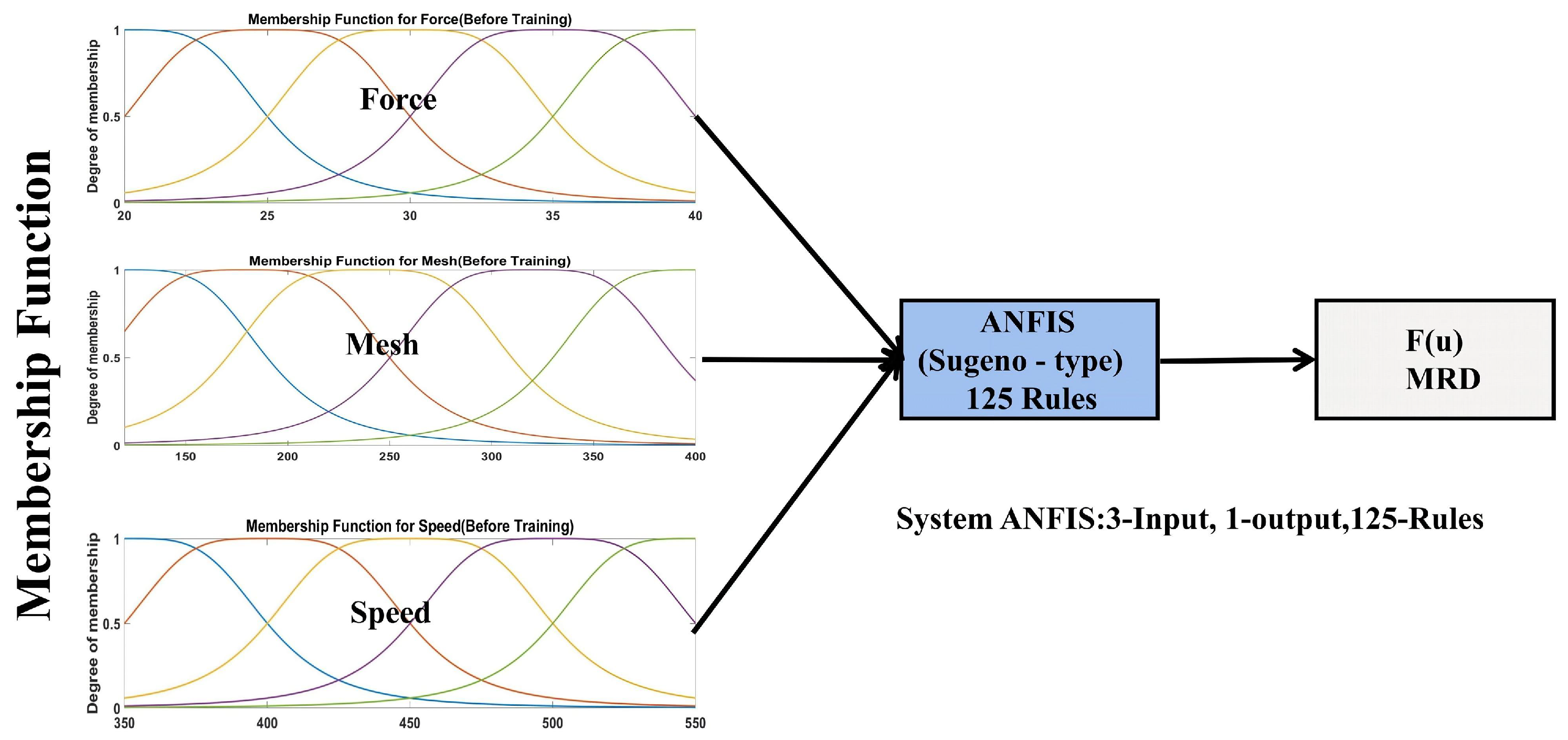
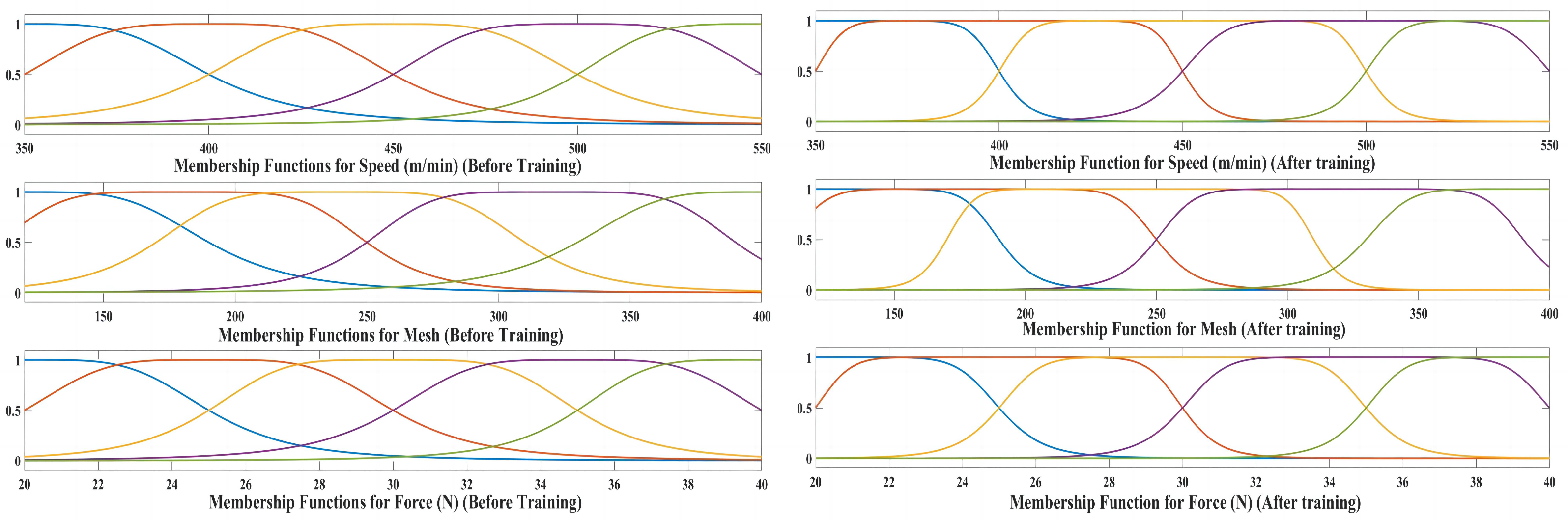
4.2.1. ANFIS Rules and Membership Function
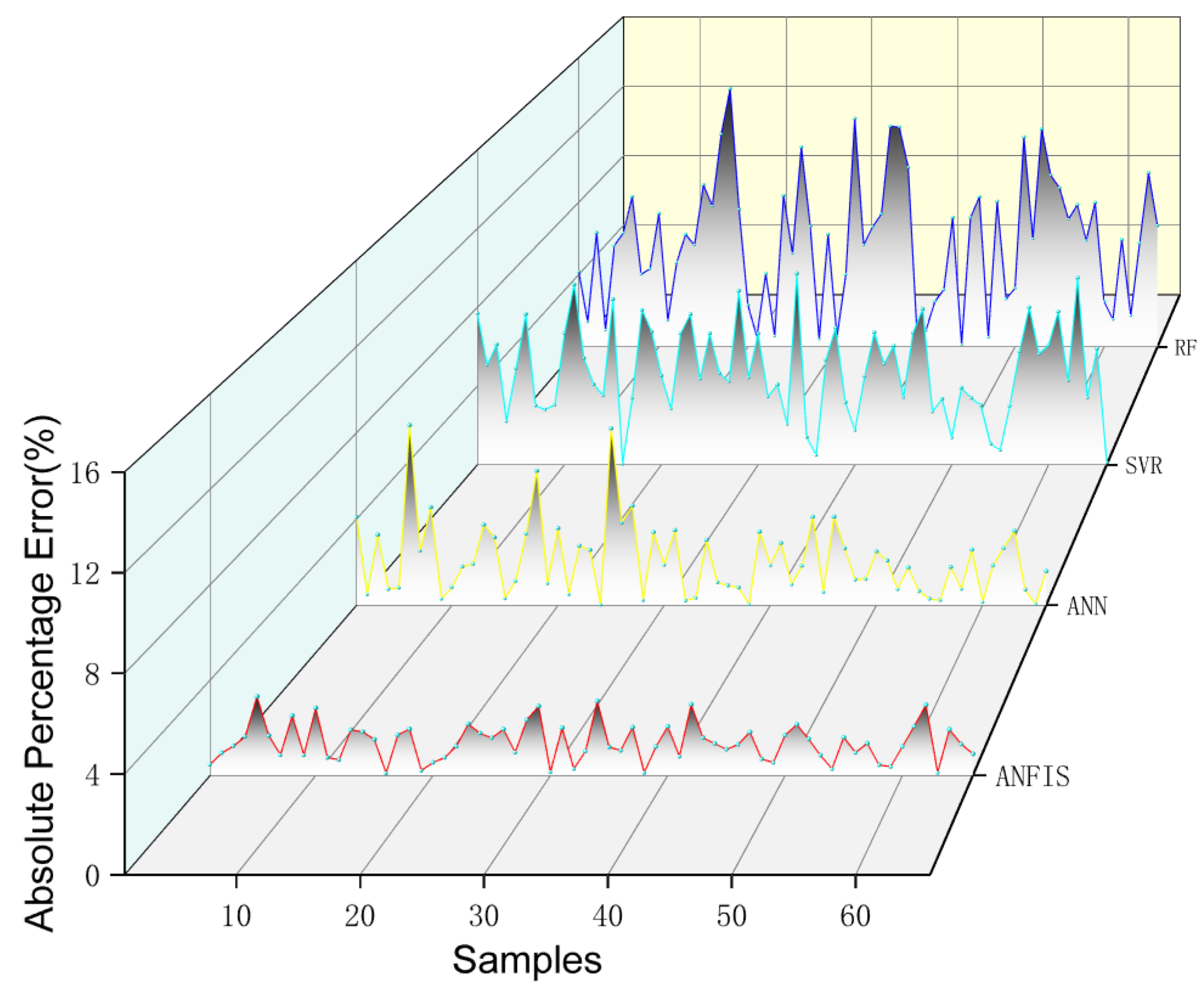
4.2.2. Training Network and Prediction Performance
4.3. ANN, SVR and RF
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Korchak, S. Performance of the Process of Grinding Steel Parts; Mashinostroenie (Mechanical Engineering): Moscow, Russia, 1974; p. 230. [Google Scholar]
- Zhu, D.; Feng, X.; Xu, X.; Yang, Z.; Li, W.; Yan, S.; Ding, H. Robotic grinding of complex components: A step towards efficient and intelligent machining–challenges, solutions, and applications. Robot. Comput. Integr. Manuf. 2020, 65, 101908. [Google Scholar] [CrossRef]
- Zhang, X.; Cabaravdic, M.; Kneupner, K.; Kuhlenkoetter, B. Real-time simulation of robot controlled belt grinding processes of sculptured surfaces. Int. J. Adv. Robot. Syst. 2004, 1, 12. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Kazerounian, K.; Gan, Z.; Sun, Y. A material removal model for robotic belt grinding process. Mach. Sci. Technol. 2014, 18, 15–30. [Google Scholar] [CrossRef]
- Yang, Z.; Chu, Y.; Xu, X.; Huang, H.; Zhu, D.; Yan, S.; Ding, H. Prediction and analysis of material removal characteristics for robotic belt grinding based on single spherical abrasive grain model. Int. J. Mech. Sci. 2021, 190, 106005. [Google Scholar] [CrossRef]
- Lv, Y.; Peng, Z.; Qu, C.; Zhu, D. An adaptive trajectory planning algorithm for robotic belt grinding of blade leading and trailing edges based on material removal profile model. Robot. Comput. Integr. Manuf. 2020, 66, 101987. [Google Scholar] [CrossRef]
- Bigerelle, M.; Hagege, B.; El Mansori, M. Mechanical modelling of micro-scale abrasion in superfinish belt grinding. Tribol. Int. 2008, 41, 992–1001. [Google Scholar] [CrossRef]
- Wang, W.; Liu, F.; Liu, Z.; Yun, C. Prediction of depth of cut for robotic belt grinding. Int. J. Adv. Manuf. Technol. 2017, 91, 699–708. [Google Scholar] [CrossRef]
- Hammann, G. Modellierung des Abtragsverhaltens Elastischer, Robotergeführter Schleifwerkzeuge; Springer: Berlin/Heidelberg, Germany, 2013; Volume 123. [Google Scholar]
- Preston, F. The theory and design of plate glass polishing machines. J. Glass Technol. 1927, 11, 214–256. [Google Scholar]
- Pandiyan, V.; Caesarendra, W.; Tjahjowidodo, T.; Praveen, G. Predictive modelling and analysis of process parameters on material removal characteristics in abrasive belt grinding process. Appl. Sci. 2017, 7, 363. [Google Scholar] [CrossRef]
- Zhe, H.; Jianyong, L.; Yueming, L.; Meng, N.; Wengang, F. Investigating the effects of contact pressure on rail material abrasive belt grinding performance. Int. J. Adv. Manuf. Technol. 2017, 93, 779–786. [Google Scholar] [CrossRef]
- Xiao, G.; Song, K.; Liu, S.; Wu, Y.; Wang, W. Comprehensive investigation into the effects of relative grinding direction on abrasive belt grinding process. J. Manuf. Process. 2021, 62, 753–761. [Google Scholar] [CrossRef]
- Pandiyan, V.; Caesarendra, W.; Glowacz, A.; Tjahjowidodo, T. Modelling of material removal in abrasive belt grinding process: A regression approach. Symmetry 2020, 12, 99. [Google Scholar] [CrossRef] [Green Version]
- Gill, S.S.; Singh, J. An Adaptive Neuro-Fuzzy Inference System modeling for material removal rate in stationary ultrasonic drilling of sillimanite ceramic. Expert Syst. Appl. 2010, 37, 5590–5598. [Google Scholar] [CrossRef]
- Khalick Mohammad, A.E.; Hong, J.; Wang, D. Polishing of uneven surfaces using industrial robots based on neural network and genetic algorithm. Int. J. Adv. Manuf. Technol. 2017, 93, 1463–1471. [Google Scholar] [CrossRef]
- Gao, K.; Chen, H.; Zhang, X.; Ren, X.; Chen, J.; Chen, X. A novel material removal prediction method based on acoustic sensing and ensemble XGBoost learning algorithm for robotic belt grinding of Inconel 718. Int. J. Adv. Manuf. Technol. 2019, 105, 217–232. [Google Scholar] [CrossRef]
- Pandiyan, V.; Shevchik, S.; Wasmer, K.; Castagne, S.; Tjahjowidodo, T. Modelling and monitoring of abrasive finishing processes using artificial intelligence techniques: A review. J. Manuf. Process. 2020, 57, 114–135. [Google Scholar] [CrossRef]
- Pandiyan, V.; Caesarendra, W.; Tjahjowidodo, T.; Tan, H.H. In-process tool condition monitoring in compliant abrasive belt grinding process using support vector machine and genetic algorithm. J. Manuf. Process. 2018, 31, 199–213. [Google Scholar] [CrossRef]
- Kecman, V. Learning and Soft Computing: Support Vector Machines, Neural Networks, and Fuzzy Logic Models; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Caesarendra, W.; Wijaya, T.; Tjahjowidodo, T.; Pappachan, B.K.; Wee, A.; Roslan, M.I. Adaptive neuro-fuzzy inference system for deburring stage classification and prediction for indirect quality monitoring. Appl. Soft Comput. 2018, 72, 565–578. [Google Scholar] [CrossRef]
- He, Z.; Li, J.; Liu, Y.; Yan, J. Single-grain cutting based modeling of abrasive belt wear in cylindrical grinding. Friction 2020, 8, 208–220. [Google Scholar] [CrossRef] [Green Version]
- Zou, L.; Liu, X.; Huang, Y.; Fei, Y. A numerical approach to predict the machined surface topography of abrasive belt flexible grinding. Int. J. Adv. Manuf. Technol. 2019, 104, 2961–2970. [Google Scholar] [CrossRef]
- Zou, L.; Wang, T.; Wang, C.; Li, Z.; Wu, Y.; Huang, Y. Modelling and analysis of the effect of nonlinear time-varying contact deformation on flexible precision grinding process. Int. J. Adv. Manuf. Technol. 2021, 115, 77–89. [Google Scholar] [CrossRef]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Luis Pérez, C. A Proposal of an Adaptive Neuro-Fuzzy Inference System for Modeling Experimental Data in Manufacturing Engineering. Mathematics 2020, 8, 1390. [Google Scholar] [CrossRef]
- Marani, M.; Songmene, V.; Zeinali, M.; Kouam, J.; Zedan, Y. Neuro-fuzzy predictive model for surface roughness and cutting force of machined Al–20 Mg2Si–2Cu metal matrix composite using additives. Neural Comput. Appl. 2020, 32, 8115–8126. [Google Scholar] [CrossRef]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-fuzzy and soft computing-a computational approach to learning and machine intelligence [Book Review]. IEEE Trans. Autom. Control 1997, 42, 1482–1484. [Google Scholar] [CrossRef]
- Ren, J.; Hao, M.; Liang, G.; Wang, S.; Lv, M. Study of subsurface damage of monocrystalline nickel in nanometric grinding with spherical abrasive grain. Phys. B Condens. Matter 2019, 560, 60–66. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Pei, L.; Sun, Z.; Yu, T.; Li, W.; Hao, X.; Hu, Y.; Yang, C. Pavement aggregate shape classification based on extreme gradient boosting. Constr. Build. Mater. 2020, 256, 119356. [Google Scholar] [CrossRef]



| (N·M) | (N·M) | |||
|---|---|---|---|---|
| Measuring range | ±1500 | ±3750 | ±240 | ±240 |
| Measurement accuracy | 1/16 | 1/8 | 1/160 | 1/160 |
| Uncertainty of measurement | 1.50% | 1.25% | 1.00% | 1.25% |
| Parameters | Unit | Levels | ||||
|---|---|---|---|---|---|---|
| Mesh | - | 120 | 180 | 240 | 320 | 400 |
| Speed | m/min | 350 | 400 | 450 | 500 | 550 |
| Force | N | 20 | 25 | 30 | 35 | 40 |
| Experiment No. | Speed (m/min) | Force (N) | Mesh | MRD (µm) | SNR (db) |
|---|---|---|---|---|---|
| 1 | 350 | 20 | 120 | 94.49 | 39.45 |
| 2 | 350 | 25 | 180 | 87.30 | 38.78 |
| 3 | 350 | 30 | 240 | 79.94 | 38.00 |
| 4 | 350 | 35 | 320 | 67.55 | 36.62 |
| 5 | 350 | 40 | 400 | 55.57 | 34.80 |
| 6 | 400 | 20 | 180 | 81.16 | 38.19 |
| 7 | 400 | 25 | 240 | 73.96 | 37.34 |
| 8 | 400 | 30 | 320 | 60.98 | 35.58 |
| 9 | 400 | 35 | 400 | 48.83 | 33.72 |
| 10 | 400 | 40 | 120 | 132.82 | 42.44 |
| 11 | 450 | 20 | 240 | 68.20 | 36.62 |
| 12 | 450 | 25 | 320 | 54.63 | 34.74 |
| 13 | 450 | 30 | 400 | 42.41 | 32.97 |
| 14 | 450 | 35 | 120 | 126.78 | 42.07 |
| 15 | 450 | 40 | 180 | 119.68 | 41.52 |
| 16 | 500 | 20 | 320 | 51.17 | 34.16 |
| 17 | 500 | 25 | 400 | 41.44 | 32.34 |
| 18 | 500 | 30 | 120 | 122.85 | 41.79 |
| 19 | 500 | 35 | 180 | 115.32 | 41.19 |
| 20 | 500 | 40 | 240 | 108.56 | 40.61 |
| 21 | 550 | 20 | 400 | 33.64 | 30.46 |
| 22 | 550 | 25 | 120 | 116.99 | 41.34 |
| 23 | 550 | 30 | 180 | 106.89 | 40.59 |
| 24 | 550 | 35 | 240 | 102.64 | 40.26 |
| 25 | 550 | 40 | 320 | 90.27 | 39.14 |
| Machining Parameter | Degrees of Freedom | Sum of Squares | Mean Square | F Ratio | (4, 12) |
|---|---|---|---|---|---|
| Speed | 4 | 2.998 | 0.749 | 3.410 | 3.259 |
| Force | 4 | 47.303 | 11.825 | 53.880 | 3.259 |
| Mesh | 4 | 231.250 | 57.812 | 263.410 | 3.259 |
| Error | 12 | 2.634 | 0.219 | - | 3.259 |
| Total | 24 | 284.185 | - | - | 3.259 |
| Parameter | Value |
|---|---|
| Neuron level | 3 |
| Size of input data set | 225 |
| Training set | |
| Testing set | |
| andMethod | Prod |
| orMethod | Max |
| defuzzification | Wtaver |
| Aggregation | Max |
| Maxepoch | 160 |
| Membership function | Gbellmf |
| Clustering Type | Grid Partitioning |
| Learning rules | Least square estimation-gradient decent algorithm |
| Cutting Depth (µm) | ANFIS | ANN | SVR | RF | ||||
|---|---|---|---|---|---|---|---|---|
| Predicted MRD (µm) | Error (%) | Predicted MRD (µm) | Error (%) | Predicted MRD (µm) | Error (%) | Predicted MRD (µm) | Error (%) | |
| 92.49 | 93.77 | 1.38 | 95.31 | 3.05 | 92.35 | 0.15 | 81.25 | 12.15 |
| 78.67 | 78.97 | 0.38 | 78.54 | 0.17 | 77.64 | 1.31 | 67.54 | 14.15 |
| 74.35 | 72.87 | 1.99 | 74.62 | 0.36 | 76.27 | 2.58 | 68.32 | 8.11 |
| 47.94 | 48.07 | 0.27 | 46.52 | 2.96 | 46.21 | 3.61 | 55.14 | 15.02 |
| 133.21 | 132.14 | 0.80 | 131.67 | 1.16 | 130.26 | 2.21 | 117.36 | 11.90 |
| 40.65 | 41.97 | 3.25 | 43.23 | 6.35 | 45.28 | 11.39 | 47.51 | 16.88 |
| 120.67 | 118.70 | 1.63 | 117.65 | 2.50 | 122.34 | 1.38 | 105.24 | 12.79 |
| 123.54 | 122.07 | 1.19 | 120.32 | 2.61 | 130.48 | 5.62 | 132.98 | 7.64 |
| 106.74 | 105.93 | 0.76 | 108.94 | 2.06 | 101.36 | 5.04 | 99.21 | 7.05 |
| 62.45 | 60.24 | 3.54 | 59.12 | 5.33 | 64.82 | 3.80 | 53.15 | 14.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, H.; Lu, X.; Cai, D.; Xiang, Y.; Chen, J.; Bao, C. Predictive Modeling and Analysis of Material Removal Characteristics for Robotic Belt Grinding of Complex Blade. Appl. Sci. 2023, 13, 4248. https://doi.org/10.3390/app13074248
Jia H, Lu X, Cai D, Xiang Y, Chen J, Bao C. Predictive Modeling and Analysis of Material Removal Characteristics for Robotic Belt Grinding of Complex Blade. Applied Sciences. 2023; 13(7):4248. https://doi.org/10.3390/app13074248
Chicago/Turabian StyleJia, Haolin, Xiaohui Lu, Deling Cai, Yingjian Xiang, Jiahao Chen, and Chengle Bao. 2023. "Predictive Modeling and Analysis of Material Removal Characteristics for Robotic Belt Grinding of Complex Blade" Applied Sciences 13, no. 7: 4248. https://doi.org/10.3390/app13074248
APA StyleJia, H., Lu, X., Cai, D., Xiang, Y., Chen, J., & Bao, C. (2023). Predictive Modeling and Analysis of Material Removal Characteristics for Robotic Belt Grinding of Complex Blade. Applied Sciences, 13(7), 4248. https://doi.org/10.3390/app13074248





