A Discrete Particle Swarm Optimization Algorithm for Dynamic Scheduling of Transmission Tasks
Abstract
:1. Introduction
1.1. Related Works
1.2. Contributions
- It is necessary to establish a mathematical model suitable for the DPSO of the DSTT;
- It is necessary to solve the DPSO’s mathematical-description problems of particle position, direction, and velocity.
- It is necessary to design specific particle-update methods.
- We build a mathematical model of the DSTT, including a task model, an evaluation model, an evaluation function, and an output of the Schedule—the mathematical model of the transmission plan—and propose a one-dimensional code to describe the Schedule, making it suitable for the calculation of the DPSO;
- We propose a DPSO to define the particle position, particle-update direction and target definition, and solve the mathematical description of the DPSO for specific problems;
- Based on the basic idea of the DPSO, and taking into account inertia retention, particle best, and global best, we use the probability-selection model to realize the particle update, and we propose random perturbation to improve the diversity of the particle population.
2. Preliminaries
2.1. Task Queue
2.2. Value Matrix
2.3. Task-Scheduling Result
2.4. Schedule
2.5. Fitness Function
2.6. Example
3. Methodologies
3.1. PSO
3.2. Algorithm Description
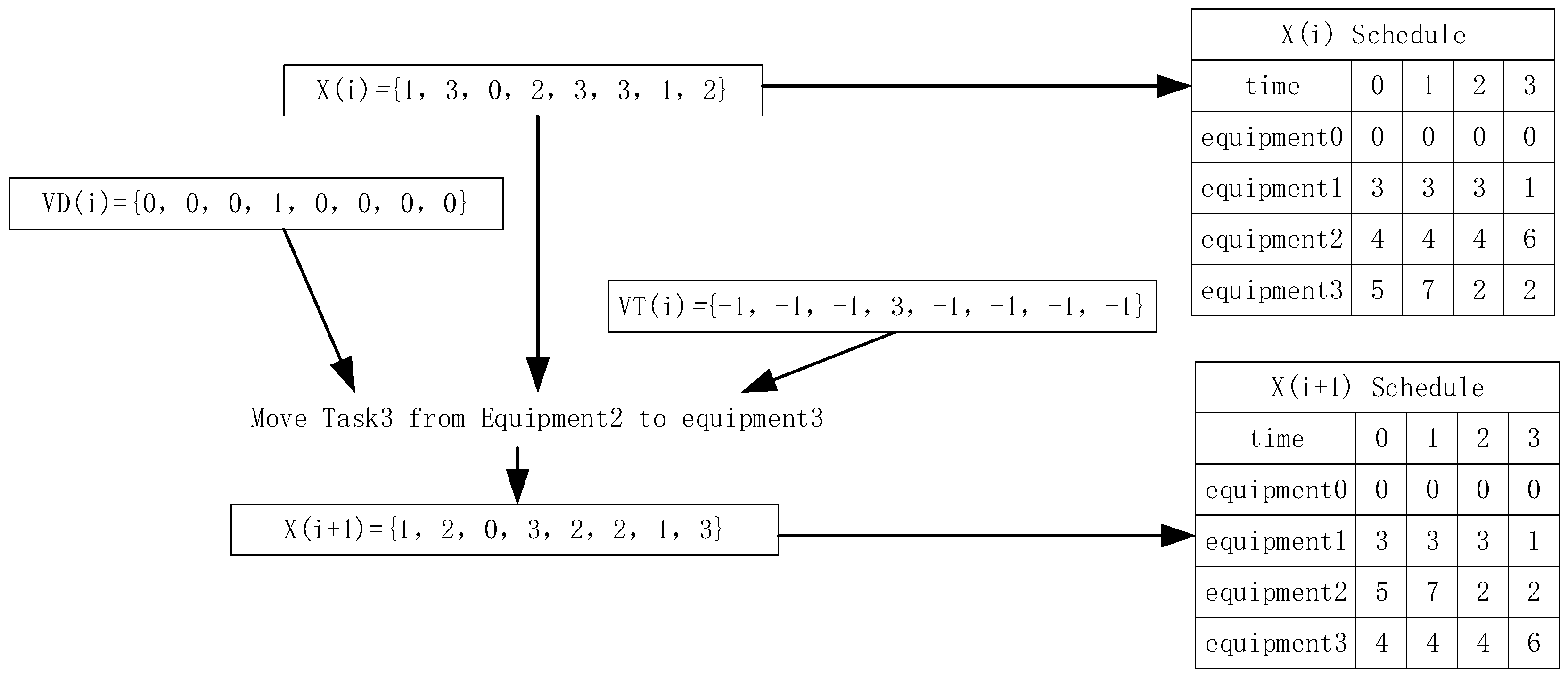
- Definition of particle position: in combination with the DSTT and the example, see Formula (15) for the definition of particle position.
- 2.
- Definition of particle-motion direction: in combination with the characteristics of data discretization in DSTT, there is no direct association management between each task. Binary processing is adopted when defining particle-motion direction, that is, each particle-motion direction is each task that can change the equipment, and is recorded as:
- 3.
- Definition of particle-motion target: the velocity displacement is defined as the serial number of the equipment to be replaced by the node representing the motion direction of particles in Schedule. The particle-motion target suitable for the operation of DSTT is defined as , which is recorded as:
- 4.
- Definition of particle-position update: according to the characteristics of DSTT, the operation of particle-velocity update is to calculate the motion direction of particles and the motion target of particles. The evaluation value of each particle task is calculated according to the particle position, and is recorded as:
3.3. Parameter
- According to Table 2, when the number of equipment and time periods is [4, 7], the influence of the parameters on the algorithm results is small. When the PBF is small and the GBF is large, the algorithm’s success rate is high. Taking the IRF of 0.1 as an example, as the PBF increases, the GBF decreases, and the success rate of the algorithm decreases gradually.
- According to Table 3, when the number of equipment and time periods is small [4, 7], the algorithm performance is evaluated by the weighted average of the number of iterations of the algorithm required to reach the global-best solution. The algorithm parameters have a great impact on the number of iterations of the algorithm. Among the parameter groups with a success rate of 100%, the parameter groups (0.2,0.2,0.6) have the lowest number of iterations.
- According to Table 4, the interval between the number of equipment and the number of time periods [4, 12] is considered globally. In the test of fixed iterations, the DPSO only achieves the maximum value of multiple parameters when the number of equipment and the number of time periods are 8. In [9, 12], some different parameter groups achieved maximum values, including (0.3,0.1,0.6), (0.5,0.1,0.4), (0.2,0.1,0.7), and (0.4,0.1,0.5).
- The groups (0.3,0.1,0.6) are better in the iterative-weighting calculation in the previous two comparison tables, but the success rate is slightly lower. The groups (0.2,0.2,0.6)’ weighted-average number of iterations is minimal. In order to ensure the comprehensiveness of the subsequent multi-algorithm experiments, use 5 groups of parameters to carry out experiments in the subsequent comparison experiments of DPSO. The list is in Table 5.
4. Experiments
4.1. Comparison Algorithm and Method
4.2. Algorithm Comparison Experiment
4.3. Summary of Experimental Analysis
4.4. Simulation Experiment
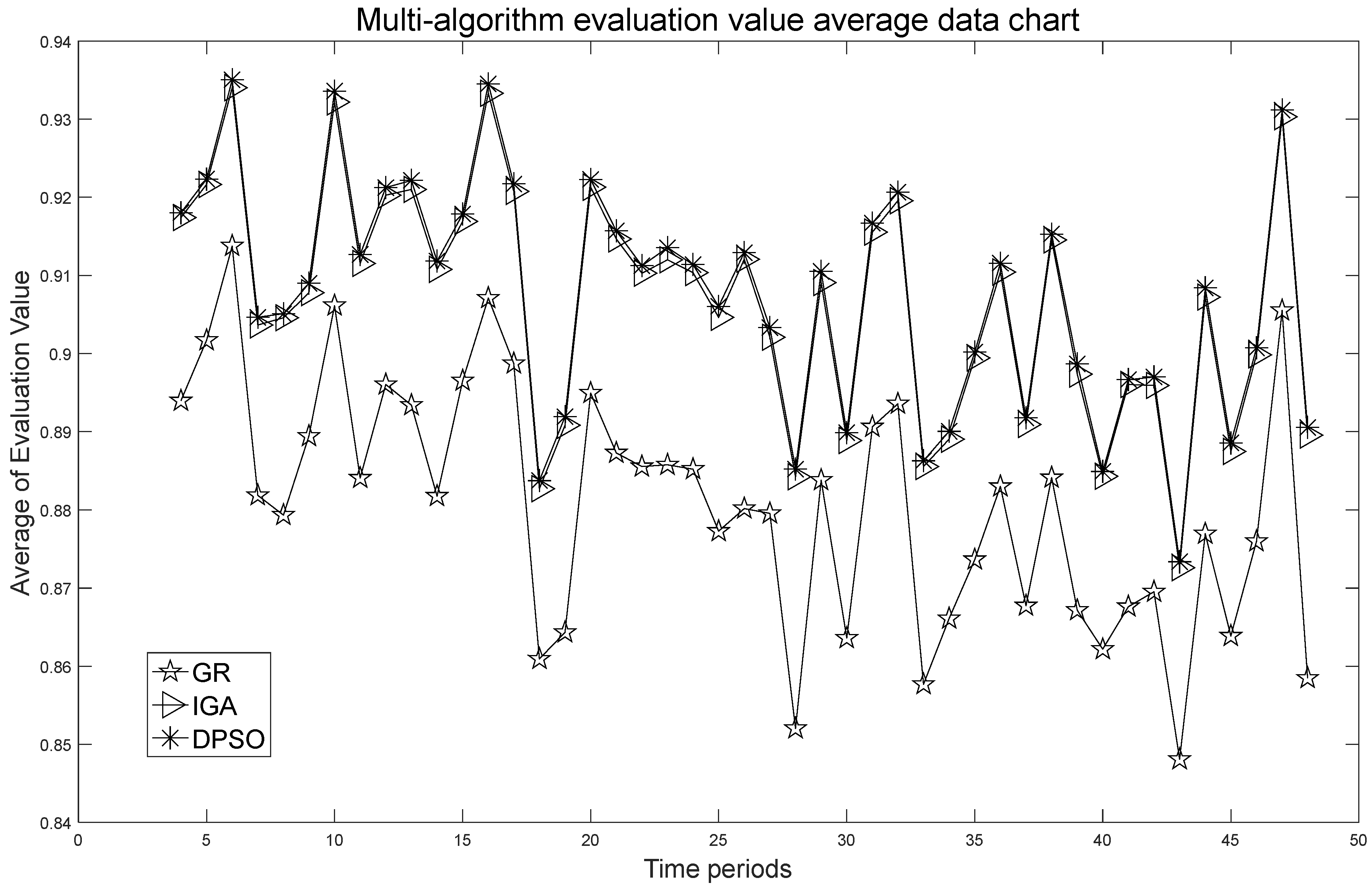
- In the simulation experiment of multiple time periods, the evaluation values of the transmission effect for all time periods are averaged. The DPSO improved the evaluation value by 3.012295% compared to the GR, and the DPSO improved the evaluation value by 0.1111146% compared to the IGA.
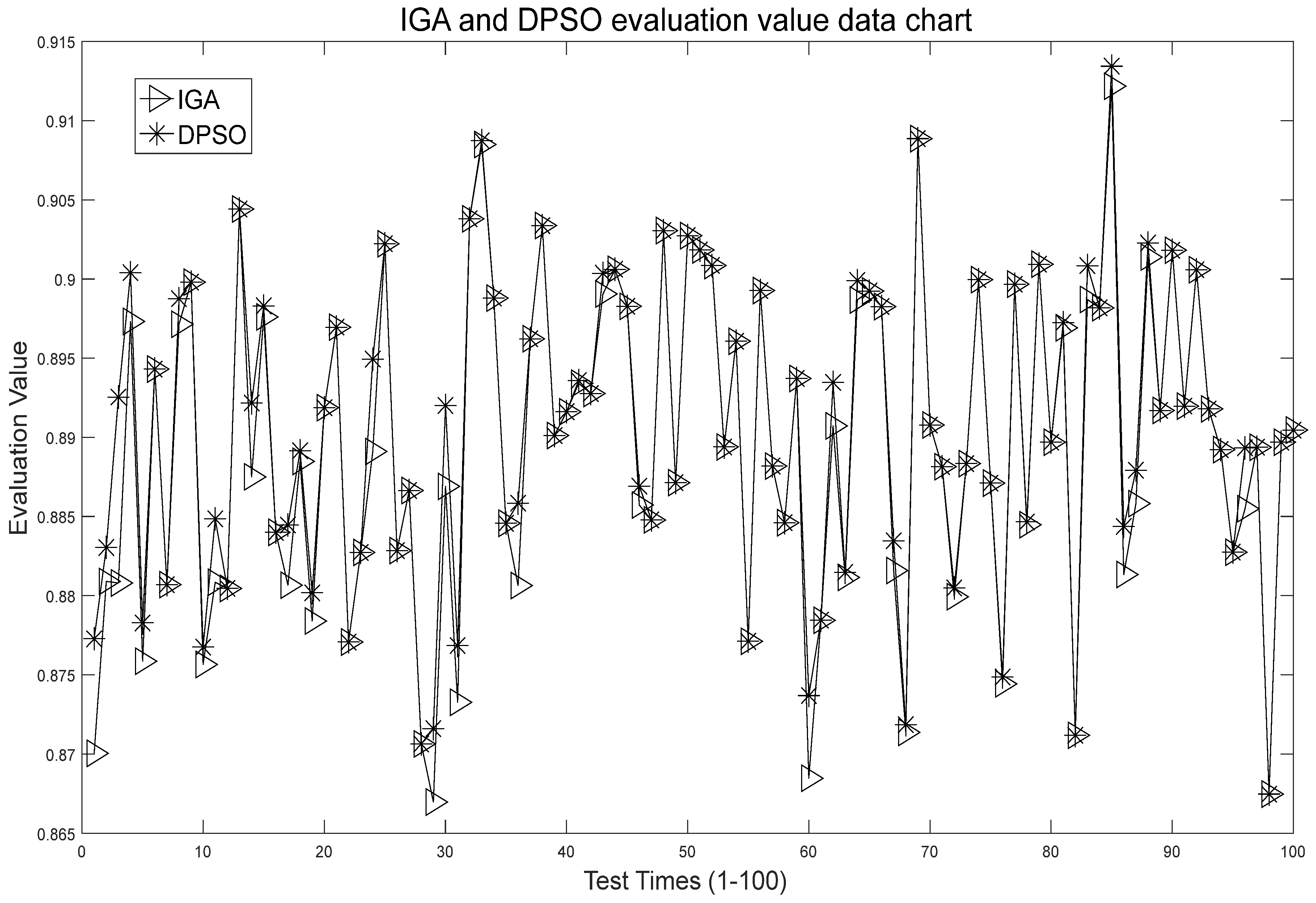
- In the simulation experiment with a maximum period of 48, the results of the DPSO were better than that of the IGA. In almost 60% of the 100 experiments, the IGA achieved the same results as the DPSO while other results were lower than that of the DPSO. The DPSO improved the evaluation value by 0.11115% compared to the IGA.
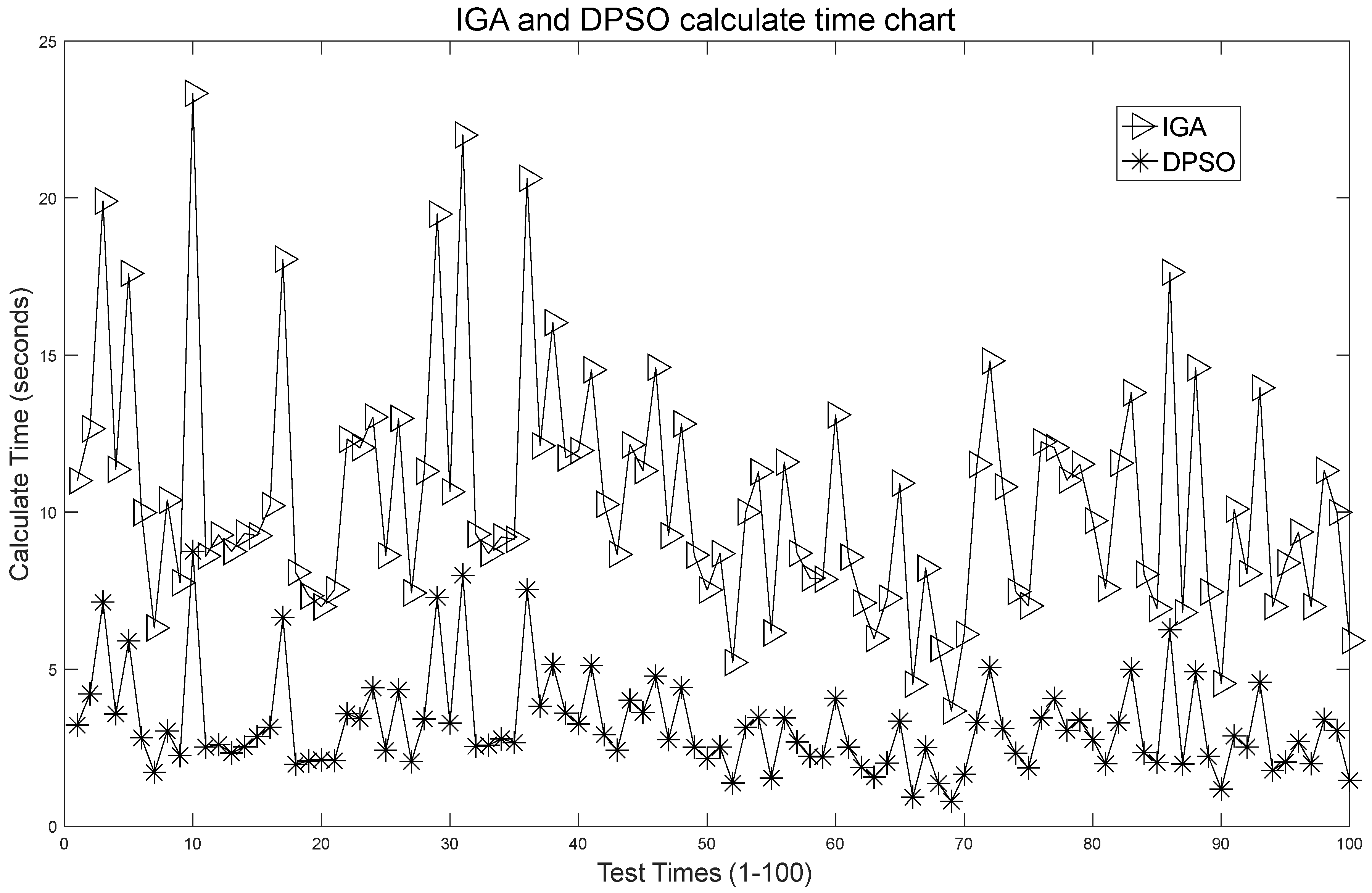
- In the simulation experiment with a maximum period of 48, in 100 experiments the average execution time of the DPSO was 3.195 s, and the average execution time of the IGA was 10.388 s. The DPSO improved the execution efficiency by 69.246%.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, M.; Xing, G.; Pang, J. Design and Implementation of Software Architecture of Intelligent Scheduling System for SW Broadcasting. Radio TV Broadcast Eng. 2007, 4, 112–116. [Google Scholar]
- Hao, W. Application of Artificial Intelligence in Radio and Television Monitoring and Supervision. Radio TV Broadcast Eng. 2019, 46, 126–128. [Google Scholar]
- Wang, X.; Yao, W. Research on Transmission Task Static Allocation Based on Intelligence Algorithm. Appl. Sci. 2023, 13, 4058. [Google Scholar] [CrossRef]
- Zhou, D.; Song, J.; Lin, C.; Wang, X. Research on Transmission Selection Optimized Evaluation Algorithm of Multi-frequency Transmitter. In 2015 International Conference on Automation, Mechanical Control and Computational Engineering; Atlantis Press: Amsterdam, The Netherlands, 2015; pp. 323–326. [Google Scholar]
- Zhou, Z.; Luo, D.; Shao, J. Immune genetic algorithm based multi-UAV cooperative target search with event-triggered mechanism. Phys. Commun. 2020, 41, 101103. [Google Scholar] [CrossRef]
- Nazarov, A.; Sztrik, J.; Kvach, A. Asymptotic analysis of finite-source M/M/1 retrial queueing system with collisions and server subject to breakdowns and repairs. Ann. Oper. Res. 2019, 277, 213–229. [Google Scholar] [CrossRef]
- Zhao, X.; Xia, X.; Wang, L. A fuzzy multi-objective immune genetic algorithm for the strategic location planning problem. Clust. Comput. 2019, 22, 3621–3641. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, Y.; Li, B. Cooperative Co-evolution with soft grouping for large scale global optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 318–325. [Google Scholar]
- Jia, Y. Distributed cooperative co-evolution with adaptive computing resource allocation for large scale optimization. IEEE Trans. Evol. Comput. 2019, 23, 188–202. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X.; Ernst, A.; Omidvar, M.N. Decomposition for large-scale optimization problems with overlapping components. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 326–333. [Google Scholar]
- Li, L.; Fang, W.; Wang, Q.; Sun, J. Differential grouping with spectral clustering for large scale global optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 334–341. [Google Scholar]
- Ismayilov, G.; Topcuoglu, H.R. Neural network-based multi-objective evolutionary algorithm for dynamic workflow scheduling in cloud computing. Future Gener. Comput. Syst. 2020, 102, 307–322. [Google Scholar] [CrossRef]
- Cabrera, A.; Acosta, A.; Almieida, F. A dynamic multi-objective approach for dynamic load balancing in heterogeneous systems. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 2421–2434. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, S.; Jiang, S. Novel prediction strategies for dynamic multi-objective optimization. IEEE Trans. Evol. Comput. 2019, 24, 260–274. [Google Scholar] [CrossRef]
- Cao, L.; Xu, L.; Goodman, E.D. Evolutionary dynamic multi-objective optimization assisted by a support vector regression predictor. IEEE Trans. Evol. Comput. 2019, 24, 305–319. [Google Scholar] [CrossRef]
- Qu, B.; Li, G.; Guo, Q. A niching multi-objective harmony search algorithm for multimodal multi-objective problems. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 1267–1274. [Google Scholar]
- Liang, J.; Xu, W.; Yue, C. Multimodal multi-objective optimization with differential evolution. Swarm Evol. Comput. 2019, 44, 1028–1059. [Google Scholar] [CrossRef]
- Qu, B.; Li, C.; Liang, J. A self-organized speciation-based multi-objective particle swarm optimizer for multimodal multi-objective problems. Appl. Soft Comput. 2020, 86, 105886. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Peng, Y.; Shang, K. A scalable multimodal multi-objective test problem. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 310–317. [Google Scholar]
- Kuppusamy, P.; Kumari, N.M.J.; Alghamdi, W.Y.; Alyami, H.; Ramalingam, R.; Javed, A.R.; Rashid, M. Job scheduling problem in fog-cloud-based environment using reinforced social spider optimization. J. Cloud Comput. 2022, 11, 99. [Google Scholar] [CrossRef]
- Tang, X.; Liu, Y.; Deng, T.; Zeng, Z.; Huang, H.; Wei, Q.; Li, X.; Yang, L. A job scheduling algorithm based on parallel workload prediction on computational grid. J. Parallel Distrib. Comput. 2023, 171, 88–97. [Google Scholar] [CrossRef]
- Jia, P.; Wu, T. A hybrid genetic algorithm for flexible job-shop scheduling problem. J. Xi’an Polytech. Univ. 2020, 10, 80–86. [Google Scholar]
- Cheng, R.; Gen, M.; Tsujimura, Y. A Tutorial Survey of Job-Shop Scheduling Problems using Genetic Algorithms-I. Representation. Comput. Ind. Eng. 1996, 30, 983–997. [Google Scholar] [CrossRef]
- Cheng, R.; Gen, M.; Tsujimura, Y. A tutorial survey of job-shop scheduling problems using genetic algorithms, part II: Hybrid genetic search strategies. Comput. Ind. Eng. 1999, 36, 343–364. [Google Scholar] [CrossRef]
- Chaudhry, I.; Khan, A. A research survey: Review of flexible job shop scheduling techniques. Int. Trans. Oper. Res. 2016, 23, 551–591. [Google Scholar] [CrossRef]
- Kim, J. Developing a job shop scheduling system through integration of graphic user interface and genetic algorithm. Mul-timed. Tools Appl. 2015, 74, 3329–3343. [Google Scholar] [CrossRef]
- Kim, J. Candidate Order based Genetic Algorithm (COGA) for Constrained Sequencing Problems. Int. J. Ind. Eng. Theory Appl. Pract. 2016, 23, 1–12. [Google Scholar]
- Park, J.; Ng, H.; Chua, T.; Ng, Y.; Kim, J. Unifified Genetic Algorithm Approach for Solving Flexible Job-Shop Scheduling Problem. Appl. Sci. 2021, 11, 6454. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Pan, Q.; Tasgetiren, M.F.; Liang, Y.C. A discrete particle swarm optimization algorithm for the permutation flowshop sequencing problem with makespan criterion. In Research and Development in Intelligent Systems XXIII, SGAI 2006; Bramer, M., Coenen, F., Tuson, A., Eds.; Springer: London, UK, 2006; pp. 19–31. [Google Scholar]
- Lian, Z.; Gi, X.; Jiao, B. A novel particle swarm optimization algorithm for permutation flow-shop scheduling to minimize makespan. Chaos Solitons Fractals 2008, 35, 851–861. [Google Scholar]
- Shi, X.; Liang, Y.; Lee, H.; Lu, C.; Wang, Q. Particle swarm optimization-based algorithms for TSP and generalized TSP. Inf. Process. Lett. 2007, 103, 169–176. [Google Scholar] [CrossRef]
- Abdel-Kader, R.F. Hybrid discrete PSO with GA operators for efficient QoS-multicast routing. Ain Shams Eng. J. 2011, 2, 21–31. [Google Scholar] [CrossRef] [Green Version]
- Roberge, V.; Tarbouchi, M.; Labonte, G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans. Ind. Inf. 2013, 9, 132–141. [Google Scholar] [CrossRef]
- Xu, S.H.; Liu, J.P.; Zhang, F.H.; Wang, L.; Sun, L.J. A combination of genetic algorithm and particle swarm optimization for vehicle routing problem with time windows. Sensors 2015, 15, 21033–21053. [Google Scholar] [CrossRef] [Green Version]
- Zheng, P.; Zhang, P.; Wang, M.; Zhang, J. A Data-Driven Robust Scheduling Method Integrating Particle Swarm Optimization Algorithm with Kernel-Based Estimation. Appl. Sci. 2021, 11, 5333. [Google Scholar] [CrossRef]
- Chen, H.-W.; Liang, C.-K. Genetic Algorithm versus Discrete Particle Swarm Optimization Algorithm for Energy-Efficient Moving Object Coverage Using Mobile Sensors. Appl. Sci. 2022, 12, 3340. [Google Scholar] [CrossRef]
- Fan, Y.-A.; Liang, C.-K. Hybrid Discrete Particle Swarm Optimization Algorithm with Genetic Operators for Target Coverage Problem in Directional Wireless Sensor Networks. Appl. Sci. 2022, 12, 8503. [Google Scholar] [CrossRef]
- GY/T 280-2014; Specifications of Interface Data for Transmitting Station Operation Management System. State Administration of Press, Publication, Radio, Film and Television: Beijing, China, 2 November 2014.
- GY/T 290-2015; Specification of Code for Data Communication Interface of Radio and Television Transmitter. State Administration of Press, Publication, Radio, Film and Television: Beijing, China, 3 March 2015.


| Parameter | Explain |
|---|---|
| number of Schedule definition periods | |
| number of equipment defined in Schedule | |
| number of Schedule tasks | |
| task of the k-th Schedule, including | |
| data description of the k-th result, including | |
| evaluation value of the transmitting effect of the i-th equipment in the j-th frequency band | |
| Schedule node data, frequency code of the i-th equipment working in the j-th time period | |
| The output result of Schedule is composed of p piece of code values |
| Parameter | Number of Equipment and Time Periods | Total | |||||
|---|---|---|---|---|---|---|---|
| IRF | PBF | GBF | 4 | 5 | 6 | 7 | |
| 0.8 | 0.1 | 0.1 | 100 | 100 | 100 | 99 | 399 |
| 0.7 | 0.1 | 0.2 | 100 | 100 | 100 | 100 | 400 |
| 0.6 | 0.2 | 0.2 | 100 | 100 | 100 | 99 | 399 |
| 0.6 | 0.1 | 0.3 | 100 | 100 | 100 | 100 | 400 |
| 0.6 | 0.2 | 0.2 | 100 | 100 | 100 | 99 | 399 |
| 0.6 | 0.3 | 0.1 | 100 | 100 | 99 | 97 | 396 |
| 0.5 | 0.1 | 0.4 | 100 | 100 | 100 | 100 | 400 |
| 0.5 | 0.2 | 0.3 | 100 | 100 | 100 | 100 | 400 |
| 0.5 | 0.3 | 0.2 | 100 | 100 | 98 | 98 | 396 |
| 0.5 | 0.4 | 0.1 | 100 | 100 | 97 | 93 | 390 |
| 0.4 | 0.1 | 0.5 | 100 | 100 | 100 | 100 | 400 |
| 0.4 | 0.2 | 0.4 | 100 | 100 | 100 | 99 | 399 |
| 0.4 | 0.3 | 0.3 | 100 | 100 | 100 | 99 | 399 |
| 0.4 | 0.4 | 0.2 | 100 | 99 | 96 | 90 | 385 |
| 0.4 | 0.5 | 0.1 | 100 | 99 | 96 | 96 | 391 |
| 0.3 | 0.1 | 0.6 | 100 | 100 | 100 | 99 | 399 |
| 0.3 | 0.2 | 0.5 | 100 | 100 | 100 | 97 | 397 |
| 0.3 | 0.3 | 0.4 | 100 | 99 | 99 | 97 | 395 |
| 0.3 | 0.4 | 0.3 | 100 | 100 | 97 | 96 | 393 |
| 0.3 | 0.5 | 0.2 | 100 | 99 | 98 | 94 | 391 |
| 0.3 | 0.6 | 0.1 | 100 | 99 | 97 | 93 | 389 |
| 0.2 | 0.1 | 0.7 | 100 | 100 | 100 | 100 | 400 |
| 0.2 | 0.2 | 0.6 | 100 | 100 | 100 | 100 | 400 |
| 0.2 | 0.3 | 0.5 | 100 | 99 | 99 | 95 | 393 |
| 0.2 | 0.4 | 0.4 | 100 | 98 | 98 | 97 | 393 |
| 0.2 | 0.5 | 0.3 | 100 | 99 | 94 | 92 | 385 |
| 0.2 | 0.6 | 0.2 | 100 | 95 | 97 | 89 | 381 |
| 0.2 | 0.7 | 0.1 | 99 | 98 | 89 | 87 | 373 |
| 0.1 | 0.1 | 0.8 | 100 | 100 | 100 | 99 | 399 |
| 0.1 | 0.2 | 0.7 | 100 | 100 | 100 | 99 | 399 |
| 0.1 | 0.3 | 0.6 | 100 | 100 | 98 | 99 | 397 |
| 0.1 | 0.4 | 0.5 | 100 | 96 | 98 | 94 | 388 |
| 0.1 | 0.5 | 0.4 | 100 | 96 | 99 | 90 | 385 |
| 0.1 | 0.6 | 0.3 | 100 | 97 | 95 | 93 | 385 |
| 0.1 | 0.7 | 0.2 | 99 | 98 | 90 | 89 | 376 |
| 0.1 | 0.8 | 0.1 | 99 | 96 | 89 | 87 | 371 |
| Parameter | Number of Equipment and Time Periods | Average Weighted | |||||
|---|---|---|---|---|---|---|---|
| IRF | PBF | GBF | 4 | 5 | 6 | 7 | |
| 0.8 | 0.1 | 0.1 | 224 | 871 | 2655 | 21,824 | 3.9881 |
| 0.7 | 0.1 | 0.2 | 112 | 599 | 2217 | 10,548 | 2.3223 |
| 0.6 | 0.2 | 0.2 | 172 | 557 | 1650 | 8722 | 2.3816 |
| 0.6 | 0.1 | 0.3 | 121 | 591 | 1836 | 5129 | 1.9570 |
| 0.6 | 0.2 | 0.2 | 113 | 439 | 3923 | 9776 | 2.4696 |
| 0.6 | 0.3 | 0.1 | 178 | 452 | 3309 | 16,446 | 3.1171 |
| 0.5 | 0.1 | 0.4 | 149 | 512 | 1569 | 8560 | 2.1828 |
| 0.5 | 0.2 | 0.3 | 132 | 367 | 1469 | 5336 | 1.7257 |
| 0.5 | 0.3 | 0.2 | 118 | 432 | 2423 | 11,878 | 2.3078 |
| 0.5 | 0.4 | 0.1 | 112 | 307 | 6163 | 25,490 | 3.7425 |
| 0.4 | 0.1 | 0.5 | 122 | 522 | 1749 | 3791 | 1.7931 |
| 0.4 | 0.2 | 0.4 | 122 | 415 | 1270 | 7374 | 1.8020 |
| 0.4 | 0.3 | 0.3 | 124 | 334 | 975 | 8476 | 1.7363 |
| 0.4 | 0.4 | 0.2 | 119 | 780 | 8287 | 35,345 | 5.2982 |
| 0.4 | 0.5 | 0.1 | 109 | 1033 | 7520 | 21,687 | 4.5165 |
| 0.3 | 0.1 | 0.6 | 149 | 443 | 1619 | 7191 | 2.0399 |
| 0.3 | 0.2 | 0.5 | 110 | 453 | 1363 | 10,859 | 2.0050 |
| 0.3 | 0.3 | 0.4 | 127 | 843 | 3195 | 12,709 | 2.9862 |
| 0.3 | 0.4 | 0.3 | 104 | 351 | 6735 | 17,436 | 3.3739 |
| 0.3 | 0.5 | 0.2 | 754 | 628 | 4604 | 19,818 | 6.9327 |
| 0.3 | 0.6 | 0.1 | 103 | 1049 | 7460 | 22,095 | 4.5122 |
| 0.2 | 0.1 | 0.7 | 139 | 567 | 1450 | 4326 | 1.9032 |
| 0.2 | 0.2 | 0.6 | 109 | 415 | 1283 | 3175 | 1.4791 |
| 0.2 | 0.3 | 0.5 | 120 | 725 | 3347 | 14,749 | 2.9821 |
| 0.2 | 0.4 | 0.4 | 119 | 1037 | 4929 | 15,402 | 3.6608 |
| 0.2 | 0.5 | 0.3 | 109 | 554 | 9827 | 28,083 | 4.8906 |
| 0.2 | 0.6 | 0.2 | 107 | 4385 | 6990 | 37,551 | 8.7769 |
| 0.2 | 0.7 | 0.1 | 498 | 1632 | 16,425 | 46,448 | 10.6003 |
| 0.1 | 0.1 | 0.8 | 133 | 455 | 1978 | 5732 | 1.9499 |
| 0.1 | 0.2 | 0.7 | 115 | 378 | 1600 | 5762 | 1.6963 |
| 0.1 | 0.3 | 0.6 | 126 | 352 | 4289 | 4313 | 2.1971 |
| 0.1 | 0.4 | 0.5 | 146 | 2829 | 5560 | 13,826 | 5.6724 |
| 0.1 | 0.5 | 0.4 | 118 | 1822 | 2081 | 29,446 | 4.7190 |
| 0.1 | 0.6 | 0.3 | 116 | 3604 | 9047 | 19,192 | 7.3423 |
| 0.1 | 0.7 | 0.2 | 614 | 2266 | 15,314 | 39,792 | 11.2526 |
| 0.1 | 0.8 | 0.1 | 612 | 2278 | 18,466 | 36,460 | 11.7022 |
| Parameter | Number of Equipment and Time Periods | Total | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IRF | PBF | GBF | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 0.8 | 0.1 | 0.1 | √ | √ | √ | 3 | ||||||
| 0.7 | 0.1 | 0.2 | √ | √ | √ | √ | 4 | |||||
| 0.6 | 0.2 | 0.2 | √ | √ | √ | 3 | ||||||
| 0.6 | 0.1 | 0.3 | √ | √ | √ | √ | 4 | |||||
| 0.6 | 0.2 | 0.2 | √ | √ | √ | 3 | ||||||
| 0.6 | 0.3 | 0.1 | √ | √ | 2 | |||||||
| 0.5 | 0.1 | 0.4 | √ | √ | √ | √ | √ | √ | 6 | |||
| 0.5 | 0.2 | 0.3 | √ | √ | √ | √ | 4 | |||||
| 0.5 | 0.3 | 0.2 | √ | √ | 2 | |||||||
| 0.5 | 0.4 | 0.1 | √ | √ | 2 | |||||||
| 0.4 | 0.1 | 0.5 | √ | √ | √ | √ | √ | √ | 6 | |||
| 0.4 | 0.2 | 0.4 | √ | √ | √ | 3 | ||||||
| 0.4 | 0.3 | 0.3 | √ | √ | √ | 3 | ||||||
| 0.4 | 0.4 | 0.2 | √ | 1 | ||||||||
| 0.4 | 0.5 | 0.1 | √ | 1 | ||||||||
| 0.3 | 0.1 | 0.6 | √ | √ | √ | √ | √ | 5 | ||||
| 0.3 | 0.2 | 0.5 | √ | √ | √ | 3 | ||||||
| 0.3 | 0.3 | 0.4 | √ | 1 | ||||||||
| 0.3 | 0.4 | 0.3 | √ | √ | 2 | |||||||
| 0.3 | 0.5 | 0.2 | √ | 1 | ||||||||
| 0.3 | 0.6 | 0.1 | √ | 1 | ||||||||
| 0.2 | 0.1 | 0.7 | √ | √ | √ | √ | √ | 5 | ||||
| 0.2 | 0.2 | 0.6 | √ | √ | √ | √ | 4 | |||||
| 0.2 | 0.3 | 0.5 | √ | 1 | ||||||||
| 0.2 | 0.4 | 0.4 | √ | 1 | ||||||||
| 0.2 | 0.5 | 0.3 | √ | 1 | ||||||||
| 0.2 | 0.6 | 0.2 | √ | 1 | ||||||||
| 0.2 | 0.7 | 0.1 | 0 | |||||||||
| 0.1 | 0.1 | 0.8 | √ | √ | √ | 3 | ||||||
| 0.1 | 0.2 | 0.7 | √ | √ | √ | 3 | ||||||
| 0.1 | 0.3 | 0.6 | √ | √ | 2 | |||||||
| 0.1 | 0.4 | 0.5 | √ | 1 | ||||||||
| 0.1 | 0.5 | 0.4 | √ | 1 | ||||||||
| 0.1 | 0.6 | 0.3 | √ | 1 | ||||||||
| 0.1 | 0.7 | 0.2 | 0 | |||||||||
| 0.1 | 0.8 | 0.1 | 0 | |||||||||
| Parameter | [4, 7] | [4, 12] | ||||
|---|---|---|---|---|---|---|
| IRF | PBF | GBF | Success Rate | Weighted Iteration | Maximum Number of Times | |
| DPSO1 | 0.5 | 0.1 | 0.4 | 100% | 2.1828 | 6 |
| DPSO2 | 0.4 | 0.1 | 0.5 | 100% | 1.7931 | 6 |
| DPSO3 | 0.3 | 0.1 | 0.6 | 99.75% | 2.0399 | 5 |
| DPSO4 | 0.2 | 0.1 | 0.7 | 100% | 1.9032 | 5 |
| DPSO5 | 0.2 | 0.2 | 0.6 | 100% | 1.4791 | 4 |
| Algorithm | Explain |
|---|---|
| ENU | Enumeration algorithm: The global-optimal solution can be obtained by traversing the running chart of all tasks and calculating the evaluation value. With the increase in the number of equipment and time periods, the iteration number increases rapidly and the algorithm’s execution time is long. |
| GR | Greedy algorithm: Find out the tasks that can obtain the best allocation among all tasks. According to this principle, until all tasks are allocated, the algorithm’s execution time is stable, the number of algorithm iterations is related to the task period, and the conflicts encountered in the allocation are backtracked [4]. |
| IGA | Improved genetic algorithm: Select the elitist-retention strategy, the discontinuous cycle replacement group crossover strategy for crossover, and the overall equipment task switching strategy for mutation. The three parameters are set as the algorithm’s optimal parameter array, with a selection factor = 0.8, a crossover factor = 0.1, and a mutation factor = 0.1. Refer to previous research results for the selection of parameters [3]. |
| DPSO | Discrete particle swarm optimization algorithm: The parameters are calculated according to the five sets of parameters in Table 5, and the corresponding statistical calculations are performed. |
| Eq. | ENU | GR | IGA | DPSO | ||
|---|---|---|---|---|---|---|
| [min, max] | Avg. | Stdea. | ||||
| 4 | 100 | 25 | 100 | [100, 100] | 100 | 0.000000 |
| 5 | 100 | 8 | 100 | [100, 100] | 100 | 0.000000 |
| 6 | 100 | 5 | 100 | [99, 100] | 99.8 | 0.447214 |
| 7 | 100 | 2 | 99 | [98, 100] | 99.6 | 0.894427 |
| 8 | N/A | 1 | 89 | [99, 100] | 99.8 | 0.447214 |
| 9 | N/A | 0 | 70 | [92, 99] | 97.2 | 2.949576 |
| 10 | N/A | 0 | 62 | [93, 100] | 97.8 | 2.774887 |
| 11 | N/A | 0 | 35 | [93, 98] | 96.8 | 2.167948 |
| 12 | N/A | 0 | 39 | [83, 97] | 93.2 | 5.932959 |
| 13 | N/A | 0 | 20 | [90, 100] | 94.8 | 3.701351 |
| 14 | N/A | 0 | 4 | [77, 97] | 88.6 | 8.049845 |
| 15 | N/A | 0 | 10 | [67, 94] | 87.4 | 11.436783 |
| Total | 400 | 41 | 728 | [1124, 1182] | 1155 | 26.870058 |
| Eq. | GR | IGA | DPSO | ||
|---|---|---|---|---|---|
| [min, max] | Avg. | Stdea. | |||
| 4 | 0.815214 | 0.838134 | [0.838134, 0.838134] | 0.838134 | 0.000000 |
| 5 | 0.874183 | 0.895642 | [0.895642, 0.895642] | 0.895642 | 0.000000 |
| 6 | 0.856763 | 0.883459 | [0.883458, 0.883459] | 0.8834588 | 0.000000 |
| 7 | 0.899497 | 0.916141 | [0.916114, 0.916156] | 0.9161528 | 0.000007 |
| 8 | 0.892468 | 0.913266 | [0.91355, 0.913556] | 0.9135548 | 0.000003 |
| 9 | 0.858319 | 0.881545 | [0.882189, 0.882289] | 0.8822652 | 0.000043 |
| 10 | 0.874637 | 0.898784 | [0.89988, 0.899956] | 0.8999352 | 0.000031 |
| 11 | 0.873344 | 0.896935 | [0.898354, 0.898388] | 0.898379 | 0.000014 |
| 12 | 0.878253 | 0.902085 | [0.903259, 0.90338] | 0.9033514 | 0.000052 |
| 13 | 0.878391 | 0.914041 | [0.916594, 0.916635] | 0.9166176 | 0.000018 |
| 14 | 0.904408 | 0.931707 | [0.934612, 0.934725] | 0.9346716 | 0.000048 |
| 15 | 0.891888 | 0.917394 | [0.920402, 0.920621] | 0.920569 | 0.000094 |
| Avg. | 0.874780 | 0.899094 | [0.900205, 0.900242] | 0.9002276 | 0.000018 |
| Eq. | IGA | DPSO | ||
|---|---|---|---|---|
| [min, max] | Avg. | Stdea. | ||
| 4 | 643 | [105, 132] | 116.4 | 10.0 |
| 5 | 2692 | [340, 552] | 446.8 | 88.4 |
| 6 | 7452 | [1674, 2088] | 1812.4 | 179.8 |
| 7 | 15,095 | [4355, 9186] | 5893.8 | 1963.8 |
| 8 | 74,431 | [7719, 11,447] | 9395.8 | 1465.2 |
| 9 | 266,112 | [36,169, 69,736] | 48,312.8 | 13,134.6 |
| 10 | 421,878 | [42,925, 88,540] | 63,079 | 16,922.1 |
| 11 | 899,103 | [108,956, 208,574] | 132,676.2 | 42,597.5 |
| 12 | 1,210,932 | [209,287, 407,190] | 309,613.4 | 90,217.6 |
| 13 | 2,211,539 | [362,240, 765,968] | 498,789 | 166,816.1 |
| 14 | 3,241,904 | [493,569, 1,381,226] | 841,163.8 | 328,465.6 |
| 15 | 4,141,849 | [735,817, 2,595,418] | 1,297,816.8 | 746,327.9 |
| Eq. | Availability | Accuracy | Efficiency | Evaluation |
|---|---|---|---|---|
| ENU | high | N/A | N/A | bad |
| GR | low | low | N/A | bad |
| IGA | middle | high | low | better |
| DPSO | high | high | high | best |
| Periods | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|
| GR | 0.893972 | 0.901704 | 0.913778 | 0.881862 | 0.879343 | 0.889435 | 0.906143 | 0.884089 | 0.896052 |
| IGA | 0.917416 | 0.92164 | 0.934022 | 0.90367 | 0.904581 | 0.907794 | 0.932187 | 0.911542 | 0.920281 |
| DPSO | 0.918031 | 0.922333 | 0.935052 | 0.904655 | 0.905095 | 0.909001 | 0.933586 | 0.912695 | 0.921244 |
| Periods | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| GR | 0.893406 | 0.881768 | 0.89654 | 0.907105 | 0.89874 | 0.860929 | 0.864331 | 0.894956 | 0.8873 |
| IGA | 0.921019 | 0.910778 | 0.916936 | 0.93331 | 0.920762 | 0.88272 | 0.890827 | 0.921293 | 0.914671 |
| DPSO | 0.922169 | 0.911839 | 0.91786 | 0.93453 | 0.921716 | 0.883748 | 0.891933 | 0.922291 | 0.915707 |
| Periods | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| GR | 0.885542 | 0.885767 | 0.885219 | 0.87728 | 0.880179 | 0.87955 | 0.852032 | 0.883815 | 0.863596 |
| IGA | 0.910287 | 0.912008 | 0.910358 | 0.904637 | 0.912072 | 0.902095 | 0.884231 | 0.909096 | 0.888886 |
| DPSO | 0.911239 | 0.913564 | 0.911396 | 0.906042 | 0.912925 | 0.90334 | 0.885226 | 0.910536 | 0.889882 |
| Periods | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| GR | 0.890629 | 0.89359 | 0.857689 | 0.866087 | 0.873645 | 0.883004 | 0.867741 | 0.88413 | 0.867158 |
| IGA | 0.915545 | 0.91956 | 0.885552 | 0.889054 | 0.899454 | 0.910442 | 0.890941 | 0.914558 | 0.897373 |
| DPSO | 0.916702 | 0.920654 | 0.886297 | 0.89005 | 0.900186 | 0.911575 | 0.891782 | 0.915296 | 0.898685 |
| Periods | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| GR | 0.862168 | 0.867621 | 0.86952 | 0.848084 | 0.876947 | 0.863869 | 0.875981 | 0.905513 | 0.858482 |
| IGA | 0.884312 | 0.896044 | 0.895931 | 0.872597 | 0.907236 | 0.887478 | 0.899854 | 0.930317 | 0.889568 |
| DPSO | 0.884925 | 0.896671 | 0.897014 | 0.873367 | 0.908403 | 0.888566 | 0.900728 | 0.931161 | 0.890556 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Yao, W. A Discrete Particle Swarm Optimization Algorithm for Dynamic Scheduling of Transmission Tasks. Appl. Sci. 2023, 13, 4353. https://doi.org/10.3390/app13074353
Wang X, Yao W. A Discrete Particle Swarm Optimization Algorithm for Dynamic Scheduling of Transmission Tasks. Applied Sciences. 2023; 13(7):4353. https://doi.org/10.3390/app13074353
Chicago/Turabian StyleWang, Xinzhe, and Wenbin Yao. 2023. "A Discrete Particle Swarm Optimization Algorithm for Dynamic Scheduling of Transmission Tasks" Applied Sciences 13, no. 7: 4353. https://doi.org/10.3390/app13074353
APA StyleWang, X., & Yao, W. (2023). A Discrete Particle Swarm Optimization Algorithm for Dynamic Scheduling of Transmission Tasks. Applied Sciences, 13(7), 4353. https://doi.org/10.3390/app13074353






