Numerical Study on Seismic Performance of Buckling-Restrained Braced Double-Pier RC Bridge with Bolted Gusset Connections
Abstract
:1. Introduction
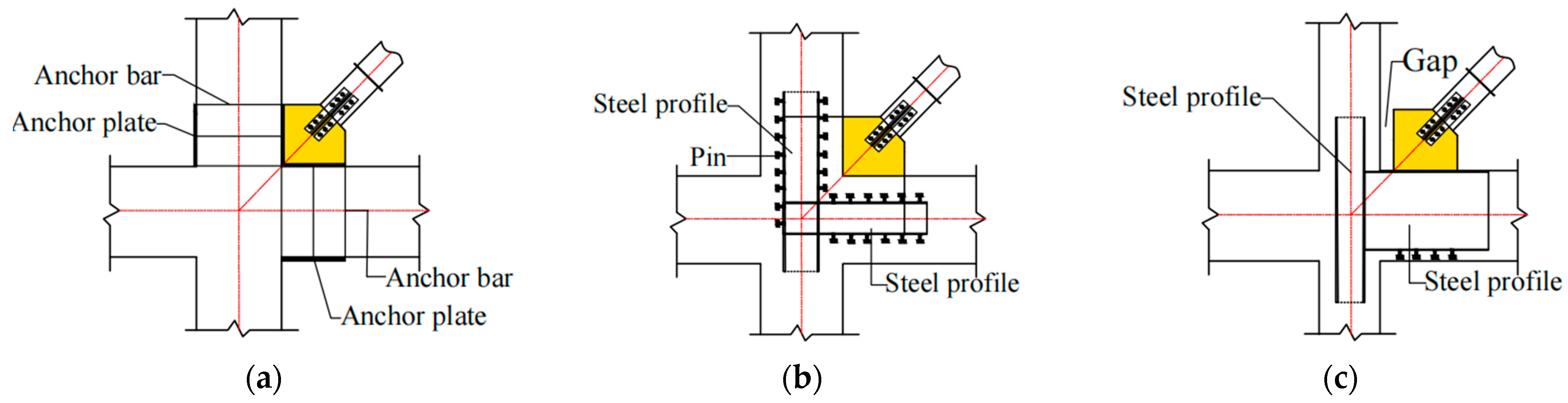
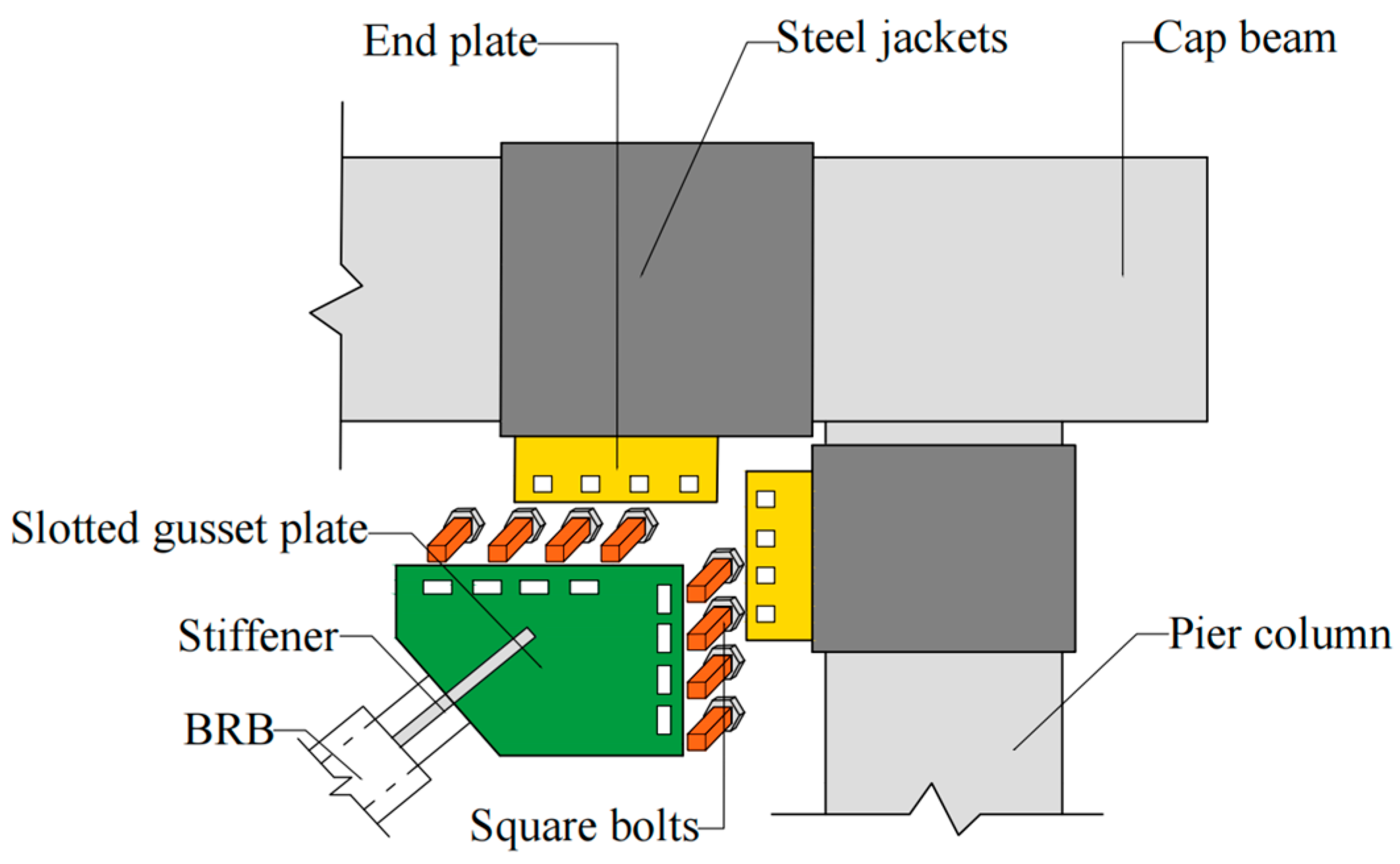
2. Bolted Gusset Connection
2.1. Configuration
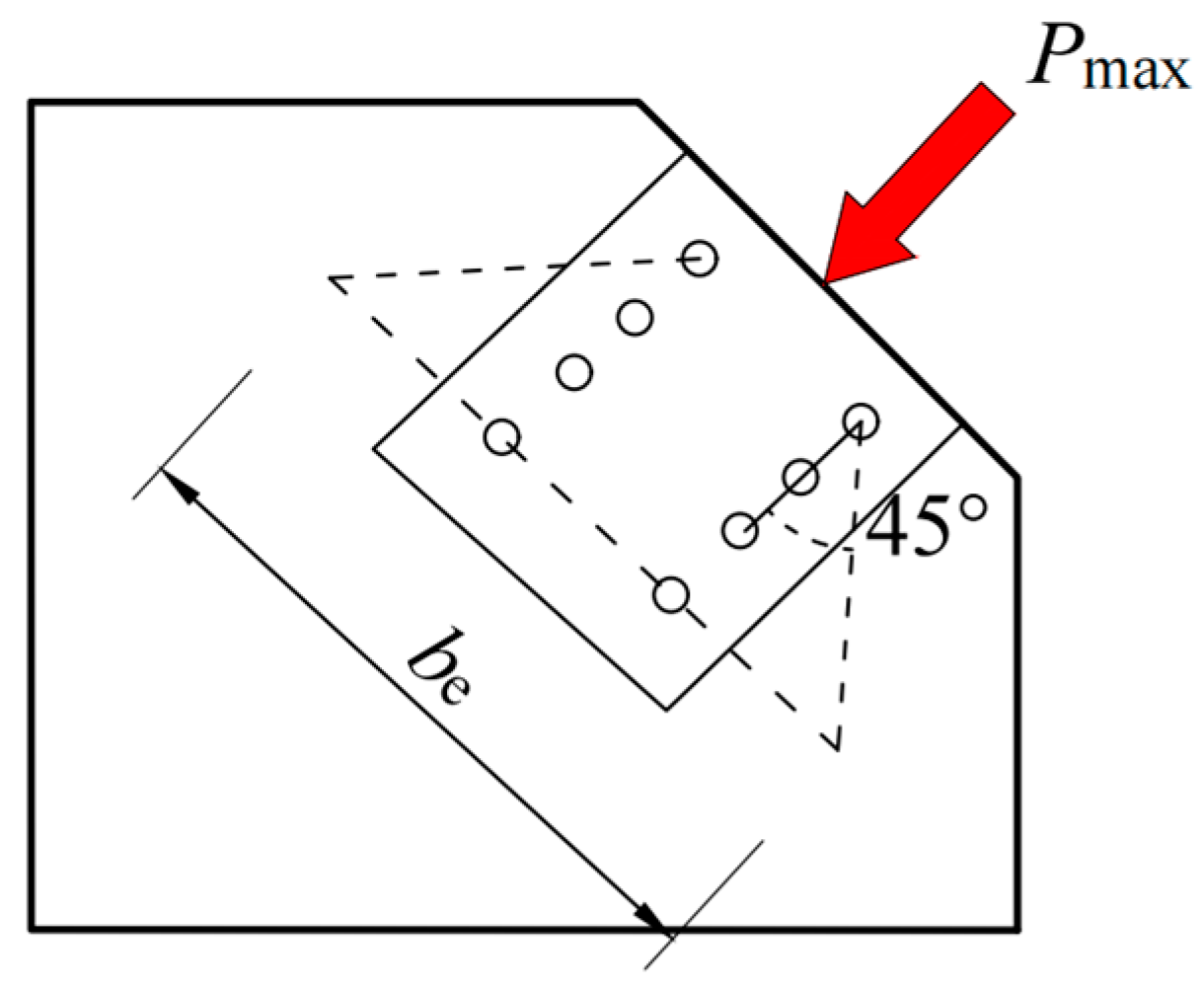
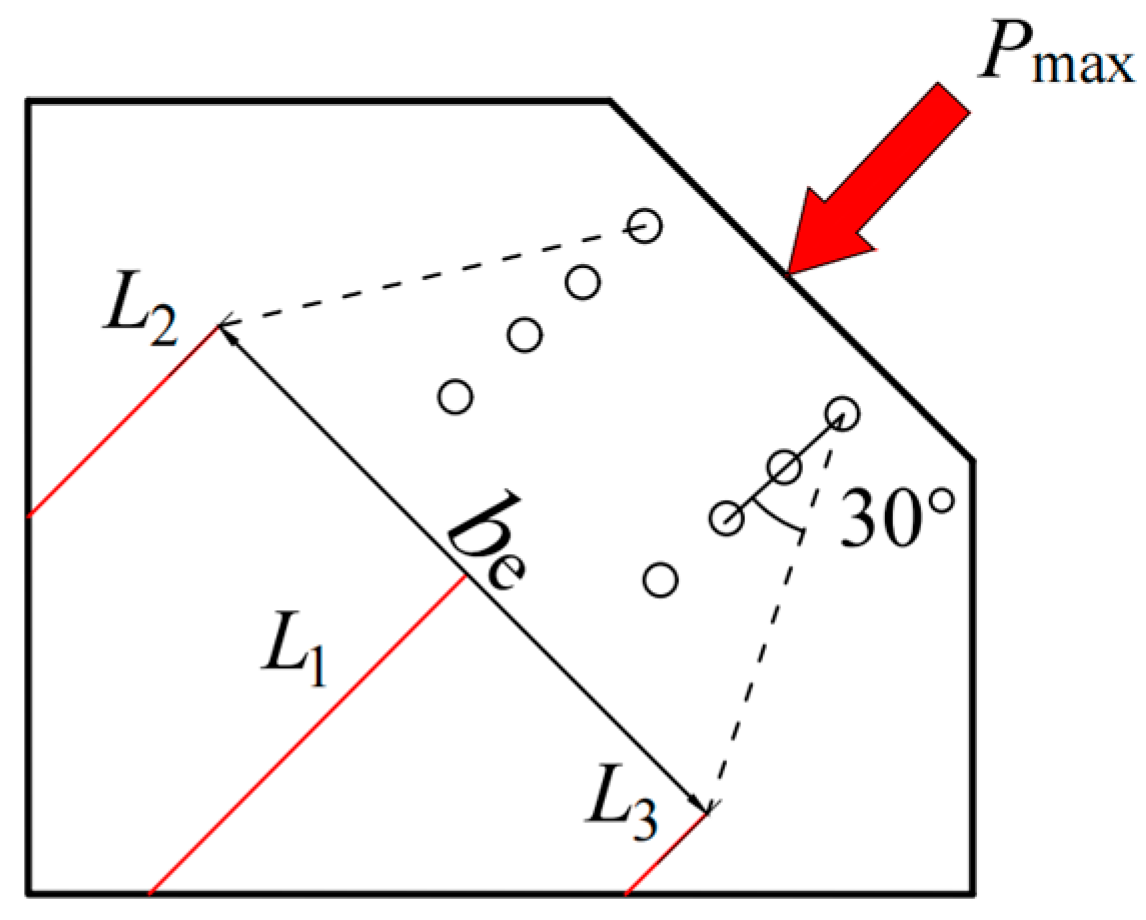
2.2. Design of Bolted Gusset Connection
3. Numerical Study
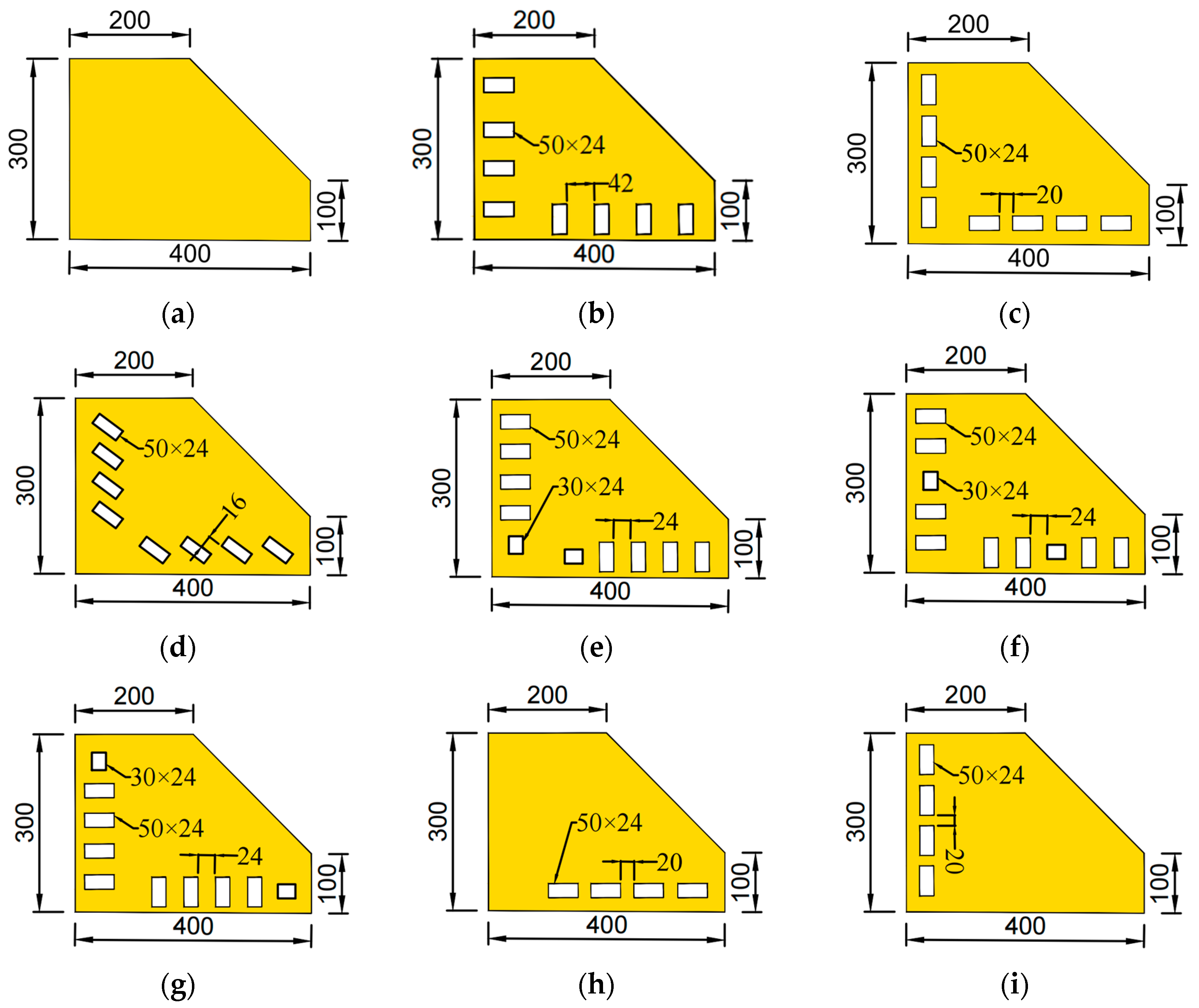
3.1. Parameters Design
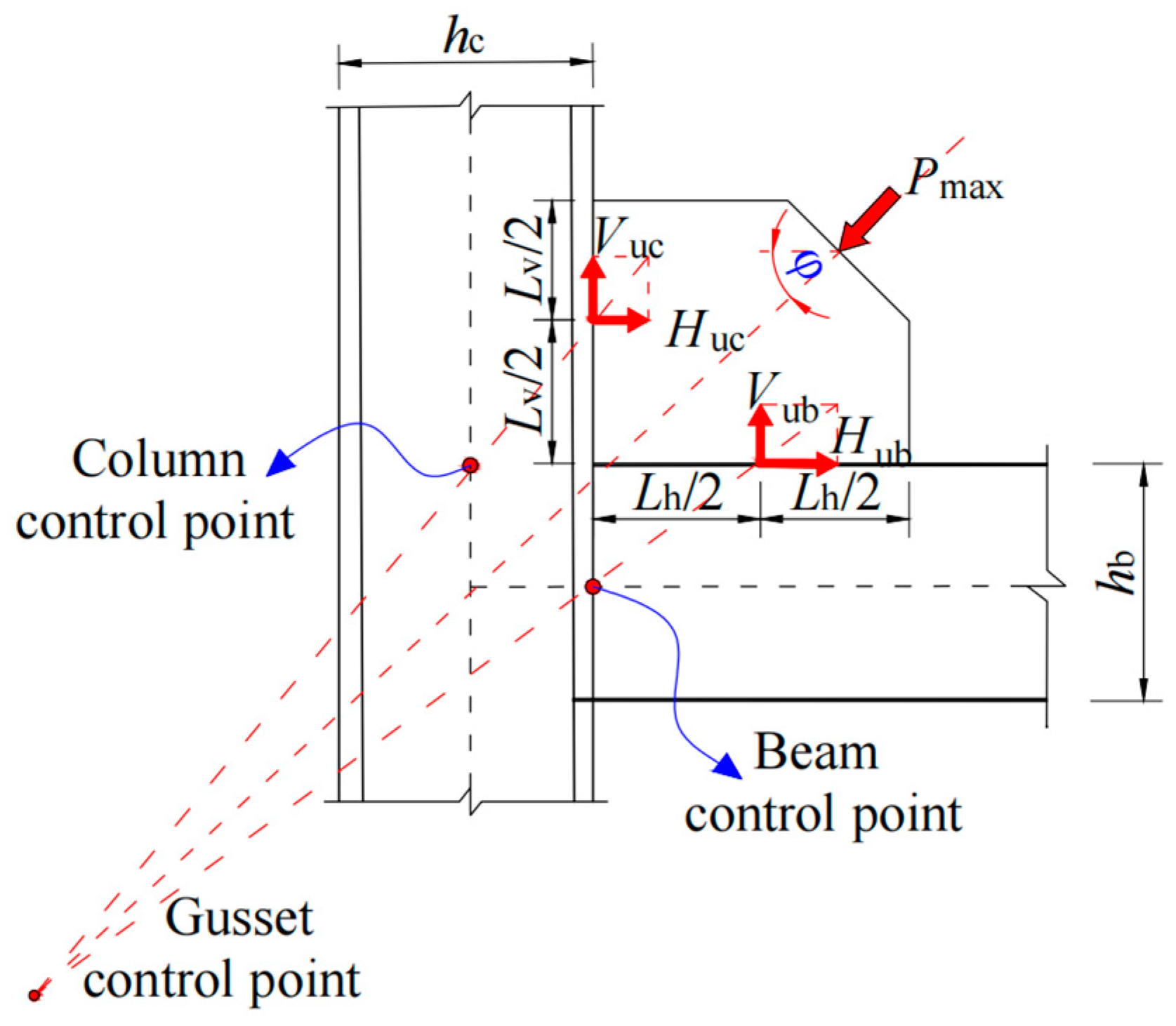
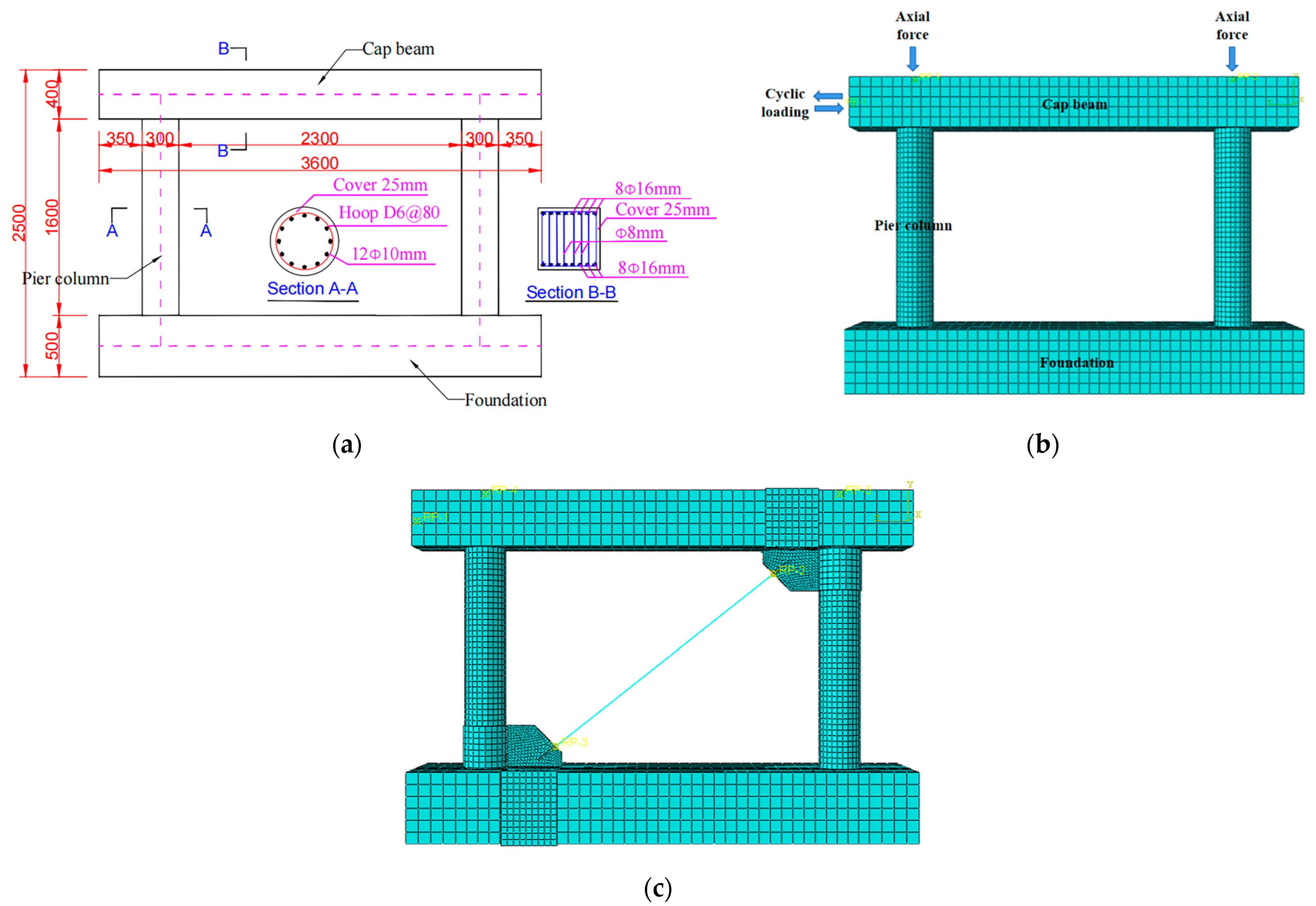
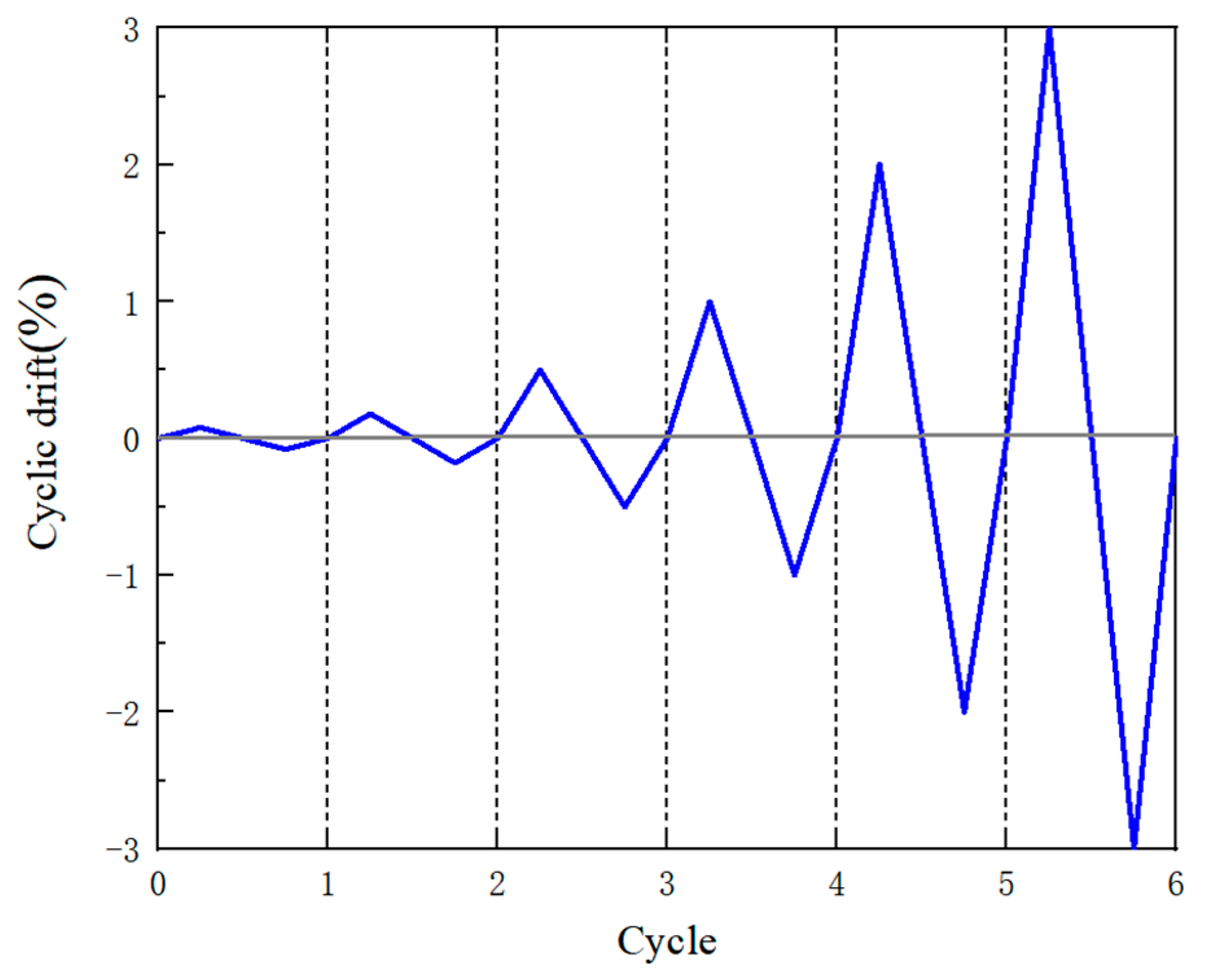
3.2. Finite Element Model
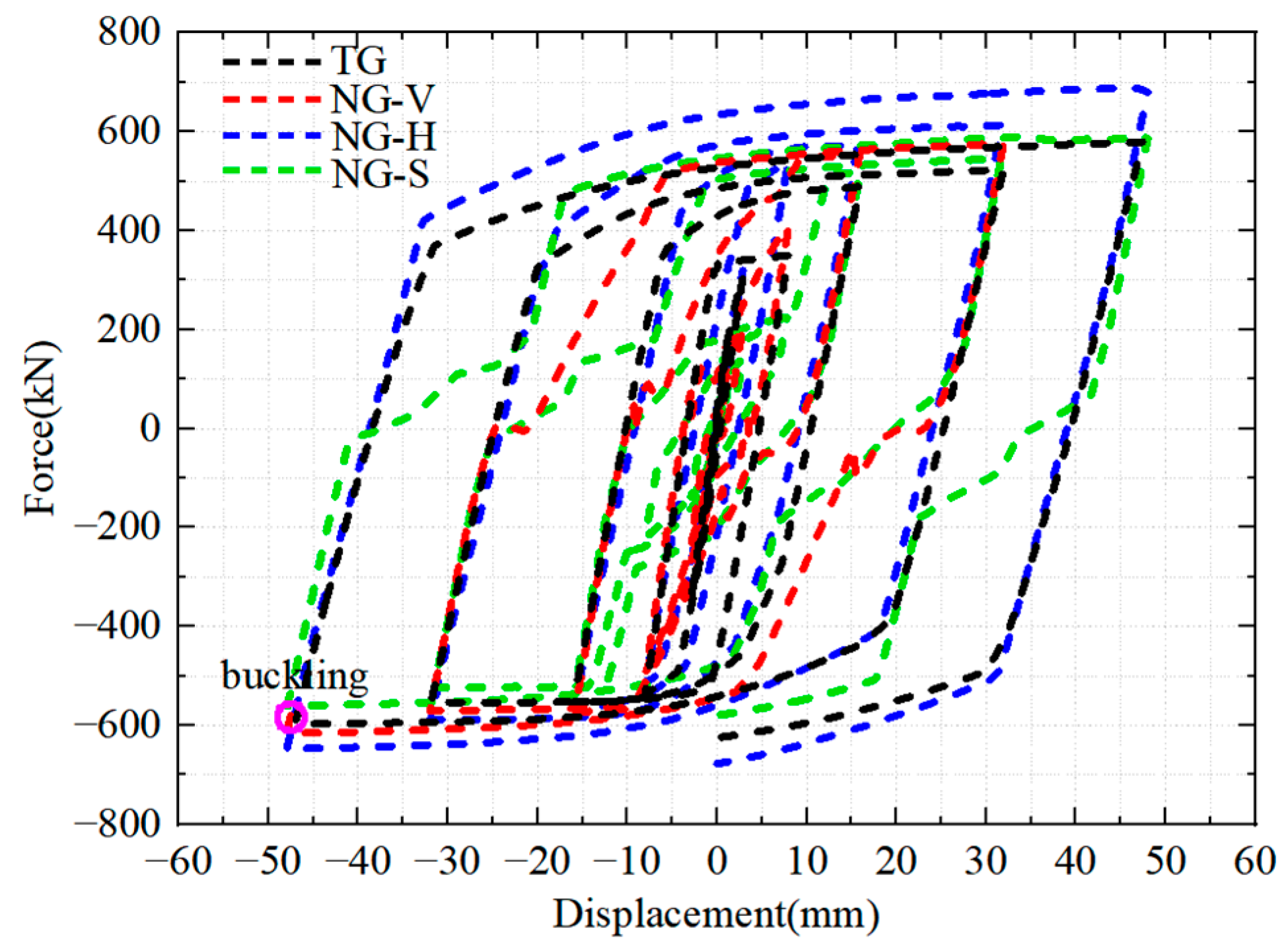
4. Results and Discussion
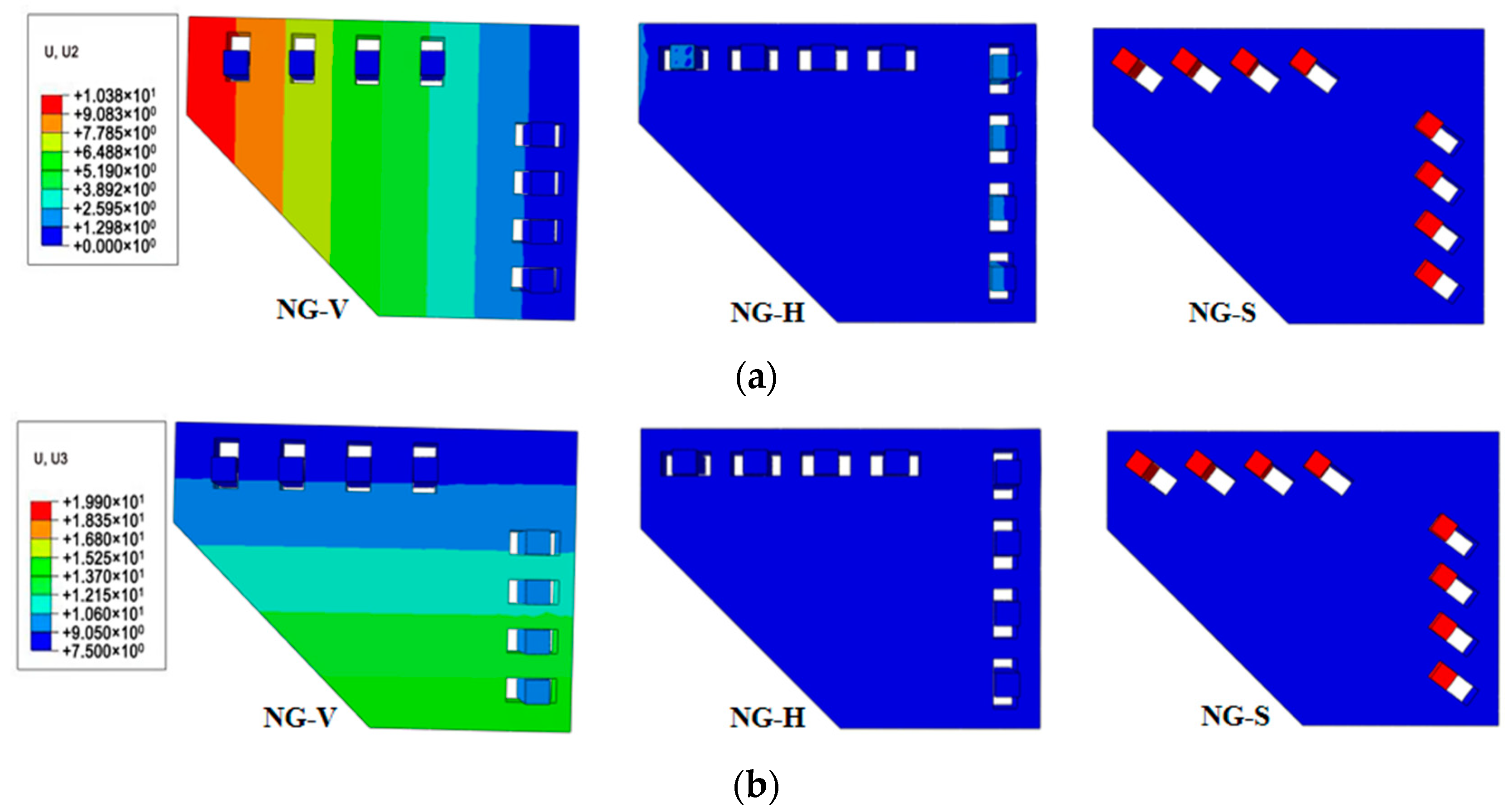
4.1. Slot Direction
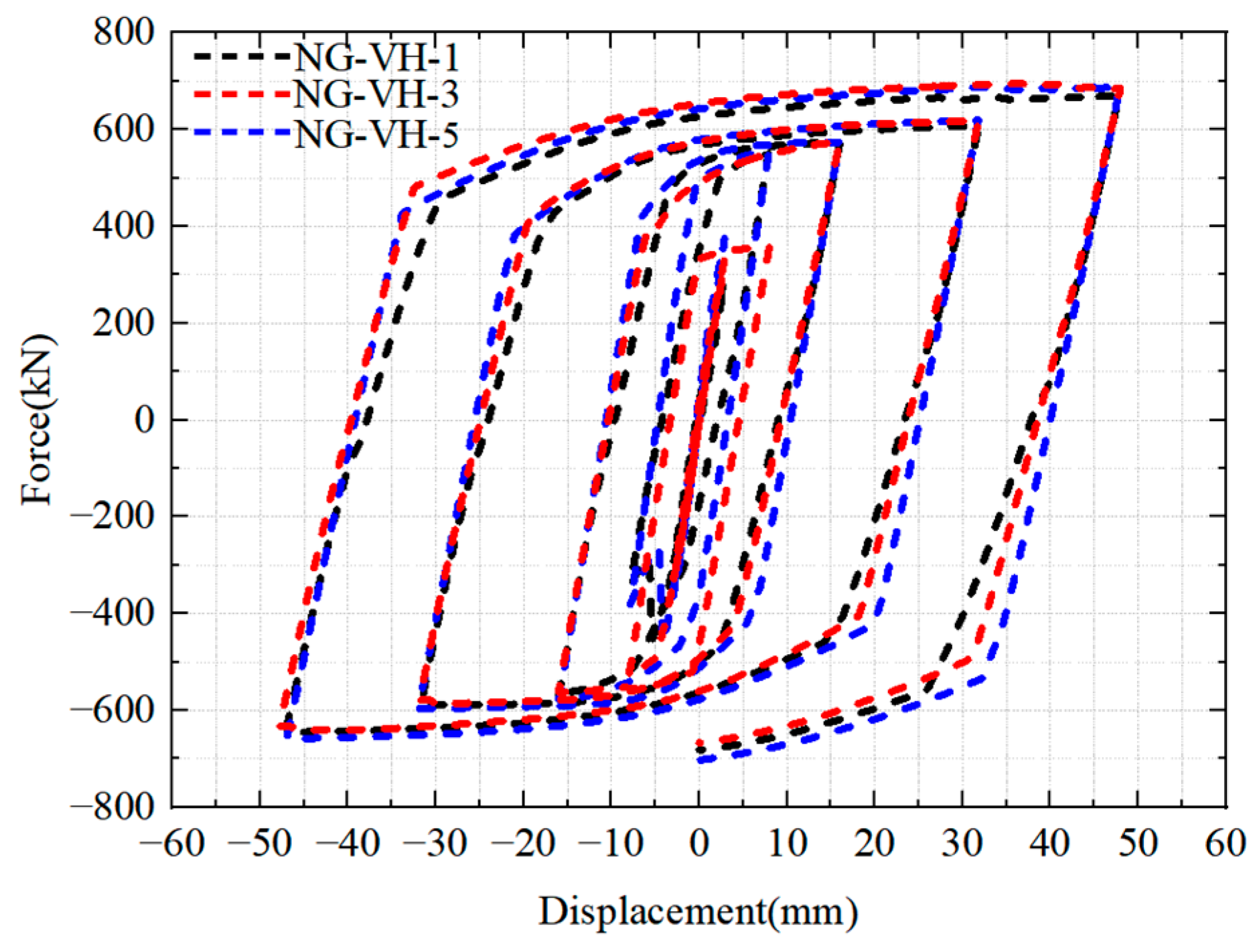
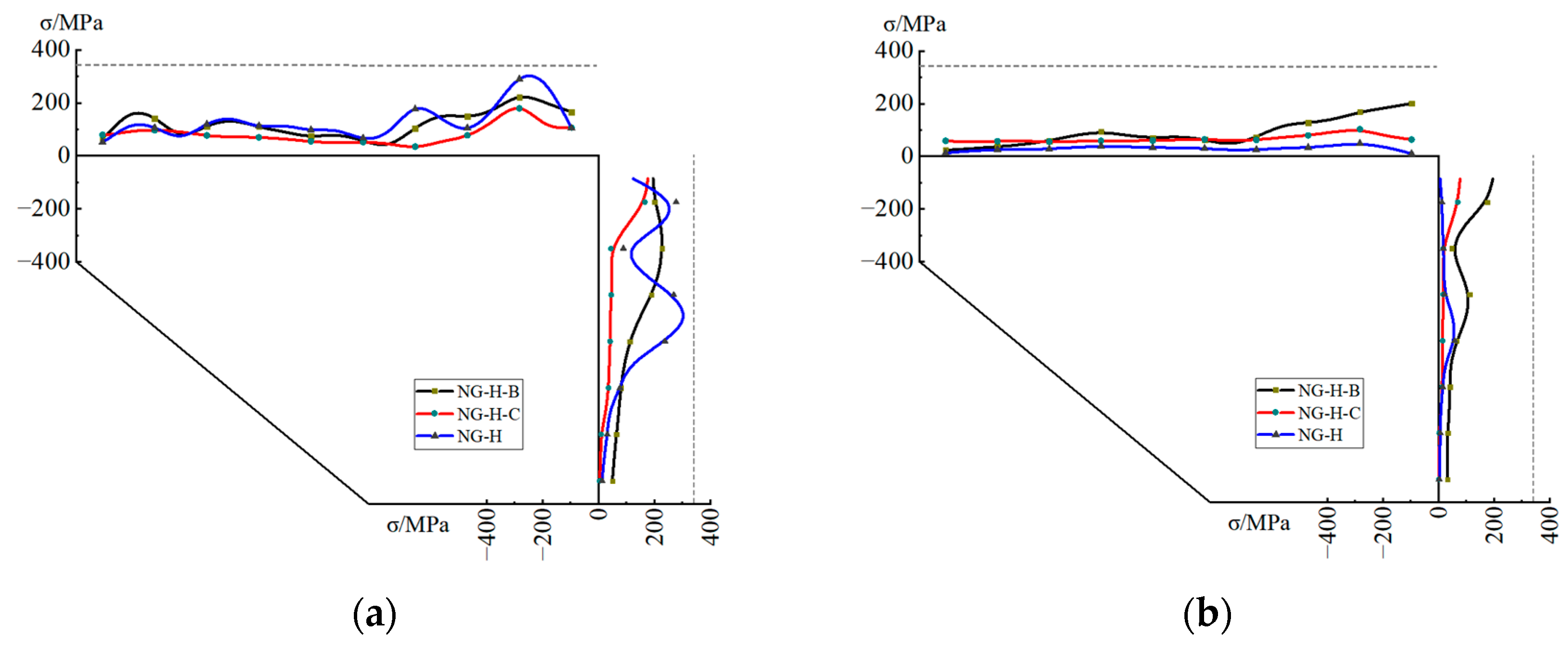
4.2. Position of the Bolt Sliding Parallel to the Gusset Interface
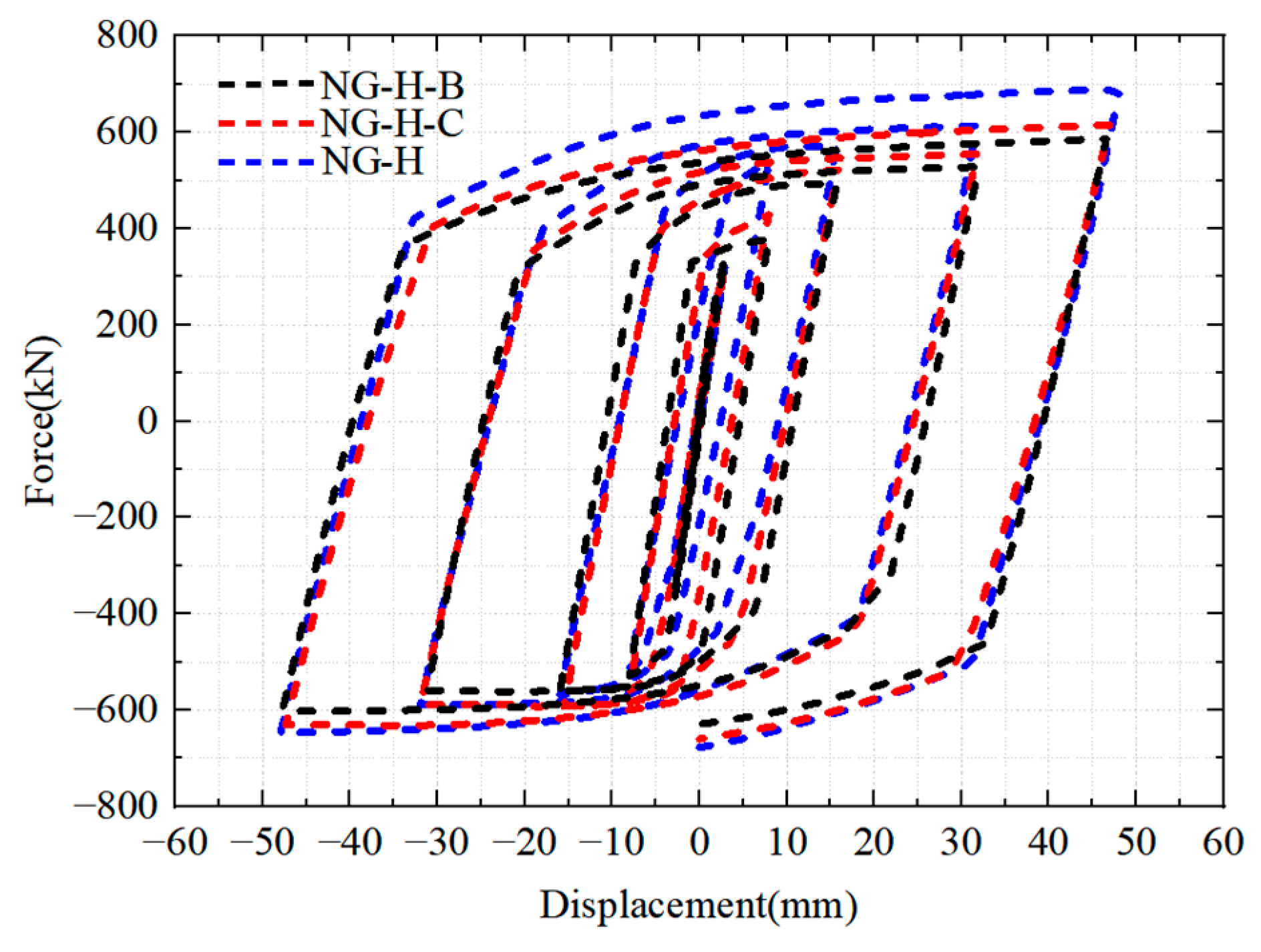
4.3. One-Sided Sliding Bolt
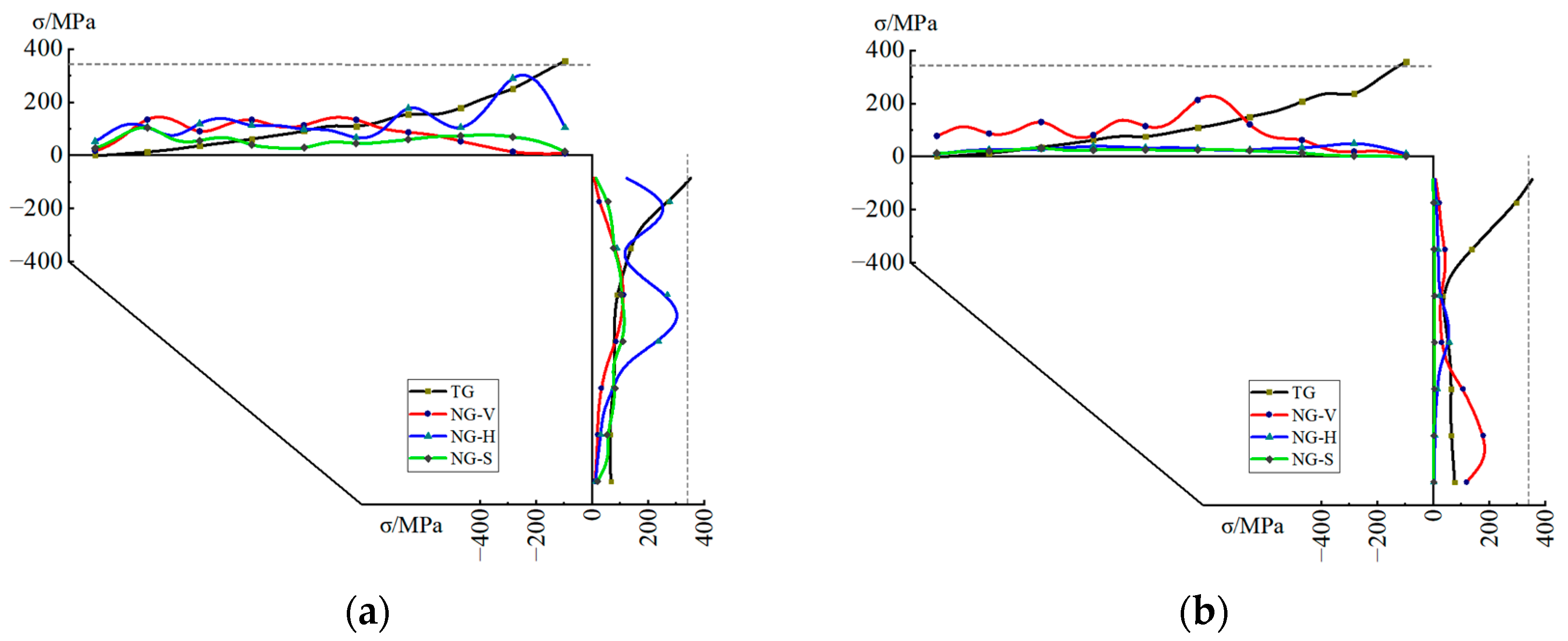
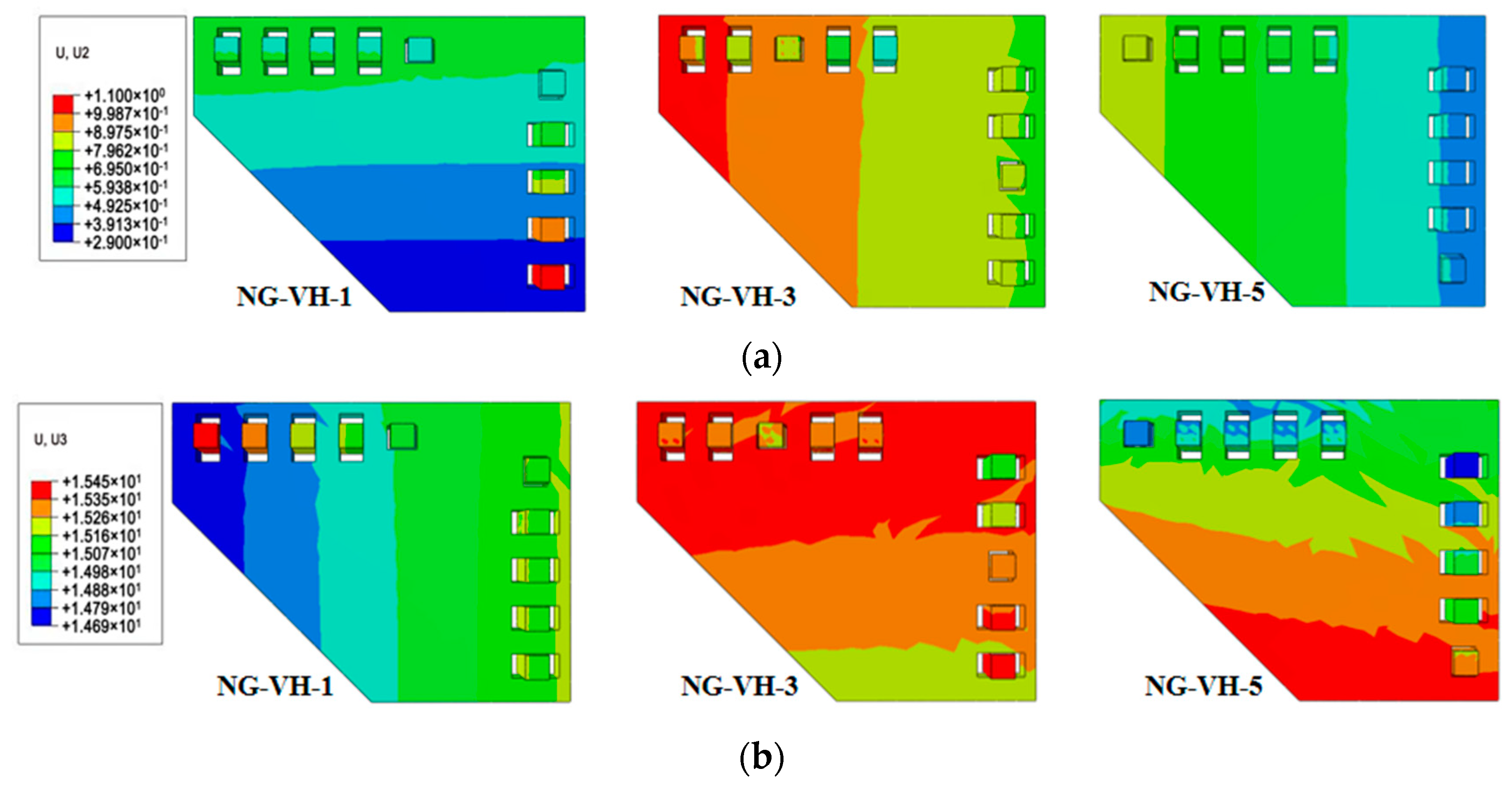
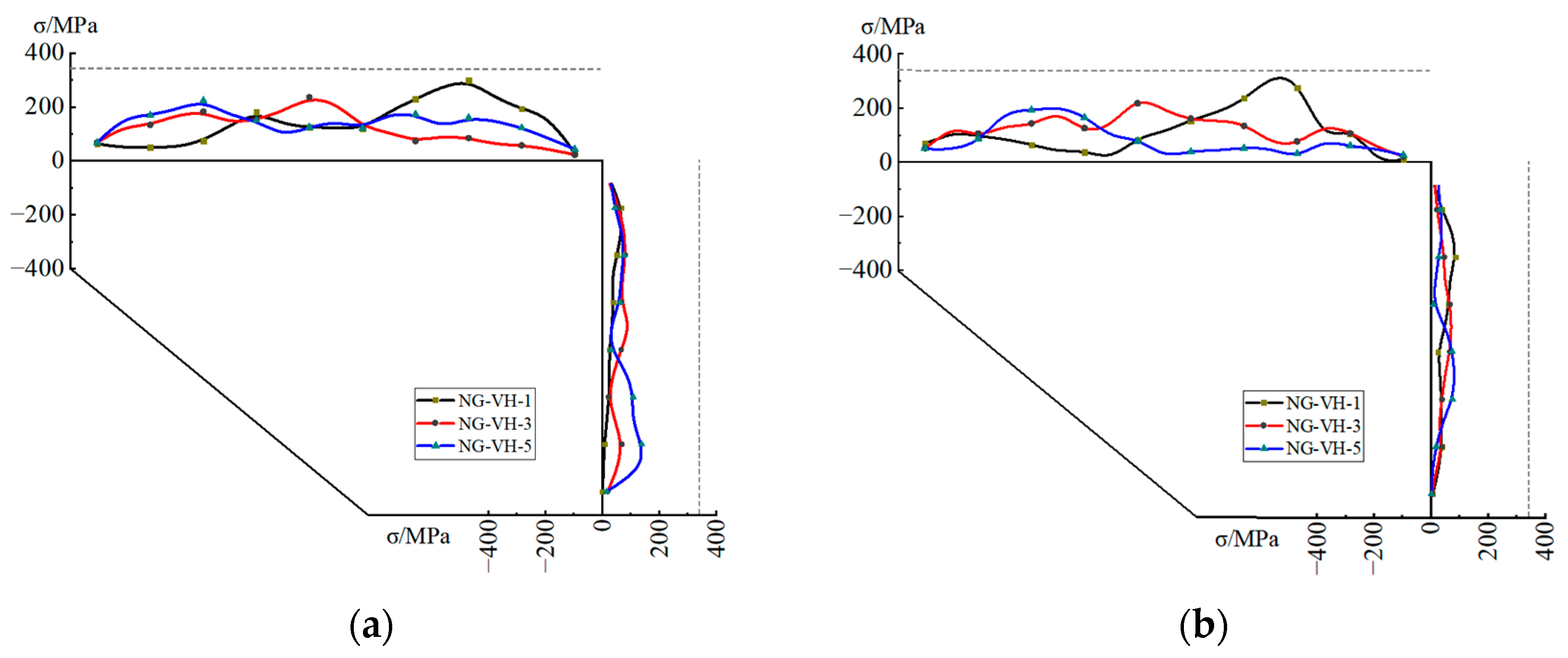
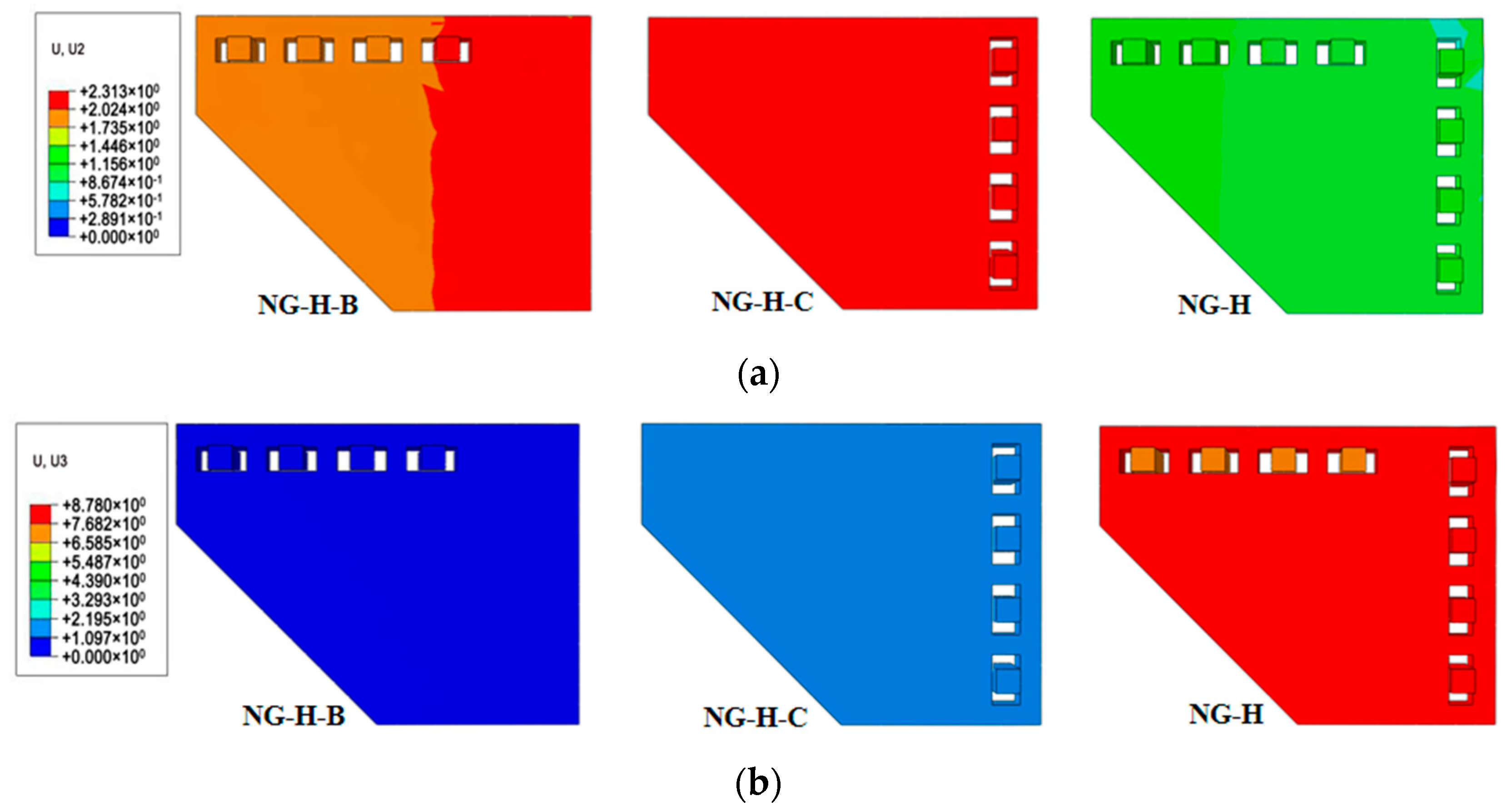
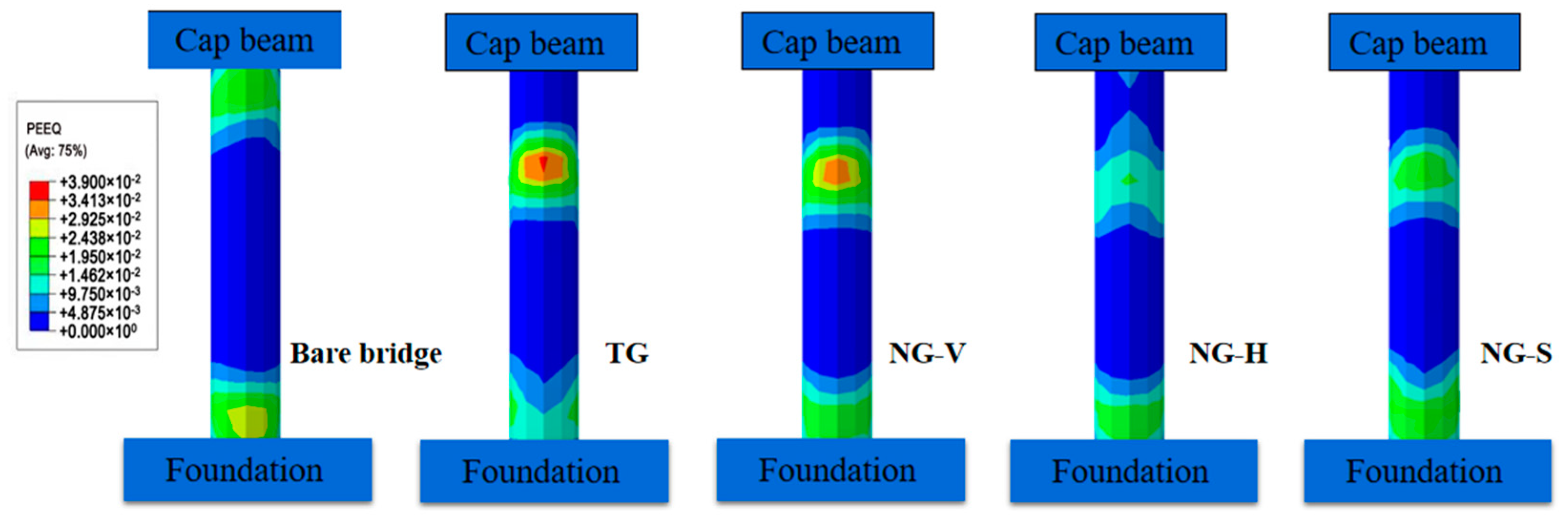
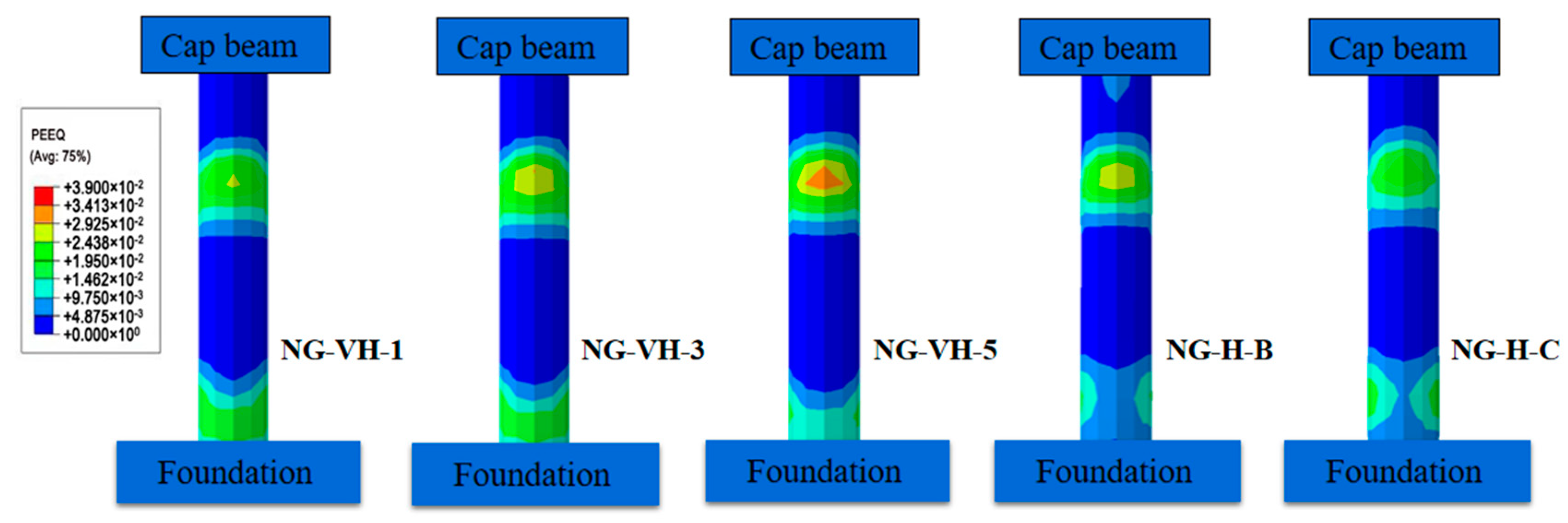
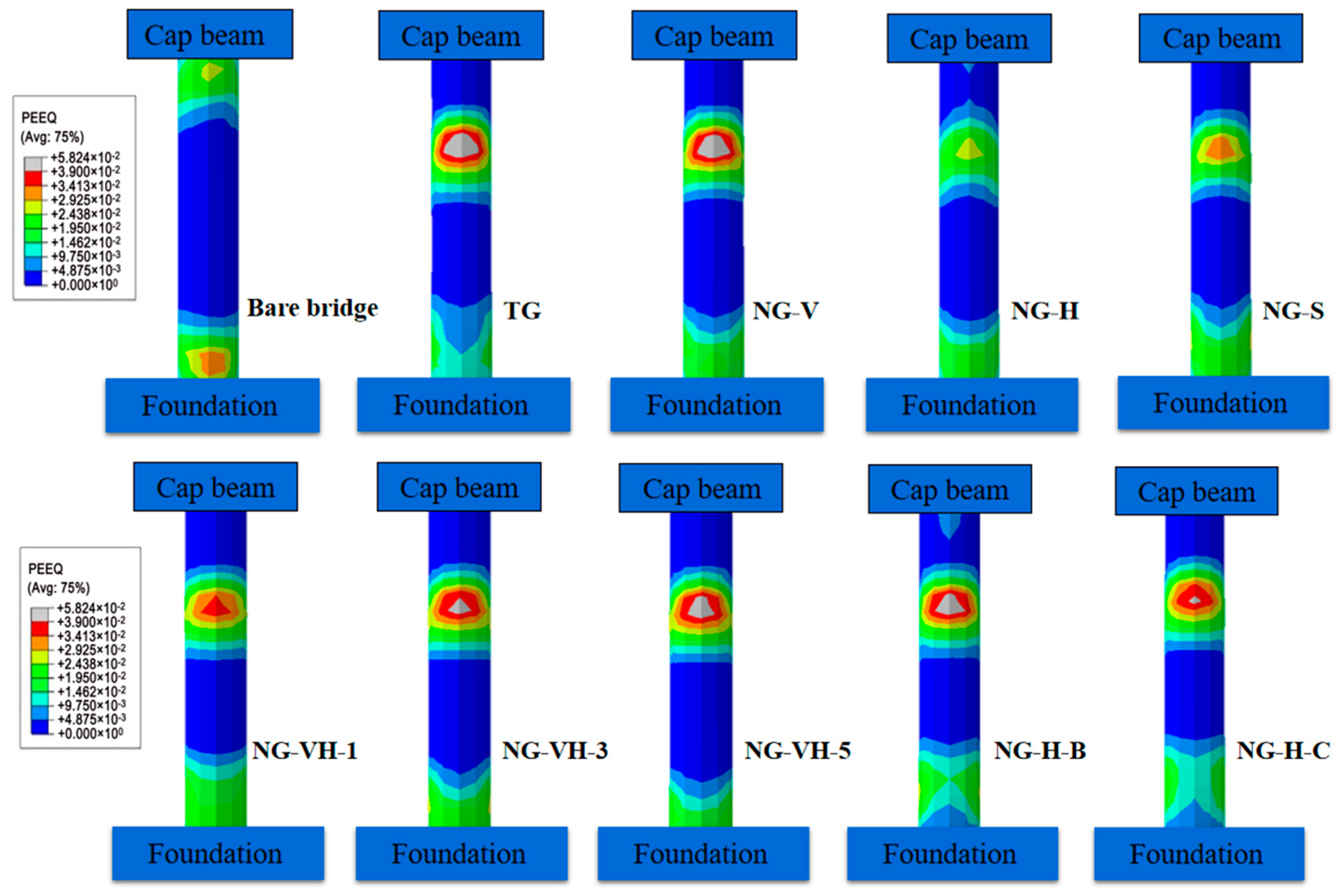
4.4. Cumulative Equivalent Plastic Strain near Column Ends
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, R.; Qiu, C.X.; Hao, D.X. Seismic response analysis of multi-story steel frames using BRB and SCB hybrid bracing system. Appl. Sci. 2020, 10, 284. [Google Scholar] [CrossRef] [Green Version]
- Sosorburam, P.; Yamaguchi, E. Seismic retrofit of steel truss bridge using buckling restrained damper. Appl. Sci. 2019, 9, 2791. [Google Scholar] [CrossRef] [Green Version]
- Freddi, F.; Tubaldi, E.; Zona, A.; Dall’Asta, A. Seismic performance of dual systems coupling moment-resisting and buckling-restrained braced frames. Earthq. Eng. Struct. Dyn. 2021, 50, 329–353. [Google Scholar] [CrossRef]
- Naqi, A.; Roy, T.; Saito, T. Time-dependent damage estimation of a high-rise steel building equipped with buckling-restrained brace under a series of earthquakes and winds. Appl. Sci. 2021, 11, 9253. [Google Scholar] [CrossRef]
- Zhang, A.L.; Wang, H.W.; Jiang, Z.Q.; Guo, K.; Niu, Z.Y. Numerical simulation analysis of double yield points assembled buckling-restrained brace with replaceable inner core. Structures 2022, 35, 1278–1294. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Dou, C.; Guo, Y.L.; Zhang, A.L. Theoretical study on design methods for pinned assembled BRB with flat core. Eng. Struct. 2017, 133, 1–13. [Google Scholar] [CrossRef]
- Zhao, J.X.; Wu, B.; Ou, J.P. Flexural demand on pin-connected buckling-restrained braces and design recommendations. J. Struct. Eng. 2012, 138, 1398–1415. [Google Scholar] [CrossRef]
- El-Bahey, S.; Bruneau, M. Buckling restrained braces as structural fuses for the seismic retrofit of reinforced concrete bridge bents. Eng. Struct. 2011, 33, 1052–1061. [Google Scholar] [CrossRef]
- Upadhyay, A.; Pantelides, C.P.; Ibarra, L. Residual drift mitigation for bridges retrofitted with buckling restrained braces or selfcentering energy dissipation devices. Eng. Struct. 2019, 199, 109663. [Google Scholar] [CrossRef]
- Xiang, N.; Alam, M.S. Displacement-based seismic design of bridge bents retrofitted with various bracing devices and their seismic fragility assessment under near-fault and far-field ground motions. Soil. Dyn. Earthq. Eng. 2019, 119, 75–90. [Google Scholar] [CrossRef]
- Shi, Y.; Zhong, Z.; Qin, H. Toggle buckling-restrained brace systems and a corresponding design method for the seismic retrofit of bridge bents. Eng. Struct. 2020, 221, 110996. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Z.; Fan, X. Seismic design and performance analysis of bridge bents retrofitted with multistage buckling-restrained braces. Structures 2023, 49, 779–791. [Google Scholar] [CrossRef]
- Chou, C.C.; Liu, J.H.; Pham, D.H. Steel buckling-restrained braced frames with single and dual corner gusset connections: Seismic tests and analyses. Earthq. Eng. Struct. Dyn. 2012, 41, 1138–1156. [Google Scholar] [CrossRef]
- Lin, P.C.; Tsai, K.C.; Wu, A.C.; Chuang, M.C. Seismic design and test of gusset connections for buckling-restrained braced frames. Earthq. Eng. Struct. Dyn. 2014, 43, 565–587. [Google Scholar] [CrossRef]
- Bai, J.L.; He, J.; Li, C.; Jin, S.S.; Yang, H. Experimental investigation on the seismic performance of a novel damage-control replaceable RC beam-to-column joint. Eng. Struct. 2022, 267, 114692. [Google Scholar] [CrossRef]
- Chen, H.M.; Bai, J.L. Seismic performance evaluation of buckling-restrained braced RC frames considering stiffness and strength requirements and low-cycle fatigue behaviors. Eng. Struct. 2022, 267, 114692. [Google Scholar] [CrossRef]
- Fahnestock, L.A.; Ricles, J.M.; Sause, R. Experimental evaluation of a large-scale buckling-restrained braced frame. ASCE J. Struct. Eng. 2007, 133, 1205–1214. [Google Scholar] [CrossRef]
- Fatemi, H.; Aghakouchak, A.A. Design and numerical evaluation of two innovative moment-free beam-gusset-column connections for BRBFs. J. Constr. Steel Res. 2021, 184, 106837. [Google Scholar] [CrossRef]
- Dong, H.; Du, X.; Han, Q. Hysteretic performance of RC double-column bridge piers with self-centering buckling-restrained braces. Bull. Earthq. Eng. 2019, 17, 3255–3281. [Google Scholar] [CrossRef]
- Dong, H.; Du, X.; Han, Q.; Bi, K. Numerical studies on the seismic performances of RC two-column bent bridges with self-centering energy dissipation braces. J. Struct. Eng. 2020, 146, 04020038. [Google Scholar] [CrossRef]
- Bazaez, R.; Dusicka, P. Cyclic behavior of reinforced concrete bridge bent retrofitted with buckling restrained braces. Eng. Struct. 2016, 119, 34–48. [Google Scholar] [CrossRef]
- Bazaez, R.; Dusicka, P. Performance assessment of multi-column RC bridge bents seismically retrofitted with buckling-restrained braces. Bull. Earthq. Eng. 2018, 16, 2135–2160. [Google Scholar] [CrossRef]
- Zhao, J.X.; Zhang, J.G.; Song, J.Y. Sliding gusset connections for improved seismic performance of BRB-RC frame: Damage-control design and subassemblage tests. Eng. Struct. 2023, 282, 115828. [Google Scholar] [CrossRef]
- Muir, L.S. Designing compact gussets with the uniform force method. Engineering 2008, 45, 13. [Google Scholar]
- Whitmore, R.E. Experimental Investigation of Stresses in Gusset Plates; Bulletin No. 16. Engineering Experiment Station; The University of Tennessee: Knoxville, TN, USA, 1952. [Google Scholar]
- American Institute of Steel Construction (AISC). Specification for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 2016. [Google Scholar]
- Thornton, W.A. Bracing connections for heavy construction. Engineering 1984, 21, 139–148. [Google Scholar]
- GB 50017-2017; Standard for Design of Steel Structures. China Building Industry Press: Beijing, China, 2018.
- Abaqus, S. CAE 6.20 User’s Manual Dassault; Systémes Inc. Provid.: Johnston, RI, USA, 2020; Volume IV. [Google Scholar]
- GB 50011-2010; Code for Seismic Design of Building. China Building Industry Press: Beijing, China, 2010.
- Fang, C.; Yam, M.C.H.; Zhou, X. Post-buckling resistance of gusset plate connections: Behaviour, strength, and design considerations. Eng. Struct. 2015, 99, 9–27. [Google Scholar] [CrossRef]


| Material | Elastic Modulus (GPa) | Yield Strength (MPa) | Ultimate Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| Q235 | 210 | 235 | 428 | 0.3 |
| Q345 | 210 | 345 | 540 | 0.3 |
| S690Q | 210 | 794 | 856 | 0.3 |
| HRB335 | 210 | 392 | 498 | 0.3 |
| Model | Yielding Load (kN) | Lateral Stiffness (kN/mm) | Cumulative Energy Dissipation (kN·m) | Vmax (kN) | Vmin (kN) |
|---|---|---|---|---|---|
| TG | 537.69 | 89.37 | 189.1 | 579.06 | −596.08 |
| NG-V | 482.94 | 80.72 | 79.17 | 575.88 | −616.19 |
| NG-H | 526.34 | 91.49 | 207.4 | 680.43 | −647.58 |
| NG-S | 531.53 | 79.58 | 142.9 | 586.83 | −560.25 |
| NG-VH-1 | 565.28 | 82.39 | 203.1 | 670.13 | −645.73 |
| NG-VH-3 | 550.16 | 88.29 | 208.4 | 684.24 | −640.23 |
| NG-VH-5 | 573.75 | 95.43 | 215.8 | 687.42 | −658.82 |
| NG-H-B | 539.73 | 95.88 | 191.9 | 586.27 | −600.04 |
| NG-H-C | 511.17 | 93.05 | 197.6 | 615.04 | −630.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Ji, P.; Cheng, P.; Xu, G. Numerical Study on Seismic Performance of Buckling-Restrained Braced Double-Pier RC Bridge with Bolted Gusset Connections. Appl. Sci. 2023, 13, 4391. https://doi.org/10.3390/app13074391
Lu J, Ji P, Cheng P, Xu G. Numerical Study on Seismic Performance of Buckling-Restrained Braced Double-Pier RC Bridge with Bolted Gusset Connections. Applied Sciences. 2023; 13(7):4391. https://doi.org/10.3390/app13074391
Chicago/Turabian StyleLu, Junkai, Pengfei Ji, Peifeng Cheng, and Guoshan Xu. 2023. "Numerical Study on Seismic Performance of Buckling-Restrained Braced Double-Pier RC Bridge with Bolted Gusset Connections" Applied Sciences 13, no. 7: 4391. https://doi.org/10.3390/app13074391
APA StyleLu, J., Ji, P., Cheng, P., & Xu, G. (2023). Numerical Study on Seismic Performance of Buckling-Restrained Braced Double-Pier RC Bridge with Bolted Gusset Connections. Applied Sciences, 13(7), 4391. https://doi.org/10.3390/app13074391







