Short-Term Power Load Forecasting Based on an EPT-VMD-TCN-TPA Model
Abstract
1. Introduction
- (1)
- Since the load series has a certain fundamental trend, the fundamental trend dominates the direction of the load series over time. The established EPT can accurately extract the fundamental trend of the load series, thus improving the accuracy of short-term load forecasting.
- (2)
- The adopted VMD decomposes the residual fluctuation series into several subseries with different center frequencies, which further reduces the non-smoothness of the fluctuation series. The number of decompositions of the VMD is determined using the ratio of residual energy, which makes the decomposed subsequences smoother.
- (3)
- The experimental results show that the EPT-VMD hybrid decomposition method proposed in this paper is effective for load prediction.
- (4)
- The TCN-TPA network is used for the prediction of individual components so that the temporal characteristics of these sequences can be better extracted. The temporal pattern attention mechanism incorporated in the TCN network can better assign different weights to different variables at the same time step compared to the ordinary attention mechanism. The temporal pattern attention mechanism enhances the impact of temporal attributes of multivariate load sequences on load prediction.
- (5)
- In further experiments, FE was used to analyze the complexity of the IMF components and to reconstruct these components using similar entropy values. The experimental results show that the EPT-VMD-FE-TCN-TPA reconstructed model using FE has higher operational efficiency compared to the EPT-VMD-TCN-TPA prediction model, but the prediction precision is reduced.
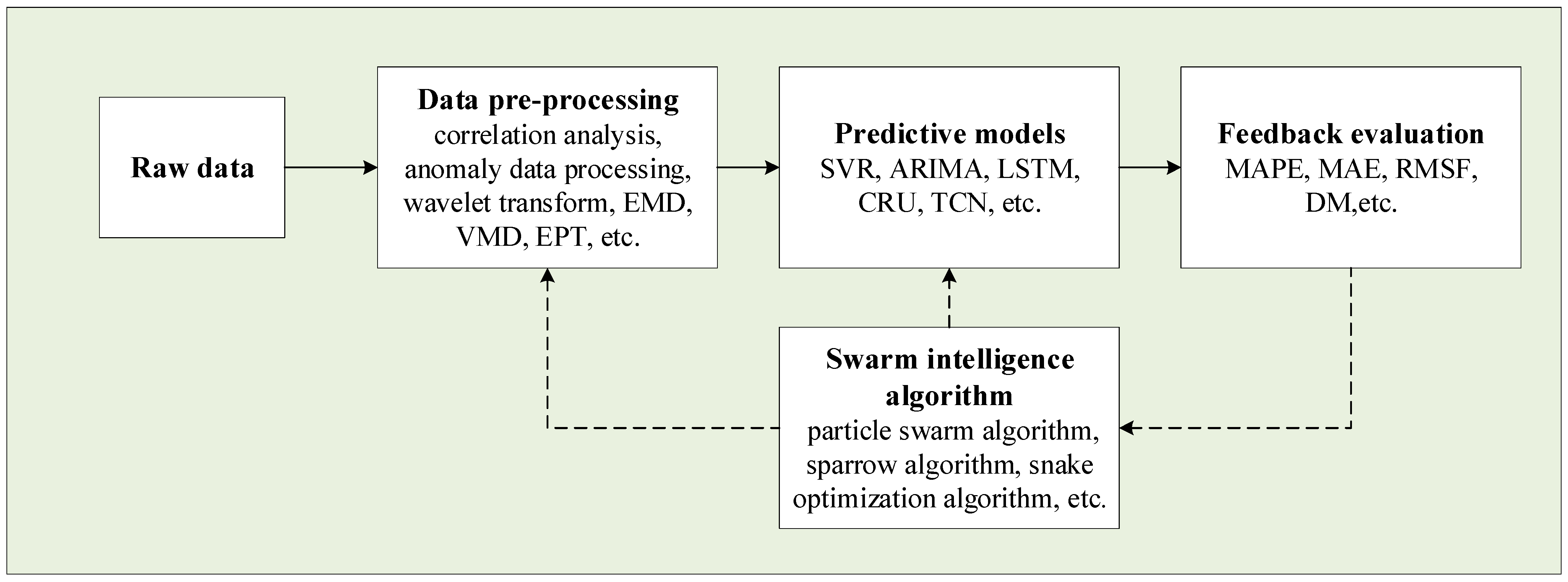
2. Related Theories and Methods
2.1. Ensemble Patch Transformation (EPT)
2.1.1. Patch Process
2.1.2. Ensemble Process
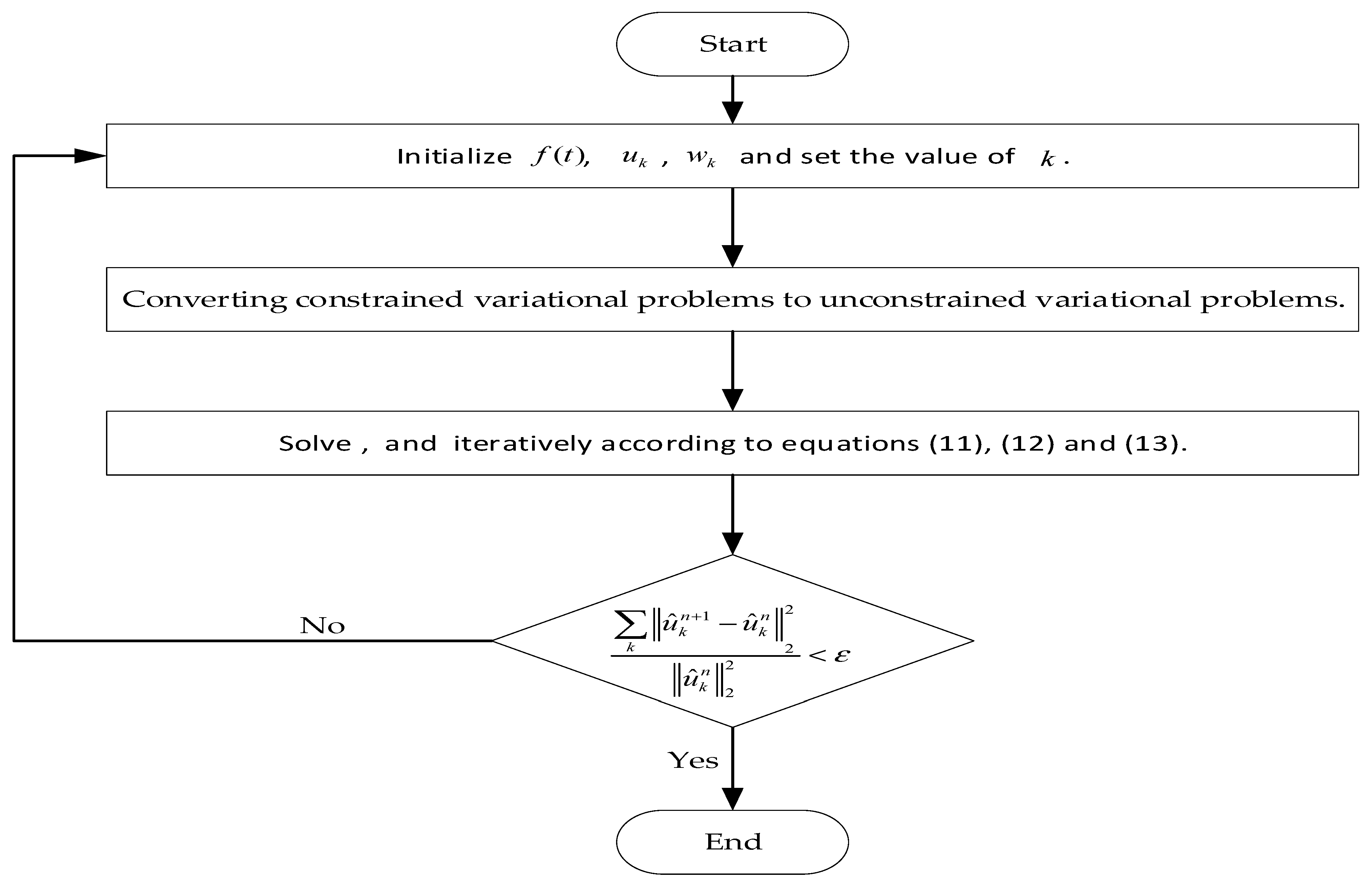
2.2. Variational Modal Decomposition (VMD)
- (1)
- Constructing variational problems.
- (2)
- Transformation of variational problems.
- (3)
- Solve the variational problem.
2.3. Fuzzy Entropy (FE)
- (1)
- Knowing an -dimensional time series , let the phase space dimension be and the phase space vector be:where denotes the spatial mean.
- (2)
- The maximum difference between the corresponding elements of and is defined as the distance .
- (3)
- Introduce the affiliation function as the following equation:where is the similar tolerance boundary width and is the similar tolerance boundary gradient.
- (4)
- Define the function.
- (5)
- Define the function.
- (6)
- When is a finite value, the value of FE can be expressed as Equation (21).
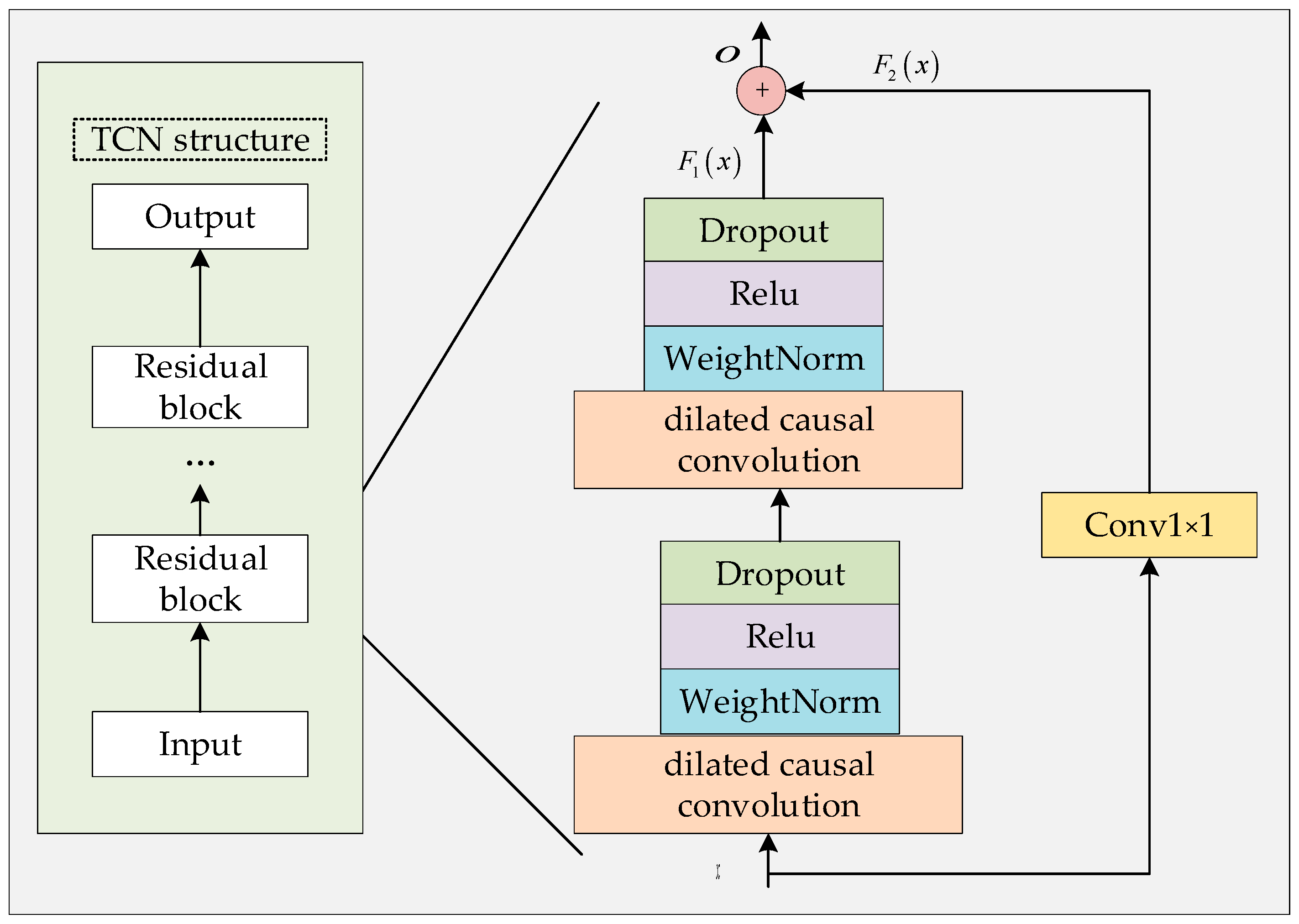
2.4. The Temporal Convolutional Network (TCN)
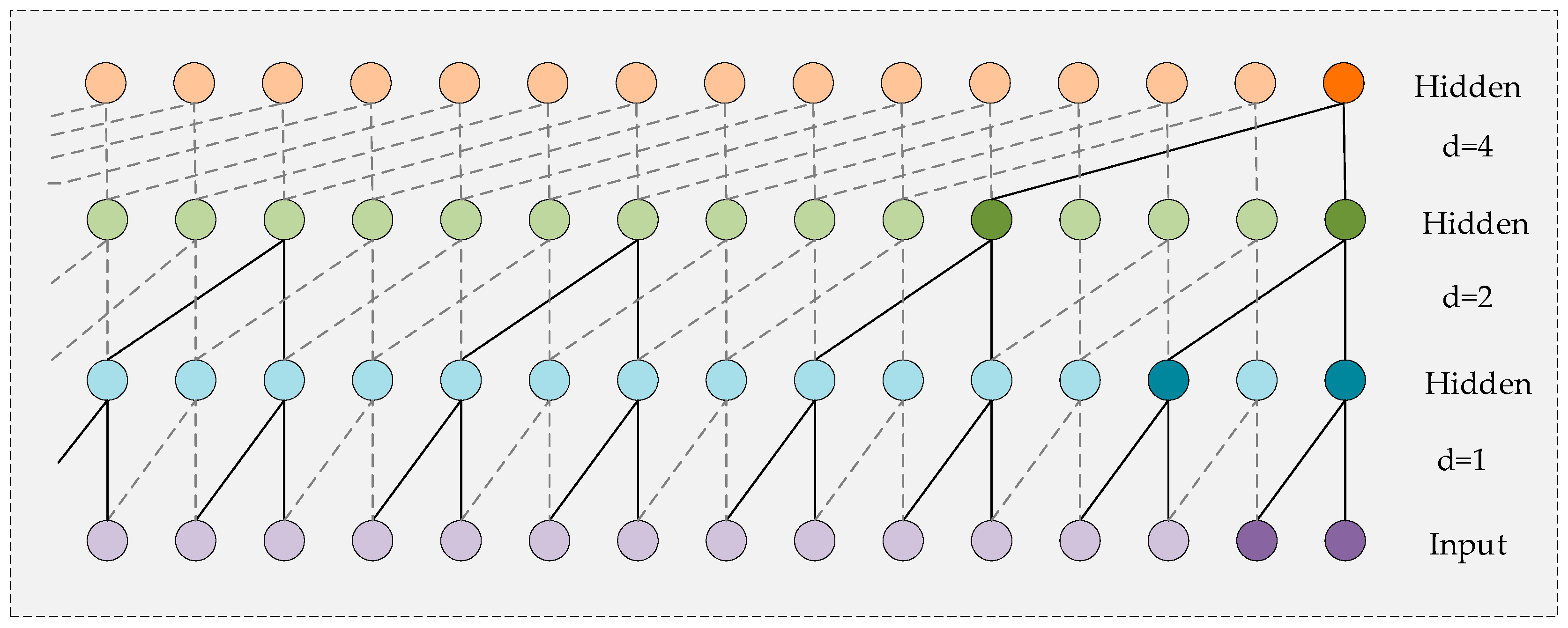
2.4.1. Causal Convolution
2.4.2. Dilated Casual Convolution
2.4.3. Residual Block
2.5. Temporal Pattern Attention (TPA)
- (1)
- The TCN processing time series.
- (2)
- CNN convolution.
- (3)
- The attention weight.
- (4)
- Fusion.
3. The Proposed EPT-VMD-TPA-TCN Model and the Restructured EPT-VMD-FE-TPA-TCN Model
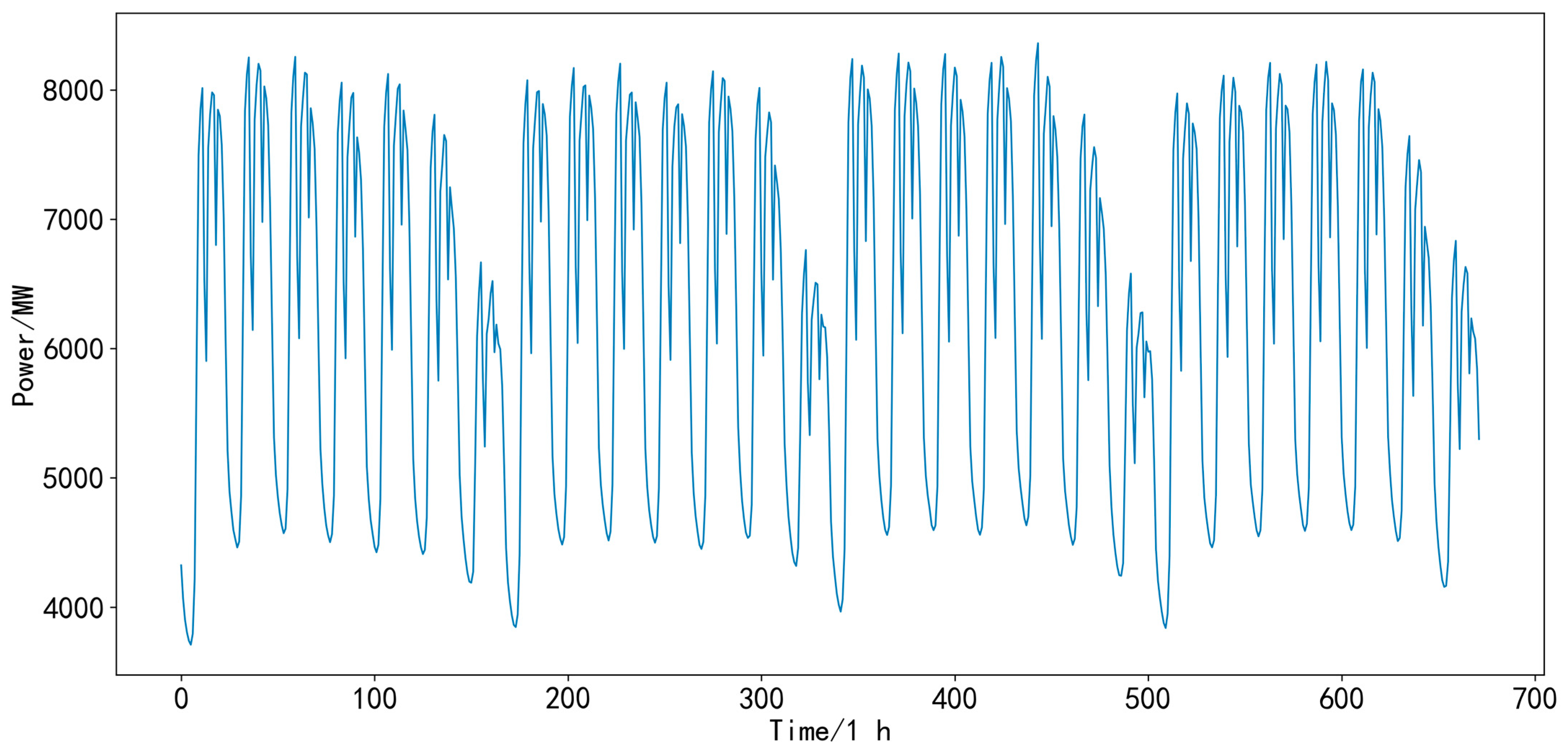
3.1. Experimental Datasets
- (1)
- Dataset (Area 1): 1 January 2012–10 January 2015 (total 1106 days, 106,176 load data collection points).
- (2)
- Training set: data from 1 January 2012–2 June 2014 (884 days, 84,864 load data collection points) were used to train the model.
- (3)
- Test set: 3 June 2014–10 January 2015 (222 days, 21,312 load data sampling points) was used for the evaluation of the model.
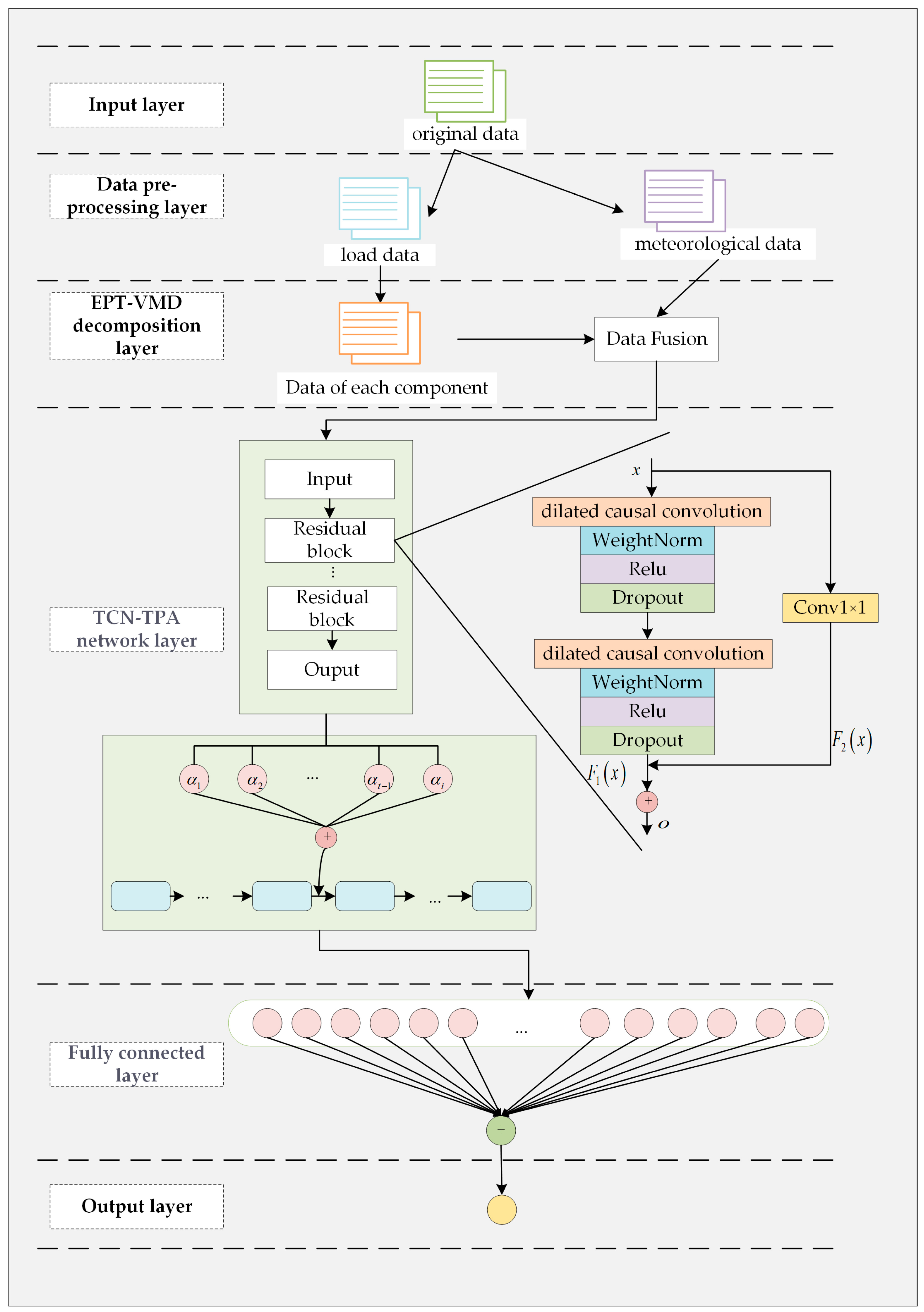
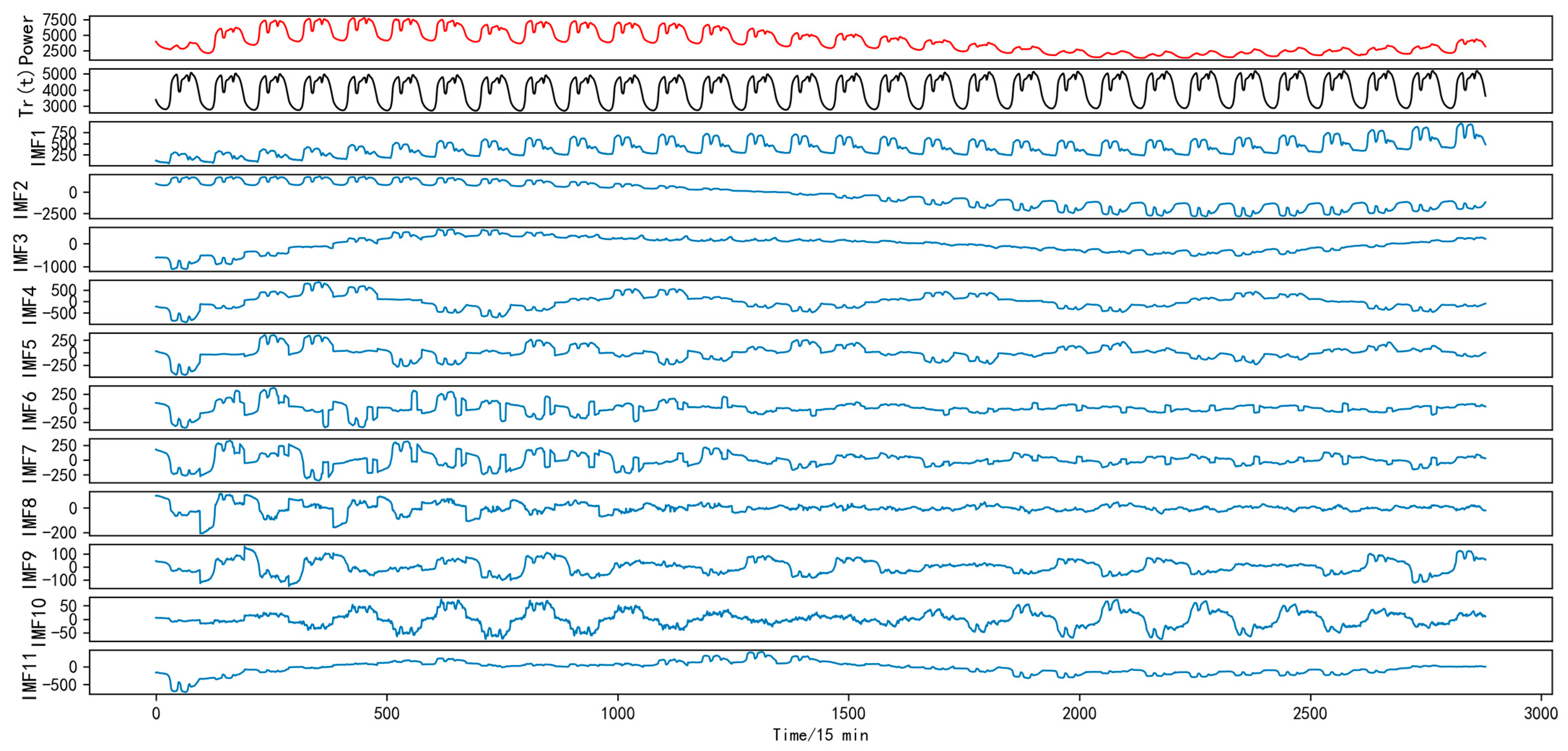
3.2. EPT-VMD Decomposition Layer
3.2.1. EPT Decomposition
3.2.2. VMD
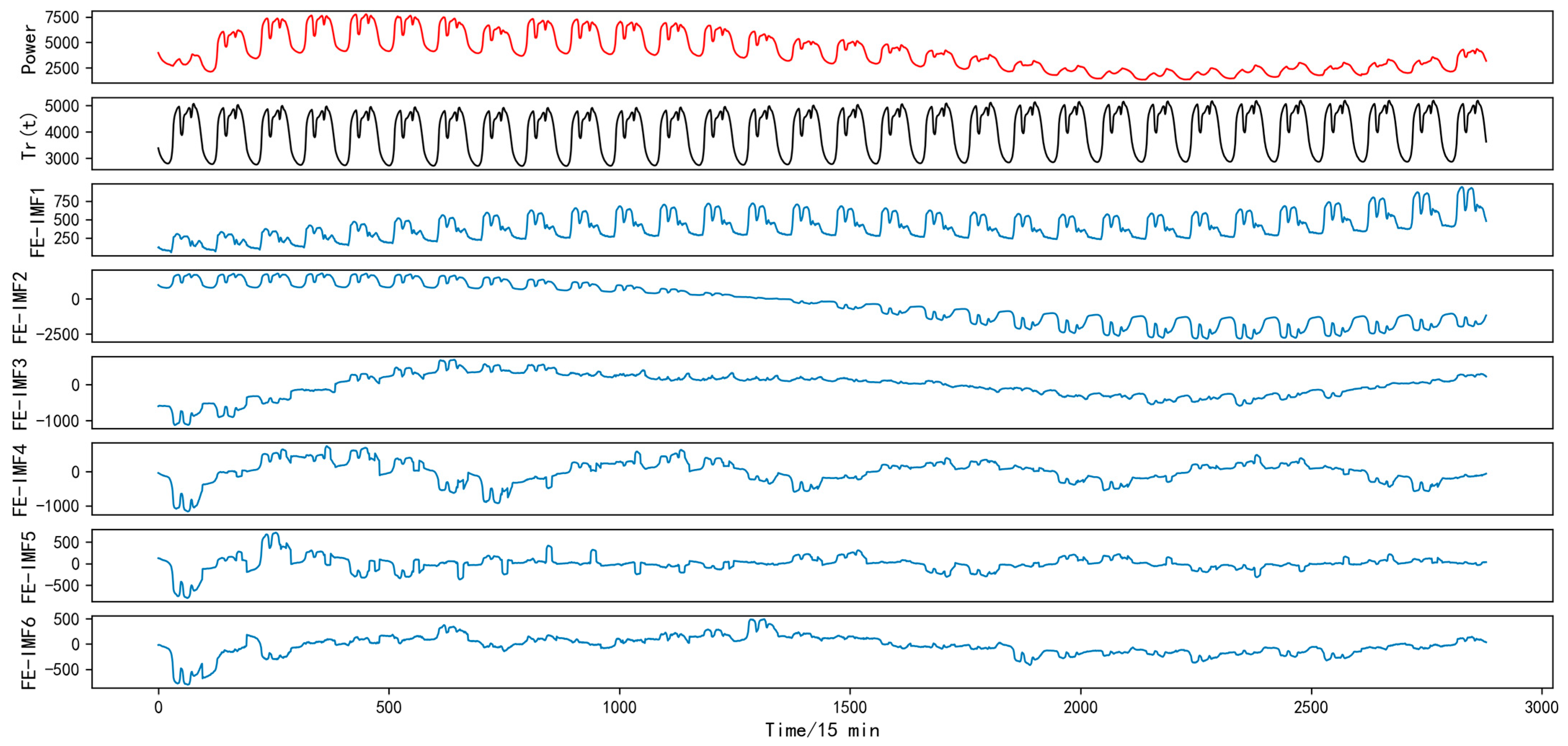
3.3. Sub-Sequence Recombination Layer
3.4. TCN-TPA Network Training and Prediction Layers
3.5. Fully Connected Prediction Result Output Layer
3.6. Workflow of the EPT-VMD-TCN-TPA Model
4. Experiments
4.1. Datasets and Experimental Environment
4.2. Data Normalization
4.3. Error Evaluation Indicators
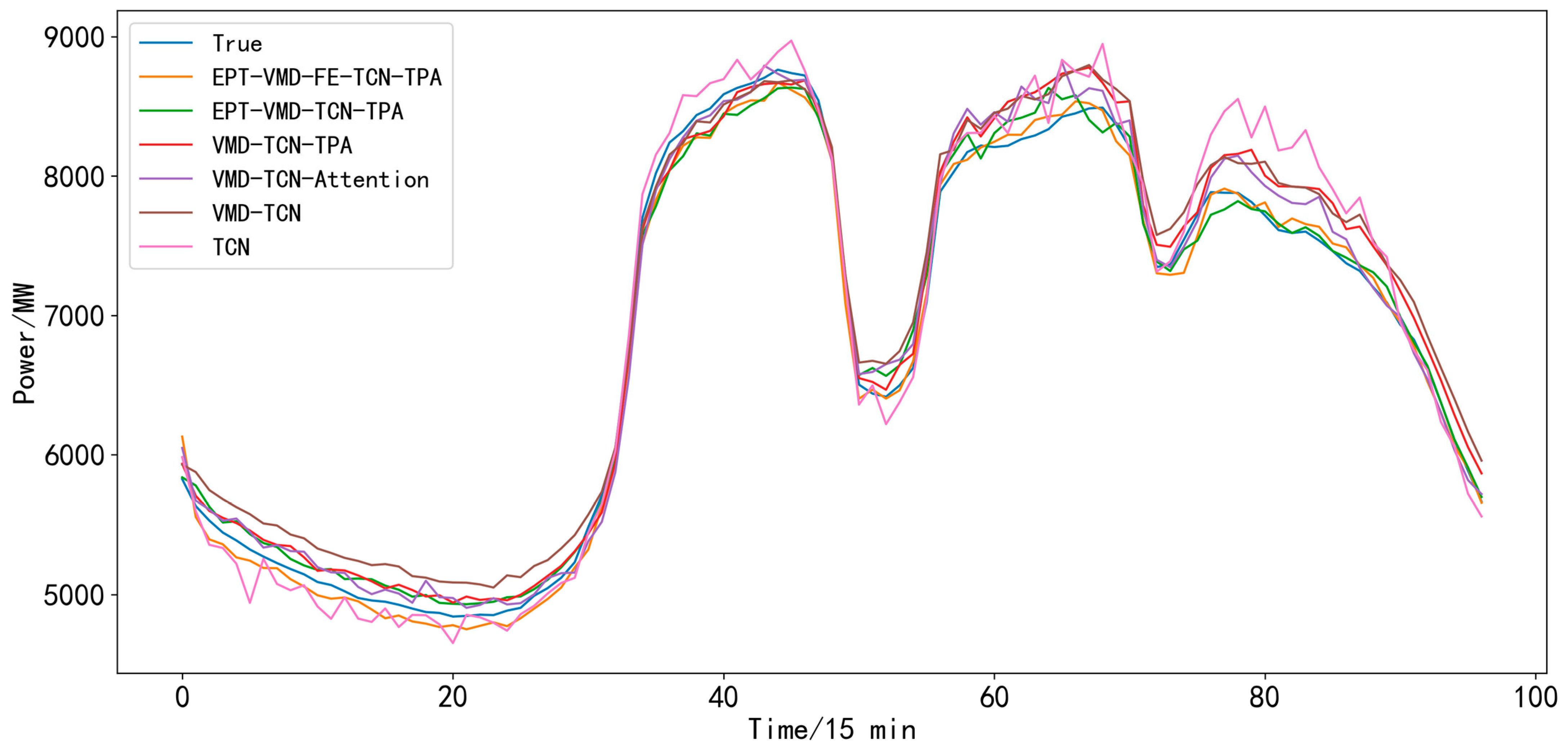
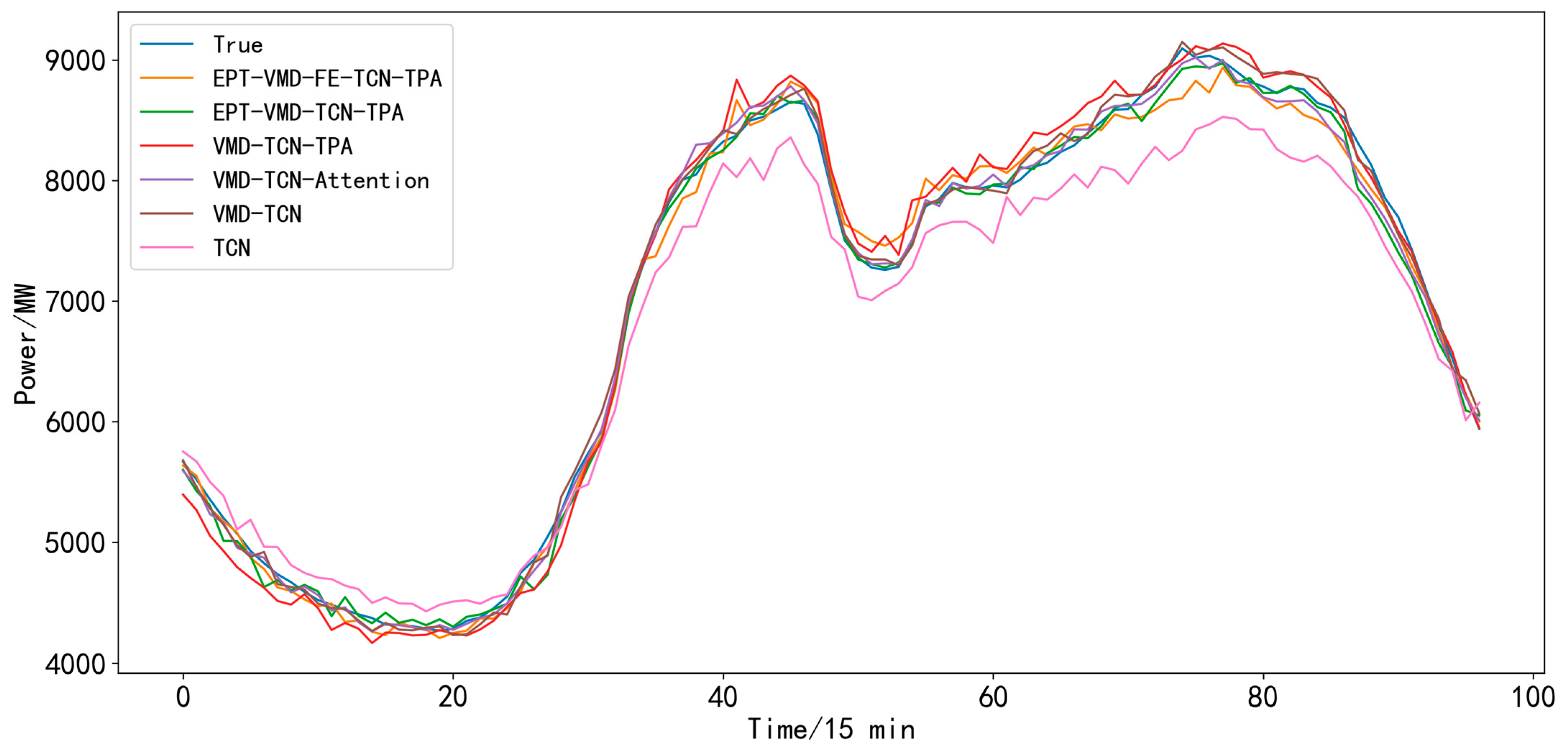
4.4. Ablation Experiments
- (1)
- TCN model [27]: This model is a more advanced model in recent years, which not only can effectively extract the features of nonlinear time series data but also can effectively solve complex problems such as gradient explosion and gradient disappearance during model training.
- (2)
- VMD-TCN model: The load data are firstly decomposed using VMD, after which the dataset is trained and predicted using the TCN network.
- (3)
- VMD-TCN-Attention model: A general attention mechanism is added to the VMD-TCN model.
- (4)
- VMD-TCN-TPA model: Based on the VMD-TCN model, the prediction capability is improved by introducing a temporal pattern attention mechanism, which is especially suitable for handling multi-task temporal prediction.
- (5)
- EPT-VMD-TCN-TPA model: Our proposed final model. Before using the VMD-TCN-TPA model, the EPT method, which extracts the trend components of the load data, is first introduced.
- (6)
- EPT-VMD-FE-TCN-TPA model: This model adds a recombination layer to the proposed EPT-VMD-TCN-TPA model in this paper and merges the similar components of the intermediate processes according to FE values.
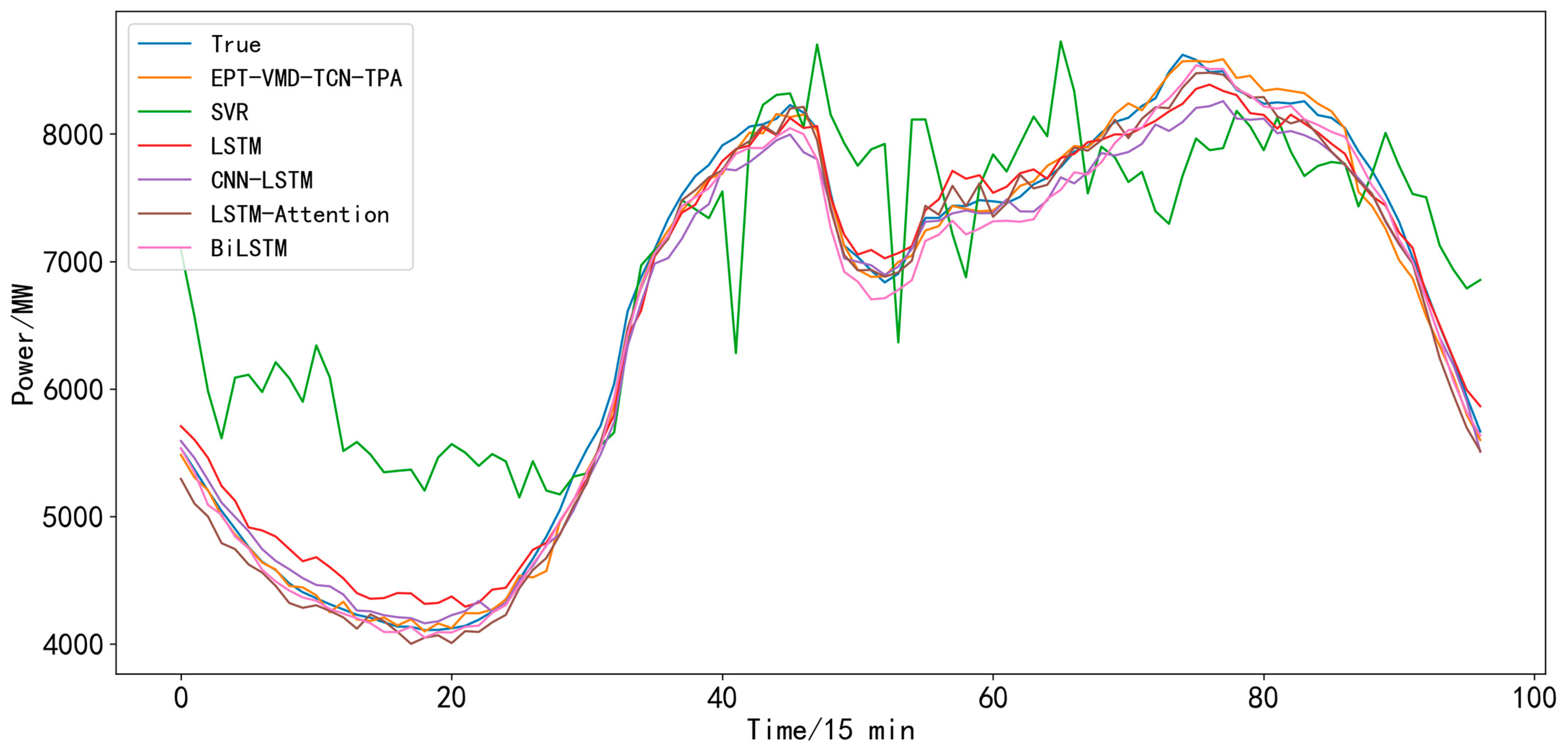
4.5. Classic Experiments
- (1)
- SVR prediction model: Support vector regression prediction model.
- (2)
- LSTM prediction model [23]: A typical recurrent neural network with memory function and gate structure, which can effectively solve the problem of gradient disappearance and gradient explosion due to excessive sequence length in RNN models.
- (3)
- CNN-LSTM prediction model [50]: By combining CNN and LSTM models, it enables the model to extract features inside the data through the convolution operation of the CNN, while using LSTM models to predict changes in the time series.
- (4)
- LSTM-Attention prediction model [22]: This model introduces the attention mechanism based on the LSTM model. The attention mechanism assigns more weight to important features, thus strengthening the connection between the whole and the local, and improving the prediction accuracy.
- (5)
- BiLSTM prediction model [25]: This model is improved on the basis of the LSTM model. Both forward and backward sequence information inputs are available to fully extract the information from the load data.
- (6)
- EPT-VMD-TCN-TPA prediction model: Our proposed final model.
- (7)
5. Experimental Results in Area 2
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fallah, S.; Deo, R.; Shojafar, M.; Conti, M.; Shamshirband, S. Computational Intelligence Approaches for Energy Load Forecasting in Smart Energy Management Grids: State of the Art, Future Challenges, and Research Directions. Energies 2018, 11, 596. [Google Scholar] [CrossRef]
- Li, J.; Luo, Y.; Wei, S. Long-Term Electricity Consumption Forecasting Method Based on System Dynamics under the Carbon-Neutral Target. Energy 2022, 244, 122572. [Google Scholar] [CrossRef]
- Nti, I.K.; Teimeh, M.; Nyarko-Boateng, O.; Adekoya, A.F. Electricity Load Forecasting: A Systematic Review. J. Electr. Syst. Inf. Technol. 2020, 7, 13. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, H.; Yan, B. A Review on Renewable Energy and Electricity Requirement Forecasting Models for Smart Grid and Buildings. Sustain. Cities Soc. 2020, 55, 102052. [Google Scholar] [CrossRef]
- Mishra, M.; Nayak, J.; Naik, B.; Abraham, A. Deep Learning in Electrical Utility Industry: A Comprehensive Review of a Decade of Research. Eng. Appl. Artif. Intell. 2020, 96, 104000. [Google Scholar] [CrossRef]
- Kuster, C.; Rezgui, Y.; Mourshed, M. Electrical load forecasting models: A critical systematic review. Sustain. Cities Soc. 2017, 35, 257–270. [Google Scholar] [CrossRef]
- Tan, F.L.; Zhang, J.; Ma, H.Z. Combined forecasting method of power load based on trend change division. J. N. China Electr. Power Univ. 2020, 47, 17–24. [Google Scholar]
- Christiaanse, W. Short-Term Load Forecasting Using General Exponential Smoothing. IEEE Trans. Power Appar. Syst. 1971, PAS-90, 900–911. [Google Scholar] [CrossRef]
- Chen, P.Y.; Fang, Y.J. Short-term load forecasting of power system for holiday point-by-point growth rate based on Kalman filtering. Eng. J. Wuhan Univ. 2020, 53, 139–144. [Google Scholar]
- Munkhammar, J.; van der Meer, D.; Widén, J. Very Short Term Load Forecasting of Residential Electricity Consumption Using the Markov-Chain Mixture Distribution (MCM) Model. Appl. Energy 2021, 282, 116180. [Google Scholar] [CrossRef]
- Wu, F.; Cattani, C.; Song, W.; Zio, E. Fractional ARIMA with an Improved Cuckoo Search Optimization for the Efficient Short-Term Power Load Forecasting. Alex. Eng. J. 2020, 59, 3111–3118. [Google Scholar] [CrossRef]
- Duan, L.; Niu, D.; Gu, Z. Long and medium term power load forecasting with multi-level recursive regression analysis. In Proceedings of the 2008 Second International Symposium on Intelligent Information Technology Application, Shanghai, China, 20–22 December 2008; pp. 514–518. [Google Scholar]
- Ceperic, E.; Ceperic, V.; Baric, A. A Strategy for Short-Term Load Forecasting by Support Vector Regression Machines. IEEE Trans. Power Syst. 2013, 28, 4356–4364. [Google Scholar] [CrossRef]
- Hu, Y.; Li, J.; Hong, M.; Ren, J.; Lin, R.; Liu, Y.; Liu, M.; Man, Y. Short Term Electric Load Forecasting Model and Its Verification for Process Industrial Enterprises Based on Hybrid GA-PSO-BPNN Algorithm—A Case Study of Papermaking Process. Energy 2019, 170, 1215–1227. [Google Scholar] [CrossRef]
- Kuhba, H.; Al-Tamemi, H.A.H. Power system short-term load forecasting using artificial neural networks. Int. J. Eng. Dev. Res. 2016, 4, 78–87. [Google Scholar]
- Imani, M. Electrical Load-Temperature CNN for Residential Load Forecasting. Energy 2021, 227, 120480. [Google Scholar] [CrossRef]
- Motepe, S.; Hasan, A.N.; Twala, B.; Stopforth, R. Power Distribution Networks Load Forecasting Using Deep Belief Networks: The South African Case. In Proceedings of the 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 9–11 April 2019; pp. 507–512. [Google Scholar]
- Wang, C.; Huang, S.; Wang, S.; Ma, Y.; Ma, J.; Ding, J. Short term load forecasting based on vmd-dnn. In Proceedings of the 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), Online, 21–24 October 2019; pp. 1045–1048. [Google Scholar]
- Zhang, B.; Wu, J.-L.; Chang, P.-C. A Multiple Time Series-Based Recurrent Neural Network for Short-Term Load Forecasting. Soft Comput. 2018, 22, 4099–4112. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Muzaffar, S.; Afshari, A. Short-Term Load Forecasts Using LSTM Networks. Energy Procedia 2019, 158, 2922–2927. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Cui, Y. Short-Term Load Forecasting Based on LSTM Networks Considering Attention Mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107818. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Gao, X.; Li, X.; Zhao, B.; Ji, W.; Jing, X.; He, Y. Short-Term Electricity Load Forecasting Model Based on EMD-GRU with Feature Selection. Energies 2019, 12, 1140. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, H. A Variant Model Based on BiLSTM for Electricity Load Prediction. In Proceedings of the 2021 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 29 July 2021; pp. 404–411. [Google Scholar]
- Niu, D.; Yu, M.; Sun, L.; Gao, T.; Wang, K. Short-Term Multi-Energy Load Forecasting for Integrated Energy Systems Based on CNN-BiGRU Optimized by Attention Mechanism. Appl. Energy 2022, 313, 118801. [Google Scholar] [CrossRef]
- Song, J.; Xue, G.; Pan, X.; Ma, Y.; Li, H. Hourly Heat Load Prediction Model Based on Temporal Convolutional Neural Network. IEEE Access 2020, 8, 16726–16741. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Chen, X.; Zeng, X.; Kong, Y.; Sun, S.; Guo, Y.; Liu, Y. Short-Term Load Forecasting for Industrial Customers Based on TCN-LightGBM. IEEE Trans. Power Syst. 2021, 36, 1984–1997. [Google Scholar] [CrossRef]
- Tang, X.; Chen, H.; Xiang, W.; Yang, J.; Zou, M. Short-Term Load Forecasting Using Channel and Temporal Attention Based Temporal Convolutional Network. Electr. Power Syst. Res. 2022, 205, 107761. [Google Scholar] [CrossRef]
- Shah, I.; Jan, F.; Ali, S. Functional Data Approach for Short-Term Electricity Demand Forecasting. Math. Probl. Eng. 2022, 2022, 6709779. [Google Scholar] [CrossRef]
- Shah, I.; Iftikhar, H.; Ali, S. Modeling and Forecasting Electricity Demand and Prices: A Comparison of Alternative Approaches. J. Math. 2022, 2022, 3581037. [Google Scholar] [CrossRef]
- Shah, I.; Iftikhar, H.; Ali, S.; Wang, D. Short-Term Electricity Demand Forecasting Using ComponentsEstimation Technique. Energies 2019, 12, 2532. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; He, Y.; Wang, Y. Short-Term Load-Forecasting Method Based on Wavelet Decomposition with Second-Order Gray Neural Network Model Combined with ADF Test. IEEE Access 2017, 5, 16324–16331. [Google Scholar] [CrossRef]
- Meng, Z.; Xie, Y.; Sun, J. Short-Term Load Forecasting Using Neural Attention Model Based on EMD. Electr. Eng. 2022, 104, 1857–1866. [Google Scholar] [CrossRef]
- Dong, P.; Bin, X.; Jun, M.; Qian, D.; Jinjin, D.; Jinjin, Z.; Qian, Z. Short-Term Load Forecasting Based on EEMD-Approximate Entropy and ELM. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 4–7 November 2019; pp. 1772–1775. [Google Scholar]
- Zhang, Z.; Hong, W.-C.; Li, J. Electric Load Forecasting by Hybrid Self-Recurrent Support Vector Regression Model with Variational Mode Decomposition and Improved Cuckoo Search Algorithm. IEEE Access 2020, 8, 14642–14658. [Google Scholar] [CrossRef]
- Yuan, F.; Che, J. An Ensemble Multi-Step M-RMLSSVR Model Based on VMD and Two-Group Strategy for Day-Ahead Short-Term Load Forecasting. Knowl. Based Syst. 2022, 252, 109440. [Google Scholar] [CrossRef]
- Cai, C.; Li, Y.; Su, Z.; Zhu, T.; He, Y. Short-Term Electrical Load Forecasting Based on VMD and GRU-TCN Hybrid Network. Appl. Sci. 2022, 12, 6647. [Google Scholar] [CrossRef]
- Kim, D.; Choi, G.; Oh, H.-S. Ensemble Patch Transformation: A Flexible Framework for Decomposition and Filtering of Signal. EURASIP J. Adv. Signal Process. 2020, 2020, 30. [Google Scholar] [CrossRef]
- Heydari, A.; Keynia, F.; Garcia, D.A.; De Santoli, L. Mid-Term Load Power Forecasting Considering Environment Emission Using a Hybrid Intelligent Approach. In Proceedings of the 2018 5th International Symposium on Environment-Friendly Energies and Applications (EFEA), Rome, Italy, 24–26 September 2018; pp. 1–5. [Google Scholar]
- Jiang, P.; Nie, Y.; Wang, J.; Huang, X. Multivariable Short-Term Electricity Price Forecasting Using Artificial Intelligence and Multi-Input Multi-Output Scheme. Energy Econ. 2023, 117, 106471. [Google Scholar] [CrossRef]
- Sekhar, C.; Dahiya, R. Robust Framework Based on Hybrid Deep Learning Approach for Short Term Load Forecasting of Building Electricity Demand. Energy 2023, 268, 126660. [Google Scholar] [CrossRef]
- Heydari, A.; Majidi Nezhad, M.; Pirshayan, E.; Astiaso Garcia, D.; Keynia, F.; De Santoli, L. Short-Term Electricity Price and Load Forecasting in Isolated Power Grids Based on Composite Neural Network and Gravitational Search Optimization Algorithm. Appl. Energy 2020, 277, 115503. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Shih, S.-Y.; Sun, F.-K.; Lee, H. Temporal Pattern Attention for Multivariate Time Series Forecasting. Mach. Learn. 2019, 108, 1421–1441. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Huang, K.; Gui, W. Non-Ferrous Metals Price Forecasting Based on Variational Mode Decomposition and LSTM Network. Knowl. Based Syst. 2020, 188, 105006. [Google Scholar] [CrossRef]
- Tran, T.N. Grid Search of Convolutional Neural Network model in the case of load forecasting. Arch. Electr. Eng. 2021, 2022, 3581037. [Google Scholar]
- Shah, I.; Iftikhar, H.; Ali, S. Modeling and Forecasting Medium-Term Electricity Consumption Using Component Estimation Technique. Forecasting 2020, 2, 163–179. [Google Scholar] [CrossRef]
- Rafi, S.H.; Nahid-Al-Masood; Deeba, S.R.; Hossain, E. A Short-Term Load Forecasting Method Using Integrated CNN and LSTM Network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]









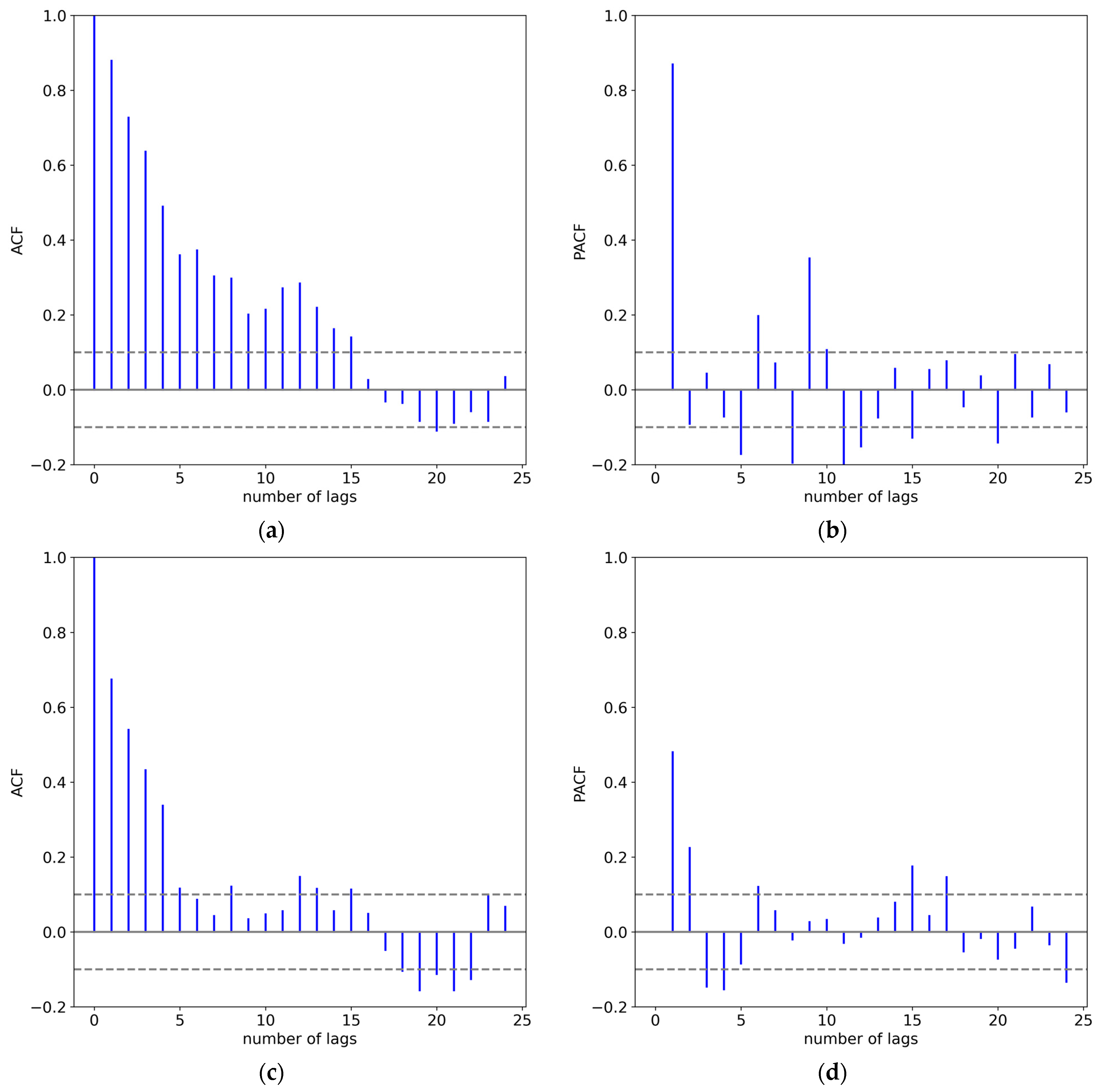
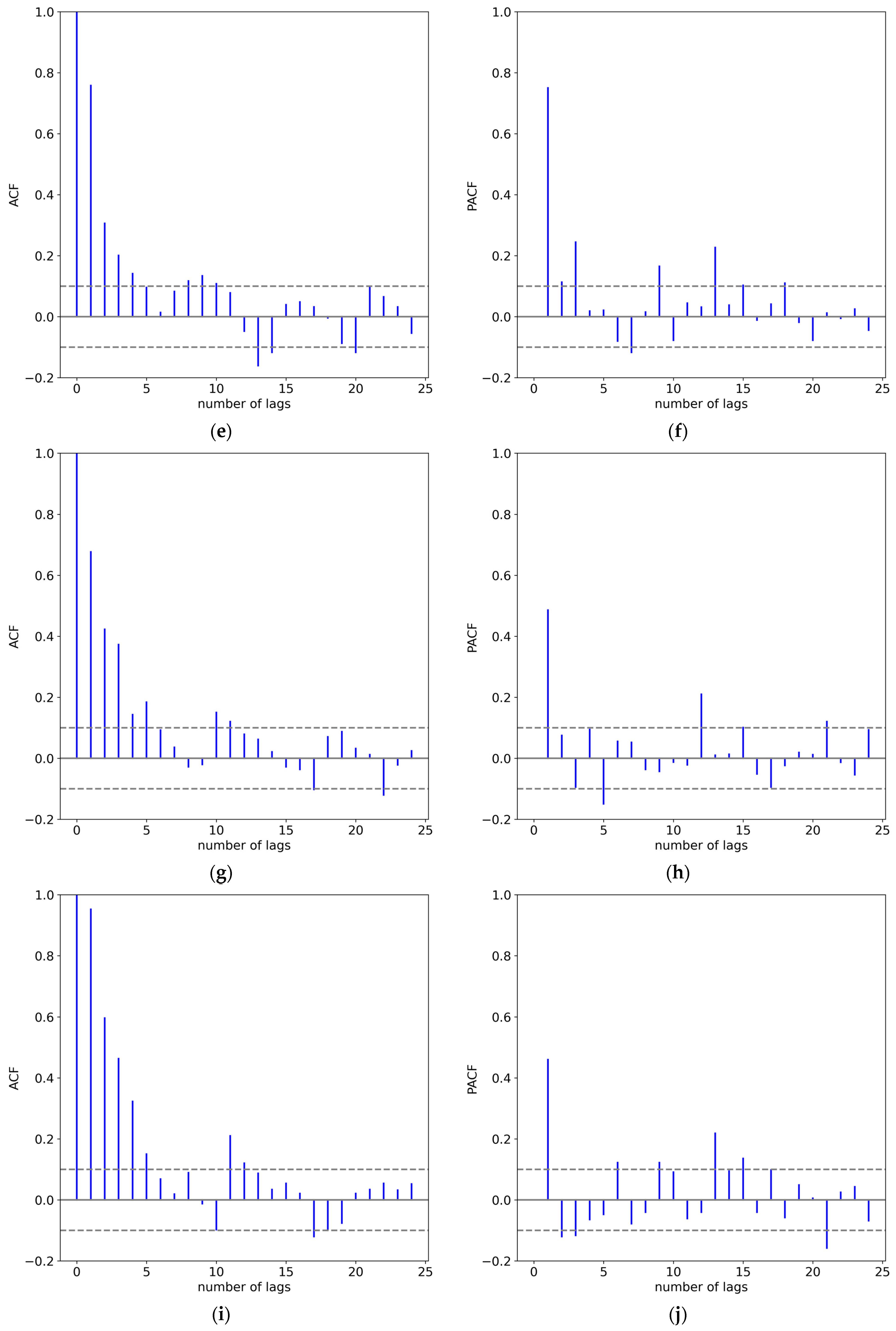
| Dataset | Samples | Range | Numbers | Mean (MW) | Max (MW) | Min (MW) | Std. (MW) |
|---|---|---|---|---|---|---|---|
| Area 1 | All samples | 1 January 2012–10 January 2015 | 106,176 | 6915.33 | 12,296.85 | 1306.08 | 2094.08 |
| Training | 1 January 2012–2 June 2014 | 84,864 | 6657.81 | 11,446.85 | 1306.08 | 2034.47 | |
| Testing | 3 June 2014–10 January 2015 | 21,312 | 7945.53 | 12,296.85 | 2267.67 | 2010.75 | |
| Area 2 | All samples | 1 January 2012–10 January 2015 | 106,176 | 7357.43 | 13,536.74 | 1986.32 | 2180.43 |
| Training | 1 January 2012–2 June 2014 | 84,864 | 7038.44 | 12,466.10 | 1986.32 | 2054.60 | |
| Testing | 3 June 2014–10 January 2015 | 21,312 | 8627.67 | 13,536.74 | 3259.12 | 2204.07 |
| Date | Max. Temperature (°C) | Min. Temperature (°C) | Avg. Temperature (°C) | Relative Humidity (avg.) | Rainfall (mm) |
|---|---|---|---|---|---|
| 1 August 2012 | 36.0 | 23.1 | 30.3 | 71.0 | 26.5 |
| 2 August 2012 | 35.6 | 27.8 | 31.9 | 61.0 | 0.0 |
| 3 August 2012 | 33.9 | 28.0 | 30.9 | 63.0 | 0.0 |
| 4 August 2012 | 31.3 | 27.8 | 29.5 | 75.0 | 0.0 |
| 5 August 2012 | 31.0 | 26.2 | 28.5 | 82.0 | 1.8 |
| 6 August 2012 | 30.8 | 24.7 | 26.9 | 87.0 | 12.3 |
| 7 August 2012 | 34.5 | 25.8 | 29.4 | 79.0 | 0.1 |
| k | Rres-Value of Area 1 | Rres-Value of Area 2 |
|---|---|---|
| 2 | 0.01588381 | 0.01149027 |
| 3 | 0.01077131 | 0.01032953 |
| 4 | 0.00584849 | 0.00780275 |
| 5 | 0.00502476 | 0.00628756 |
| 6 | 0.00412682 | 0.00523697 |
| 7 | 0.00386909 | 0.00402301 |
| 8 | 0.00370431 | 0.00331197 |
| 9 | 0.00360939 | 0.00285365 |
| 10 | 0.00356238 | 0.00239487 |
| 11 | 0.00338015 | 0.00198062 |
| 12 | 0.00335977 | 0.00197231 |
| 13 | 0.00334251 | 0.00197134 |
| 14 | 0.00333611 | 0.00197128 |
| 15 | 0.00332795 | 0.00197123 |
| Recombinant Sequences | FE-IMF1 | FE-IMF2 | FE-IMF3 | FE-IMF4 | FE-IMF5 | FE-IMF6 |
|---|---|---|---|---|---|---|
| Components | IMF1 | IMF2 | IMF3 + IMF10 | IMF4 + IMF7 | IMF5 + IMF6 | IMF8 + IMF9 + IMF11 |
| Processor | Memory | Python | TensorFlow | Keras |
|---|---|---|---|---|
| Intel(R) Core (TM) i5-7200U CPU @ 2.50 GHz 2.70 GHz | 4 G | 3.8 | 2.11.0 | 2.11.0 |
| Items | Number of Residual Blocks | Convolution Kernel Size | Number of Convolution Kernels | Dilation Rate | Number of Iterations | Dropout |
|---|---|---|---|---|---|---|
| Value | 3 | 3 | 20 | (1,2,4) | 100 | 0.1 |
| Items | Learning Rate | Loss Function | Optimizer | Activation Functions | Batch-Size |
|---|---|---|---|---|---|
| Value | 0.001 | MSE | Adam | ReLU | 64 |
| Model | MAPE (%) | RMSE (MW) | MAE (MW) | R2 | Time (s) |
|---|---|---|---|---|---|
| TCN | 2.84 | 247.9006 | 181.3514 | 0.9774 | 34.040 |
| VMD-TCN | 2.59 | 187.9851 | 147.2761 | 0.9870 | 390.934 |
| VMD-TCN-Attention | 1.58 | 133.4030 | 102.7410 | 0.9934 | 383.140 |
| VMD-TCN-TPA | 1.54 | 122.1089 | 98.6245 | 0.9945 | 427.891 |
| EPT-VMD-TCN-TPA | 1.25 | 110.2692 | 82.3180 | 0.9955 | 443.232 |
| EPT-VMD-FE-TCN-TPA | 1.86 | 168.9959 | 121.6994 | 0.9895 | 296.137 |
| Model | TCN | VMD-TCN | VMD-TCN-Attention | VMD-TCN-TPA | EPT-VMD-TCN-TPA | EPT-VMD-FE-TCN-TPA |
|---|---|---|---|---|---|---|
| TCN | nan | 0.0112 (−2.538) | 0.0007 (−3.386) | 0.0003 (−3.590) | 0.0002 (−3.765) | 0.0110 (−2.543) |
| VMD-TCN | 0.0112 (2.538) | nan | 0.0877 (−1.708) | 0.0472 (−1.985) | 0.0260 (−2.227) | 0.5255 (−0.635) |
| VMD-TCN-Attention | 0.0007 (3.386) | 0.0877 (1.708) | nan | 0.0083 (−2.642) | 0.0000 (−8.145) | 0.0106 (2.555) |
| VMD-TCN-TPA | 0.0003 (3.590) | 0.0472 (1.985) | 0.0083 (2.642) | nan | 0.0066 (−2.716) | 0.0021 (3.073) |
| EPT-VMD-TCN-TPA | 0.0002 (3.765) | 0.0260 (2.227) | 0.0000 (8.145) | 0.0066 (2.716) | nan | 0.0001 (4.018) |
| EPT-VMD-FE-TCN-TPA | 0.0110 (2.543) | 0.5255 (0.635) | 0.0106 (−2.555) | 0.0021 (−3.073) | 0.0001 (−4.018) | nan |
| Model | MAPE (%) | RMSE (MW) | MAE (MW) | R2 | Time (s) |
|---|---|---|---|---|---|
| SVR | 16.07 | 1309.0193 | 1022.1499 | 0.3689 | 11.666 |
| LSTM | 3.48 | 320.5932 | 222.2477 | 0.9621 | 39.803 |
| CNN-LSTM | 3.27 | 291.7813 | 203.8683 | 0.9686 | 45.583 |
| LSTM-Attention | 3.82 | 379.4524 | 229.1554 | 0.9470 | 57.898 |
| BiLSTM | 3.15 | 273.6259 | 200.7860 | 0.9724 | 93.655 |
| EPT-VMD-TCN-TPA | 1.25 | 110.2692 | 82.3180 | 0.9955 | 443.232 |
| Model | SVR | LSTM | CNN-LSTM | LSTM-Attention | BiLSTM | EPT-VMD-TCN-TPA | EPT-VMD-FE-TCN-TPA |
|---|---|---|---|---|---|---|---|
| SVR | nan | 0.0000 (−5.779) | 0.0000 (−5.828) | 0.0000 (−6.444) | 0.0000 (−5.502) | 0.0000 (−5.649) | 0.0000 (−5.603) |
| LSTM | 0.0000 (5.779) | nan | 0.0010 (−3.289) | 0.3682 (0.899) | 0.2256 (−1.212) | 0.0018 (−3.127) | 0.0082 (−2.644) |
| CNN-LSTM | 0.0000 (5.828) | 0.0010 (3.289) | nan | 0.2191 (1.229) | 0.6427 (−0.464) | 0.0058 (−2.759) | 0.0274 (−2.205) |
| LSTM-Attention | 0.0000 (6.444) | 0.3682 (−0.899) | 0.2191 (−1.229) | nan | 0.2869 (−1.065) | 0.0087 (−2.821) | 0.0179 (−2.608) |
| BiLSTM | 0.0000 (5.502) | 0.2256 (1.212) | 0.6427 (0.464) | 0.2869 (1.065) | nan | 0.0000 (−4.811) | 0.0003 (−3.587) |
| EPT-VMD-TCN-TPA | 0.0000 (5.649) | 0.0018 (3.127) | 0.0058 (2.758) | 0.0087 (2.821) | 0.0000 (4.811) | nan | 0.0001 (4.018) |
| EPT-VMD-FE-TCN-TPA | 0.0000 (5.604) | 0.0082 (2.644) | 0.0275 (2.205) | 0.0179 (2.608) | 0.0003 (3.587) | 0.0001 (−4.018) | nan |
| Model | MAPE (%) | RMSE (MW) | MAE (MW) | R2 | Time (s) |
|---|---|---|---|---|---|
| TCN | 3.02 | 279.9281 | 207.6085 | 0.9681 | 31.759 |
| VMD-TCN | 1.68 | 147.2106 | 116.8644 | 0.9912 | 356.854 |
| VMD-TCN-Attention | 1.63 | 144.1170 | 110.6246 | 0.9915 | 379.672 |
| VMD-TCN-TPA | 1.60 | 140.2134 | 109.3452 | 0.9919 | 411.754 |
| EPT-VMD-TCN-TPA | 1.58 | 137.6182 | 107.2617 | 0.9923 | 424.006 |
| EPT-VMD-FE-TCN-TPA | 2.02 | 170.3671 | 135.1109 | 0.9882 | 243.455 |
| Model | MAPE (%) | RMSE (MW) | MAE (MW) | R2 | Time (s) |
|---|---|---|---|---|---|
| SVR | 13.11 | 1103.4697 | 882.2721 | 0.5045 | 6.910 |
| LSTM | 3.64 | 355.7457 | 249.5678 | 0.9485 | 32.688 |
| CNN-LSTM | 3.26 | 294.3930 | 222.8188 | 0.9647 | 79.906 |
| LSTM-Attention | 3.85 | 383.7617 | 265.7952 | 0.9401 | 73.906 |
| BiLSTM | 2.64 | 254.9352 | 178.6009 | 0.9736 | 131.753 |
| EPT-VMD-TCN-TPA | 1.58 | 137.6182 | 107.2617 | 0.9923 | 424.006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zan, S.; Zhang, Q. Short-Term Power Load Forecasting Based on an EPT-VMD-TCN-TPA Model. Appl. Sci. 2023, 13, 4462. https://doi.org/10.3390/app13074462
Zan S, Zhang Q. Short-Term Power Load Forecasting Based on an EPT-VMD-TCN-TPA Model. Applied Sciences. 2023; 13(7):4462. https://doi.org/10.3390/app13074462
Chicago/Turabian StyleZan, Shifa, and Qiang Zhang. 2023. "Short-Term Power Load Forecasting Based on an EPT-VMD-TCN-TPA Model" Applied Sciences 13, no. 7: 4462. https://doi.org/10.3390/app13074462
APA StyleZan, S., & Zhang, Q. (2023). Short-Term Power Load Forecasting Based on an EPT-VMD-TCN-TPA Model. Applied Sciences, 13(7), 4462. https://doi.org/10.3390/app13074462





