Mechanical Properties and Constitutive Relationship of Cretaceous Frozen Sandstone under Low Temperature
Abstract
:1. Introduction
2. Test Plan
2.1. Sample Preparation
2.2. Test Equipment
2.3. Test Design
3. Mechanical Test Results of Cretaceous Red Sandstone
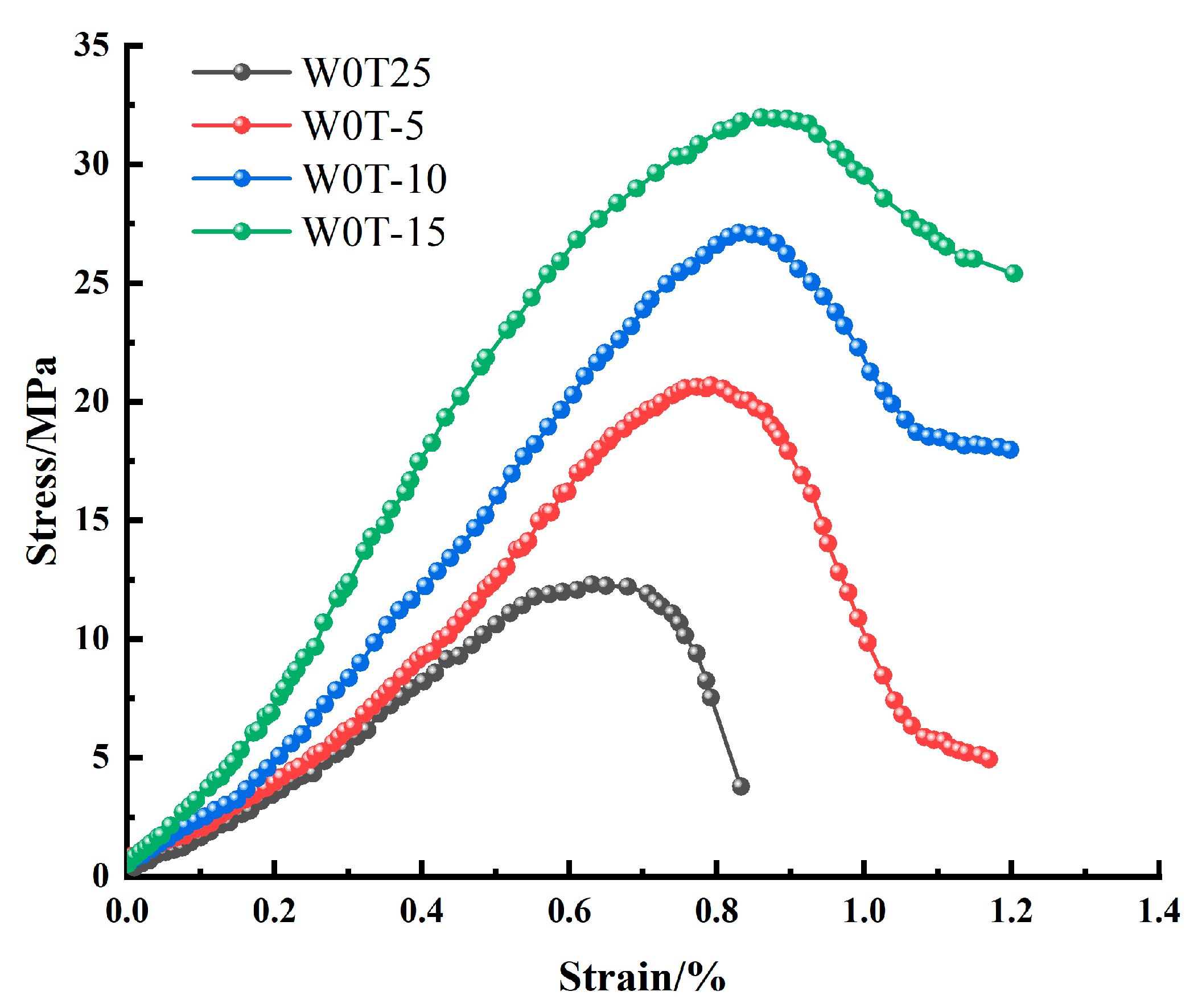
3.1. Uniaxial Compression Test of Cretaceous Red Sandstone
3.2. Triaxial Compression Test of Cretaceous Red Sandstone
3.3. Analysis of Mechanical Properties of Rock
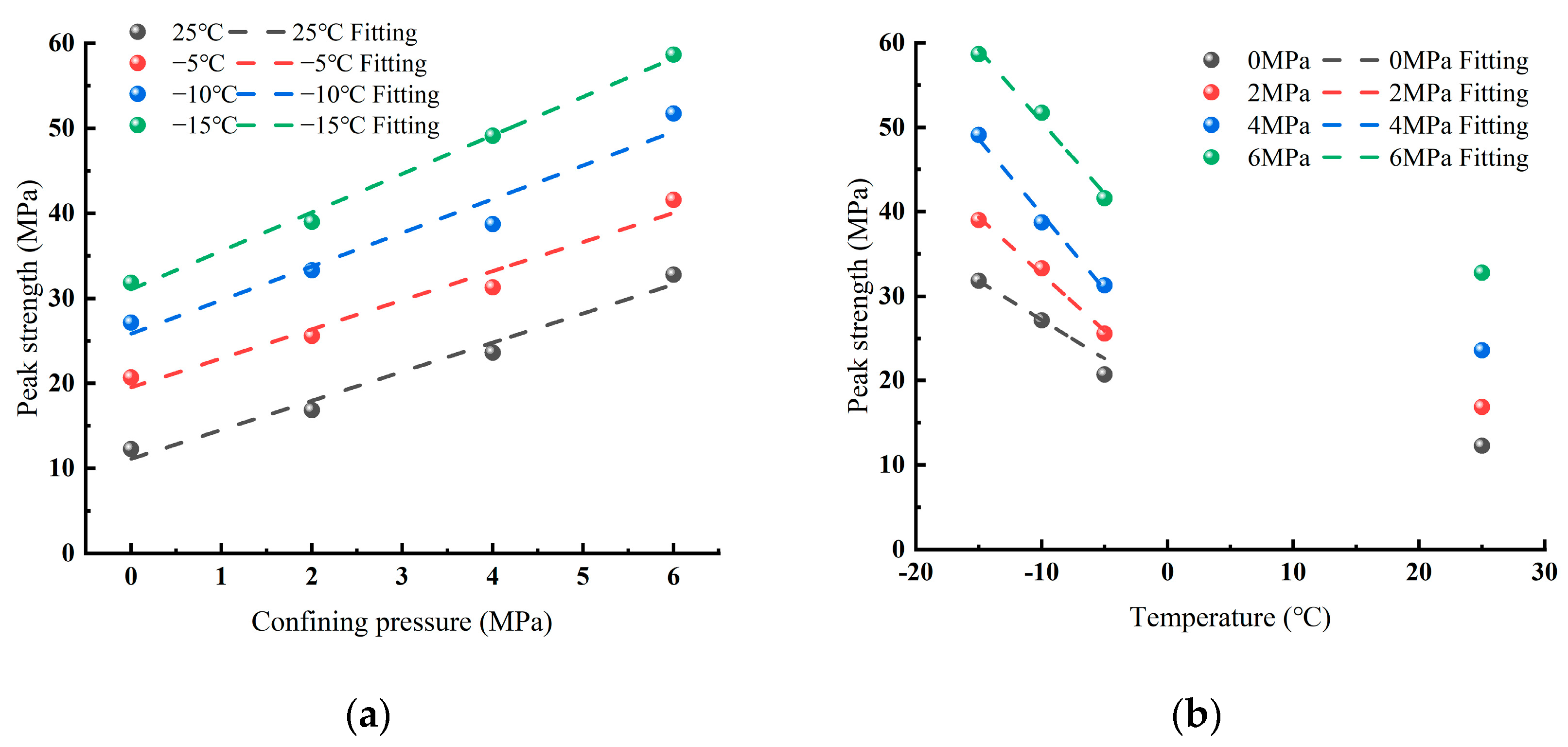
3.3.1. Relationship between the Freezing Temperature/Confining Pressure and the Peak Intensity of Sandstone
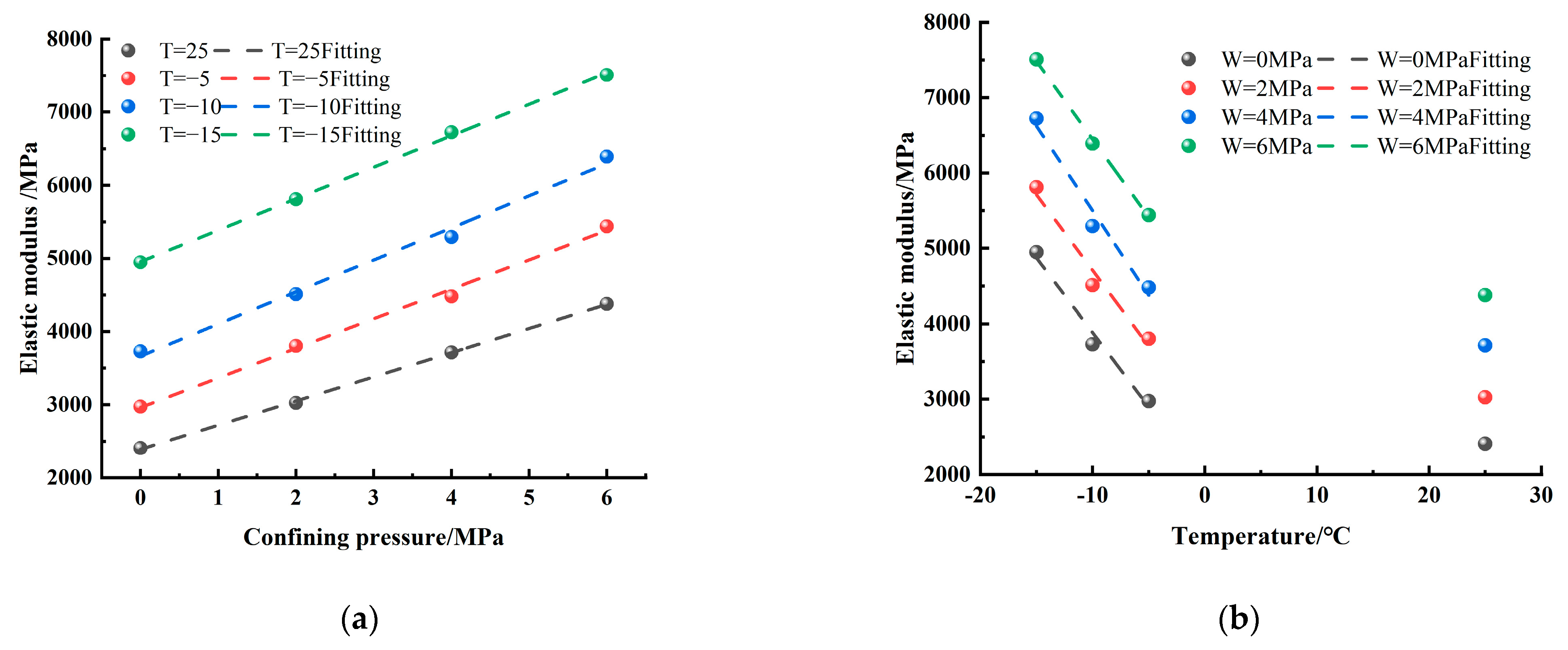
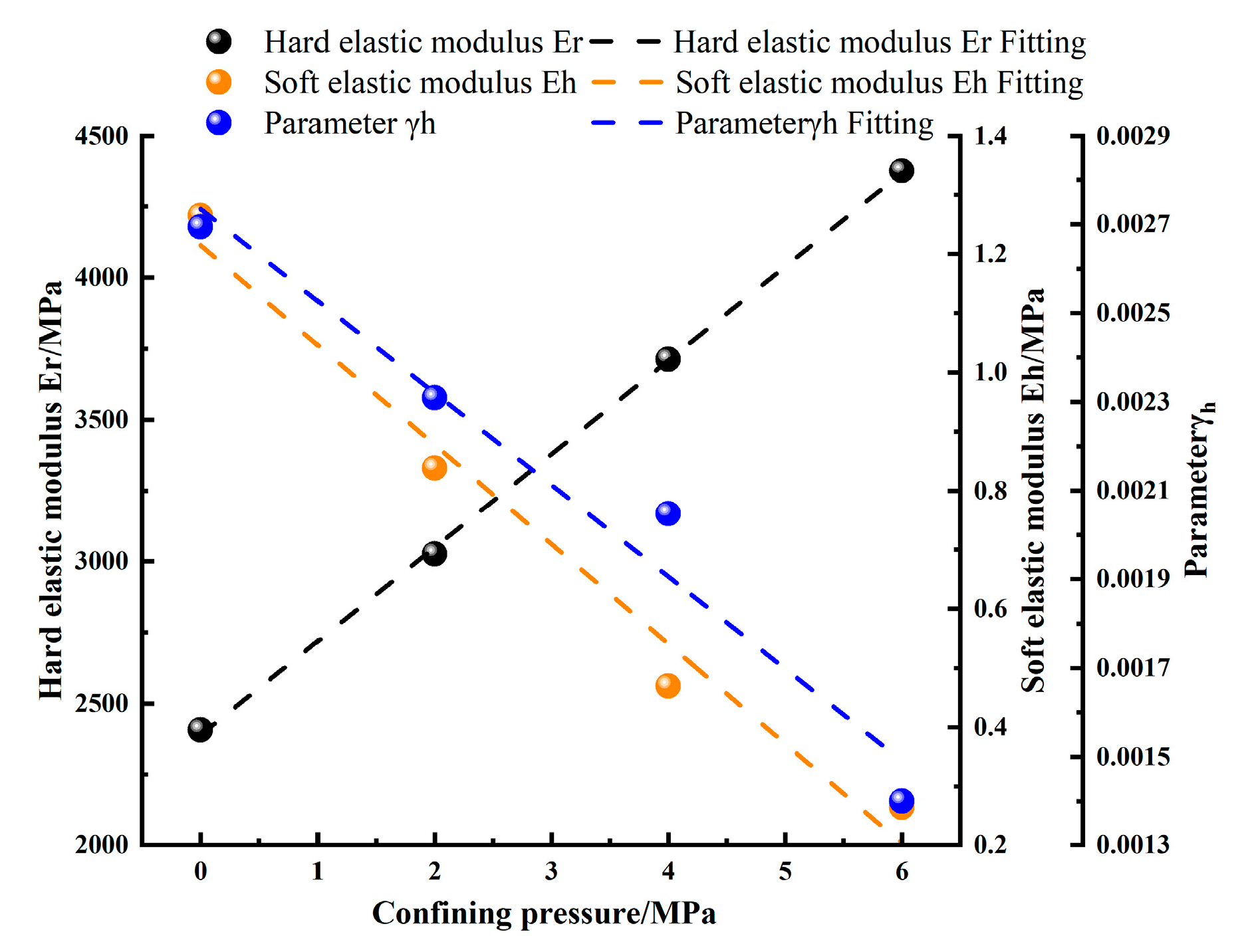
3.3.2. Relationship between the Freezing Temperature/Confining Pressure and the Elastic Modulus of Sandstone
3.3.3. Relationship between the Freezing Temperature/Confining Pressure and Poisson’s Ratio of Sandstone
4. Constitutive Relationship
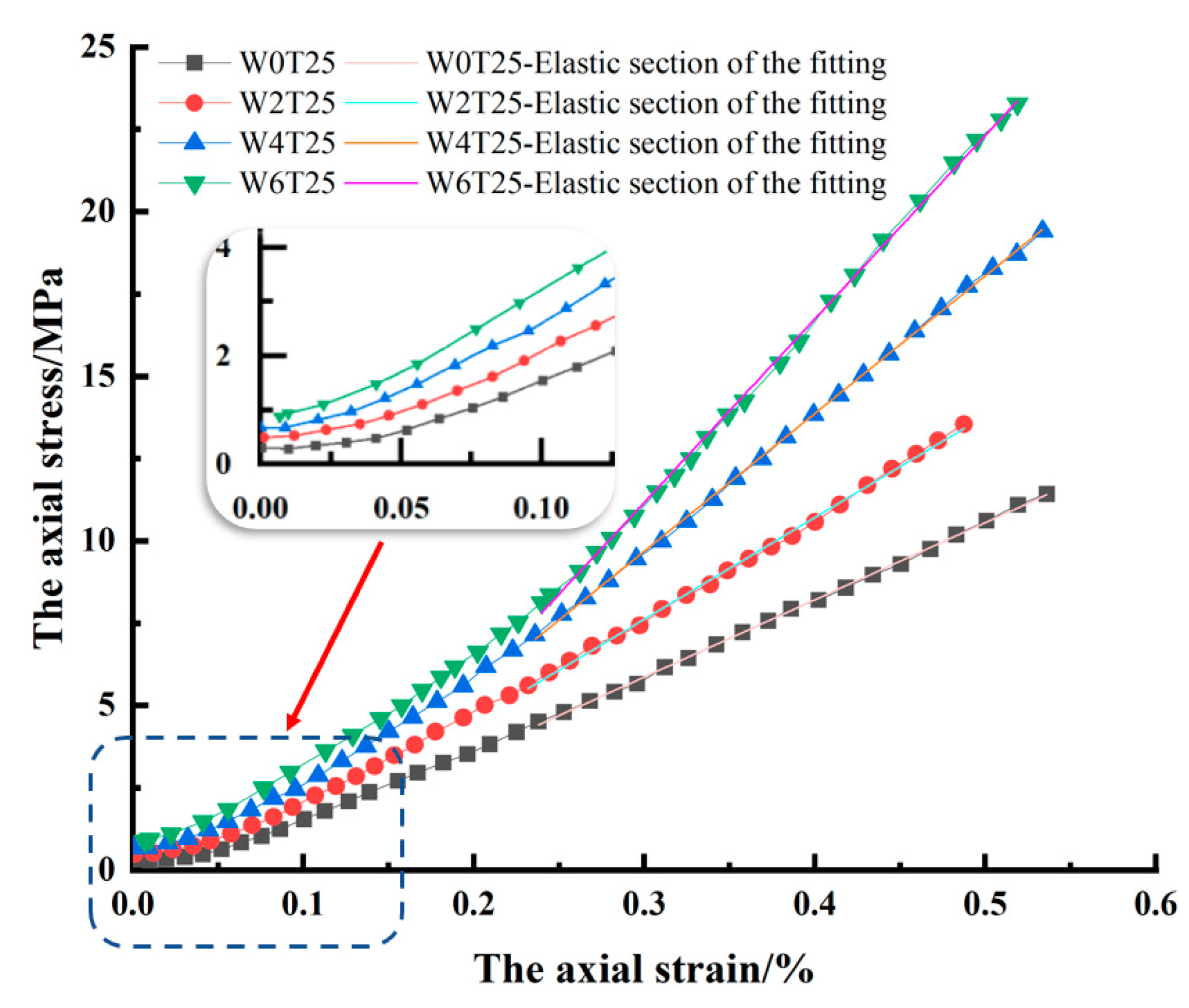
4.1. Constitutive Relationship before Yield Point
4.2. Constitutive Relationship after the Yield Point
- On the basis of the D-P strength criterion, the damage-softening constitutive model of rock is more suitable for describing the stress–strain curve of rock, especially beyond the yield point, with a high fitting degree.
- The stress before the yield point described by the constitutive relation is generally high, and it cannot be used to accurately describe the crack compaction and elastic deformation stages of Cretaceous red sandstone under 3D stress.
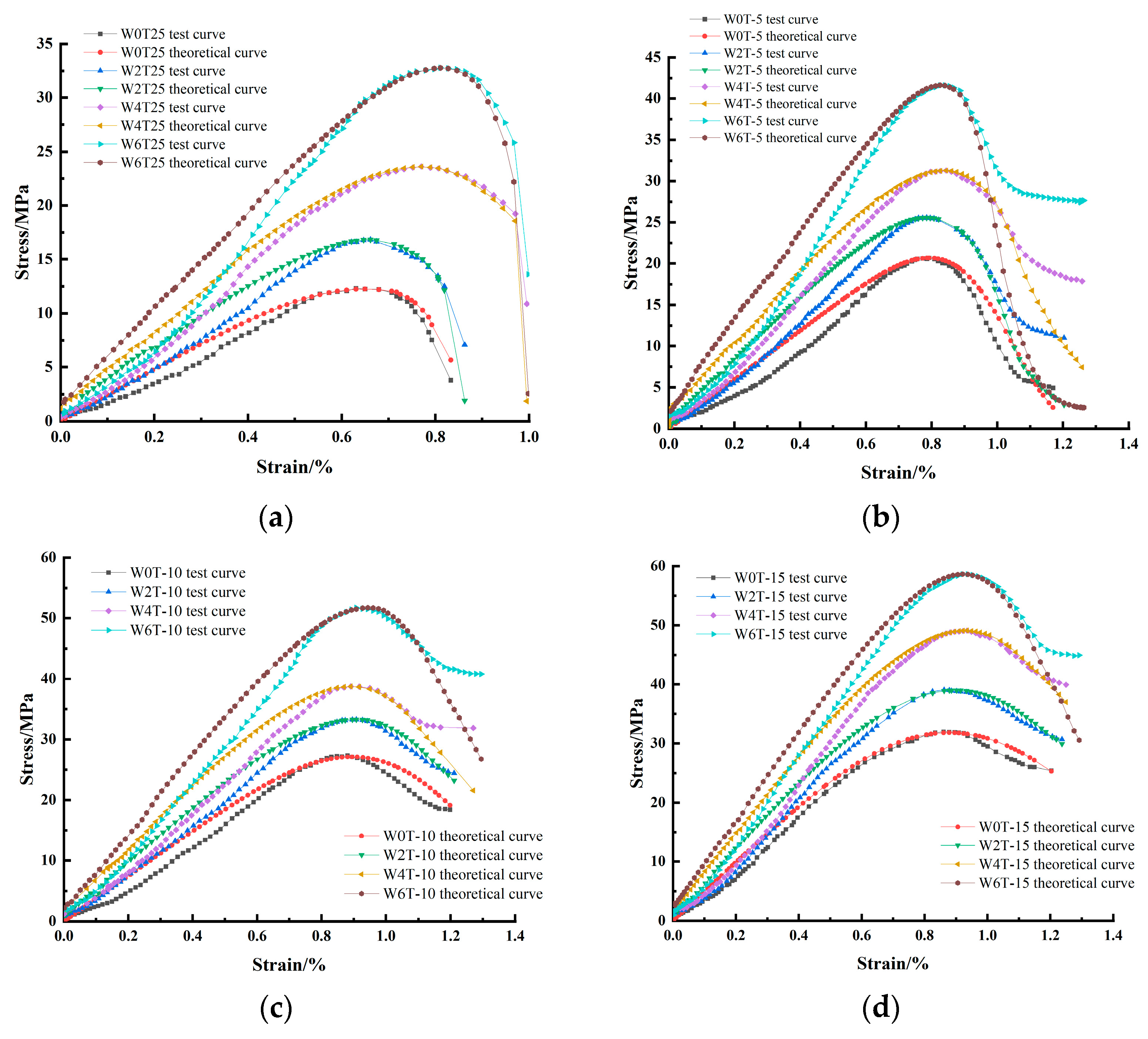
- Compared with the test curve under high confining pressure, the model curve is more consistent with the test stress–strain curve obtained under low confining pressure, and under the negative temperature state, the fitting degree of the model curve rises with the decrease in the temperature, which may be ascribed to the increase in the elastic modulus of rock as the temperature decreases.
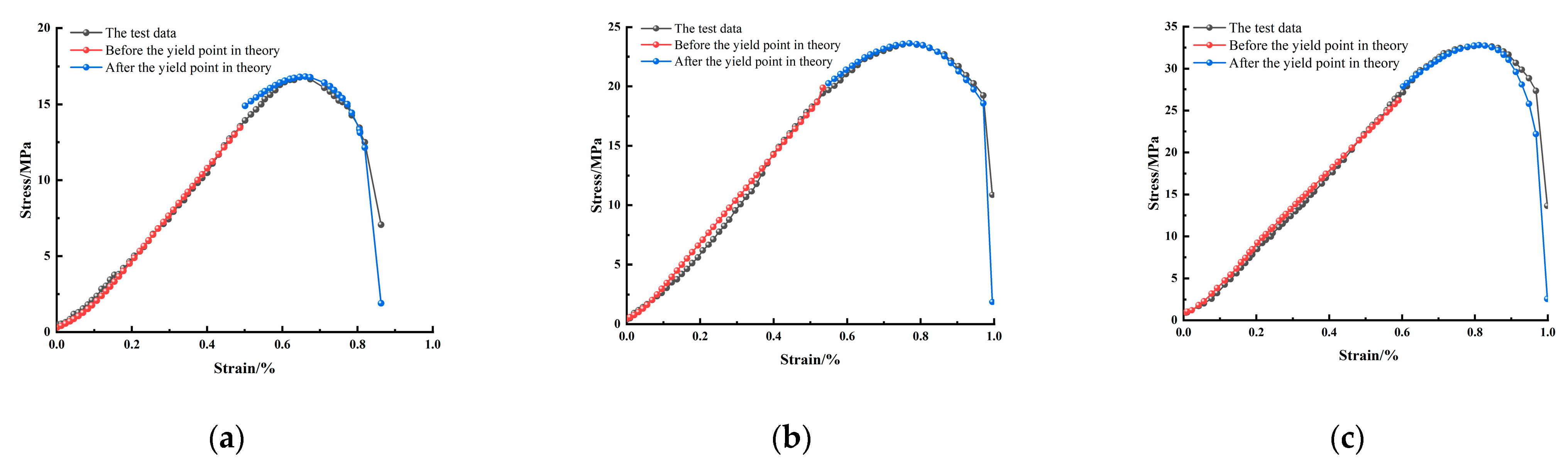
4.3. Model Validation
5. Conclusions
- Triaxial compression tests were conducted on the frozen samples of weakly cemented red sandstone in the Luohe Formation of Lower Cretaceous in Lijiagou air-return shaft of Wenjiapo Mine under different confining pressures. The stress–strain curves of rock subjected to triaxial compression exhibited four phases: crack compaction, elastic deformation, yielding phase, and failure phase. Different from the deformation characteristics under confining pressure, there was no strain-softening stage behind the peak of rock under uniaxial compression, which manifested as a sudden stress drop and rock failure.
- The peak strength and the elastic modulus of rock increased with the decrease in the temperature when the confining pressure was constant and showed a linear growth trend under negative temperature conditions, but the rate of growth gradually decreased. When the test temperature was constant, as the confining pressure increased, the peak strength and the elastic modulus increased, while the Poisson’s ratio decreased.
- The TPHM was able to effectively describe the constitutive relationship of rock before the yield point. On the basis of the Lemaitre strain equivalence hypothesis, the micro-elements in the sandstone were assumed to obey Weibull distribution. According to the D-P criterion, the damage constitutive relationship of rock was established to describe the stress–strain relationship after the yield point.
- The results based on the constitutive relationship were compared with the test results. The absolute error between the two was not more than 1 MPa, and the relative error was less than 5%. This indicated that the established constitutive model was not only better able to describe the rock fracture compression and elastic stages before the yield point, but also revealed the post-peak strain softening section, verifying the applicability and rationality of the model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.L.; Lu, B.; Yang, R.S.; Lin, H.; Wang, S.S.; Liu, C.H. Cemented backfilling mining technology with continuous mining and continuous backfilling method for underground coal mine and typical engineering cases. J. China Coal Soc. 2022, 47, 1055–1071. (In Chinese) [Google Scholar]
- Chen, Y.L.; Cui, H.D.; Li, M.; Pu, H.; Liu, F.M.; Zhang, L.Y. Dynamic mechanical properties and failure mechanism of saturated coal-measure sandstone in open pit mine with damage under real-time low-temperature conditions. J. China Coal Soc. 2022, 47, 1168–1179. (In Chinese) [Google Scholar]
- Yao, Z.S.; Cheng, H.; Rong, C.X. Shaft structural design and optimization of deep freezing bedrock shaft in west area. J. China Coal Soc. 2010, 35, 760–764. (In Chinese) [Google Scholar]
- Yuan, L. Theory and technology considerations on high-quality development of coal main energy security in China. Bull. Chin. Acad. Sci. 2023, 38, 11–22. (In Chinese) [Google Scholar]
- Dong, S.N.; Liu, H.X.; Wang, H. Reserch status and prospect on the mechanism of dynamic sand inrush at weakly cemented strata in working face with thick bedrock. J. China Coal Soc. 2022, 47, 274–285. (In Chinese) [Google Scholar]
- Li, H.; Li, J.; Li, L.; Xu, H.; Wei, J. Prevention of water and sand inrush during mining of extremely thick coal seams under unconsolidated Cenozoic alluvium. Bull. Eng. Geol. Environ. 2020, 79, 3271–3283. [Google Scholar] [CrossRef]
- Li, Q.H.; Li, S.X. Experimental study on mechanical properties of ultra-deep sandstone. Chin. J. Rock Mech. Eng. 2021, 40, 948–957. [Google Scholar]
- Tan, W.H.; Wang, P.F.; Wang, J.L.; Liu, J.J.; Ma, X.W. Mechanical properties of granite under uniaxial compression based on CT technology. J. Basic Sci. Eng. 2020, 28, 1489–1498. (In Chinese) [Google Scholar]
- Meng, Z.P.; Peng, S.P.; Zhang, S.H. Triaxial test on physical and mechanical properties of sandstone for different diagenesis degree. Chin. J. Geotech. Eng. 2003, 25, 140–143. (In Chinese) [Google Scholar]
- Meng, Q.B.; Liu, J.F.; Xie, L.X.; Pu, H.; Yang, Y.G.; Huang, B.X.; Qian, W. Experimental mechanical strength and deformation characteristics of deep damaged–fractured rock. Bull. Eng. Geol. Environ. 2021, 81, 32. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, W.; Zhang, S.; Mu, Y.; Li, G. Experimental investigation of the path-dependent strength and deformation behaviours of frozen loess. Eng. Geol. 2020, 265, 105449. [Google Scholar] [CrossRef]
- Li, Q.L.; Wang, M.; Fu, Q.; Li, T.; Liu, D.; Hou, R.; Li, H.; Cui, S.; Ji, Y. Short-term influence of biochar on soil temperature, liquid moisture content and soybean growth in a seasonal frozen soil area. J. Environ. Manag. 2020, 266, 110609. [Google Scholar] [CrossRef]
- Yoshikawa, T.; Noda, T. Triaxial test on water absorption compression of unsaturated soil and its soil-water-air-coupled elastoplastic finite deformation analysis. Soils Found. 2020, 60, 1151–1170. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, C.Q.; Bai, Y. Investigation of damage evolution and its model of rock-like brittle materials. Rock Soil Mech. 2021, 42, 2344–2354. (In Chinese) [Google Scholar]
- Li, W.T.; Li, S.C.; Feng, X.D.; Li, S.C.; Yuan, C. Study of post-peak strain softening mechanical properties of rock based on mohr-coulomb criterion. Chin. J. Rock Mech. Eng. 2011, 30, 1460–1466. (In Chinese) [Google Scholar]
- Zhang, C.H.; Zhao, Q.S.; Huang, L.; Ye, S.; Yu, Y.J. Post-peak strain softening mechanical model of rock considering confining pressure effect. Rock Soil Mech. 2010, 31, 193–197. (In Chinese) [Google Scholar]
- Lu, Y.H.; Chen, M.; Yuan, J.B.; Jin, Y.; Teng, X.Q. Borehole instability mechanism of a deviated well in anisotropic formations. Acta Pet. Sin. 2013, 34, 563–568. (In Chinese) [Google Scholar]
- Cao, W.G.; Zhao, M.H.; Tang, X.J. Study on simulation of statistical damage in the full process of rock failure. Chin. J. Geotech. Eng. 2003, 34, 184–187. (In Chinese) [Google Scholar]
- Cao, W.G.; Fang, Z.L.; Tang, X.J. A study of statistical constitutive model for soft and damage rocks. Chin. J. Rock Mech. Eng. 1998, 17, 628–633. (In Chinese) [Google Scholar]
- Huang, H.F.; Ju, N.P.; Li, L.; Xiao, J.W.; Li, M.; Bai, J.; Lv, X.T. Improved Harris function based statistical damage softening model for rocks. J. Eng. Geol. 2018, 26, 520–527. (In Chinese) [Google Scholar]
- Zhang, W.Z.; Chen, C.X.; Yu, M.Y. Study of mechanical properties and constitutive relation of weathered sandstone. Rock Soil Mech. 2009, 30, 33–36. (In Chinese) [Google Scholar]
- Muralha, J.; Grasselli, G.; Tatone, B.; Blümel, M.; Chryssanthakis, P.; Jiang, Y.J. ISRM suggested method for laboratory determination of the shear strength of rock joints: Revised version. Rock Mech. Rock Eng. 2014, 47, 291–302. [Google Scholar] [CrossRef]
- Wang, J.B.; Zhang, Q.; Song, Z.P.; Zhang, Y.W. Creep properties and damage constitutive model of salt rock under uniaxial compression. Int. J. Damage Mech. 2020, 29, 902–922. [Google Scholar] [CrossRef]
- Yan, Z.Q.; Li, Z.; Tan, Y.Z.; Ma, L.J.; Yu, L.Y.; Li, H.Y. Coupling effects of strain rate and low temperature on the dynamic mechanical properties of frozen water-saturated sandstone. Water 2022, 14, 3513. [Google Scholar] [CrossRef]
- Yu, J.; Fu, G.F.; Chen, X.; Guo, X.Y. Experimental study on mechanical properties of sandstone after freezing-thawing cycles under triaxial confining pressure unloading. Chin. J. Rock Mech. Eng. 2015, 34, 2001–2009. (In Chinese) [Google Scholar]
- Zhang, H.M.; Meng, X.Z.; Liu, X.Y. Establishment of constitutive model and analysis of damage characteristics of frozen-thawed rock under load. Arab. J. Geosci. 2021, 14, 1277. [Google Scholar] [CrossRef]
- Li, L.C.; Zhao, Y. Investigation on nonlinear elastic behaviour of rocks based on a two-part hooke’s model. Chin. J. Rock Mech. Eng. 2012, 31, 2119–2126. (In Chinese) [Google Scholar]
- Zhao, Y.; Liu, H.H. An elastic stress–strain relationship for porous rock under anisotropic stress conditions. Rock Mech. Rock Eng. 2012, 45, 389–399. [Google Scholar] [CrossRef]
- Azam, S.; Hojjatollah, R.; Ali, N. An anisotropic continuum damage mechanics model for the simulation of yield surface evolution and ratcheting. Int. J. Appl. Mech. 2022, 14, 2250044. [Google Scholar]
- Peng, Z.X.; Zeng, Y.W. Microcrack propagation-based damage mechanics model of rock. J. Northeast. Univ. (Nat. Sci.) 2022, 43, 1784–1791. (In Chinese) [Google Scholar]
- Hou, J.L.; Lv, J.N.; Ricoeur, A.; Hu, Y.F.; Zuo, H.; Chen, Y.H.; Li, Q. The M-integral in fracture and damage mechanics: A review of developments and applications. Eng. Fract. Mech. 2022, 273, 108741. [Google Scholar] [CrossRef]
- Zhao, S.L.; Yang, Z.J.; Fu, X.D.; Fang, Z. Shear damage mechanism of coarse-grained materials considering strain localization. Rock Soil Mech. 2023, 44, 31–42. (In Chinese) [Google Scholar]
- Morro, A. A phase-field approach to continuum damage mechanics. Materials 2022, 15, 7671. [Google Scholar] [CrossRef] [PubMed]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Krajcinovic, D.; Silva, M.A.G. Statistical aspects of the continuous damage theory. Int. J. Solids Struct. 1982, 18, 551–562. [Google Scholar] [CrossRef]
- Zhao, G.J.; Chen, C.; Yan, H. A thermal damage constitutive model for oil shale based on weibull statistical theory. Math. Probl. Eng. 2019, 2019, 4962586. [Google Scholar] [CrossRef] [Green Version]
- Bu, P.; Li, Y.L.; Li, Y.; Wen, L.F.; Wang, J.; Zhang, X. Creep damage coupling model of concrete based on the statistical damage theory. J. Build. Eng. 2023, 63, 105437. [Google Scholar] [CrossRef]
- Liu, C.X.; Yang, L.D.; Cao, W.G. A statistical damage softening constitutive model for rock and back analysis of parameters. Chin. J. Undergr. Space Eng. 2007, 3, 453–457. (In Chinese) [Google Scholar]
- Huang, H.F.; Ju, N.P.; Lan, K.W.; Li, M.; Kong, W.; Guo, L.Y. Statistical damage softening model for rock and back analysis of its parameters. J. Yangtze River Sci. Res. Inst. 2018, 35, 102–106. (In Chinese) [Google Scholar]
- Pan, J.L.; Guo, Q.F.; Tian, L.M.; Wu, X.; Wang, M. Study on rock statistical damage softening constitutive model and its parameters based on the unified strength theory. Min. Res. Dev. 2019, 39, 38–42. (In Chinese) [Google Scholar]
- Walton, G.; Sinha, S. Challenges associated with numerical back analysis in rock mechanics. J. Rock Mech. Geotech. Eng. 2022, 14, 2058–2071. [Google Scholar] [CrossRef]
- Zhao, H.B.; Chen, B.R.; Li, S.J.; Li, Z.; Zhu, C. Updating the models and uncertainty of mechanical parameters for rock tunnels using Bayesian inference. Geosci. Front. 2021, 12, 230–242. [Google Scholar] [CrossRef]
- Liu, X.S.; Ning, J.G.; Tan, Y.L.; Gu, Q.H. Damage constitutive model based on energy dissipation for intact rock subjected to cyclic loading. Int. J. Rock Mech. Min. Sci. 2016, 85, 27–32. [Google Scholar] [CrossRef]
- Pan, J.L.; Cai, M.F.; Li, P.; Guo, Q.F. A damage constitutive model of rock-like materials containing a single crack under the action of chemical corrosion and uniaxial compression. J. Cent. South Univ. 2022, 29, 486–498. [Google Scholar] [CrossRef]
- Zhu, Z.N.; Tian, H.; Wang, R.; Jiang, G.S.; Dou, B.; Mei, G. Statistical thermal damage constitutive model of rocks based on Weibull distribution. Arab. J. Geosci. 2021, 14, 495. [Google Scholar] [CrossRef]
- Fang, Y.; Yao, Z.S.; Huang, X.W.; Li, X.W.; Diao, N.H.; Hu, K.; Li, H. Permeability evolution characteristics and microanalysis of reactive powder concrete of drilling shaft lining under stress-seepage coupling. Constr. Build. Mater. 2022, 331, 127336. [Google Scholar] [CrossRef]
- Li, H.C.; Zhang, S. A constitutive damage model of rock based on the assumption of modified Lemaitre strain equivalence hypothesis. Rock Soil Mech. 2017, 38, 1321–1326, 1334. (In Chinese) [Google Scholar]
- Shi, Z.M.; Li, J.T.; Wang, J.; Chen, J.; Lin, H.; Cao, P. Experimental and numerical study on fracture characteristics and constitutive model of sandstone under freeze-thaw-fatigue. Int. J. Fatigue 2023, 166, 107236. [Google Scholar] [CrossRef]
- Fang, Y.; Yao, Z.S.; Huang, X.W.; Li, X.W.; Xu, Y.J.; Hu, K.; Shu, S.Y. Durability analysis and damage constitutive modeling of fiber-reinforced reactive powder concrete of drilling shaft in porous water-bearing rock stratum. Case. Stud. Constr. Mater. 2023, 18, e01911. [Google Scholar] [CrossRef]






| Natural Moisture Content/% | Saturated Water Content/% | Dry Density/g·cm−3 | Saturation Density/g·cm−3 | Porosity/% |
|---|---|---|---|---|
| 5.18 | 8.69 | 2.12 | 2.23 | 23.61 |
| Experimental Temperature | Confining Pressure | |||
|---|---|---|---|---|
| 0 MPa (No Confining Pressure) | 2 MPa | 4 MPa | 6 MPa | |
| 25 °C | W0T25 | W2T25 | W4T25 | W6T25 |
| −5 °C | W0T-5 | W2T-5 | W4T-5 | W6T-5 |
| −10 °C | W0T-10 | W2T-10 | W4T-10 | W6T-10 |
| −15 °C | W0T-15 | W2T-15 | W4T-15 | W6T-15 |
| Specimen Number | σmax/MPa | E/MPa | μ |
|---|---|---|---|
| W0T25 | 12.242 | 2407.36 | 0.249 |
| W0T-5 | 20.689 | 2973.21 | 0.239 |
| W0T-10 | 27.122 | 3728.39 | 0.230 |
| W0T-15 | 31.812 | 4947.37 | 0.210 |
| W2T25 | 16.827 | 3026.18 | 0.234 |
| W2T-5 | 25.557 | 3802.13 | 0.226 |
| W2T-10 | 33.277 | 4507.64 | 0.216 |
| W2T-15 | 38.981 | 5807.88 | 0.197 |
| W4T25 | 23.611 | 3713.07 | 0.222 |
| W4T-5 | 31.276 | 4478.78 | 0.216 |
| W4T-10 | 38.704 | 5292.02 | 0.204 |
| W4T-15 | 49.109 | 6723.26 | 0.187 |
| W6T25 | 32.784 | 4376.91 | 0.213 |
| W6T-5 | 41.582 | 5439.73 | 0.207 |
| W6T-10 | 51.706 | 6390.49 | 0.196 |
| W6T-15 | 58.642 | 7507.74 | 0.180 |
| Confining Pressure/MPa | Absolute Deviation /MPa | /% |
|---|---|---|
| 2 | 0.312 | 3.28 |
| 4 | 0.526 | 3.82 |
| 6 | 0.706 | 3.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, S.; Yao, Z.; Xu, Y.; Wang, C.; Hu, K. Mechanical Properties and Constitutive Relationship of Cretaceous Frozen Sandstone under Low Temperature. Appl. Sci. 2023, 13, 4504. https://doi.org/10.3390/app13074504
Shu S, Yao Z, Xu Y, Wang C, Hu K. Mechanical Properties and Constitutive Relationship of Cretaceous Frozen Sandstone under Low Temperature. Applied Sciences. 2023; 13(7):4504. https://doi.org/10.3390/app13074504
Chicago/Turabian StyleShu, Siyuan, Zhishu Yao, Yongjie Xu, Chen Wang, and Kun Hu. 2023. "Mechanical Properties and Constitutive Relationship of Cretaceous Frozen Sandstone under Low Temperature" Applied Sciences 13, no. 7: 4504. https://doi.org/10.3390/app13074504
APA StyleShu, S., Yao, Z., Xu, Y., Wang, C., & Hu, K. (2023). Mechanical Properties and Constitutive Relationship of Cretaceous Frozen Sandstone under Low Temperature. Applied Sciences, 13(7), 4504. https://doi.org/10.3390/app13074504







