Restenosis Investigation of Two-Stent Placement in the Artery Bifurcation with Different Stenting Techniques Using Computational Fluid Dynamics Analysis

Abstract

The in-stent restenosis may still occur in patients with a coronary bifurcation stenting. The purpose of this study is to investigate the restenosis effect in the relationships between the bifurcation angles of the coronary artery and three types of stenting techniques (T-stenting, Culotte, and Kissing techniques), for comparing two kinds of arterial shapes using computational fluid dynamics (CFD) analysis. The finite element models of two types of the coronary arteries were reconstructed using stereolithography (STL) data of an artificial artery from reverse engineering laser scanning, and then each artery was further modified to add three kinds of the bifurcation angles, including 80°, 113°, and 142°. The low TAWSS of the two arteries were mainly concentrated at the LCX branch; a more essential discovery was that the low TAWSS area ration was in proportion to the bifurcation angle. The smallest low TAWSS of the T-stenting and Kissing techniques was detected in the arteries A and B, respectively. Both Culotte and Kissing techniques always showed a higher OSI than the T-stenting, and a high OSI was meaningfully located at the LCX branch. The CFD study concluded that the large bifurcation angle of an artery using a long stent at the LCX side branch with the T-stenting technique has a high risk of stenting restenosis.

1. Introduction

Coronary artery stenosis is a common cardiovascular disease. Arterial narrowing is mainly caused by plaques of lipid, platelet accumulation, and endothelial cell proliferation [1]. It has been reported that the hemodynamics and the geometry of the coronary arteries are closely related to the stenosis of plaque accumulation. Coronary artery narrowing often occurs at the bifurcation with complex blood flow [2]. Additionally, a coronary artery bifurcation angle may affect wall shear stress, the plaque distribution, and the size of plaque [3]. Coronary stenting is considered to be a standard treatment for the coronary artery stenosis. So far, many different stenting techniques have been developed for coronary artery bifurcation stenosis, such as T-stenting, Culotte, and Kissing. In the case of coronary bifurcation after stenting, some patients experience adverse postoperative effects, such as stent thrombosis and restenosis with endothelial hyperplasia [4,5]. The coronary bifurcation stenting, as a standard treatment, has been applied in arterial stenosis. The techniques of a simple one-stent are applied for treating stenosis in the bifurcation region for a long time [6,7,8,9], but a severe stenosis can still be detected after a stenting treatment [10,11,12,13]. Therefore, the complex stenting techniques, such as a two-stent application, are developed to improve the effects of stenosis in the artery bifurcation [14]. The problems of restenosis by using two-stent techniques have confirmed some harmful complications [15,16,17]. Stent restenosis is a complex biological process that is related to the injury, inflammation, and local blood disorder caused by stent implantation. Previous in vitro studies have indicated that low wall shear stress (less than 0.5 Pa) contributes to the development of incipient atherosclerosis, transforming smaller fibrotic masses into high-risk plaques [18].

The stenting techniques for coronary artery bifurcation have been evidenced as an important issue to prevent coronary bifurcation lesions. Kumsars et al. [19] indicated that the bifurcation stenosis was significantly located at the large side brunch of the artery, compared with simpler and two-stent stenting techniques. Freixa et al. [20] evaluated long-term outcomes using a two-stent technique for the treatment of coronary bifurcations; the results showed that the application of the crush and Culotte techniques was associated with a low risk of bifurcation stenosis. Moreover, the bifurcation angle, balloon-inflated final stage, and side branch diameter were the main important variables to influence the bifurcation stenosis. Chen et al. [21] have mentioned that stenting techniques were developed for decreasing stenosis near the bifurcation region. The innovative design and structure of the stent could decrease a risk of stenting stenosis, but the efficiencies of new stenting techniques or complex in-stent structures are still unclear. Therefore, the investigation of stenting restenosis is considered to be an important concern to analyze with the artery bifurcation model in the hemodynamic analysis.

Computational fluid dynamics (CFD) is a numerical-based method to analyze and solve problems of fluid flows. Perktold et al. [22] first demonstrated that the CFD could be used to provide detailed data on hemodynamic conditions of carotid artery bifurcation. Moreover, the CFD appeared as a practical tool for investigating local hemodynamics of the carotid artery to provide important hemodynamic information that was beyond the capabilities of experimental measurements. The CFD investigation can offer essential evidence into the biomechanical effects of stenting techniques and provide a framework for the quantitative assessment of hemodynamics in the coronary artery segment. Previous studies [23,24] have been evidenced to investigate hemodynamic effects with different stenting techniques through the CFD simulation. For now, the analysis of the CFD has been widely used in the field of cardiovascular medicine [25]. Combining mathematics, physics, and clinical methods has improved the understanding and applications of interventional cardiology from stent design to implantation. Fluid dynamics and deformation force analysis could improve stent-based interventional treatment of coronary artery disease by restoring and achieving a more physiological hemodynamic profile. In recent years, many stenting techniques for coronary artery bifurcation have been developed to improve curative effects of coronary bifurcation lesions. However, stent restenosis cannot be entirely avoided in patients with stent treatment. Many studies have indicated influenced factors of the coronary restenosis—including coronary artery shape, bifurcation angle, stent structure and stenting technology. However, a definite cause of the stent restenosis is still unclear, particularly in the relationship between the arterial bifurcation angles and the stenting techniques. The CFD was considered to investigate the effects of stent restenosis in the local region of the coronary artery bifurcation that could be confirmed to provide a reliable result for evaluating stent restenosis. Therefore, the aim of this study is to investigate the stent restenosis effects on the relationships between bifurcation angles of the coronary artery, and three types of stenting techniques for comparing two kinds of artery shapes using computational fluid dynamics analysis.

2. Materials and Methods

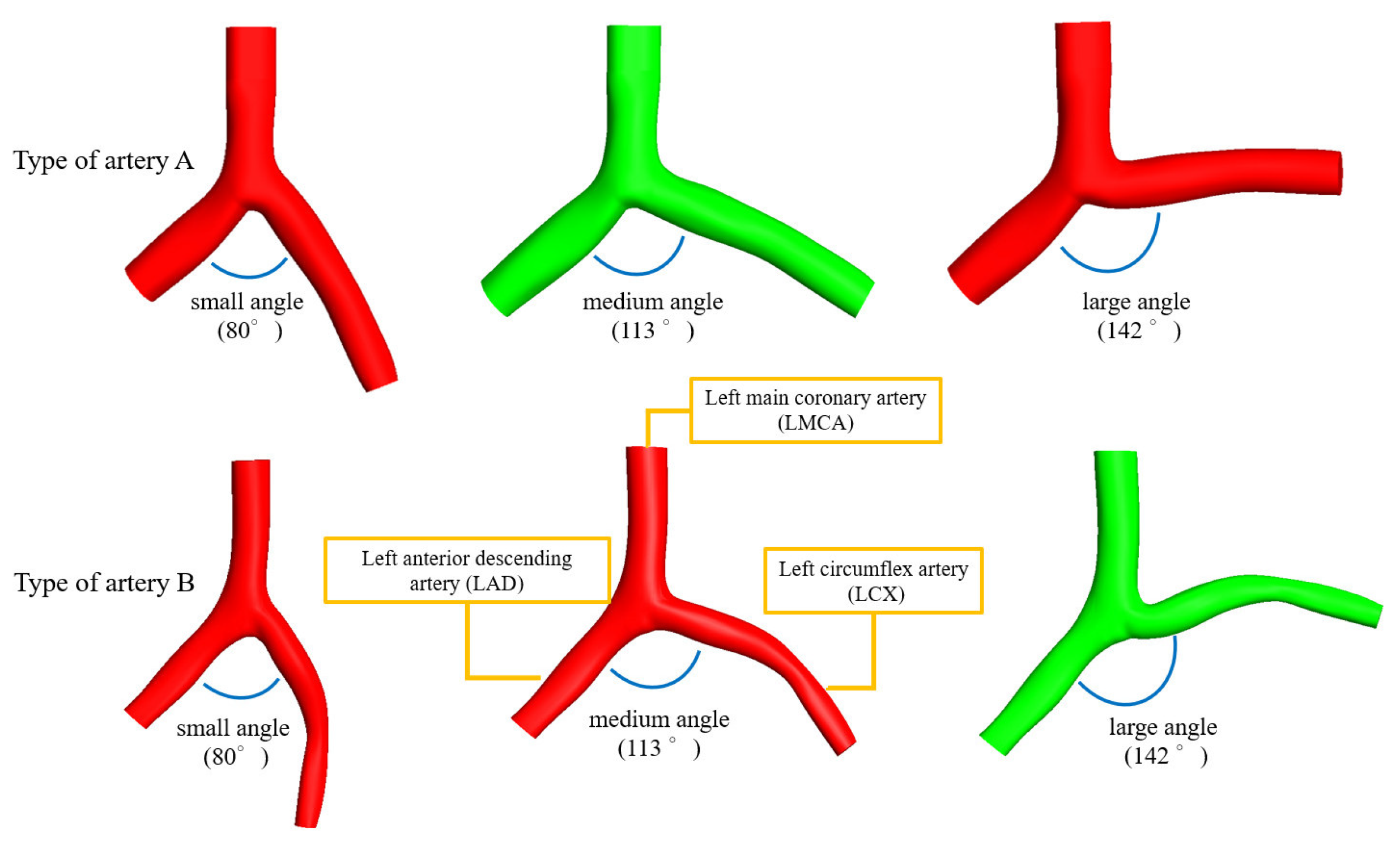
The left coronary artery bifurcation models were reconstructed based on a reverse engineering (RE) technique by scanning two different shapes of artificial medical-trained coronary artery models by Nextengine (Nextengine Inc., Santa Monica, CA, USA). Each RE-based model was further transferred into a software of Geomagic Essentials (Geomagic Inc., Morrisville, NC, USA) for a surfacing process to generate a solid model of the basic coronary bifurcation artery. Two basic solid coronary artery bifurcation models (called artery A and artery B) with different shapes were generated with green color models, as shown in Figure 1. The left coronary artery bifurcation model in this study was composed of the left main coronary artery (LMCA), left anterior descending artery (LAD), and left circumflex artery (LCX), as shown in Figure 1. One of the two coronary artery models was larger in diameter and straighter in both the LCX and LAD side branches. Another model was smaller in diameter and more curved in the LCX side branch. These two types of the arterial models could reflect the majority of patients in a group of stenting stenosis in a clinic, not just presenting with the idealized model. The average diameters of LMCA, LAD, and LCX of the artery A are 4.4 mm, 3.9 mm, and 3.8 mm, respectively, and the original bifurcation angle of the artery A is 113°. The average diameters of LMCA, LAD, and LCX of the artery B are 3.5 mm, 2.9 mm, and 2.5 mm, respectively, and the original bifurcation angle of the artery B is 142°. Previous studies have pointed out that the bifurcation angles of the left coronary artery were different for each patient [26,27]. In order to investigate the restenosis effects of the coronary artery bifurcation angles, this study defines three ranges for the coronary artery bifurcation angles: (a) small angle—the bifurcation angle was less than 90°; (b) medium angle—the bifurcation angle was between 90° and 120°; (c) large angle—the bifurcation angle was more than 120°. Hence, three types of bifurcation angles of the arteries A and B in the small, medium, and large angles were remodeled in 80, 113, and 142°, respectively. The variations of the bifurcation angles were mainly changed between the LAD and LCX arteries by a computer-aided procedure (SolidWorks 2010, SolidWorks Corp, Concord, MA, USA) to generate new models with different bifurcation angles. Three bifurcation angle models in the arteries A and B are also showed in Figure 1. The coronary artery models of this study were reconstructed from a human anatomical-based silicon model of the left coronary artery by reverse engineering scanning. The two silicon models of the left coronary artery have precise geometry to reflect the artery’s contour, surface feature, and inlet and outlet diameters. The two models are mainly to replicate two types of left coronary arteries in size and shape of the human subjects. The two models are not reconstructed through a CAD procedure. The CAD arterial model has uniformity in the artery shape for each artery branch, particularly in the bifurcation region, and also reflects non-reality geometry. Hence, the two anatomically based models of this study can provide a reliable artery size and shape to investigate the stenting stenosis problem, but are not idealized models.

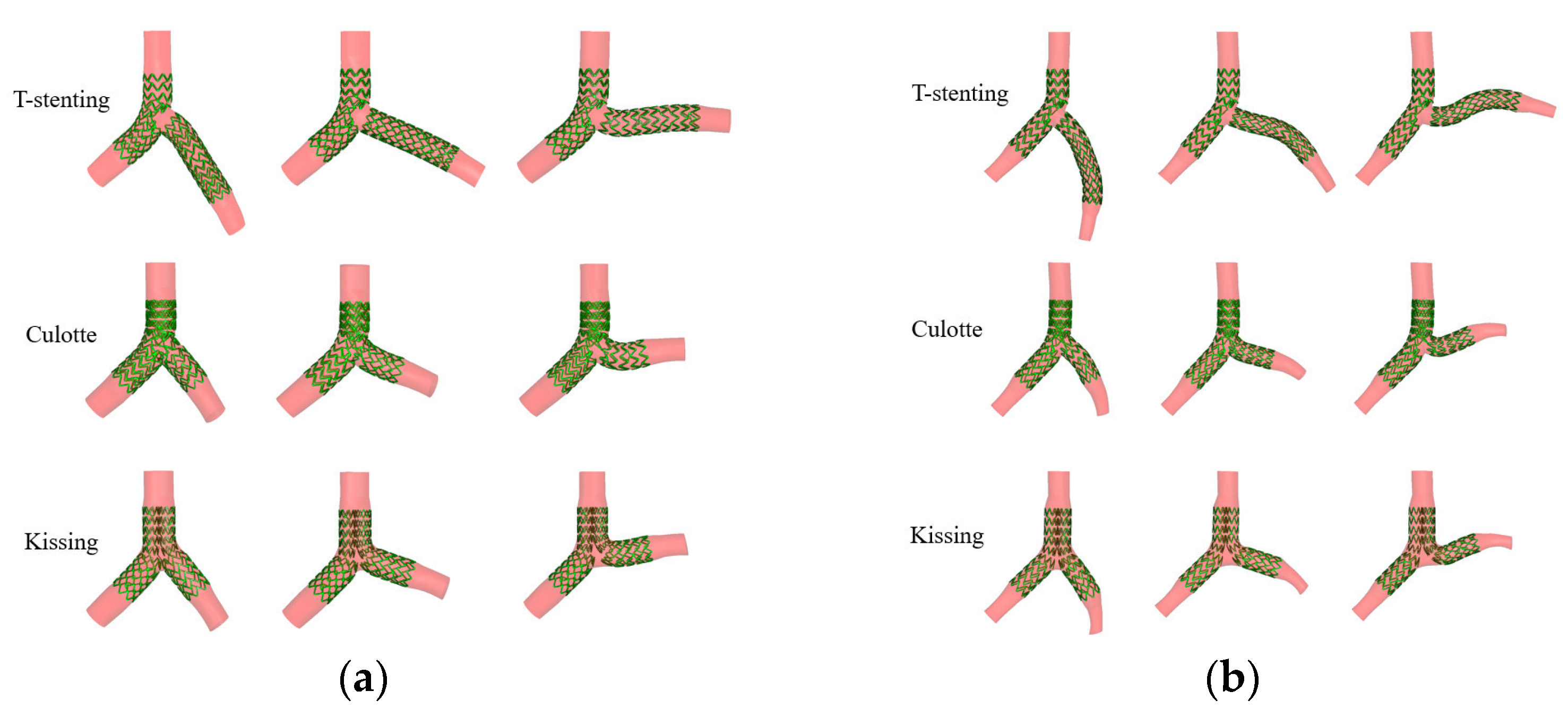
Bifurcation lesions are one of the complex lesion subsets to treat with percutaneous coronary interventions. However, bifurcation interventions have a lower rate of practical success and a higher rate of stent restenosis. This study selected bifurcation lesion in the location of the ostium of each branch as an investigating object of the clinical problem. Hence, two-stent techniques were selected for this type of bifurcation lesion. A number of two-stent techniques are available for clinic, but effects of stenting restenosis are still unclear. Three types of two-stent techniques are selected in this study, including T-stenting, Culotte, and Kissing. The stent positioning, balloon inflation, and crush operation are followed by the surgeon’s treatment protocol.

The stent CAD model of this study was considered to construct according to the Boston stent of non- and inflated-structures (Figure 2) using the SolidWorks 2010. The stent model, that was 15 mm in length and 0.8 mm in strut thickness, contained 10 strut units. Three stenting techniques—T-stenting, Culotte, and Kissing—in the bifurcation region of the left coronary artery were selected for investigating the restenosis effects after the stenting process. In the stent model reconstruction of structure expansion, the two-stent inflation is performed in the transparent silicon model of the regional coronary artery bifurcation, and then a micro-CT is executed to obtain images of the inflated stent in order to understand the truss deformation in between the two stents. The stent images are chipped in some truss and have a severely deformed structure if the stent model reconstructs directly from micro-CT. Hence, the authors developed a method of stent reconstruction combining CAD and CT images to obtain a perfect stenting model without the truss and structure chipped. The model from the CT image-based reconstruction as a template model of the inflated stent is reconstructed first; although, this stent model is a chipped structure in the contact region of the two-stent inflation. Then, the CAD model of the stent can be designed and corrected step-by-step through a 3D structure alignment between the CT image-based model and CAD-based model. The perfect inflation model of the two-stent structure can be obtained according to the CT image-based model, excluding the chipped truss structure of the two-stent inflation. The perfect structure of the two-stent stenting can then be obtained for investigating the effects of stenting restenosis with the three types of stenting techniques.

The contact condition between the stent and the arterial wall under the stent placement was applied totally expansion to lock into place inside the artery. Hence, a half strut thickness of the inflated stent was embedded into the arterial wall in all models to consider a universal contact condition between the stent and the arterial wall. The deformation of the arterial wall could influence blood flow and cause variations of wall shear stress. Hence, this assumption could simplify a complex combination in the relationship between the stent and the arterial wall. The three stenting techniques of the coronary artery bifurcation models in the arteries A and B are shown in Figure 3. The element type of Mesh200 was selected to mesh the artery and stent in the tetrahedral shape with 10 nodes. The criterion of the convergence testing was considered to stop increasing in elements when the value of the percent relative error (PRR) was less than 5%. Hence, element numbers of the artery with an inflated two-stent model were approximately 3,938,265 to obtain the convergence criterion. The convergence elements were applied and meshed for whole arterial models of the CFD simulation.

All stenting bifurcation models were performed in the CFD analysis using the CFX module of the ANSYS Workbench 16 (ANSYS Inc., Canonsburg, PA, USA). The non-Newtonian Casson model was selected to describe the blood’s shear-thinning behavior [28]. The blood density and the dynamic viscosity of the blood were assumed at 1060 kg/m³ and 0.0035 Pa∙s, respectively [29]. The pulsatile flow rate was applied as an inlet boundary condition at the left main coronary artery (Figure 4) [30].

A constant zero pressure boundary condition was applied at the outlet. Moreover, both the arterial wall and stent were rigid with a no-slip boundary condition. The hemodynamic evaluations of the CFD analysis included flow velocity (FV), time-averaged wall shear stress (TAWSS), and oscillatory shear index (OSI). Wall shear stress (WSS) is used to associate dynamic behaviors of blood flow with potential clinical outcomes. The instantaneous WSS is defined as

$$WSS={\mathcal{T}}_t-\left({\mathcal{T}}_t·n\right)n.$$

(1)

The WSS can be further calculated as a time-averaged index over a cardiac cycle. The formula is defined as

$$TAWSS=\frac{1}{T}{{\displaystyle \int }}_0^T\left|WSS\right|dt$$

(2)

where T is the period of one cardiac cycle. In vitro studies have demonstrated that low TAWSS (<0.5 Pa) is associated with promoting endothelial cell proliferation and plaque growth [31]. The OSI is a non-dimensional scalar variable; it represents the change of direction of the WSS vector from a predominant blood flow direction during the cardiac cycle. The value of the OSI distribution is computed from 0 to 0.5; both values 0 and 0.5 represent a region of unidirectional flow and full-oscillatory flow, respectively. The high OSI (>0.2) has been considered to increase endothelia cell proliferation and to cause higher vessel wall permeability [32]. The formula of the OSI is defined as below

$$OSI=\frac{1}{2}\left(1-\frac{\left|{{\displaystyle \int }}_0^{T}WSSdt\right|}{{{\displaystyle \int }}_0^T\left|WSS\right|dt}\right)$$

(3)

The four consecutive cardiac cycles were simulated for investigating the stenting restenosis with different stenting techniques by the CFD simulation. Moreover, final results were taken from the fourth cycle for comparing the effects of stenting restenosis with different stenting techniques. This determination of cardiac cycles was cited as a reference from Beier et al. in 2016 [33]. Hence, this study set four cardiac cycles to perform simulation to provide the results of the TAWSS and OSI values.

3. Results

The results of the blood FV of the three bifurcation angles in the two arteries with the three stenting techniques is shown in Figure 5. The comparing group without stenting models—in the two types of arteries A and B—showed that the laminar flow was detected in the three angles of the bifurcation arteries. However, stenting techniques were applied in the arteries A and B to cause recirculatory flow at the leading edge of the LCX. The recirculatory flow became more pronounced when the bifurcation angles were increased. Among the three stenting techniques, the LCX flow velocity of the T-stenting was lower than the Culotte and Kissing. An additional low-velocity region was observed at the bifurcation carina when the Kissing bifurcation angle increased. The flow velocity of the artery A was higher than the artery B for comparing whole models.

The results of the wall pressure distribution of the three bifurcation angles in the two arteries with the three stenting techniques is shown in Figure 6. The comparing group without the stenting models in the two types of arteries A and B showed that the bifurcation carinal had a higher wall pressure. The higher wall pressure of the arteries A and B by T-stenting occurred on the LMCA and bifurcation carinal. The wall pressure of the artery A with T-stenting was more pronounced when the bifurcation was increased. In contrast, the wall pressure of the artery B had a reverse tendency. In the model of Culotte stenting, the higher wall pressure of the artery A was concentrated on the LMCA stent inlet and bifurcation carinal. However, as for the artery B, it was concentrated on the inlet of the LMCA and bifurcation. The higher wall pressures of the two arteries were more pronounced when the bifurcation angles were decreased. In the model of the Kissing stenting, the higher wall pressure of the artery A was concentrated on the inlet of the LMCA stent. However, as for the higher wall pressure of the artery B, both the LMCA and LCX presented with a high wall pressure. A decreased tendency of the wall pressure was discovered when the bifurcation angle was increased. Moreover, the wall pressure of the artery B was higher than the artery A for comparing whole models.

The distribution of the specific low TAWSS threshold only demonstrated less than 0.5 Pa of the three bifurcation angles with the three stenting techniques in the two arteries, as shown in Figure 7. The specific low TAWSS in the artery A was wider than that in the artery B. The region of the specific low TAWSS in the artery A by the T-stenting was concentrated on the proximal site of the lateral LAD and the proximal site of the lateral LCX. In addition, the region of the specific low TAWSS was concentrated on the proximal site of the lateral LCX and the distal site of the medial LCX in the artery B. In the models of Culotte stenting, the region of the specific low TAWSS of the artery A was similarly concentrated on the proximal site of the LMCA, the proximal site of the lateral LAD, and the proximal site of the lateral LCX. However, as for the region of the specific low TAWSS of the artery B, it was concentrated on the proximal site of the lateral LCX. In the models of the Kissing stenting, the region of the specific low TAWSS of the artery A was concentrated on the proximal site of the lateral LAD, the proximal site of the lateral LCX, and the bifurcation carina. However, as for the region of the specific low TAWSS of the artery B, it was concentrated on the LCX and bifurcation carina. Moreover, the regions of the specific low TAWSS of the arteries A and B were significantly detected to increase tendency when the bifurcation angles of the artery were enlarged.

For further understanding the area ratio of the TAWSS in the percentage of less than 0.5 Pa, the TAWSS area of the artery with less than 0.5 Pa divided by the whole TAWSS area of the artery was calculated. The critical TAWSS (<0.5 Pa) area ratio of the two arteries with the three stenting techniques in the three bifurcation angles is shown in Figure 8. The critical TAWSS area ratio in the artery A was larger than that of the artery B. Moreover, both the arteries A and B in the critical TAWSS area ratio were significantly detected to increase when the bifurcation angles of the artery were enlarged. The largest critical TAWSS area ratio of the artery A was obtained at the T-stenting technique. The ranks of the critical TAWSS area ratio in the models of large bifurcation angles were T-stenting (25.30%) > Culotte (20.93%) > Kissing (13.80%). The largest critical TAWSS area ratio of the artery B was detected at the Kissing technique. The ranks of the critical TAWSS area ratio were Kissing (12.02%) > Culotte (7.54%) > T-stenting (7.43%). The rank of the critical TAWSS area ratio in the arteries A and B models of medium bifurcation angles were Culotte (19.11%) > T-stenting (18.52%) > Kissing (11.96%), and Kissing (10.47%) > Culotte (7.42%) > T-stenting (7.04%), respectively. The ranks of the critical TAWSS area ratio in the arteries A and B models of small bifurcation angles were Culotte (18.60%) > T-stenting (16.59%) > Kissing (9.99%), and Kissing (9.35%) > Culotte (6.76%) > T-stenting (6.59%), respectively.

The specific regions of the OSI value larger than 0.2 were considered a higher risk of stenting restenosis after placement of a two-stent operation. The figure presentation of the specific regions was further presented in the sections of result and discussion. The results of the specific OSI distribution are shown in Figure 9. The larger 0.2 in the OSI value of the artery A by the T-stenting was mainly concentrated on the LCX branch. The larger 0.2 in the OSI value of the artery B by the T-stenting was also concentrated on the LCX branch, particularly on the proximal site of the lateral LCX branch. In the models of the Culotte stenting, the larger 0.2 in the OSI value of the artery A was mainly focused on the proximal site of the LAD and LCX branches. In contrast, the larger 0.2 in the OSI value of the artery B was concentrated on the proximal site of the lateral LCX branch. In the models of the Kissing stenting, the larger 0.2 in the OSI of the artery A was mainly concentrated on the lateral LCX branch and bifurcation carina. Likewise, the larger 0.2 in the OSI value of the artery B was also focused on the lateral LCX branch and bifurcation carina. The larger 0.2 in the OSI values of the two arteries became more pronounced when the bifurcation angles were augmented.

For evaluation of the arterial OSI, the arteries selected were three perpendicular sections to the proximal LMCA, LAD, and LCX near the bifurcation region to calculate the OSI variations. Each section was uniformly picked, with 50 points of the OSI on the arterial section edge. The section contour of the arteries was further divided into four regions—A, B, C, and D regions—to evaluate the differences of the OSI. The 12 o’clock position was selected from the OSI as the initial capture point, from number 1 to number 50, in a clockwise manner (Figure 10). The comparisons of the mean OSI (mean values larger than 0.2 to collect for calculating) of the two arteries are shown in Figure 11a. Those larger than 0.2 of the OSI represented that a high risk of a stenting restenosis was confirmed in the clinical report. The results indicated that the tendency of the OSI for the three types of bifurcation angles in each arterial branch with the three stenting techniques in the artery A was larger than that in the artery B. The peak OSI in the LMCA, LAD, and LCX branches of the large bifurcation angle was detected in the Kissing (0.31), Culotte (0.32), and Culotte (0.33) techniques, respectively. The peak OSI in the LMCA, LAD, and LCX branches of the medium bifurcation angle was detected in the Kissing (0.30), Kissing (0.33), and Culotte (0.33) techniques, respectively. The peak OSI in the LMCA, LAD, and LCX branches of the small bifurcation angle was detected in the Culotte (0.31), Kissing (0.30), and Culotte (0.32) techniques, respectively. The comparing results indicated that the large OSI (>0.2 threshold) distributions were significantly located at the LCX branch to cause a high risk of the stenting restenosis (Figure 11b). The most significant high-risk regions of the stenting restenosis in the LCX with three types of the large, medium, and small angles were detected at the C-D, C, and C regions, respectively. This result revealed that the restenosis region was mainly concentrated at the lateral-inferior site of the LCX branch.

4. Discussion

The standard treatment of a coronary artery bifurcation stenosis is performed by a technique of coronary artery stenting [34]. The in-stent restenosis may still occur after coronary bifurcation stenting in the clinic. In-stent restenosis is caused by chronic inflammatory symptoms of the persistent mechanism stress by the metal stent [35], or the stent-induced disturbances of blood flow changes the wall shear stress of the endothelial cell that causes the endothelial cell dysfunction [36]. Coronary artery bifurcation is a predilection of restenosis because of the complex hemodynamic local blood flow that the coronary bifurcation contributes to the restenosis [37,38,39]. Time-average wall shear stress and Oscillatory shear index of computational fluid dynamics analysis have been used as parameters to evaluate hemodynamics. Wall shear stress is the shear stress that the fluid acts on the arterial wall, and has a recognized effect on the arterial wall biology [40]. Stent implantation affects the regional arterial geometry by changing the local blood flow, causing the turbulence flow [41,42]. Low wall shear stress (<0.5 Pa) induces neointimal and increases the risk of inflammatory symptoms [43,44]. The OSI is a non-dimensional scalar variable that explains the degree of deviation of the WSS from the antegrade flow direction. A high oscillatory shear stress index (OSI > 0.2) is associated with an increased risk of neointimal hyperplasia, inflammation, and thrombosis [43,44]. Therefore, both TAWSS < 0.5 Pa and OSI > 0.2 were selected as the restenosis threshold of detrimental hemodynamic indicators.

The velocity results showed that the artery B was higher than the artery A, and the velocity of the LAD was higher than the LCX in this study. The different stenting techniques showed that the velocity was lower at the leading edges of LAD and LCX, and the recirculatory flow concentrates at the leading edge of the LCX proximal, which becomes more obvious as the bifurcation increases. The recirculatory flow in the T-stenting was more significant than other stenting techniques. The T-stenting was a small area of the coronary bifurcation into the LCX proximal without stent coverage. In the two other stenting techniques, the stent extends completely from the main branch to the side branches. In the T-stenting, the small area without stent coverage at the proximal LCX induced blood recirculatory when the blood flux moved through from the LMCA into the bifurcation branch of a segment of the area without stent coverage, and then blood flowed into a stent-covered area of the LCX branch to further disturb the obviously blood-steady situation influenced by the structure of the stent strut. The Kissing technique was detected in a particular area without stent attachment at the bifurcation carina, which was evidenced to increase extensively in proportion to the bifurcation angles, to confirmeffects of the low-velocity recirculatory near the bifurcation carina.

In addition, the index of the artery wall pressure was also considered an important role to investigate the stenting restenosis with three types of stenting techniques in the different arteries. Thubrikar et al. [45] indicated that the arterial wall pressure and accompanying stretch is one of the contributing factors to the atherosclerotic lesions. Excessive wall pressure will cause atherosclerotic plaques and the plaques to rupture [46]. In the wall pressure distribution, results showed that the three stenting techniques caused the wall pressure to significantly increase in the two arteries. In the three stenting techniques, the wall pressure of the artery B with the Kissing stenting technique had the most significant increase than the other models.

The distribution of the specific low TAWSS in the artery A was wider than the artery B, and the area of the specific low TAWSS seemed to be increased with the bifurcation degree. According to the outcomes of the specific low TAWSS, it was shown that the T-stenting of the artery A could provide the worst presentation with a large bifurcation angle, but the best performance was the Kissing technique. The specific low TAWSS of the artery B displayed that there was no obvious difference in the performance of the specific low TAWSS between the T-stenting and Culotte techniques. The kissing technique was easier to cause the specific low TAWSS than the other two techniques in the artery B.

The trend of the TAWSS was confirmed as the same distribution with the blood velocity in this study. The distribution of the specific low TAWSS in the artery A was wider than the artery B, and the distribution of the specific low TAWSS expended with the bifurcation degree increases. In the T-stenting, the specific low TAWSS of the artery A was distributed at the lateral site of the LAD and whole LCX, but the specific low TAWSS of the artery B was only distributed at the lateral site of the LCX. The velocity of the T-stenting of the lateral LAD was lower than that of the medial one in the artery A models. Moreover, a significant blood reflux was located at the proximal LCX, and the low blood flow velocity was also detected in this whole branch. The blood flow velocity of the LAD and the LCX of the lateral site was lower than that of the medial one in the artery B models. The position of the specific low TAWSS was evidenced to obviously locate at the region of the low blood flow velocity. In the Culotte technique, the specific low TAWSS in the arteries A and B was mainly concentrated at the leading edges of the LAD and LCX, as well as the LCX, respectively. However, the specific low TAWSS in the T-stenting and the Kissing were not discovered at the LMCA branch. The Culotte technique that caused the TAWSS was that a double-layer structure of stenting in the LMCA induced small backflows of the blood flow within the two layers of struts. The specific low TAWSS under the Kissing application in the artery A was concentrated on the regions of the lateral LAD, lateral LCX, and bifurcation carina. The specific low TAWSS in the artery B was concentrated on the lateral LCX and bifurcation carina. The bifurcation carina without any stent coverage in the Kissing technique could cause a reflection of low velocity turbulence to generate the specific low TAWSS response. The LCX distribution of the specific low TAWSS in the Kissing technique was wider than the other two stenting techniques in the model of the artery B. The Kissing technique was inserted two stents to cause diameter expansion of the LMCA branch in the artery B; therefore, the blood velocity of the LAD and the LCX revealed a lower tendency than the other two stenting techniques. In other words, the Kissing technique could result in a more separated distribution of the specific low TAWSS than the other two stenting techniques in the artery B. The expansion effect of the Kissing operation in the LMCA branch of the artery A was not a pronounced tendency, due to an original larger diameter to reduce the effects of both low velocity and the specific low TAWSS. According to the low TAWSS area ratio, it was shown that the T-stenting of the artery A could provide the worst presentation with a large bifurcation angle, but the best performance was the Kissing technique. The low TAWSS area ratio of the artery B displayed that there was no obvious difference in performance of the low TAWSS between the T-stenting and Culotte techniques. The Kissing technique was easier to cause a low TAWSS than the other two techniques in the artery B.

The inflated two-stent structure in the coronary artery bifurcation could cause a complex blood flow to change both wall shear stress and a steady flow condition. The index of the OSI had been used to investigate the effects of the restenosis in the side branch after a stenting operation in a clinic. The higher OSI values (>0.2) were associated with a significant risk of neointima hyperplasia, inflammation, and thrombosis. This study indicated that the higher OSI value was mainly detected at the LCX branch proportionate to the bifurcation angles. The blood flow from the LMCA to the bifurcation region and the structure of stent could cause an obvious disturbance in flow, and that could cause wall shear stress of an adjacent region’s oscillations. Hence, the OSI value of lesion-caused capacity would be rapidly raised at the LCX branch.

The result of the arterial branches revealed that the OSI of the LCX was maxed among three branches, and then when located at the LMCA, the LAD showed minimally in the arteries A and B. Both Culotte and Kissing techniques in the stenting structures around the bifurcation area were more complex than the T-stenting. Moreover, the usage of double stents in a deformed structure could interfere with the blood flow velocity and disturbance, resulting in the OSI increasing and a high risk of restenosis. Furthermore, according to the OSI distribution of the arterial branches, the high OSI was mainly concentrated at the regions C and D, which was located at the lateral side of the LCX arterial wall. Importantly, the distribution tendency of the OSI was consistent with the blood flow in the LCX branch.

The CFD results of the low TAWSS and the OSI in the three branches of the two types of arteries indicated that the LCX branch near bifurcation was evidence of a high risk of stenting restenosis. This outcome was the same as the clinical consequence of bifurcation-induced restenosis by using the double-stent technique. The previous literatures have pointed out that the stenosis rate at the LCX branch is approximately 12% [47,48]. The distributions of the blood flow velocity and wall shear stress presented that the inflated truss structure of the in-stent disturbed the blood flow on the lateral side of the arterial wall and generated recirculatory flow, causing the local effect of the low blood flow velocity. The low TAWSS significantly affected lipid and platelet deposition. The outcome of this study was consistent with the experimental results of an in vitro bifurcation model by Yazdani [49]. In terms of bifurcation angle effects, the results of the three bifurcation angles in this study indicated that the large bifurcation angle could cause recirculatory flow and increase the area of low wall shear stress. This finding is also consistent with an in vitro study in a research report by Nakazawa [50]. The stent expansion by balloon inflation could change the boundary layer separation on the lateral side of the arterial wall to generate recirculatory flows. In a clinical observation, the large bifurcation angle in the artery could lead to larger recirculatory flows. Chen et al. [51] proposed that the stent length in the LCX branch would be affected by local hydrodynamics by using the double stent technique. The factor of a longer stent in the side branch may cause low wall stress and a high OSI, which will adversely affect the hemodynamics of the side branch. The T-stenting in this study had placed a complete stent on the LCX branch, but both of the Culotte and Kissing techniques had only a half stent structure on the LCX branch. Therefore, the distribution of the low TAWSS and high OSI in the T-stenting technique is indeed greater than both of the Culotte and Kissing techniques. This outcome is consistent with the previous research of Chen’s study [51].

The result of this study indicated that the T-stenting technique was evidenced as the worst performance with the quantitative process of the TAWSS and the OSI. In other worlds, the restenosis probability of the T-stenting technique is higher than with the Culotte and Kissing techniques. Although the T-stenting is worse than the other two stenting techniques, each stenting technique has some problems of potential hemodynamic. For example, the Culotte technique in the LMCA branch performed a layer overlap of two metal stents, causing a blood disturbance in the overlapped region. On the other hand, the Kissing technique also puts two stents into the LMCA branch, which may cause excessive stress on the arterial wall to induce turbulent flow and low wall shear stress in the non-stent covered part of the bifurcation carina to further generate restenosis.

Currently, the numerical analysis of the CFD is used to investigate blood-flow-related hemodynamics and the local blood environment after stent implantation. The important influencing factors of fluid dynamics in stent implantation includes stent geometry, stent implantation technique, and coronary artery bifurcation geometry. The patient-specific CFD model with indicators such as wall shear stress and oscillatory shear index can be calculated to predict stenting technique evaluations and understand pre- and post-treatment outcomes. According to the CFD analysis, this study has some limitations as discussed below. There are only two anatomy-based artery samples performed in this study. In the future, this study will increase the arterial geometric type of the coronary stenosis patients to understand the influence of the specific age and gender to provide more complete outcomes. Moreover, the coronary arterial wall is assumed as a rigid material to neglect deformations of the arterial wall initiating by heart pulsation. Furthermore, a stent is a perfectly assumed expansion to a cylindrical shape, and completely contacts and inserts into the arterial inner wall. The contact depth between the stent and arterial wall is uniformly embedded for all of the models. Finally, the outlet conditions of each branch were simplified with a constant pressure to interact between the bold flow and two-stenting in the CFD simulation.