PID Control Model Based on Back Propagation Neural Network Optimized by Adversarial Learning-Based Grey Wolf Optimization

Abstract

In processes of industrial production, the online adaptive tuning method of proportional-integral-differential (PID) parameters using a neural network is found to be more appropriate than a conventional controller with PID for controlling different industrial processes with varying characteristics. However, real-time implementation and high reliability require the adjustment of specific model parameters. Therefore, this paper proposes a PID controller that combines a back-propagation neural network (BPNN) and adversarial learning-based grey wolf optimization (ALGWO). To enhance the unpredictable behavior and capacity for exploration of the grey wolf, this study develops a new parameter-learning technique. Alpha gray wolves use the random walk of levy flight as their hunting method. In beta and delta gray wolves, a search strategy centering on the top gray wolf is employed, and in omega gray wolves, the decision wolves handle the confrontation strategy. A fair balance between exploration and exploitation can be achieved, as evidenced by the success of the adversarial learning-based grey wolf optimization technique in ten widely used benchmark functions. The effectiveness of different activation functions in conjunction with ALGWO were evaluated in resolving the parameter adjustment issue of the BPNN model. The results demonstrate that no unique activation function outperforms others in different controlled systems, but their fitnesses are significantly inferior to those of the conventional PID controller.

1. Introduction

In control manufacturing, standard PID control algorithms are frequently utilized as a control strategy, providing the benefits of unequivocal simplicity and excellent performance [1], among others. PID control algorithms, alongside traditional methods, are mainly used for control-parameter optimization [2,3]. However, the PID control algorithm has several drawbacks, including difficulty in parameter setting and susceptibility to disturbance. More PID tuning algorithms, such as neural networks [4], machine learning [5,6], and heuristic algorithms [7,8], should be developed for use in actual control processes to address these issues.

However, as controlled systems become increasingly complex, there is a growing need for control strategies that can handle time-varying behavior and time delays. The complexity of the controlled system contributes to the frequently subpar control effects of a PID controller [9,10]. At present, many intelligent algorithms have been developed. Systems with time-varying and hysteresis delays can benefit significantly from these approaches [11,12]. By manually modifying the control rules, the expert PID control algorithm can be applied to specific simulation systems [13]. Fuzzy PID control can be included in the controller using a lookup table, making it simpler to obtain better control effects [14,15,16,17,18,19]. However, the expert PID and fuzzy PID controllers always have subpar timing precision and limited anti-interference capabilities. Due to the benefits of rapid adjustment velocity and excellent accuracy [20,21], the neural network PID control approaches have been applied in numerous complicated systems [22,23,24]. In 2022. Wang et al. [25] used the PSO-BPNN-PID algorithm to control the nutrient solution, and the simulation results demonstrated that the reaction time and accuracy of the control system were superior to those of the conventional PID control method. The same year, a BPNN-PID controller was developed using a Xilinx field-programmable gate array (FPGA) technology in [26]. The findings revealed that the suggested system exhibited fast convergence and dependable performance. To better regulate the delay system in 2023, a particle swarm optimization-radial basis function (PSO-RBF) is utilized in place of a traditional PID controller [27]. In general, BP neural network research has thus shown positive results.

In addition, to achieve effective controller performance, these parameters of the BPNN-PID controller must be properly optimized. Moreover, heuristic methods are typically used in the process of parameter optimization [28,29,30,31,32]. In 2018, the BP neural network was optimized using a mind evolutionary algorithm to predict wave heights; the model achieved great accuracy and a fast running time [33]. In 2021, using an algorithm known as the water cycle method, Zhang et al. [34] improved the BP neural network model for landside prediction. In 2022, it was proposed that the Boost circuit’s dynamic and generally pro capabilities be improved by combining a genetic algorithm with BP neural network PID control (GA-BP-PID) [35]. Therefore, an ALGWO-BPNN control model is proposed in this paper as a better way to control time-varying and time delay systems. The primary contributions of the proposed controller are as follows:

• The GWO technique is used to propose and optimize a PID control model based on a BPNN. Considering that the GWO algorithm is not necessarily the best for solving complex problems, a stochastic adjustment convergence factor formula is proposed, and the beta and delta are adjusted in combination with a differential evolution (DE). With the enhanced GWO method, the connection weight of the BPNN achieved a verifiably better control effect.
• Several benchmark functions are selected to analyze ALGWO.
• Some activation functions for the output layer of the BPNN model are analyzed and compared.
• The ALGWO-BPNN model is simulated and compared with the conventional PID controller.

2. Related Works

2.1. Back Propagation Neural Network

Using the error back propagation technique, a multilayer feedforward neural network is called to become a back propagation neural network. Due to its nature, it has outstanding performance in nonlinear mapping, such as function approximation and pattern recognition.

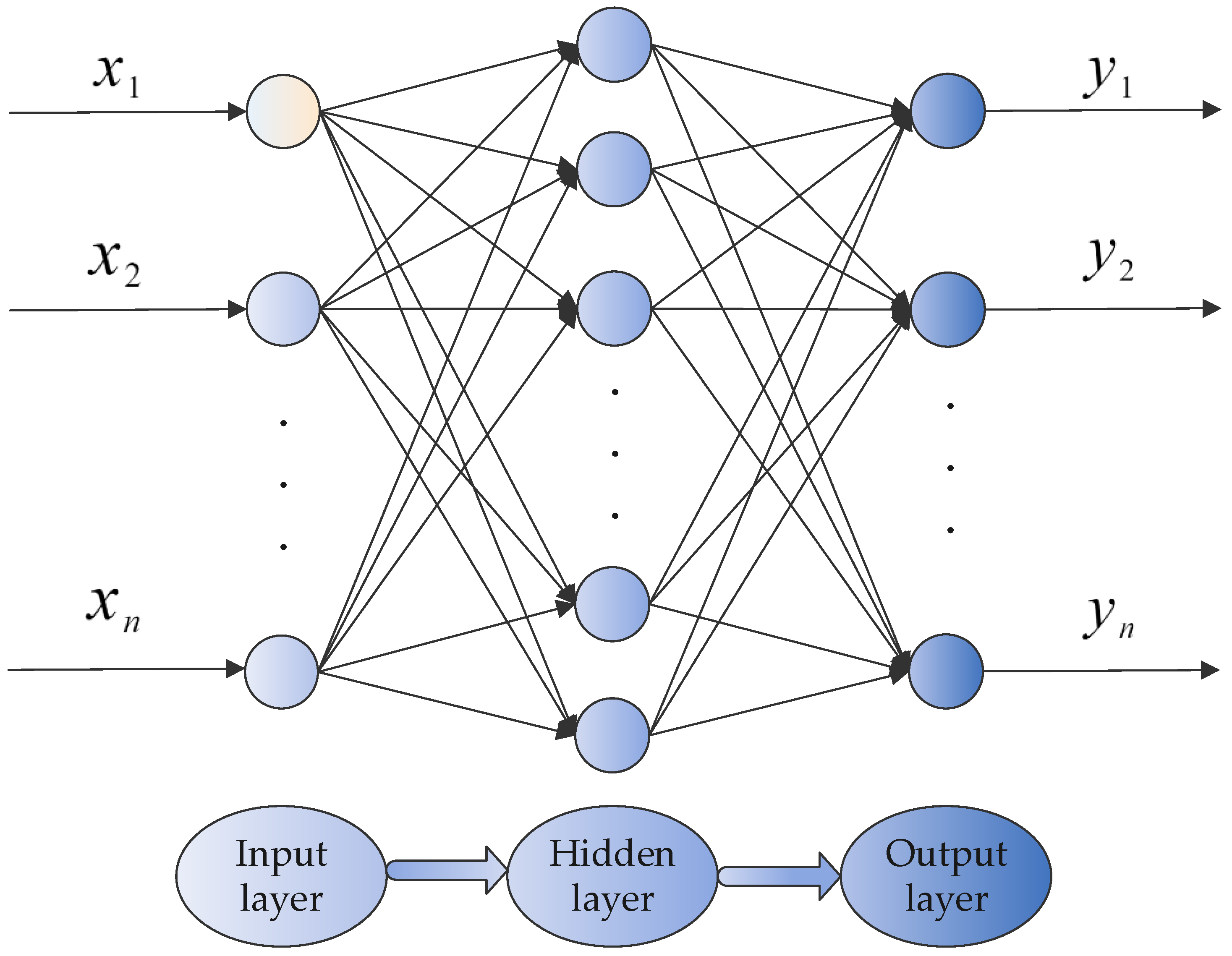
There are three layers in a back propagation neural network model: input, hidden, and output. The structure of the fundamental BPNN model is depicted in Figure 1. The input layer deals with the kind and volume of input. By the quantity of control layers and activation functions, the hidden layer introduces the possibility for nonlinear mapping. The output layer is in charge of producing certain information.

Output of the neuron model structure is usually expressed as a nonlinear combination of input and weight, as shown in (1).

$${\hat{y}}_j=f({\displaystyle \sum _{i=1}^n{w}_{ij}}{x}_i-b_{ij})$$

(1)

where ${\hat{y}}_j$ is output of the neuron, $x_i$ is output of the neuron, $b_{ij}$ and $w_{ij}$ are the bias and weight of the neuron, and $f()$ is an activation function.

Typical loss function for optimization is shown in (2).

$$E={\displaystyle \sum _{i=1}^n{({\widehat{y}}_i-y_i)}^2}$$

(2)

where ${\widehat{y}}_i$ is the truth value and $E$ is a loss function.

Gradient Descent (GD) technology is typically used for weight minimization [36].

$$w_i{}_j=w_i{}_j-\eta \frac{\partial E(w_i{}_j)}{\partial w_i{}_j}$$

(3)

where $\eta$ is a learning rate.

2.2. Grey Wolf Optimization Algorithm

Authors of [37] examined the grey wolf’s social behavior before modeling it and creating an algorithm for the grey wolf’s optimization.

The pros and cons of the actual problems’ remedies are used to categorize the entire grey wolf population. The best option is designated as the alpha $(\alpha )$, the second best option is designated as the beta $(\beta )$, the third best option is designated as the delta $(\delta )$, and the remaining gray wolves are designated as the omega $(\omega )$.

The following describes how gray wolves’ behavior toward nearby prey is mathematically modeled:

$${\overrightarrow{D}}_i=\left|{\overrightarrow{W}}_{prey}\cdot {\overrightarrow{X}}_{prey}-{\overrightarrow{X}}_i\right|$$

(4)

$${\overrightarrow{X}}_i={\overrightarrow{X}}_{prey}-{\overrightarrow{A}}_i\cdot {\overrightarrow{D}}_i$$

(5)

where ${\overrightarrow{X}}_{prey}$ is the position of the prey, ${\overrightarrow{X}}_i$ is the position vector of the grey wolf, and ${\overrightarrow{A}}_i$ and ${\overrightarrow{W}}_{prey}$ are coefficient vectors.

The ${\overrightarrow{A}}_i$ and ${\overrightarrow{W}}_{prey}$ are calculated as follows:

$${\overrightarrow{A}}_i=2\cdot rand\cdot \overrightarrow{a}-\overrightarrow{a}$$

(6)

$${\overrightarrow{W}}_{prey}=2\cdot rand$$

(7)

where $\overrightarrow{a}$ decreases linearly and rand are random vectors.

Because we do not know where the prey is, we can only roughly determine where the gray wolf is by using our decision-making level to mimic the gray wolf’s hunting behavior. Through the following, each gray wolf can update its location:

$$\left\{\begin{array}{c}{\overrightarrow{D}}_{\alpha }=\left|{\overrightarrow{W}}_{\alpha }\cdot {\overrightarrow{X}}_{\alpha }-\overrightarrow{X}\right|\\ {\overrightarrow{D}}_{\beta }=\left|{\overrightarrow{W}}_{\beta }\cdot {\overrightarrow{X}}_{\beta }-\overrightarrow{X}\right|\\ {\overrightarrow{D}}_{\delta }=\left|{\overrightarrow{W}}_{\delta }\cdot {\overrightarrow{X}}_{\delta }-\overrightarrow{X}\right|\end{array}\right.$$

(8)

$$\left\{\begin{array}{c}{\overrightarrow{X}}_{i\alpha }=\left|{\overrightarrow{X}}_{\alpha }-{\overrightarrow{A}}_{\alpha }\cdot {\overrightarrow{D}}_{\alpha }\right|\\ {\overrightarrow{X}}_i{}_{\beta }=\left|{\overrightarrow{X}}_{\beta }-{\overrightarrow{A}}_{\beta }\cdot {\overrightarrow{D}}_{\beta }\right|\\ {\overrightarrow{X}}_{i\delta }=\left|{\overrightarrow{X}}_{\delta }-{\overrightarrow{A}}_{\delta }\cdot {\overrightarrow{D}}_{\delta }\right|\end{array}\right.$$

(9)

$${\overrightarrow{X}}_i=\frac{{\overrightarrow{X}}_{i\alpha }+{\overrightarrow{X}}_{i\beta }+{\overrightarrow{X}}_{i\delta }}{3}$$

(10)

3. Model Optimization

The standard grey wolf optimization algorithm has all omega members update their positions until they hit the termination conditions and discover the best answer (alpha) by learning from the first three best leaders. Even when the alpha falls into the local optimum, the standard grey wolf optimization algorithm still has good performance and the ability of fast collection, but the effect is relatively general when solving the problem of complex search space. As a conclusion, the proposed ALGWO enhances strategy optimization from two perspectives, namely the adaptive weight and gray wolf location update methods, predicated on the standard GWO.

3.1. Random Adjustment Strategy

The parameter established by the grey wolf algorithm to balance the capabilities of exploration and exploitation is called the convergence factor. The non-decreasing strategy increases the probability of selecting a larger step size at the beginning of the iteration, increasing the exploration capabilities. At the end of the iteration, the grey wolf is forced to select a smaller step size to increase its development capabilities. The convergence factor $\overrightarrow{a}$ in this study has the potential to take on a greater or smaller value during the algorithm’s iterative procedure by applying the random selection technique. Hence, by achieving a smaller value in the early stages, the convergence speed can be sped up, and by acquiring a higher value in the latter stages, the local optimum can be jumped. These three curves are shown in Figure 2.

$$a_1=2-2\ast \frac{t}{T}$$

(11)

$$a_2=2-2\ast \mathit{ln}(1+\frac{t}{T}(e-1))$$

(12)

$$a_3=2-2\ast \frac{e^{\frac{t}{T}}-1}{e-1}$$

(13)

3.2. Decision-making Level Update Scheme

Since the alpha gray wolf already represents the optimal value in the current population of gray wolves, and since the gray wolf does not benefit from the gray wolf’s optimal solution, the location update in this study uses levy flight instead of the sub-optimal or third optimal solutions.

$${\overrightarrow{X}}_{\alpha }={\overrightarrow{X}}_{\alpha }+\overrightarrow{s}$$

(14)

where $\overrightarrow{s}$ is calculated from the formula proposed by Mantegna.

The differential evolution idea is utilized to update the position to strengthen the leadership influence of the alpha gray wolf over potential leaders in beta and delta gray wolves because of the differential evolution algorithm’s strong local search capability in multimodal function search and grey wolf.

$$\left\{\begin{array}{c}{\overrightarrow{X}}_{\beta }={\overrightarrow{X}}_{\beta }+\overrightarrow{F}\cdot ({\overrightarrow{X}}_{\alpha }-{\overrightarrow{X}}_{\delta })\\ {\overrightarrow{X}}_{\delta }={\overrightarrow{X}}_{\delta }+\overrightarrow{F}\cdot ({\overrightarrow{X}}_{\alpha }-{\overrightarrow{X}}_{\beta })\end{array}\right.$$

(15)

The populations of the beta $(\beta )$ and the delta $(\delta )$ are set to one or more, and $\overrightarrow{F}$ is the variation factor. It declines in line with the amount of iterations from 0.6 to 0.3.

The entire grey wolf group may slip into the local optimum and lose the ability to perform global searches under the formula and formula update if the alpha $(\alpha )$, beta $(\beta )$, and delta $(\delta )$ grey wolves are in the local optimum in the multimodal function. Hence, the conflict between candidate leaders and leaders can be employed to resolve the decline in optimization accuracy induced by this condition.

$$\left\{\begin{array}{c}{\overrightarrow{X}}_i=\frac{{\overrightarrow{X}}_{i\alpha }+{\overrightarrow{X}}_{i\beta }+{\overrightarrow{X}}_{i\delta }}{3}, r>q\\ {\overrightarrow{X}}_i=\frac{{\overrightarrow{X}}_{i\alpha }-{\overrightarrow{X}}_{i\beta }-{\overrightarrow{X}}_{i\delta }}{3}, r\le q\end{array}\right.$$

(16)

where the beta $(\beta )$ and the delta $(\delta )$ are the second and third candidate solutions of the problem; q is the preset selection threshold, and it decreases linearly with the number of iterations from 0.9 to 0.6.

3.3. PID Controller Based on Back Propagation Neural Network

The back propagation neural network maps the input, output, and the errors nonlinearly to the PID controller’s three parameters, $k_p$, $k_i$, and $k_d$. In addition, the BP neural network has three neuron points for the input layer, five for the buried layer, and three for the output layer. The frequently employed Tanh function is utilized in the hidden layer.

$$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

(17)

The three no-negative gain parameters of the PID control scheme are output by BP neural networks, hence sigmoid functions and other functions with no-negative output values are applied.

$$g(x)=ub\cdot \frac{1}{1+e^{-x}}$$

(18)

$$t(x)=ub\cdot \frac{e^x}{e^x+e^{-x}}$$

(19)

$$h(x)=\min (\max (0,x),ub)$$

(20)

where $ub$ is upper bound of the output. It is employed to regulate the output range.

The structure of the PID control scheme based on a back propagation neural network is shown in Figure 3.

3.4. Structure of the Total Algorithm

The search space in this paper consists of the network weight and hyperparameters, since they have a major impact on the performance of the back propagation neural network model. The system’s process is shown in Figure 4.

4. Results and Discussion

4.1. Experiment Settings

Ten different test functions are employed to gauge the performance of the proposed method in order to demonstrate its usefulness. To guarantee a fair comparison, the population size in this paper is fixed at 30 and the number of iterations is set at 1000. The parameters of different algorithms that might be used are displayed in

Table 1. Parameter setups of different algorithms.

Algorithm	Values of the Parameters
GWO	a = 2 (linear reduction during iteration)
SOGWO [38]	a = 2 (linear reduction during iteration)
PSO	$c_1=2,c_2=2,w_{Max}=0.9,w_{Min}=0.2$
DE	F = 0.5, CR = 0.5

. In order to avoid random variation, tests are carried out 10 times independently.

However, additional analysis is required to determine how well the ALGWO-BPNN-PID algorithm performs in control issues. In order to assess the superiority of the ALGWO-BPNN control technique, the four tests are also performed using the fitness value, overshoot, and settling time performances. The simulation’s settings are similar. As a controller model, the incremental digital PID is employed. The sampling interval is set at one. The g(x) and the other function are the activation functions described above. The output control signal of the controller is restricted to [−10, 10]. Equation (21) is used to assess the algorithm’s effectiveness.

$$J={\displaystyle \underset{0}{\overset{\infty }{\int }}(w_1\left|e(t)\right|}{+w}_2{u}^2(t))dt$$

(21)

where $e(t)$ is the system error and $u(t)$ is the controller output, and $w_1$ and $w_2$ are the weights, with values of 0.001 and 0.999. Furthermore, overshoot will cause the fitness to increase more quickly.

4.2. Test Systems

4.2.1. Test System 1

Six unimodal functions are included in the test functions. PSO and GWO are contrasted with the suggested ALGWO algorithm’s solution. The unimodal test functions are described in

Table 2. Details of the unimodal test function.

Function Name	Expression	Search Space	Dim
F1	$\mathrm{F}1={\displaystyle \sum _{i=1}^n{x}_i^2}$	[−100,100]	30
F2	$\mathrm{F}2={\displaystyle \sum _{i=1}^n\left|x_i\right|}-{\displaystyle \prod _{i=1}^n\left|x_i\right|}$	[−10,10]	30
F3	$\mathrm{F}3={\displaystyle \sum _{i=1}^n{({\displaystyle \sum _{j=1}^i{x}_j})}^2}$	[−100,100]	30
F4	$\mathrm{F}4=\underset{i}{\max }\left\{\left|x_i\right|,1\le i\le n\right\}$	[−100,100]	30
F5	$\mathrm{F}5={\displaystyle \sum _{i=1}^n\left[100{(x_{i+1}-x_i^2)}^2+{(x_i-1)}^2\right]}$	[−30,30]	30
F6	$\mathrm{F}6={\displaystyle \sum _{i=1}^n{(|x_i+0.5|)}^2}$	[−100,100]	30

. Figure 5 displays the two-dimensional parameter space for these six unimodal functions to show them more easily.

The average and standard deviations for ten independent runs used to assess the resilience and average accuracy of algorithms are shown in

Table 3. Comparison results of three algorithms on six groups of benchmark functions.

Base Function		GWO	ALGWO	PSO
F1	STD	6.69 × 10−70	0	1.40 × 10−11
	AVE	2.49 × 10−70	0	5.48 × 10−12
F2	STD	3.49 × 10−41	0	1.01 × 10−5
	AVE	3.89 × 10−41	3.01 × 10−238	7.24 × 10−6
F3	STD	1.57 × 10−20	0	3.47 × 100
	AVE	8.72 × 10−21	0	7.16 × 100
F4	STD	2.04 × 10−17	0	1.20 × 10−1
	AVE	1.77 × 10−17	2.70 × 10−206	3.90 × 10−1
F5	STD	8.78 × 10−1	4.90 × 10−1	3.46 × 101
	AVE	2.66 × 101	2.62 × 101	5.04 × 101
F6	STD	2.71 × 10−1	1.09 × 100	1.59 × 10−11
	AVE	3.00 × 10−1	3.58 × 10−1	8.16 × 10−12

. For each function, the best results are displayed in bold. Figure 6 shows the convergence curves of the six test functions.

As shown in Table 3, the ALGWO algorithm indications are usually noticeably better than those of other algorithms. Figure 6 illustrates that the ALGWO algorithm provides better solution outcomes and faster convergence. As a result, the ALGWO method performs the best overall when solving unimodal test functions when compared to other algorithms.

4.2.2. Test System 2

Four multimodal functions are included in the test functions. They are compared to four metaheuristic algorithms that are currently in use. PSO, DE, GWO, and SOGWO are the algorithms utilized for comparison.

Table 4. Details of the multimodal test function.

Function Name	Expression	Search Space	Dim
F8	$\mathrm{F}8={\displaystyle \sum _{i=1}^n-x_i\sin (\sqrt{\left|x_i\right|})}$	[−500,500]	30
F9	$\mathrm{F}9={\displaystyle \sum _{i=1}^n\left[x_i^2-10\cos (2\pi x_i)+10\right]}$	[−5.12,5.12]	30
F10	$\mathrm{F}10=-20e^{-0.2\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{x}_i^2}}}-e^{\frac{1}{n}{\displaystyle \sum _{i=1}^n\cos (2\pi x_i)}}+20+e$	[−32,32]	30
F11	$\mathrm{F}11=\frac{1}{4000}{\displaystyle \sum _{i=1}^n{x}_i^2}-{\displaystyle \prod _{i=1}^n\cos (\frac{x_i}{\sqrt{i}})+1}$	[−600,600]	30

displays the specifics of the multimodal test function. The two-dimensional parameter space of these four unimodal functions is depicted in Figure 7.

Table 5. Comparison results of five algorithms on four groups of benchmark functions.

Base Function		GWO	ALGWO	SOGWO	PSO	DE
F8	STD	8.45 × 102	1.26 × 103	7.11 × 102	8.35 × 102	6.86 × 102
	AVE	−5.98 × 103	−5.98 × 103	−6.44 × 103	−6.80 × 103	−5.97 × 103
F9	STD	0	0	0	8.22 × 100	1.57 × 101
	AVE	0	0	0	3.47 × 101	2.57 × 102
F10	STD	1.49 × 10−15	0	2.39 × 10−15	3.59 × 10−6	7.20 × 10−1
	AVE	1.43 × 10−14	4.44 × 10−15	1.40 × 10−14	2.56 × 10−6	1.72 × 10−1
F11	STD	0	0	0	7.30 × 10−3	2.67 × 100
	AVE	0	0	0	7.10 × 10−3	3.63 × 10−1

contains the average and standard deviation for ten independent runs. The convergence rates of the four test functions for several algorithms are displayed in Figure 8.

Table 5 demonstrates that, despite the ALGWO algorithm’s poor performance in the multimodal test function in the F8 function, the average search accuracy achieves the minimum value of 4.44 × 10⁻¹⁵ in F10 and the optimal solution of 0 in F9 and F11. As a result, the ALWO algorithm’s indication is much superior to that of other algorithms. Figure 8 shows that, for the test functions of F10 and F11, the ALGWO algorithm yields superior solution outcomes and accelerates convergence speed. Therefore, when solving multimodal test functions, the ALGWO method generally outperforms other algorithms.

4.2.3. Test System 3

The first-order linear system is chosen for testing in order to confirm the superiority of the ALGWO-BPNN in the PID control process, and the model transfer function is indicated in (22). The value of the ub is 10, so the mapping range of the activation function is set to 0 to 10. The control findings are shown in

Table 6. The comparison of final fitness of algorithms on test system 3.

Algorithm		$\mathit{g}(\mathit{x})$	$\mathit{t}(\mathit{x})$	$\mathit{h}(\mathit{x})$	PID
GWO	AVE	277.2945	295.4016	280.0701	301.2233
	STD	13.5263	13.4028	13.5383	0.2515
ALGWO	AVE	275.7396	280.0453	278.7984	301.0937
	STD	2.4216	12.3446	11.8726	0.2811

and Figure 9. The best performance is demonstrated by the $g(x)$ activation function. The convergence characteristics can be seen in Figure 10.

$$G(s)=\frac{1.7}{320s+1}$$

(22)

The variance and standard deviation of utilizing the ALGWO method are noticeably lower, as seen in Table 6, as compared to using the GWO algorithm. For instance, the PID control system utilizing the g(x) BPNN reduces the standard deviation from 13.5263 to 2.4216 and also lowers the average value by 1.5. As a result, it has improved resilience and average accuracy. The average value is decreased by roughly 20 after using the BPNN model, so the average accuracy is increased. The g(x) activation function has a better impact when utilized as an activation function.

As shown in Figure 9, the controllers employing BPNN-PID outperform the PID controllers in reducing overshoot when the system reference value changes. As shown in Figure 10, the ALGWO algorithm is used to control the BPNN-PID control scheme in comparison to GWO, and it approaches the ideal solution at iteration 200 with a faster convergence rate, demonstrating ALWO’s more deterministic global search capability and quicker discovery speed of high-dimensional optimal solutions. The optimization values utilizing the ALGWO algorithm are 275.7396 and 301.0937, respectively, in terms of optimization accuracy. It is shown that both in high-dimensional and low-dimensional scenarios, it is superior to GWO. According to the convergence curve, the ALGWO algorithm needs 60 iterations to find the local optimal solution and 90 iterations to depart from it. Compared to the 150 iterations needed by the GWO method, this is a huge reduction. As a result, ALGWO can eliminate local optimal solutions more quickly.

4.2.4. Test System 4

For testing, the second-order linear system is used, and formula 23 illustrates the model transfer function. The activation function’s mapping range is set to 0 to 30. The performance characteristics and step response data are displayed in

Table 7. Performance characteristics on test system 4.

Algorithm	Overshoot (%)	Rising Time (s)	Settling Time (s)	Fitness
GWO and $g(x)$	0.62	3	3	1.0651
GWO and $t(x)$	0	2	4	1.0234
GWO and $h(x)$	0	2	2	1.0978
GWO and PID	10	2	3	11.9876
ALGWO and $g(x)$	0.02	2	3	1.0360
ALGWO and $t(x)$	0	2	4	1.0238
ALGWO and $h(x)$	0	2	2	1.0804
ALGWO and PID	6	2	4	11.8913

and Figure 11.

$$G(s)=\frac{133}{s^2+25s}$$

(23)

Table 7 demonstrates how the ALGWO method has lower fitness than the GWO algorithm in some control schemes. As an illustration, the average precision is decreased in a BPNN PID control system applied to g(x) from 1.0651 to 1.0360, and the overshoot index is also decreased from 0.62% to 0.02%. The average accuracy is therefore increased by the ALWO technique. In terms of whether to use BPNN technology or not, the average accuracy decreased from 11.8913 to 1.0238, which significantly indicates that the ALGWO-BPNN-PID control scheme is more effective in second-order linear systems. Furthermore, the g(x) activation function has better results, as shown in Table 7.

As can be clearly seen from Figure 11, the maximum value of the tracking values decreased from 1.10 to 1.007. As a result, ALGWO-BPNN-PID controllers have a lot of benefits over traditional PID controllers in terms of reducing overshoot.

4.2.5. Test System 5

The first-order plus time delay model is selected for testing, and the model transfer function is shown in (24). The mapping range of the activation function is set to 0 to 30.

Table 8. The comparison of final fitness of algorithms on test system 5.

Algorithm		$\mathit{g}(\mathit{x})$	$\mathit{t}(\mathit{x})$	$\mathit{h}(\mathit{x})$	PID
GWO	AVE	24.9222	25.0190	24.8169	27.0366
	STD	0.6144	0.7097	0.6658	0.0773
ALGWO	AVE	24.1989	23.8964	24.8090	27.0068
	STD	0.1029	0.1883	0.6113	0.0245

shows the mean value and standard deviation of 10 runs.

Table 9. Performance characteristics on test system 5.

Algorithm	Overshoot (%)	Rising Time (s)	Settling Time (s)	Fitness
GWO and $g(x)$	0.06	34	41	24.2989
GWO and $t(x)$	0	38	49	25.0178
GWO and $h(x)$	0	35	44	24.7274
GWO and PID	0.18	41	52	26.9809
ALGWO and $g(x)$	0	35	45	24.2034
ALGWO and $t(x)$	0	34	44	23.9817
ALGWO and $h(x)$	0	30	36	24.2842
ALGWO and PID	0.11	41	53	26.9800

and Figure 12 illustrate the performance characteristics and step response outputs represented by one of the results, while Figure 13 displays the 10-time average convergence characteristics of several algorithms.

$$G(s)=\frac{1.7e^{-10s}}{320s+1}$$

(24)

As shown in Table 8, compared to the control scheme using GWO and PID, the control scheme using ALGWO-BPNN-PID reduces the fitness from 27.0366 to 23.8964, improving the average accuracy. Between them, the activation function of t(x) achieves the best effect, with the lowest average fitness of 23.8964. As can be seen from Table 9, using the ALGWO-BPNN-PID control scheme causes, the overshoot to decrease from 0.18% to 0.00%, the rise time to increase by about 5s, and the adjustment time to decrease by about 8s. Between the schemes, the control scheme using the g(x) activation function has a better overall effect.

As can be clearly seen in Figure 12, the response speed of the GWO-PID control scheme is slower, reaching 0.98 in about 52 seconds, while the BPNN-PID control scheme is advanced to about 45 seconds. As can be seen from Figure 13, the ALGWO-BPNN-PID control scheme has a faster convergence speed and better optimization accuracy, with a decrease of about two. Therefore, the ALGWO-BPNN-PID control scheme has more advantages in the first-order plus time-delay model.

4.2.6. Test System 6

The time-varying model is selected for testing, and the model’s difference equation is displayed as follows. The mean value and standard deviation for 10 runs are displayed in

Table 10. The comparison of final fitness of algorithms on test system 6.

Algorithm		$\mathit{g}(\mathit{x})$	$\mathit{t}(\mathit{x})$	$\mathit{h}(\mathit{x})$	PID
GWO	AVE	40.8749	46.6955	41.2529	56.4116
	STD	0.61855	8.8126	1.2789	0
ALGWO	AVE	40.2174	41.1174	40.5169	49.2536
	STD	0.5555	0.6698	0.6763	6.6099

. The mapping range of the activation function is set to 0 to 30. Figure 14 shows the step response, while Figure 15 displays the comparison results. The results demonstrate that the ALGWO-BPNN method shows the optimal control effect in slow time-varying systems.

$$w=1-0.8\times e^{-0.1k}$$

(25)

$$y(k)=0.9969\times w\times y(k-1)+0.0053\times u(k-1)$$

(26)

First, as shown in Table 10, using the ALGWO method produces lower variances and standard deviations compared to using the GWO algorithm. For example, a PID control system using t(x) BPNN reduced the standard deviation from 8.8126 to 0.6698, and also reduced the average value by 5.5. Therefore, it improves elasticity and average accuracy. Then, the final average fitness is reduced by roughly 10, making the ALGWO-BPNN-PID controllers significantly superior to conventional PID controllers. Finally, the g(x) activation function has a better impact when used as an activation function, with a fitness of 40.2174.

Figure 14 shows that the controller employing BPNN-PID outperforms the PID controller in terms of reaction speed, shortening the time by around ten seconds, when tracking the unit step response. As seen in Figure 15, the ALGWO algorithm is employed to regulate the BPNN-PID control scheme in comparison to GWO, and by iteration 100, it comes close to an optimal solution, demonstrating ALGWO’s superior global search capabilities. The optimization values for the ALGWO method are 49.2536 and 40.5169, respectively, in terms of optimization accuracy. This demonstrates that it outperforms GWO. In conclusion, GWO-BPNN-PID controllers have better performance when applied to slow time-varying systems.

5. Conclusions

The most popular type of industrial process control is PID control, which has been utilized extensively in the metallurgical industry, the electromechanical industry, and other industries. However, as the controlled system becomes increasingly complex, the time-varying and time-delayed systems of the PID control algorithm exert only a general control effect. In this paper, an incremental PID control algorithm based on a BP neural network was selected. Furthermore, by utilizing a novel natural excitation optimization technique, namely the gray wolf optimization algorithm based on confrontation learning, we sought to enhance the control impact of the BPNN-PID controller. In the first step, a fresh adversarial search approach for GWO was suggested. Ten test functions were used to evaluate the ALGWO algorithm. This technique performs better than other algorithms because it can increase convergence speed and search capability. The ALGWO-BPNN model is based on the ALGWO algorithm, which was the second step. To achieve real-time online modification of the PID control parameters and acquire the optimal control rules, the key parameters of the BPNN were adjusted using ALGWO. In addition, the impact of changing the activation function on BPNN was discussed and comparative tests were conducted using the conventional PID control. The findings indicate that the ALGWO-BPNN controller exerts a superior control effect compared to the conventional PID controller in time-varying or time-delay systems.