Neural Network-Assisted Interferogram Analysis Using Cylindrical and Flat Reference Beams
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Foundations
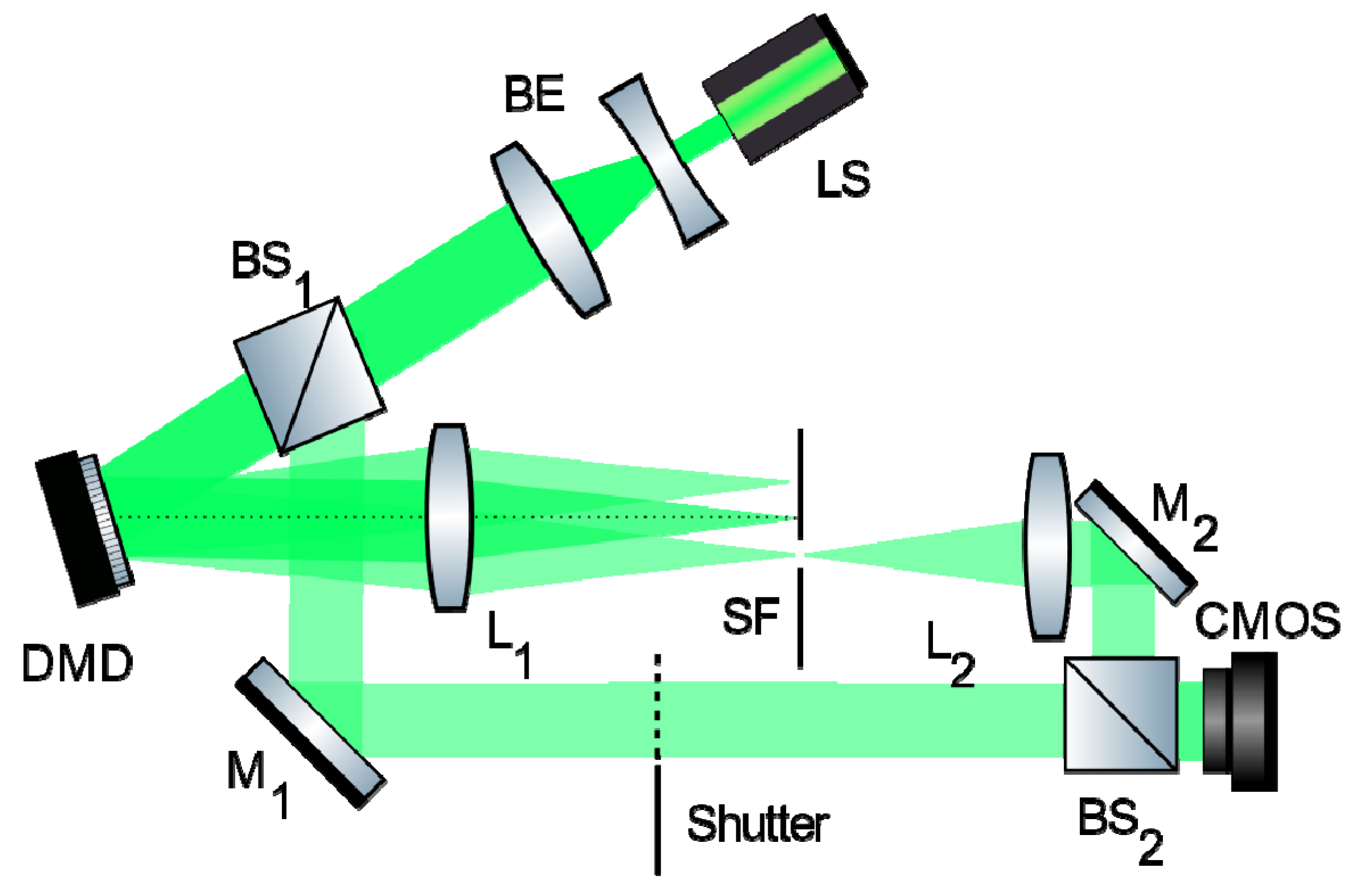
2.2. Optical Setup
2.3. Neural Network
- -
- at the first stage, the tensor is convoluted with a 1 × 1 kernel. This operation is called “pointwise convolution.”
- -
- at the second stage, standard convolution is performed. After that, the results of the convolution of the tensor obtained as a result of applying the “pointwise convolution” operation to the input tensor are summed up with all the filters of the layer and form the output tensor of the layer. This operation is called “depthwise convolution.”
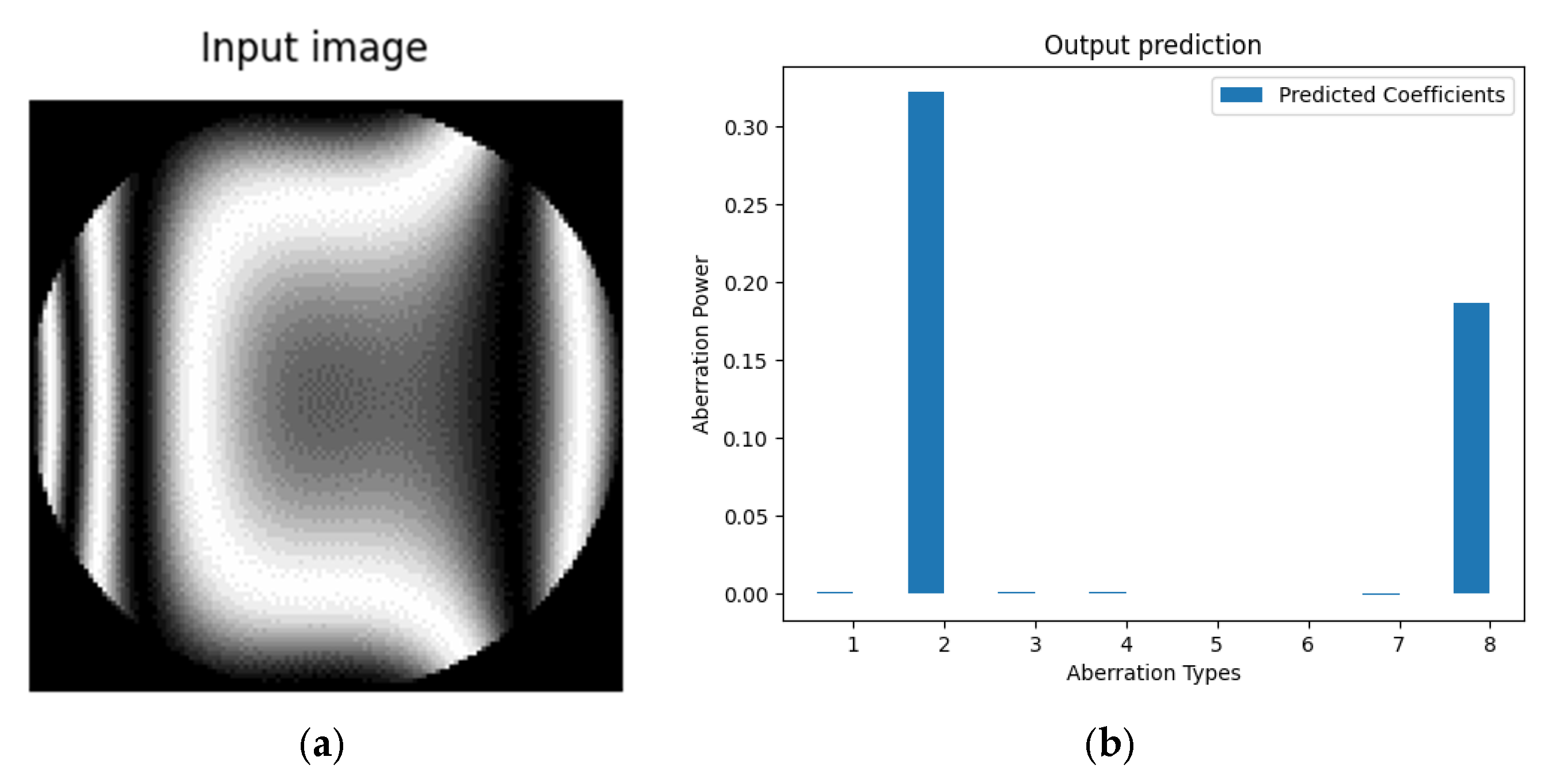
3. Results
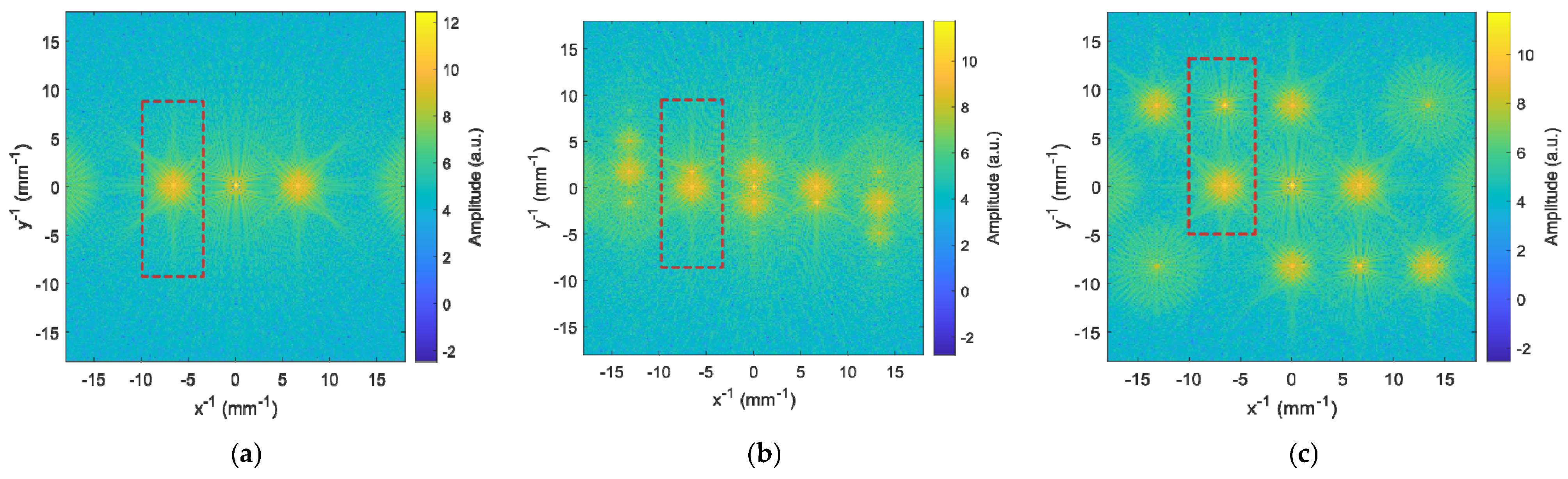
3.1. Numerical Simulation
3.2. Experimental Formation of Interferograms
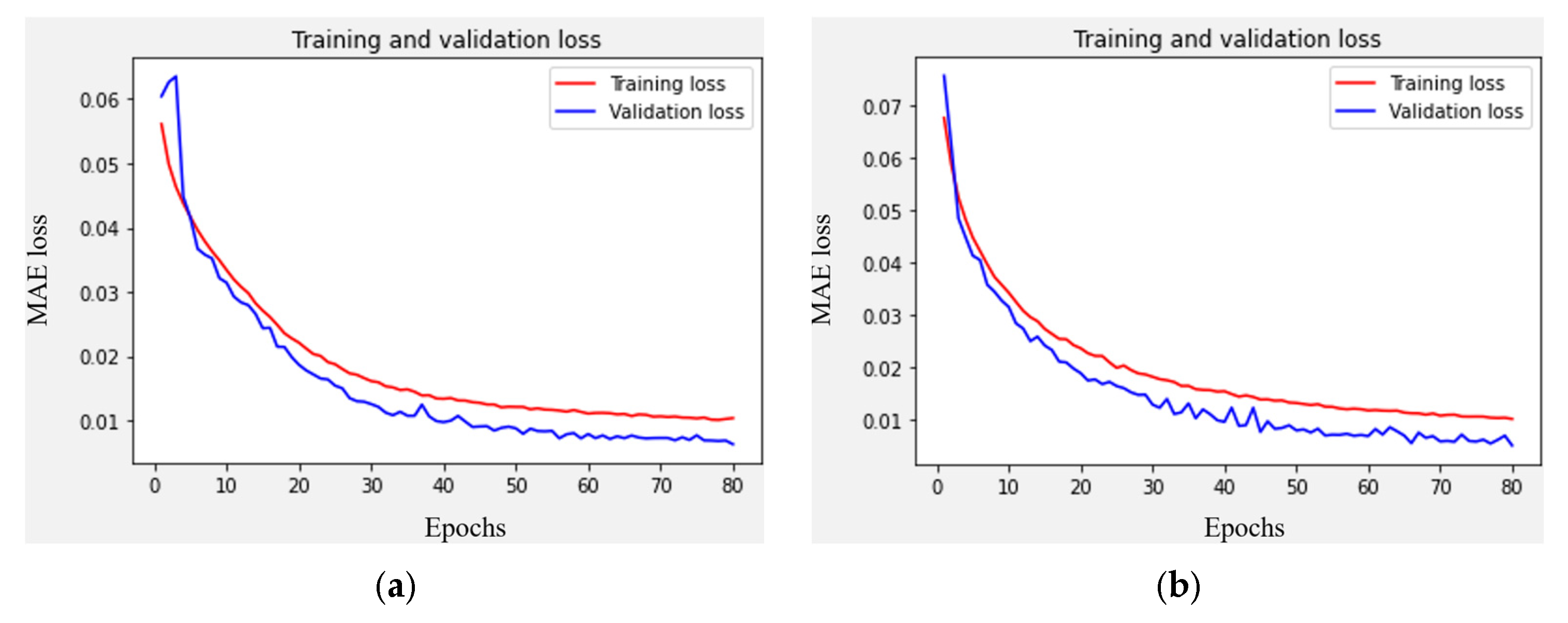
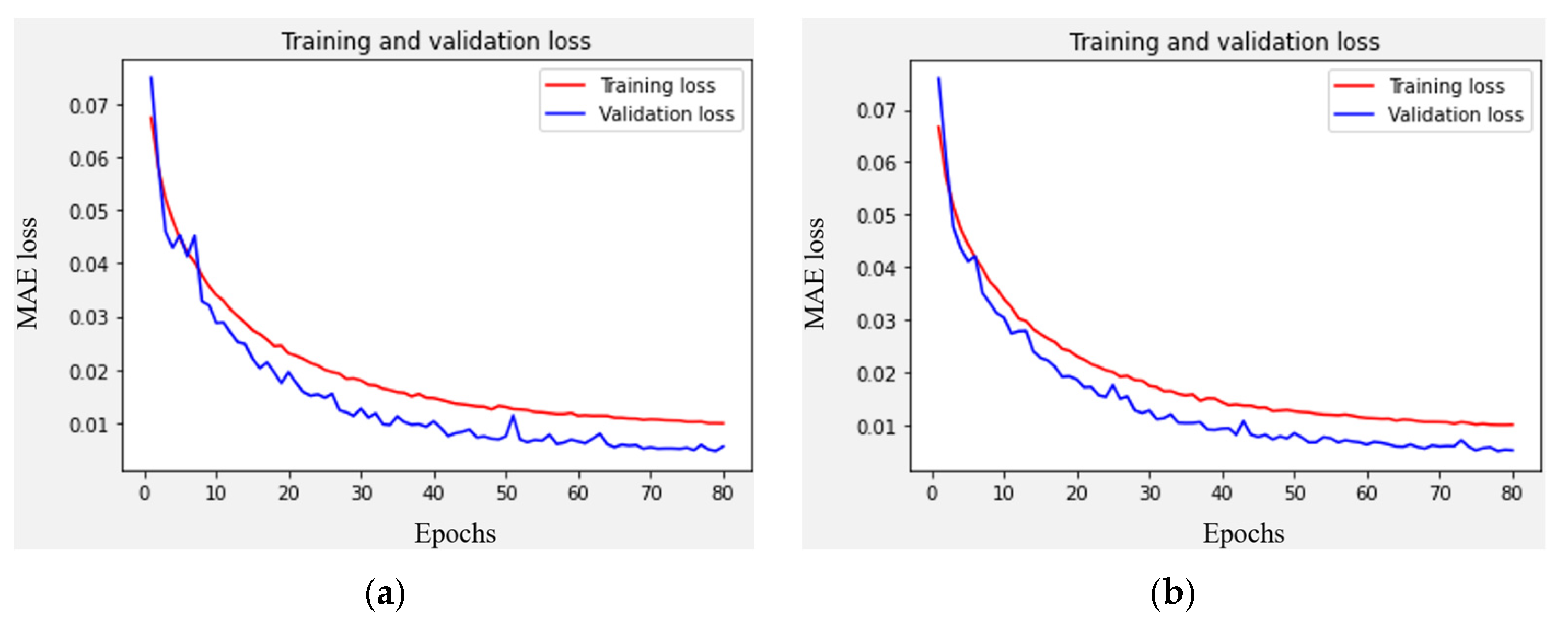
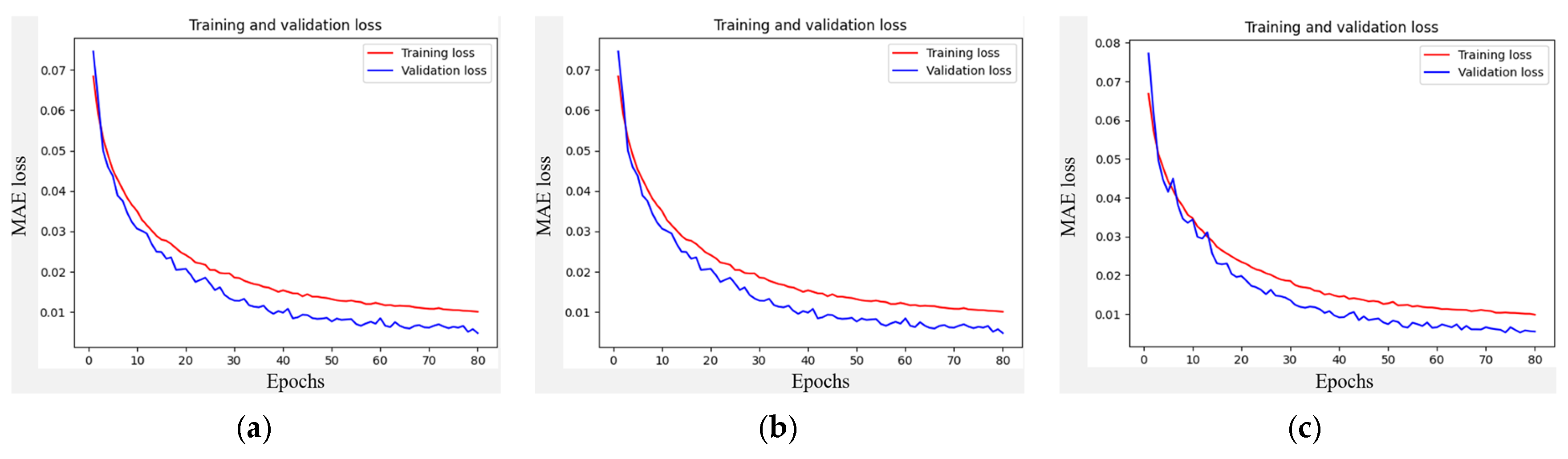
3.3. Neural Network Training
3.3.1. Modeling Dataset
3.3.2. Experimental Dataset
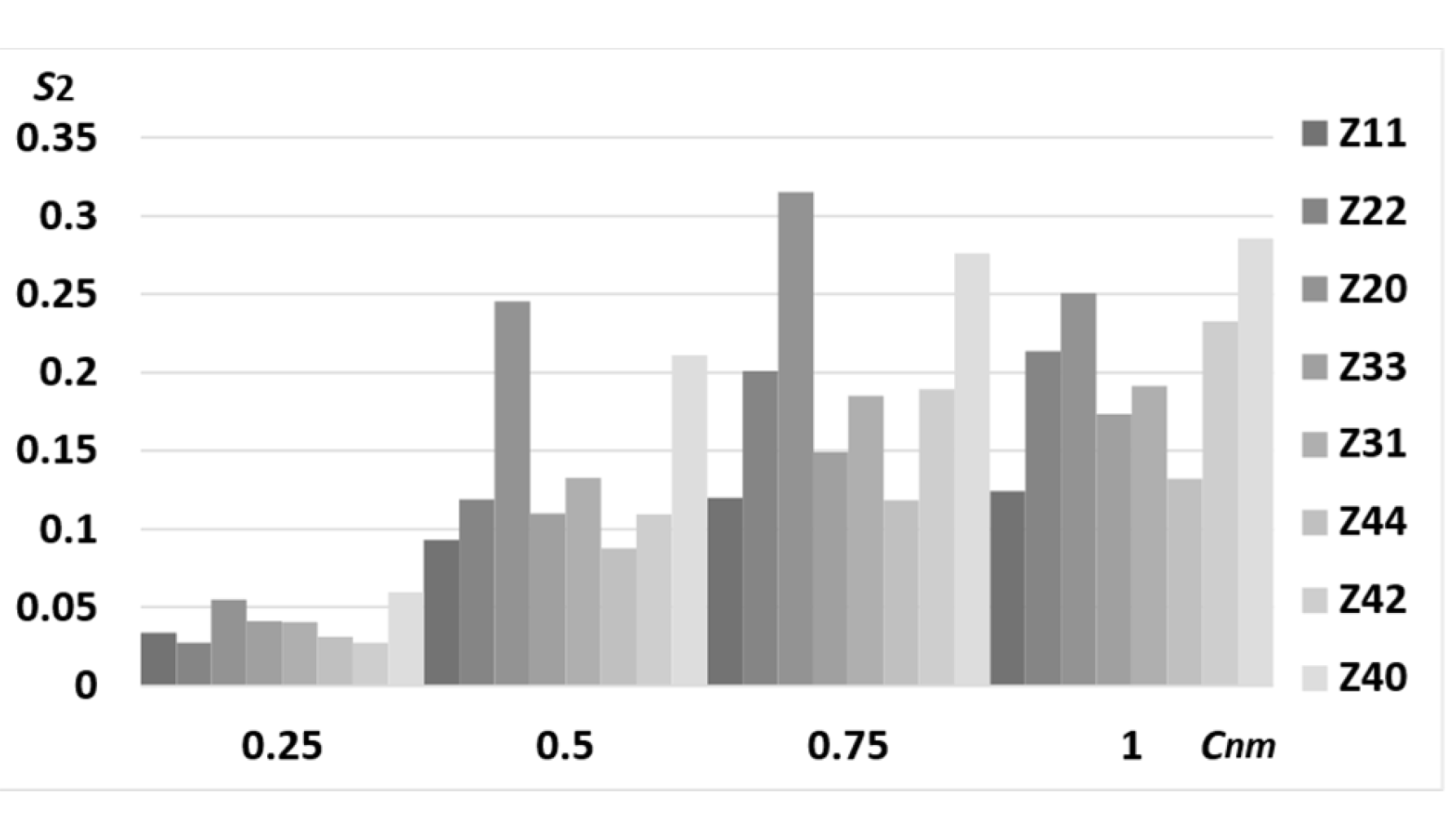
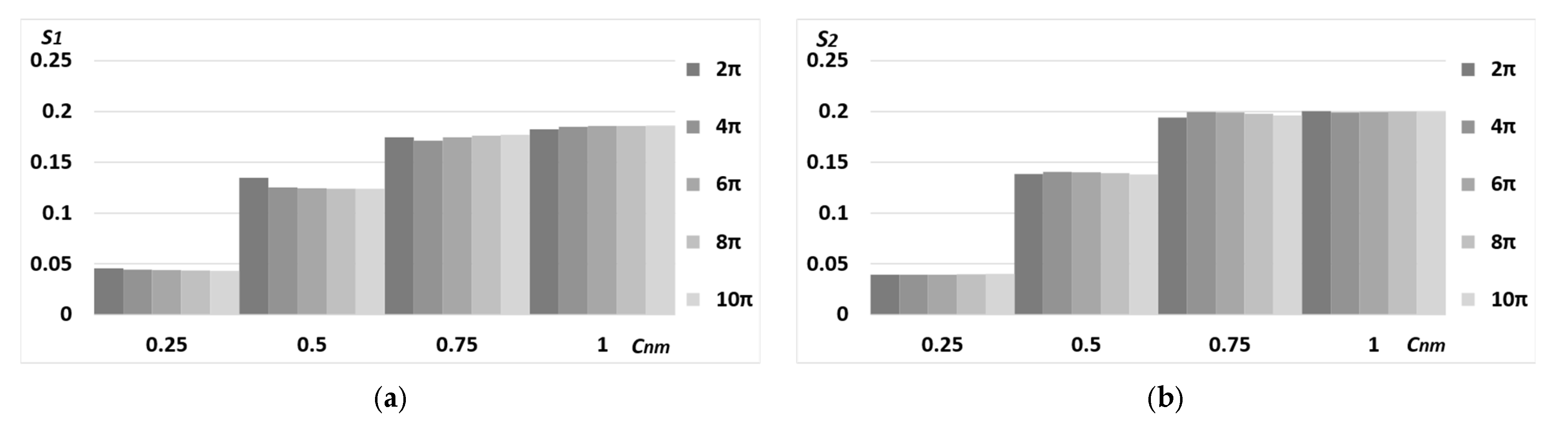
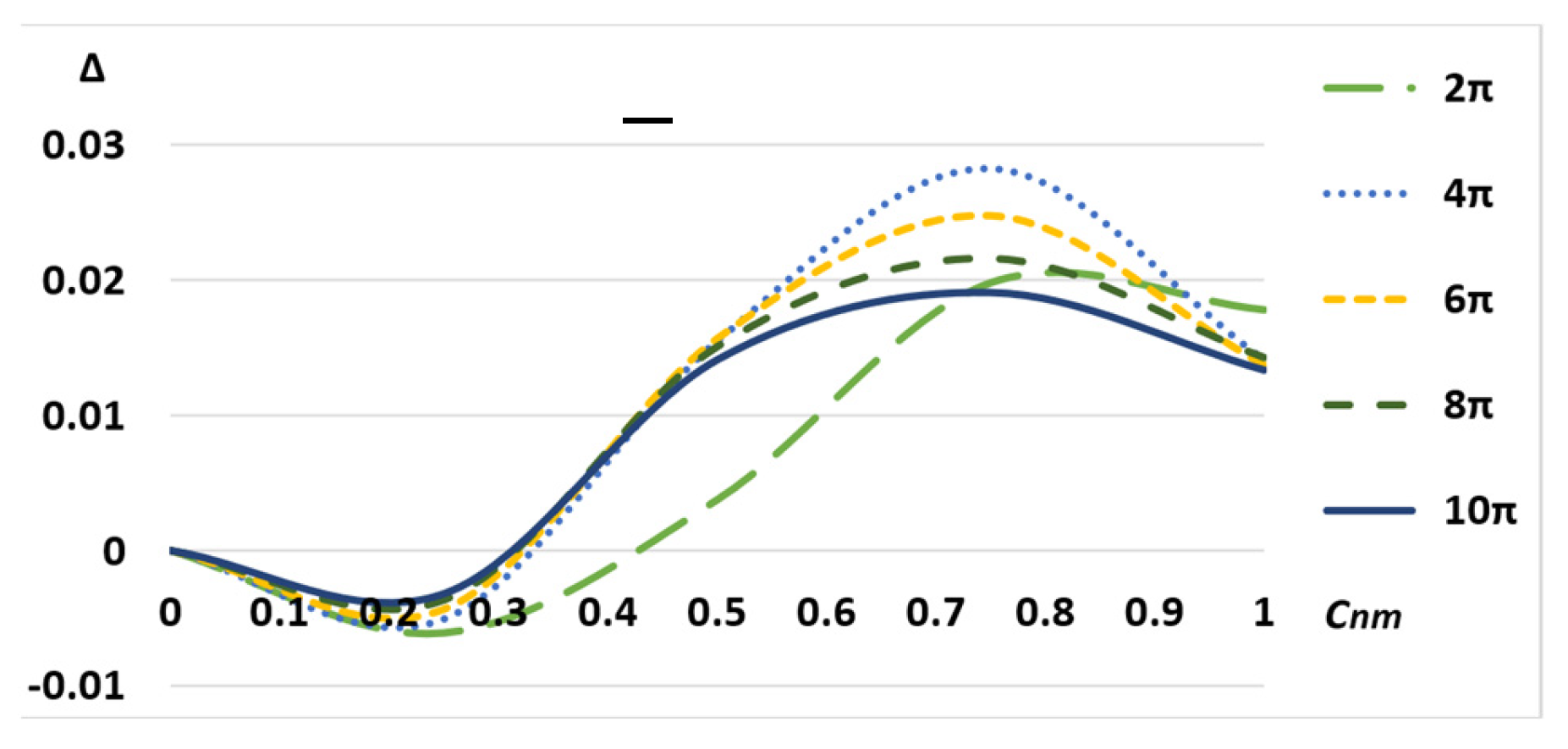
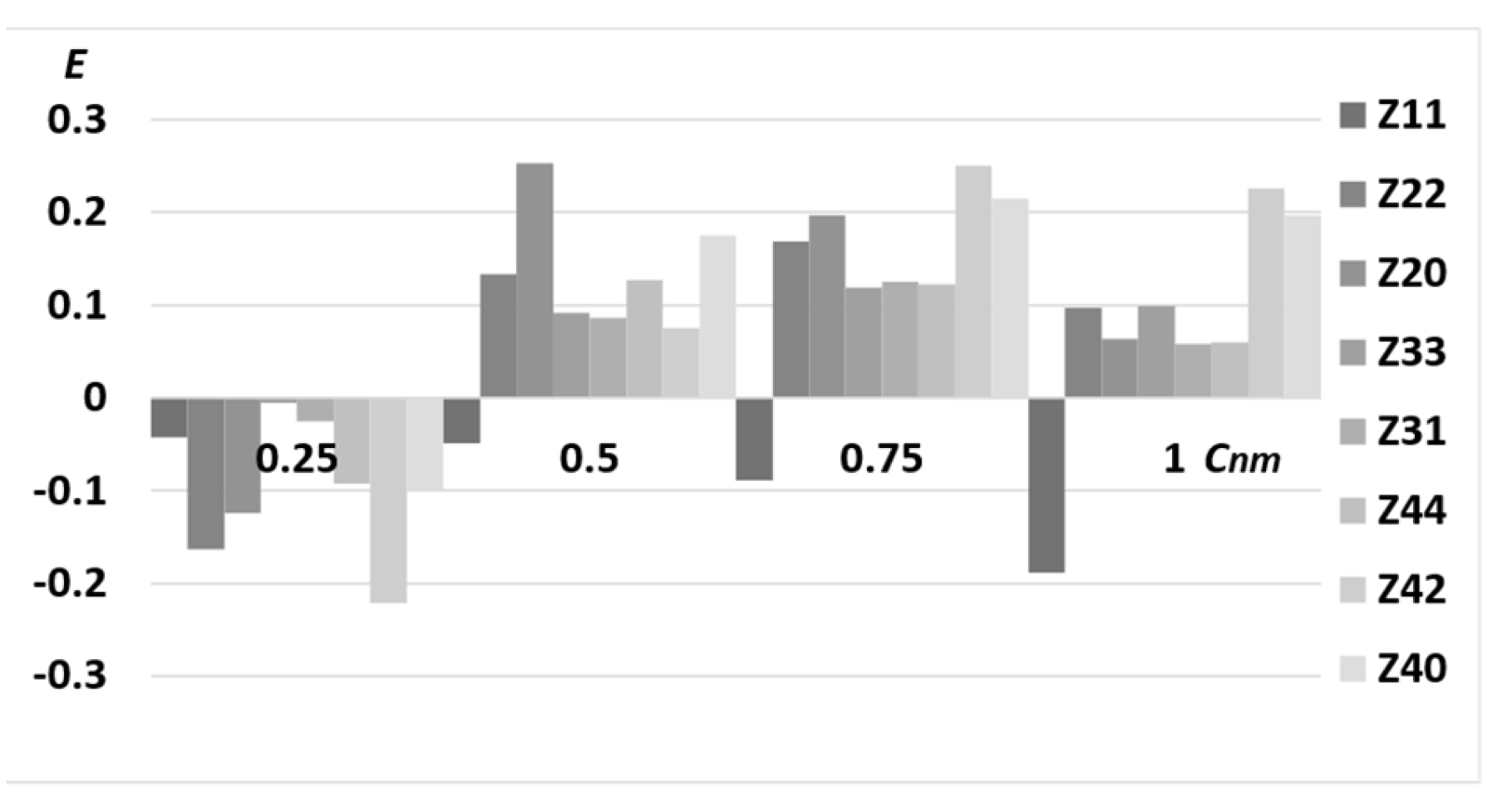
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Park, J.-H.; Lee, B. Holographic techniques for augmented reality and virtual reality near-eye displays. Light Adv. Manuf. 2022, 3, 1. [Google Scholar] [CrossRef]
- Booth, M.; Andrade, D.; Burke, D.; Patton, B.; Zurauskas, M. Aberrations and adaptive optics in superresolution microscopy. Microscopy 2015, 64, 251–261. [Google Scholar] [CrossRef]
- Klebanov, I.M.; Karsakov, A.V.; Khonina, S.N.; Davydov, A.N.; Polyakov, K.A. Wavefront aberration compensation of space telescopes with telescope temperature field adjustment. Comput. Opt. 2017, 41, 30–36. [Google Scholar] [CrossRef]
- Gu, Z.; Wang, Y.; Ju, G. Computation of misalignment and primary mirror astigmatism figure error of two-mirror telescopes. J. Astron. Telesc. Instrum. Syst. 2018, 4, 019002. [Google Scholar] [CrossRef]
- Lombardo, M.; Lombardo, G. Wave aberration of human eyes and new descriptors of image optical quality and visual performance. J. Cataract Refract. Surg. 2010, 36, 313–320. [Google Scholar] [CrossRef] [PubMed]
- Khorin, P.A.; Khonina, S.N.; Karsakov, A.V.; Branchevskiy, S.L. Analysis of corneal aberration of the human eye. Comput. Opt. 2016, 40, 810–817. [Google Scholar] [CrossRef]
- Bisch, N.; Guan, J.; Booth, M.J.; Salter, P.S. Adaptive optics aberration correction for deep direct laser written waveguides in the heating regime. Appl. Phys. A. 2019, 125, 364. [Google Scholar] [CrossRef]
- Bian, Y.; Li, Y.; Li, W.; Hong, X.; Qiu, J.; Chen, E.; Li, L.; Wu, J. The impact of optical system aberration and fiber positioning error on the FMF coupling efficiency of an FSO receiver under atmospheric turbulence. J. Opt. 2022, 24, 085701. [Google Scholar] [CrossRef]
- Cabriel, C.; Bourg, N.; Dupuis, G.; Lévêque-Fort, S. Aberration-accounting calibration for 3D single-molecule localization microscopy. Opt. Lett. 2018, 43, 174. [Google Scholar] [CrossRef]
- Kuschmierz, R.; Scharf, E.; Ortegón-González, D.F.; Glosemeyer, T.; Czarske, J.W. Ultra-thin 3D lensless fiber endoscopy using diffractive optical elements and deep neural networks. Light Adv. Manuf. 2021, 2, 1. [Google Scholar] [CrossRef]
- Ellerbroek, B.L.; Vogel, C.R. Inverse problems in astronomical adaptive optics. Inverse Probl. 2009, 25, 063001. [Google Scholar] [CrossRef]
- Ji, N. Adaptive optical fluorescence microscopy. Nat. Methods 2017, 14, 374–380. [Google Scholar] [CrossRef]
- Bouchez, A.H.; Angeli, G.Z.; Ashby, D.S.; Bernier, R.; Conan, R.; McLeod, B.A.; Quirós-Pacheco, F.; Van Dam, M.A. An overview and status of GMT active and adaptive optics. Proc. SPIE 2018, 10703, 107030W. [Google Scholar] [CrossRef]
- Khorin, P.A.; Porfirev, A.P.; Khonina, S.N. Adaptive detection of wave aberrations based on the multichannel filter. Photonics 2022, 9, 204. [Google Scholar] [CrossRef]
- Zepp, A.; Gladysz, S.; Stein, K.; Osten, W. Simulation-based design optimization of the holographic wavefront sensor in closed-loop adaptive optics. Light: Adv. Manuf. 2022, 3, 27. [Google Scholar] [CrossRef]
- Platt, B.C.; Shack, R. History and principles of Shack-Hartmann wavefront sensing. J. Refract. Surg. 2001, 17, S573–S577. [Google Scholar] [CrossRef] [PubMed]
- Hongbin, Y.; Guangya, Z.; Siong, C.F.; Feiwen, L.; Shouhua, W.A. Tunable Shack-Hartmann wavefront sensor based on a liquid-filled microlens array. J. Micromech. Microeng. 2008, 18, 105017. [Google Scholar] [CrossRef]
- Fauvarque, O. General formalism for Fourier-based wave front sensing: Application to the pyramid wave front sensors. J. Astron. Telesc. Instrum. Syst. 2017, 3, 019001. [Google Scholar] [CrossRef]
- Hutterer, V.; Ramlau, R.; Shatokhina, I. Real-time adaptive optics with pyramid wavefront sensors: A theoretical analysis of the pyramid sensor model. Inverse Prob. 2019, 35, 34. [Google Scholar] [CrossRef]
- Karpeev, S.V.; Pavelyev, V.S.; Khonina, S.N.; Kazanskiy, N.L. High-effective fiber sensors based on transversal mode selection. Proc. SPIE Int. Soc. Opt. Eng. 2005, 5854, 163–169. [Google Scholar]
- Fang, Z.; Chin, K.; Qu, R.; Cai, H. Fundamentals of Optical Fiber Sensors; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2012; ISBN 978-0-470-57540-6. [Google Scholar]
- Khonina, S.N.; Karpeev, S.V.; Paranin, V.D. Birefringence detection of a gradient-index lens based on astigmatic transformation of a Bessel beam. Optik 2018, 164, 679–685. [Google Scholar] [CrossRef]
- Booth, M.J. Direct measurement of Zernike aberration modes with a modal wavefront sensor. Proc. SPIE 2003, 5162, 79–90. [Google Scholar]
- Porfirev, A.P.; Khonina, S.N. Experimental investigation of multi-order diffractive optical elements matched with two types of Zernike functions. Proc. SPIE 2016, 9807, 98070E. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Porfirev, A.P. Wavefront Aberration Sensor Based on a Multichannel Diffractive Optical Element. Sensors 2020, 20, 14. [Google Scholar] [CrossRef] [PubMed]
- Khorin, P.A.; Volotovskiy, S.G.; Khonina, S.N. Optical detection of values of separate aberrations using a multi-channel filter matched with phase Zernike functions. Comput. Opt. 2021, 45, 525–533. [Google Scholar] [CrossRef]
- Malacara, D. Optical Shop Testing; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Takeda, M. Fourier fringe analysis and its application to metrology of extreme physical phenomena: A review. Appl. Opt. 2013, 52, 20. [Google Scholar] [CrossRef]
- Gao, W.; Huyen, N.T.; Loi, H.S.; Kemao, Q. Real-time 2D parallel windowed Fourier transform for fringe pattern analysis using Graphics Processing Unit. Opt. Express 2009, 17, 23147–23152. [Google Scholar] [CrossRef]
- Zhang, R.; Guo, H.; Asundi, A.K. Geometric analysis of influence of fringe directions on phase sensitivities in fringe projection profilometry. Appl. Opt. 2016, 55, 7675–7687. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Zhang, C.; Zhou, C.; Jiang, K.; Fang, M. Circular fringe projection profilometry. Opt. Lett. 2016, 41, 4951–4954. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, H.; Qiao, J.; Zhou, C.; Zhang, L.; Hu, G.; Geng, H. Three-dimensional measurement based on optimized circular fringe projection technique. Opt. Express 2019, 27, 2465–2477. [Google Scholar] [CrossRef]
- Ma, Y.; Yin, D.; Wei, C.; Feng, S.; Ma, J.; Nie, S.; Yuan, C. Real-time 3-D shape measurement based on radial spatial carrier phase shifting from circular fringe pattern. Opt. Commun. 2019, 450, 6–13. [Google Scholar] [CrossRef]
- Chen, Q.; Han, M.; Wang, Y.; Chen, W. An Improved Circular Fringe Fourier Transform Profilometry. Sensors 2022, 22, 6048. [Google Scholar] [CrossRef]
- Iwata, K.; Kusunoki, F.; Moriwaki, K.; Fukuda, H.; Tomii, T. Three-dimensional profiling using the Fourier transform method with a hexagonal grating projection. Appl. Opt. 2008, 47, 2103–2108. [Google Scholar] [CrossRef] [PubMed]
- Porras-Aguilar, R.; Falaggis, K.; Ramos-Garcia, R. Optimum projection pattern generation for grey-level coded structured light illumination systems. Opt. Lasers Eng. 2017, 91, 242–256. [Google Scholar] [CrossRef]
- Porras-Aguilar, R.; Falaggis, K. Absolute phase recovery in structured light illumination systems: Sinusoidal vs. intensity discrete patterns. Opt. Lasers Eng. 2016, 84, 111–119. [Google Scholar] [CrossRef]
- Belashov, A.V.; Petrov, N.V.; Semenova, I.V. Method for calculating the dynamic phase delay in holographic interferometry without phase unwrapping. Comput. Opt. 2014, 38, 710–716. [Google Scholar] [CrossRef]
- Belashov, A.V.; Petrov, N.V.; Semenova, I.V. Digital off-axis holographic interferometry with simulated wavefront. Opt. Express 2014, 22, 28363–28376. [Google Scholar] [CrossRef]
- Rivenson, Y.; Zhang, Y.; Günaydın, H.; Teng, D.; Ozcan, A. Phase recovery and holographic image reconstruction using deep learning in neural networks. Light Sci. Appl. 2018, 7, 17141. [Google Scholar] [CrossRef]
- Andersen, T.; Owner-Petersen, M.; Enmark, A. Neural networks for image-based wavefront sensing for astronomy. Opt. Lett. 2019, 44, 4618–4621. [Google Scholar] [CrossRef]
- Jia, P. Astronomical image restoration and point spread function estimation with deep neural networks. Astron. J. 2020, 159, 183. [Google Scholar] [CrossRef]
- Rodin, I.A.; Khonina, S.N.; Serafimovich, P.G.; Popov, S.B. Recognition of wavefront aberrations types corresponding to single Zernike functions from the pattern of the point spread function in the focal plane using neural networks. Comput. Opt. 2020, 44, 923–930. [Google Scholar] [CrossRef]
- Khorin, P.A.; Dzyuba, A.P.; Serafimovich, P.G.; Khonina, S.N. Neural networks application to determine the types and magnitude of aberrations from the pattern of the point spread function out of the focal plane. J. Phys. Conf. Ser. V. 2021, 2086, 012148. [Google Scholar] [CrossRef]
- Pinilla, S.; Mishra, K.V.; Shevkunov, I.; Soltanalian, M.; Katkovnik, V.; Egiazarian, K. Unfolding-Aided Bootstrapped Phase Retrieval in Optical Imaging: Explainable AI reveals new imaging frontiers. IEEE Signal Process. Mag. 2023, 40, 46–60. [Google Scholar] [CrossRef]
- Tang, X.; Zhu, J.; Zhong, P.; Chen, Y.; Zhang, B.; Hu, H. Reliable wavefront reconstruction from a single lateral shearing interferogram using Bayesian convolutional neural network. Opt. Lasers Eng. 2023, 160, 107281. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Z.; Dou, J.; Liu, Z. Fast demodulation of single-shot interferogram via convolutional neural network. Opt. Commun. 2021, 487, 126813. [Google Scholar] [CrossRef]
- Khonina, S.N.; Khorin, P.A.; Serafimovich, P.G.; Dzuyba, A.P.; Georgieva, A.O.; Petrov, N.V. Analysis of the wavefront aberrations based on neural networks processing of the interferograms with a conical reference beam. Appl. Phys. B. 2022, 128, 60. [Google Scholar] [CrossRef]
- Georgieva, A.O.; Belashov, A.V.; Petrov, N.V. Complex wavefront manipulation and holographic correction based on digital micromirror device: A study of spatial resolution and discretisation. Proc. SPIE 2020, 11294, 112940B. [Google Scholar] [CrossRef]
- Georgieva, A.; Belashov, A.V.; Petrov, N.V. Optimization of DMD-based independent amplitude and phase modulation by analysis of target complex wavefront. Sci. Rep. 2022, 12, 7754. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Sherif, S.S.; Cathey, W.T.; Dowski, E.R. Phase plate to extend the depth of field of incoherent hybrid imaging systems. Appl. Opt. 2004, 43, 2709–2721. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V. Generalized apodization of an incoherent imaging system aimed for extending the depth of focus. Pattern Recognit. Image Anal. 2015, 25, 626–631. [Google Scholar] [CrossRef]
- Khonina, S.N.; Volotovskiy, S.G.; Dzyuba, A.P.; Serafimovich, P.G.; Popov, S.B.; Butt, M.A. Power phase apodization study on compensation defocusing and chromatic aberration in the imaging system. Electronics 2021, 10, 1327. [Google Scholar] [CrossRef]
- Lee, W.H. Binary synthetic holograms. Appl. Opt. 1974, 13, 1677–1682. [Google Scholar] [CrossRef] [PubMed]
- Liebling, M.; Blu, T.; Unser, M. Complex-Wave Retrieval from a Single off-Axis Hologram. J. Opt. Soc. Am. A. 2004, 21, 367. [Google Scholar] [CrossRef] [PubMed]
- Katkovnik, V.; Shevkunov, I.A.; Petrov, N.V.; Egiazarian, K. Wavefront Reconstruction in Digital Off-Axis Holography via Sparse Coding of Amplitude and Absolute Phase. Opt. Lett. 2015, 40, 2417. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Guo, Y.; Zhong, L.; Min, L.; Wang, J.; Wu, Y.; Chen, K.; Wei, K.; Rao, C. Adaptive optics based on machine learning: A review. Opto-Electron. Adv. 2022, 5, 200082. [Google Scholar] [CrossRef]
- Kaiser, L.; Gomez, A.N.; Chollet, F. Depthwise Separable Convolutions for Neural Machine Translation. arXiv 2017. [Google Scholar] [CrossRef]
- Khorin, P.A.; Volotovskiy, S.G. Analysis of the threshold sensitivity of a wavefront aberration sensor based on a multi-channel diffraction optical element. Proc. SPIE 2021, 11793, 117930B. [Google Scholar]

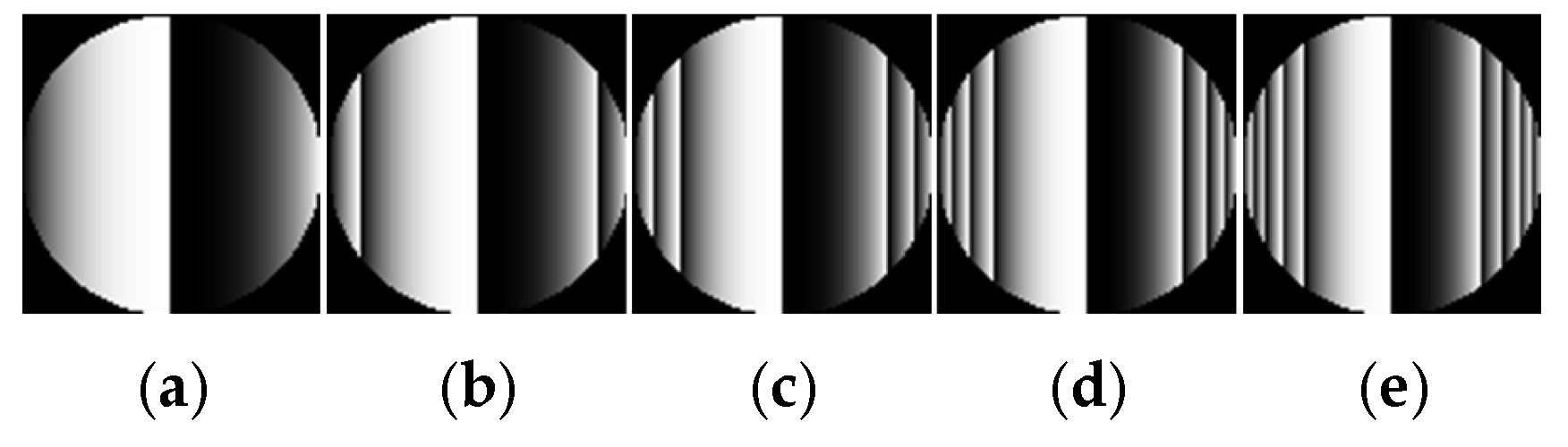


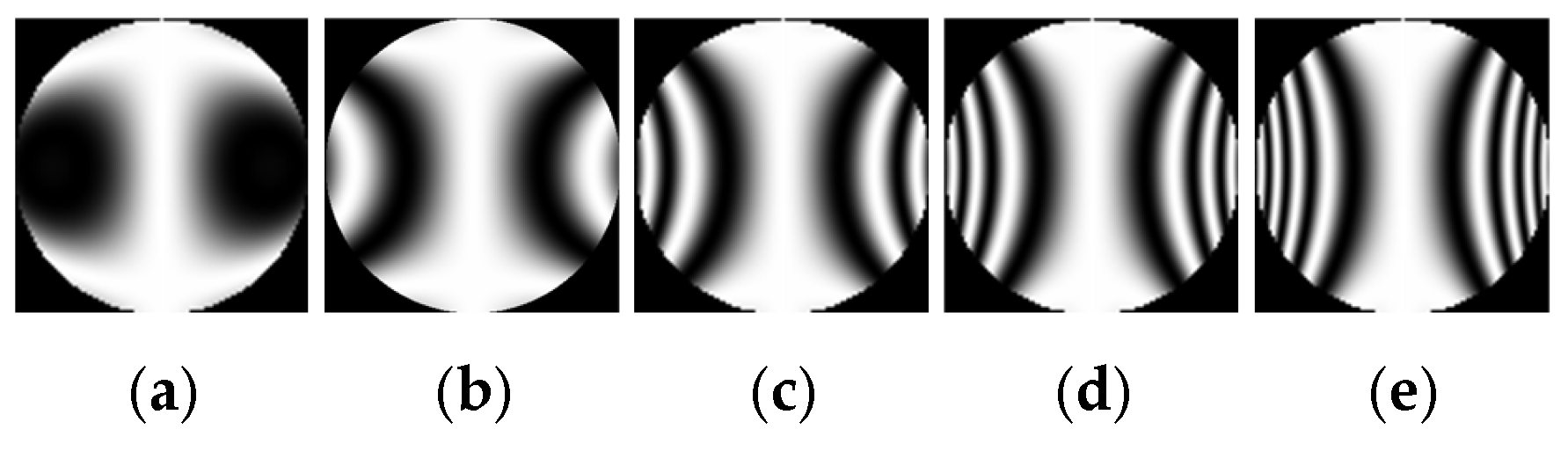

| Aberration Type Phase W(x,y) | Linear Interferogram , | Cylindrical Interferogram , |
|---|---|---|
- tilt |   |   |
- astigmatism |   |   |
- defocus |   |   |
- trefoil |   |   |
- coma |   |   |
- quadrafoil |   |   |
- secondary ast. |   |   |
- spherical |   |   |
| Images of Linear Interferograms | Images of Cylindrical Interferograms | ||||
|---|---|---|---|---|---|
| 2π | 4π | 6π | 2π | 4π | 6π |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
| Aberration Type Phase W(x,y) | Linear Interferogram , | Cylindrical Interferogram , |
|---|---|---|
- tilt |   |   |
- astigmatism |   |  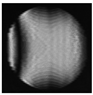 |
- defocus |  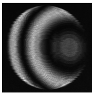 |   |
- trefoil |   |   |
- coma |  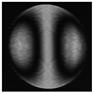 | 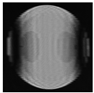 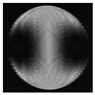 |
- quadrafoil |   |   |
- secondary ast. |   | 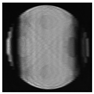 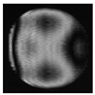 |
- spherical | 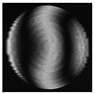  | 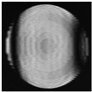 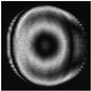 |
| Images of Linear Interferograms | Images of Cylindrical Interferograms | ||||
|---|---|---|---|---|---|
| 2π | 4π | 6π | 2π | 4π | 6π |
 |  |  |  | 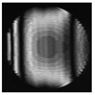 | 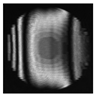 |
 |  |  |  | 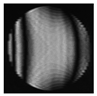 |  |
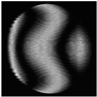 |  |  | 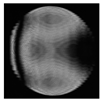 | 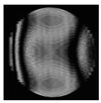 | 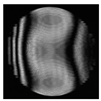 |
| Model Phase Distribution | Reconstructed Phase Distribution | Interferogram |
|---|---|---|
 |  | 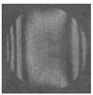 |
 |  |  |
 |  | 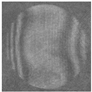 |
| Type Angle | Linear | Cylindrical |
|---|---|---|
| α = 2π | 0.0063 | 0.0050 |
| α = 4π | 0.0065 | 0.0047 |
| α = 6π | 0.0068 | 0.0050 |
| Images of Cylindrical Interferograms | |||||
|---|---|---|---|---|---|
| 0.30 | |||||
| 0.05 | 0.15 | 0.25 | 0.35 | 0.45 | |
| Interf. |  |  |  |  |  |
| Type Angle | Cylindrical Model Interferogram | Cylindrical Experimental Interferogram |
|---|---|---|
| α = 2π | 0.0050 | 0.0049 |
| α = 4π | 0.0047 | 0.0046 |
| α = 6π | 0.0050 | 0.0052 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khorin, P.A.; Dzyuba, A.P.; Chernykh, A.V.; Georgieva, A.O.; Petrov, N.V.; Khonina, S.N. Neural Network-Assisted Interferogram Analysis Using Cylindrical and Flat Reference Beams. Appl. Sci. 2023, 13, 4831. https://doi.org/10.3390/app13084831
Khorin PA, Dzyuba AP, Chernykh AV, Georgieva AO, Petrov NV, Khonina SN. Neural Network-Assisted Interferogram Analysis Using Cylindrical and Flat Reference Beams. Applied Sciences. 2023; 13(8):4831. https://doi.org/10.3390/app13084831
Chicago/Turabian StyleKhorin, Pavel A., Alexey P. Dzyuba, Aleksey V. Chernykh, Aleksandra O. Georgieva, Nikolay V. Petrov, and Svetlana N. Khonina. 2023. "Neural Network-Assisted Interferogram Analysis Using Cylindrical and Flat Reference Beams" Applied Sciences 13, no. 8: 4831. https://doi.org/10.3390/app13084831
APA StyleKhorin, P. A., Dzyuba, A. P., Chernykh, A. V., Georgieva, A. O., Petrov, N. V., & Khonina, S. N. (2023). Neural Network-Assisted Interferogram Analysis Using Cylindrical and Flat Reference Beams. Applied Sciences, 13(8), 4831. https://doi.org/10.3390/app13084831








