Aerothermoelastic Analysis of Conical Shell in Supersonic Flow
Abstract
:1. Introduction
2. Dynamic Model
2.1. Model Description
2.2. Constrained Mode
2.3. Dynamic Equation
3. Comparison and Convergence Studies
4. Numerical Results and Discussions
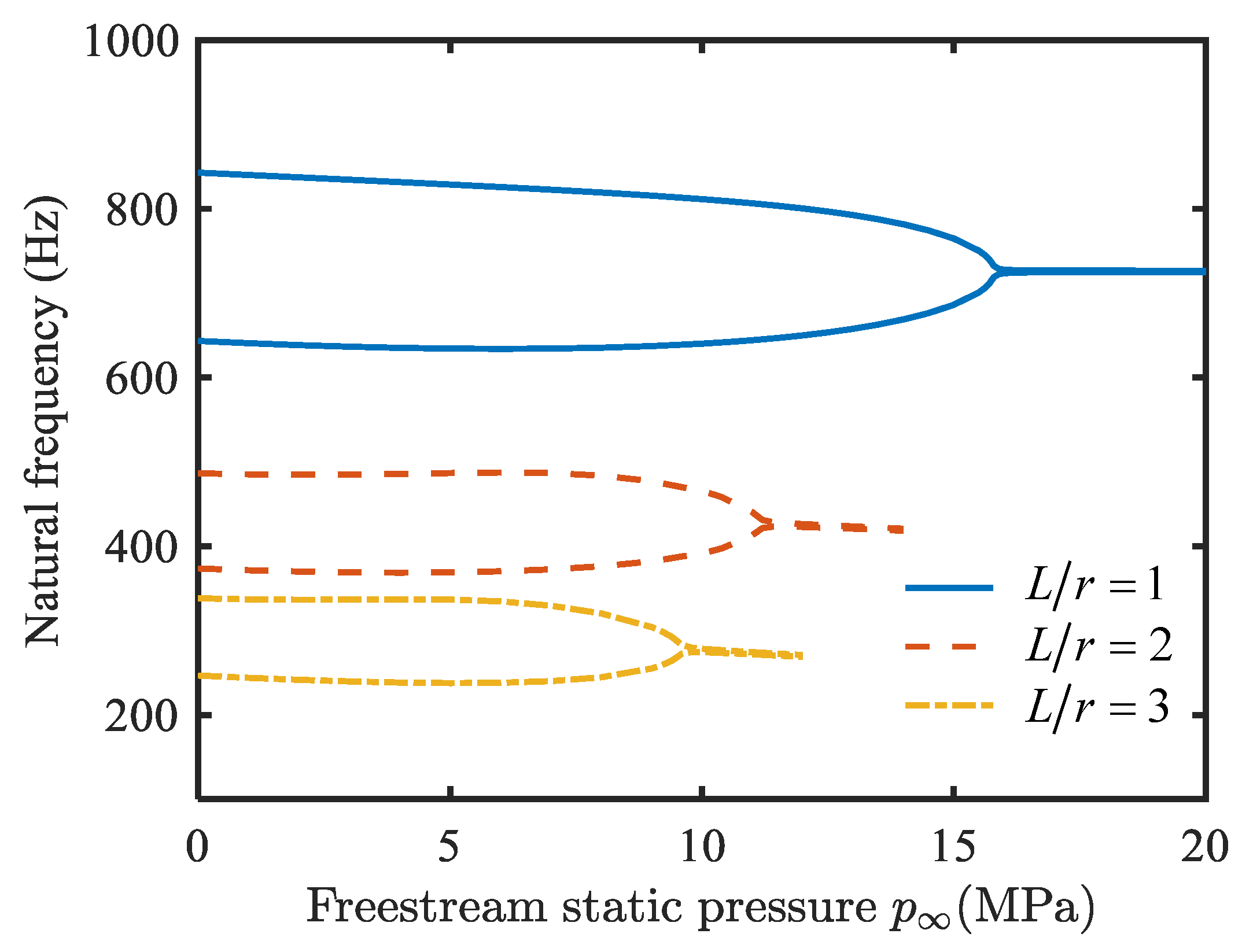
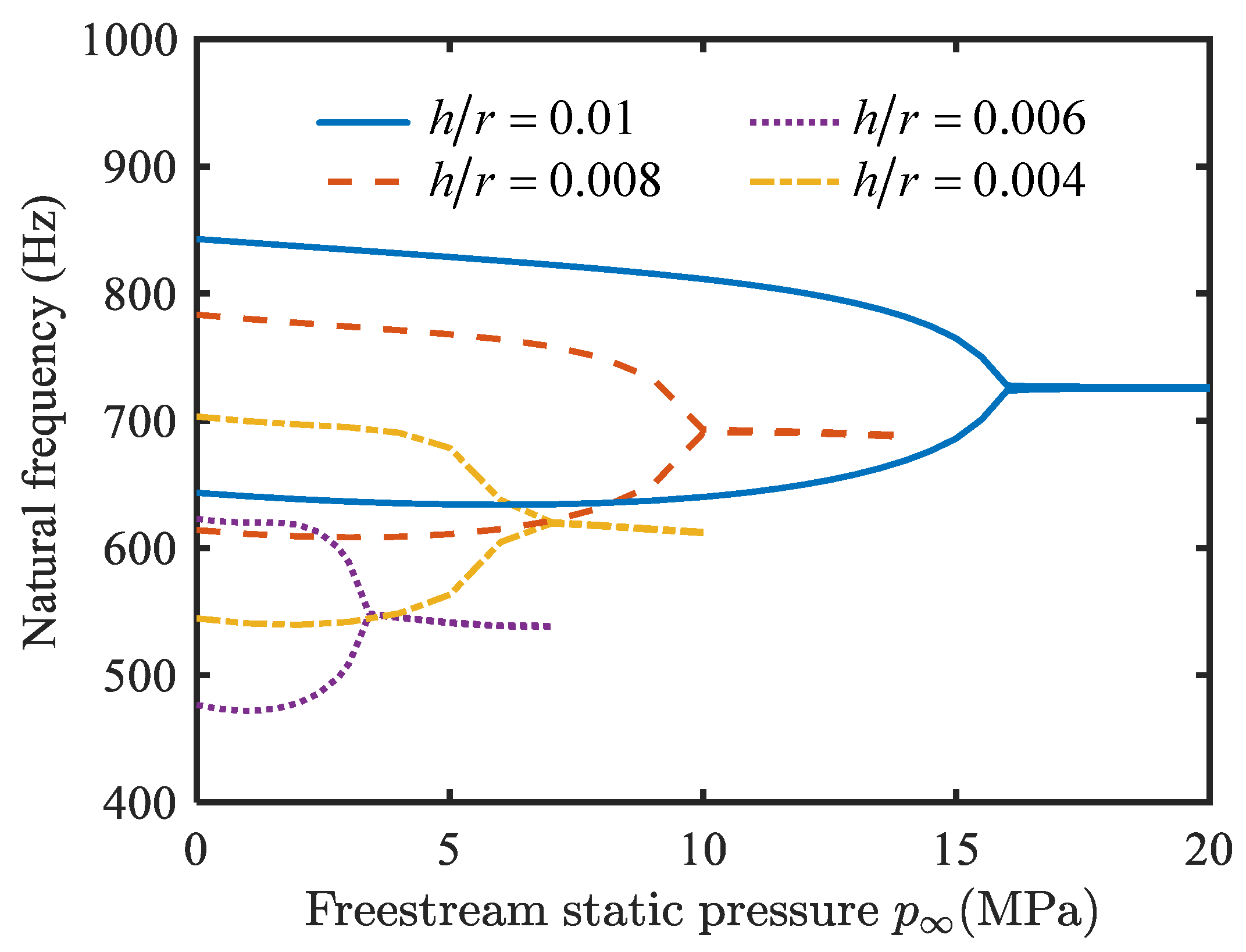
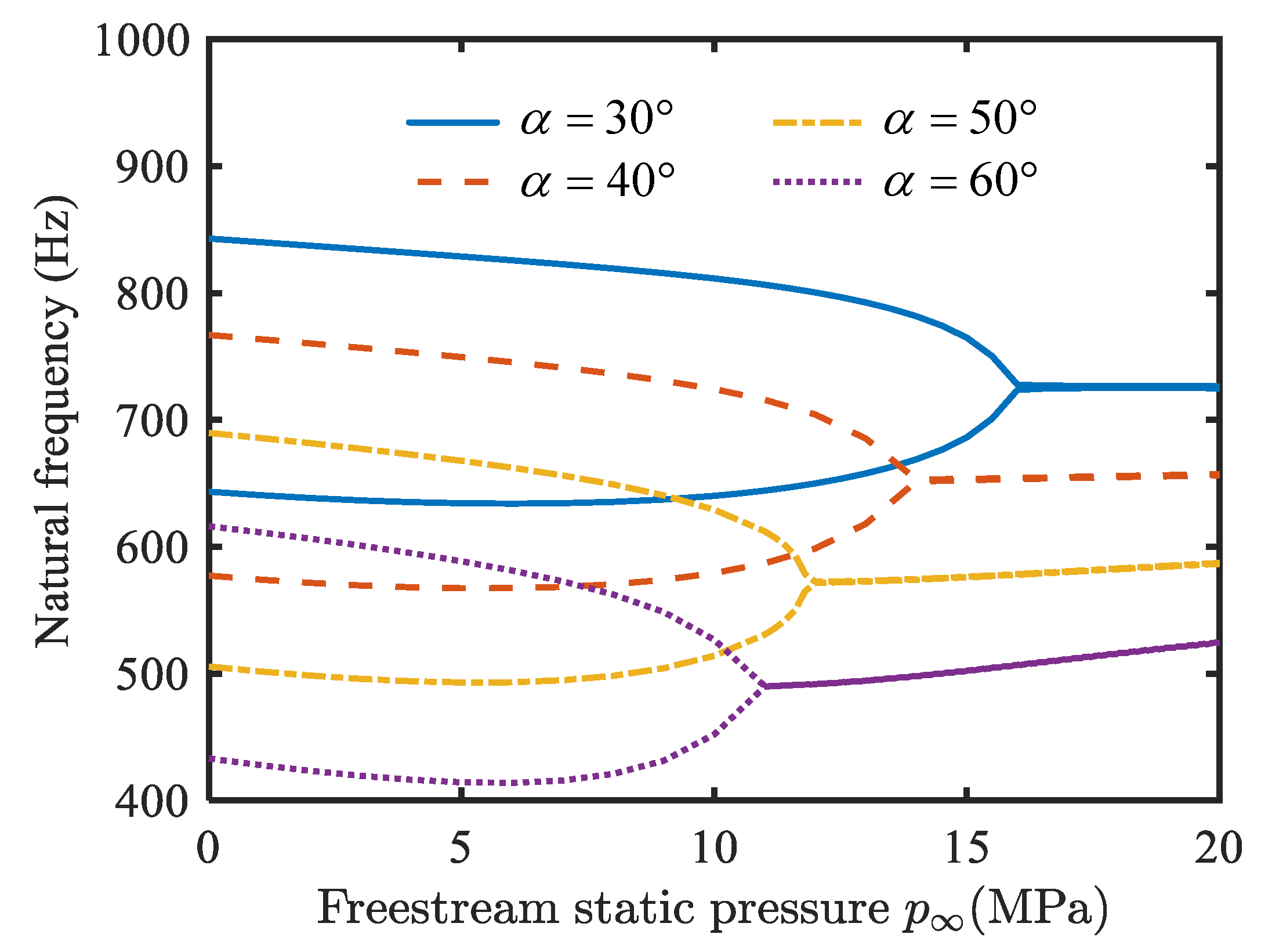
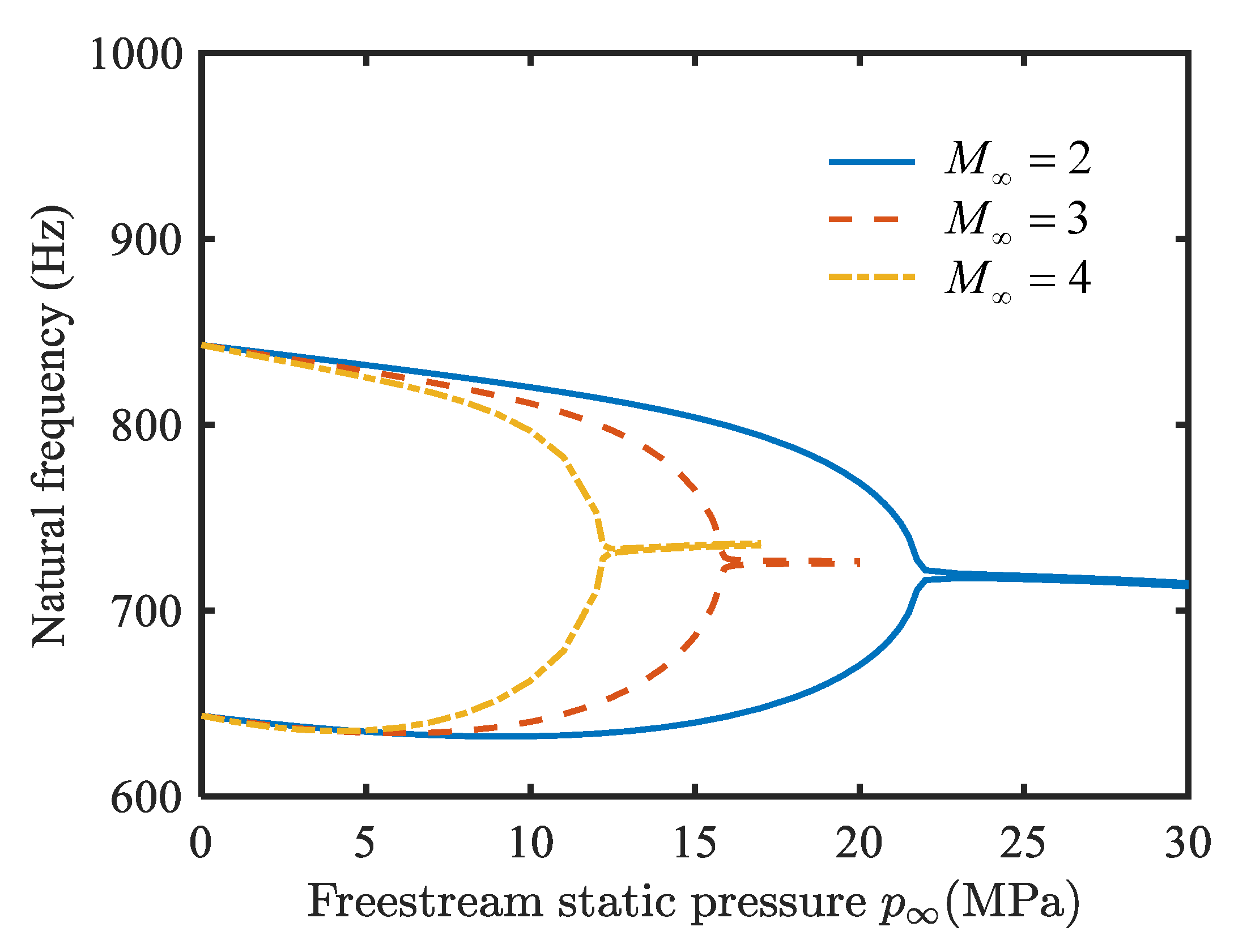
4.1. Natural Vibration Characteristics Analysis
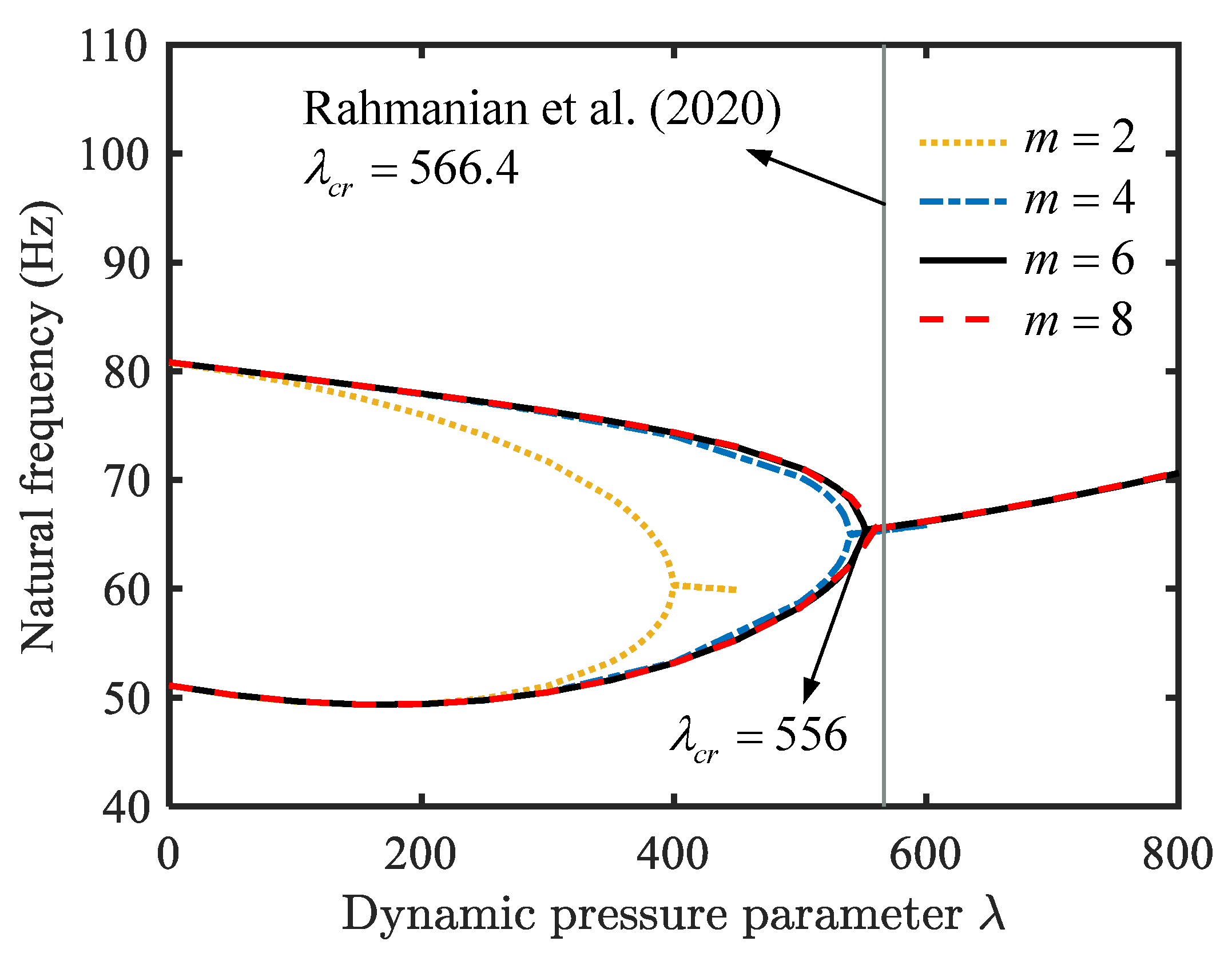
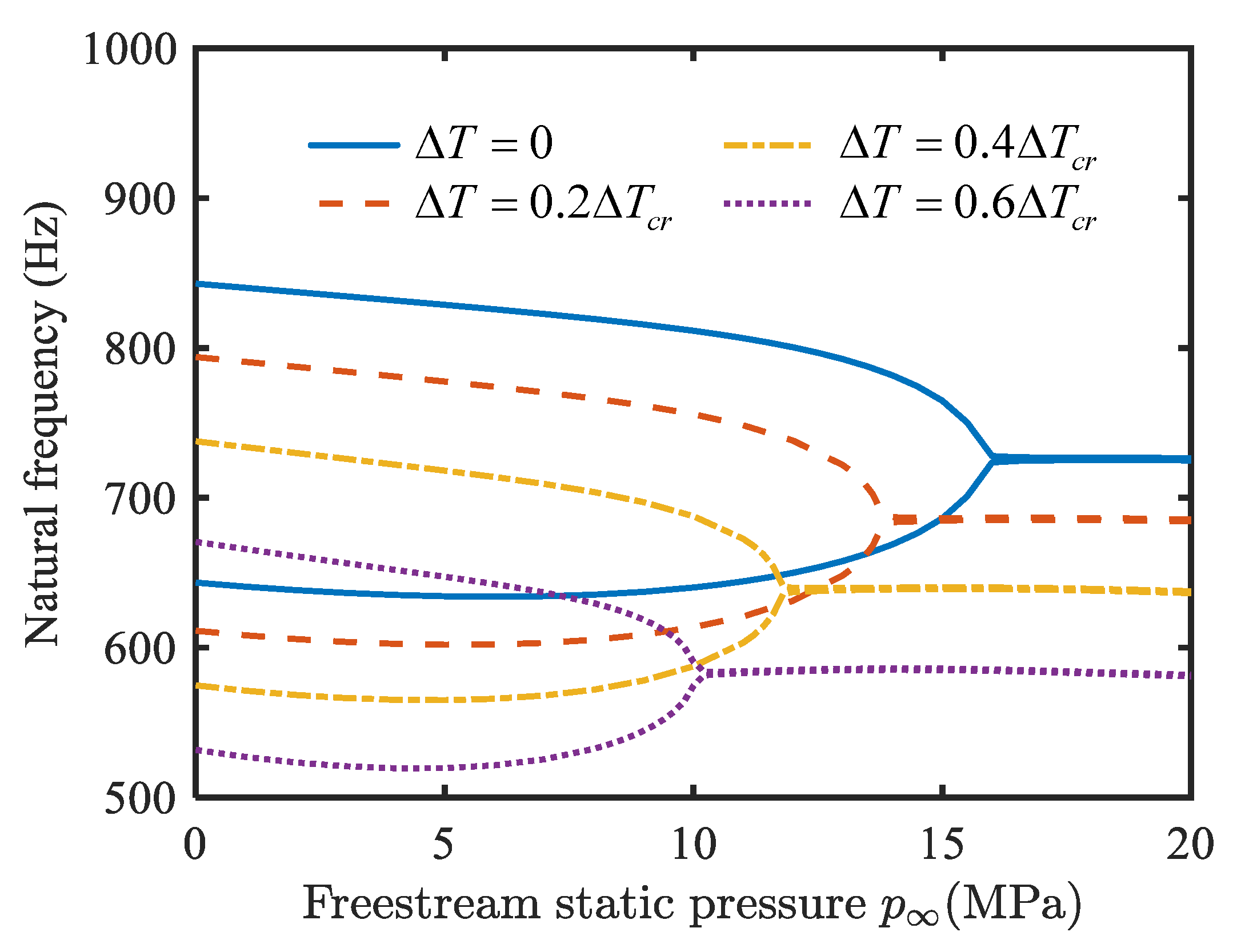
4.2. Aerothermoelastic Stability Analysis
5. Conclusions
- (1)
- For thin-walled conical shells, the linear temperature assumption is reasonable.
- (2)
- With an increase in temperature change, the fundamental frequency of the conical shell decreases gradually, and finally drops to zero. As the static pressure of the free-stream increases, two adjacent natural frequencies converge, which can cause flutter.
- (3)
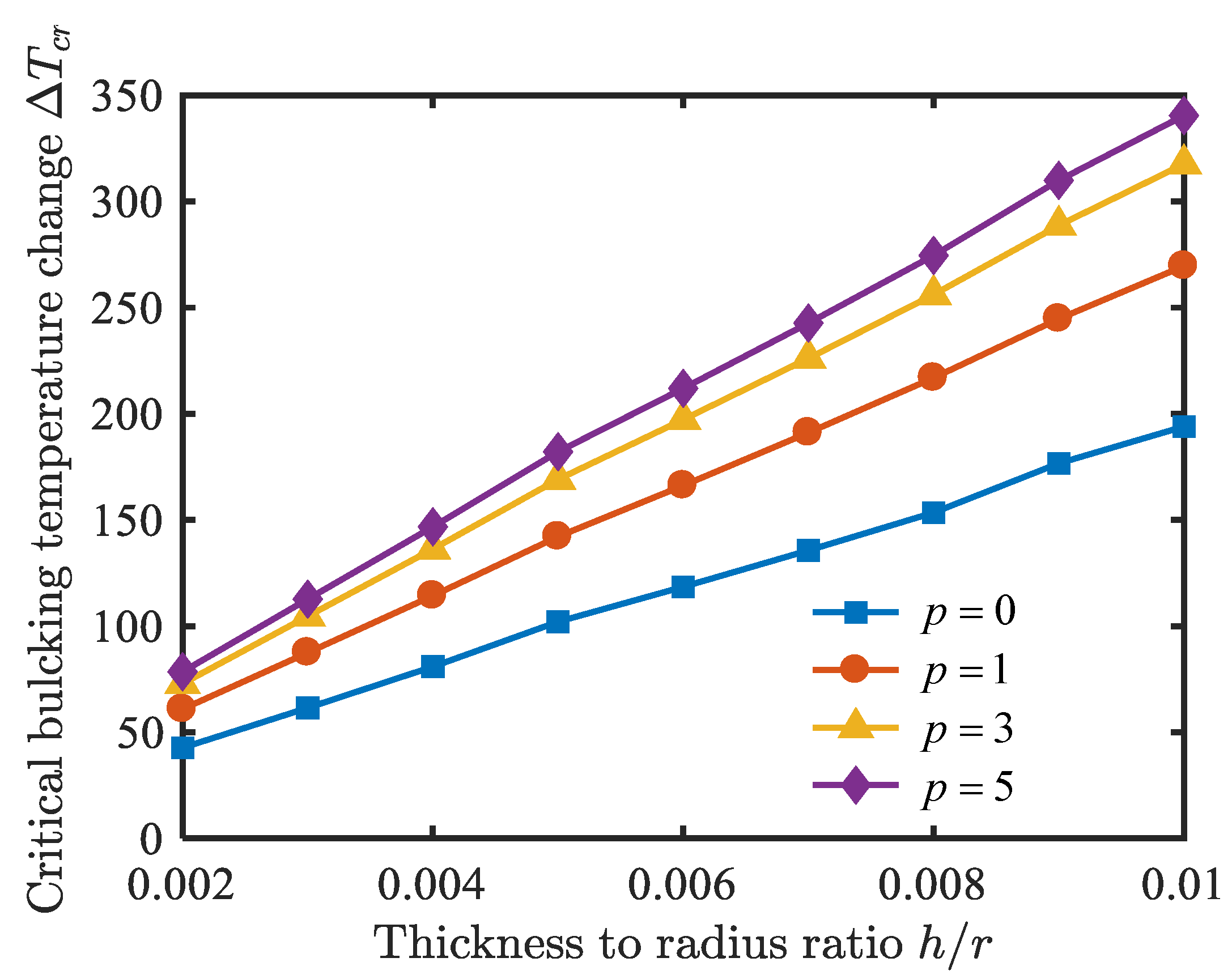
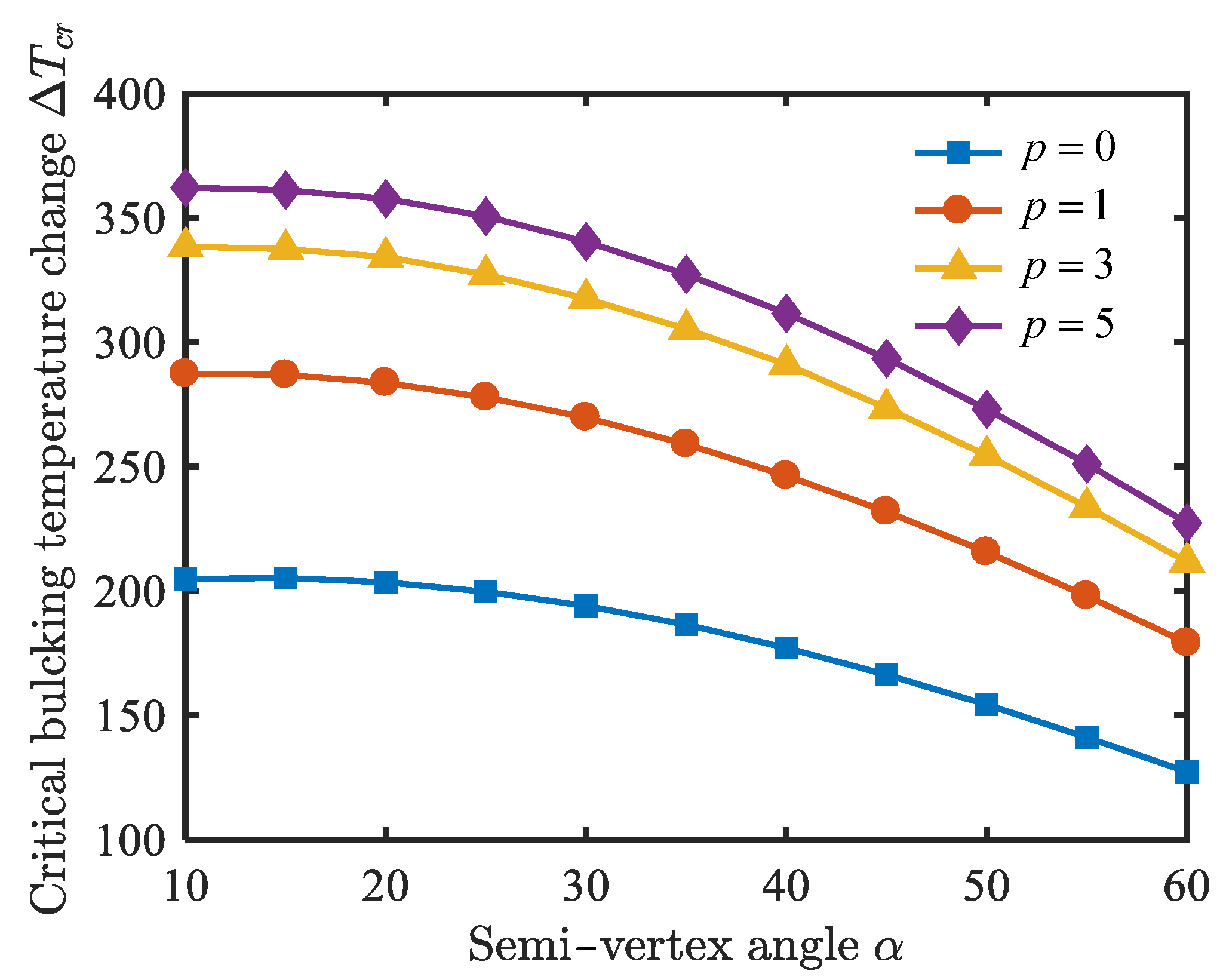
- The natural frequencies of the conical shell are proportional to the ratio of thickness to radius, and inversely proportional to the ratio of length to radius and semi-vertex angle.
- (4)
- With an increase in the length-to-radius ratio, the critical buckling temperature change increases slightly, and the critical free-stream static pressure decreases obviously; the critical buckling temperature change and the critical free-stream static pressure are enhanced by raising the thickness-to-radius ratio; the critical buckling temperature change and the critical free-stream static pressure decrease when the semi-vertex angle is enhanced.
- (5)
- The critical flutter pressure of conical shell is intensified with a decrease in the Mach number and temperature.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amabili, M.; Pellicano, F. Nonlinear supersonic flutter of circular cylindrical shells. AIAA J. 2001, 39, 564–573. [Google Scholar] [CrossRef]
- Amabili, M.; Pellicano, F. Multimode approach to nonlinear supersonic flutter of imperfect circular cylindrical shells. J. Appl. Mech.-Trans. ASME 2002, 69, 117–129. [Google Scholar] [CrossRef]
- Haddadpour, H.; Mahmoudkhani, S.; Navazi, H.M. Supersonic flutter prediction of functionally graded cylindrical shells. Compos. Struct. 2008, 83, 391–398. [Google Scholar] [CrossRef]
- Shin, W.H.; Oh, I.K.; Lee, I. Nonlinear flutter of aerothermally buckled composite shells with damping treatments. J. Sound Vib. 2009, 324, 556–569. [Google Scholar] [CrossRef]
- Song, Z.G.; Li, F.M. Aerothermoelastic analysis and active flutter control of supersonic composite laminated cylindrical shells. Compos. Struct. 2013, 106, 653–660. [Google Scholar] [CrossRef]
- Sabri, F.; Lakis, A.A. Efficient hybrid finite element method for flutter prediction of functionally graded cylindrical shells. J. Vib. Acoust.-Trans. ASME 2014, 136, 011002. [Google Scholar] [CrossRef]
- Bochkarev, S.A.; Lekomtsev, S.V.; Matveenko, V.P. Aeroelastic stability of heated functionally graded cylindrical shells containing fluid. Mech. Adv. Mater. Struct. 2017, 24, 1391–1400. [Google Scholar] [CrossRef]
- Asadi, H. Numerical simulation of the fluid-solid interaction for CNT reinforced functionally graded cylindrical shells in thermal environments. Acta Astronaut. 2017, 138, 214–224. [Google Scholar] [CrossRef]
- Zhang, L.W.; Song, Z.G.; Liew, K.M. Modeling aerothermoelastic properties and active flutter control of nanocomposite cylindrical shells in supersonic airflow under thermal environments. Comput. Methods Appl. Mech. Eng. 2017, 325, 416–433. [Google Scholar] [CrossRef]
- Chai, Y.Y.; Song, Z.G.; Li, F.M. Investigations on the aerothermoelastic properties of composite laminated cylindrical shells with elastic boundaries in supersonic airflow based on the Rayleigh-Ritz method. Aerosp. Sci. Technol. 2018, 82–83, 534–544. [Google Scholar] [CrossRef]
- Lin, H.G.; Cao, D.Q.; Shao, C.H. An admissible function for vibration and flutter studies of FG cylindrical shells with arbitrary edge conditions using characteristic orthogonal polynomials. Compos. Struct. 2018, 185, 748–763. [Google Scholar] [CrossRef]
- Bochkarev, S.A.; Lekomtsev, S.V. Stability of functionally graded circular cylindrical shells under combined loading. Mech. Compos. Mater. 2019, 55, 349–362. [Google Scholar] [CrossRef]
- Fazilati, J.; Khalafi, V.; Shahverdi, H. Three-dimensional aero-thermo-elasticity analysis of functionally graded cylindrical shell panels. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 1715–1727. [Google Scholar] [CrossRef]
- Mahmoudkhani, S. Aerothermoelastic analysis of imperfect FG cylindrical shells in supersonic flow. Compos. Struct. 2019, 225, 111160. [Google Scholar] [CrossRef]
- Guo, H.L.; Zur, K.K.; Ouyang, X. New insights into the nonlinear stability of nanocomposite cylindrical panels under aero-thermal loads. Compos. Struct. 2023, 303, 116231. [Google Scholar] [CrossRef]
- Mei, C.; Abdel-Motagly, K.; Chen, R. A review of nonlinear panel flutter at supersonic and hypersonic speeds. Appl. Mech. Rev. 1999, 52, 321–332. [Google Scholar] [CrossRef]
- Shishaeva, A.; Aksenov, A.; Vedeneev, V. The effect of external perturbations on nonlinear panel flutter at low supersonic speed. J. Fluids Struct. 2022, 111, 103570. [Google Scholar] [CrossRef]
- Abdukhakimov, F.A.; Vedeneev, V.V. Effect of Yaw Angle on Flutter of Rectangular Plates at Low Supersonic Speeds. AIAA J. 2022, 60, 4256–4266. [Google Scholar] [CrossRef]
- Vedeneev, V.V.; Nesterov, V.A. Effect of Nonequilibrium Reacting Flow on Flutter at Hypersonic Flight Speed. AIAA J. 2019, 57, 2222–2226. [Google Scholar] [CrossRef]
- Bhangale, R.K.; Ganesan, N.; Padmanabhan, C. Linear thermoelastic buckling and free vibration behavior of functionally graded truncated conical shells. J. Sound Vib. 2006, 292, 341–371. [Google Scholar] [CrossRef]
- Naj, R.; Boroujerdy, M.S.; Eslami, M.R. Thermal and mechanical instability of functionally graded truncated conical shells. Thin-Walled Struct. 2008, 46, 65–78. [Google Scholar] [CrossRef]
- Talebitooti, M. Thermal effect on free vibration of ring-stiffened rotating graded conical shell with clamped ends. Mech. Adv. Mater. Struct. 2016, 25, 155–165. [Google Scholar] [CrossRef]
- Shakouri, M. Free vibration analysis of functionally graded rotating conical shells in thermal environment. Compos. Part B-Eng. 2019, 163, 574–584. [Google Scholar] [CrossRef]
- Dixon, S.C.; Hudson, M.L. Flutter, Vibration, and Buckling of Truncated Orthotropic Conical Shells with Generalized Elastic Edge Restraint; TN D-5759; NASA: Washington, DC, USA, 1970. [Google Scholar]
- Bismarcknasr, M.N.; Costasavio, H.R. Finite-element solution of the supersonic flutter of conical shells. AIAA J. 1979, 17, 1148–1150. [Google Scholar] [CrossRef]
- Vasil’ev, A.V. Flutter of conical shells under external flow of a supersonic gas. Mosc. Univ. Mech. Bull. 2015, 70, 23–27. [Google Scholar] [CrossRef]
- Sabri, F.; Lakis, A.A. Hybrid finite element method applied to supersonic flutter of an empty or partially liquid-filled truncated conical shell. J. Sound Vib. 2010, 329, 302–316. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, Z.; Gao, Y. The flutter of truncated conical shell subjected to internal supersonic air flow. Multidiscip. Model. Mater. Struct. 2014, 10, 18–35. [Google Scholar]
- Mehri, M.; Asadi, H.; Wang, Q. On dynamic instability of a pressurized functionally graded carbon nanotube reinforced truncated conical shell subjected to yawed supersonic airflow. Compos. Struct. 2016, 153, 938–951. [Google Scholar] [CrossRef]
- Bakhtiari, M.; Lakis, A.A.; Kerboua, Y. Nonlinear supersonic flutter of truncated conical shells. J. Mech. Sci. Technol. 2020, 34, 1375–1388. [Google Scholar] [CrossRef]
- Afshari, H.; Ariaseresht, Y.; Koloor, S.S.R.; Amirabadi, H.; Bidgoli, M.O. Supersonic flutter behavior of a polymeric truncated conical shell reinforced with agglomerated CNTs. Waves Random Complex Media 2022, 23. [Google Scholar] [CrossRef]
- Rahmanian, M.; Javadi, M. A unified algorithm for fully-coupled aeroelastic stability analysis of conical shells in yawed supersonic flow to identify the effect of boundary conditions. Thin-Walled Struct. 2020, 155, 106910. [Google Scholar] [CrossRef]
- Mahmoudkhani, S.; Haddadpour, H.; Navazi, H.M. Supersonic flutter prediction of functionally graded conical shells. Compos. Struct. 2010, 92, 377–386. [Google Scholar] [CrossRef]
- Hao, Y.X.; Yang, S.W.; Zhang, W.; Yao, M.H.; Wang, A.W. Flutter of high-dimension nonlinear system for a FGM truncated conical shell. Mech. Adv. Mater. Struct. 2018, 25, 47–61. [Google Scholar] [CrossRef]
- Shen, H.S.; Noda, N. Postbuckling of FGM cylindrical shells under combined axial and radial mechanical loads in thermal environments. Int. J. Solids Struct. 2005, 42, 4641–4662. [Google Scholar] [CrossRef]
- Sun, S.; Cao, D.; Han, Q. Vibration studies of rotating cylindrical shells with arbitrary edges using characteristic orthogonal polynomials in the rayleigh–ritz method. Int. J. Mech. Sci. 2013, 68, 180–189. [Google Scholar] [CrossRef]
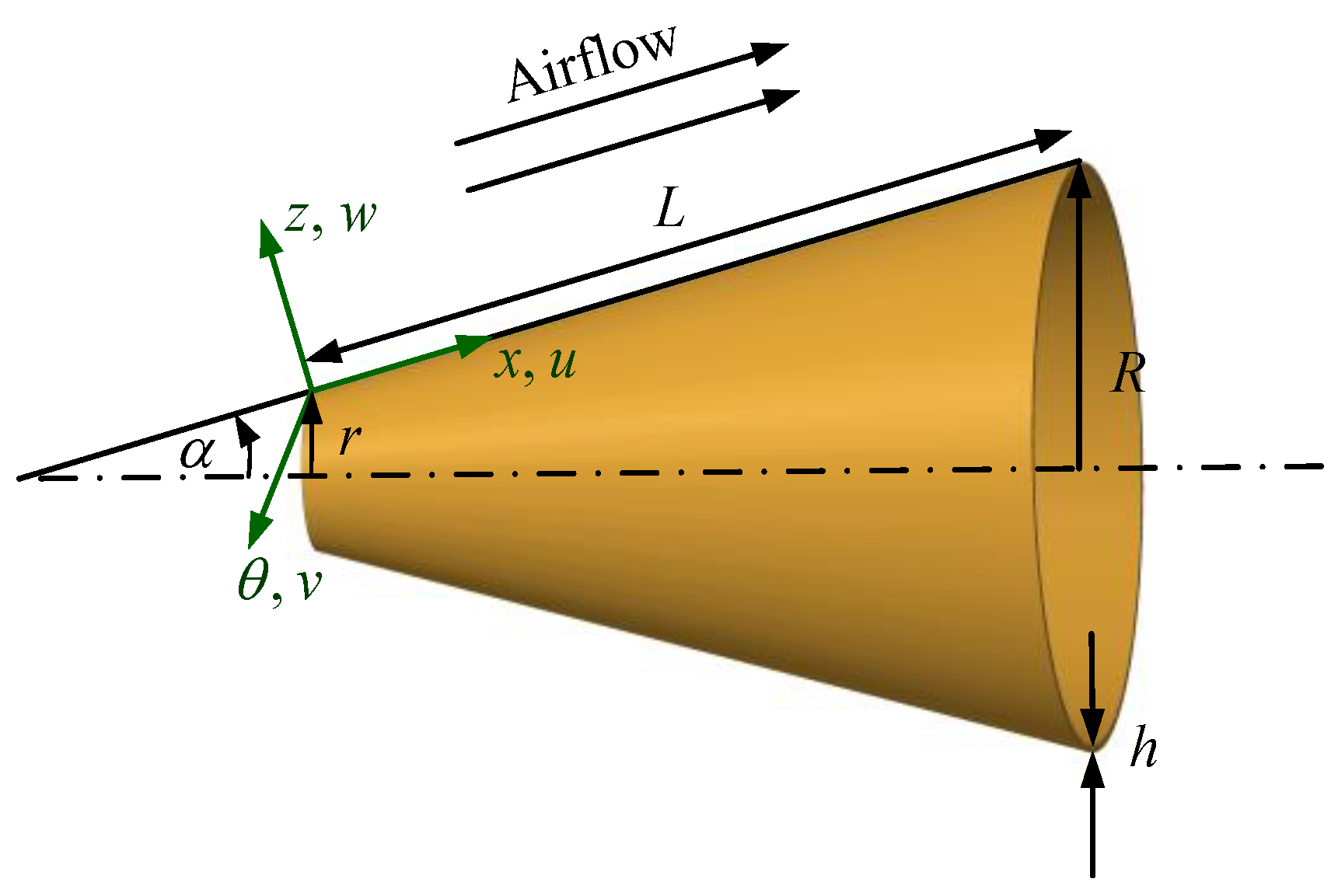



| α | Shakouri [23] | Present Results | ||||||
|---|---|---|---|---|---|---|---|---|
| N = 5 | N = 6 | N = 7 | N = 8 | N = 9 | N = 10 | |||
| L/r = 1 | 30° | 0.85746 | 0.87708 | 0.86008 | 0.85790 | 0.85765 | 0.85740 | 0.85740 |
| 60° | 0.44767 | 0.45785 | 0.44823 | 0.44817 | 0.44769 | 0.44766 | 0.44766 | |
| L/r = 5 | 30° | 0.30770 | 0.31969 | 0.31730 | 0.30935 | 0.30914 | 0.30796 | 0.30794 |
| 60° | 0.14467 | 0.16803 | 0.15799 | 0.14986 | 0.14682 | 0.14511 | 0.14493 | |
| Property | P−1 | P0 | P1 | P2 | P3 | |
|---|---|---|---|---|---|---|
| (pa) | SUS304 | 0 | 201.04 × 109 | 3.079 × 10−4 | −6.534 × 10−7 | 0 |
| Si3N4 | 0 | 348.43 × 109 | −3.070 × 10−4 | 2.130 × 10−7 | −8.946 × 10−11 | |
| SUS304 | 0 | 0.31 | 0 | 0 | 0 | |
| Si3N4 | 0 | 0.24 | 0 | 0 | 0 | |
| (kg/m3) | SUS304 | 0 | 8166 | 0 | 0 | 0 |
| Si3N4 | 0 | 2370 | 0 | 0 | 0 | |
| (1/K) | SUS304 | 0 | 12.330 × 10−6 | 8.086 × 10−4 | 0 | 0 |
| Si3N4 | 0 | 5.8723 × 10−6 | 9.095 × 10−4 | 0 | 0 | |
| k (W/m°K) | SUS304 | 0 | 15.379 | 0 | 0 | 0 |
| Si3N4 | 0 | 13.723 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zeng, L.; Zhao, C.; Sun, S.; Yang, Y. Aerothermoelastic Analysis of Conical Shell in Supersonic Flow. Appl. Sci. 2023, 13, 4850. https://doi.org/10.3390/app13084850
Wang M, Zeng L, Zhao C, Sun S, Yang Y. Aerothermoelastic Analysis of Conical Shell in Supersonic Flow. Applied Sciences. 2023; 13(8):4850. https://doi.org/10.3390/app13084850
Chicago/Turabian StyleWang, Min, Leilei Zeng, Changying Zhao, Shupeng Sun, and Yang Yang. 2023. "Aerothermoelastic Analysis of Conical Shell in Supersonic Flow" Applied Sciences 13, no. 8: 4850. https://doi.org/10.3390/app13084850
APA StyleWang, M., Zeng, L., Zhao, C., Sun, S., & Yang, Y. (2023). Aerothermoelastic Analysis of Conical Shell in Supersonic Flow. Applied Sciences, 13(8), 4850. https://doi.org/10.3390/app13084850






