Configuration Optimization and Response Prediction Method of the Clamping Robot for Vibration Suppression of Cantilever Workpiece
Abstract
:1. Introduction
- Providing a solution for dynamics modelling of the ARGW system with approximately closed-loop structure;
- The influence laws of different clamping robot configurations on the vibration responses of the workpiece are studied;
- The vibration suppression effect on the workpiece is improved by optimizing the clamping robot configuration.
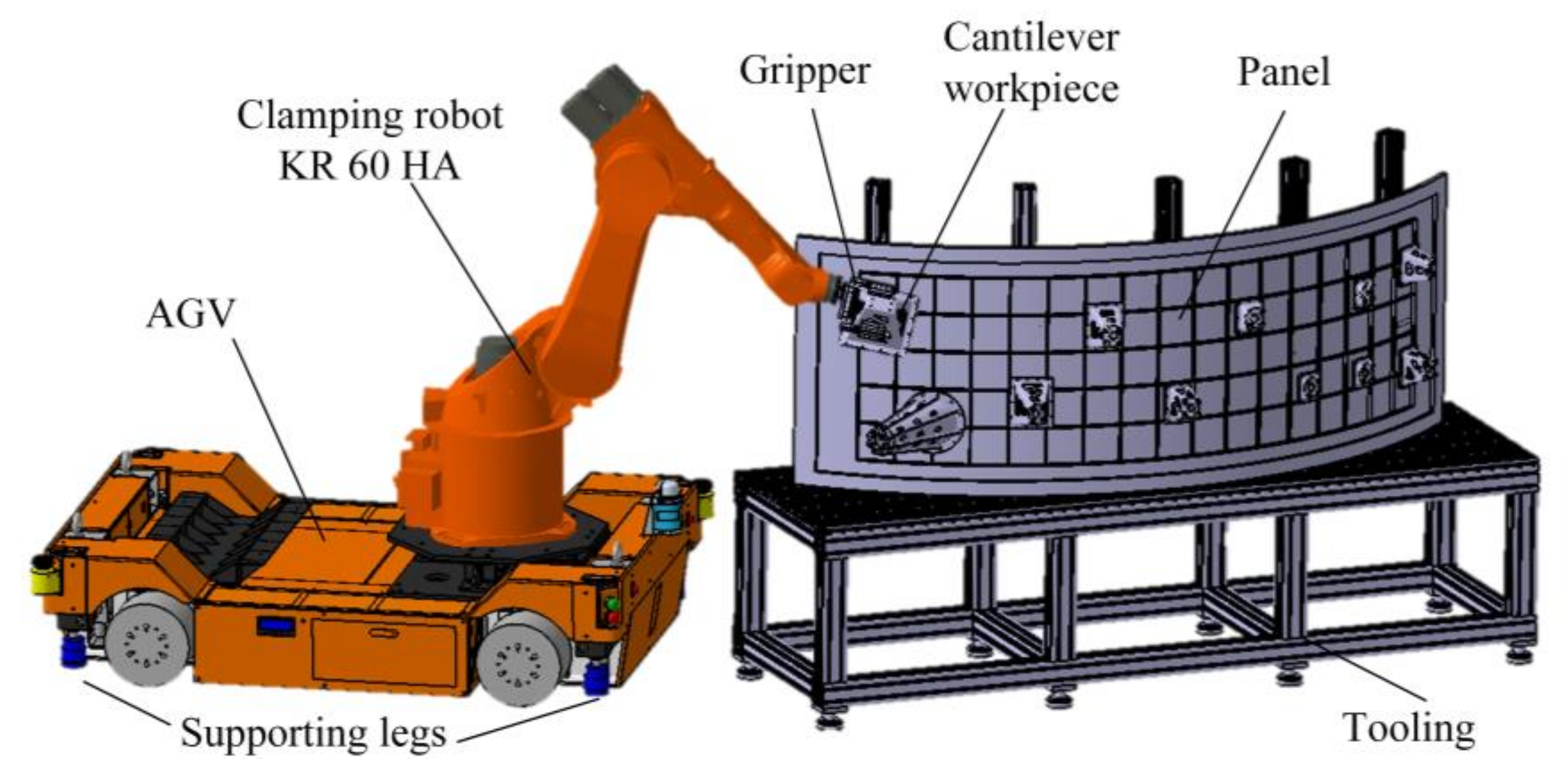
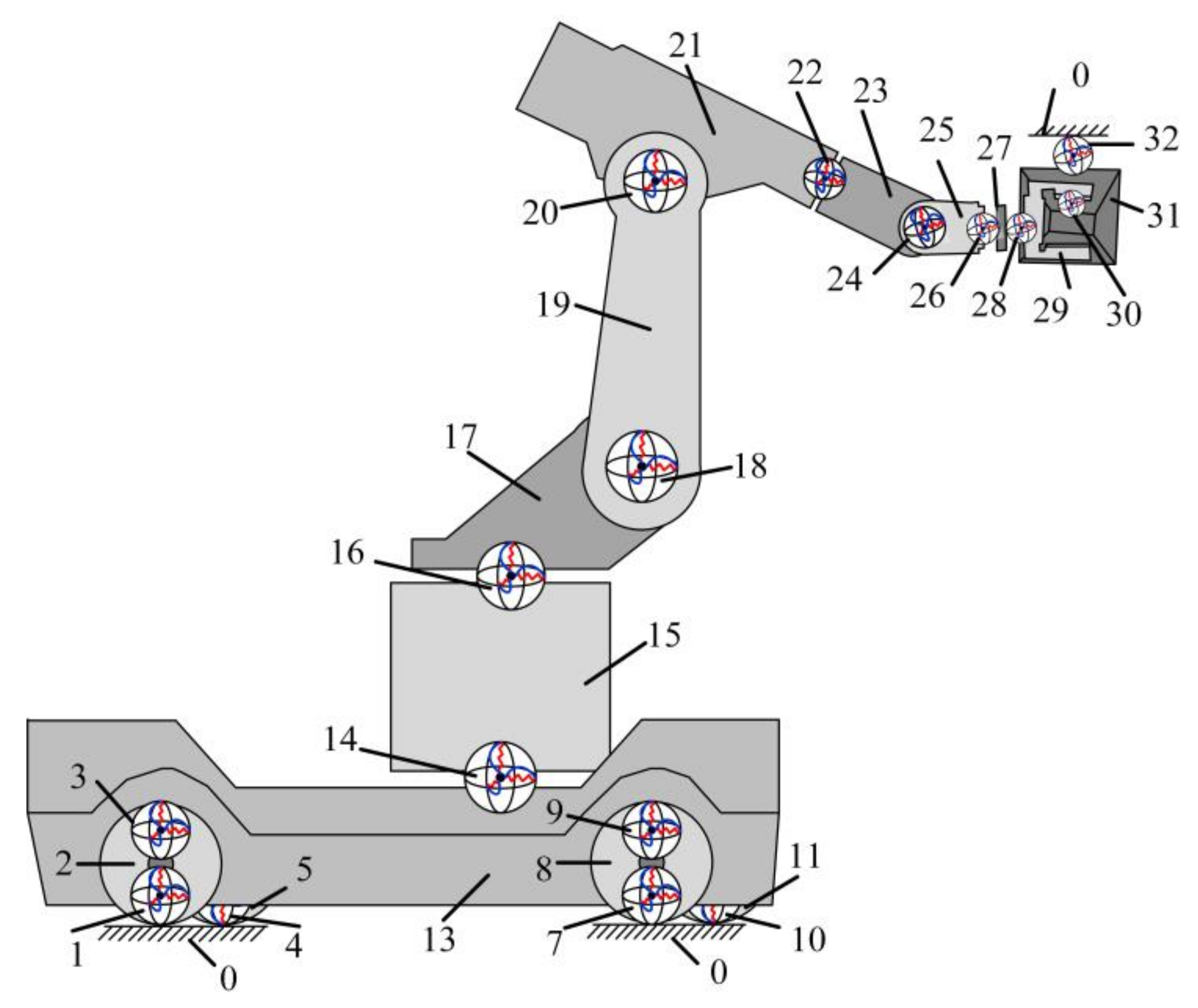
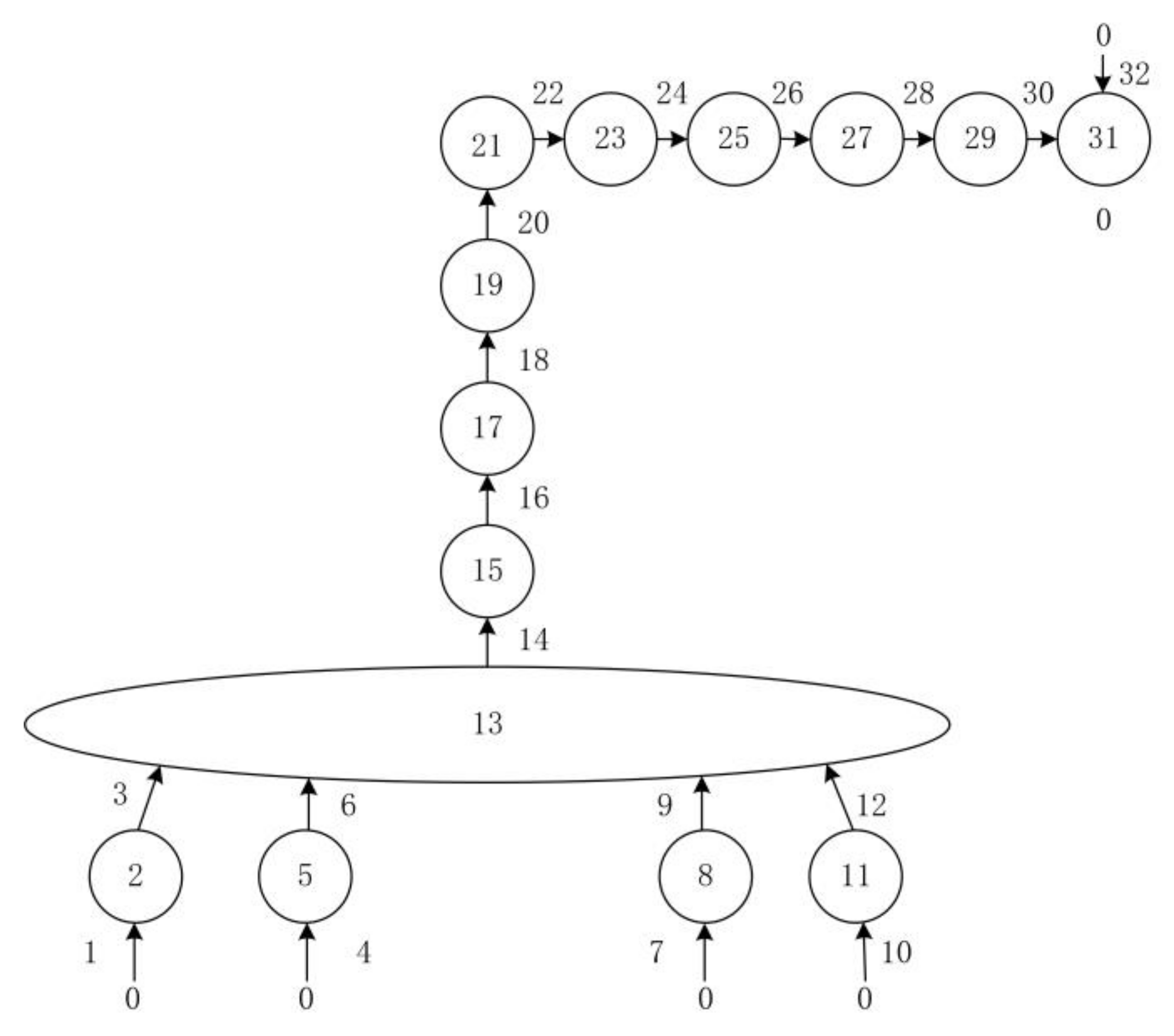
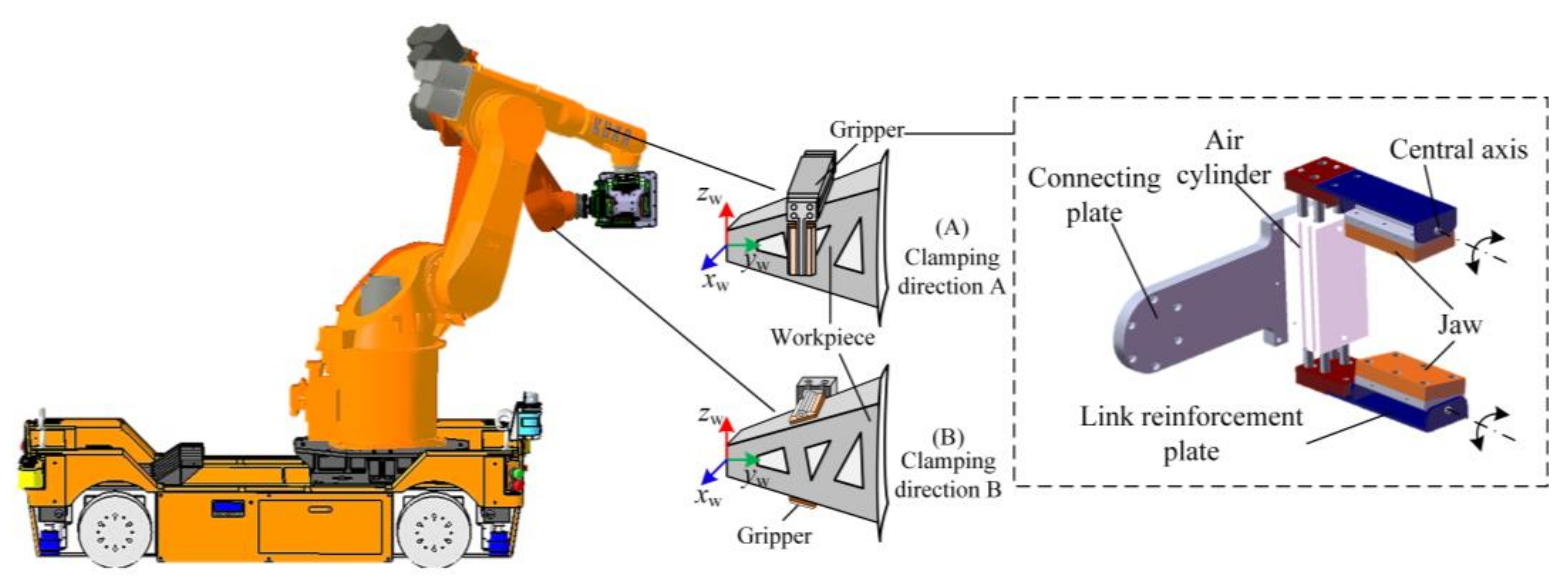
2. System Composition and Dynamic Model
3. Dynamics Responses of the Workpiece under Different Clamping Robot Configurations
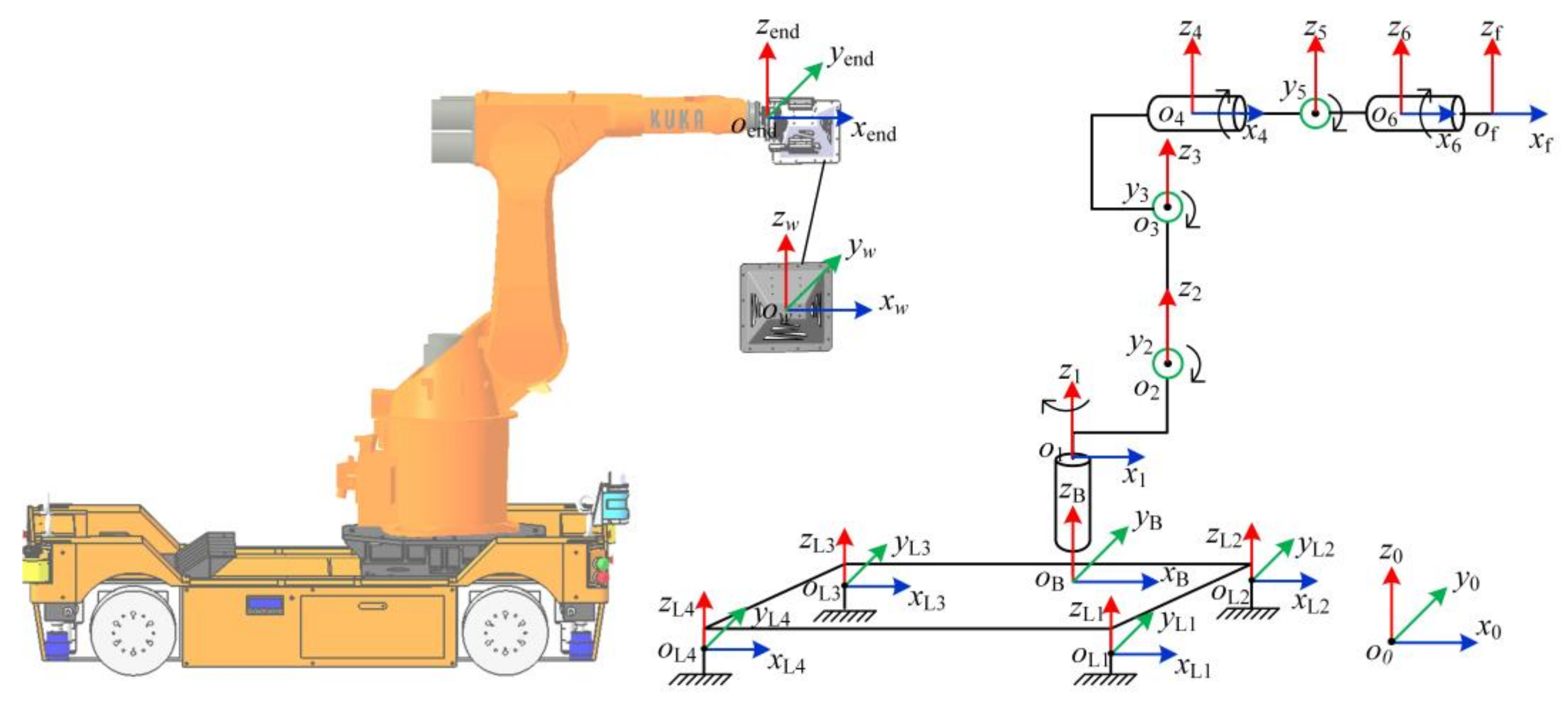
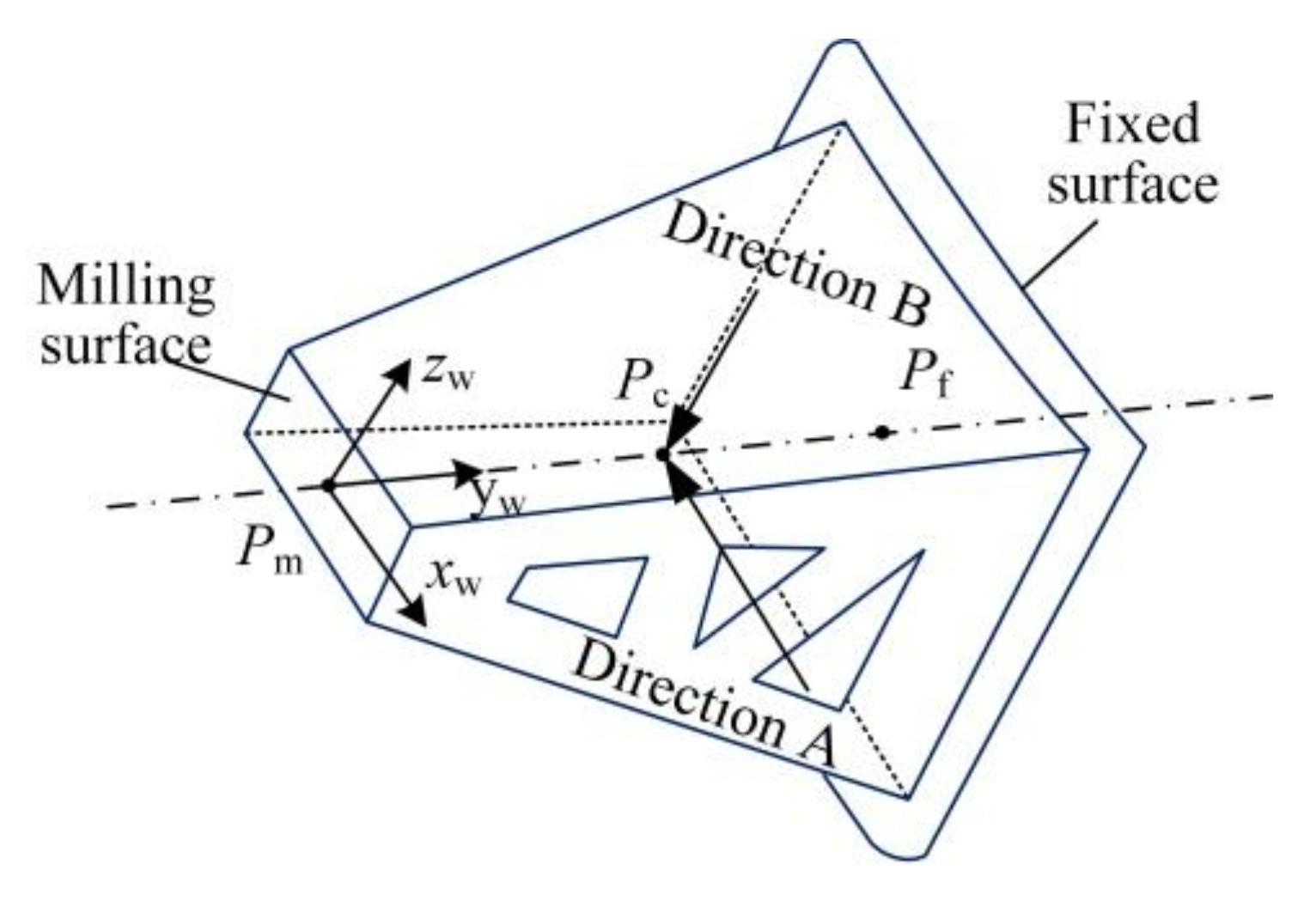
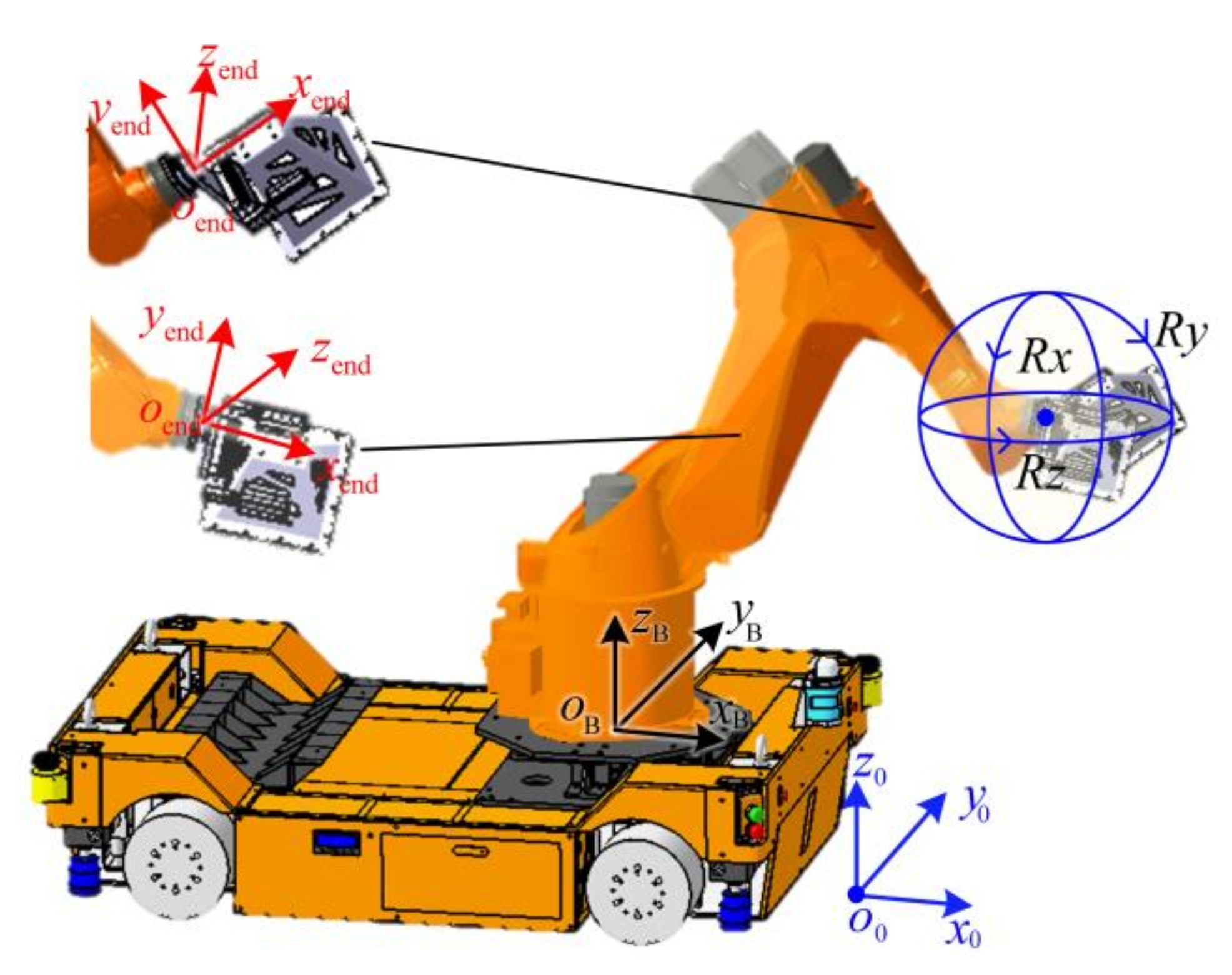
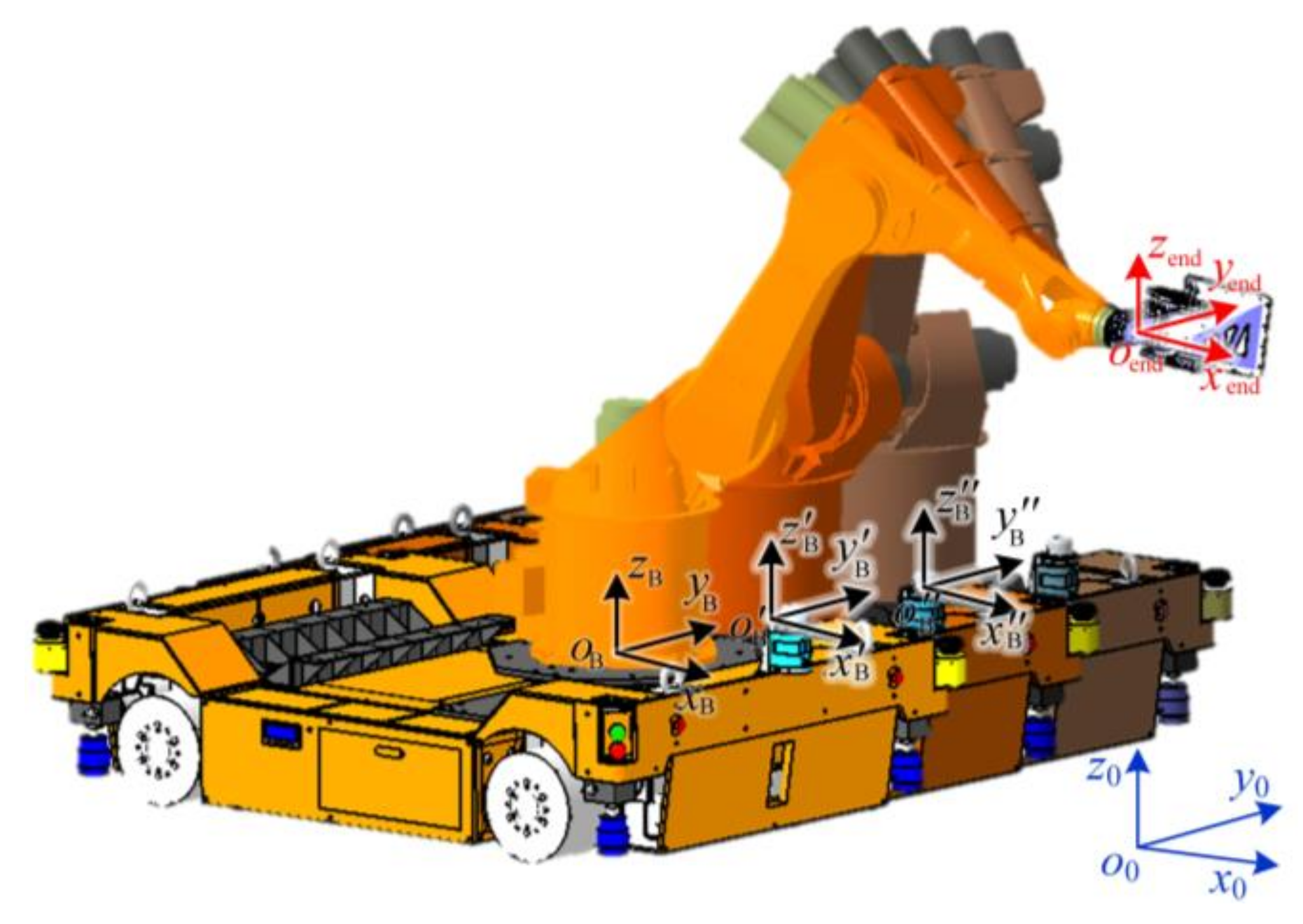
3.1. Coordinate Systems of the ARGW System
3.2. Dynamics Response of the Workpiece
4. Dynamics Simulation and Configuration Optimization Method
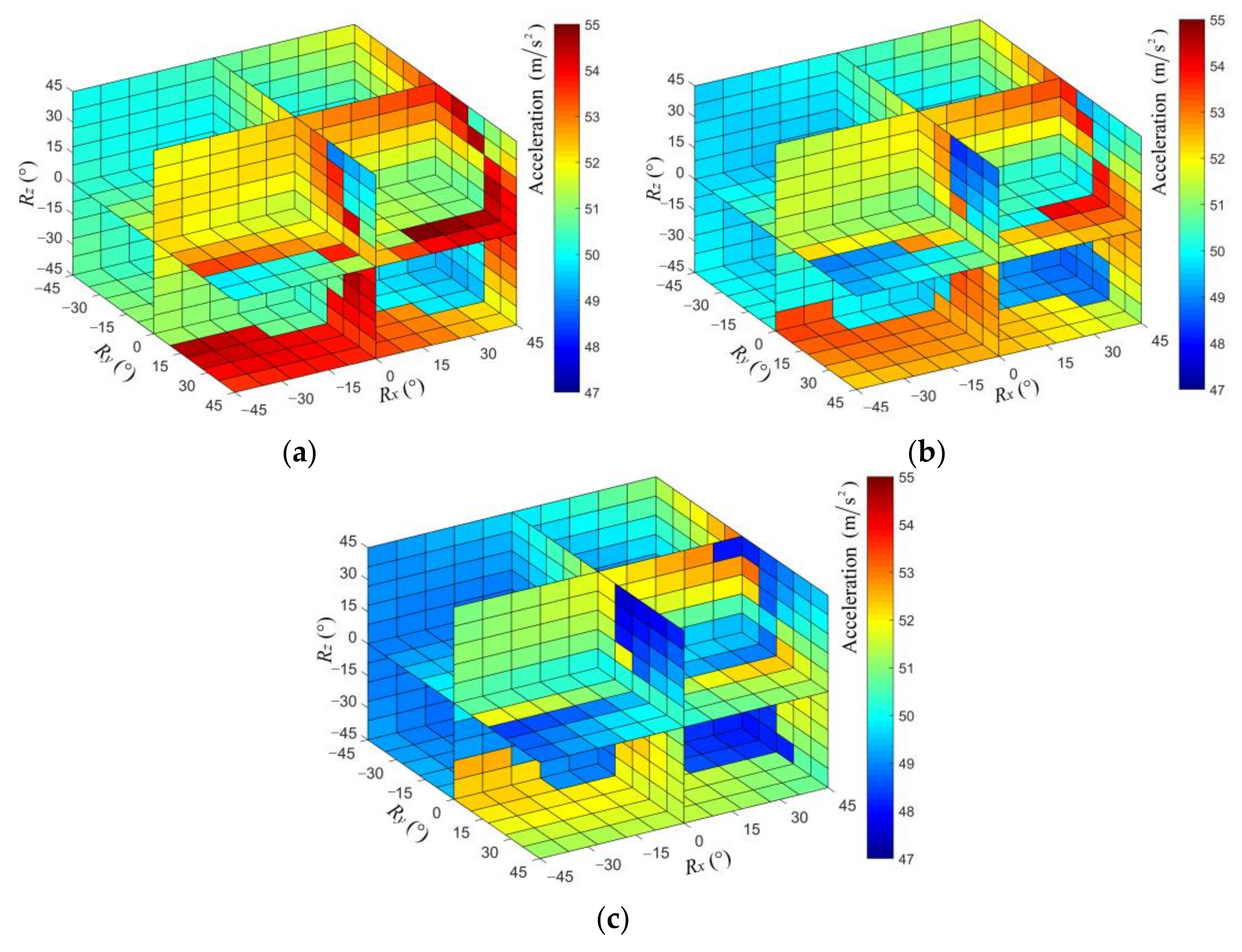
4.1. Vibration Suppression Effects of Different Postures
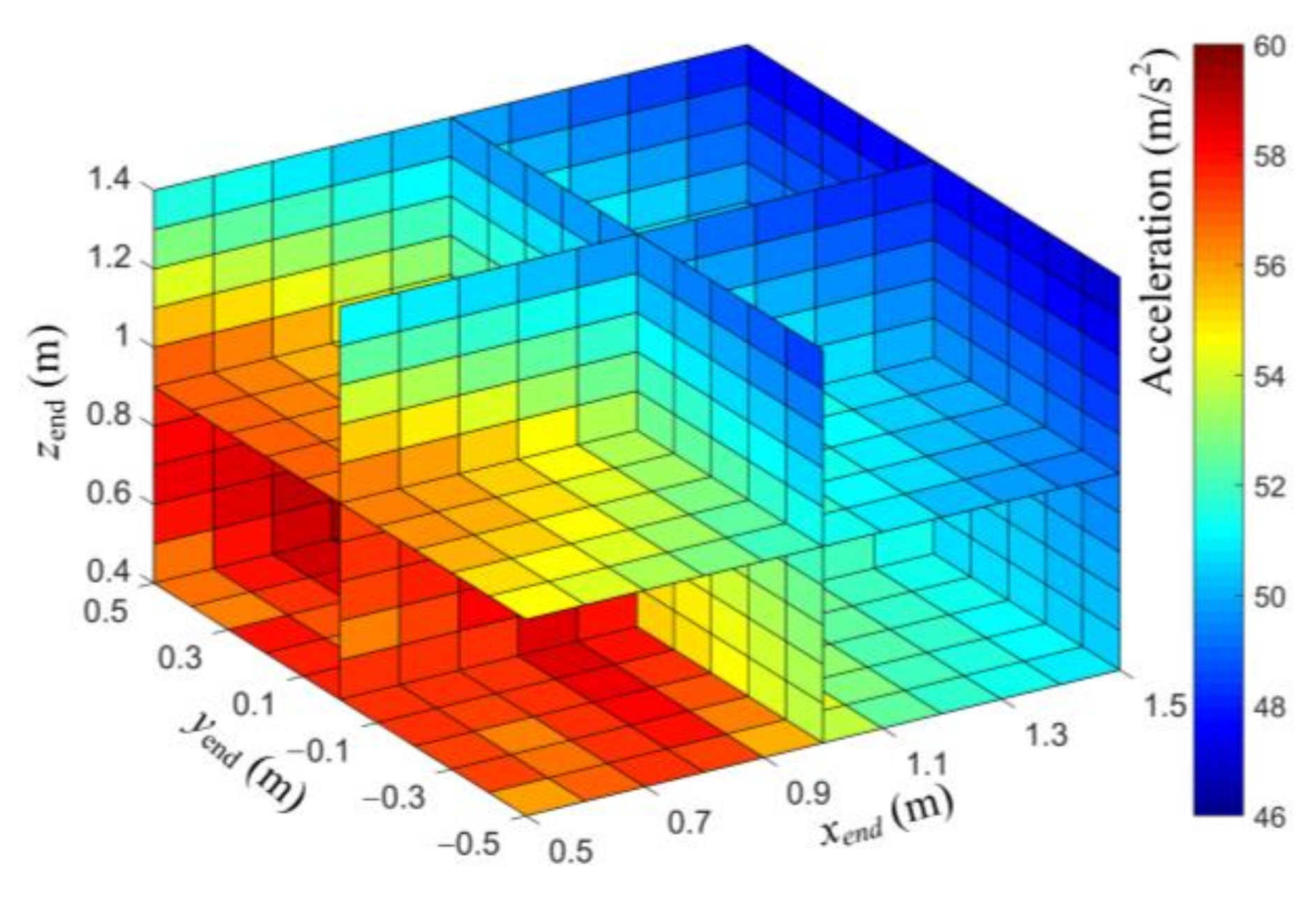
4.2. Vibration Suppression Effects of Different Positions
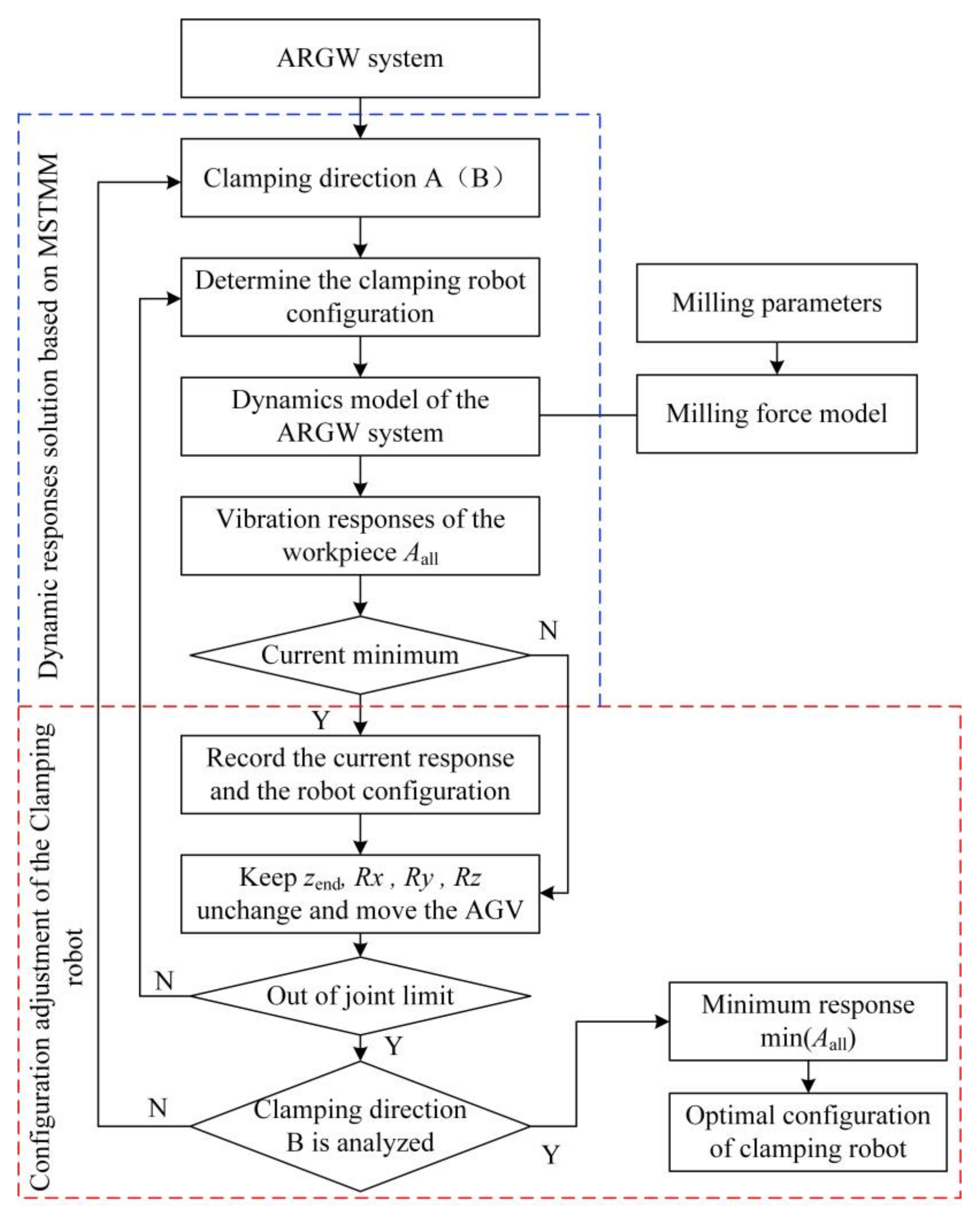
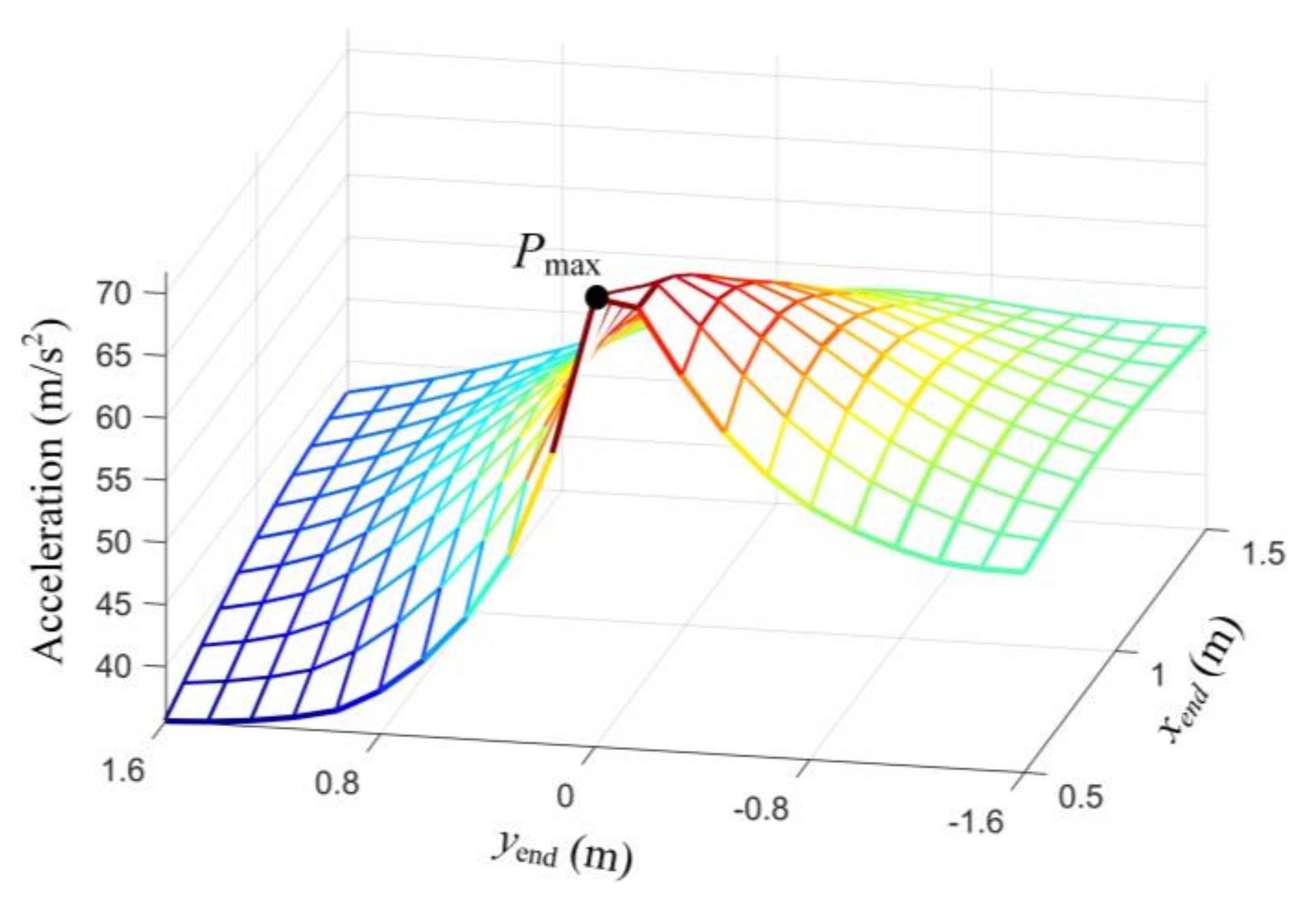
4.3. Configuration Optimization Mothed of the Clamping Robot
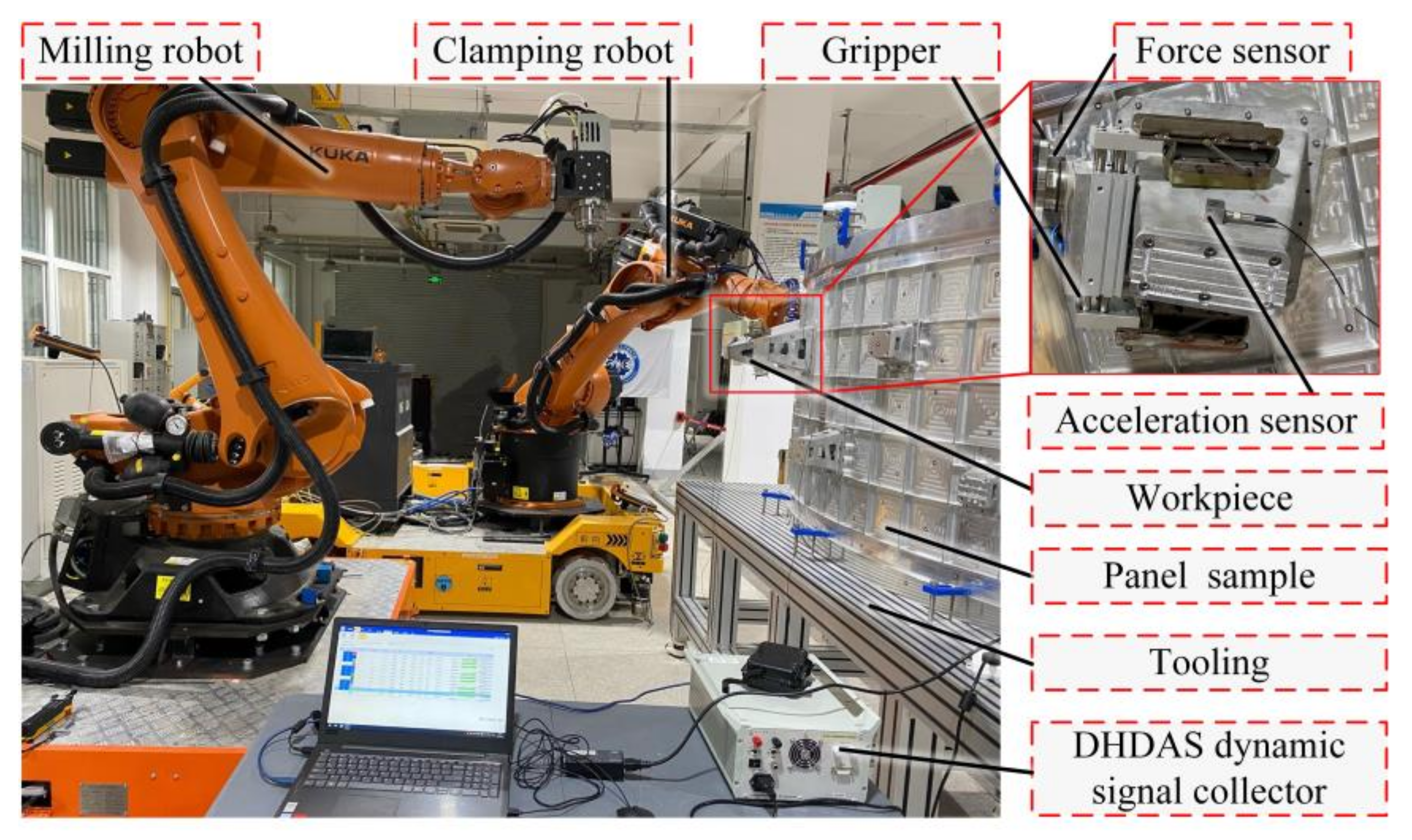
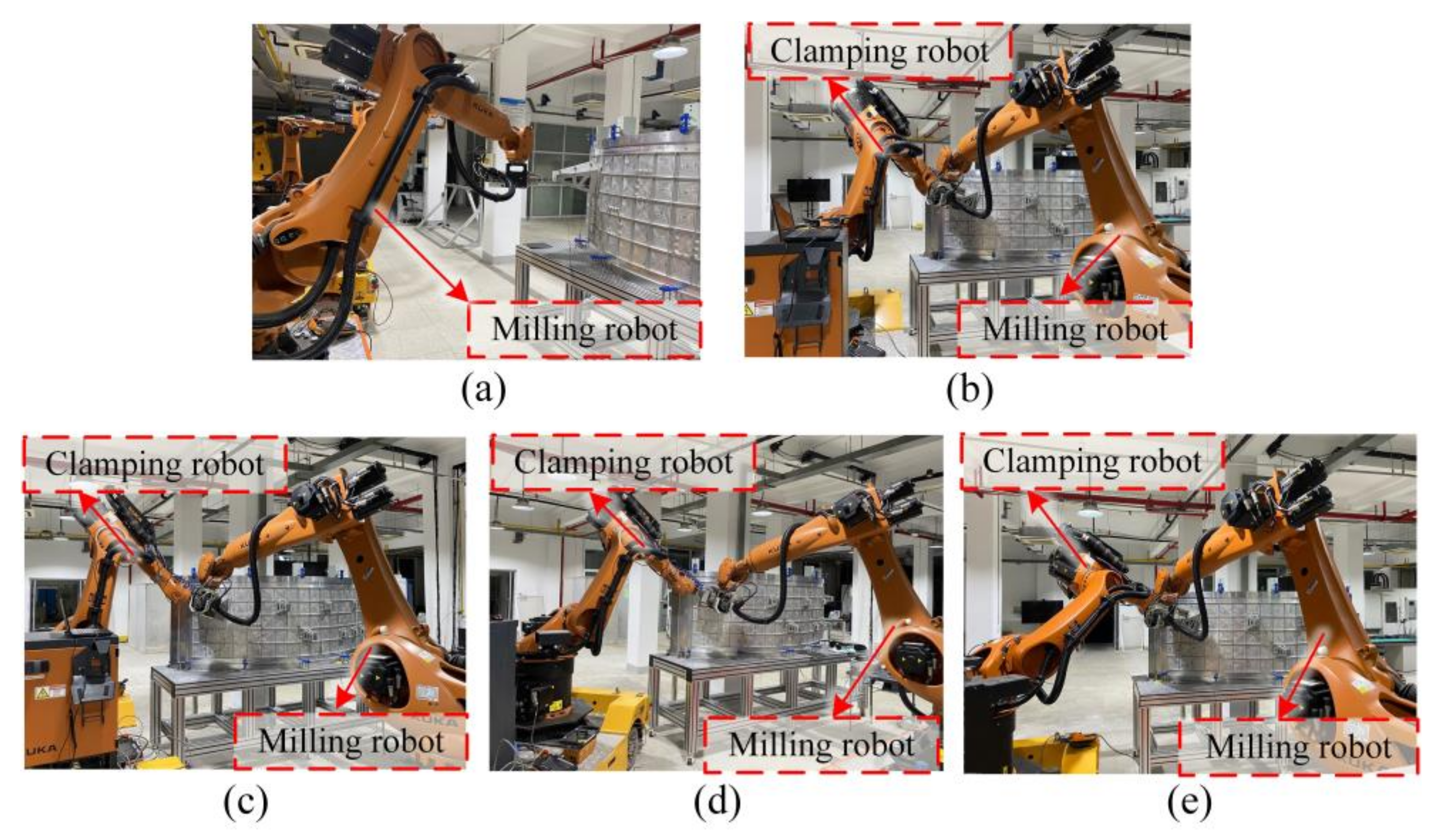
5. Verification Experiments
5.1. Verification of the ARGW System Dynamics Model
5.2. Verification of the Configuration Optimization Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Yang, Y.; Xiao, M.; Wan, M.; Zhang, W. A Gaussian process regression-based surrogate model of the varying workpiece dynamics for chatter prediction in milling of thin-walled structures. Int. J. Mech. Syst. Dyn. 2022, 2, 117–130. [Google Scholar] [CrossRef]
- Zeng, Y.; Tian, W.; Li, D.; He, X.; Liao, W. An error-similarity-based robot positional accuracy improvement method for a robotic drilling and riveting system. Int. J. Adv. Manuf. Technol. 2016, 88, 2745–2755. [Google Scholar] [CrossRef]
- Zhao, B.; Zeng, L.; Wu, Z.; Xu, K. A continuum manipulator for continuously variable stiffness and its stiffness control formulation. Mech. Mach. Theory 2020, 149, 103746. [Google Scholar] [CrossRef]
- Cen, L.; Melkote, S.N. Effect of Robot Dynamics on the Machining Forces in Robotic Milling. Procedia Manuf. 2017, 10, 486–496. [Google Scholar] [CrossRef]
- Moreira, A.P.; Neto, P.; Vidal, F. Special Issue on Advances in Industrial Robotics and Intelligent Systems. Appl. Sci. 2023, 13, 1352. [Google Scholar] [CrossRef]
- Schneider, U.; Posada, J.R.D.; Verl, A. Automatic Pose Optimization for Robotic Processes. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- Zhang, D.; Yuan, H.; Cao, Z. Environmental adaptive control of a snake-like robot with variable stiffness actuators. IEEE/CAA J. Autom. Sin. 2020, 7, 745–751. [Google Scholar] [CrossRef]
- Guo, Y.; Dong, H.; Ke, Y. Stiffness-oriented posture optimization in robotic machining applications. Robot. Comput.-Integr. Manuf. 2015, 35, 69–76. [Google Scholar] [CrossRef]
- Hyuseyin, C.; Neil, D.S.; Erdem, O. Cartesian Stiffness Optimization for Serial Arm Robots. Procedia CIRP 2018, 77, 566–569. [Google Scholar]
- Zhang, J.; Liao, W.; Bu, Y.; Tian, W.; Hu, J. Stiffness properties analysis and enhancement in robotic drilling application. Int. J. Adv. Manuf. Technol. 2020, 106, 5539–5558. [Google Scholar] [CrossRef]
- Jiao, J.; Tian, W.; Liao, W.; Zhang, L.; Bu, Y. Processing configuration off-line optimization for functionally redundant robotic drilling tasks. Robot. Auton. Syst. 2018, 110, 112–123. [Google Scholar] [CrossRef]
- Yang, L.; Huan, Z.; Han, D. Posture optimization methodology of 6R industrial robots for machining using performance evaluation indexes. Robot. Comput.-Integr. Manuf. 2017, 48, 59–72. [Google Scholar]
- Léger, J.; Angeles, J. Off-line programming of six-axis robots for optimum five-dimensional tasks. Mech. Mach. Theory 2016, 100, 155–169. [Google Scholar] [CrossRef]
- Yin, B.; Wenhe, L.; Wei, T.; Jin, Z.; Lin, Z. Stiffness analysis and optimization in robotic drilling application. Precis. Eng. 2017, 49, 388–400. [Google Scholar]
- Cvitanic, T.; Nguyen, V.; Melkote, S.N. Pose optimization in robotic machining using static and dynamic stiffness models. Robot. Comput.-Integr. Manuf. 2020, 66, 101992. [Google Scholar] [CrossRef]
- Gang, X.; Ye, D.; LiMin, Z. Stiffness-based pose optimization of an industrial robot for five-axis milling. Robot. Comput.-Integr. Manuf. 2019, 55, 19–28. [Google Scholar]
- Mousavi, S.; Gagnol, V.; Bouzgarrou, B.C.; Ray, P. Stability optimization in robotic milling through the control of functional. Robot. Comput.-Integr. Manuf. 2018, 50, 181–192. [Google Scholar] [CrossRef]
- Chen, C.; Peng, F.; Yan, R.; Fan, Z.; Li, Y.; Wei, D. Posture-dependent stability prediction of a milling industrial robot based on inverse distance weighted method. Procedia Manuf. 2018, 17, 993–1000. [Google Scholar] [CrossRef]
- Lukić, B.; Petrič, T.; Žlajpah, L.; Jovanović, K. KUKA LWR Robot Cartesian Stiffness Control Based on Kinematic Redundancy. Adv. Serv. Ind. Robot. 2020, 310–318. [Google Scholar] [CrossRef]
- Yao, J.; Qian, C.; Zhang, Y.; Yu, G. Multi-Objective Redundancy Optimization of Continuous-Point Robot Milling Path in Shipbuilding. Comput. Model. Eng. Sci. 2023, 134, 1283–1303. [Google Scholar] [CrossRef]
- Bian, C.; Jiang, J.; Ke, Y. End stiffness modeling for automatic horizontal dual-machine cooperative drilling and riveting system. Int. J. Adv. Manuf. Technol. 2019, 104, 1521–1530. [Google Scholar] [CrossRef]
- Marie, S.; Courteille, E.; Maurine, P. Elasto-geometrical modeling and calibration of robot manipulators: Application to machining and forming applications. Mech. Mach. Theory 2013, 69, 13–43. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.; Gagnol, V.; Bouzgarrou, B.C.; Ray, P. Control of a Multi Degrees Functional Redundancies Robotic Cell for Optimization of the Machining Stability. Procedia CIRP 2017, 58, 269–274. [Google Scholar] [CrossRef]
- Garnier, S.; Subrin, K.; Waiyagan, K. Modelling of Robotic Drilling. Procedia CIRP 2017, 58, 416–421. [Google Scholar] [CrossRef]
- Guo, Y.; Dong, H.; Wang, G.; Ke, Y. Vibration analysis and suppression in robotic boring process. Int. J. Mach. Tools Manuf. 2016, 101, 102–110. [Google Scholar] [CrossRef]
- Cui, G.; Li, B.; Tian, W.; Liao, W.; Zhao, W. Dynamic modeling and vibration prediction of an industrial robot in manufacturing. Appl. Math. Model. 2022, 105, 114–136. [Google Scholar] [CrossRef]
- Xiong, G.; Ding, Y.; Zhu, L. A Feed-Direction Stiffness Based Trajectory Optimization Method for a Milling Robot. In Proceedings of the 10th International Conference on Intelligent Robotics and Applications, Wuhan, China, 16–18 August 2017; pp. 184–195. [Google Scholar]
- Chen, C.; Peng, F.; Yan, R.; Li, Y.; Wei, D.; Fan, Z.; Tang, X.; Zhu, Z. Stiffness performance index based posture and feed orientation optimization in robotic milling process. Robot. Comput.-Integr. Manuf. 2019, 55, 29–40. [Google Scholar] [CrossRef]
- Caro, S.; Dumas, C.; Garnier, S.; Furet, B. Workpiece Placement Optimization in Robotic-based Manufacturing. IFAC Proc. Vol. 2013, 46, 819–824. [Google Scholar] [CrossRef] [Green Version]
- Shen, N.; Guo, Z.; Li, J.; Tong, L.; Zhu, K. A practical method of improving hole position accuracy in the robotic drilling process. Int. J. Adv. Manuf. Technol. 2018, 96, 2973–2987. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, R.; Liu, Z.; Duan, J.; Qin, J. Process Simulation and Optimization of Arc Welding Robot Workstation Based on Digital Twin. Machines 2023, 11, 53. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Liu, W.Z.; Gao, J.G.; Liu, C.R. The Location Optimization of the Mission Space Based on the Stiffness of Robot. Adv. Mater. Res. 2014, 889–890, 1126–1131. [Google Scholar] [CrossRef]
- Liao, Z.-Y.; Li, J.-R.; Xie, H.-L.; Wang, Q.-H.; Zhou, X.-F. Region-based toolpath generation for robotic milling of freeform surfaces with stiffness optimization. Robot. Comput.-Integr. Manuf. 2020, 64, 101953. [Google Scholar] [CrossRef]
- Tao, B.; Zhao, X.; Ding, H. Mobile-robotic machining for large complex components: A review study. Sci. China Technol. Sci. 2019, 62, 1388–1400. [Google Scholar] [CrossRef]
- Ma, H.; Wu, J.; Xiong, Z. Active chatter control in turning processes with input constraint. Int. J. Adv. Manuf. Technol. 2020, 108, 3737–3751. [Google Scholar] [CrossRef]
- Li, G.; Zhu, W.; Dong, H.; Ke, Y. Stiffness-oriented performance indices defined on two-dimensional manifold for 6-DOF industrial robot. Robot. Comput.-Integr. Manuf. 2021, 68, 102076. [Google Scholar] [CrossRef]
- He, F.-X.; Liu, Y.; Liu, K. A chatter-free path optimization algorithm based on stiffness orientation method for robotic milling. Int. J. Adv. Manuf. Technol. 2018, 101, 2739–2750. [Google Scholar] [CrossRef]
- Li, B.; Cui, G.; Tian, W.; Liao, W. Vibration suppression of an industrial robot with AGV in drilling applications by configuration optimization. Appl. Math. Model. 2022, 112, 614–634. [Google Scholar] [CrossRef]
- Rui, X.; Zhang, J.; Wang, X.; Rong, B.; He, B.; Jin, Z. Multibody system transfer matrix method: The past, the present, and the future. Int. J. Mech. Syst. Dyn. 2022, 2, 3–26. [Google Scholar] [CrossRef]
- Rui, X.; Wang, X.; Zhou, Q.; Zhang, J. Transfer matrix method for multibody systems (Rui method) and its applications. Sci. China Technol. Sci. 2019, 62, 712–720. [Google Scholar] [CrossRef]
- Miao, Y.; Wang, G.; Rui, X. Simulation and adaptive control of back propagation neural network proportional–integral–derivative for special launcher using new version of transfer matrix method for multibody systems. J. Vib. Control 2019, 26, 757–768. [Google Scholar] [CrossRef]

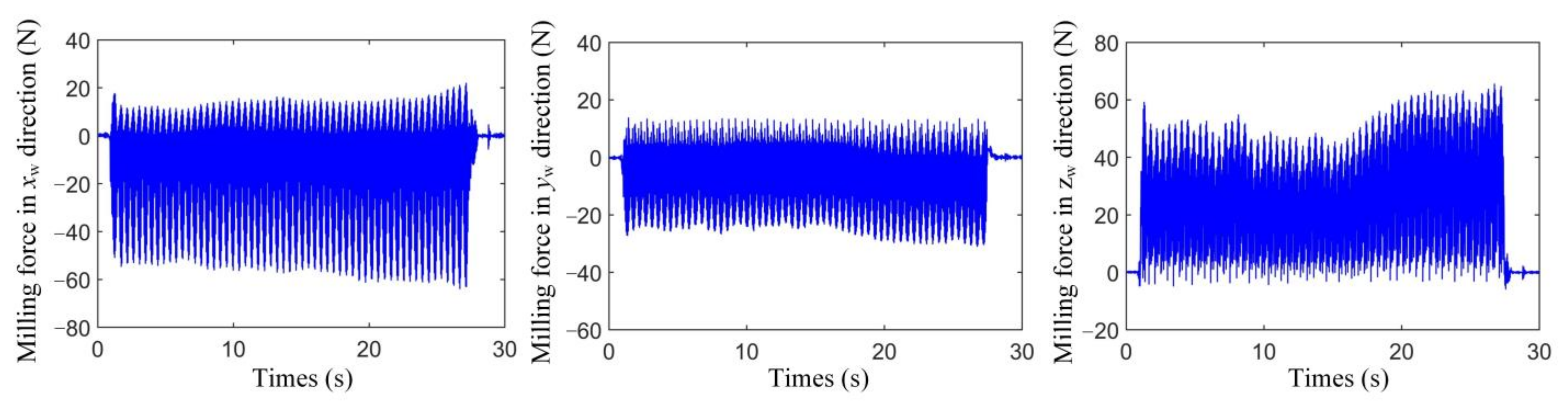
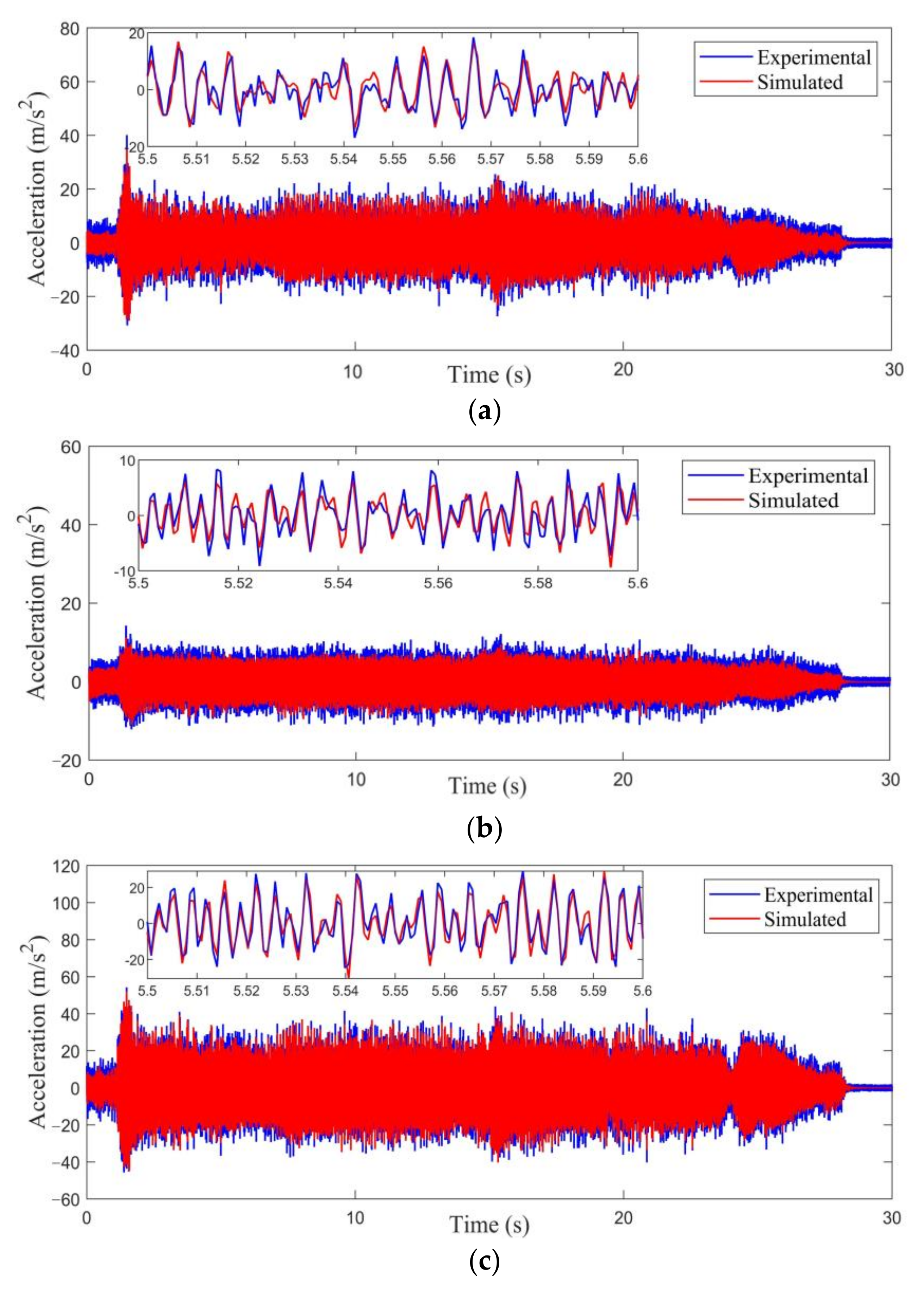


| Feed Rate (mm/s) | Rotational Speed (r/min) | Milling Width (mm) | Milling Depth (mm) |
|---|---|---|---|
| 2.5 | 6000 | 8.0 | 1.0 |
| Group | ||||||
|---|---|---|---|---|---|---|
| Config. 1 | 56.85 | −54.88 | 95.82 | −248.27 | 42.74 | −147.21 |
| Config. 2 | 61.13 | −58.51 | 101.86 | −241.47 | 40.89 | −152.49 |
| Config. 3 | 47.09 | −52.77 | 92.24 | 102.02 | 49.46 | −142.27 |
| Config. 4 | 37.73 | −29.41 | 49.91 | 86.66 | 36.88 | 243.70 |
| Group | Non- Clamping | Config. 1 | Config. 2 | Config. 3 | Config. 4 |
|---|---|---|---|---|---|
| Ra (μm) | 1.684 | 0.921 | 0.801 | 0.611 | 0.576 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Tian, W.; Li, B.; Miao, Y. Configuration Optimization and Response Prediction Method of the Clamping Robot for Vibration Suppression of Cantilever Workpiece. Appl. Sci. 2023, 13, 4863. https://doi.org/10.3390/app13084863
Wang P, Tian W, Li B, Miao Y. Configuration Optimization and Response Prediction Method of the Clamping Robot for Vibration Suppression of Cantilever Workpiece. Applied Sciences. 2023; 13(8):4863. https://doi.org/10.3390/app13084863
Chicago/Turabian StyleWang, Pinzhang, Wei Tian, Bo Li, and Yunfei Miao. 2023. "Configuration Optimization and Response Prediction Method of the Clamping Robot for Vibration Suppression of Cantilever Workpiece" Applied Sciences 13, no. 8: 4863. https://doi.org/10.3390/app13084863
APA StyleWang, P., Tian, W., Li, B., & Miao, Y. (2023). Configuration Optimization and Response Prediction Method of the Clamping Robot for Vibration Suppression of Cantilever Workpiece. Applied Sciences, 13(8), 4863. https://doi.org/10.3390/app13084863






