Design of an Adaptive Algorithm for Feeding Volume–Traveling Speed Coupling Systems of Rice Harvesters in Southern China
Abstract
:1. Introduction
2. Methods
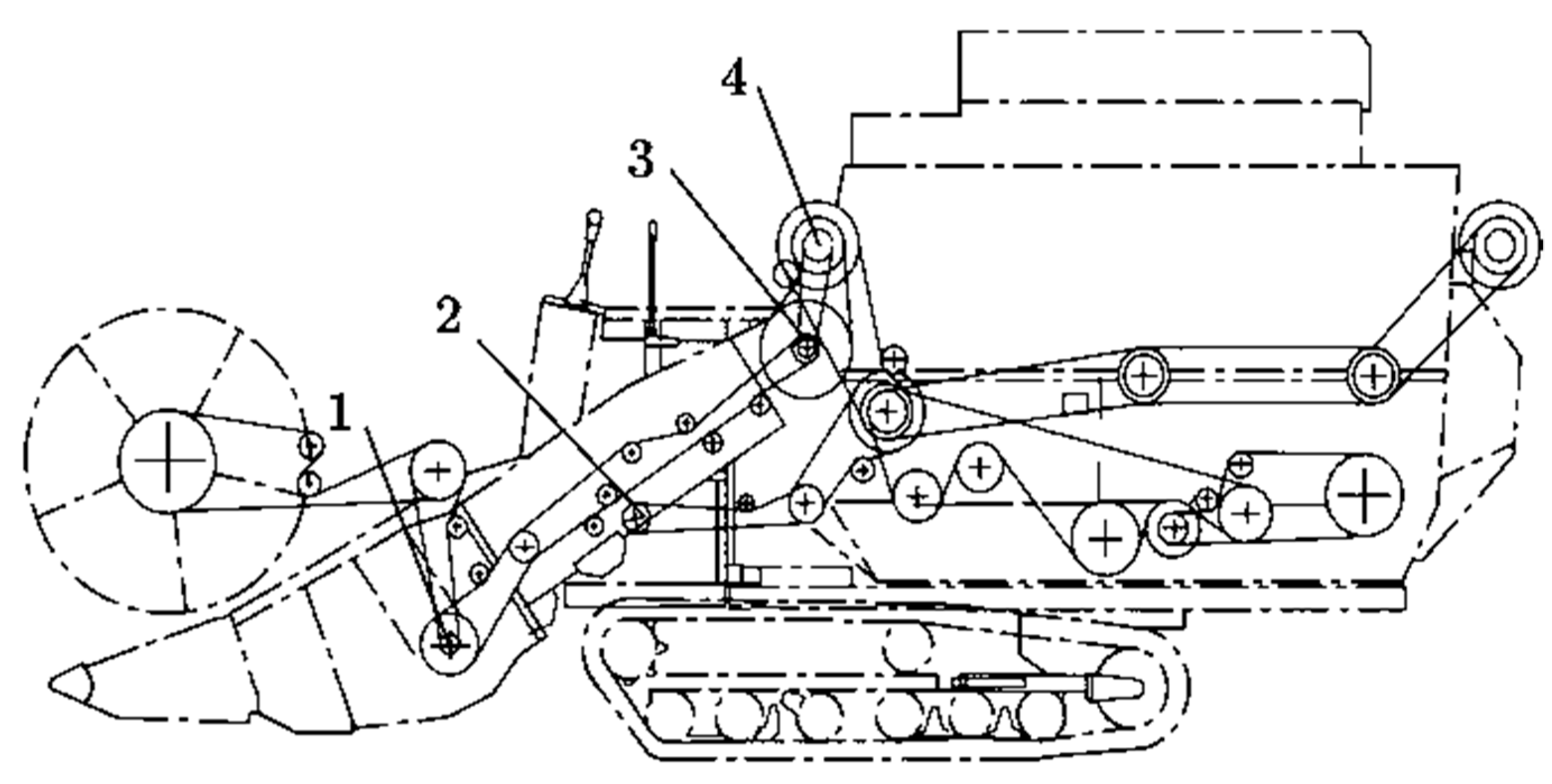
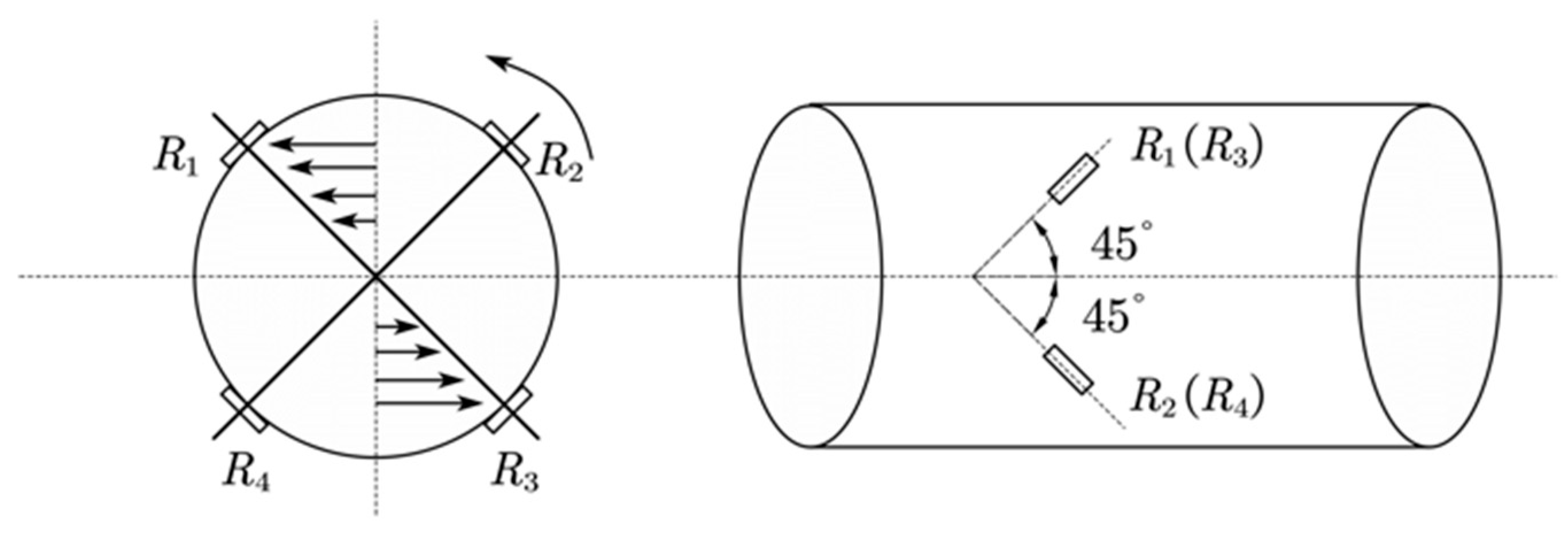
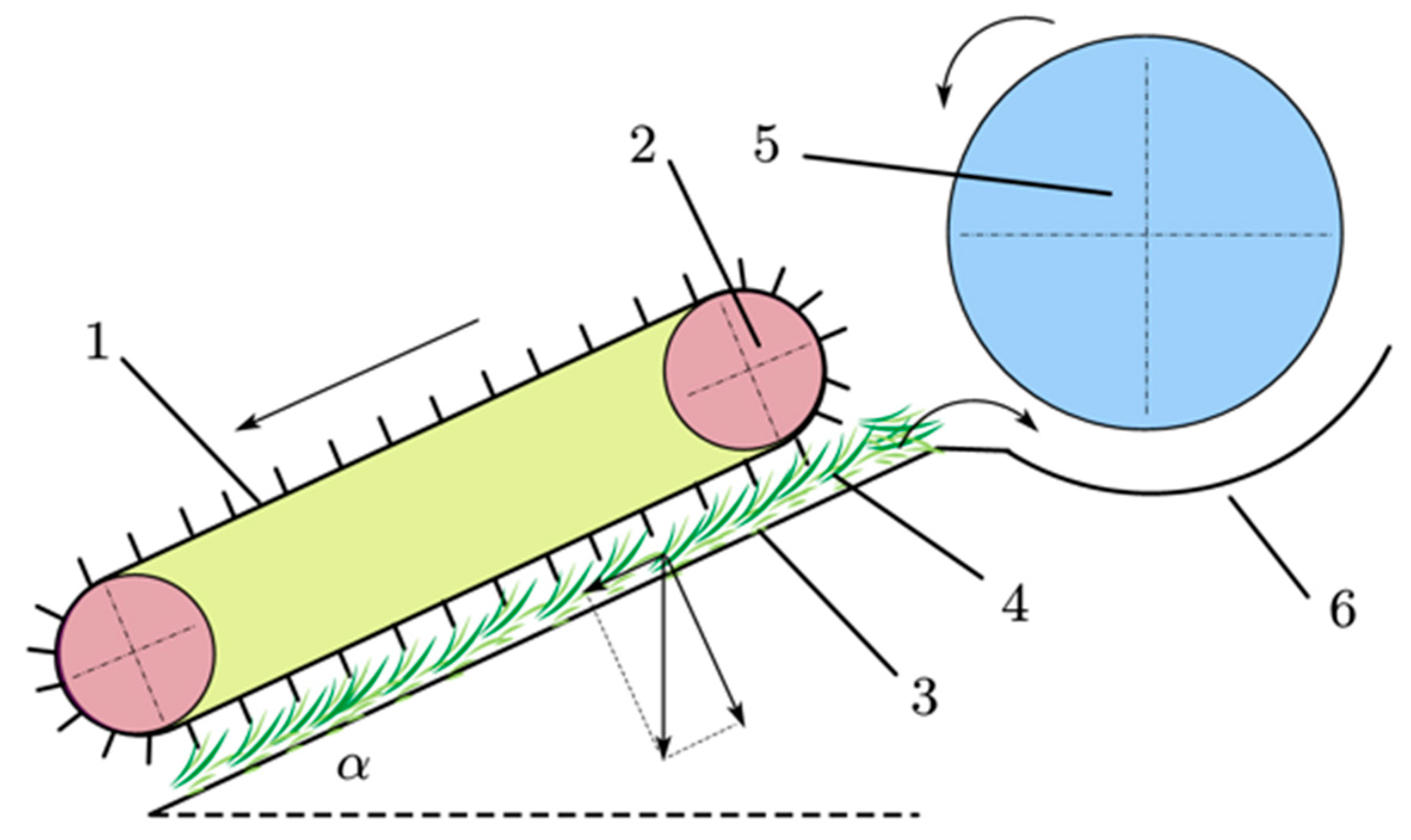
2.1. Detection Scheme Selection
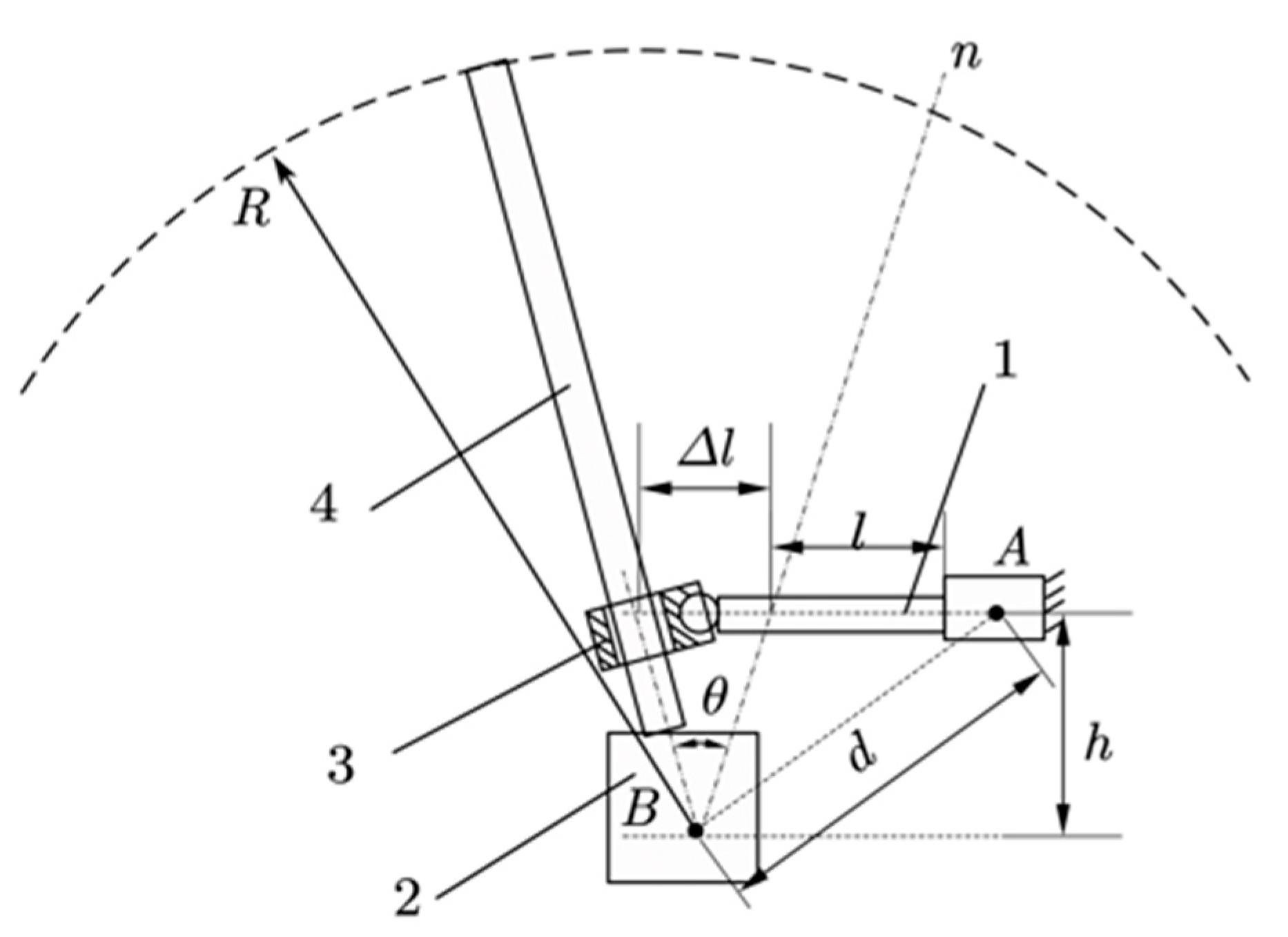
2.2. Detection Principle and Calculation Method
3. System Design
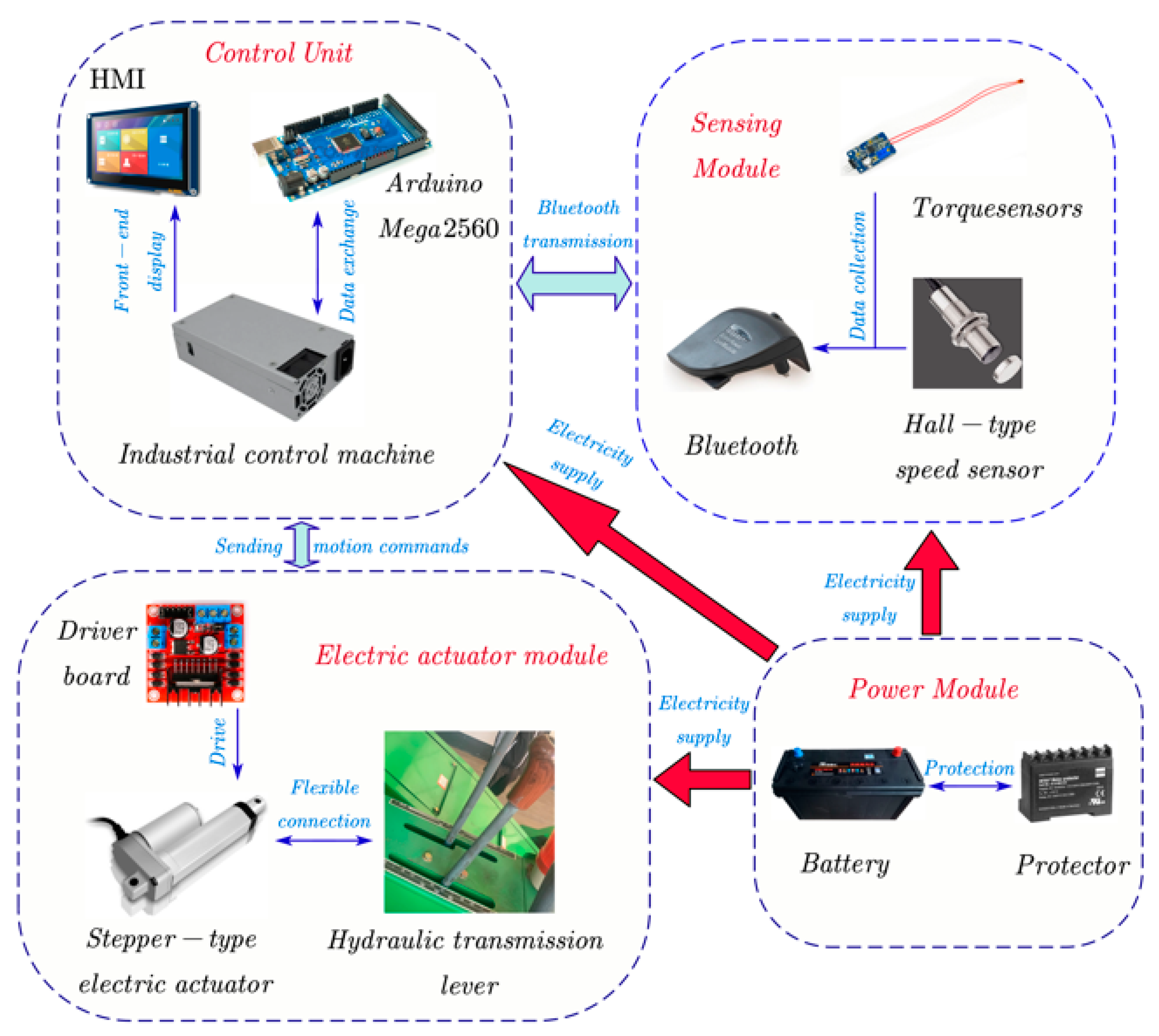
3.1. Control System Hardware Framework
3.2. Electric Actuator Module
4. Algorithm Design
4.1. Optimal Traveling Speed Calculation Strategy
- When and are both in a reasonable state, the absolute value of the relative error between its value and the rated value belongs to [0, 0.1]; then, the traveling speed at this time is ;
- When there is an abnormality between and , i.e., the absolute value of the relative error between at least one set of values and the rated value belonging to [0.1, 0.2], adjust the speed to 0.8 and observe the subsequent values. If all values return to a reasonable state within 3 s, adjust the speed to ; otherwise, decelerate to 0.4;
- When the harvester fails, i.e., the absolute value of the relative error between any value and the rated value is constantly >20%, the speed is immediately reduced to 0 m/s and the machine is stopped for inspection.where is the optimal traveling speed of the harvester, m/s; = 1,2, are the error values of and , respectively; are the rated values of and , respectively; and is the data update time, s.
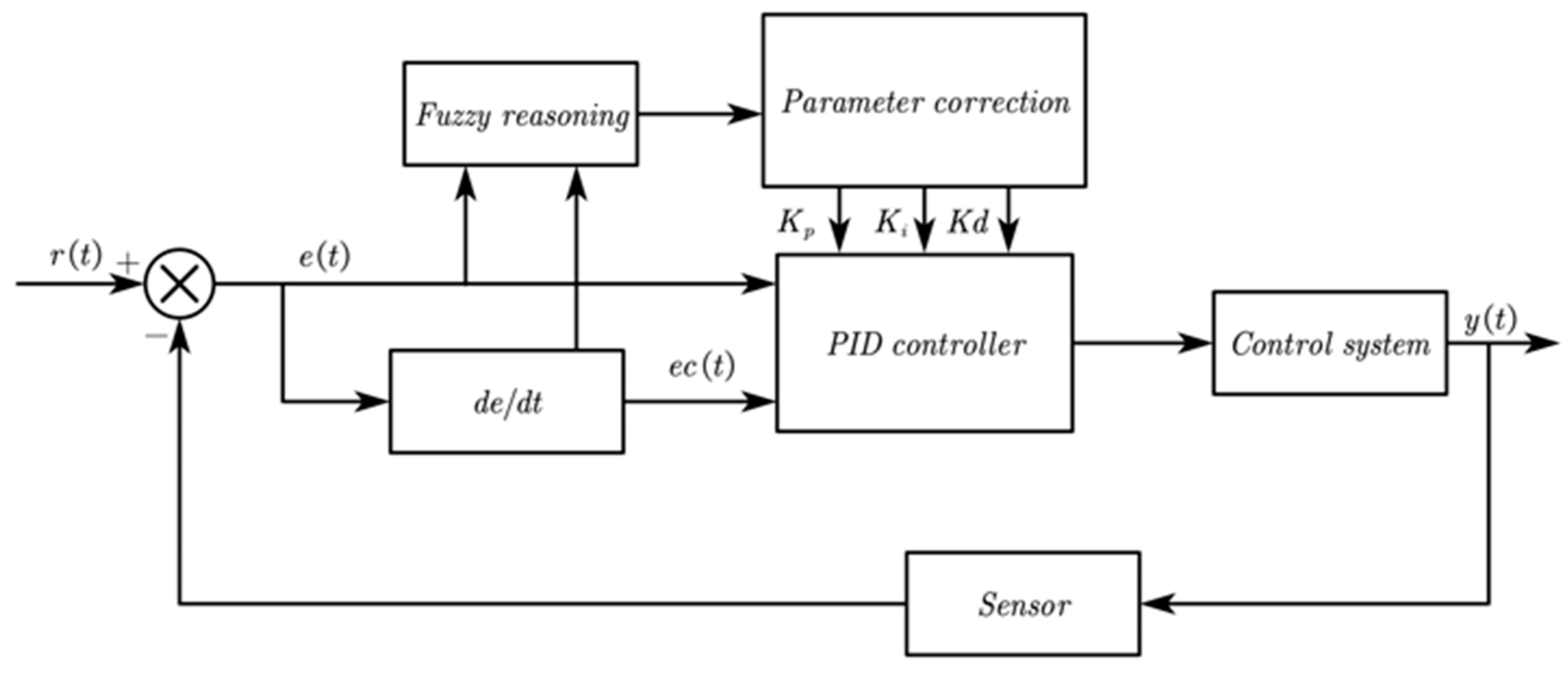
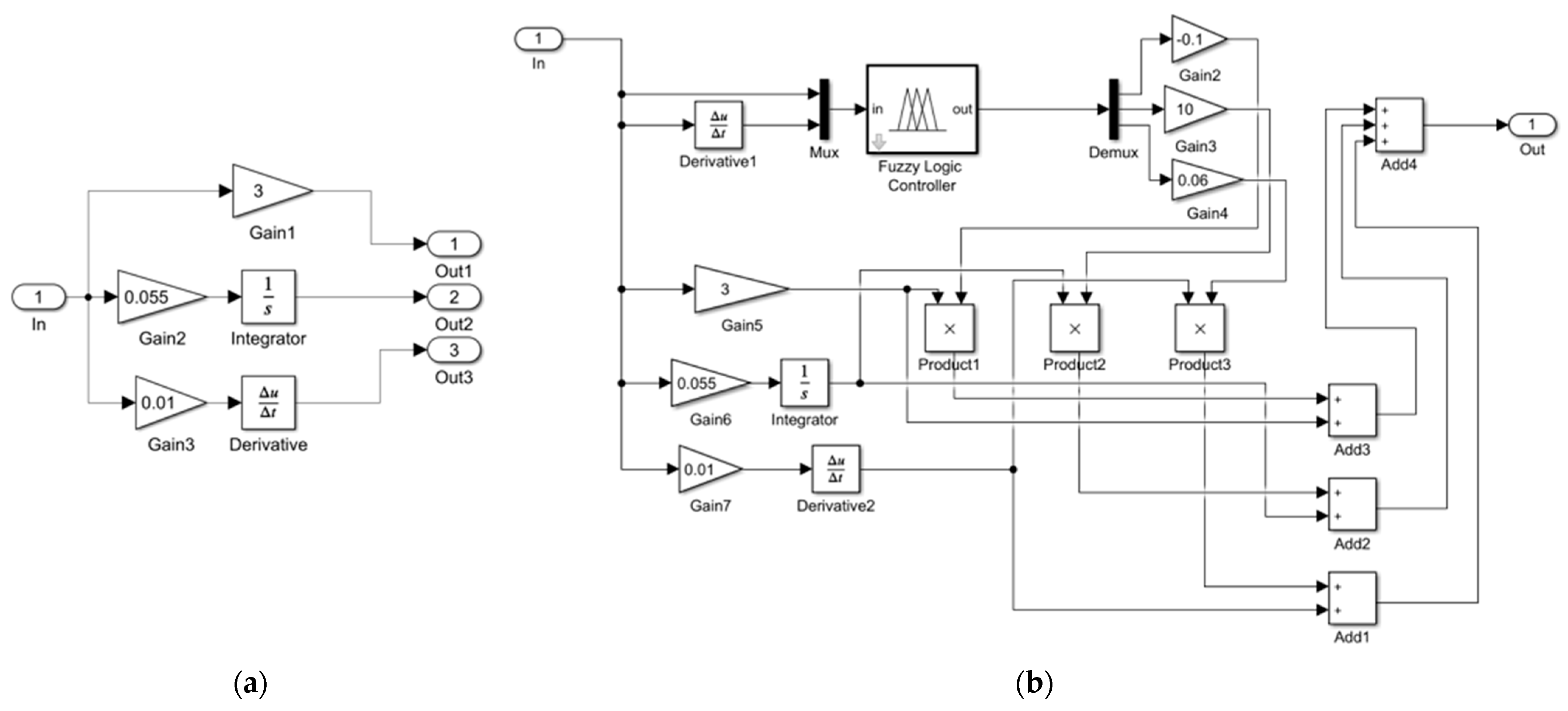
4.2. Adaptive Fuzzy PID for Coupling System
4.2.1. Domain of Discourse and Fuzzy Subset Determination
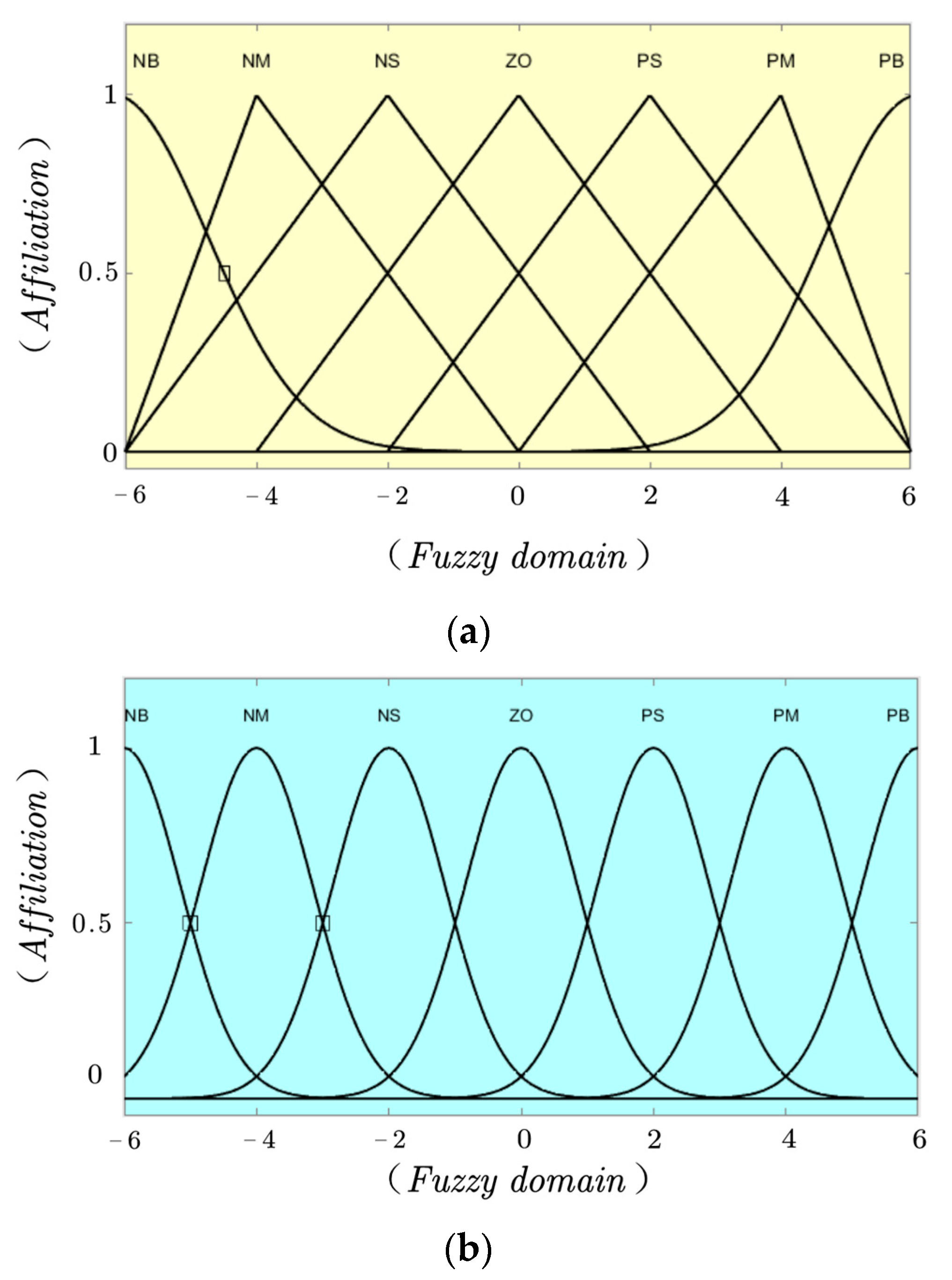
4.2.2. Affiliation Function Selection
4.2.3. Fuzzy Rules Design
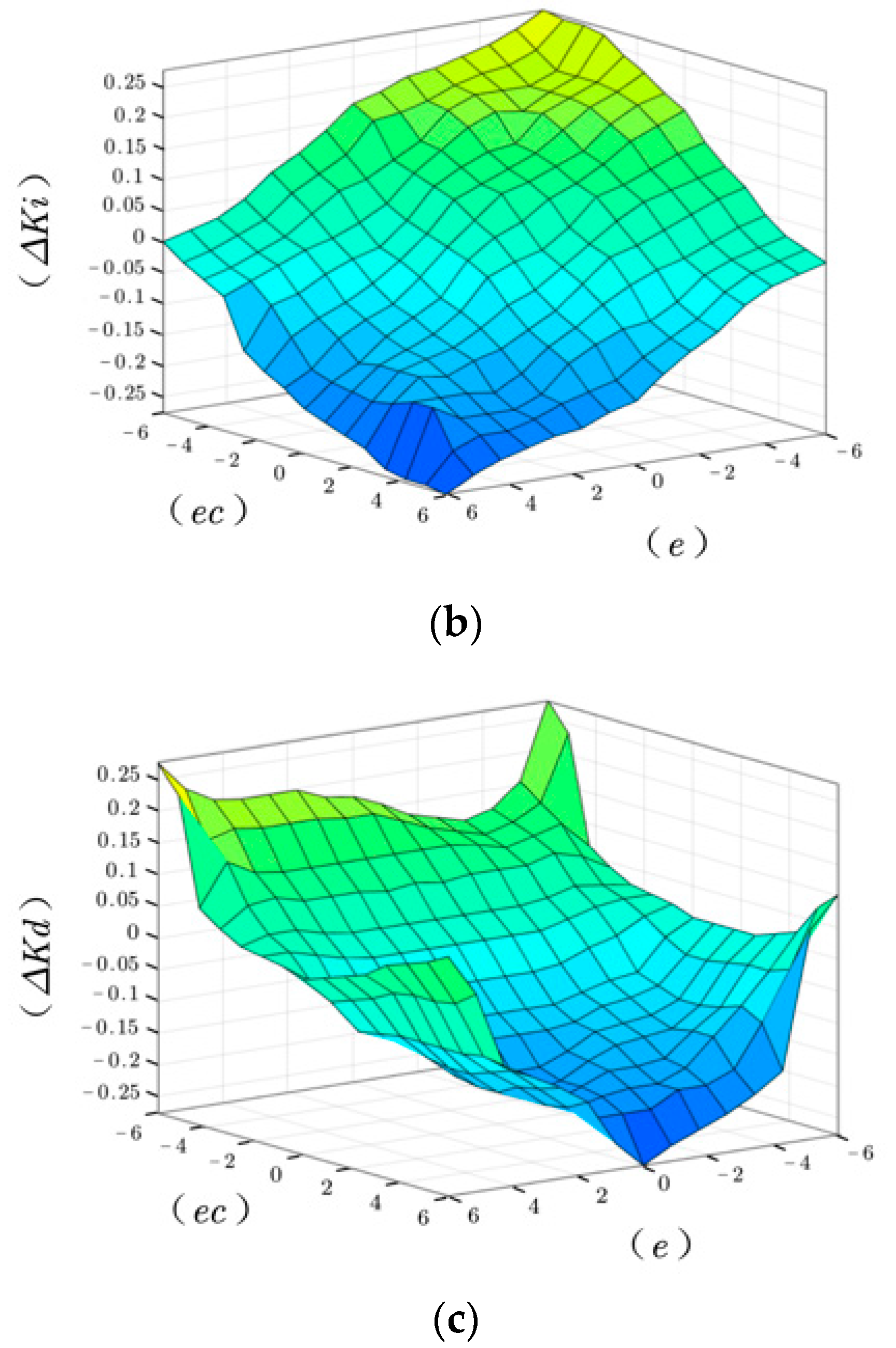
4.2.4. Inference and Defuzzification
5. Experiment and Analysis
5.1. Simulation Experiments
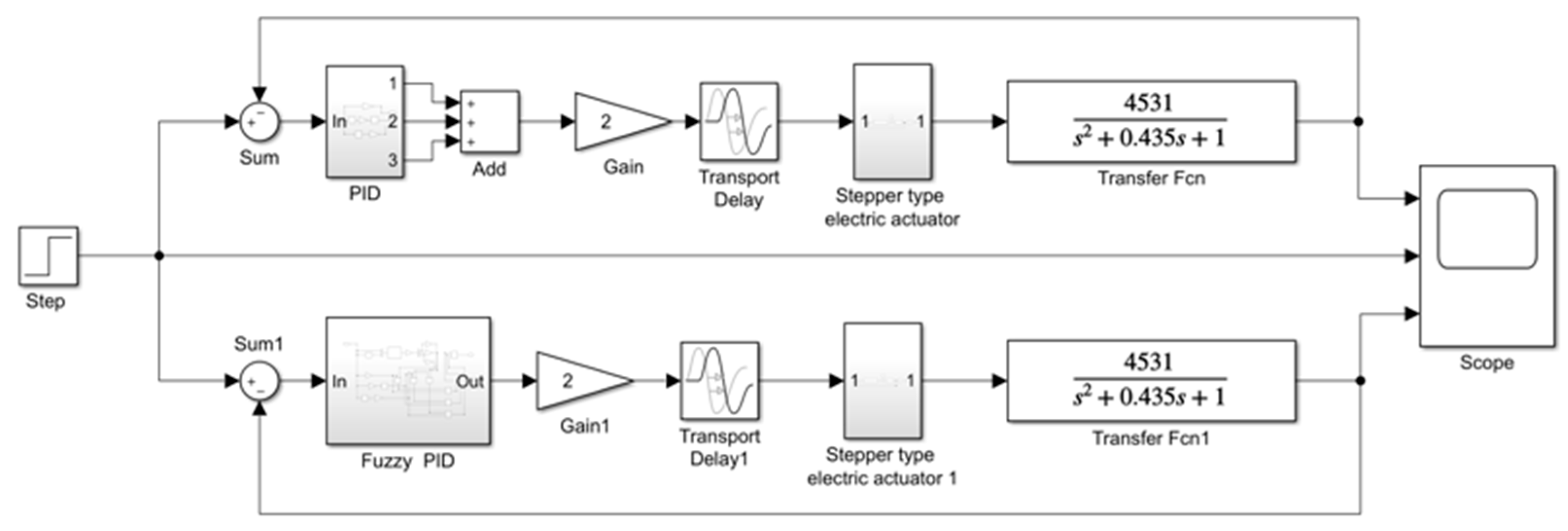
5.1.1. Pusher Voltage–Motor Speed Coupling Model
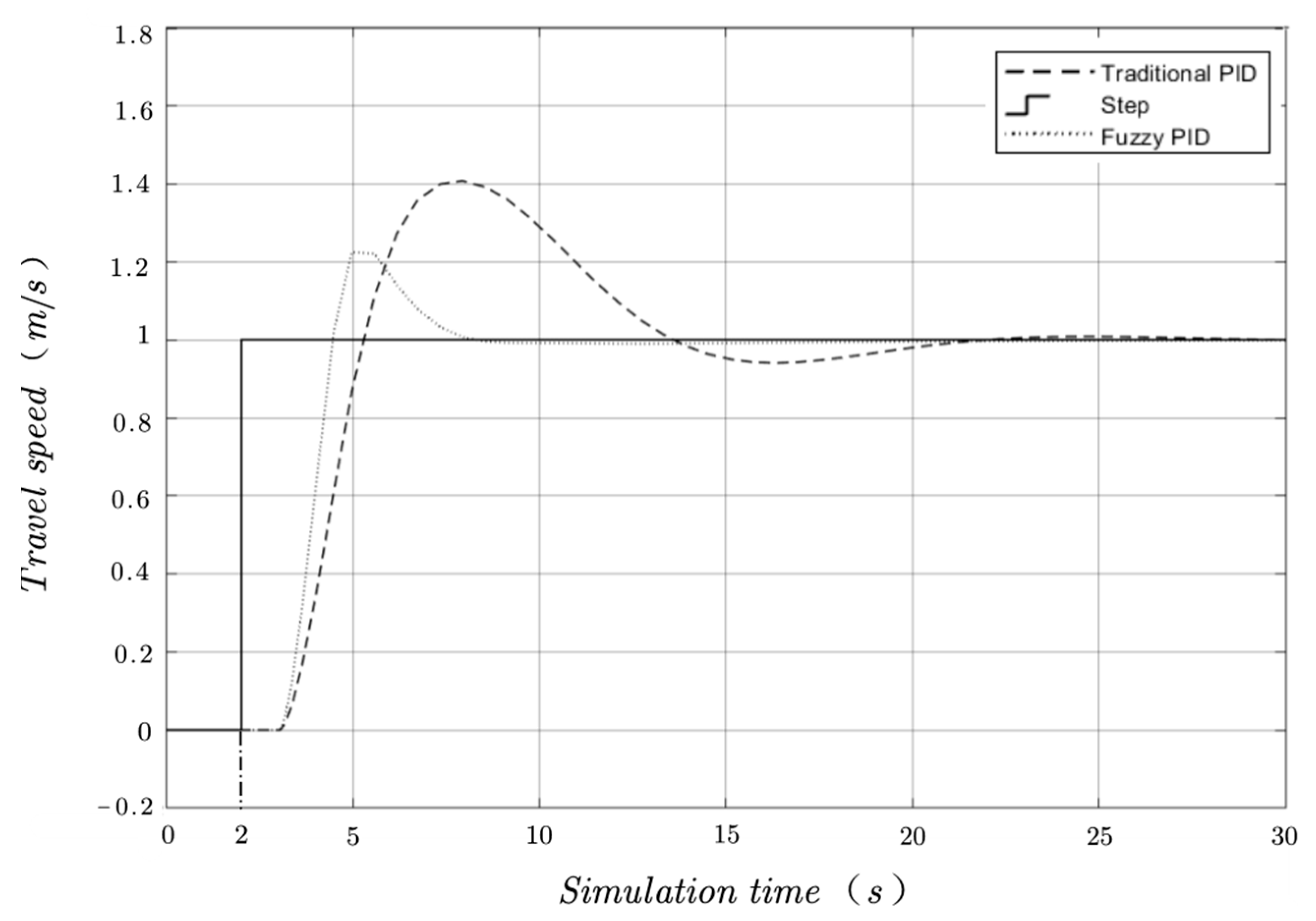
5.1.2. Simulation Comparison Test between Fuzzy PID and a Traditional PID System
5.2. Field Trials
5.2.1. Trial Conditions
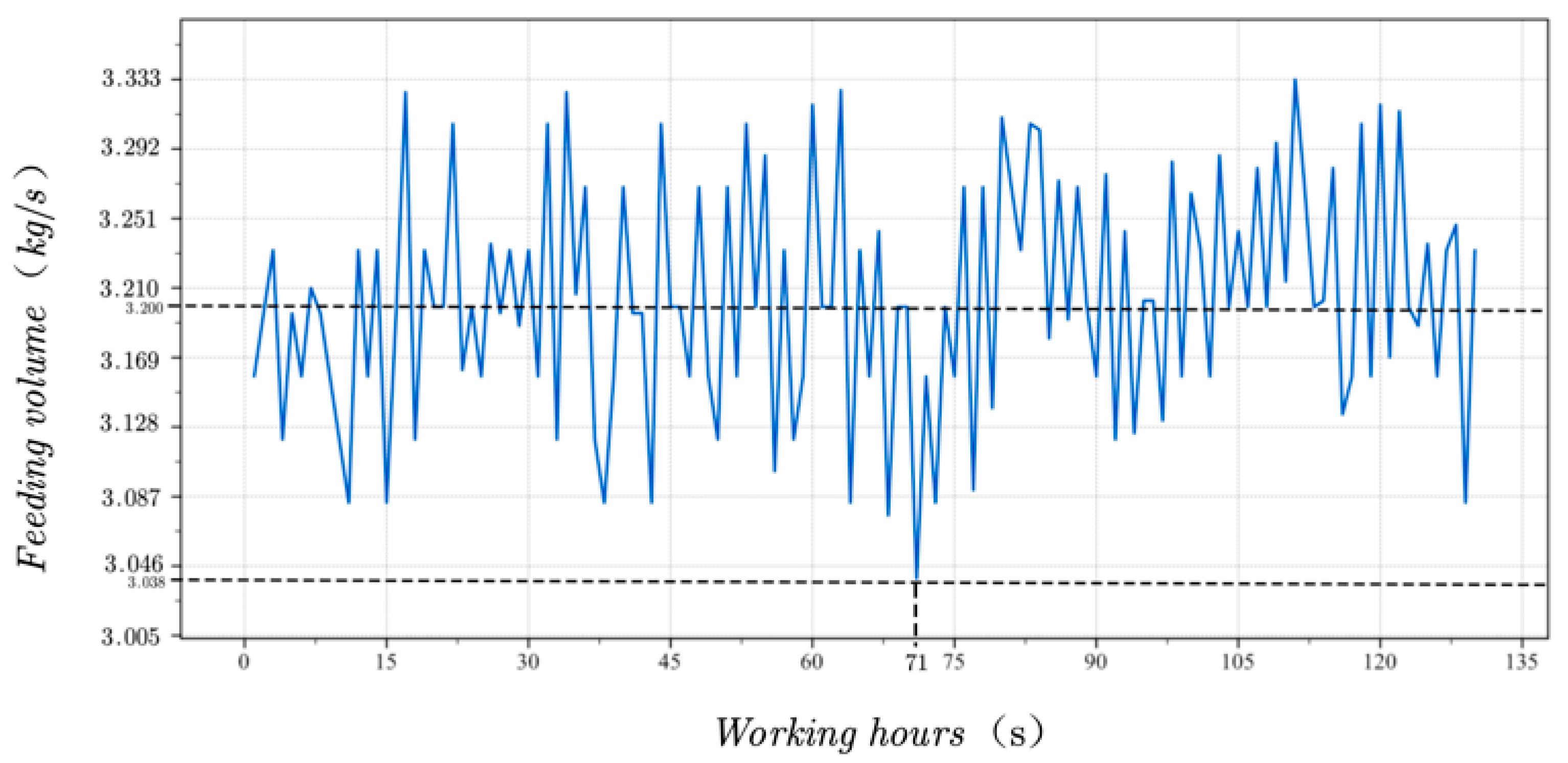
5.2.2. Experiment and Analysis
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, F.; Zhang, L.; Zhou, X.; Guo, X.; Zhu, Y.; Liu, M.; Xiong, H.; Jiang, P. The ratoon rice system with high yield and high efficiency in China: Progress, trend of theory and technology. Field Crops Res. 2021, 272, 108282. [Google Scholar] [CrossRef]
- Li, C.; Bremer, P.; Harder, M.K.; Lee, M.S.; Parker, K.; Gaugler, E.C.; Mirosa, M. A systematic review of food loss and waste in China: Quantity, impacts and mediators. J. Environ. Manag. 2021, 303, 114092. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wang, X.; Li, J.; Zhang, Q. Deep attributed network representation learning of complex coupling and interaction. Knowl.-Based Syst. 2021, 212, 106618. [Google Scholar] [CrossRef]
- Da Silveira, F.; Lermen, F.H.; Amaral, F.G. An overview of agriculture 4.0 development: Systematic review of descriptions, technologies, barriers, advantages, and disadvantages. Comput. Electron. Agric. 2021, 189, 106405. [Google Scholar] [CrossRef]
- Sood, S.; Singh, H. Computer vision and machine learning based approaches for food security: A review. Multimed. Tools Appl. 2021, 80, 27973–27999. [Google Scholar] [CrossRef]
- Sabzi, S.; Abbaspour-Gilandeh, Y.; Javadikia, H. Machine vision system for the automatic segmentation of plants under different lighting conditions. Biosyst. Eng. 2017, 161, 157–173. [Google Scholar] [CrossRef]
- Federico, D.; Matteo, C.; Daniele, D.A.; Andrea, A.; Francesco, T.; Matteo, S.S. Modeling, control design and experimental automatic calibration of a leveling system for combine harvesters. Control Eng. Pract. 2023, 132, 105411. [Google Scholar]
- Nevavuori, P.; Narra, N.; Lipping, T. Crop yield prediction with deep convolutional neural networks. Comput. Electron. Agric. 2019, 163, 104859. [Google Scholar] [CrossRef]
- Ma, W.; Zhu, Z.; Zhou, X. Agricultural mechanization and cropland abandonment in rural China. Appl. Econ. Lett. 2022, 29, 526–533. [Google Scholar] [CrossRef]
- Li, R.; Cheng, Y.; Xu, J.; Li, Y.; Ding, X.; Zhao, S. Research on on-line monitoring system of hydraulic actuator of combine harvester. Processes 2022, 10, 35. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, H.; Sun, H.; Wang, P.; Cao, Q. Experimental Study on Electric Harvesting of Combine Harvester. J. Phys. Conf. Ser. 2022, 2218, 012064. [Google Scholar] [CrossRef]
- Wang, G.; Wang, L.; Yang, Y.; You, X. Optimal Design of Harvesting Speed and Forward Speed of Harvester Based on Adaptive Control System. J. Sens. 2022, 2022, 4176942. [Google Scholar] [CrossRef]
- Chen, J.; Lian, Y.; Zou, R.; Zhang, S.; Ning, X.; Han, M. Real-time grain breakage sensing for rice combine harvesters using machine vision technology. Int. J. Agric. Biol. Eng. 2020, 13, 194–199. [Google Scholar] [CrossRef]
- Kounalakis, T.; Triantafyllidis, G.A.; Nalpantidis, L. Deep learning-based visual recognition of rumex for robotic precision farming. Comput. Electron. Agric. 2019, 165, 104973. [Google Scholar] [CrossRef]
- Saleem, M.H.; Potgieter, J.; Arif, K.M. Automation in agriculture by machine and deep learning techniques: A review of recent developments. Precis. Agric. 2021, 22, 2053–2091. [Google Scholar] [CrossRef]
- Darwin, B.; Dharmaraj, P.; Prince, S.; Popescu, D.E.; Hemanth, D.J. Recognition of bloom/yield in crop images using deep learning models for smart agriculture: A review. Agronomy 2021, 11, 646. [Google Scholar] [CrossRef]
- Liu, T.; Ma, Y.; Yang, W.; Ji, W.; Wang, R.; Jiang, P. Spatial-temporal interaction learning based two-stream network for action recognition. Inf. Sci. 2022, 606, 864–876. [Google Scholar] [CrossRef]
- Looh, G.A.; Xie, F.; Zhang, Z.; Mangeh Iii, F.C. Development of Small Agricultural Machines in China: 4LZ–0.8 Mini Combine Harvester. Development 2019, 6, 9849–9854. [Google Scholar]
- Li, H. Research and Prospect of crawler chassis of agricultural machinery in mountainous and hilly areas. In Proceedings of the 2021 International Conference on Control and Intelligent Robotics, Guangzhou, China, 18–20 June 2021. [Google Scholar]
- Chapagain, T.; Raizada, M.N. Agronomic challenges and opportunities for smallholder terrace agriculture in developing countries. Front. Plant Sci. 2017, 8, 331. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Li, Y.; Qing, Y. Current status and prospect of research on combine harvester header for rape. IOP Conf. Ser. Earth Environ. Sci. 2021, 742, 012001. [Google Scholar] [CrossRef]
- Li, W.; Shuo, L.; Dianji, L.; Ghay, E. Multi-Sensor Signal Acquisition and Data Processing Analysis of Combine Harvester. INMATEH-Agric. Eng. 2021, 63, 335–344. [Google Scholar]
- Jiang, T.; Guan, Z.; Li, H.; Mu, S.; Wu, C.; Zhang, M.; Wang, G.; Chen, X. A feeding quantity monitoring system for a combine harvester: Design and experiment. Agriculture 2022, 12, 153. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, R.; Ou, H.; Zhang, Z.; Zhang, M.; Li, H. Analysis and comparison of feed rate detection methods of combine harvester based on power detection. Trans. Chin. Soc. Agric. Mach. 2020, 5, 5. [Google Scholar]
- Zhao, R.; Qin, D.; Chen, B.; Wang, T.; Wu, H. Thermal Management of Fuel Cells Based on Diploid Genetic Algorithm and Fuzzy PID. Appl. Sci. 2023, 13, 520. [Google Scholar] [CrossRef]
- Borase, R.P.; Maghade, D.K.; Sondkar, S.Y.; Pawar, S.N. A review of PID control, tuning methods and applications. Int. J. Dyn. Control 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Maghfiroh, H.; Ramelan, A.; Adriyanto, F. Fuzzy-PID in BLDC Motor Speed Control Using MATLAB/Simulink. J. Robot. Control JRC 2022, 3, 8–13. [Google Scholar] [CrossRef]
- Chi, K.; Hsiao, Y.; Chen, C. Robust Feedback Linearization Control Design for Five-Link Human Biped Robot with Multi-Performances. Appl. Sci. 2023, 13, 76. [Google Scholar] [CrossRef]
- Li, F.; Shang, C.; Li, Y.; Yang, J.; Shen, Q. Approximate reasoning with fuzzy rule interpolation: Background and recent advances. Artif. Intell. Rev. 2021, 54, 4543–4590. [Google Scholar] [CrossRef]
- Hu, H.; Zha, M.; Chang, L.; Kong, W. Design of Double Redundancy Controller for Electric Actuator Based on Dual three-phase PMSM. In Proceedings of the 2021 IEEE 2nd China International Youth Conference on Electrical Engineering (CIYCEE), Chengdu, China, 15–17 December 2021. [Google Scholar]
- Sain, D.; Mohan, B.M. Modeling, simulation and experimental realization of a new nonlinear fuzzy PID controller using Center of Gravity defuzzification. ISA Trans. 2021, 110, 319–327. [Google Scholar] [CrossRef]








| Variables | The Basic Domain | Based on |
|---|---|---|
| [−6, 6] | The traveling speed variation fluctuated greatly during the test, and the limit deviation was 6 m/s. | |
| [−6, 6] | The test’s rate of change in deviation was significant; the range was determined by simulation tests. | |
| [−6, 6] | Affects the speed at which the system adjusts. In mountainous hilly areas, the speed and direction of the machine needed to be adjusted frequently, so the value should be extended. Determine the range by simulation test. | |
| [−0.3, 0.3] | Affects the system’s steady-state error; too large will lead to overshoot. Determine the range by simulation test. | |
| [−0.3, 0.3] | Affects the system response speed; too large will lead to a long response time. Determine the range by simulation test. |
| e | NB | NM | NS | ZO | PS | PM | PB | |
|---|---|---|---|---|---|---|---|---|
| ec | ||||||||
| NB | PB/NB/PS | PB/NB/NS | PM/NM/NB | PM/NM/NB | PS/NS/NB | ZO/ZO/NM | ZO/ZO/PS | |
| NM | PB/NB/PS | PB/NB/NS | PM/NM/NB | PS/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/ZO/ZO | |
| NS | PM/NB/ZO | PM/NM/NS | PM/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/PS/NS | NS/PS/ZO | |
| ZO | PM/NM/ZO | PM/NM/NS | PS/NS/NS | ZO/ZO/NS | NS/PS/NS | NM/PM/NS | NM/PM/ZO | |
| PS | PS/NM/ZO | PS/NS/ZO | ZO/ZO/ZO | NS/PS/ZO | NS/PS/ZO | NM/PM/ZO | NM/PB/ZO | |
| PM | PS/ZO/PS | ZO/ZO/PS | NS/PS/PS | NM/PS/PS | NM/PM/PS | NM/PB/PS | NB/PB/PB | |
| PB | ZO/ZO/PB | ZO/ZO/PM | NM/PS/PM | NM/PM/PM | NM/PM/PS | NB/PB/PS | NB/PB/PB | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, L.; Liu, T.; Jiang, P.; Xie, F.; Zhou, J.; Yang, W.; Qi, A. Design of an Adaptive Algorithm for Feeding Volume–Traveling Speed Coupling Systems of Rice Harvesters in Southern China. Appl. Sci. 2023, 13, 4876. https://doi.org/10.3390/app13084876
Deng L, Liu T, Jiang P, Xie F, Zhou J, Yang W, Qi A. Design of an Adaptive Algorithm for Feeding Volume–Traveling Speed Coupling Systems of Rice Harvesters in Southern China. Applied Sciences. 2023; 13(8):4876. https://doi.org/10.3390/app13084876
Chicago/Turabian StyleDeng, Lexing, Tianyu Liu, Ping Jiang, Fangping Xie, Junchi Zhou, Wenhan Yang, and Aolin Qi. 2023. "Design of an Adaptive Algorithm for Feeding Volume–Traveling Speed Coupling Systems of Rice Harvesters in Southern China" Applied Sciences 13, no. 8: 4876. https://doi.org/10.3390/app13084876
APA StyleDeng, L., Liu, T., Jiang, P., Xie, F., Zhou, J., Yang, W., & Qi, A. (2023). Design of an Adaptive Algorithm for Feeding Volume–Traveling Speed Coupling Systems of Rice Harvesters in Southern China. Applied Sciences, 13(8), 4876. https://doi.org/10.3390/app13084876






