Stray Magnetic Field Measurement Method of Magnetic Hysteresis Curve of Open-Ended Sensor and Actuator Cores
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
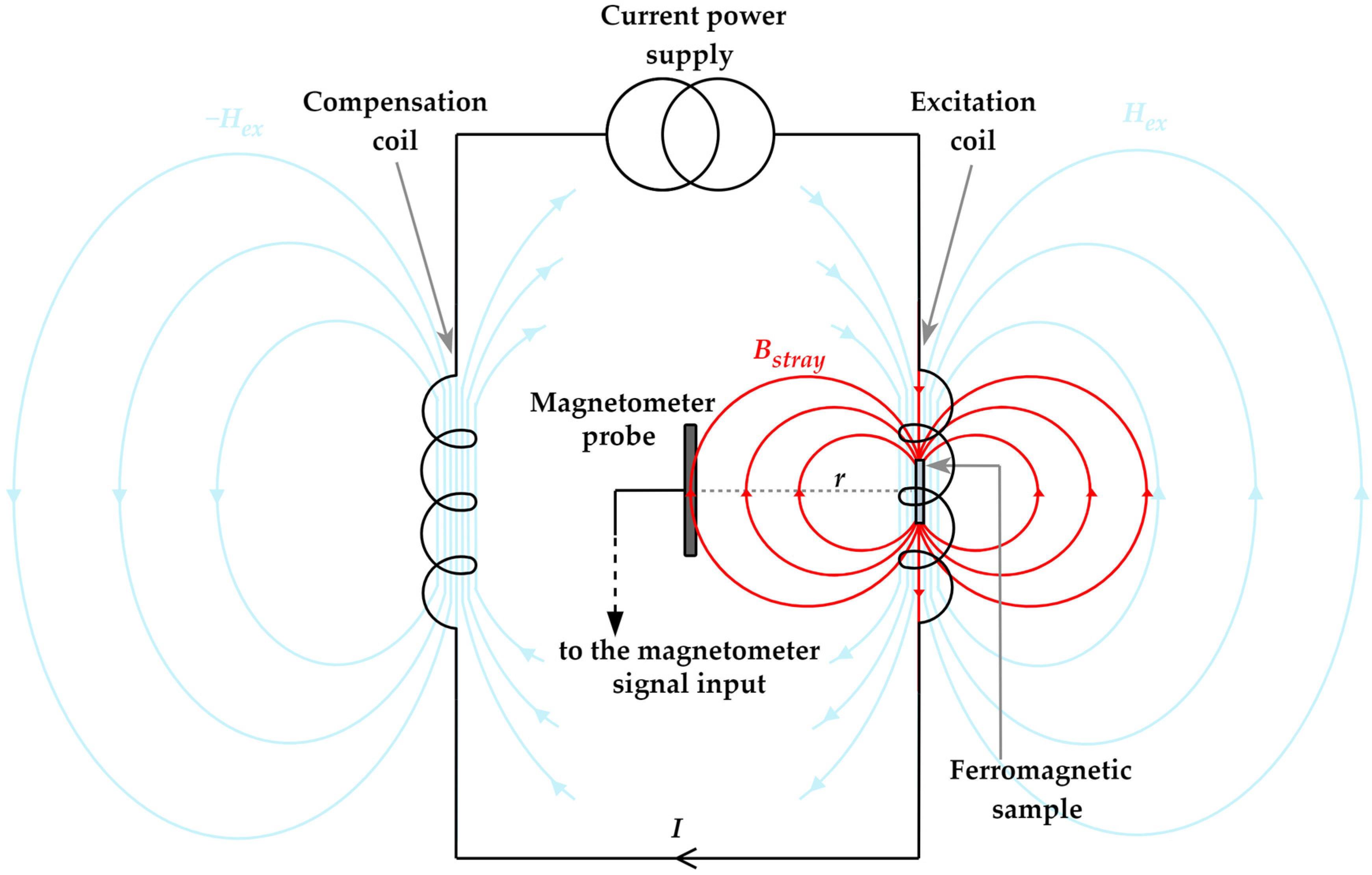
2.1. Principle of the Measurement Method
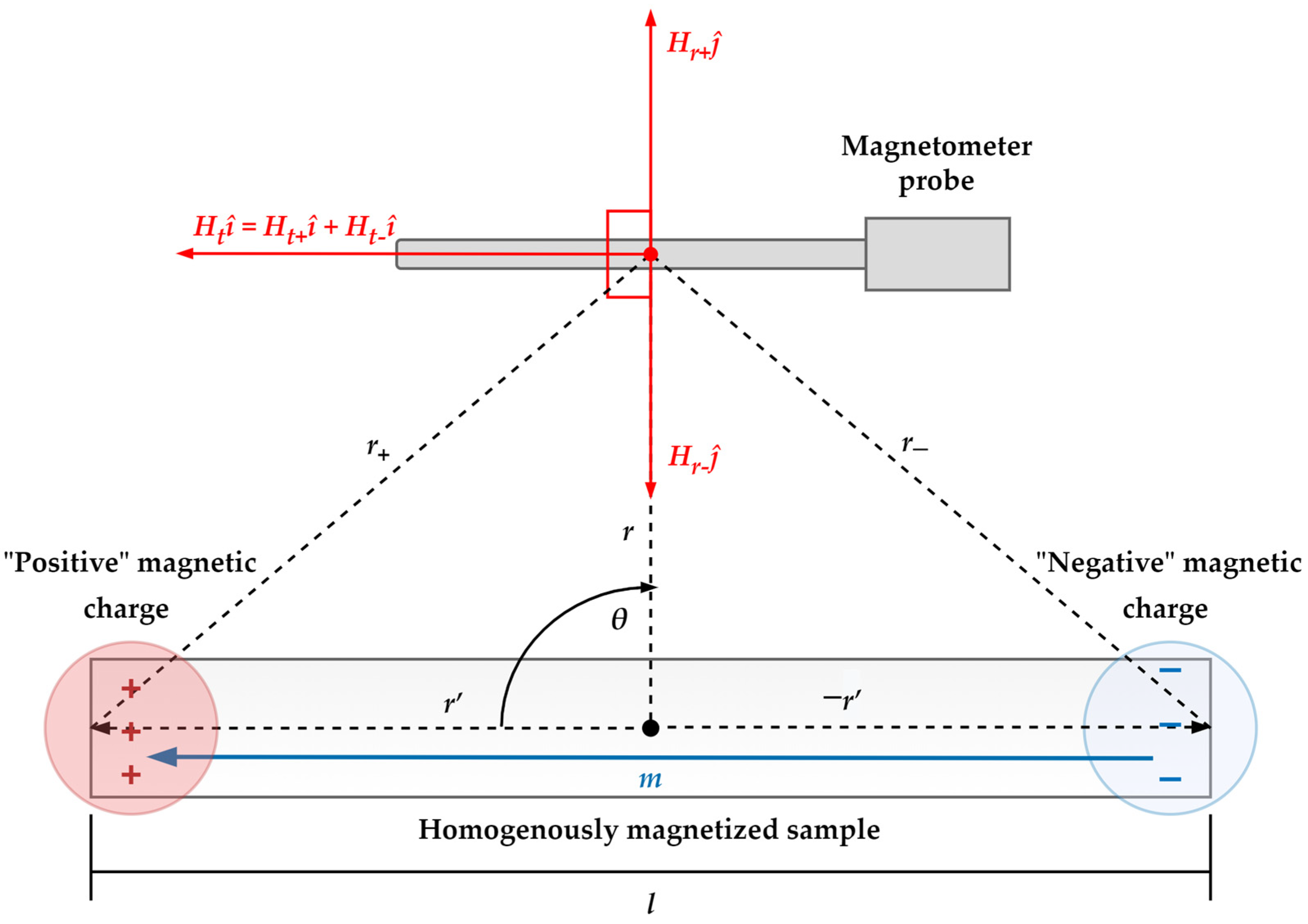
2.2. Mathematical Apparatus for Magnetic Hysteresis Curve Reconstruction
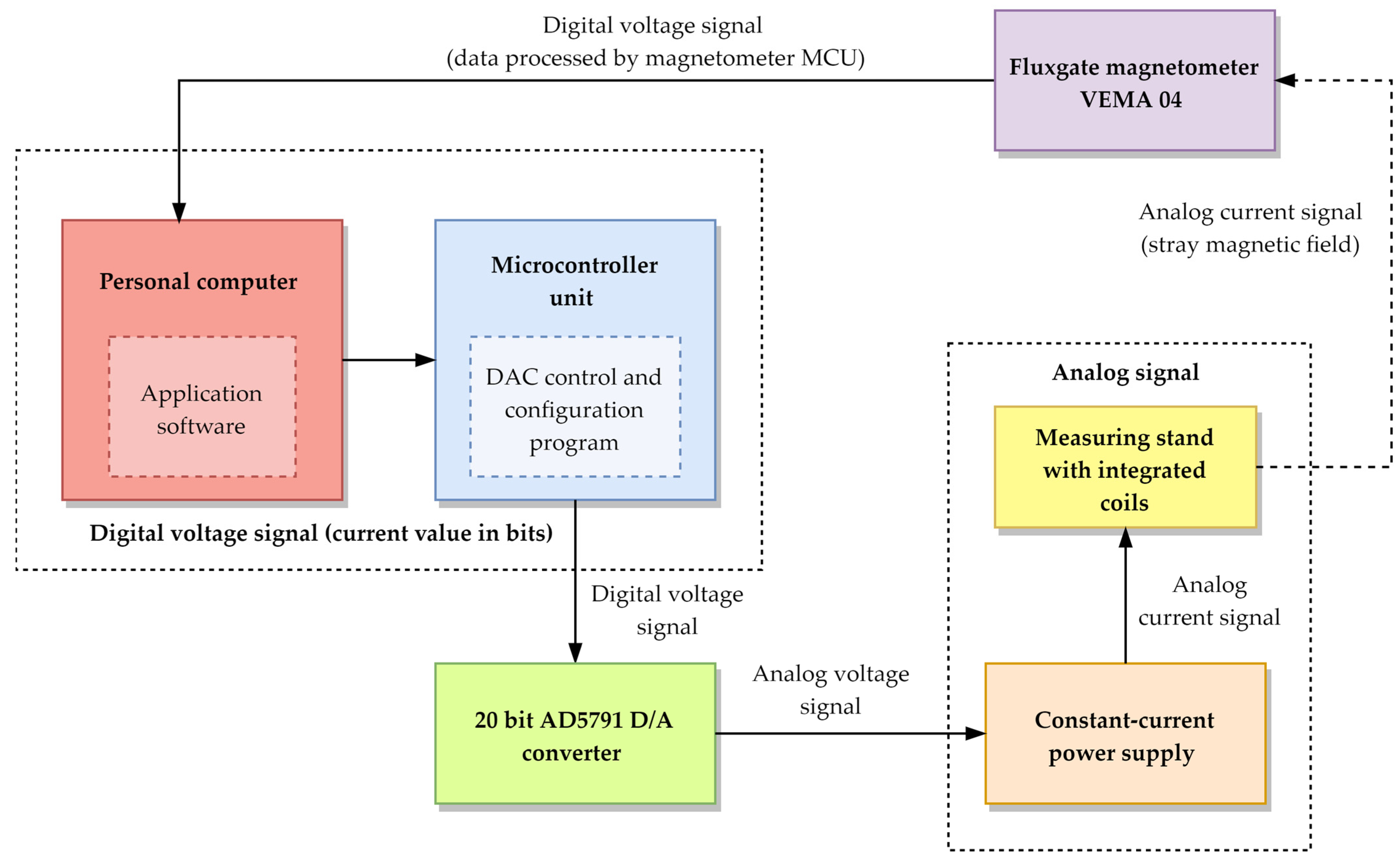
2.3. Measurement Chain
- Relax-type fluxgate magnetometer VEMA 04 developed at the Department of Aviation Technical Studies at the Faculty of Aeronautics of the Technical University of Košice. The total range and sensitivity of the VEMA magnetometer are up to ±50,000 nT and 3.5 nT, respectively. The sample rate of a used model is about 500 Hz [47].
- Measuring stand with integrated magnetizing (excitation) and compensation coils, between which a sensing probe holder is located. The total length and radius of the coils are 290 mm and 50 mm, respectively. Both coils can generate a relatively identical but opposite magnetic field with a magnitude of 3896.55 A/m per ampere at their midpoint, from which the magnetic field drop is at a distance of 50 mm less than 2% (Note that the magnetized sample should be during the measurement process constantly exposed to a homogenous magnetic field). A skeleton of the measuring stand was made by an additive manufacturing process based on fused depositing modeling technology.
- Evaluation board with high precision 20-bit AD5791 digital to analog converter enables to generate bipolar supply up to ±15 V.
- Arduino Mega 2560 microcontroller unit (MCU) based on the ATmega2560 microprocessor with an integrated program intended for control and configuration of the D/A controller.
- A personal computer with application software [48] that defines and controls the measuring process, statistically processes the measured data in order to reduce measurement uncertainties, calculates the magnetization characteristics according to the integrated mathematical apparatus, and provides its real-time visualization using a graphical user interface.
- Constant-current power supply with input ranges up to ±3 V.
3. Results and Discussion
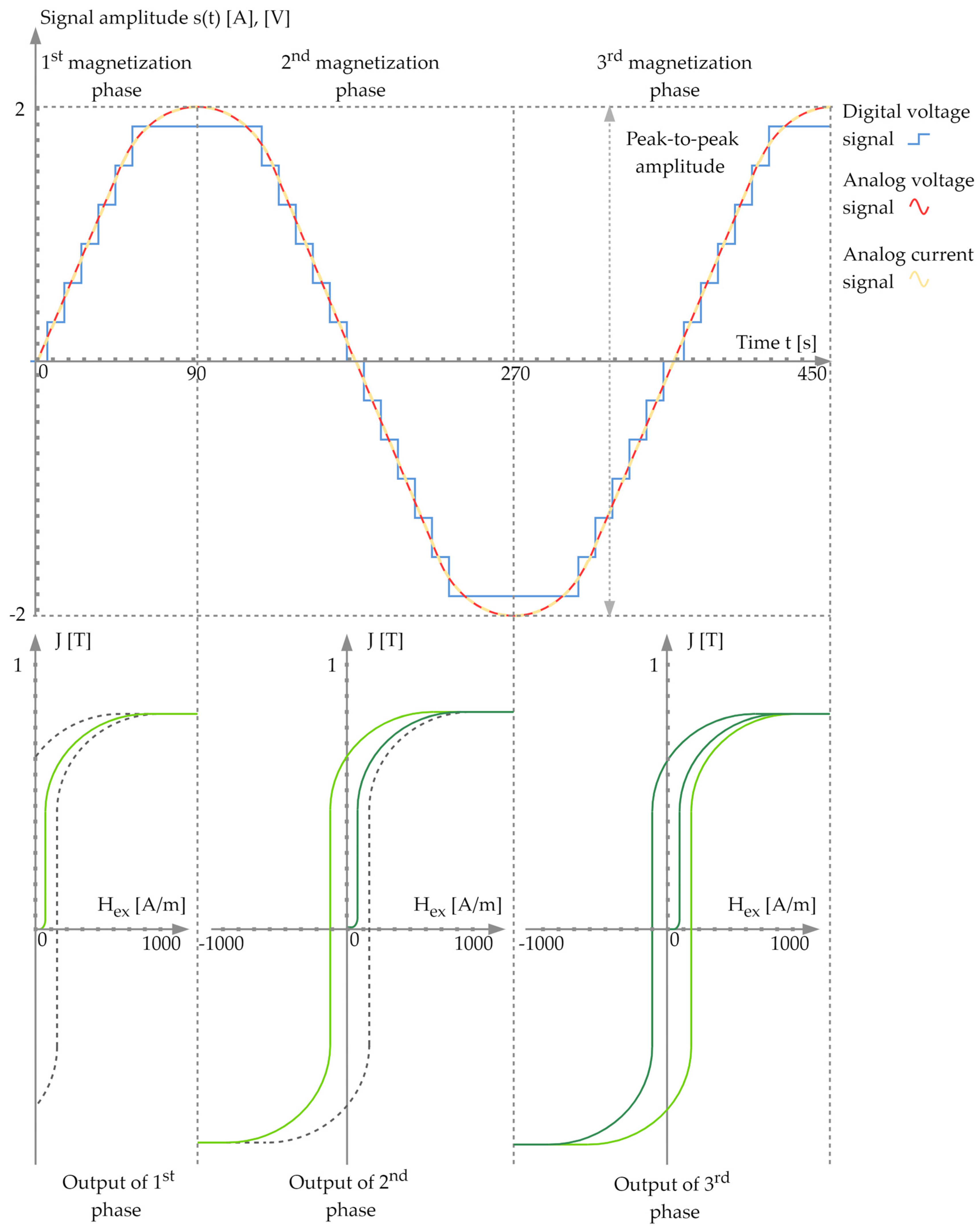
3.1. Measurement of Magnetic Hysteresis Curve of Actuator Core
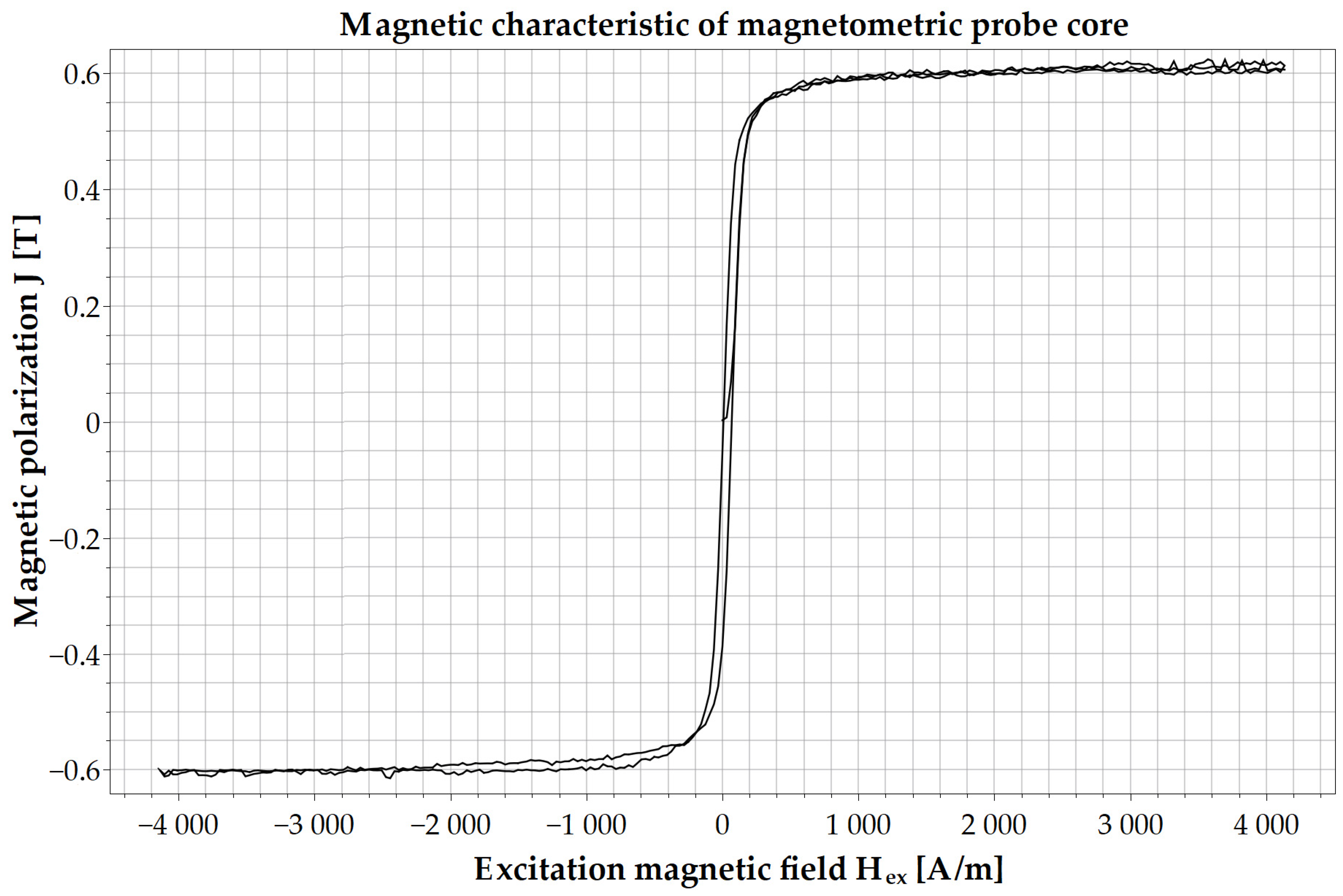
3.2. Measurement of Magnetic Hysteresis Curve of Magnetometric Relax-Type Probe Core
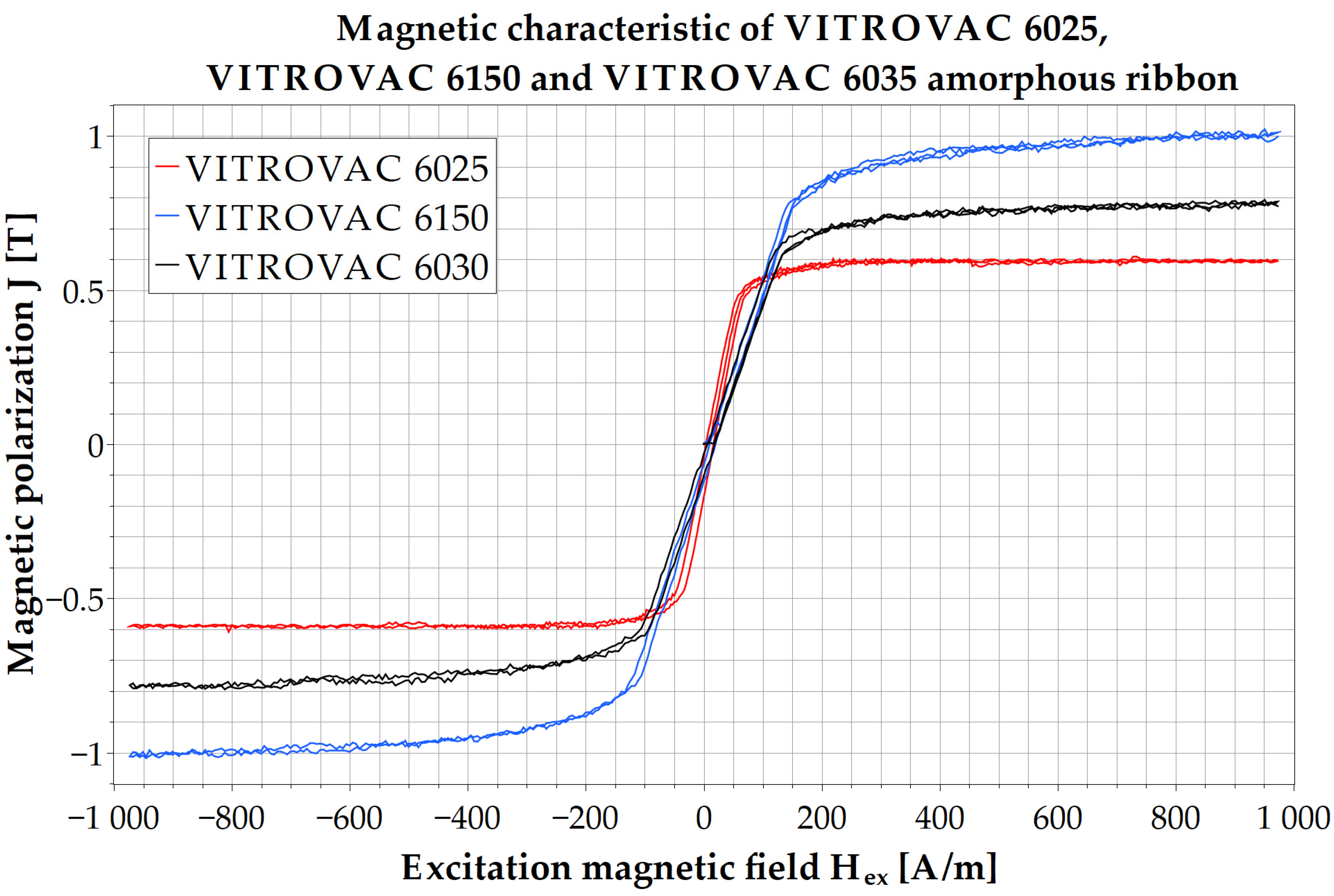
3.3. Supplementary Measurements of Magnetic Hysteresis Curves of Co-Based Amorphous Ribbons
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nanosats. Available online: https://www.nanosats.eu/ (accessed on 10 March 2023).
- Nanosats. Available online: https://www.nanosats.eu/img/fig/Nanosats_years_2023-01-01_large.png (accessed on 10 March 2023).
- Chiu, Y.-C.; Chang, L.C.; Chao, C.-K.; Tai, T.-Y.; Cheng, K.-L.; Liu, H.-T.; Tsai-Lin, R.; Liao, C.-T.; Luo, W.-H.; Chiu, G.-P.; et al. Lessons Learned from IDEASSat: Design, Testing, on Orbit Operations, and Anomaly Analysis of a First University CubeSat Intended for Ionospheric Science. Aerospace 2022, 9, 110. [Google Scholar] [CrossRef]
- Issa, H.; Marpu, P.; Jallad, A.H.; Al Marar, A. Mission Operations and Science Plan for the MeznSat CubeSat Mission for Greenhouse Gases Monitoring. In Proceedings of the IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 5454–5457. [Google Scholar] [CrossRef]
- Lim, B.; Mauro, D.; De Rosee, R.; Sorgenfrei, M.; Vance, S. CHARM: A CubeSat water vapor radiometer for earth science. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1022–1025. [Google Scholar] [CrossRef]
- Orger, N.C.; Cay, Y.; Kaymaz, Z.; Berat Karyot, T.; Nikbay, M. Optimization of a plasma instrument design for a CubeSat with space weather research. In Proceedings of the International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 16–19 June 2015. [Google Scholar] [CrossRef]
- Doyle, M.; Gloster, A.; Griffin, M.; Hibbett, M.; Kyle, J.; O’Toole, C.; Mangan, J.; Murphy, D.; Wong, N.L.; Akarapu, S.K.R.; et al. Design, development, and testing of flight software for EIRSAT-1: A university-class CubeSat enabling astronomical research. Softw. Cyberinfrastructure Astron. VII 2022, 12189, 445–463. [Google Scholar] [CrossRef]
- Berg, W.; Kummerow, C.; Reising, S.; Chandrasekar, V.; Schulte, R.; Goncharenko, Y.; Kilmer, B.; Brown, S.; Lim, B.; Pad-manabhan, S.; et al. Demonstrating the viability of the TEMPEST-D CubeSat radiometer for science applications. In Proceedings of the IEEE International Geoscience and remote sensing symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019. [Google Scholar] [CrossRef]
- Misra, S.; Brown, S.; Jarnot, R.; Felten, C.; Bendig, R.; Kocz, J.; McKelvey, C.; Ball, C.; Chen, C.-C.; O’Brien, A.; et al. CubeSat radiometer radio frequency interference technology (Cub-eRRT) validation mission: Enabling future resource-constrained science missions. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018. [Google Scholar] [CrossRef]
- Fields, R.; Sun, X.; Abshire, J.B.; Beck, J.; Rawlings, R.M.; Sullivan, W.; Hinkley, D. A linear mode photon-counting (LMPC) detector array in a CubeSat to enable Earth science lidar measurements. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar] [CrossRef]
- Mazzarella, L.; Lowe, C.; Lowndes, D.; Joshi, S.K.; Greenland, S.; McNeil, D.; Mercury, C.; Macdonald, M.; Rarity, J.; Oi, D.K.L. QUARC: Quantum Research Cubesat—A Constellation for Quantum Communication. Cryptography 2020, 4, 7. [Google Scholar] [CrossRef] [Green Version]
- Capannolo, A.; Zanotti, G.; Lavagna, M.; Epifani, E.M.; Dotto, E.; Della Corte, V. Challenges in LICIA Cubesat trajectory design to support DART mission science. Acta Astronaut. 2021, 182, 208–218. [Google Scholar] [CrossRef]
- Lightholder, J.; Thompson, D.R.; Castillo-Rogez, J.; Basset, C. Near Earth asteroid scout CubeSat science data retrieval op-timization using onboard data analysis. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019. [Google Scholar] [CrossRef]
- Bakken, S.; Henriksen, M.B.; Birkeland, R.; Langer, D.D.; Oudijk, A.E.; Berg, S.; Pursley, Y.; Garrett, J.L.; Gran-Jansen, F.; Honoré-Livermore, E.; et al. HYPSO-1 CubeSat: First Images and In-Orbit Characterization. Remote Sens. 2023, 15, 755. [Google Scholar] [CrossRef]
- Ramiaramanantsoa, T.; Bowman, J.D.; Shkolnik, E.L.; Loyd, R.O.P.; Ardila, D.R.; Jewell, A.; Barman, T.; Basset, C.H.; Beasley, M.; Cheng, S.; et al. Onboard dynamic image exposure control for the Star–Planet Activity Research CubeSat (SPARCS). Mon. Not. R. Astron. Soc. 2022, 509, 5702–5712. [Google Scholar] [CrossRef]
- Ramiaramanantsoa, T.; Bowman, J.D.; Shkolnik, E.L.; Loyd, R.O.P.; Ardila, D.R.; Barman, T.; Basset, C.; Beasley, M.; Cheng, S.; Gamaunt, J.; et al. Time-resolved photometry of the high-energy radiation of M dwarfs with the Star-Planet Activity Research Cubesat. Astron. Nachr. 2022, 343, e210068. [Google Scholar] [CrossRef]
- Gibson, B.M. Miniaturized ring-down spectrometer for CubeSat-based planetary science. Appl. Opt. 2019, 58, 1941–1949. [Google Scholar] [CrossRef]
- Mason, J.P.; Woods, T.N.; Caspi, A.; Chamberlin, P.C.; Moore, C.; Jones, A.; Kohnert, R.; Li, X.; Palo, S.; Solomon, S.C. Miniature X-ray solar spectrometer: A sci-ence-oriented, university 3U CubeSat. J. Spacecr. Rocket. 2016, 53, 328–339. [Google Scholar] [CrossRef] [Green Version]
- Kim, G.N.; Park, S.Y.; Lee, T.; Kang, D.E.; Jeon, S.; Son, J.; Kim, N.; Park, Y.; Song, Y. Development of CubeSat Systems in Formation Flying for the Solar Science Demonstration: The CANYVAL-C Mission. Adv. Space Res. 2021, 68, 4434–4455. [Google Scholar] [CrossRef]
- Garrick-Bethell, I.; Lin, R.P.; Sanchez, H.; Jaroux, B.A.; Bester, M.; Brown, P.; Cosgrove, D.; Dougherty, M.K.; Halekas, J.S.; Hemingway, D.; et al. Lunar magnetic field measurements with a cubesat. Proceeding of the SPIE 8739, Sensors and Systems for Space Applications VI, Baltimore, MD, USA, 21 May 2013. [Google Scholar] [CrossRef]
- Jeong-Ah, L.; Sang-Young, P.; Youngkwang, K.; Jonghee, B.; Donghun, L.; Gwanghyeok, J. Mission orbit design of CubeSat impactor measuring lunar local magnetic field. J. Astr. S. Sci. 2017, 34, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Mateos, I.; Sánchez-Mínguez, R.; Ramos-Castro, J. Design of a CubeSat payload to test a magnetic measurement system for space-borne gravitational wave detectors. Sen. Act. A Phys. 2018, 273, 311–316. [Google Scholar] [CrossRef] [Green Version]
- Carletta, S.; Nascetti, A.; Gosikere Matadha, S.S.; Iannascoli, L.; Baratto de Albuquerque, T.; Maipan Davis, N.; Schirone, L.; Impresario, G.; Pirrotta, S.; Brucato, J.R. Characterization and Testing of the Passive Magnetic Attitude Control System for the 3U AstroBio CubeSat. Aerospace 2022, 9, 723. [Google Scholar] [CrossRef]
- Williams, A.; Yamrick, K.; Asundi, S.; Wriggers, W.; Liu, Z. An Experimental Approach to Mapping of Magnetic Fields of CubeSat Attitude Actuator Representations. In Proceedings of the IEEE Aerospace Conference, Byg Sky, Montana, 7–14 March 2020. [Google Scholar] [CrossRef]
- Cervettini, G.; Pastorelli, S.; Park, H.; Lee, D.Y.; Romano, M. Development and experimentation of a CubeSat magnetic attitude control system testbed. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1345–1350. [Google Scholar] [CrossRef]
- Miyagusuku, R.; Arias, K.R.; Villota, E. Hybrid magnetic attitude control system under CubeSat standards. In Proceedings of the IEEE Aerospace Conference Proceedings 2012, Big Sky, MT, USA, 3–10 March 2012; pp. 1–9. [Google Scholar] [CrossRef]
- Musilova, M.; Smelko, M.; Lipovsky, P.; Kapus, J.; Zavodsky, O.; Slosiar, R. skCUBE very-low-frequency radio waves detector and whistlers. In Proceedings of the International Conference on Mechanical and Aerospace Engineering (ICMAE), Prague, Czech Republic, 22–25 July 2017. [Google Scholar] [CrossRef]
- Pál, A.; Ohno, M.; Mészáros, L.; Werner, N.; Ripa, J.; Frajt, M.; Hirade, N.; Hudec, J.; Kapuš, J.; Koleda, M. GRBAlpha: A 1U CubeSat mission for validating timing-based gamma-ray burst localization. In Proceedings of the Space Telescopes and Instrumentation 2020: Ultraviolet to Gamma Ray, Online, 14–18 December 2020. [Google Scholar] [CrossRef]
- Ripa, J.; Pal, A.; Ohno, M.; Werner, N.; Meszaros, L.; Csak, B.; Dafčíková, M.; Dániel, V.; Dudáš, J.; Frajt, M. Early results from GRBAlpha and VZLUSAT-2. In Proceedings of the Space Telescopes and Instrumentation 2022: Ultraviolet to Gamma Ray, Montréal, QC, Canada, 17–23 July 2022. [Google Scholar] [CrossRef]
- Kliment, T.; Praslička, D.; Lipovský, P.; Draganová, K.; Závodský, O. Calibration of magnetometer for small satellites using neural network. A. Phys. Pol. A 2017, 131, 1129–1131. [Google Scholar] [CrossRef]
- Polik, Z.; Kuczmann, M. Measuring and control the hysteresis loop by using analog and digital integrators. J. Optoel. Adv. Mat. 2008, 10, 1861–1865. [Google Scholar]
- Zhao, X.; Liu, X.; Zhao, Z.; Zou, X.; Xiao, Y.; Li, G. Measurement and modeling of hysteresis characteristics in ferromagnetic materials under DC magnetizations. AIP Adv. 2019, 9, 025111. [Google Scholar] [CrossRef] [Green Version]
- Shirane, T.; Ito, M. Measurement of Hysteresis Loop on Soft Magnetic Materials Using Lock-In Amplifier. In IEEE Transactions on Magnetics; IEEE: Piscataway, NJ, USA, 2012; Volume 48, pp. 1437–1440. [Google Scholar] [CrossRef]
- Najgebauer, M.; Gryś, S.; Hiergeist, R. Uncertainty of hysteresis loop measurements in magnetic materials. Zesz. Nauk. Wydziału Elektrotechniki I Autom. Politech. Gdańskiej 2018, 59, 149–152. [Google Scholar] [CrossRef]
- Stupakov, O. Controllable Magnetic Hysteresis Measurement of Electrical Steels in a Single-Yoke Open Configuration. In IEEE Transactions on Magnetics; IEEE: Piscataway, NJ, USA, 2012; Volume 48, pp. 4718–4726. [Google Scholar] [CrossRef]
- Jinghui, W.; Dayi, S.; Wei, C. A new pulse measurement method for magnetization characteristics of small loss angle core. EIT Power Elec. 2021, 14, 51–62. [Google Scholar] [CrossRef]
- Morino, H.; Ishihara, Y.; Todaka, T. Measuring method of magnetic characteristics in any direction for silicon steel. J. Magn. Mag. Mat. 1992, 112, 115–119. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, M.; Li, Y. Measurement and Simulation of Magnetic Properties of Nanocrystalline Alloys under High-Frequency Pulse Excitation. Materials 2023, 16, 2850. [Google Scholar] [CrossRef]
- Lu, H.Y.; Zhu, J.G.; Hui, S.Y.R. Measurement and Modeling of Thermal Effects on Magnetic Hysteresis of Soft Ferrites. In IEEE Transactions on Magnetics; IEEE: Piscataway, NJ, USA, 2007; Volume 43, pp. 3952–3960. [Google Scholar] [CrossRef]
- Vrijsen, N.H.; Jansen, J.W.; Compter, J.C.; Lomonova, E.A. Measurement method for determining the magnetic hysteresis effects of reluctance actuators by evaluation of the force and flux variation. Rev. Sci. Instrum. 2013, 84, 075003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oravec, M.; Hesko, F.; Szőke, Z.; Smelko, M.; Gazda, T. Magnetometry for security applications. In Advances in Physical, Social & Occupational Ergonomics; AHFE 2021, Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2021; Volume 273, pp. 236–243. [Google Scholar] [CrossRef]
- Lipovský, P.; Novotňák, J.; Blažek, J. Possible Utilization of Low Frequency Magnetic Fields in Short Range Multirotor UAV Detection System. In Proceedings of the 11th International Conference on Air Transport–INAIR 2022, Returning to the Skies, Bratislava, Slovakia, 24–25 November 2022; Volume 65, pp. 106–115. [Google Scholar] [CrossRef]
- Lipovský, P.; Draganová, K.; Novotňák, J.; Szőke, Z.; Fiľko, M. Indoor Mapping of Magnetic Fields Using UAV Equipped with Fluxgate Magnetometer. Sensors 2021, 21, 4191. [Google Scholar] [CrossRef]
- Krishnan, K.M. Magnetostatic energy. In Fundamentals and Applications of Magnetic Materials, 1st ed.; Oxford University Press: Oxford, UK, 2016; pp. 347–348. [Google Scholar]
- Coey, J.M.D. Magnetic field calculations. In Magnetism and Magnetic Materials, 1st ed.; Cambridge University Press: New York, NY, USA, 2010; pp. 43–49. [Google Scholar]
- BENDA Oldrich. Feromagnetizmus; Slovenské Vydavate’stvo Technickej Literatúry: Bratislava, Slovakia, 1963. [Google Scholar]
- Hudák, J.; Blažek, J.; Praslička, D.; Mikita, I.; Lipovský, P.; Gonda, P. Sensitivity of VEMA-04.1 Magnetometer. J. Electr. Eng. 2010, 61, 28–31. [Google Scholar]
- Kašper, P.; Lipovský, P.; Šmelko, M. Application Software of Modular System for Magnetic Characteristics Measurement. In Proceedings of the 2022 16th International Scientific Conference on New Trends in Aviation Development, Nový Smokovec–High Tatras, Slovakia, 24–25 November 2022; pp. 95–100. [Google Scholar] [CrossRef]
- Hilzinger, R.; Rodewald, W. Magnetic field calculations. Magnetic properties of amorphous alloys. In Magnetic Materials, Fundamental, Product, Properties, Applications, 1st ed.; Seitfudem, G., Ed.; Publicis Publishing: Erlangen, Germany, 2013; p. 277. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kašper, P.; Šmelko, M.; Kessler, J.; Lipovský, P.; Draganová, K. Stray Magnetic Field Measurement Method of Magnetic Hysteresis Curve of Open-Ended Sensor and Actuator Cores. Appl. Sci. 2023, 13, 4885. https://doi.org/10.3390/app13084885
Kašper P, Šmelko M, Kessler J, Lipovský P, Draganová K. Stray Magnetic Field Measurement Method of Magnetic Hysteresis Curve of Open-Ended Sensor and Actuator Cores. Applied Sciences. 2023; 13(8):4885. https://doi.org/10.3390/app13084885
Chicago/Turabian StyleKašper, Patrik, Miroslav Šmelko, Jaroslav Kessler, Pavol Lipovský, and Katarína Draganová. 2023. "Stray Magnetic Field Measurement Method of Magnetic Hysteresis Curve of Open-Ended Sensor and Actuator Cores" Applied Sciences 13, no. 8: 4885. https://doi.org/10.3390/app13084885
APA StyleKašper, P., Šmelko, M., Kessler, J., Lipovský, P., & Draganová, K. (2023). Stray Magnetic Field Measurement Method of Magnetic Hysteresis Curve of Open-Ended Sensor and Actuator Cores. Applied Sciences, 13(8), 4885. https://doi.org/10.3390/app13084885









