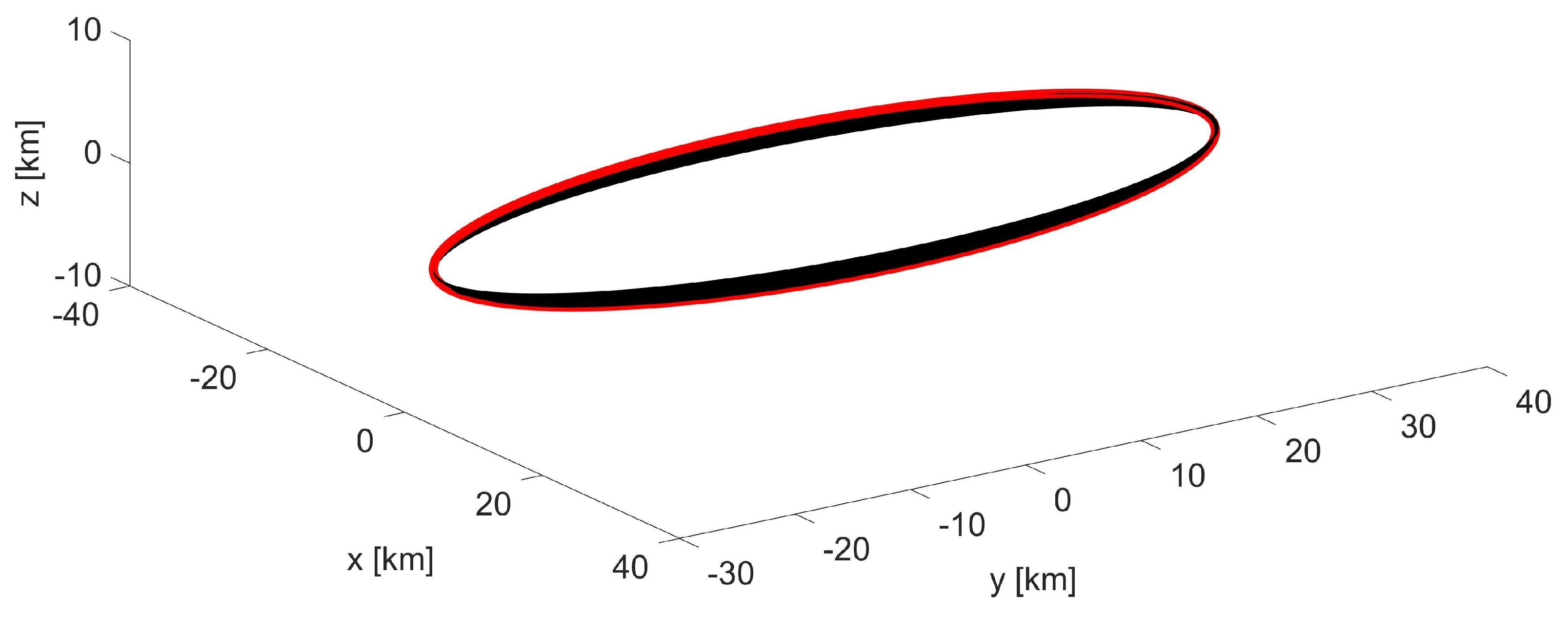
Figure 1.
SSO formation: -invariant bounded trajectory (black) in ; the first orbit is plotted in red.
Figure 1.
SSO formation: -invariant bounded trajectory (black) in ; the first orbit is plotted in red.
Figure 2.
SSO formation: trajectory (black) in resulting from non-invariant initial conditions; the first orbit is plotted in red.
Figure 2.
SSO formation: trajectory (black) in resulting from non-invariant initial conditions; the first orbit is plotted in red.
Figure 3.
SSO formation: time behavior of y component.
Figure 3.
SSO formation: time behavior of y component.
Figure 4.
SSO formation: time behavior of z component.
Figure 4.
SSO formation: time behavior of z component.
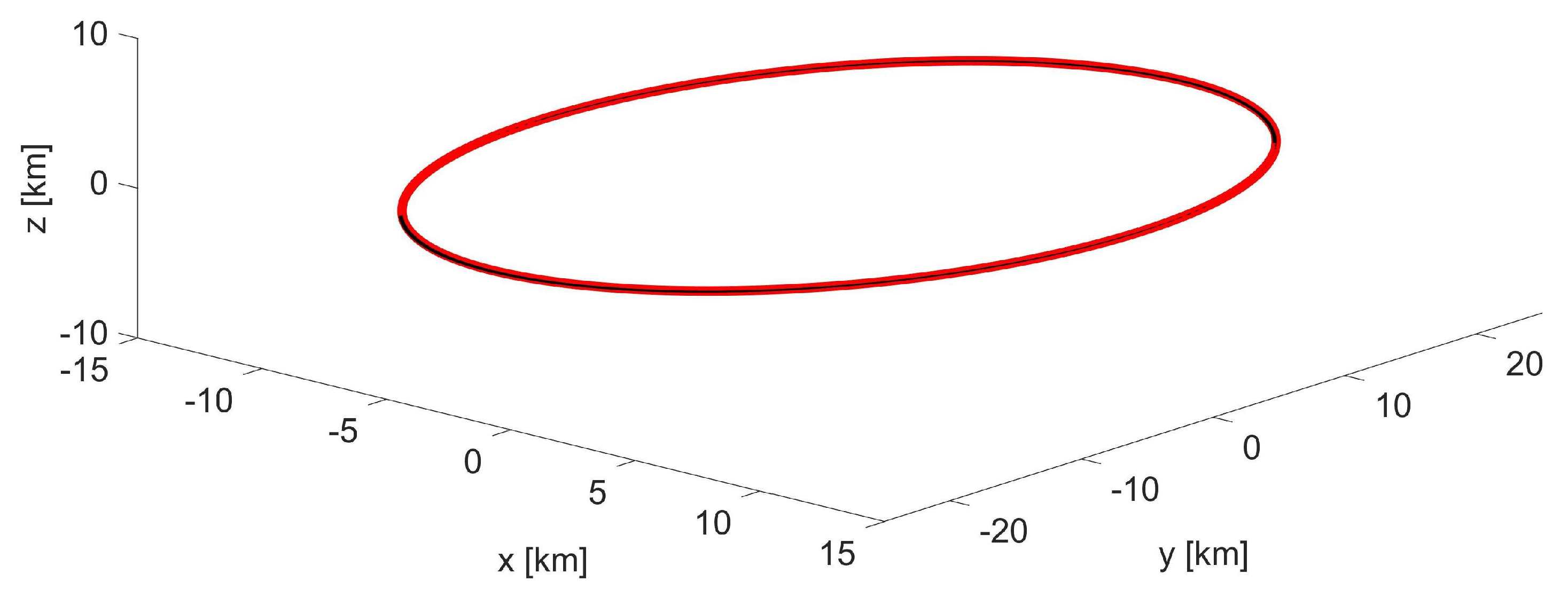
Figure 5.
Mid-inclination LEO formation: -invariant bounded trajectory (black) in ; the first orbit is plotted in red.
Figure 5.
Mid-inclination LEO formation: -invariant bounded trajectory (black) in ; the first orbit is plotted in red.
Figure 6.
Mid-inclination LEO formation: trajectory (black) in resulting from non-invariant initial conditions; the first orbit is plotted in red.
Figure 6.
Mid-inclination LEO formation: trajectory (black) in resulting from non-invariant initial conditions; the first orbit is plotted in red.
Figure 7.
Mid-inclination LEO formation: time behavior of y component.
Figure 7.
Mid-inclination LEO formation: time behavior of y component.
Figure 8.
Mid-inclination LEO formation: time behavior of z component.
Figure 8.
Mid-inclination LEO formation: time behavior of z component.
Figure 9.
Mid-inclination eccentric LEO formation: trajectory in resulting from -invariant and -invariant initial conditions; the first orbit is plotted in red.
Figure 9.
Mid-inclination eccentric LEO formation: trajectory in resulting from -invariant and -invariant initial conditions; the first orbit is plotted in red.
Figure 10.
Mid-inclination eccentric LEO formation: time behavior of y component for -invariant and -invariant initial conditions.
Figure 10.
Mid-inclination eccentric LEO formation: time behavior of y component for -invariant and -invariant initial conditions.
Figure 11.
Lunar formation: -invariant bounded trajectory (black) in ; the first orbit is plotted in red.
Figure 11.
Lunar formation: -invariant bounded trajectory (black) in ; the first orbit is plotted in red.
Figure 12.
Lunar formation: trajectory (black) in resulting from non-invariant initial conditions; the first orbit is plotted in red.
Figure 12.
Lunar formation: trajectory (black) in resulting from non-invariant initial conditions; the first orbit is plotted in red.
Figure 13.
Lunar formation: time behavior of y component.
Figure 13.
Lunar formation: time behavior of y component.
Figure 14.
Guidance strategy: transfer of the reconnaissance satellite into a -invariant bounded trajectory in about the target object.
Figure 14.
Guidance strategy: transfer of the reconnaissance satellite into a -invariant bounded trajectory in about the target object.
Figure 15.
Guidance strategy: detail of the injection point between the departure trajectory and the target orbit in ; the arrow indicates the direction of the provided.
Figure 15.
Guidance strategy: detail of the injection point between the departure trajectory and the target orbit in ; the arrow indicates the direction of the provided.
Figure 16.
Guidance strategy: projection of the trajectory onto the plane; the amplitude of the z component does not change after the maneuver.
Figure 16.
Guidance strategy: projection of the trajectory onto the plane; the amplitude of the z component does not change after the maneuver.
Table 1.
SSO formation: orbit parameters chief satellite.
Table 1.
SSO formation: orbit parameters chief satellite.
| semimajor axis | | 6919 km |
| eccentricity | e | 0.002 |
| inclination | i | 97.79 deg |
| local time ascending node | - | 11:00 am |
| epoch (UTC) | - | 24 January 2023 12:00:00 |
Table 2.
SSO formation: initial state of deputy satellite.
Table 2.
SSO formation: initial state of deputy satellite.
| Hamiltonian Variables | Position/Velocity Components |
|---|
| 0 | x | 9.7806 km |
| (1 + j) · | y | −19.5611 km |
| (1 + j) · | z | −0.9781 km |
| 0 | | −14.2517 m/s |
| (−1 − j) · | | −21.4989 m/s |
| (−1 − j) · | | 0 m/s |
Table 3.
SSO formation: maximum and minimum value of the position coordinates for the first and the last orbit.
Table 3.
SSO formation: maximum and minimum value of the position coordinates for the first and the last orbit.
| First Orbit | Last Orbit |
|---|
| 16.2582 km | | 16.2606 km |
| −16.2572 km | | −16.2724 km |
| 38.8642 km | | 38.9342 km |
| −26.1207 km | | −26.0483 km |
| 0.9807 km | | 0.9426 km |
| −0.9781 km | | −0.9370 km |
Table 4.
Mid-inclination LEO formation: orbit parameters of chief satellite.
Table 4.
Mid-inclination LEO formation: orbit parameters of chief satellite.
| semimajor axis | | 6919 km |
| eccentricity | e | 0 |
| inclination | i | 52 deg |
| RAAN | | 0 deg |
| epoch (UTC) | - | 24 January 2023 12:00:00 |
Table 5.
Mid-inclination LEO formation: initial state of deputy satellite.
Table 5.
Mid-inclination LEO formation: initial state of deputy satellite.
| Hamiltonian Variables | Position/Velocity Components |
|---|
| 0 | x | 9.7849 km |
| (1 + j) · | y | −19.5697 km |
| (1 + j) · | z | −9.7849 km |
| 0 | | −7.5402 m/s |
| (−1 − j) · | | −21.5257 m/s |
| (−1 − j) · | | 0.2797 m/s |
Table 6.
Mid-inclination LEO formation: maximum and minimum value of the position coordinates for the first and the last orbit.
Table 6.
Mid-inclination LEO formation: maximum and minimum value of the position coordinates for the first and the last orbit.
| First Orbit | Last Orbit |
|---|
| 11.9577 km | | 11.9611 km |
| −11.9724 km | | −11.9790 km |
| 18.0742 km | | 19.2724 km |
| −29.8000 km | | −28.5862 km |
| 9.5223 km | | 9.5223
km |
| −9.4888 km | | −9.4888 km |
Table 7.
Mid-inclination eccentric LEO formation: orbit parameters of chief satellite.
Table 7.
Mid-inclination eccentric LEO formation: orbit parameters of chief satellite.
| semimajor axis | | 7153 km |
| eccentricity | e | 0.05 |
| inclination | i | 48 deg |
| RAAN | | 0 deg |
| argument of pericenter | | 30 deg |
| epoch (UTC) | - | 24 January 2023 12:00:00 |
Table 8.
Mid-inclination eccentric LEO formation: -invariant initial state of deputy satellite.
Table 8.
Mid-inclination eccentric LEO formation: -invariant initial state of deputy satellite.
| x | −0.7156 km |
| y | 0.2700 km |
| z | −0.3202 km |
| −0.0724 m/s |
| 1.6135 m/s |
| 0.3773 m/s |
Table 9.
Mid-inclination eccentric LEO formation: -invariant initial state of deputy satellite.
Table 9.
Mid-inclination eccentric LEO formation: -invariant initial state of deputy satellite.
| Hamiltonian Variables | Position/Velocity Components |
|---|
| 0 | x | −0.7156 km |
| (−1.069 + j0.072) · | y | 0.2700 km |
| (−3.165 − j4.125) · | z | −0.3202 km |
| 0 | | −0.0724 m/s |
| (−0.072 + j1.069) · | | 1.6142 m/s |
| (4.125 + j3.165) · | | 0.4173 m/s |
Table 10.
Lunar formation: orbit parameters of chief satellite.
Table 10.
Lunar formation: orbit parameters of chief satellite.
| semimajor axis | | 6038 km |
| eccentricity | e | 0 |
| inclination | i | 40 |
| RAAN | | 0 |
| epoch (UTC) | - | 24 January 2023 12:00:00 |
Table 11.
Lunar formation: initial state of deputy satellite.
Table 11.
Lunar formation: initial state of deputy satellite.
| Hamiltonian Variables | Position/Velocity Components |
|---|
| 0 | x | 8.5390 km |
| j · | y | −17.0780 km |
| (1 + j) · | z | 0.8539 km |
| 0 | | −1.2744 m/s |
| −1 · | | −2.5523 m/s |
| (−1 − j) · | | −0.1274 m/s |
Table 12.
Lunar formation: maximum and minimum value of the position coordinates for the first and the last orbit.
Table 12.
Lunar formation: maximum and minimum value of the position coordinates for the first and the last orbit.
| First Orbit | Last Orbit |
|---|
| 12.0678 km | | 12.0679 km |
| −12.0669 km | | −12.0673 km |
| 24.0799 km | | 24.0799 km |
| −24.1878 km | | −24.4185 km |
| 1.2091 km | | 1.2103
km |
| −1.2043 km | | −1.2055 km |
Table 13.
Guidance strategy: orbit parameters of target object.
Table 13.
Guidance strategy: orbit parameters of target object.
| semimajor axis | | 6828 km |
| eccentricity | e | 0 |
| inclination | i | 62 deg |
| RAAN | | 0 deg |
| true anomaly | | 0 deg |
| epoch (UTC) | - | 24 January 2023 12:00:00 |
Table 14.
Guidance strategy: orbit parameters of reconnaissance satellite.
Table 14.
Guidance strategy: orbit parameters of reconnaissance satellite.
| semimajor axis | | 6835 km |
| eccentricity | e | 0.033 |
| inclination | i | 62 deg |
| RAAN | | deg |
| argument of perigee | | deg |
| true anomaly | | deg |
| epoch (UTC) | - | 24 January 2023 12:00:00 |
Table 15.
Guidance strategy: initial state of reconnaissance satellite.
Table 15.
Guidance strategy: initial state of reconnaissance satellite.
| Hamiltonian Variables | Position/Velocity Components |
|---|
| | x | 9.6562 km |
| (0.11 − 2.04j) · | y | −19.3123 km |
| (1 + j) · | z | 9.6563 km |
| −3 · | | −242.2476 m/s |
| (2.04 − 0.11j) · | | −21.1209 m/s |
| (−1 − j) · | | −1.2055 m/s |
Table 16.
Lunar formation: state of reconnaissance satellite after the maneuver.
Table 16.
Lunar formation: state of reconnaissance satellite after the maneuver.
| Hamiltonian Variables | Position/Velocity Components |
|---|
| 0 | x | 9.6562 km |
| (1 + j) · | y | −19.3123 km |
| (1 + j) · | z | 9.6563 km |
| 0 | | −10.8052 m/s |
| (−1 − j) · | | −21.6630 m/s |
| (−1 − j) · | | −1.2060 m/s |