Data Fusion-Based Structural Damage Identification Approach Integrating Fractal and RCPN
Abstract
1. Introduction
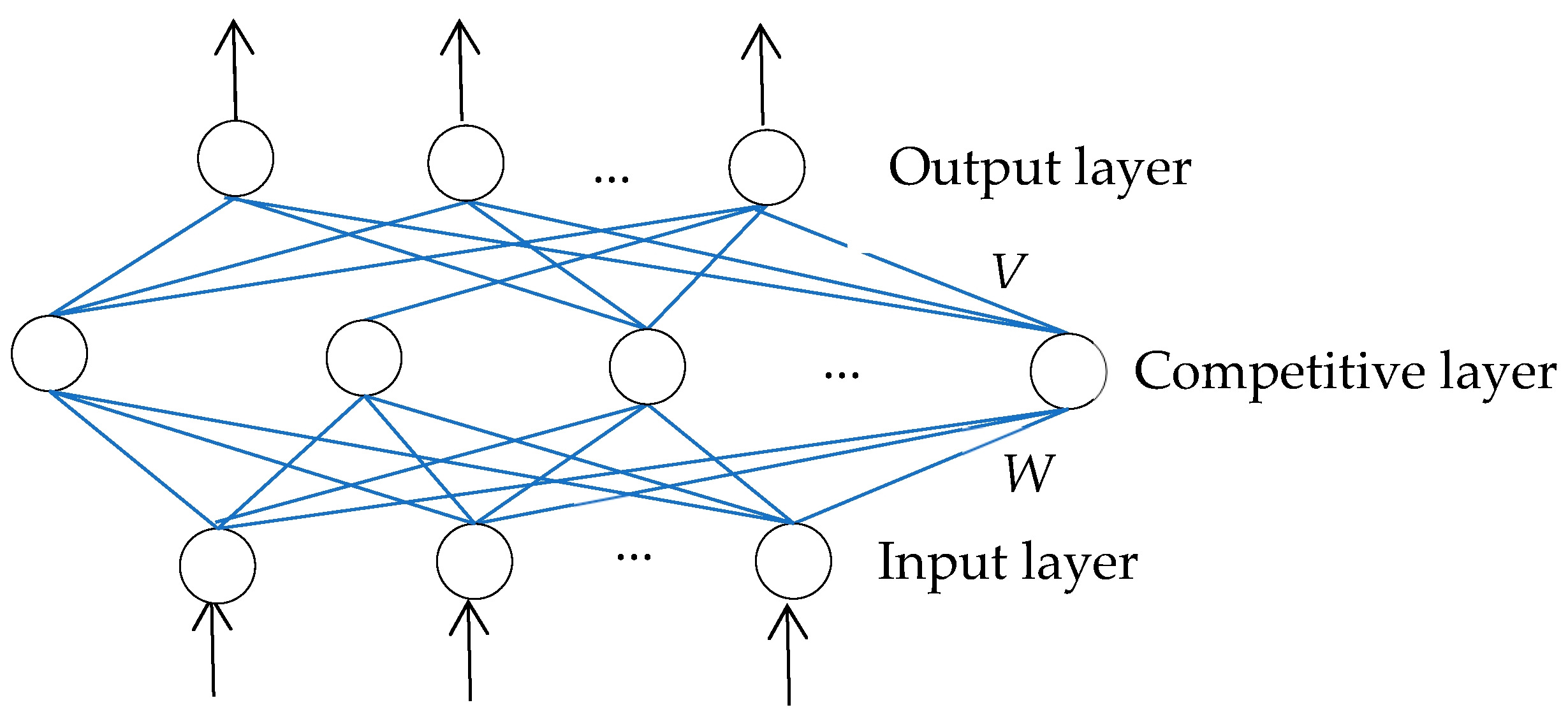
2. Counter-Propagation Network (CPN)
- (1)
- Initialize.
- (2)
- The connection weight vector Wj is normalized as follows:
- (3)
- The input activation value of each neuron in the competitive layer is obtained, namely the sum of weighted input:
- (4)
- Find the vector Wg, which is closest to Ak in the connection weight vector Wj:
- (5)
- Adjust the connection weight vector Wg:where, is the learning rate, 0 < < 1.
- (6)
- The connection weight vector Wg is re-normalized as above, step (3).
- (7)
- Adjusting the connection weight vector Vl from the winning neuron in the competition layer to the neuron in the output layer:where, is learning rate and . According to step (5), Equations (6)–(14) can be simplified as:
- (8)
- The weighted input of each neuron in the output layer is solved and taken as the actual output value of the output neuron; , l = 1, 2, ..., M, can then be reduced to .
- (9)
- Return to step (2) until the p input modes training is complete.
- (10)
- Then t = t + 1, the input mode Ak is re-provided to the network learning and ends when t = T.
3. Structural Damage Identification Methods
3.1. Data Preprocessing
3.2. Fractal Features Extraction
3.3. Revised Counter-Propagation Network (RCPN)
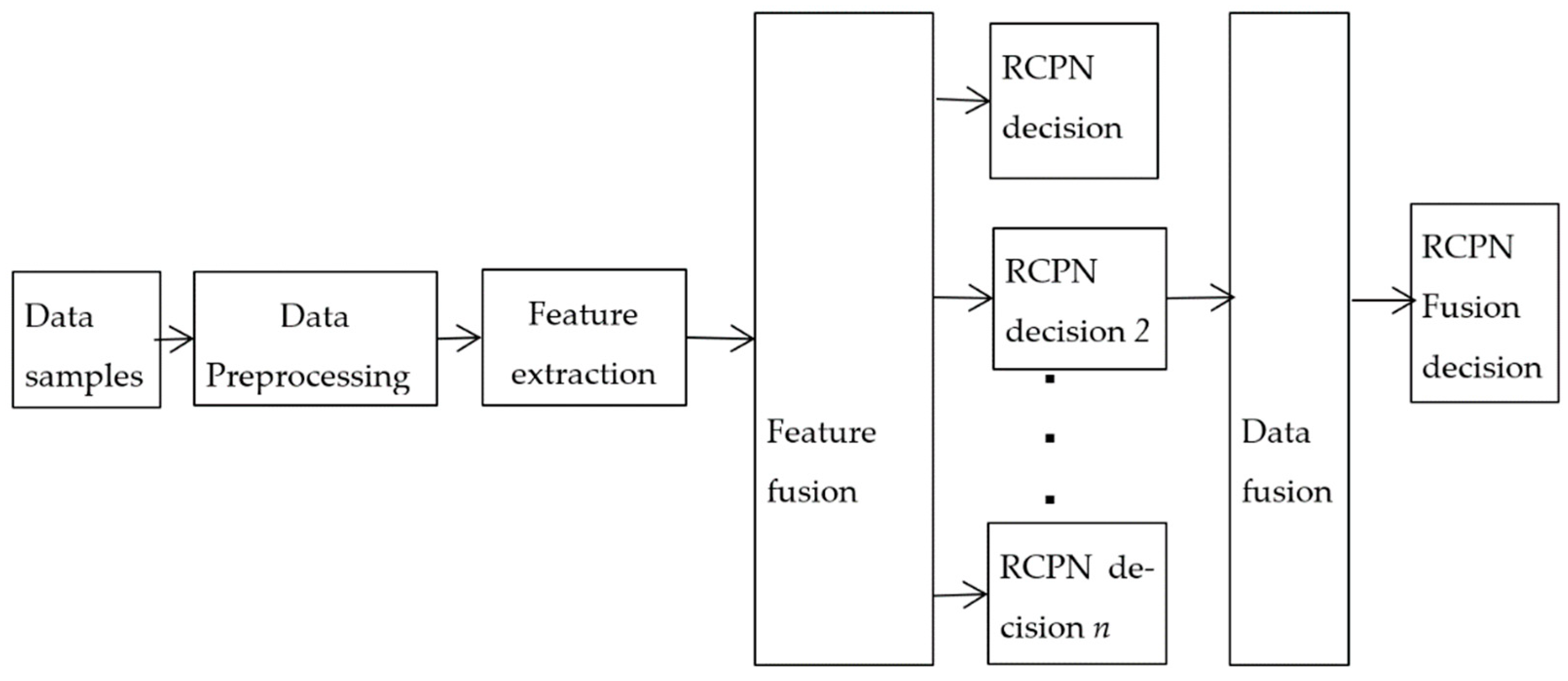
3.4. Fusion Decision and Results Output of RCPN
4. Damage Identification of ASCE Benchmark Structure [41]
4.1. Numerical Model
4.2. Damage Detection Results of Single RCPN Classifier
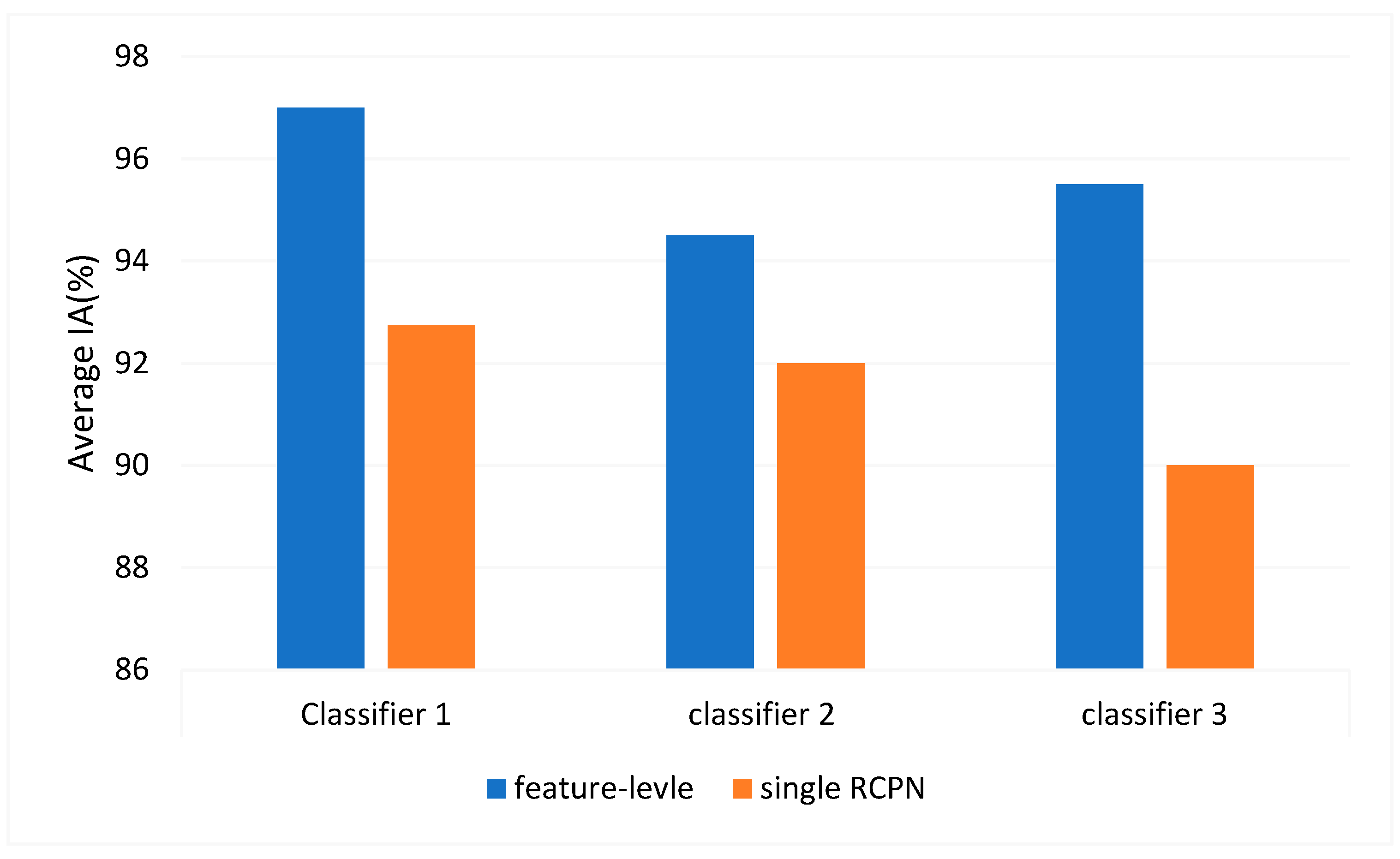
4.3. Damage Detection Results of Feature-Level Fusion Model
4.4. Damage Detection Results of Decision—Level Fusion Model
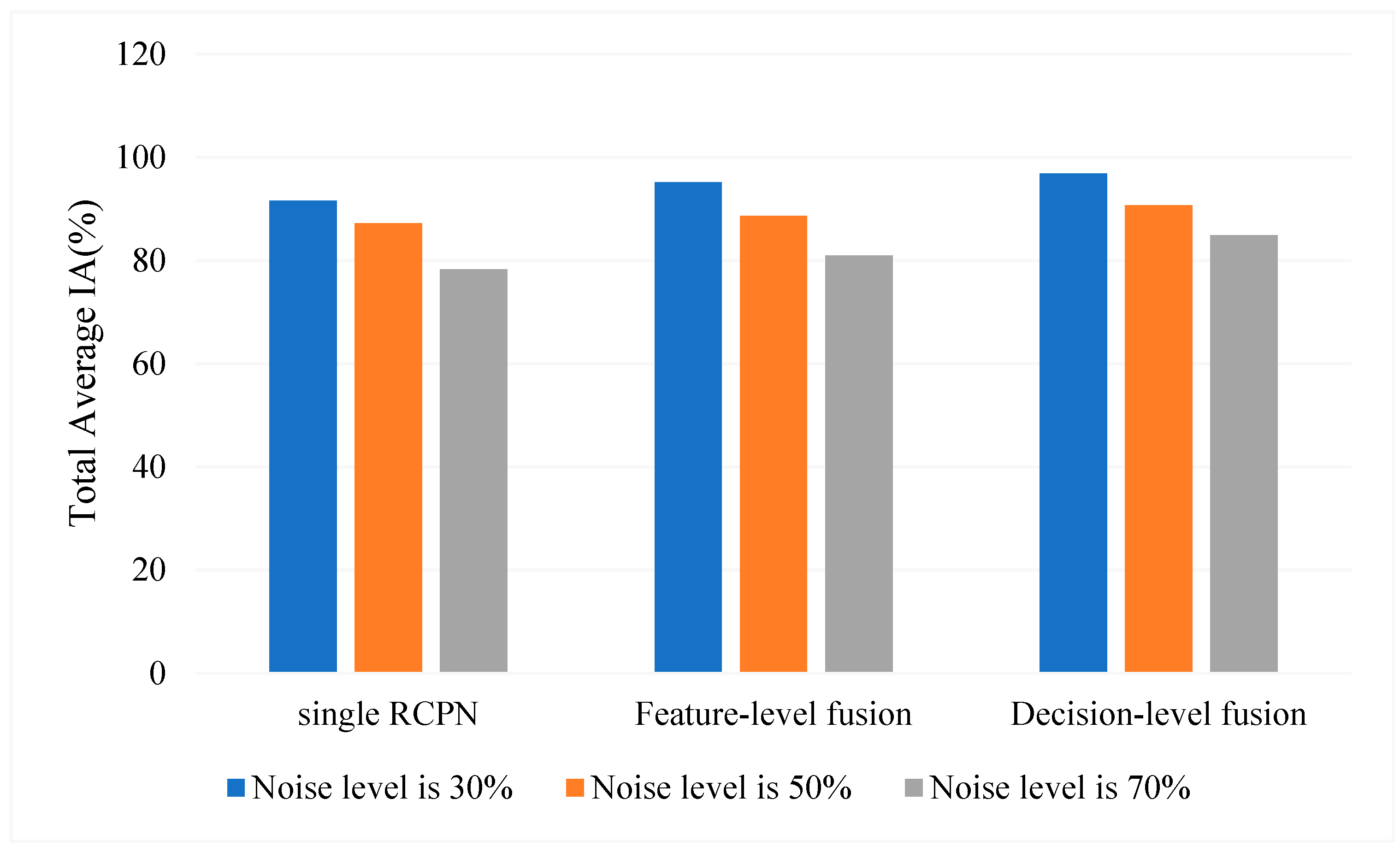
4.5. Comparison and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Tao, T.; Li, A.; Zhang, Y. Structural health monitoring system for Sutong Cable-stayed Bridge. Smart Struct. Syst. 2016, 18, 317–334. [Google Scholar] [CrossRef]
- Liu, T.; Xu, H.; Ragulskis, M.; Cao, M.; Ostachowicz, W. A Data-Driven Damage Identification Framework Based on Transmissibility Function Datasets and One-Dimensional Convolutional Neural Networks: Verification on a Structural Health Monitoring Benchmark Structure. Sensors 2020, 20, 1059. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.M.; Wang, H.; Wan, H.P.; Mao, J.X.; Xu, Y.C. Anomaly detection of structural health monitoring data using the maximum likelihood estimation-based Bayesian dynamic linear model. Struct. Health Monit. 2021, 20, 2936–2952. [Google Scholar] [CrossRef]
- Scianna, A.M.; Christenson, R. Probabilistic Structural Health Monitoring Method Applied to the Bridge Health Monitoring Benchmark Problem. Transport. Res. Rec. 2018, 2131, 92–97. [Google Scholar] [CrossRef]
- Alrasheedi, A.F.; Alnowibet, K.A.; Saxena, A.; Sallam, K.M.; Mohamed, A.W. Chaos Embed Marine Predator (CMPA) Algorithm for Feature Selection. Mathematics 2022, 10, 1411. [Google Scholar] [CrossRef]
- Dessi, D.; Camerlengo, G. Damage identification techniques via modal curvature analysis: Overview and comparison. Mech. Syst. Signal Process. 2015, 52–53, 181–205. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Output-only damage detection using vehicle-induced displacement response and mode shape curvature index. Struct. Control Health Monit. 2016, 23, 1088–1107. [Google Scholar] [CrossRef]
- Stutz, L.; Rangel, I.; Rangel, L.; Corrêa, R.; Knupp, D. Structural damage identification built on a response surface model and the flexibility matrix. J. Sound Vib. 2018, 434, 284–297. [Google Scholar] [CrossRef]
- Ghannadi, P.; Kourehli, S.S. Structural damage detection based on MAC flexibility and frequency using moth-flame algorithm. Struct. Eng. Mech. 2019, 70, 649–659. [Google Scholar]
- Li, Y.; Cheng, L.; Yam, L.; Wong, W.O. Identification of damage locations for plate-like structures using damage sensitive indices: Strain modal approach. Comput. Struct. 2002, 80, 1881–1894. [Google Scholar] [CrossRef]
- Thue Nguyen, Q.; Livaŏglu, R. Modal strain energy based enhanced approaches for damage detection and severity estimation. Eng. Fail. Anal. 2023, 146, 107142. [Google Scholar] [CrossRef]
- Gillich, G.-R.; Praisach, Z.-I. Modal identification and damage detection in beam-like structures using the power spectrum and time–frequency analysis. Signal Process. 2014, 96, 29–44. [Google Scholar] [CrossRef]
- Yu, Z.; Xia, H.; Goicolea, J.M.; Xia, C. Bridge Damage Identification from Moving Load Induced Deflection Based on Wavelet Transform and Lipschitz Exponent. Int. J. Struct. Stab. Dyn. 2016, 16, 1550003. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Y.; Luo, Q.; Li, Q. Vibration-based damage identification in composite plates using 3D-DIC and wavelet analysis. Mech. Syst. Signal Process. 2022, 173, 108890. [Google Scholar] [CrossRef]
- Lo Iacono, F.; Navarra, G.; Pirrotta, A. A damage identification procedure based on Hilbert transform: Experimental validation. Struct. Control Health Monit. 2012, 19, 146–160. [Google Scholar] [CrossRef]
- Xiang, H.; Nie, Z.; Gao, R.; Ma, H. Pattern Matching-Based Structural Damage Identification Using Mode Shape Difference Ratio with Limited Sensors. Int. J. Struct. Stab. Dyn. 2023, 1–23, 2350106. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, C.; Guo, B. Transfer-learning guided Bayesian model updating for damage identification considering modeling uncertainty. Mech. Syst. Signal Process. 2021, 166, 108426. [Google Scholar] [CrossRef]
- Shi, B.; Qiao, P. A new surface fractal dimension for displacement mode shape-based damage identification of plate-type structures. Mech. Syst. Signal Process. 2018, 103, 139–161. [Google Scholar] [CrossRef]
- Huang, Y.; Li, H.; Wu, S.; Yang, Y. Fractal dimension based damage identification incorporating multi-task sparse Bayesian learning. Smart Mater. Struct. 2018, 27, 075020. [Google Scholar] [CrossRef]
- Ramezani, M.; Bahar, O. Structural damage identification for elements and connections using an improved genetic algorithm. Smart Struct. Syst. 2021, 28, 643–660. [Google Scholar]
- Ghannadi, P.; Kourehli, S.S.; Mirjalili, S. The Application of PSO in Structural Damage Detection: An Analysis of the Previously Released Publications (2005–2020). Frat. Ed Integrità Strutt. 2022, 16, 460–489. [Google Scholar] [CrossRef]
- Lei, Y.; Zuo, M.J. Gear crack level identification based on weighted K nearest neighbor classification algorithm. Mech. Syst. Signal Process. 2009, 23, 1535–1547. [Google Scholar] [CrossRef]
- Sarmadi, H.; Karamodin, A. A novel anomaly detection method based on adaptive Mahalanobis-squared distance and one-class kNN rule for structural health monitoring under environmental effects. Mech. Syst. Signal Process. 2019, 140, 106495. [Google Scholar] [CrossRef]
- Lei, J.; Cui, Y.; Shi, W. Structural damage identification method based on vibration statistical indicators and support vector machine. Adv. Struct. Eng. 2022, 25, 1310–1322. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, B.; Zhu, X.; Li, S. Damaged cable identification in cable-stayed bridge from bridge deck strain measurements using support vector machine. Adv. Struct. Eng. 2022, 25, 754–771. [Google Scholar] [CrossRef]
- Rabiej, M.; Rabiej, S. Application of the artificial neural network for identification of polymers based on their X-ray diffraction curves. Comput. Mater. Sci. 2020, 186, 110042. [Google Scholar] [CrossRef]
- Ye, L.; Su, Z.; Yang, C.; He, Z.; Wang, X. Hierarchical development of training database for artificial neural network-based damage identification. Compos. Struct. 2006, 76, 224–233. [Google Scholar] [CrossRef]
- González-Pérez, C.A.; González, J.V. Identification of Structural Damage in a Vehicular Bridge using Artificial Neural Networks. Struct. Health Monit. 2010, 10, 33–48. [Google Scholar] [CrossRef]
- Li, J.; Dackermann, U.; Xu, Y.-L.; Samali, B. Damage identification in civil engineering structures utilizing PCA-compressed residual frequency response functions and neural network ensembles. Struct. Control Health Monit. 2015, 18, 207–226. [Google Scholar] [CrossRef]
- Gu, J.; Gul, M.; Wu, X. Damage detection under varying temperature using artificial neural networks. Struct. Control. Health Monit. 2017, 24, e1998. [Google Scholar] [CrossRef]
- Aziz, R.M.; Mahto, R.; Goel, K.; Das, A.; Kumar, P.; Saxena, A. Modified Genetic Algorithm with Deep Learning for Fraud Transactions of Ethereum Smart Contract. Appl. Sci. 2023, 13, 697. [Google Scholar] [CrossRef]
- Sony, S.; Gamage, S.; Sadhu, A.; Samarabandu, J. Multiclass Damage Identification in a Full-Scale Bridge Using Optimally Tuned One-Dimensional Convolutional Neural Network. J. Comput. Civ. Eng. 2022, 36, 04021035. [Google Scholar] [CrossRef]
- Li, D.; Liang, Z.-L.; Ren, W.-X.; Yang, D.; Wang, S.-D.; Xiang, S.-L. Structural damage identification under nonstationary excitations through recurrence plot and multi-label convolutional neural network. Measurement 2021, 186, 110101. [Google Scholar] [CrossRef]
- Puruncajas, B.; Vidal, Y.; Tutivén, C. Vibration-Response-Only Structural Health Monitoring for Offshore Wind Turbine Jacket Foundations via Convolutional Neural Networks. Sensors 2020, 20, 3429. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, S.; Singh, R.K.; Singh, U.P.; Jain, S. Biogeography particle swarm optimization based counter propagation network for sketch based face recognition. Multimedia Tools Appl. 2018, 78, 9801–9825. [Google Scholar] [CrossRef]
- Jiang, S.F.; Lin, J. Structural damage identification based on rough set and revised counter-propagation network. J. Vib. Shock 2011, 30, 1–645. [Google Scholar]
- Zhou, L.; Sun, H.; He, Z. Fractal dimension-based damage imaging for composites. Shock Vib. 2013, 20, 164539. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, C.; Zhang, T.; Wang, N.; Chen, L.; Jie, G. Acoustic emission fractal characteristics analysis of steel fiber reinforced concrete during uniaxial tensile damage. Mater. Test. 2020, 62, 329–336. [Google Scholar] [CrossRef]
- Woods, J.E.; Yang, Y.-S.; Chen, P.-C.; Lau, D.T.; Erochko, J. Automated Crack Detection and Damage Index Calculation for RC Structures Using Image Analysis and Fractal Dimension. J. Struct. Eng. 2021, 147, 04021019. [Google Scholar] [CrossRef]
- Rolo, A. A method for the correlation dimension estimation for on-line condition monitoring of large rotating machinery. Mech. Syst. Signal Process. 2005, 19, 939–954. [Google Scholar] [CrossRef]
- Johnson, E.A.; Lam, H.F.; Katafygiotis, L.S.; Beck, J.L. Phase I IASC-ASCE Structural Health Monitoring Benchmark Problem Using Simulated Data. J. Eng. Mech. 2004, 130, 3–15. [Google Scholar] [CrossRef]



| Damage Pattern | Damage Simulation |
|---|---|
| 1 | Remove all support from the first layer |
| 2 | Remove all supports from Layers 1 and 3 |
| 3 | Remove 1 brace from 1st layer |
| 4 | Remove 1 brace each from the 1st and 3rd layers |
| Noise Level ε (%) | Classifier | IA of Damage Patterns (%) | Average IA(%) | Total Average IA (%) | |||
|---|---|---|---|---|---|---|---|
| Pattern 1 | Pattern 2 | Pattern 3 | Pattern 4 | ||||
| 30 | NC1 | 96 | 94 | 91 | 90 | 92.75 | 91.6 |
| NC2 | 91 | 95 | 89 | 93 | 92 | ||
| NC3 | 94 | 91 | 83 | 88 | 90 | ||
| 50 | NC1 | 93 | 89 | 85 | 81 | 87 | 87.25 |
| NC2 | 90 | 95 | 80 | 82 | 86.75 | ||
| NC3 | 89 | 91 | 84 | 88 | 88 | ||
| 70 | NC1 | 83 | 85 | 71 | 73 | 78 | 78.3 |
| NC2 | 81 | 87 | 74 | 71 | 78.25 | ||
| NC3 | 82 | 85 | 73 | 75 | 78.75 | ||
| Noise Level ε (%) | Feature-Level Fusion Methods | IA of Damage Patterns (%) | Average IA(%) | Total Average IA (%) | |||
|---|---|---|---|---|---|---|---|
| Pattern 1 | Pattern 2 | Pattern 3 | Pattern 4 | ||||
| 30 | Classifier 1 (NC1 + NC2) | 99 | 99 | 97 | 96 | 97 | 95.2 |
| Classifier 2 (NC2 + NC3) | 97 | 97 | 91 | 93 | 94.5 | ||
| Classifier 3 (NC1+NC3) | 98 | 96 | 94 | 94 | 95.5 | ||
| Classifier 4 (NC1 + NC2 + NC3) | 96 | 98 | 91 | 90 | 93.75 | ||
| 50 | Classifier 1 (NC1 + NC2) | 94 | 97 | 82 | 81 | 88.5 | 88.7 |
| Classifier 2 (NC2 + NC3) | 96 | 92 | 80 | 82 | 87.5 | ||
| Classifier 3 (NC1 + NC3) | 95 | 95 | 85 | 87 | 90.5 | ||
| Classifier 4 (NC1 + NC2 + NC3) | 93 | 94 | 81 | 85 | 88.25 | ||
| 70 | Classifier 1 (NC1 + NC2) | 87 | 85 | 76 | 75 | 80.75 | 81.0 |
| Classifier 2 (NC2 + NC3) | 87 | 89 | 75 | 74 | 81.25 | ||
| Classifier 3 (NC1 + NC3) | 84 | 88 | 76 | 79 | 81.75 | ||
| Classifier 4 (NC1 + NC2 + NC3) | 83 | 86 | 78 | 74 | 80.25 | ||
| Noise Level ε (%) | Decision-Level Fusion Methods | IA of Damage Patterns (%) | Average IA(%) | Total Average IA (%) | |||
|---|---|---|---|---|---|---|---|
| Pattern1 | Pattern2 | Pattern 3 | Pattern4 | ||||
| 30 | 1 (classifier 1 + 2) | 98 | 99 | 97 | 96 | 97.5 | 96.9 |
| 2 (classifier 2 + 3) | 99 | 98 | 96 | 95 | 97 | ||
| 3 (classifier 1 + 2 + 3) | 98 | 97 | 95 | 95 | 96.25 | ||
| 50 | 1 (classifier 1 + 2) | 96 | 96 | 84 | 85 | 90.25 | 90.7 |
| 2 (classifier 2 + 3) | 97 | 95 | 86 | 89 | 91.75 | ||
| 3 (classifier 1 + 2 + 3) | 96 | 95 | 84 | 85 | 90 | ||
| 70 | 1 (classifier 1 + 2) | 90 | 92 | 78 | 80 | 85 | 84.9 |
| 2 (classifier 2 + 3) | 91 | 91 | 79 | 82 | 85.75 | ||
| 3 (classifier 1 + 2 + 3) | 89 | 90 | 78 | 79 | 84 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Li, M. Data Fusion-Based Structural Damage Identification Approach Integrating Fractal and RCPN. Appl. Sci. 2023, 13, 5289. https://doi.org/10.3390/app13095289
Fu C, Li M. Data Fusion-Based Structural Damage Identification Approach Integrating Fractal and RCPN. Applied Sciences. 2023; 13(9):5289. https://doi.org/10.3390/app13095289
Chicago/Turabian StyleFu, Chun, and Ming Li. 2023. "Data Fusion-Based Structural Damage Identification Approach Integrating Fractal and RCPN" Applied Sciences 13, no. 9: 5289. https://doi.org/10.3390/app13095289
APA StyleFu, C., & Li, M. (2023). Data Fusion-Based Structural Damage Identification Approach Integrating Fractal and RCPN. Applied Sciences, 13(9), 5289. https://doi.org/10.3390/app13095289





