Optimization of Damping in a Semi-Active Car Suspension System with Various Locations of Masses
Abstract
1. Introduction
2. Methods
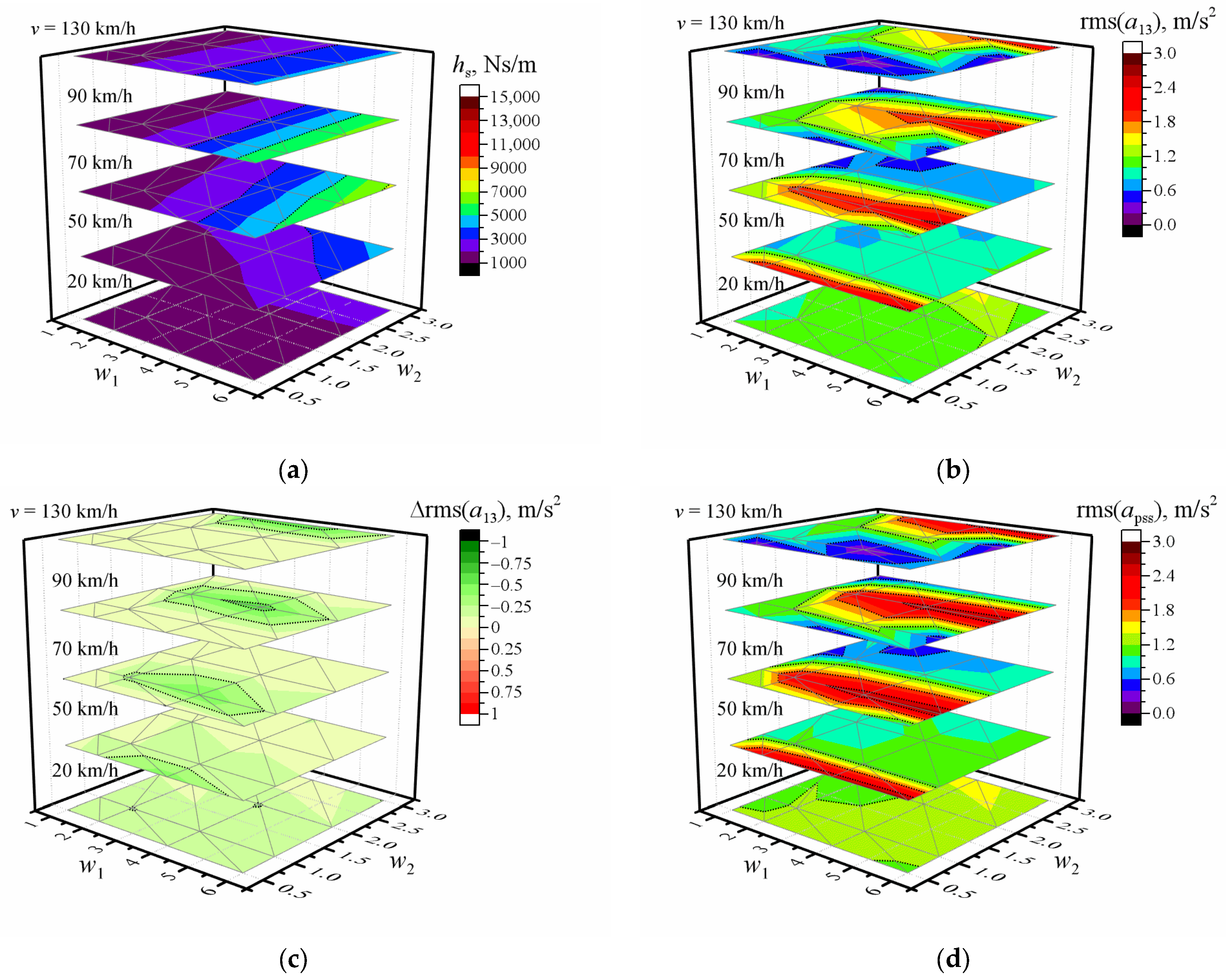
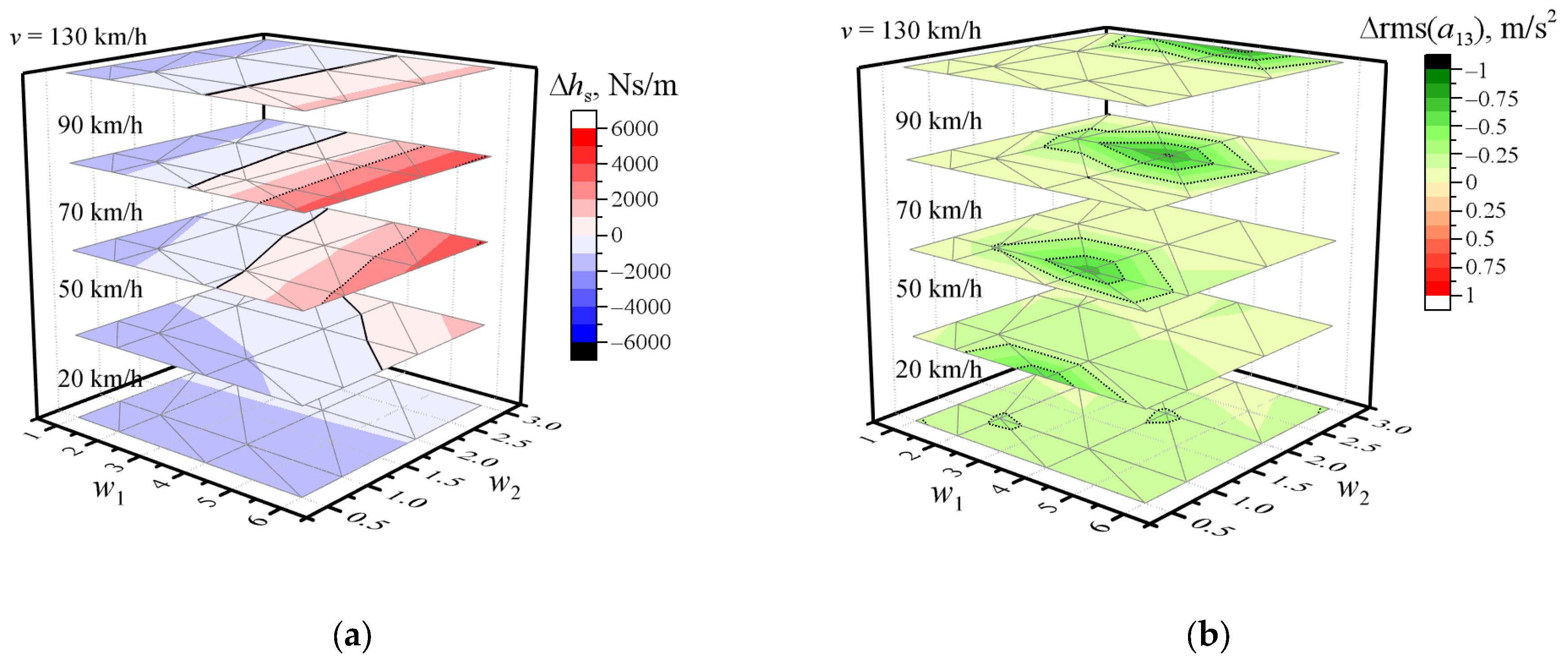
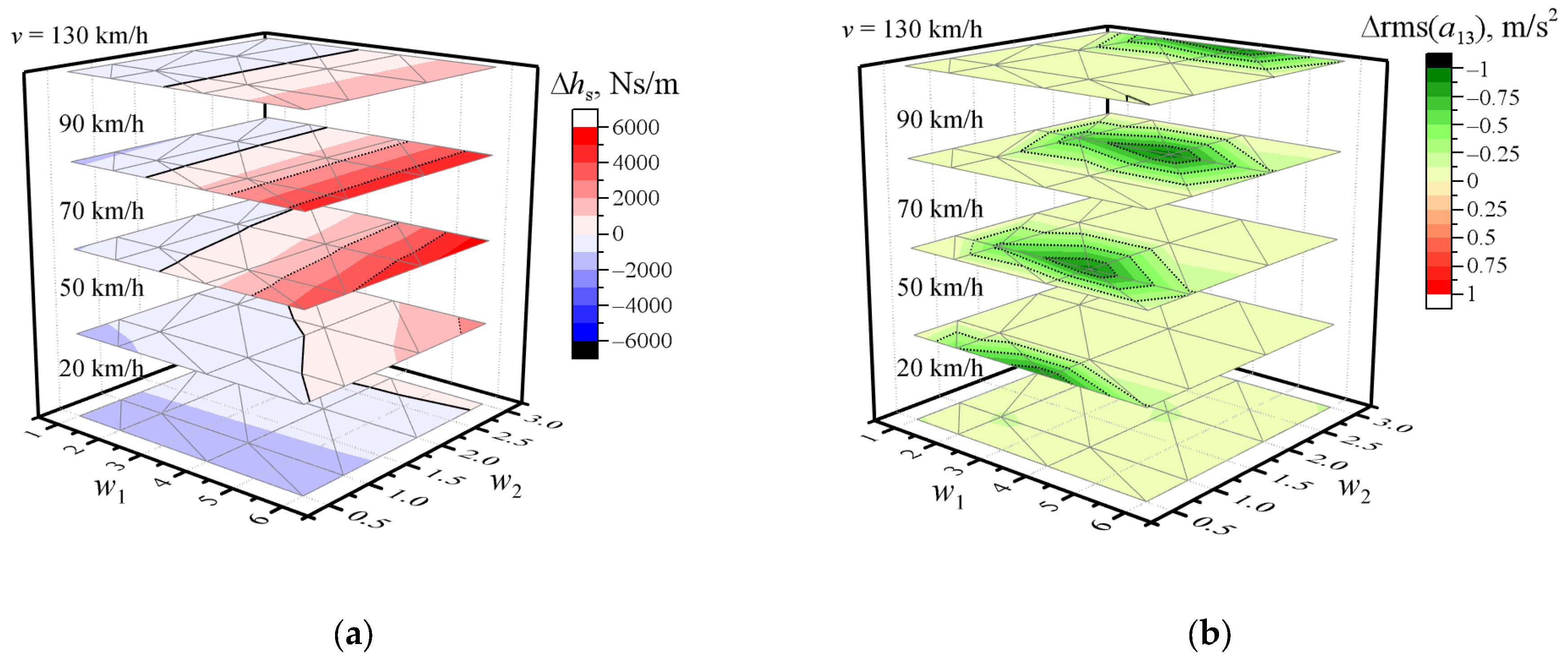
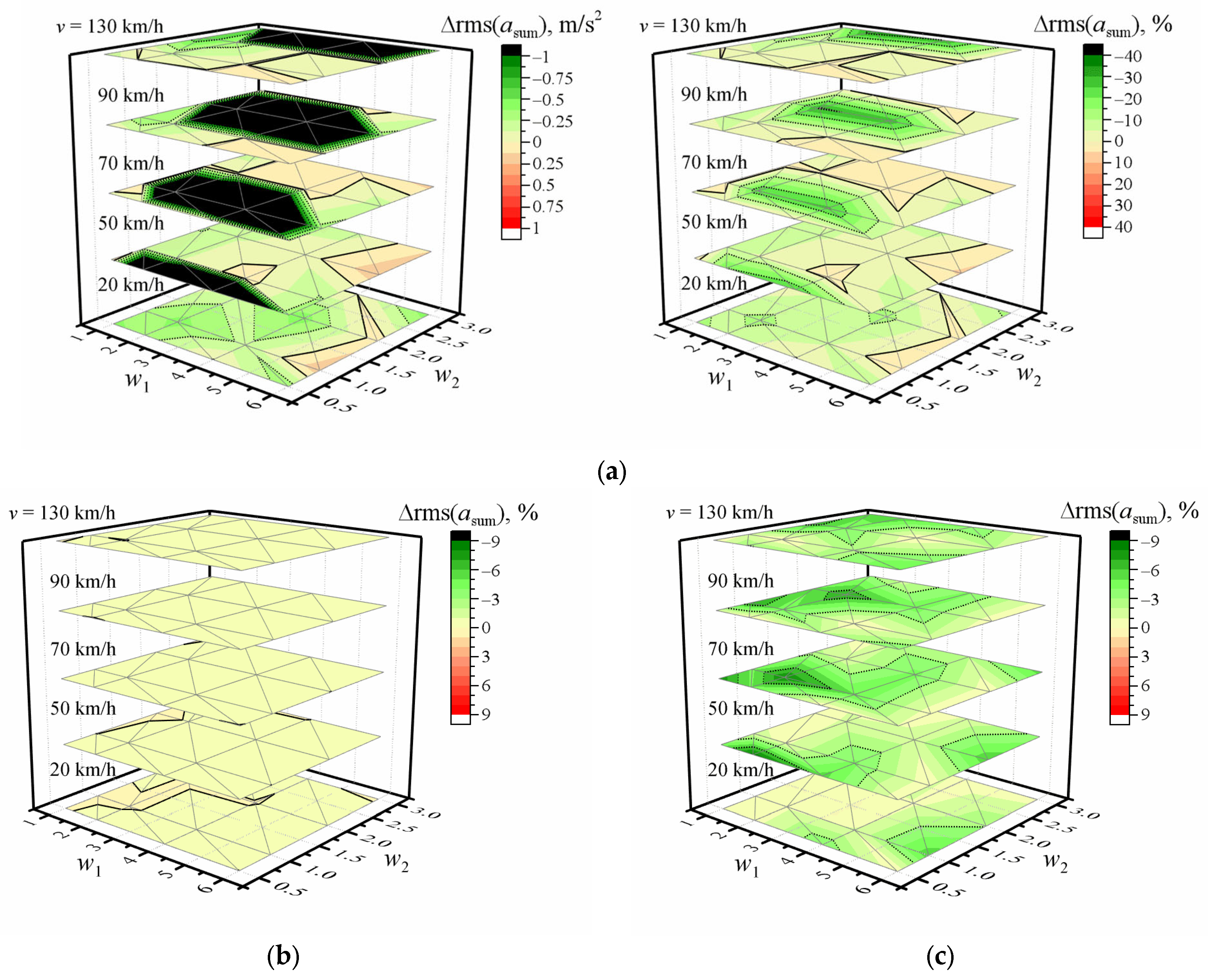
3. Results and Discussion
- When fixed waviness index = w1:
- Higher damping values are needed, increasing values of w2 at low speed (differences amount to several hundreds);
- This difference decreases with increasing speed (down to several tens);
- Higher w1 values significantly increase damping values when the speed is more than 50 km/h;
- It reaches the maximum when w1 = 6 and the speed is 70 km/h or 90 km/h.
- When fixed waviness index = w2:
- The differences of damping amount to several tens at 20 km/h speed;
- This difference increases with increasing speed and reaches the maximum at 70 km/h or 90 km/h speed.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Múčka, P.; Gagnon, L. Influence of tyre–road contact model on vehicle vibration response. Veh. Syst. Dyn. 2015, 53, 1227–1246. [Google Scholar] [CrossRef]
- Karnopp, D.; Crosby, M.J.; Harwood, R.A. Vibration Control Using Semi-Active Force Generators. J. Eng. Ind. 1974, 96, 619–626. [Google Scholar] [CrossRef]
- Sharp, R.S.; Crolla, D.A. Road Vehicle Suspension System Design—A review. Veh. Syst. Dyn. 1987, 16, 167–192. [Google Scholar] [CrossRef]
- Ma, X.; Wong, P.K.; Zhao, J. Practical multi-objective control for automotive semi-active suspension system with nonlinear hydraulic adjustable damper. Mech. Syst. Signal Process. 2019, 117, 667–688. [Google Scholar] [CrossRef]
- Savaresi, S.M.; Poussot-Vassal, C.; Spelta, C.; Sename, O.; Dugard, L. Chapter 2—Semi-Active Suspension Technologies and Models. In Semi-Active Suspension Control Design for Vehicles; Savaresi, S.M., Poussot-Vassal, C., Spelta, C., Sename, O., Dugard, L., Eds.; Butterworth-Heinemann: Boston, MA, USA, 2010; pp. 15–39. ISBN 978-0-08-096678-6. [Google Scholar]
- Soliman, A.; Kaldas, M. Semi-active suspension systems from research to mass-market—A review. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1005–1023. [Google Scholar] [CrossRef]
- Ride Performance Innovation, Accelerated SM Electronic Damper Technologies. Available online: https://www.tenneco.com/assets/1/7/5498-Electronic_Damper_Technologies-9.8.pdf (accessed on 3 January 2023).
- Bedük, M.D.; Çalışkan, K.; Henze, R.; Küçükay, F. Advanced parameter analysis for damper influence on ride dynamics. J. Vib. Control 2018, 24, 1393–1411. [Google Scholar] [CrossRef]
- Mavroudakis, B.; Eberhard, P. Mode Decoupling Vehicle Suspension System Applied to a Race Car. In III European Conference on Computational Mechanics: Solids, Structures and Coupled Problems in Engineering: Book of Abstracts; Springer: Berlin/Heidelberg, Germany, 2006; p. 771. [Google Scholar] [CrossRef]
- Els, P.S.; Theron, N.J.; Uys, P.E.; Thoresson, M.J. The ride comfort vs. handling compromise for off-road vehicles. J. Terramechanics 2007, 44, 303–317. [Google Scholar] [CrossRef]
- Morales, A.L.; Nieto, A.J.; Chicharro, J.M.; Pintado, P. A semi-active vehicle suspension based on pneumatic springs and magnetorheological dampers. J. Vib. Control 2018, 24, 808–821. [Google Scholar] [CrossRef]
- Nieto, A.J.; Morales, A.L.; Chicharro, J.M.; Pintado, P. An adaptive pneumatic suspension system for improving ride comfort and handling. J. Vib. Control 2016, 22, 1492–1503. [Google Scholar] [CrossRef]
- Hać, A. Optimal Linear Preview Control of Active Vehicle Suspension. Veh. Syst. Dyn. 1992, 21, 167–195. [Google Scholar] [CrossRef]
- Barak, P. Passive Versus Active and Semi-Active Suspension from Theory to Application in North American Industry; SAE Technical Paper 922140; SAE International: Warrendale, PA, USA, 1992. [Google Scholar] [CrossRef]
- Ballo, I. Comparison of the properties of active and semiactive suspension. Veh. Syst. Dyn. 2007, 45, 1065–1073. [Google Scholar] [CrossRef]
- Lajqi, S.; Pehan, S. Designs and optimizations of active and semi-active non-linear suspension systems for a terrain vehicle. Stroj. Vestn. J. Mech. Eng. 2012, 58, 732–743. [Google Scholar] [CrossRef]
- Youn, I.; Hać, A. Semi-active suspensions with adaptive capability. J. Sound Vib. 1995, 180, 475–492. [Google Scholar] [CrossRef]
- Wu, T.H.; Lan, C.C. A wide-range variable stiffness mechanism for semi-active vibration systems. J. Sound Vib. 2016, 363, 18–32. [Google Scholar] [CrossRef]
- Tchamna, R.; Lee, M.; Youn, I. Attitude control of full vehicle using variable stiffness suspension control. Optim. Control Appl. Methods 2015, 36, 936–952. [Google Scholar] [CrossRef]
- Spelta, C.; Previdi, F.; Savaresi, S.M.; Bolzern, P.; Cutini, M.; Bisaglia, C.; Bertinotti, S.A. Performance analysis of semi-active suspensions with control of variable damping and stiffness. Veh. Syst. Dyn. 2011, 49, 237–256. [Google Scholar] [CrossRef]
- Jayachandran, R.; Krishnapillai, S. Modeling and optimization of passive and semi-active suspension systems for passenger cars to improve ride comfort and isolate engine vibration. J. Vib. Control 2013, 19, 1471–1479. [Google Scholar] [CrossRef]
- Huang, H.; Sun, S.; Chen, S.; Li, W. Numerical and experimental studies on a new variable stiffness and damping magnetorheological fluid damper. J. Intell. Mater. Syst. Struct. 2019, 30, 1639–1652. [Google Scholar] [CrossRef]
- Kumar, J.; Bhushan, G. Dynamic analysis of quarter car model with semi-active suspension based on combination of magneto-rheological materials. Int. J. Dyn. Control 2023, 11, 482–490. [Google Scholar] [CrossRef]
- Savaresi, S.; Poussot-Vassal, C.; Spelta, C.; Sename, O.; Dugard, L. Semi-Active Suspension Control Design for Vehicles; Butterworth-Heinemann: Boston, MA, USA, 2010; ISBN 9780080966786. [Google Scholar]
- Brezas, P.; Smith, M.C.; Hoult, W. A clipped-optimal control algorithm for semi-active vehicle suspensions: Theory and experimental evaluation. Automatica 2015, 53, 188–194. [Google Scholar] [CrossRef]
- Zhao, L.L.; Zhou, C.C.; Yu, Y.W. A research on optimal damping ratio control strategy for semi-active suspension system. Automot. Eng. 2018, 40, 41–47. [Google Scholar]
- Sayers, M.W.; Gillespie, T.D.; Queiroz, C.A.V. International Road Roughness Experiment: A Basis for Establishing a Standard Scale for Road Roughness Measurements; World Bank: Washington, DC, USA, 1986; ISBN 0821305891/9780821305898. [Google Scholar]
- Sayers, M.W.; Karamihas, S.M. The Little Book of Profiling-Basic Information about Measuring and Interpreting Road Profile; Regent of the University of Michigan: New York, NY, USA, 1998. [Google Scholar]
- Loprencipe, G.; Cantisani, G. Unified analysis of road pavement profiles for evaluation of surface characteristics. Mod. Appl. Sci. 2013, 7, 1–14. [Google Scholar] [CrossRef]
- Nguyen, T.; Lechner, B.; Wong, Y.D. Response-based methods to measure road surface irregularity: A state-of-the-art review. Eur. Transp. Res. Rev. 2019, 11, 43. [Google Scholar] [CrossRef]
- Tomizuka, M. “Optimum Linear Preview Control with Application to Vehicle Suspension”—Revisited. J. Dyn. Syst. Meas. Control 1976, 98, 309–315. [Google Scholar] [CrossRef]
- Louam, N.; Wilson, D.A.; Sharp, R.S. Optimal Control of a Vehicle Suspension Incorporating the Time Delay between Front and Rear Wheel Inputs. Veh. Syst. Dyn. 1988, 17, 317–336. [Google Scholar] [CrossRef]
- Louam, N.; Wilson, D.A.; Sharp, R.S. Optimization and Performance Enhancement of Active Suspensions for Automobiles under Preview of the Road. Veh. Syst. Dyn. 1992, 21, 39–63. [Google Scholar] [CrossRef]
- Hrovat, D. Optimal suspension performance for 2-D vehicle models. J. Sound Vib. 1991, 146, 93–110. [Google Scholar] [CrossRef]
- Soliman, A.M.A.; Crolla, D.A. Preview control for a semi-active suspension system. Int. J. Veh. Des. 1996, 17, 384–397. [Google Scholar]
- Sugasawa, F.; Kobayashi, H.; Kakimoto, T.; Shiraishi, Y.; Tateishi, Y. Electronically controlled shock absorber system used as a road sensor which utilizes super sonic waves. SAE Trans. 1985, 94, 15–25. [Google Scholar] [CrossRef]
- Rauh, J.; Ammon, D. System dynamics of electrified vehicles: Some facts, thoughts, and challenges. Veh. Syst. Dyn. 2011, 49, 1005–1020. [Google Scholar] [CrossRef]
- Tseng, H.E.; Hrovat, D. State of the art survey: Active and semi-active suspension control. Veh. Syst. Dyn. 2015, 53, 1034–1062. [Google Scholar] [CrossRef]
- Yang, Z.; Shi, C.; Zheng, Y.; Gu, S. A study on a vehicle semi-active suspension control system based on road elevation identification. PLoS ONE 2022, 17, e0269406. [Google Scholar] [CrossRef] [PubMed]
- Basargan, H.; Mihály, A.; Gáspár, P.; Sename, O. Cloud-based adaptive semi-active suspension control for improving driving comfort and road holding. IFAC Pap. 2022, 55, 89–94. [Google Scholar] [CrossRef]
- Pham, T.P.; Sename, O.; Tho Phan, C.; Bao Tran, G.Q. H∞ Observer for Road Profile Estimation in an Automotive Semi-active Suspension System Using Two Accelerometers. In Proceedings of 10th International Conference on Mechatronics and Control Engineering; Springer: Singapore, 2023; pp. 121–134. [Google Scholar] [CrossRef]
- Van Quynh, L.; Van Cuong, B.; Tan, H.A.; Huan, C.C. Modified Skyhook Control for Semi-active Electric Vehicle Suspension. In Proceedings of the Advances in Engineering Research and Application; Nguyen, D.C., Vu, N.P., Long, B.T., Puta, H., Sattler, K.-U., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 839–845. [Google Scholar]
- Jana, D.; Nagarajaiah, S. Data-driven full-field vibration response estimation from limited measurements in real-time using dictionary learning and compressive sensing. Eng. Struct. 2023, 275, 115280. [Google Scholar] [CrossRef]
- Lenkutis, T.; Viržonis, D.; Čerškus, A.; Dzedzickis, A.; Šešok, N.; Bučinskas, V. An Automotive Ferrofluidic Electromagnetic System for Energy Harvesting and Adaptive Damping. Sensors 2022, 22, 1195. [Google Scholar] [CrossRef]
- Lenkutis, T.; Čerškus, A.; Sitiajev, N.E.; Dumbrava, K.; Staugaitė, I.; Šešok, N.; Dzedzickis, A.; Bučinskas, V. Extraction of information from a PSD for the control of vehicle suspension. In Automation 2021: Recent Achievements in Automation, Robotics and Measurement Techniques; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Čerškus, A.; Lenkutis, T.; Šešok, N.; Dzedzickis, A.; Viržonis, D.; Bučinskas, V. Identification of road profile parameters from vehicle suspension dynamics for control of damping. Symmetry 2021, 13, 1149. [Google Scholar] [CrossRef]
- Turnip, A.; Hong, K.S. Road-frequency based optimisation of damping coefficients for semi-active suspension systems. Int. J. Veh. Des. 2013, 63, 84–101. [Google Scholar] [CrossRef]
- Lozia, Z. The use of a linear quarter-car model to optimize the damping in a passive automotive suspension system—A follow-on from many authors’ works of the recent 40 years. Arch. Motoryz. 2016, 71, 39–71. [Google Scholar] [CrossRef]
- Lozia, Z.; Zdanowicz, P. Optimization of damping in the passive automotive suspension system with using two quarter-car models. IOP Conf. Ser. Mater. Sci. Eng. 2016, 148, 012014. [Google Scholar] [CrossRef]
- Verros, G.; Natsiavas, S.; Papadimitriou, C. Design optimization of quarter-car models with passive and semi-active suspensions under random road excitation. JVC/J. Vib. Control 2005, 11, 581–606. [Google Scholar] [CrossRef]
- Marzbanrad, J.; Poozesh, P.; Damroodi, M. Improving vehicle ride comfort using an active and semi-active controller in a half-car model. JVC/J. Vib. Control 2013, 19, 1357–1377. [Google Scholar] [CrossRef]
- Bouazara, M.; Richard, M.J. An optimization method designed to improve 3-D vehicle comfort and road holding capability through the use of active and semi-active suspensions. Eur. J. Mech. A/Solids 2001, 20, 509–520. [Google Scholar] [CrossRef]
- Koulocheris, D.; Papaioannou, G.; Chrysos, E. A comparison of optimal semi-active suspension systems regarding vehicle ride comfort. IOP Conf. Ser. Mater. Sci. Eng. 2017, 252, 012022. [Google Scholar] [CrossRef]
- Makowski, M. Algorithm for Damping Control in Vehicle Suspension Equipped with Magneto-Rheological Dampers. In Springer Proceedings in Mathematics and Statistics; Springer: New York, NY, USA, 2018; Volume 248, pp. 235–247. ISBN 9783319965970. [Google Scholar]
- Yonglin, Z.; Jiafan, Z. Numerical simulation of stochastic road process using white noise filtration. Mech. Syst. Signal Process. 2006, 20, 363–372. [Google Scholar] [CrossRef]
- Shinozuka, M.; Jan, C.M. Digital simulation of random processes and its applications. J. Sound Vib. 1972, 25, 111–128. [Google Scholar] [CrossRef]
- Sun, L. Simulation of pavement roughness and IRI based on power spectral density. Math. Comput. Simul. 2002, 61, 77–88. [Google Scholar] [CrossRef]
- Ngwangwa, H.M.; Heyns, P.S.; Labuschagne, F.J.J.; Kululanga, G.K. Reconstruction of road defects and road roughness classification using vehicle responses with artificial neural networks simulation. J. Terramechanics 2010, 47, 97–111. [Google Scholar] [CrossRef]
- Agostinacchio, M.; Ciampa, D.; Olita, S. The vibrations induced by surface irregularities in road pavements—A Matlab® approach. Eur. Transp. Res. Rev. 2014, 6, 267–275. [Google Scholar] [CrossRef]
- Dharankar, C.S.; Hada, M.K.; Chandel, S. Numerical generation of road profile through spectral description for simulation of vehicle suspension. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1957–1967. [Google Scholar] [CrossRef]
- Kansake, B.A.; Frimpong, S. Analytical modelling of dump truck tire dynamic response to haul road surface excitations. Int. J. Min. Reclam. Environ. 2020, 34, 1–18. [Google Scholar] [CrossRef]
- ISO 8608:2016. Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data. ISO: London, UK, 2016. Available online: https://www.iso.org/obp/ui/#iso:std:iso:8608:ed-2:v1:en (accessed on 11 March 2021).
- Andrén, P. Power spectral density approximations of longitudinal road profiles. Int. J. Veh. Des. 2006, 40, 2–14. [Google Scholar] [CrossRef]
- Lenkutis, T.; Čerškus, A.; Šešok, N.; Dzedzickis, A.; Bučinskas, V. Road Surface Profile Synthesis: Assessment of Suitability for Simulation. Symmetry 2020, 13, 68. [Google Scholar] [CrossRef]
- Bucinskas, V.; Mitrouchev, P.; Sutinys, E.; Sesok, N.; Iljin, I.; Morkvenaite-Vilkonciene, I. Evaluation of Comfort Level and Harvested Energy in the Vehicle Using Controlled Damping. Energies 2017, 10, 1742. [Google Scholar] [CrossRef]
- Crolla, D.A. Vehicle Dynamics—Theory into Practice. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 1996, 210, 83–94. [Google Scholar] [CrossRef]
- Gobbi, M.; Levi, F.; Mastinu, G. Multi-objective stochastic optimisation of the suspension system of road vehicles. J. Sound Vib. 2006, 298, 1055–1072. [Google Scholar] [CrossRef]
- Ghafouri, J.; Sakhavati, A.; Jovari, R.; Gharehpetian, G.B. PI controller for quarter vehicle active suspension system with optimized gains using PSO algorithm. In Proceedings of the 2nd International Conference on Control, Instrumentation and Automation, Shiraz, Iran, 27–29 December 2011; pp. 379–383. [Google Scholar] [CrossRef]
- Els, P.S.; Uys, P.E.; Snyman, J.A.; Thoresson, M.J. Gradient-based approximation methods applied to the optimal design of vehicle suspension systems using computational models with severe inherent noise. Math. Comput. Model. 2006, 43, 787–801. [Google Scholar] [CrossRef]
- Els, P.S.; Uys, P.E. Investigation of the applicability of the dynamic-Q optimisation algorithm to vehicle suspension design. Math. Comput. Model. 2003, 37, 1029–1046. [Google Scholar] [CrossRef]
- Hrovat, D.; Hubbard, M. A comparison between jerk optimal and acceleration optimal vibration isolation. J. Sound Vib. 1987, 112, 201–210. [Google Scholar] [CrossRef]
- Taghipour, M.; Shahriari, D.; Shahsavari, A. Active Suspension Systems With Optimal Jerk Control. In Proceedings of the ASME 8th Biennial Conference on Engineering Systems Design and Analysis, Torino, Italy, 4–7 July 2006; pp. 359–364. [Google Scholar] [CrossRef]
- ISO 2631-1:1997. Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration—Part 1: General Requirements. ISO: London, UK, 1997. Available online: https://www.iso.org/obp/ui/#iso:std:iso:2631:-1:ed-2:v2:en (accessed on 17 January 2023).
- Wu, J.; Zhou, H.; Liu, Z.; Gu, M. Ride Comfort Optimization via Speed Planning and Preview Semi-Active Suspension Control for Autonomous Vehicles on Uneven Roads. IEEE Trans. Veh. Technol. 2020, 69, 8343–8355. [Google Scholar] [CrossRef]
- Uys, P.E.; Els, P.S.; Thoresson, M. Suspension settings for optimal ride comfort of off-road vehicles travelling on roads with different roughness and speeds. J. Terramechanics 2007, 44, 163–175. [Google Scholar] [CrossRef]
| Road Type | Car Model | Remarks | Refs. |
|---|---|---|---|
| Asphalt, concrete, rough | Quarter-car | Modified skyhook control | [47] |
| Sinusoidal and random road | Full-car (7DOF) | LIDAR and diagonal recurrent neural network control model | [23] |
| ISO class B, C, D | Quarter-car | Optimized damping using three criteria or modified criteria; various speeds | [48,49] |
| Good and poor quality | Quarter-car | Optimized damping and stiffness | [50] |
| Random (max elevation 50 mm) | Full-car (12DOF) | Optimized damping and stiffness; separated engine | [21] |
| Random (standard deviation 10 mm) | Quarter-car | Genetic algorithm | [51] |
| Main road profile | 3D model with driver | Optimized damping and stiffness for passive, semi-active, and active suspensions | [52] |
| Bump 50 mm | Half-car | C-K figures; genetic algorithm; various control methods | [53] |
| hs, Ns/m | |||||
|---|---|---|---|---|---|
| Waviness | 20 km/h | 50 km/h | 70 km/h | 90 km/h | 130 km/h |
| w1 = 1; w2 = 0.5 | 1131 | 1153 | 1141 | 1106 | 1291 |
| w1 = 2; w2 = 0.5 | 1129 | 1191 | 1410 | 1378 | 1658 |
| w1 = 4; w2 = 0.5 | 1122 | 1390 | 2433 | 2687 | 2701 |
| w1 = 6; w2 = 0.5 | 1116 | 1953 | 4729 | 5739 | 4148 |
| w1 = 1; w2 = 1 | 1326 | 1351 | 1280 | 1170 | 1319 |
| w1 = 2; w2 = 1 | 1319 | 1408 | 1598 | 1478 | 1690 |
| w1 = 4; w2 = 1 | 1312 | 1688 | 2735 | 2881 | 2726 |
| w1 = 6; w2 = 1 | 1299 | 2382 | 5267 | 5944 | 4160 |
| w1 = 1; w2 = 2 | 1856 | 1844 | 1581 | 1295 | 1357 |
| w1 = 2; w2 = 2 | 1839 | 1941 | 1973 | 1663 | 1725 |
| w1 = 4; w2 = 2 | 1808 | 2375 | 3324 | 3197 | 2752 |
| w1 = 6; w2 = 2 | 1776 | 3375 | 6297 | 6272 | 4175 |
| w1 = 1; w2 = 3 | 2747 | 2412 | 1858 | 1402 | 1378 |
| w1 = 2; w2 = 3 | 2689 | 2565 | 2317 | 1811 | 1748 |
| w1 = 4; w2 = 3 | 2596 | 3170 | 3867 | 3422 | 2767 |
| w1 = 6; w2 = 3 | 2512 | 4585 | 7280 | 6508 | 4180 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čerškus, A.; Ušinskis, V.; Šešok, N.; Iljin, I.; Bučinskas, V. Optimization of Damping in a Semi-Active Car Suspension System with Various Locations of Masses. Appl. Sci. 2023, 13, 5371. https://doi.org/10.3390/app13095371
Čerškus A, Ušinskis V, Šešok N, Iljin I, Bučinskas V. Optimization of Damping in a Semi-Active Car Suspension System with Various Locations of Masses. Applied Sciences. 2023; 13(9):5371. https://doi.org/10.3390/app13095371
Chicago/Turabian StyleČerškus, Aurimas, Vygantas Ušinskis, Nikolaj Šešok, Igor Iljin, and Vytautas Bučinskas. 2023. "Optimization of Damping in a Semi-Active Car Suspension System with Various Locations of Masses" Applied Sciences 13, no. 9: 5371. https://doi.org/10.3390/app13095371
APA StyleČerškus, A., Ušinskis, V., Šešok, N., Iljin, I., & Bučinskas, V. (2023). Optimization of Damping in a Semi-Active Car Suspension System with Various Locations of Masses. Applied Sciences, 13(9), 5371. https://doi.org/10.3390/app13095371







