Geographical Distribution of Global Radiation and Sunshine Duration over the Island of Cyprus

Abstract

In this work, hourly measurements of global solar irradiances obtained from pyranometers and sunshine duration data using either Kipp & Zonen CSD3 automatic sensors or Campbell–Stokes sunshine recorders were assessed through an extensive quality control procedure and statistical analysis on the measured and derived solar parameters for all the actinometric stations installed in various locations over the island of Cyprus, covering mainly the period 2019–2021. This information is useful for engineers concerning the solar energy capture systems and energy efficiency who can therefore take knowledge of the local radiation levels. Monthly mean hourly values of global radiation and sunshine duration are calculated and shown through isoline diagrams. During June or July, daily global irradiations ranged between 25 MJ/m² and 30 MJ/m², with the lowest occurring in the mountainous locations. On the other hand, in January or December, they ranged between 6.5 MJ/m² and 10.5 MJ/m². The total annual number of hours of sunshine duration ranged between 2500 and 3500, with the lowest values recorded at the mountainous sites. The clearness index and relative sunshine duration were used for the classification of the weather conditions over the island. Furthermore, the interrelationships between the said indices were used for the estimation of global radiation. This work has specifically contributed to the characterization and analysis of hourly and daily solar global radiation. Furthermore, the measurements on the ground level could be compared with satellite observations in order to improve the geographical distribution of global radiation, especially in areas where no measurements exist. The analysis could be also extended for the other shortwave radiation components (Direct, Diffuse and Photosynthetic Active Radiation (PAR)) in order to assess the solar radiation regime over the island.

1. Introduction

Solar radiation is the main source of energy that affects the atmospheric environment [1], climate [2] and ecosystems [3]. The knowledge of the local solar radiation profile is important for the design solar energy systems. Information on solar energy is used in many applications that seek to optimize the capture of solar energy, so that it is possible to reach energy savings and carry out sustainable energy consumption [4,5,6]. Furthermore, solar radiation data are essential for applications in meteorology, agriculture, crop modeling as well as in the health sector [3,7]. Two elements of solar radiation components are the most popular elements registered by weather stations: (i) global irradiance data measured on a horizontal surface and (ii) sunshine duration (SD). The SD is recorded as long the direct normal solar irradiance exceeds the value of 120 W/m². However, the sunshine duration is a parameter of secondary significance in the determination of the climatology at a site, while the prime parameters are temperature, humidity, wind, precipitation, and solar radiation [8,9,10,11]. Nevertheless, sunshine duration is important in estimating solar radiation [11]. Additionally, solar radiation fractions, such as the direct and diffuse fractions to global radiation, are required for several applications. For example, the direct component is a basic input to predict the performances and to design concentrating solar plants [8]. Different models can be found in the literature to estimate these two components.

The solar radiation intensity is affected by the presence of the atmospheric constituents [12,13,14], the variations in the amount and texture of clouds as well as by the Sun-Earth geometry [1]. Therefore, clouds and aerosols are the main factors that play a significant role in determining the solar radiation climate at a site. These factors vary over space and time, causing an analogous variability in solar radiation.

The estimation of global irradiance and the prediction of its components, i.e., direct, diffuse and reflected radiation, has been widely discussed in the literature. Since the pioneer contribution by Liu and Jordan [15], several models and comparative analyses have been presented and discussed. An extensive review of the measurements and modeling of all shortwave radiation components has been given by Badescu [11] and more recently by Wald [16]. Generally, two categories of solar radiation models can be distinguished. In the first category belong models that are based on meteorological data, such as cloudiness, sunshine duration, and turbidity of the atmosphere [17,18,19,20,21]. Details about the computation procedure of the said models are given by Myers [22]. In the second category belong models that use the decomposition method where the global irradiance is split into its direct and diffuse components and are basically based on clearness index and diffuse or direct fractions. In this category, we could classify the models of Orgill and Hollands [23], Erbs et al. [24], Skartveit et al. [25], and Boland et al. [26] could be classified, to mention just some of them. The separation models are still highly popular [27]. They are often described as site-dependent in the literature because they are essentially empirical in nature. The Bolland model was found to perform satisfactorily at different sites of the world. Furthermore, in order to cover wide areas on Earth, satellite observations are supplied [28,29].

The solar radiation climate provides the levels, trends, and frequencies of global radiation and its components. Indicative studies for different parts of the world have been published in the literature. For example, Diabatė et al. [30] presented the solar climate of Africa, while Kambezidis [5] reported the solar climate of Athens. More recently, Kambezidis [2] presented the solar climate and the sky-status climatology of Greece [31]. The first study was based on the hourly values of solar parameters obtained from typical meteorological years (TMYs) for 43 locations in Greece. In his second study, he investigated the sky conditions climatology based on the clearness index (k_t) and diffuse fraction (k_d). For this purpose, he defined the following limits for sky conditions: for clear 0 < k_d < 0.26, for intermediate 0.26 < k_d < 0.78, and for overcast skies 0.78 < k_d < 1. In a recent paper, Kambezidis et al. [32] developed a mathematical method to determine the said limits, using 14 sites from different locations around the world. Another recent study that describes the solar radiation climatology for Camagüey of Cuba was presented by Antuña-Sánchez et al. [33]. Apeh et al. [34] studied the variation of the radiation indices in Alice of South Africa in order to characterize the solar climate of the area.

Regarding Cyprus, an assessment of the solar radiation climate was presented by Jacovides et al. [35], while a number of works were published in the last five years that investigate the statistics of various shortwave and longwave solar radiation components based on measurements at two locations [6,36]. An attempt was made by the project Solargis [37] to present an annual map of the island with respect to the average global and direct horizontal radiation, based mainly on satellite data. However, no such study has been conducted for the whole island using ground surface measurements. Therefore, the present work provides an analysis of the global radiation and sunshine duration as well as the classification of sky types based on clearness index. The measurement sites were classified into four categories according to their elevation and their distance from the coast, i.e., coastal (0–300 m], inland plain (0–300 m], semi-mountainous (300 to 800 m] and mountainous (>800 m) locations. The first objective of this work was to assess the measurements obtained by pyranometers and sunshine duration sensors through an extensive quality control procedure and perform statistical analysis on the measured and derived parameters. This information will be useful to engineers concerned to solar energy capture systems and energy efficiency who can therefore take knowledge of the local radiation levels. Furthermore, global radiation can be used to estimate other radiation components such as UV, Reflected, and PAR radiation [36].

The paper is organized as follows: Section 2 describes the materials and methods that were used to estimate extraterrestrial irradiances, including the quality control procedure that was followed for both hourly and daily values. Section 3 presents a detail statistical analysis of global radiation and the derived radiation indices for both hourly and daily values. The analysis covers the daily variation, the monthly variability, the statistical relationships between global radiation and sunshine duration, as well as the geographical distribution of the relevant parameters through isoline diagrams. Section 4 concludes this paper and provides suggestions for future research.

2. Materials and Methods

Hourly data of global horizontal irradiance (G) were obtained from automatic weather stations located in different parts of the island, covering mainly the period 2019–2021. Most of the pyranometers were supplied by the Kipp & Zonen Company. For the sunshine duration data, Kipp & Zonen CSD3 sunshine duration sensors were used. The sensors faced south with a slope (β) of 35° (local latitude) from the horizontal plane. The sunshine duration sensor, at the same time, measures the direct normal irradiance (B_n) in W/m². The measured normal irradiance is less accurate than the value obtained by pyrhiliometers, which are installed on a solar tracker system. The experimental error of CSD3 recorders for direct normal irradiance ranged between 5% and 10% (Kipp and Zonen, personal communication).

The photosynthetic active radiation was measured by the PAR-LITE Quantum Sensor of Kipp & Zonen company in μmol/s/m² with an experimental error of about 5%. This measurement represents the number of photons between 400 and 700 nm incidents on a square meter per second. The conversion factor of 4.57 μmol/J proposed by McCree [38] was used to convert the Photosynthetic Photon Flux Density (PPFD) into its energy alternative (PAR) in W/m². All sensors were factory calibrated. Additionally, the stations were equipped with air temperature and relative humidity sensors, which are installed at the screen level of 1.2 m above the surface. Also, wind speed and direction are measured at a height of 10 m. The coordinates of the stations, the type of the models of the radiation equipment and their calibration factors, as well as their period of measurements are presented in Table 1a, while the position of the stations is also shown in Figure 1. Table 1b shows the meteorological stations equipped with Campbell–Stokes sunshine recorders operated in different periods. Recently, no stations are operated with this type of sunshine recorder. The stations were classified into coastal, plain (0 to 300 m], semi-mountainous (300 to 800 m], and mountainous (800 to 1750 m). The geographical distribution of the stations was considered satisfactory.

Regarding the climate, Cyprus has an intense Mediterranean climate with the typical seasonal rhythm strongly marked in respect of temperature and rainfall. Hot and dry summers last from mid-May to mid-October and mild, rainy, rather changeable, winters last from November to mid-March, separated by short autumn and spring seasons. Periodically, the island is under the effect of the Saharan Air Layer, which is characterized by high content of mineral dust. Dust conditions are more frequent in spring and autumn, although they are observed in some cases in winter and summer.

The annual mean temperature for Cyprus varies from year to year, from 16.1 °C to 19.7 °C, with an average of 17.5 °C. Daily temperatures during the hottest months of July and August ranged between 30 °C on the central plain and 24 °C on the Troodos Mountains. The average maximum temperatures for these two months ranged between 27 °C in the mountains areas and 38 °C in plain areas. In January, the coolest month, the indicative daily temperature was 10 °C on the central plain and 3 °C on the higher parts of the Troodos Mountains, while the average minimum temperatures were 5 °C and 0 °C, respectively. The mean annual precipitation varied from year to year and from place to place. The lowest mean annual precipitation for Cyprus was 213 mm in 1972–1973 and the highest was 759 mm in 1968–1969. The mean annual precipitation for the period 1961–1990 was 503 mm. The wettest months are normally December, January, and February and the driest are July, August, and September. Statistical analysis of rainfall reveals a decreasing trend of rainfall amounts in the last 30 years.

The annual average daily global radiation was 19.5 MJ/m² for the coastal stations, about 19.0 MJ/m² for the inland plain and semi-mountainous areas, while for the mountainous areas it was about 17.5 MJ/m². The mean annual daily sunshine duration was about 8.8 h in coastal and inland plain areas, while in the mountainous areas it was about 7.5 h. Over the whole summer, six months have an average of 11.5 h of bright sunshine per day, while in winter this was reduced to 5.5 h in the cloudiest months, of December and January.

2.1. Estimation of Global Solar and Extraterrestrial Irradiances on a Horizontal Surface

The irradiance falling on a plain at normal incidence at the top of the atmosphere (G_0n) can be estimated from the following equation [16]:

$$G_{0n}=G_{sc}\ast [1+0.033\ast \cos (360\ast d_n/365)](\mathrm{W}/{\mathrm{m}}^2)$$

(1)

where d_n is the day of the year (1.365) and G_sc is the solar constant (1367 W/m²). Then, the irradiance on a horizontal plain at the top of the atmosphere can be estimated by the following equation:

$$G_0=G_{0n}\ast \cos {\theta }_z=G_{0n}\ast (\cos \varphi \ast \cos \delta \ast \cos \omega +\sin \varphi \ast \sin \delta )(\mathrm{W}/{\mathrm{m}}^2)$$

(2)

where θ_z is the solar zenith angle (SZA), which is given by:

$$\cos {\theta }_z=\cos \varphi \ast \cos \delta \ast \cos \omega +\sin \varphi \ast \sin \delta$$

(3)

ϕ is the latitude of the location, δ is the solar declination angle (deg), and ω is the hour angle (deg). The solar declination and hour angles are estimated by the following equations:

$$\delta =23.45\ast \sin [360\ast (284+d_n)/365]$$

(4)

$$\omega =180\ast (t-12)/12$$

(5)

where t is the hour of the day.

The daily total global irradiation, which is obtained by a horizontal plain at the top of the atmosphere (G_0d), is given by the following equation:

$$G_{0d}=(24\ast 3.6/\pi )\ast G_{0n}\ast [(\cos \varphi \ast \cos \delta \ast \sin {\omega }_s+(\pi \ast {\omega }_s/180)\ast \sin \varphi \ast \sin \delta )](\mathrm{kJ}/{\mathrm{m}}^2)$$

(6)

where ω_s is the sunset hour angle and is given by:

$${\omega }_s={\cos }^{-1}(-\tan \varphi \ast \tan \delta )$$

(7)

The daily values of the radiation components are obtained from the sums of the hourly values. Furthermore, the astronomical day length (S_0d), which is the computed time during which the center of the solar disk is above an altitude of zero degrees (without allowance for atmospheric refraction), is given by:

$$S_{0d}=(1/7.5)\ast {\cos }^{-1}(-\tan \varphi \ast \tan \delta )\left(\mathrm{h}\right)$$

(8)

The clear-sky irradiance was estimated using the Haurwitz [39] model, which is a function of the zenith angle. This model was tested by Ianetz [40] in Israel showing high performance. The equation involved in the said model is shown below:

$$G_c=1098\ast \cos {\theta }_z\ast \exp (-0.057/\cos {\theta }_z)$$

(9)

Almost a similar equation was obtained using the maximum values of global irradiances of the actinometric station of Farmakas:

$$G_c=2170.5\ast {(\cos {\theta }_z)}^{-0.175}\ast \exp (-0.578/\cos {\theta }_z)$$

(10)

The horizontal beam irradiance (B) can be calculated from the normal beam irradiance (B_n) from the following equation [16]:

$$B=B_n\ast \cos {\theta }_z$$

(11)

Then, the hourly diffuse irradiance (D) is the difference of global (G) and direct horizontal irradiance (B):

$$D=G-B$$

(12)

Estimation of Radiation Indices and Classification of the Sky Conditions

For the classification of the sky conditions, we use the clearness index (k_t), which is defined as the ratio of global irradiance (G) to the extraterrestrial irradiance (G₀) both measured on horizontal surfaces:

$$k_t=G/G_0$$

(13)

The upper bound of the k_t ratio is 1, although it can be slightly higher than 1 during partially cloudy conditions, when total irradiance may be enhanced due to the reflection of solar irradiance from the base of the clouds and from the scattering of direct irradiance due to cloud particles. Such periods of enhanced solar irradiance may last from several seconds to some minutes depending on the cloud motion [41].

Four sky categories have been proposed by Pashiardis et al. [6], based on the relation between hourly irradiances of global, direct and diffuse radiation, and the clearness index (k_t), as well as the relative sunshine duration (σ = S_d/S_0d):

Class I: Cloudy: k_t ≤ 0.35 or σ ≤ 0.3

Class II: Partially cloudy with predominance of diffuse component: 0.35 < k_t ≤ 0.55 or 0.3 < σ ≤ 0.6

Class III: Partially cloudy with predominance of direct component: 0.55 < k_t ≤ 0.65 or 0.6 < σ ≤ 0.85

Class IV: Clear sky: k_t > 0.65 or σ > 0.85

For the stations equipped with the CSD3 sunshine sensors, the following radiation indices can be also calculated:

$$k_b=B/G$$

(14)

$$k_d=D/G$$

(15)

2.2. Quality Control Process

2.2.1. Quality Control of Hourly Values

Fingerprint plots demonstrating the variation of each radiation component are used to check for any major problems with the data before testing every single variable. In these plots, the x-axis represents a day in the year and the y-axis represents an hour of the day, with a color scale from blue to red showing the various levels of the presented variables. The graphs of all the stations do not show any major problem with the measurements.

The quality control procedures for the solar irradiances are based on checking whether the measurements are within certain limits, such as physically possible limits (PPL) and extremely rare limits (ERL) as proposed by BSRN network [42]. The PPL process checks extremely large errors in radiation data, while the ERL process identifies cases that exceed the rare limits over very short time periods. The lower bound of the limits is naturally zero, although BSRN suggests −4 W/m² for PPL and −2 W/m² for ERL lower limits of the radiation components. The upper bound of these limits is shown in

Table 2. The upper bounds for the “physically possible” (PPL) and “extremely rare” (ERL) limits as proposed by BSRN group, which are used for checking the radiation parameters.

Parameter	Upper Bound (W/m2)
	PPL	ERL
Global Irradiance (G)	$1.5\ast G_{0n}\ast {(\cos {\theta }_z)}^{1.2}+100$	$1.2\ast G_{0n}\ast {(\cos {\theta }_z)}^{1.2}+50$
Direct Normal Irradiance (Bn)	$G_{0n}$	$0.95\ast G_{0n}\ast {(\cos {\theta }_z)}^{0.2}+10$
Direct Horizontal. Irr (B)	$G_{0n}\ast \cos {\theta }_z$	$0.95\ast G_{0n}\ast {(\cos {\theta }_z)}^{1.2}+10$
Diffuse Irradiance (D)	$0.95\ast G_{0n}\ast {(\cos {\theta }_z)}^{1.2}+50$	$0.75\ast G_{0n}\ast {(\cos {\theta }_z)}^{1.2}+30$

.

The following plot illustrates the various tests outlined in the preceding paragraphs based on the hourly measurements. Figure 2 shows the highest limits of global irradiances as a function of solar zenith angle, at Pentakomo (coastal location). Similar graphs were obtained from the other locations. The analysis shows that all the data are within the proposed limits. Lefkara Dam and Zygi were excluded from the analysis because they did not pass these quality control limits.

The comparison tests were concentrated on the ratios of k_b, k_d, and k_t. The ratio k_b is always lower than 1. The upper bound of the k_d ratio is 1, although it can be slightly higher than 1 (i.e., 1.15). This usually occurs in the morning after sunrise or in the afternoon before sunset when the solar elevation angle is low, and the diffuse irradiance is slightly higher than that of global irradiance due to the cosine effect of the lower sun angles. Therefore, to avoid this problem, cases of diffuse irradiances below 5° of sun elevation angle were excluded from the dataset [43]. Only few observations were considered invalid when low k_d values are associated with low k_t values. This occurs when the sensor was covered with environmental debris.

The step test was based on time consistency, which compares the difference between successive measurements. If the difference exceeds an allowed value, then both observations are flagged as suspects. Estevez et al. [44] proposed the following values for different variables: for hourly global irradiance, the limit was 555 W/m², and for hourly temperature, it was set to 7 °C, while for relative humidity he suggested the value was 45%. The dataset confirmed the limits of the above variables.

Finally, the persistency test was applied to check the variability of the measurements. When a sensor fails, it will often report a constant value. No days have been detected with a constant value.

2.2.2. Quality Control of Daily Values

The quality control process was also extended to the daily sums of global solar irradiation and daily sunshine duration values. Firstly, the daily values of global irradiation (G_d) were checked against the extraterrestrial daily irradiation (G_0d). The daily values of G_d should be lower than G_0d, but they should be higher than the lower limit of $0.03\ast G_{0d}$ during overcast conditions [45]. As can be seen in Figure 3, G_d is lower than the upper limit of G_0d and it is generally higher than the lower limit.

The second test was a comparison test between the extreme values of daily sums of global irradiation and the respective daily sums on clear days. The daily sums should only exceed the clear-sky values with high atmospheric transparency by a small amount, i.e., $G_d<1.1\ast G_{cd}$.

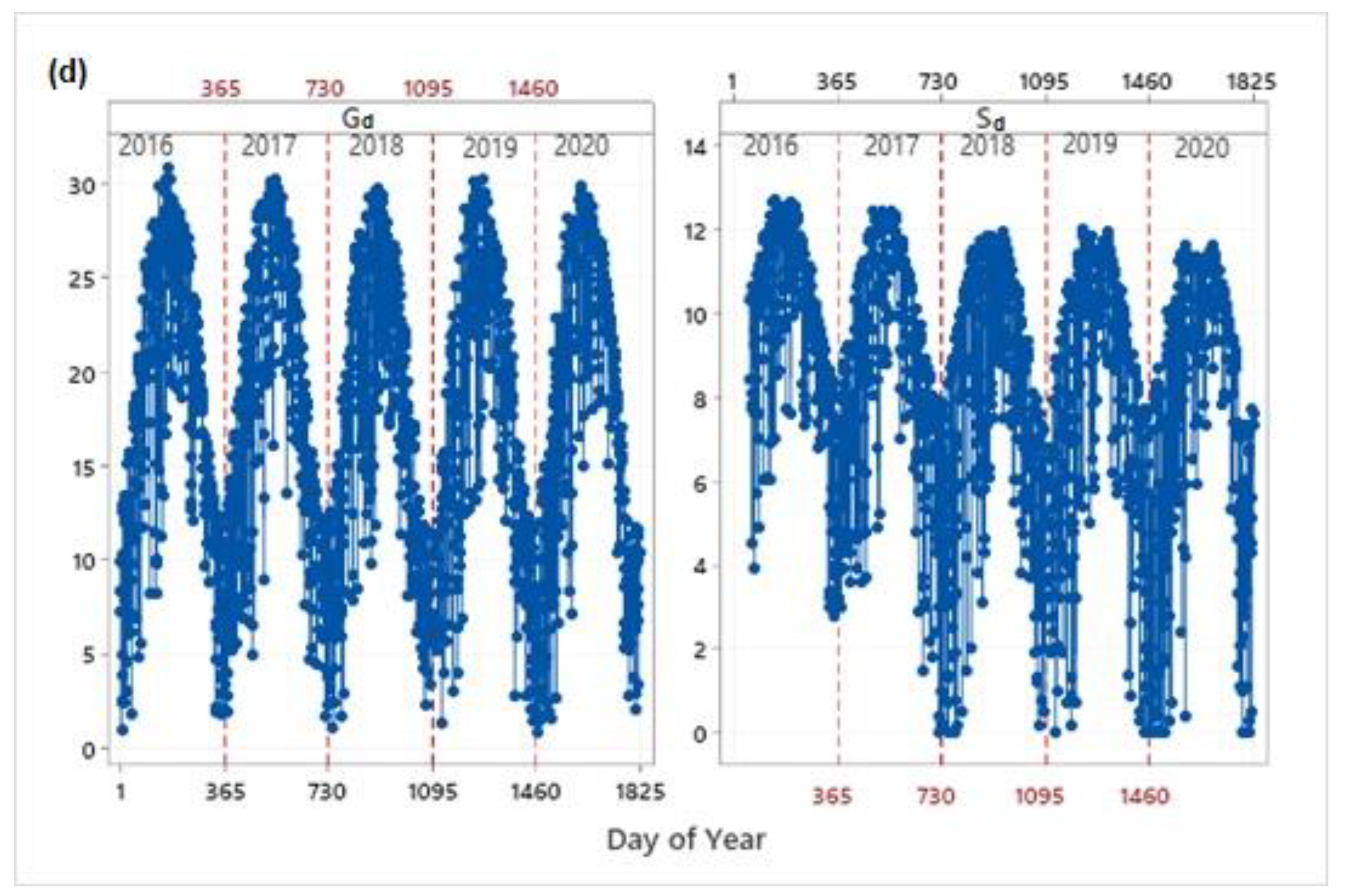
Finally, the daily sums of sunshine duration (S_d) should not exceed the daylength (S_0d) i.e., $S_d<S_{0d}$. All the values passed this test (Figure 4). Similar graphs were obtained from the other locations.

The time series plots of the daily irradiation in MJ/m² and daily sunshine duration for the selected stations are shown in Figure 5. The highest daily global irradiation reached the value of 31.9 MJ/m² at Kambos, while at the rest stations it was slightly below 31 MJ/m². Athalassa recorded the highest daily sunshine duration reaching the value of 13.9 h, while it was lower at the mountainous site reaching the value of 12.7 h.

3. Results and Discussion

3.1. Daily Values

3.1.1. Monthly Mean Daily Global Irradiation and Mean Daily Sunshine Duration

Daily global solar radiation was analyzed and compared in this study. Figure 6 shows the temporal evolution of daily global irradiation at the selected stations. The data revealed a common evolution shape with maxima in summer and minima in winter, due to the daily minimum solar zenith angle and daylength (astronomical factors) variation during the year. Large fluctuations occurred in spring and autumn during the transition from cold to warm weather and vice versa. The lowest values were recorded at Prodromos, which is located at an elevation of 1380 m. The highest differences between the stations were observed during the summer months (about 5 MJ/m²), while during the winter months they were generally lower than 4 MJ/m².

Table 3. Monthly mean daily global irradiation and monthly mean daily values (MJ/m²) in the four seasons of the year for the four groups of stations.

Station/Month	Class	1	2	3	4	5	6	7	8	9	10	11	12	Spring	Summer	Autumn	Winter	Year
Larnaca AP	c	9.4	13.8	18.1	23.4	28.0	29.7	28.7	25.9	21.8	16.7	10.9	9.0	23.2	28.1	16.5	10.7	19.9
Limassol P.	c	9.6	13.8	18.2	23.1	26.8	27.9	27.3	23.9	20.1	15.6	11.2	8.7	22.7	26.4	15.6	10.7	18.9
Limassol H.	c	10.5	12.8	18.2	22.8	26.1	27.7	27.0	24.5	21.8	16.3	12.3	9.3	22.4	26.4	16.8	10.9	19.4
Pafos AP	c	9.3	12.9	18.3	23.5	27.7	29.6	26.3	22.9	22.1	17.0	11.3	8.1	23.1	26.3	16.8	10.1	19.8
Polis	c	8.6	13.8	18.1	23.6	28.3	30.1	29.3	25.8	22.1	16.4	11.6	8.3	23.3	28.4	16.7	10.2	19.7
Pentakomo	c	10.1	13.5	18.0	22.3	27.3	28.4	27.6	24.2	20.2	15.0	11.2	8.8	22.5	26.7	15.5	10.8	18.9
Avdimou	c	9.1	14.0	17.6	22.6	26.7	27.5	27.5	25.5	21.5	16.3	11.3	8.7	22.3	26.9	16.4	10.6	19.2
Mean	c	9.5	13.5	18.1	23.0	27.3	28.7	27.7	24.7	21.4	16.2	11.4	8.7	22.8	27.0	16.3	10.6	19.4
Frenaros	p	9.1	13.4	17.3	22.6	27.3	28.1	28.0	25.2	21.1	15.5	10.7	8.5	22.4	27.1	15.7	10.3	19.4
Mennoyia	p	9.6	13.4	17.6	22.7	24.7	28.1	27.9	25.3	20.8	16.3	11.4	9.0	21.7	27.1	16.2	10.7	19.0
Athalassa	p	9.5	14.3	17.8	22.6	27.7	28.3	28.1	25.7	21.0	15.9	9.6	8.7	22.7	27.4	15.5	10.8	18.3
Mamari	p	8.7	13.6	16.7	24.8	27.3	28.8	28.7	26.2	21.6	16.4	11.2	7.9	22.9	27.9	16.4	10.1	19.4
Mean	p	9.2	13.7	17.3	23.2	26.7	28.3	28.2	25.6	21.1	16.0	10.7	8.5	22.4	27.4	15.9	10.5	19.0
Choulou	sm	8.5	12.3	17.2	21.3	24.5	28.9	28.4	26.1	21.4	16.3	10.9	8.6	21.0	27.8	16.2	9.8	18.7
Mathiatis	sm	9.0	12.2	16.5	20.7	26.5	26.5	27.9	24.7	20.2	15.3	10.7	8.1	21.2	26.4	15.4	9.8	18.4
Kalopanayiotis	sm	7.3	11.2	15.5	20.0	26.3	26.4	27.5	24.5	19.5	14.5	9.7	7.2	20.6	26.1	14.6	8.6	17.5
Xyliatos	sm	9.2	12.0	18.1	22.5	24.7	28.1	29.0	26.5	22.0	15.9	10.7	8.1	21.8	27.9	16.2	9.8	19.2
Mallia	sm	8.9	13.2	16.7	22.0	26.7	28.2	28.0	25.6	21.6	16.2	11.1	8.5	21.8	27.3	16.3	10.2	19.4
Kambos	sm	9.1	12.3	17.3	22.1	27.4	27.7	28.8	25.9	21.9	16.1	12.1	8.7	22.2	27.4	16.7	10.0	20.4
Mean	sm	8.7	12.2	16.9	21.4	26.0	27.6	28.3	25.5	21.1	15.7	10.9	8.2	21.4	27.1	15.9	9.7	18.9
Farmakas	m	7.8	11.1	16.4	21.2	23.9	25.8	27.6	24.3	19.8	14.4	10.1	7.7	20.5	25.9	14.8	8.9	17.5
Kilani	m	7.6	11.8	15.6	20.7	25.6	26.3	26.4	24.2	20.4	15.6	10.9	8.0	20.7	25.6	15.6	9.1	17.8
Agros	m	8.3	11.9	16.9	20.9	22.5	25.1	26.0	23.9	20.4	15.3	10.9	8.1	20.1	25.0	15.6	9.4	17.7
Kyperounda	m	8.5	12.6	16.3	20.6	26.5	25.8	27.5	24.2	20.0	15.2	10.8	8.1	21.1	25.8	15.3	9.7	18.1
Amiantos	m	8.3	11.7	16.3	20.0	25.8	25.7	25.9	23.0	19.8	15.1	10.2	7.7	20.7	24.9	15.1	9.3	17.5
Prodromos	m	6.4	9.9	13.9	18.9	24.7	23.4	23.8	22.4	18.7	14.1	9.5	7.1	19.2	23.2	14.1	7.8	16.2
Mean	m	7.8	11.5	15.9	20.4	24.8	25.3	26.2	23.7	19.8	15.0	10.4	7.8	20.4	25.1	15.1	9.0	17.5

presents the monthly mean daily values in MJ/m² of all the measurement stations. The highest mean daily global solar horizontal irradiation was recorded in June or July and it was almost 29 MJ/m² in the coastal areas and about 28 MJ/m² in inland plain and semi-mountainous areas. In contrast, it was about 26 MJ/m² in the mountainous areas. The geographical distribution of the mean daily global irradiation for the four seasons of the year, as well as for the annual mean daily for the island of Cyprus, is presented in Figure 7. The contour lines on the map were based on the spline method using the ArcGIS software. Spring consisted of the months March, April, and May, while summer comprises June, July, and August. The months in autumn were September, October, and November, while winter consisted of December, January, and February. In winter, the average daily irradiation ranged from 8 MJ/m² (in the mountainous sites) to 11 MJ/m² (in plain and coastal sites). In summer, it ranged from 24 MJ/m² to 28 MJ/m², while the annual daily average ranged from 17 to 20 MJ/m².

Figure 8 shows the monthly mean daily sunshine duration in hours and tents for all stations. The lowest values were recorded in the mountainous stations with an annual average of 7.5 h. The highest differences between the stations were observed during the summer months (about 3 h), while during the winter months they were generally lower than 2 h.

Table 4. Monthly mean daily and seasonal sunshine duration in hours for the four groups of stations.

Station/Month	Elev. (m)	Type	Class	1	2	3	4	5	6	7	8	9	10	11	12	Spring	Summer	Autumn	Winter	Year
Larnaca AP	2	CS	c	5.6	7.2	8.2	10.0	10.8	12.8	13.0	12.2	10.6	8.9	7.2	5.7	9.6	12.7	8.9	6.2	7.4
Pafos AP	8	CS	c	4.6	5.6	7.4	9.2	11.0	11.9	11.2	10.4	10.4	8.5	6.2	4.7	9.2	11.2	8.4	5.0	8.7
Pafos Kato	10	CS	c	6.2	6.9	7.7	8.5	11.1	12.3	12.4	12.0	10.9	9.3	7.7	6.6	9.1	12.2	9.3	6.6	9.3
Polis	22	CSD3	c	4.4	7.3	8.4	10.0	12.2	13.3	13.4	12.5	11.3	9.4	7.0	4.0	10.2	13.0	9.2	5.2	9.4
Akrotiri	23	CS	c	5.1	7.2	8.4	10.3	11.0	13.0	12.7	11.9	10.9	9.0	6.8	4.1	9.9	12.5	8.9	5.5	9.1
Pentakomo	23	CSD3	c	6.3	7.4	8.5	9.9	12.1	12.4	12.6	12.1	11.1	9.6	7.4	5.9	10.2	12.4	9.4	6.6	9.7
Akhelia	45	CS	c	6.0	7.0	7.8	9.5	11.2	12.6	12.6	11.8	10.7	9.0	7.7	5.9	9.5	12.3	9.1	6.3	9.3
Mean			c	5.5	6.9	8.1	9.6	11.3	12.6	12.6	11.8	10.8	9.1	7.2	5.3	9.7	12.3	9.0	5.9	9.0
Xylofagou	49	CS	p	5.7	7.0	8.0	9.3	11.1	12.3	12.3	11.9	10.6	8.8	6.8	5.8	9.5	12.2	8.7	6.1	9.1
Akhna Forest	50	CS	p	6.5	6.7	8.0	9.6	10.5	12.0	12.3	11.8	10.6	8.8	7.1	5.7	9.4	12.0	8.8	6.3	9.1
Avdimou	51	CSD3	p	5.3	6.8	8.1	8.9	10.5	10.9	11.1	10.7	10.5	8.6	7.2	5.6	9.2	10.9	8.8	5.9	8.7
Chrysochou	67	CS	p	5.2	6.0	6.8	8.3	9.8	11.7	12.1	11.2	9.9	8.3	6.4	5.6	8.3	11.6	8.2	5.6	8.4
Evretou	110	CS	p	5.4	6.1	7.7	9.2	10.3	11.7	11.7	11.4	10.4	8.3	6.4	4.9	9.1	11.6	8.4	5.4	8.7
Mennoyia	140	CSD3	p	5.4	6.7	7.8	9.7	10.3	12.2	12.6	11.9	10.3	9.0	7.0	5.8	9.3	12.2	8.8	6.0	9.1
Nicosia	155	CS	p	5.7	6.8	7.2	8.9	10.9	12.6	12.6	12.0	10.1	8.3	6.8	5.6	9.0	12.4	8.4	6.0	9.0
Athalassa	158	CHP1	p	5.1	7.6	7.9	9.0	12.0	12.5	12.8	12.2	10.8	9.0	5.1	5.5	9.6	12.5	8.3	6.1	9.2
Gerolakos	166	CS	p	5.9	6.4	8.1	9.6	10.6	12.1	12.4	11.8	10.3	8.8	7.5	5.5	9.4	12.1	8.9	5.9	9.2
Mean			p	5.6	6.7	7.7	9.2	10.7	12.0	12.2	11.7	10.4	8.7	6.7	5.5	9.2	12.0	8.6	5.9	8.9
Choulou	316	CSD3	sm	4.4	6.0	7.3	8.3	9.9	12.5	12.5	11.6	9.9	8.3	6.4	4.9	8.5	12.2	8.2	5.1	8.5
Mathiatis	395	CSD3	sm	5.4	6.4	7.8	9.2	11.9	12.1	13.0	11.9	10.4	8.2	6.6	5.4	9.6	12.3	8.4	5.7	9.1
Kalopanayiotis	587	CSD3	sm	3.1	4.6	5.8	7.1	9.7	10.0	10.5	9.4	8.0	6.5	4.8	3.5	7.5	10.0	6.4	3.7	6.9
Mallia	633	CSD3	sm	4.8	5.9	7.6	8.4	10.4	11.4	11.9	11.1	10.6	8.0	7.5	5.6	8.8	11.4	8.7	5.4	8.8
Kambos	634	CSD3	sm	5.3	6.3	7.4	9.1	11.5	11.8	12.3	11.7	9.7	8.4	6.5	5.5	9.3	11.9	8.2	5.7	8.8
Saittas	640	CS	sm	4.1	5.9	7.0	8.6	10.1	11.8	11.7	11.2	10.1	8.1	5.6	4.3	8.6	11.5	7.9	4.8	8.2
Mean			sm	4.5	5.8	7.1	8.5	10.6	11.6	12.0	11.1	9.8	7.9	6.2	4.8	8.7	11.6	8.0	5.1	8.4
Farmakas	833	CSD3	m	3.4	4.6	6.4	7.9	8.8	9.5	10.3	9.4	8.1	6.5	4.9	3.9	7.7	9.7	6.5	4.0	7.0
Agros	998	CSD3	m	4.8	5.9	8.0	9.2	9.9	10.5	11.1	10.7	9.6	8.1	6.4	5.1	9.1	10.8	8.0	5.3	8.4
Amiantos	1355	CSD3	m	3.8	4.8	6.3	7.1	9.8	9.8	10.1	8.9	8.3	6.8	5.2	4.1	7.7	9.6	6.7	4.2	7.1
Prodromos	1380	CS	m	4.3	5.2	6.0	7.1	9.1	10.3	10.9	9.6	8.3	6.8	5.6	4.4	7.4	10.3	6.9	4.6	7.6
Mean			m	4.1	5.1	6.7	7.8	9.4	10.0	10.6	9.7	8.6	7.1	5.5	4.3	8.0	10.1	7.0	4.5	7.5

presents the monthly mean daily values in hours and tenths of all the measurement stations. The highest mean daily sunshine duration was recorded in June or July, and it was almost 12.5 h in the coastal areas and about 12 h in inland plain and semi-mountainous areas. In contrast, it was about 10 h in the mountainous areas. The geographical distribution of the mean daily sunshine duration for the four seasons, as well as for the annual mean daily values for the island of Cyprus, is presented in Figure 9. In winter, the average daily sunshine duration ranged between 4 and 5 h/d, while it was around 6 h/d in coastal and inland plain areas. In summer, it ranged between 10 and 11 h/d in the mountainous areas, while it ranged between 12 and 13 h/d in the coastal and inland plain areas.

As is indicated from the above tables and the geographical distribution of monthly mean daily global radiation and mean daily sunshine duration, both elements decreased with the elevation. Figure 10 shows the relationships between the seasonal and yearly mean values of global irradiation with the elevation. The slopes of the regression lines ranged from −0.0010 in autumn to −0.0021 in spring. The slope in summer (−0.0019) was close to that in spring, while in winter it was −0.0014. The yearly slope was −0.0016. Generally, the Pearson correlation coefficients were higher than 0.70, indicating strong relationships between the mean daily global irradiation and the elevation.

The respective seasonal and yearly relationships of the mean daily sunshine duration and the elevation are presented in Figure 11. Spring and winter showed similar slopes (−0.0013), while summer and autumn showed a slope around −0.0017. The yearly slope was −0.0012.

3.1.2. Monthly Variability of Daily Global Radiation and Sunshine Duration

The variability of the daily values of global radiation and sunshine duration was also demonstrated through the boxplots of each month of the year (Figure 12). The boxplots present the mean and median, the IQR, as well as the outliers of each variable. The smooth curve represents the mean daily values of each month of the year. As it is indicated from the length of the boxplots, the spring, autumn, and winter seasons showed the greatest variability. Outliers were observed mainly in the summer months. As it can be seen, the daily irradiation ranged mainly between 3 and 32 MJ/m².

Table 5. Basic descriptive statistics and percentiles of the daily global irradiation (MJ/m²) for each month of the year for the selected stations: (a) Pentakomo, (b) Athalassa, (c) Kambos, (d) Agros.

(a)
Pentakomo			Descriptive Statistics and Percentiles of Daily Global Irradiation (MJ/m2)
Month	N	Mean	StDev	Min	10%	20%	30%	40%	50%	60%	70%	80%	90%	Max
1	75	10.1	2.8	2.8	6.5	7.8	8.5	9.3	10.3	10.9	12.1	12.5	13.7	15.5
2	76	13.5	4.0	1.9	6.7	10.4	12.8	14.0	14.5	15.1	15.9	16.7	17.9	18.4
3	71	18.0	4.5	3.1	11.4	14.4	16.3	18.0	18.8	19.9	20.7	21.9	23.0	23.9
4	84	22.3	4.7	9.7	14.2	18.2	21.4	22.7	23.7	25.1	25.5	26.1	26.7	27.8
5	81	27.3	2.8	16.6	24.4	25.7	26.7	27.6	28.1	28.6	29.1	29.3	29.6	30.3
6	71	28.4	2.5	16.1	25.5	28.0	28.3	28.7	28.9	29.4	29.7	29.9	30.0	30.4
7	83	27.6	0.9	25.1	26.4	26.8	27.2	27.5	27.6	27.8	27.9	28.4	28.7	29.8
8	84	24.2	1.4	18.3	22.3	23.1	23.5	24.1	24.4	24.7	24.9	25.5	25.9	27.2
9	90	20.2	1.7	16.3	17.8	18.5	19.3	19.7	20.0	20.9	21.3	21.7	22.4	24.4
10	85	15.0	3.0	3.2	10.8	13.5	14.3	14.9	15.7	16.2	16.7	17.1	18.1	19.7
11	85	11.2	2.3	4.4	7.7	9.3	10.4	10.9	11.8	12.4	12.7	13.0	13.5	14.6
12	76	8.8	2.7	1.7	4.0	6.6	7.7	8.9	9.8	10.4	10.8	11.0	11.2	12.7
Year	961	18.9	7.4	1.7	9.0	11.5	13.7	16.4	19.1	22.1	24.6	26.8	28.4	30.4
(b)
Athalassa			Descriptive Statistics and Percentiles of Daily Global Irradiation (MJ/m2)
Month	N	Mean	StDev	Min	10%	20%	30%	40%	50%	60%	70%	80%	90%	Max
1	31	9.5	2.7	3.2	5.6	7.2	7.8	8.5	9.1	10.2	11.3	12.6	12.8	14.0
2	28	14.3	3.5	3.9	9.8	11.6	12.8	14.2	14.7	15.8	16.1	17.6	18.1	18.4
3	31	17.8	4.2	7.6	11.5	14.5	16.7	17.2	18.3	19.2	20.0	21.8	22.7	23.8
4	30	22.6	5.0	12.2	13.7	15.4	22.0	23.2	23.7	24.3	26.7	26.9	27.4	27.9
5	31	27.7	1.7	22.6	25.0	26.3	26.6	27.6	28.0	28.7	28.9	29.1	29.3	29.8
6	30	28.3	2.7	21.1	22.6	27.2	28.4	29.1	29.2	29.4	29.8	29.9	30.5	30.9
7	31	28.1	0.8	26.3	27.2	27.4	27.7	27.8	28.1	28.3	28.5	28.7	29.0	30.4
8	31	25.7	1.5	21.9	23.5	24.1	25.3	25.6	25.8	26.3	26.7	26.8	27.3	27.9
9	30	21.0	1.4	17.4	19.0	19.7	20.2	20.5	21.1	21.4	22.1	22.4	22.6	23.0
10	31	15.9	2.2	11.8	13.2	13.8	14.3	15.0	15.4	17.0	17.3	17.4	19.0	19.6
11	30	9.6	2.8	2.9	6.1	7.5	7.8	8.4	10.2	11.1	11.5	12.0	12.6	13.4
12	31	8.7	2.5	1.9	4.1	7.6	8.3	8.9	9.3	9.8	10.7	10.8	10.9	11.2
Year	365	19.1	7.8	1.9	8.0	11.1	13.5	16.8	19.7	22.6	25.8	27.6	28.7	30.9
(c)
Kambos			Descriptive Statistics and Percentiles of Daily Global Irradiation (MJ/m2)
Month	N	Mean	StDev	Min	10%	20%	30%	40%	50%	60%	70%	80%	90%	Max
1	55	9.1	3.5	2.0	4.7	5.4	6.7	7.5	8.8	10.6	11.3	12.2	13.9	16.5
2	56	12.3	4.5	3.1	5.7	8.4	9.7	11.4	12.3	13.3	15.5	16.9	18.2	20.8
3	62	17.3	6.1	2.3	6.8	11.5	14.9	17.0	19.7	20.1	21.5	22.3	23.7	25.9
4	77	22.1	6.0	6.4	13.3	16.4	18.6	21.8	23.4	25.8	27.0	27.3	28.0	29.6
5	92	27.4	4.3	9.1	21.4	25.7	27.3	28.2	28.8	29.2	29.7	30.0	30.9	31.9
6	90	27.7	3.4	14.5	22.1	25.3	27.6	28.3	28.8	29.2	29.7	30.2	30.7	31.2
7	92	28.8	1.7	19.4	27.5	28.2	28.4	28.6	28.9	29.0	29.6	29.9	30.4	31.5
8	93	25.9	2.2	17.2	23.2	24.4	25.4	25.8	26.1	26.6	27.0	27.4	28.4	30.0
9	77	21.9	3.1	11.5	19.0	20.0	21.8	22.4	22.8	23.2	23.5	24.0	24.6	26.5
10	84	16.1	4.1	3.8	10.5	12.7	14.3	15.6	16.5	17.7	19.0	20.1	21.1	22.9
11	56	12.1	3.4	3.5	7.4	8.8	10.1	11.0	12.3	13.6	14.5	15.3	16.5	17.0
12	61	8.7	2.8	2.5	5.4	6.4	7.0	7.7	8.4	9.6	10.3	10.9	12.8	14.1
Year	895	20.4	8.0	2.0	8.4	11.8	15.3	19.2	22.2	24.5	27.1	28.5	29.6	31.9
(d)
Agros			Descriptive Statistics and Percentiles of Daily Global Irradiation (MJ/m2)
Month	N	Mean	StDev	Min	10%	20%	30%	40%	50%	60%	70%	80%	90%	Max
1	141	8.3	3.8	0.9	2.5	4.6	6.1	7.3	8.3	9.6	10.5	12.3	13.3	15.5
2	132	11.9	4.5	1.3	5.6	7.5	9.8	11.4	12.5	13.7	14.7	15.6	17.5	19.1
3	150	16.9	5.3	2.6	7.8	12.4	14.9	17.0	18.4	19.7	20.3	21.1	22.5	25.7
4	147	20.9	5.8	5.0	11.5	15.9	18.9	20.8	22.6	24.4	25.1	25.9	26.7	28.6
5	148	22.5	5.7	7.2	13.4	16.7	19.7	22.8	24.4	25.7	26.6	27.3	28.0	30.1
6	145	25.1	4.8	9.8	17.5	21.1	22.8	25.6	26.9	28.1	28.7	29.2	29.5	30.8
7	153	26.0	2.8	18.0	21.6	23.5	25.0	26.3	26.9	27.3	27.9	28.4	28.4	30.2
8	153	23.9	3.3	13.5	18.6	21.1	22.3	23.9	25.2	25.9	26.3	26.6	27.1	27.9
9	150	20.4	3.6	10.2	18.1	16.8	18.6	20.3	21.3	22.2	23.0	23.6	24.6	26.1
10	151	15.3	3.9	2.7	9.7	11.4	13.2	14.8	16.0	17.1	18.2	18.8	19.5	21.9
11	141	10.9	3.2	2.2	6.1	8.0	9.0	10.5	11.5	12.7	13.4	13.6	14.4	16.2
12	148	8.1	3.2	1.5	2.9	4.7	6.4	7.3	8.3	9.7	10.7	11.4	11.8	12.4
Year	1759	17.7	7.6	0.9	7.2	10.3	12.6	15.0	18.2	20.8	23.3	25.7	27.3	30.8

shows the mean daily values and their standard deviations as well as the percentiles of the daily global irradiation for each month of the year for the whole period of measurements. The highest daily global irradiation was almost 32 MJ/m² and it was recorded at Kambos, while it was about 31 MJ/m² at the rest stations. The median (50 percentile) was about 27 MJ/m² at the mountainous site, and about 29 MJ/m² at the rest of the sites in June.

3.1.3. Daily Clearness Index and Relative Sunshine Duration

The clearness index (K_T) for a particular time interval is defined as the ratio of the global radiation to the extraterrestrial radiation. It is an objective measure of the influence of cloud cover on the solar radiation flux. In this analysis, clearness index is classified in four groups, as it was earlier stated.

The monthly averages of the clearness index for all the stations are illustrated in Figure 13a. Generally, the coastal and inland plain stations showed higher K_T values throughout the year. The annual average of K_T of the first group was 0.617 and the second group was 0.583. The average values of the daily clearness index ranged between 0.495 in January and 0.685 in July for the first group, while they ranged between 0.445 in January and 0.668 in July for the second group of the stations. The linear relationship between the annual mean K_T and elevation is demonstrated in Figure 13b. As it is indicated, the annual mean K_T decreased with elevation.

Table 6. (a) Monthly daily average of global irradiation (MJ/m²) according to the classification of the daily clearness index (K_T). (b) Monthly number of days according to the classification of the daily clearness index (K_T). The asterisk denotes a missing value.

(a)
Station/Month	Class	1	2	3	4	5	6	7	8	9	10	11	12	Year
Coastal	Cloudy	4.6	5.1	7.2	10.5	9.9	12.1	*	10.6	9.4	5.9	5.1	4.1	6.5
&	Pc_D	8.3	10.5	14.0	16.1	18.1	20.1	20.6	19.2	15.6	11.3	8.9	7.9	13.3
Plain	Pc_B	11.1	14.0	18.1	21.6	24.3	25.8	25.1	23.4	19.7	14.8	11.8	10.2	18.3
	Clear	13.2	16.4	21.2	25.8	28.4	29.3	28.4	25.7	21.9	17.9	13.5	11.5	21.1
Semi-Montainous	Cloudy	4.3	5.3	6.5	9.8	10.9	12.6	13.7	13.2	10.3	6.2	5.1	4.0	7.3
&	Pc_D	8.3	10.6	13.6	16.5	18.5	19.9	19.5	18.3	14.7	11.5	8.8	7.6	14.0
Montainous	Pc_B	11.0	13.9	18.0	21.7	24.3	25.1	24.8	22.7	19.2	15.1	11.7	10.2	18.1
	Clear	13.2	16.5	21.2	26.1	28.4	29.3	28.6	26.4	22.4	18.2	14.0	11.7	21.3
(b)
Station/Month	Class	1	2	3	4	5	6	7	8	9	10	11	12	Year
Coastal	Cloudy	5	2	2	1	0	0	0	0	0	1	2	6	21
&	Pc_D	10	5	6	4	1	1	0	1	1	3	8	8	49
Plain	Pc_B	7	5	7	5	4	2	3	6	8	9	9	7	72
	Clear	6	12	14	19	25	26	27	23	22	18	9	7	208
Semi-Montainous	Cloudy	9	6	4	4	1	1	0	0	0	2	4	8	39
&	Pc_D	9	8	9	7	4	5	3	4	5	7	9	11	80
Montainous	Pc_B	5	4	6	6	6	6	5	5	6	7	7	5	69
	Clear	4	9	11	13	19	18	23	21	19	15	9	6	166

shows the monthly average of global irradiation and the number of days in each month of the year according to the above classification. The average global irradiation was almost similar in both groups. The annual average of global irradiation was about 7 MJ/m² on cloudy days and about 21 MJ/m² on clear days. However, the annual number of cloudy days was 21 (about 6%) for the first group and almost twice (39) for the second group representing 11% of the annual number of days. The respective number for partially cloudy days was 121 and 149 days, while the days that were classified as clear days were 208 (57%) and 166 (45%), respectively. As it can be seen, the summer months were classified mainly as clear days. The discrepancy between the numbers of days in the corresponding to the four types of the days was a result of the fact of the different missing days in each of the month.

The monthly average frequency of days according to their type gives an initial indication of the relative viability of different solar collector types. For example, concentrating solar collectors operate best under clear day conditions and, to a much lesser extent, under partially cloudy days. The major difference between day types was the significant reduction in the beam radiation, which also affects the global irradiation level. Regarding the global radiation, the reduction factor for partially cloudy days to that on clear days ranged from 0.73 to 0.78. Almost similar figures were obtained by Kudish and Ianetz [46] at Beer Sheva in Israel.

The monthly means and their standard deviations of the relative sunshine duration (σ) of four stations are presented in

Table 7. Monthly means and standard deviation of relative sunshine (σ) of stations representing the four classification groups.

Relative Sunshine (σ)
	Pentakomo		Athalassa		Kambos		Agros
Month	Mean	StDev	Mean	StDev	Mean	StDev	Mean	StDev
1	0.634	0.266	0.510	0.260	0.530	0.281	0.485	0.268
2	0.697	0.289	0.708	0.240	0.589	0.280	0.554	0.264
3	0.721	0.276	0.654	0.253	0.632	0.265	0.684	0.233
4	0.769	0.216	0.691	0.276	0.701	0.234	0.714	0.202
5	0.871	0.102	0.868	0.091	0.826	0.144	0.715	0.166
6	0.868	0.096	0.868	0.118	0.826	0.108	0.735	0.129
7	0.896	0.026	0.912	0.043	0.871	0.046	0.788	0.077
8	0.911	0.042	0.920	0.039	0.878	0.049	0.808	0.092
9	0.910	0.037	0.892	0.068	0.795	0.102	0.789	0.121
10	0.861	0.173	0.815	0.123	0.762	0.187	0.730	0.179
11	0.729	0.226	0.501	0.284	0.641	0.266	0.631	0.232
12	0.607	0.288	0.572	0.272	0.563	0.246	0.521	0.255
Year	0.793	0.219	0.748	0.246	0.720	0.233	0.688	0.215

. The monthly means of the coastal and inland plain areas ranged between 0.510 and 0.920. The respective means for semi-mountainous stations ranged between 0.530 and 0.880, while at the higher locations they ranged between 0.485 and 0.810. Generally, the annual average decreased from 0.793 to 0.688 with an increase in elevation.

3.1.4. Statistical Relationships

The linear relationship between the daily clearness index (K_T) and the daily relative sunshine duration (σ) for Kambos is shown in Figure 14a, while the relationship between the daily global radiation (G_d) and the daily sunshine duration (S_d) is also expressed as a quadratic equation as shown in Figure 14b. Similar relationships were obtained for the other stations that measure global and sunshine duration. Both equations are associated with high coefficients of determination (

Table 8. (a) Linear (K_T vs. σ) and quadratic equations (G_d vs. S_d) for the estimation of daily global irradiation (MJ/m²). (b) Linear equations between K_T vs. σ and G_d vs. S_d for the estimation of mean monthly daily global irradiation (MJ/m²).

(a)
Station	Elevation (m)	Period	Linear Equation (KT vs. σ)	R2	Quadratic Equation (Gd vs. Sd)	R2
Larnaka AP	2	2013–2015	KT = 0.261 + 0.528*σ	0.91
Larnaka AP	2	2020–2021	KT = 0.323 + 0.527*σ	0.70	Gd = 0.781 + 3.160*Sd − 0.066*Sd2	0.72
Pafos AP	8	2020–2021	KT = 0.231 + 0.561*σ	0.89	Gd = 5.539 + 0.421*Sd + 0.123*Sd2	0.88
Polis	22	2019–2021	KT = 0.239 + 0.519*σ	0.85	Gd = 6.193 − 0.054*Sd + 0.136*Sd2	0.91
Pentakomo	23	2019–2021	KT = 0.210 + 0.507*σ	0.87	Gd = 7.230 − 0.773*Sd + 0.185*Sd2	0.89
Avdimou	51	2019–2021	KT = 0.180 + 0.615*σ	0.89	Gd = 6.621 − 0.847*Sd + 0.237*Sd2	0.87
Menoyia	140	2013–2017	KT = 0.242 + 0.505*σ	0.91	Gd = 6.073 + 0.277*Sd + 0.116*Sd2	0.85
Athalassa	158	2020–2021	KT = 0.281 + 0.455*σ	0.90	Gd = 6.656 − 0.109*Sd + 0.138*Sd2	0.89
Athalassa	158	2013–2015	KT = 0.260 + 0.498*σ	0.91
Choulou	316	2011–2013	KT = 0.219 + 0.559*σ	0.93	Gd = 5.453 + 0.481*Sd + 0.107*Sd2	0.90
Mathiatis	395	2019–2021	KT = 0.166 + 0.574*σ	0.92	Gd =4.912 + 0.190*Sd + 0.123*Sd2	0.93
Kalopanayiotis	587	2019–2021	KT = 0.176 + 0.685*σ	0.95	Gd = 4.180 + 0.777*Sd + 0.135*Sd2	0.94
Mallia	633	2019–2021	KT = 0.174 + 0.610*σ	0.93	Gd =6.497 − 0.140*Sd + 0.163*Sd2	0.88
Kambos	634	2019–2021	KT = 0.181 + 0.617*σ	0.90	Gd = 5.440 + 0.257*Sd + 0.132*Sd2	0.92
Farmakas	833	2019–2021	KT = 0.168 + 0.701*σ	0.95	Gd = 3.940 + 0.961*Sd − 0.117*Sd2	0.93
Agros	998	2019–2021	KT = 0.099 + 0.693*σ	0.88	Gd = 3.936 + 0.265*Sd + 0.146*Sd2	0.92
Amiantos	1355	2019–2021	KT = 0.170 + 0.686*σ	0.93	Gd = 3.988 + 1.092*Sd + 0.095*Sd2	0.90
(b)
Station	Elevation (m)	Period	Linear Equation (KT vs. σ)	R2	Linear Equation (Gd vs. Sd)	R2
Larnaka AP	2	2020–2021	KT = 0.389 + 0.412*σ	0.578	Gd = 0.358 + 2.645*Sd	0.753
Pafos AP	8	2020–2021	KT = 0.203 + 0.599*σ	0.888	Gd = −3.153 + 2.641*Sd	0.943
Polis	22	2019–2021	KT = 0.294 + 0.449*σ	0.810	Gd = −2.441 + 2.353*Sd	0.901
Pentakomo	23	2019–2021	KT = 0.273 + 0.431*σ	0.728	Gd = −6.915 + 2.692*Sd	0.897
Avdimou	51	2019–2021	KT = 0.212 + 0.572*σ	0.837	Gd = −8.278 + 3.143*Sd	0.896
Menoyia	140	2013–2017	KT = 0.286 + 0.447*σ	0.952	Gd = −5.001 + 2.642*Sd	0.930
Choulou	316	2011–2013	KT = 0.244 + 0.523*σ	0.968	Gd = −2.897 + 2.542*Sd	0.942
Mathiatis	395	2019–2021	KT = 0.204 + 0.523*σ	0.967	Gd = −4.543 + 2.516*Sd	0.962
Kalopanayiotis	587	2019–2021	KT = 0.198 + 0.646*σ	0.986	Gd = −2.010 + 2.816*Sd	0.965
Mallia	633	2019–2021	KT = 0.178 + 0.605*σ	0.946	Gd = −5.694 + 2.878*Sd	0.926
Kambos	634	2019–2021	KT = 0.237 + 0.539*σ	0.902	Gd = −3.940 + 2.654*Sd	0.939
Farmakas	833	2019–2021	KT = 0.200 + 0.643*σ	0.985	Gd = −2.933 + 2.932*Sd	0.970
Agros	998	2019–2021	KT = 0.195 + 0.554*σ	0.887	Gd = −4.891 + 2.699*Sd	0.931
Amiantos	1355	2019–2021	KT = 0.219 + 0.602*σ	0.961	Gd = −2.471 + 2.821*Sd	0.945

a). The residuals (the difference between the observed and estimated data) are normally distributed and the plots of residuals versus the fitted values show no obvious patterns or clusters suggesting that the assumption of constant variance has not been violated (not shown here). The standard error of the residuals (S) is shown on the legend of the graph. In the case of the linear equations (K_T vs. σ), the intercept ranged between 0.100 and 0.280, while the slopes ranged between 0.455 and 0.700. The sum of the intercept and the slope indicates the amount of global radiation reaching the ground on a clear day. The average sum of the constants of all the sites was 0.788. Table 8b presents the linear equations of the monthly means of daily values.

3.2. Hourly Values

3.2.1. Hourly Global Irradiances as a Function of Solar Zenith Angle and Clearness Index

The variation of the hourly measured global radiation with the solar zenith angle and the associated clearness index is illustrated in Figure 15 for the station of Pentakomo. Similar graphs were obtained from the other stations. High global irradiances are associated with high clearness index. Global irradiance decreased almost exponentially with increasing the SZA for a given k_t interval. The top three layers of k_t show the clear-sky conditions. This relationship can be expressed as:

$$G=G_{max}\ast {(\cos {\theta }_z)}^b$$

(16)

where G_max is the maximum global irradiance for each k_t interval and b describes how G changes with the cosine of the SZA. The dependence of G_max on k_t can be described by the cubic equation as:

$$G_{\mathit{max}}=a+c\ast k_t+d\ast k_t^2+e\ast k_t^3$$

(17)

In the second step, b was obtained from analyzing the relationship between hourly G and the cosine of the zenith angle using a non-linear statistical method. The value of b was estimated to range between 0.8 and 0.9 for all the sites.

3.2.2. Diurnal Variation of Hourly Global Irradiances

The daily variation of the average hourly global irradiance for the selected stations is shown in Figure 16. The figure shows that the hourly average global irradiance fluctuates between 400 W/m² in January and 950 W/m² in July at local noon. Slightly lower values were observed at Agros (mountainous site). The curves of each month of global irradiances were symmetrical around the local noon. As it can be seen, the curves can be classified in five groups with similarities with respect to their variation. Starting from the top curves, the first group represents the summer months (June, July, and August) and slightly below it is the second with the months of April, May, and September. March and October compose the third group, which is followed by the group of the months of February and November, and the last group is the winter months of January and December.

3.2.3. Monthly Variability

The variability of the four shortwave hourly irradiances is demonstrated with the graph of boxplots for each month of the year (Figure 17). The smooth line represents the mean values of irradiances for each month of the year. As can be seen, no outliers were observed for the hourly global irradiances. In all cases, the median values were very close to the means. The highest variability was observed in the summer months, as is indicated by the length of the boxes. The highest values of the coastal and inland plain sites reached the value of 1000 W/m², while in the mountainous sites they exceed the value of 1100 W/m² during the summer months. The highest monthly mean values of the hourly irradiances were recorded in June or July and the lowest in December or January. Generally, the monthly mean hourly global irradiances range between 250 and 550 W/m².

3.2.4. Frequency Distribution of Global Irradiances

The annual histograms and the cumulative density frequency curves (CDF) for the global irradiances for Pentakomo are shown in Figure 18. The sites show a similar pattern with respect to their frequency distribution. Regarding the CDF curves, the percentiles of the global irradiances can be obtained from the graph. For example, the 70 percentile represents a value of 600 W/m² for the hourly global irradiances. The figures indicate that, in 70% of the hourly irradiances, these are less than above values.

3.2.5. Hourly Clearness Indices (k_t)

The monthly variability of each index for the four selected stations is presented in Figure 19. Monthly means of k_t ranged mainly between 0.5 and 0.65 with the highest occurring in summer. Slightly lower values were observed at the mountainous sites (0.4 to 0.6). All graphs show the lowest variability during the summer season. On the other hand, outliers were recorded mainly during the summer season.

The monthly statistics of the classification of the different sky conditions defined by the selected intervals of the clearness index (k_t) are presented in

Table 9. Monthly statistics of global irradiance under all and different sky conditions for the four selected sites. The asterisk denotes a missing value.

Pentakomo
	G (W/m2)				Gcld (W/m2)				Gpc (W/m2)				Gclr (W/m2)
Month	Mean	StDev	Min	Max	Mean	StDev	Min	Max	Mean	StDev	Min	Max	Mean	StDev	Min	Max
1	279	172.3	0	654	129	67.5	3	272	269	128.1	48	528	407	169.1	88	654
2	366	221.1	0	816	118	69.0	0	300	265	141.4	69	600	513	169.0	115	816
3	420	266.8	0	934	161	90.7	11	384	358	185.5	47	729	596	215.3	92	934
4	495	292.9	22	1007	194	110.4	22	420	318	187.7	60	806	712	190.4	127	1007
5	548	314.8	0	1012	164	96.1	56	364	291	180.8	64	822	744	206.9	86	1012
6	563	311.8	30	991	250	123.6	36	415	266	158.0	44	822	777	171.4	156	991
7	549	309.5	31	981	67	*	67	67	272	160.2	45	763	788	148.3	275	981
8	506	301.6	16	971	161	86.1	62	331	310	164.1	64	695	761	144.2	392	971
9	464	268.9	15	905	160	57.0	44	302	307	169.6	46	698	703	130.3	307	905
10	383	228.7	2	808	139	63.9	2	303	290	153.1	50	659	563	185.3	86	808
11	297	186.5	0	701	128	63.2	28	271	288	118.8	85	538	486	111.6	159	701
12	248	163.7	0	582	114	65.9	0	257	253	116.7	58	479	421	114.0	106	582
Year	439	284.8	0	1012	141	82.8	0	420	291	159.1	44	822	664	210.0	86	1012
Athalassa
	G (W/m2)				Gcld (W/m2)				Gpc (W/m2)				Gclr (W/m2)
Month	Mean	StDev	Min	Max	Mean	StDev	Min	Max	Mean	StDev	Min	Max	Mean	StDev	Min	Max
1	302	174.7	1	715	119	64.2	4	277	280	109.2	66	525	490	114.9	125	715
2	414	215.4	2	880	135	74.6	9	328	272	128.3	75	589	549	151.6	139	880
3	463	257.2	1	1121	149	95.7	1	384	353	168.2	64	745	625	191.8	119	1121
4	532	289.9	7	1109	152	104.8	7	427	338	181.1	69	800	714	201.5	150	1109
5	608	284.7	24	1088	157	111.3	24	428	281	169.8	61	787	739	198.6	225	1088
6	601	301.9	23	1139	180	107.4	23	444	271	162.8	60	796	763	199.2	221	1139
7	606	290.0	30	1081	123	104.7	30	396	254	134.8	65	801	763	174.4	322	1081
8	586	278.2	34	1078	135	96.5	34	367	259	139.5	65	780	741	164.3	300	1078
9	525	240.2	40	865	128	99.9	40	366	278	139.0	63	727	680	125.7	226	865
10	442	208.9	21	854	134	85.7	21	342	275	127.0	63	625	588	118.9	133	854
11	299	183.8	5	765	115	71.8	5	290	277	108.2	70	562	503	99.6	133	765
12	287	167.7	0	701	103	62.4	3	260	246	92.4	66	467	462	76.8	213	701
Year	490	277.5	0	1139	130	85.5	1	444	281	143.7	60	801	674	193.0	119	1139
Kambos
	G (W/m2)				Gcld (W/m2)				Gpc (W/m2)				Gclr (W/m2)
Month	Mean	StDev	Min	Max	Mean	StDev	Min	Max	Mean	StDev	Min	Max	Mean	StDev	Min	Max
1	317	180.9	48	757	145	53.3	48	269	292	101.2	66	528	493	142.1	117	757
2	346	230.2	29	849	142	70.6	29	320	298	145.0	67	639	544	200.0	119	849
3	472	275.0	26	978	170	91.4	26	366	355	167.2	72	738	658	216.4	228	978
4	513	307.3	25	1075	169	93.5	25	415	337	189.8	64	797	758	205.9	174	1075
5	600	313.1	50	1117	150	100.9	50	405	314	198.3	60	828	780	203.7	185	1117
6	594	311.9	46	1102	131	108.9	46	434	337	168.2	77	837	795	185.2	308	1102
7	635	308.8	42	1071	98	61.7	42	357	258	127.9	65	672	789	185.0	303	1071
8	598	300.1	42	1043	117	68.5	42	361	276	139.1	77	806	766	183.0	184	1043
9	544	275.0	39	978	124	86.5	39	361	315	158.6	77	756	687	190.9	194	978
10	471	227.5	16	889	169	75.3	16	316	319	148.3	70	618	580	189.9	117	889
11	379	198.3	26	780	126	65.5	26	280	267	117.4	82	519	499	155.2	140	780
12	291	171.8	26	652	115	56.8	26	247	287	93.7	83	481	460	129.7	118	652
Year	517	297.3	16	1117	140	82.4	16	434	307	158.8	60	837	705	216.1	117	1117
Agros
	G (W/m2)				Gcld (W/m2)				Gpc (W/m2)				Gclr (W/m2)
Month	Mean	StDev	Min	Max	Mean	StDev	Min	Max	Mean	StDev	Min	Max	Mean	StDev	Min	Max
1	245	191.3	4	782	93	66.7	4	288	259	119.3	45	523	478	133.2	88	782
2	330	235.2	2	874	109	80.2	2	325	297	145.5	67	640	557	164.6	160	874
3	431	272.8	6	992	140	100.5	6	386	326	169.1	46	712	654	188.0	168	992
4	483	303.3	9	1077	140	104.4	9	419	383	180.5	49	794	746	189.1	167	1077
5	481	321.7	13	1112	139	96.5	13	447	378	195.9	48	828	816	162.3	316	1112
6	515	329.3	13	1134	132	116.3	13	443	371	194.7	73	828	805	198.9	305	1134
7	535	338.8	12	1092	92	89.6	12	446	400	176.0	65	820	818	177.3	290	1092
8	547	307.5	21	1050	118	92.1	21	413	394	172.1	83	794	769	175.5	202	1050
9	499	277.3	14	1016	145	104.7	14	403	277	174.5	82	733	673	179.4	148	1016
10	408	248.2	2	881	109	81.4	2	320	272	155.9	47	662	585	161.7	88	881
11	337	201.6	6	816	98	54.5	6	245	272	120.3	78	555	510	122.2	156	816
12	249	179.3	6	645	89	60.9	6	257	255	115.3	50	490	461	105.9	128	645
Year	437	297.3	2	1134	115	90.4	2	447	334	175.9	45	828	687	207.7	88	1134

. The table indicates that global irradiances ranged between 500 and 750 W/m² during clear-sky conditions, while during partially cloudy conditions they ranged between 200 and 400 W/m². In contrast, they ranged between 100 and 200 W/m² during cloudy conditions. However, at the mountainous site, they were slightly higher than 100 W/m² during overcast conditions throughout the year. Regarding the case of all sky conditions, they ranged mainly between 250 and 550 W/m².

3.2.6. Annual Sky Status

Figure 20 shows the annual hours of the stations for the duration of overcast skies (DOS), intermediate skies (DIS), and for clear skies (DCS). The stations were arranged according to their elevation. It can be seen that the hour ranges for the three types of skies were [296–1479 h], [789–1901 h], and [1075–2359 h] for DOS, DIS, and DCS. The average values for the three types of skies were 840.7 ± 368.4 h, 1239.7 ± 276.6 h, and 1819.8 ± 323.2 h, respectively. These results show that the intermediate and clear-sky conditions over Cyprus prevailed all over the year. The effect of elevation toward the annual hours of the duration of each sky type is demonstrated in Figure 21. As is expected, the figure shows that the hours of overcast skies (DOS) increased at high elevation sites. On the other hand, the annual hours of DIS and DCS slightly decreased with elevation. This indicates that intermediate and clear sky conditions prevailed over the whole island, while overcast conditions were more frequently expected in the mountainous areas. The coefficient of determination (R²) for the DOS conditions was 0.64, which was higher than the respective values of the other two sky conditions.

4. Conclusions

Hourly data of global horizontal irradiance (G) were obtained from the automatic weather stations of Cyprus, covering mainly the period 2019–2021. Mostly, Kipp & Zonen pyranometers were used for the measurement of global radiation. For the sunshine duration measurements, Kipp & Zonen CSD3 sunshine duration sensors were used. The sensors, at the same time, measured the direct normal irradiance (B_n) in W/m², which, however, was less accurate than the measurements of this variable through the pyrhiliometers that are installed on solar tracking systems. Generally, the data of 28 automatic weather stations that were either in operation or closed, measuring the global radiation, were used for the assessment of solar radiation data. Furthermore, 18 stations equipped with Campbell–Stokes sunshine recorders, operating in different periods, were used to estimate global radiation. The stations were classified according to their location and their elevation, as coastal, inland plain, semi-mountainous, and mountainous stations. The first objective of the study was the assessment of the hourly and daily measurements of global solar radiation and sunshine duration data. For this purpose, the data underwent an extensive quality control process for both hourly and daily values, which was followed by a statistical analysis of the global radiation and the derived indices. In this way, the geographical distribution of global radiation over the island of Cyprus was assessed.

A detail quality control procedure was implemented on the radiation components, which are based on the suggested limits proposed by the BSRN group. The tests include physically possible limits (PPL) and extremely rare limits (ERL). Additionally, the data were tested according to the values of the clearness index of k_t, which is always lower than 1. Finally, step and persistency tests were applied on the hourly dataset. The daily values were also tested against the extraterrestrial irradiation and the estimated highest daily sums on clear days as well as by comparing the daily global radiation with the daily sunshine duration. Generally, all data are within the specified limits. However, the data of two stations (Lefkara Dam and Zygi) were excluded from the analysis because most of the data were outside the PPL and ERL limits, either due to problems of wrong installation or to the presence of trees in the surrounding area, which thus affected the incidence of global irradiance. The statistical analysis was demonstrated mainly through the graphs of boxplots, where the basic statistics of each location are presented and, at the same time, the stations can be compared on a monthly basis.

From this investigation, the following results can be highlighted:

Monthly mean daily values of global irradiation either measured or estimated from the daily sunshine duration are shown by means of isolines diagrams. These values are considered representative of the solar radiation behavior along a typical year and can be useful for exploiting solar energy applications. Seasonal analysis allows the highlighting of the differences between summer and winter irradiation conditions. June and July were found to be the months with the highest values of mean daily global radiation. During these months, daily global irradiation ranged between 25 MJ/m² and 30 MJ/m², with the lowest occurring in the mountainous locations. On the other hand, in January or December, they ranged between 6.5 MJ/m² and 10.5 MJ/m². Regarding the annual variation of the mean daily global irradiation, it is shown that it ranged between 16 MJ/m² and 20 MJ/m². The maximum of daily global solar horizontal irradiation was reached in June or July and it was almost 32 MJ/m².

The annual daily average of sunshine duration ranged between 7.0 h and 9.5 h with the lowest values occurring in the mountainous locations. The monthly mean daily values ranged between 3 and 6.5 h in January, while they ranged between 10 and 13.5 h in June or July. The maximum daily value was almost 14 h and it occurred in the summer months. The total annual number of hours of sunshine duration ranged between 2500 and 3500, with the lowest values recorded at the mountainous sites.

The monthly mean daily relative sunshine duration in the coastal and inland plain locations ranged between 0.5 in January and 0.9 in July. Slightly lower values were recorded in the mountainous sites. Linear relationships were established between the daily clearness index (K_T) and the daily relative sunshine duration (σ), while quadratic relationships were established between the daily global radiation (G_d) and the daily sunshine duration (S_d). Both equations are associated with high coefficients of determination. In the case of the linear equations (K_T vs. σ), the intercept ranged between 0.100 and 0.280, while the slope ranged between 0.455 and 0.700. The sum of the intercept and the slope indicates the amount of global radiation reaching the ground on a clear day. The average sum of the constants of all the sites was 0.788.

Generally, the coastal and inland plain stations showed higher K_T values than the mountainous sites, throughout the year. The annual average of K_T of the first group was 0.617 and the second group was 0.583. The average values of the daily clearness index ranged between 0.495 in January and 0.685 in July for the first group, while they ranged between 0.445 in January and 0.668 in July for the second group of the stations. A linear relationship between the annual mean K_T and elevation showed the decrease in the annual mean K_T with elevation.

The average global irradiation was almost similar in both groups of stations. The annual average of global irradiation was about 7 MJ/m² on cloudy days and about 21 MJ/m² on clear days. However, the annual number of cloudy days was 21 (about 6%) for the first group and almost twice (39) for the second group, representing 11% of the annual number of days. The respective number for partially cloudy days was 121 and 149 days, while the days that are classified as clear days were 208 (57%) and 166 (45%), respectively. As can be seen, the summer months were classified mainly as clear days. The monthly average frequency of days according to their type gives an initial indication of the relative viability of different solar collector types. For example, concentrating solar collectors operate best under clear day conditions and to a much lesser extent, under partially cloudy days. The major difference between day types was the significant reduction in the beam radiation, which also affects the global irradiation level. Regarding the global radiation, the reduction factor for partially cloudy days to that on clear days ranged from 0.73 to 0.78.

The monthly means of hourly clearness indices (k_t) ranged mainly between 0.5 and 0.65 with the highest occurring in summer. Slightly lower values were observed at the mountainous sites (0.4 to 0.6). During clear-sky conditions, global irradiances ranged between 500 and 750 W/m², while during partially cloudy conditions they ranged between 200 and 400 W/m². In contrast, they ranged between 100 and 200 W/m² during cloudy conditions. However, at the mountainous sites, they were slightly higher than 100 W/m² during overcast conditions throughout the year. Regarding the case of all sky conditions, they ranged mainly between 250 and 550 W/m².

Regarding the duration of the annual hours of the stations during overcast skies (DOS), they ranged between 296 and 1479 h, for intermediate skies (DIS) they ranged between 789 and 1901 h, while for clear skies (DCS) they ranged between 1075 and 2359 h. The average values for the three types of skies were 840.7 ± 368.4 h, 1239.7 ± 276.6 h, and 1819.8 ± 323.2 h, respectively. These results show that the intermediate and clear sky conditions over Cyprus prevailed throughout the year, while overcast conditions were more frequently expected in the mountainous areas.

This work has specifically contributed to the characterization and analysis of hourly and daily solar global radiation. Furthermore, the measurements on the ground level could be compared with satellite observations in order to improve the geographical distribution of global radiation, especially in areas where no measurements exist. The analysis could be also extended for the other shortwave radiation components (Direct, Diffuse and Photosynthetic Active Radiation (PAR)) in order to assess the solar radiation regime over the island. The results of this paper are of the utmost importance to scientists and engineering working in the field of solar energy, which includes both solar thermal collectors and systems and photovoltaic systems. The input power to these systems is solar radiation, and therefore knowing this with some accuracy is very important. With the knowledge of global solar radiation on horizontal surfaces, we can estimate the solar radiation on inclined surfaces [8], and therefore we can assess more accurately the efficiency of photovoltaic systems.