Optimization of a Virtual Synchronous Control Parameter for a Wind Turbine Generator Considering the Physical Constraint Boundary of Primary Frequency Regulation
Abstract
:1. Introduction
- Based on the WTG model controlled by VSG, in order to evaluate the frequency regulation capability of WTG more comprehensively and accurately, the primary frequency regulation dead zone is modeled. Then, the evaluation index expression of the whole process of frequency response after the load disturbance is derived through time domain analysis;
- Based on the frequency regulation capacity margin of WTG, this paper proposes a method of frequency regulation capability evaluation by considering both the speed limit of the rotor and the capacity limit of the converter. According to the proposed method, the real-time frequency regulation capacity of WTG is quantified by optimizing the frequency regulation coefficient.
2. Frequency Regulation Strategy of WTG Based on VSG Control
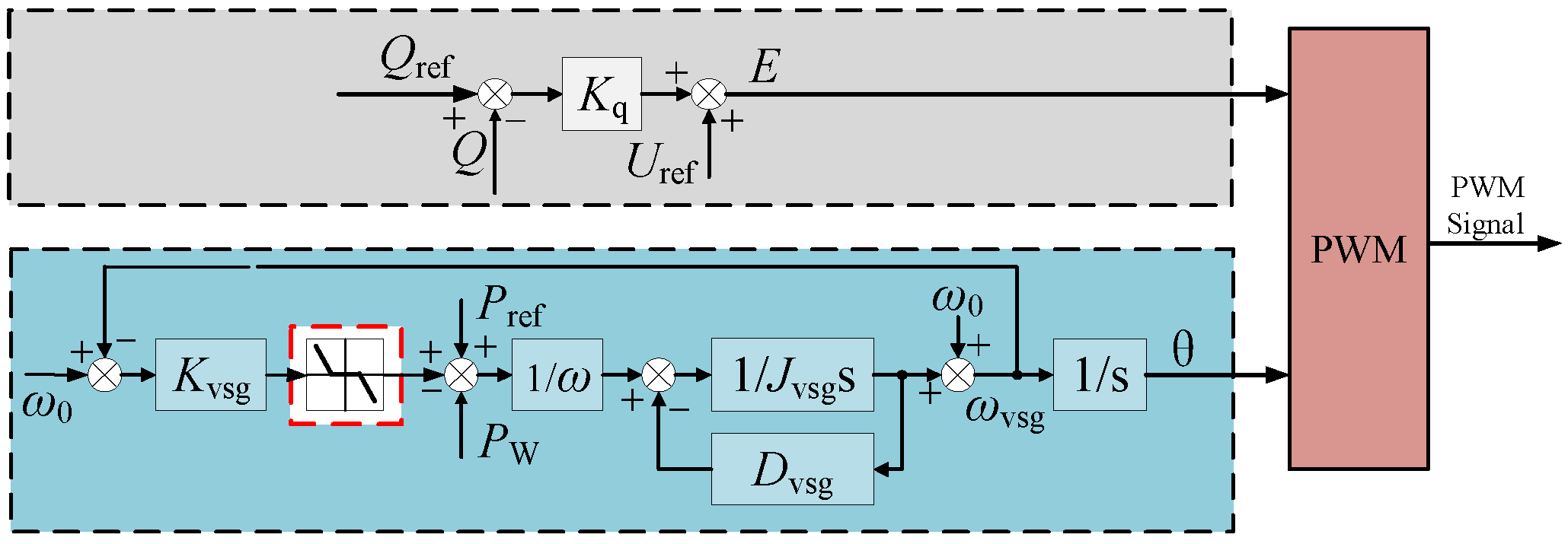
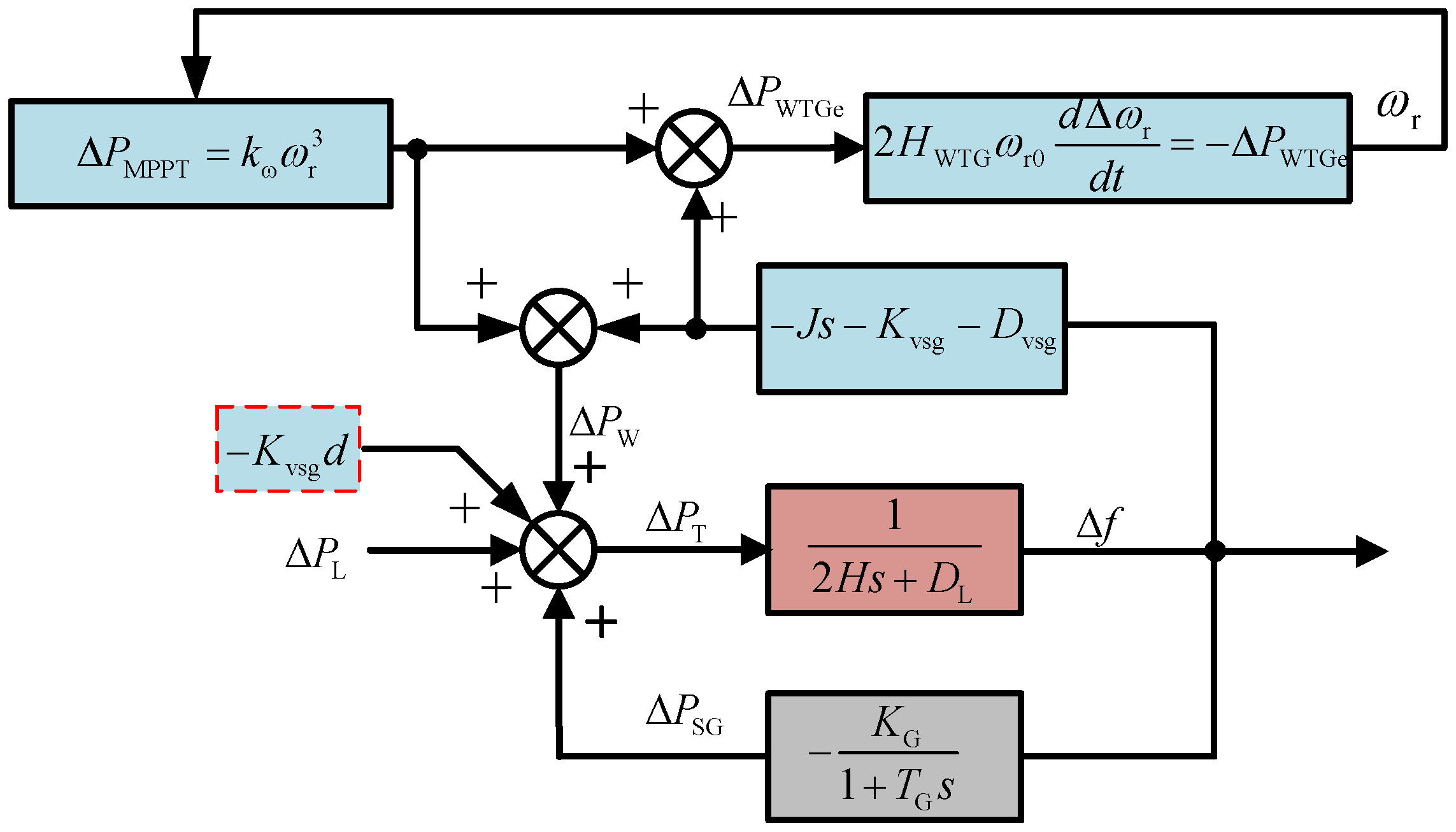
2.1. VSG Control
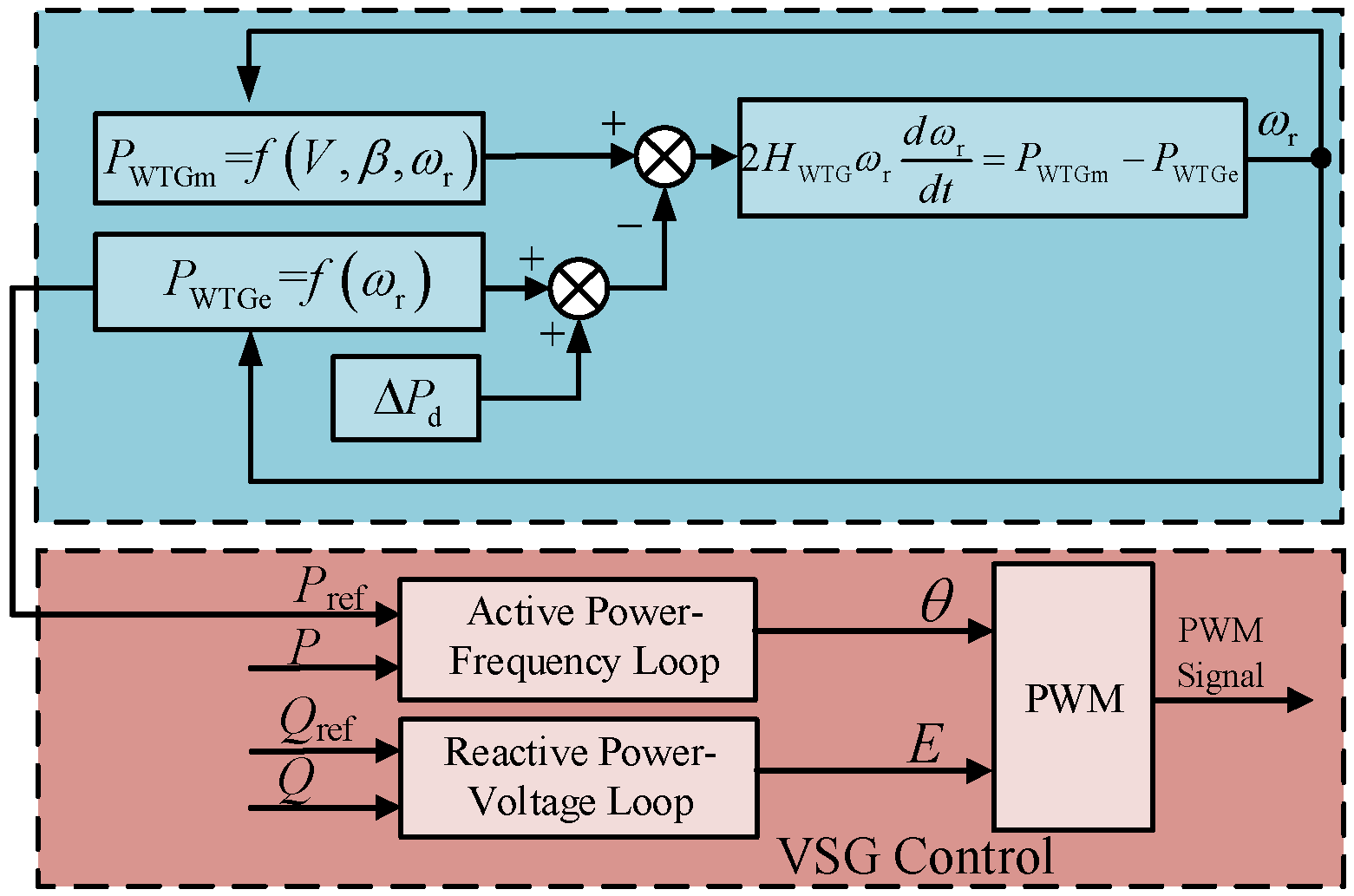
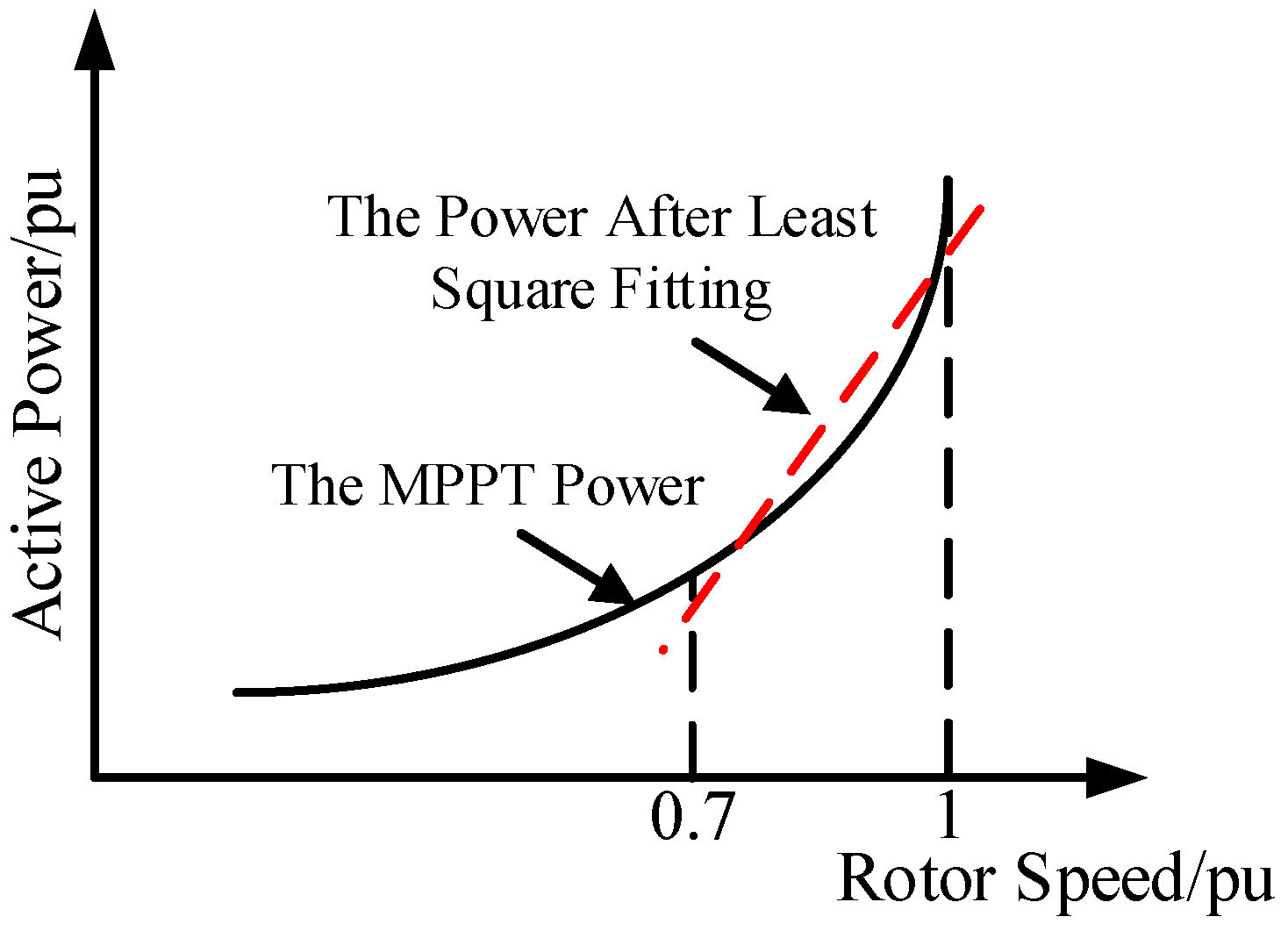
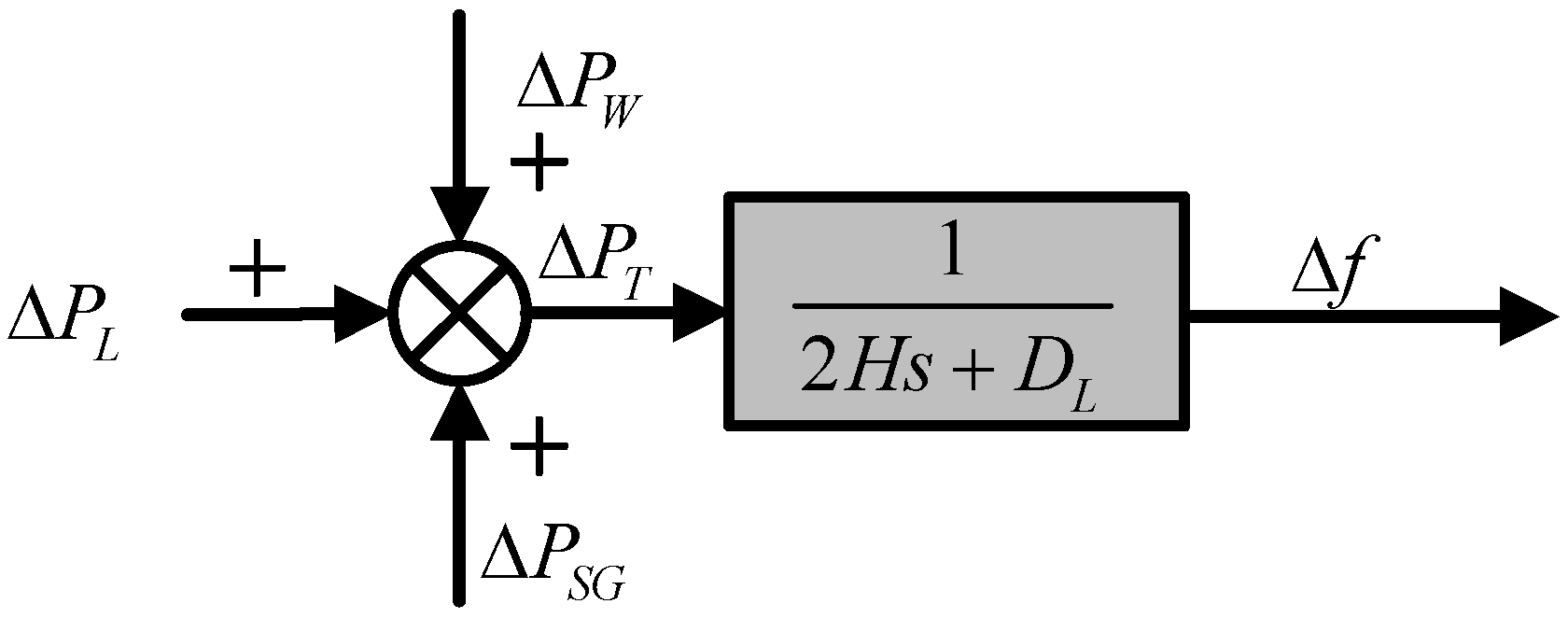
2.2. Frequency Regulation Control Model of WTG
3. Frequency Response Analysis Considering the PFR Dead Zone
3.1. The Expression of Frequency Response for WTG
3.2. The Modeling of the PFR Dead Zone
3.3. Establishment and Quantification of a Frequency Response Model
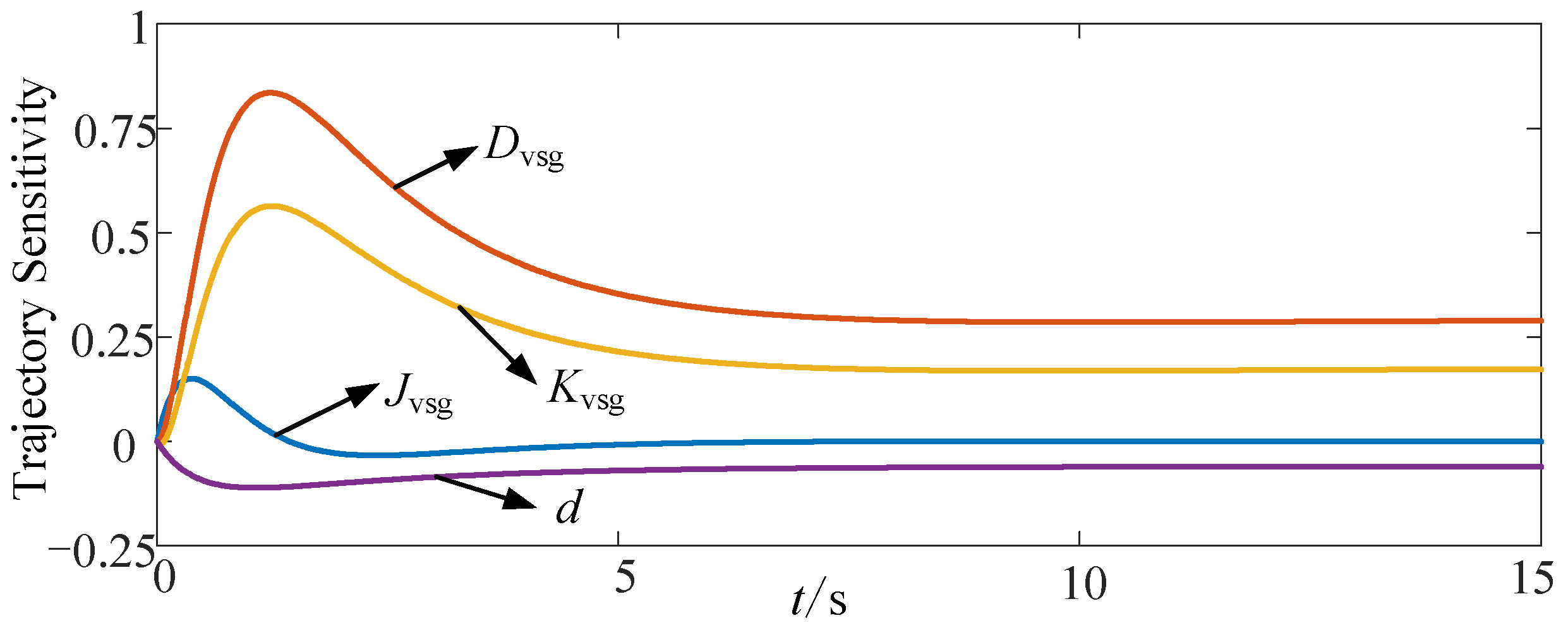
4. Trajectory Sensitivity Analysis
5. Optimization of the Virtual Damping Parameter Based on the Physical Constraint Boundary of Frequency Regulation
5.1. The Speed Limit of the Rotor
5.2. The Capacity Limit of the Converter
6. Simulation Results
6.1. The Simulation System
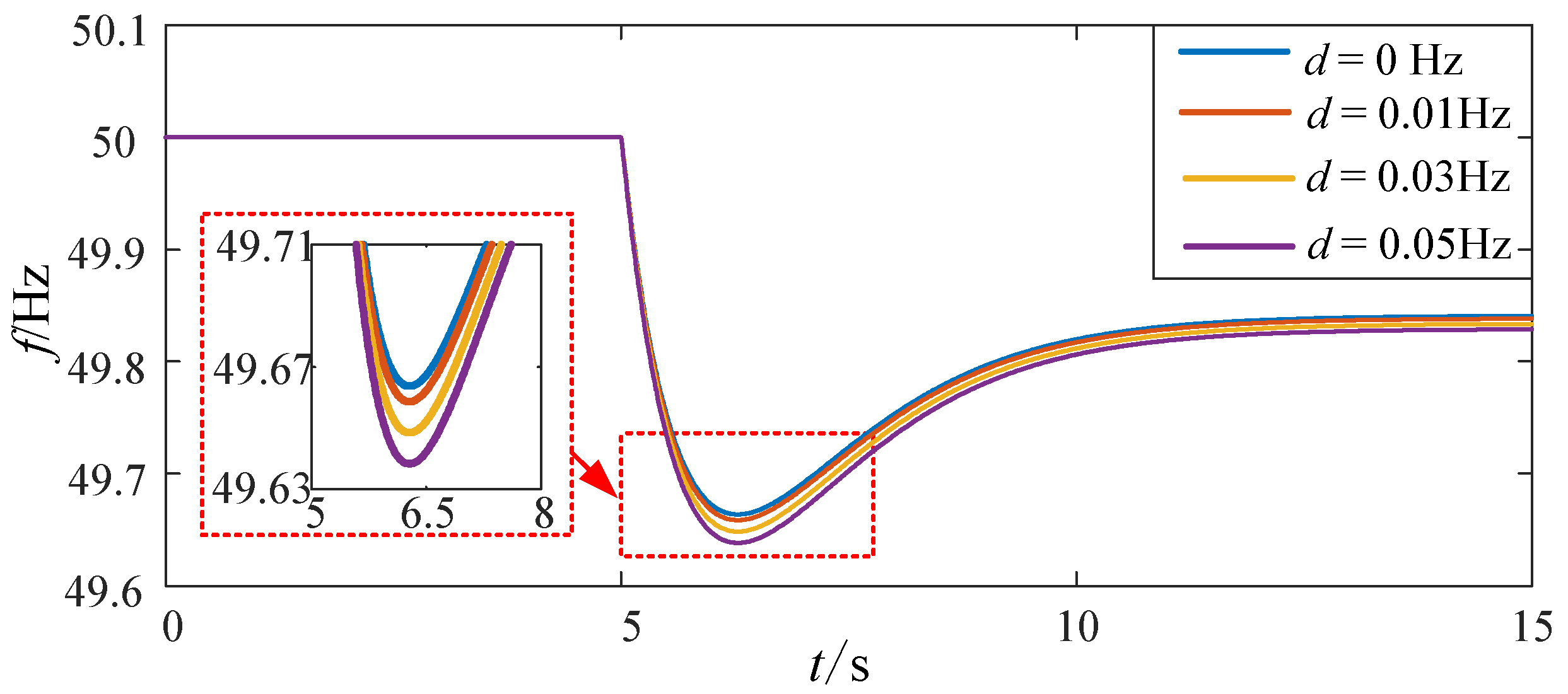
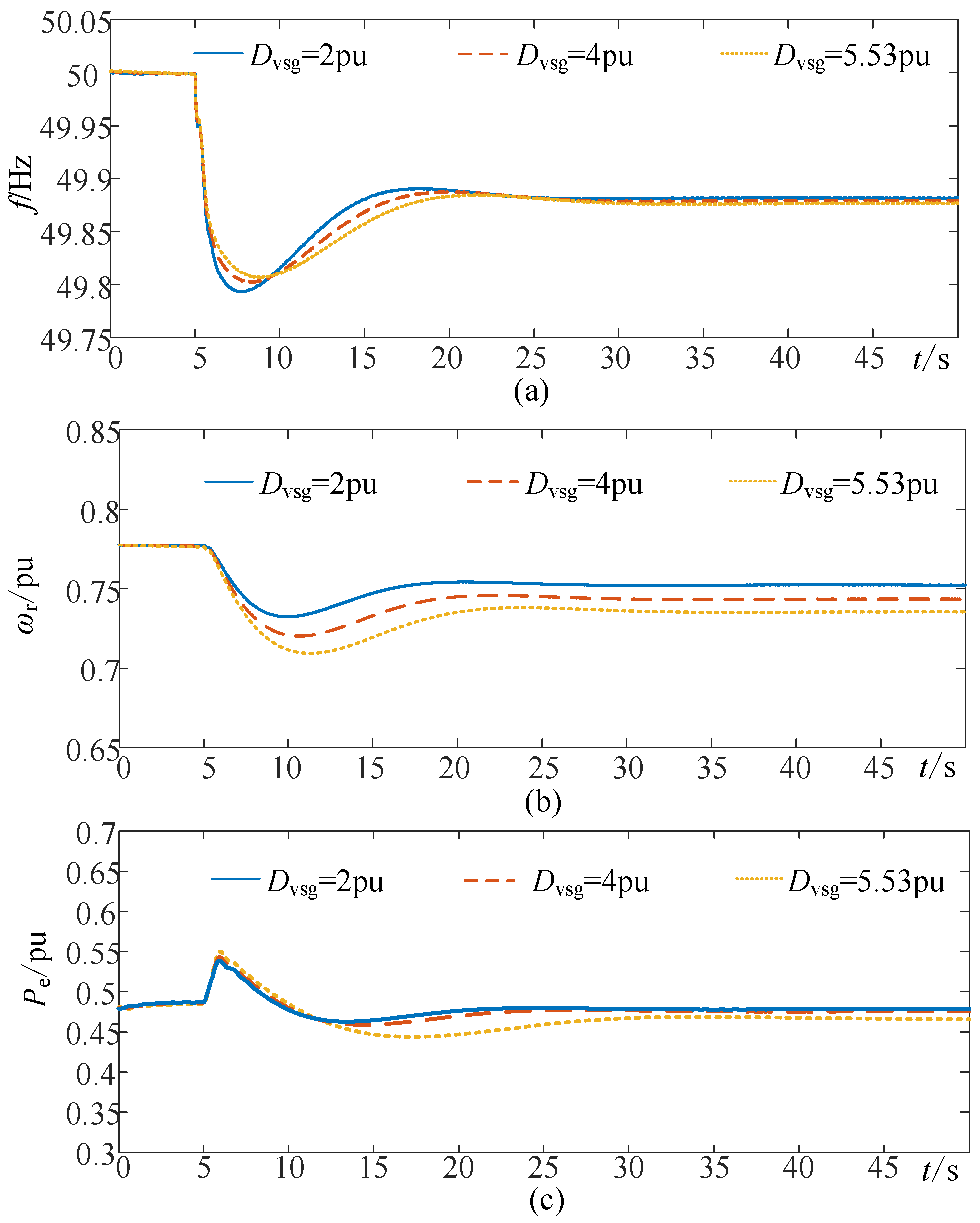
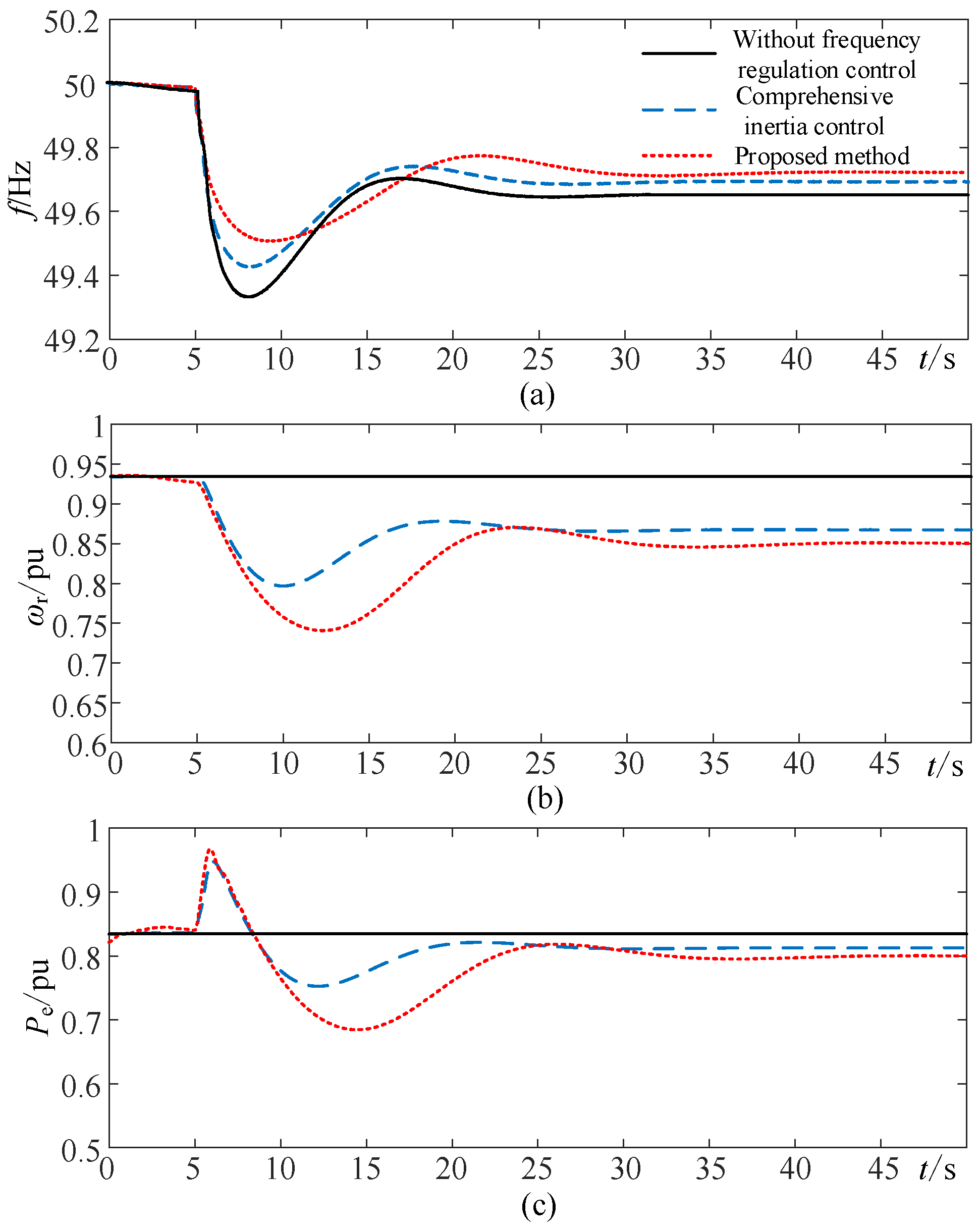
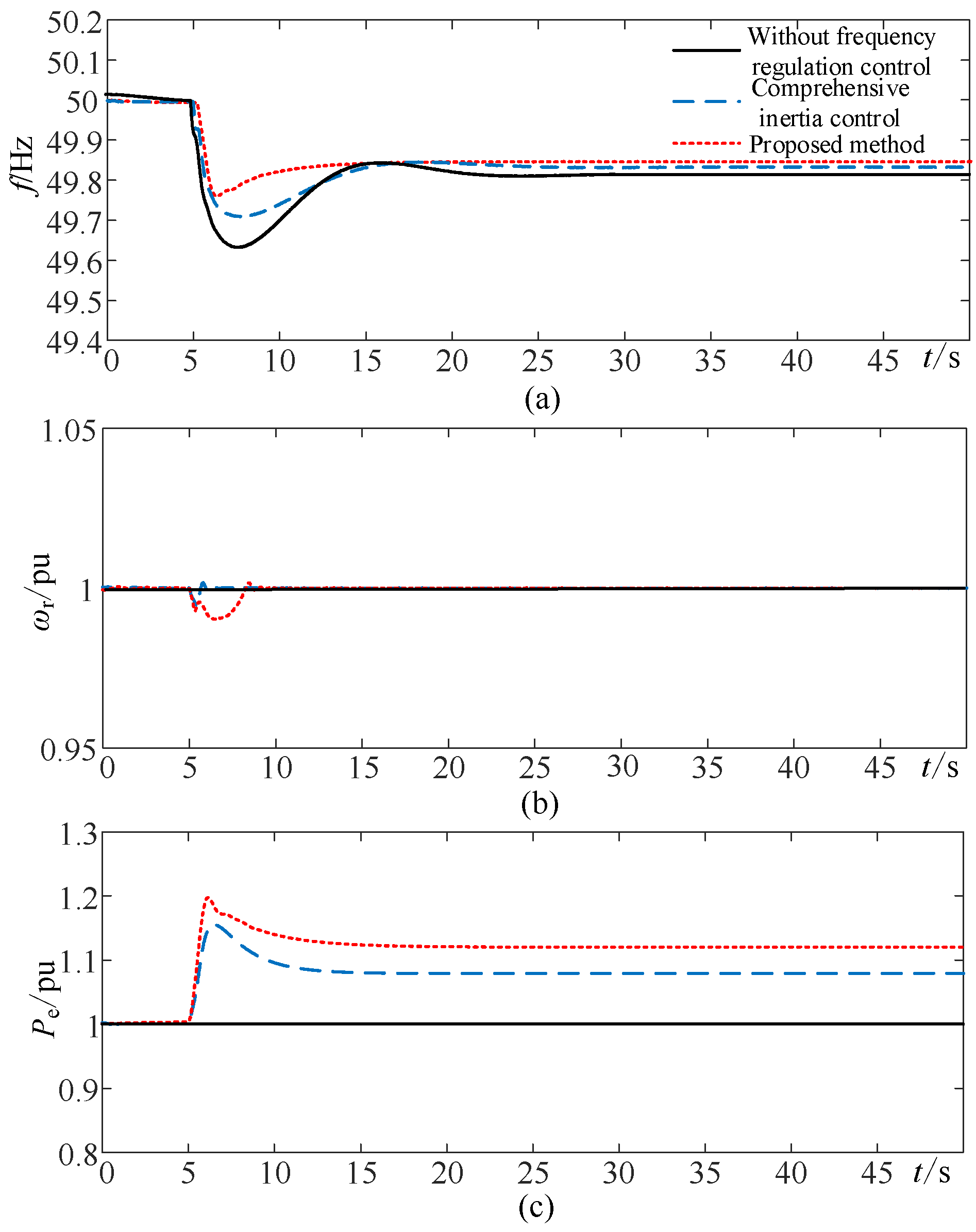
6.2. Case Studies
7. Conclusions
- The frequency regulation capability of WTG can be evaluated more comprehensively and accurately by quantifying the influence of the PFR dead zone on the system frequency response. Additionally, the frequency response model of the WTG based on VSG control is established, and the time domain analytic expression of the whole frequency response process is obtained;
- The trajectory sensitivity of each frequency regulation parameter is calculated, and the intensity of influence for each parameter on the dynamic frequency process is analyzed. As a result, the virtual damping parameter that plays a key role in the frequency modulation process is determined;
- Considering the different operating conditions and the dynamic frequency response process comprehensively, the optimization value of the virtual damping coefficient is determined based on the constraints of rotor speed and converter capacity so that WTG can make full use of available frequency regulation capacity and improve the frequency support capability. Hence, the proposed scheme has a certain engineering value for the optimization of the frequency regulation control parameter of WTG based on VSG control.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| MPPT | maximum power point tracking |
| PFR | primary frequency regulation |
| SG | synchronous generator |
| VSG | virtual synchronous generator |
| WTG | wind turbine generator |
| Pref | active power reference value (pu) |
| PW | output active power (pu) |
| PWTGe | electromagnetic power (pu) |
| PWTGm | mechanical power (pu) |
| PMPPT | output active power in MPPT mode (pu) |
| ΔPd | correction amount of electromagnetic power (pu) |
| ∆Pref | deviation of active power reference value (pu) |
| ∆Pf | output active power of PFR (pu) |
| ∆Pw | deviation of output active power (pu) |
| ∆PSG | output power variation of SG (pu) |
| ∆f | deviation of frequency (Hz) |
| Δωr | deviation of rotor speed (pu) |
| ω0 | rated angular frequency value (pu) |
| ωvsg | output angular frequency value (pu) |
| ωr | rotor speed (pu) |
| ωr0 | initial rotor speed (pu) |
| V | wind speed (m/s) |
| β | pitch angle (°) |
| Kvsg | the PFR coefficient |
| Jvsg | virtual inertia |
| Dvsg | virtual damping |
| Qref | reactive power reference value (pu) |
| Q | output reactive power (pu) |
| Uref | given value of output voltage amplitude (pu) |
| E | output voltage (pu) |
| Kq | reactive power-voltage droop regulation coefficient |
| kω | maximum power tracking coefficient |
| HWTG | inertia time constant of the WTG (s) |
| H | inertial time constant of the power system (s) |
| d | PFR dead zone (Hz) |
| DL | damping coefficient of system load |
| TG | turbine reheat time constant (s) |
| KG | PFR coefficient of SG (pu) |
References
- Singh, N.; Boruah, D.; De Kooning, J.D.M.; De Waele, W.; Vandevelde, L. Impact Assessment of Dynamic Loading Induced by the Provision of Frequency Containment Reserve on the Main Bearing Lifetime of a Wind Turbine. Energies 2023, 16, 2851. [Google Scholar] [CrossRef]
- Tu, G.; Li, Y.; Xiang, J. Coordinated Rotor Speed and Pitch Angle Control of Wind Turbines for Accurate and Efficient Frequency Response. IEEE Trans. Power Syst. 2022, 5, 3566–3576. [Google Scholar] [CrossRef]
- Ravanji, M.H.; Cañizares, C.A.; Parniani, M. Modeling and Control of Variable Speed Wind Turbine Generators for Frequency Regulation. IEEE Trans. Sustain. Energy 2020, 11, 916–927. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, B.; Xu, K.; Zhang, Y.; Hao, S.; Hu, Q. An Improved Over-Speed Deloading Control of Wind Power Systems for Primary Frequency Regulation Considering Turbulence Characteristics. Energies 2023, 16, 2813. [Google Scholar] [CrossRef]
- Afifi, M.A.; Marei, M.I.; Mohamad, A.M.I. Modelling, Analysis and Performance of a Low Inertia AC-DC Microgrid. Appl. Sci. 2023, 13, 3197. [Google Scholar] [CrossRef]
- Sun, P.; Yao, J.; Zhao, Y.; Fang, X.; Cao, J.Y. Stability Assessment and Damping Optimization Control of Multiple Grid-connected Virtual Synchronous Generators. IEEE Trans. Energy Convers. 2021, 36, 3555–3567. [Google Scholar] [CrossRef]
- Australian Energy Market Operator. Update Report: Black System Event in South Australia on 28 September 2016; Australian Energy Market Operation Limited: Melbourne, Australia, 2016. [Google Scholar]
- Chen, M.; Zhou, D.; Blaabjerg, F. Active Power Oscillation Damping Based on Acceleration Control in Paralleled Virtual Synchronous Generators System. IEEE Trans. Power Electron. 2021, 8, 9501–9510. [Google Scholar] [CrossRef]
- Shadoul, M.; Ahshan, R.; AlAbri, R.S.; Al-Badi, A.; Albadi, M.; Jamil, M. A Comprehensive Review on a Virtual-Synchronous Generator: Topologies, Control Orders and Techniques, Energy Storages, and Applications. Energies 2022, 15, 8406. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Q.; Zhou, J.; Guerrero, J.M.; Wang, R.; Lashab, A. Optimal Frequency Control for Virtual Synchronous Generator Based AC Microgrids via Adaptive Dynamic Programming. IEEE Trans. Smart Grid 2023, 14, 4–16. [Google Scholar] [CrossRef]
- Xiong, X.; Wu, C.; Hu, B.; Pan, D.; Blaabjerg, F. Transient Damping Method for Improving the Synchronization Stability of Virtual Synchronous Generators. IEEE Trans. Power Electron. 2021, 36, 7820–7831. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, T.; Wang, S.; Dong, Y.; Chen, Z. Comprehensive Coordinated Control Strategy of PMSG-Based Wind Turbine for Providing Frequency Regulation Services. IEEE Access 2019, 7, 63944–63953. [Google Scholar] [CrossRef]
- Wang, S.; Tomsovic, K. Fast Frequency Support From Wind Turbine Generators with Auxiliary Dynamic Demand Control. IEEE Trans. Power Syst. 2019, 34, 3340–3348. [Google Scholar] [CrossRef]
- Cardenas, R.; Pena, R.; Alepuz, S.; Asher, G. Overview of Control Systems for the Operation of DFIGs in Wind Energy Applications. IEEE Trans. Ind. Electron. 2013, 60, 2776–2798. [Google Scholar] [CrossRef]
- Wilches-Bernal, F.; Chow, H.; Sanchez-Gasca, J. A Fundamental Study of Applying Wind Turbines for Power System Frequency Control. IEEE Trans. Power Syst. 2016, 31, 1496–1505. [Google Scholar] [CrossRef]
- Van de Vyver, J.; De Kooning, J.D.M.; Meersman, B.; Vandevelde, L.; Vandoorn, T.L. Droop Control as an Alternative Inertial Response Strategy for the Synthetic Inertia on Wind Turbines. IEEE Trans. Power Syst. 2016, 31, 1129–1138. [Google Scholar] [CrossRef]
- Ghosh, S.; Kamalasadan, S.; Senroy, N. Doubly Fed Induction Generator (DFIG)-Based Wind Farm Control Framework for Primary Frequency and Inertial Response Application. IEEE Trans. Power Syst. 2016, 31, 1861–1871. [Google Scholar] [CrossRef]
- Arani, M.F.M.; Mohamed, Y.A.R.I. Dynamic Droop Control for Wind Turbines Participating in Primary Frequency Regulation in Microgrids. IEEE Trans. Smart Grid 2018, 9, 5742–5751. [Google Scholar] [CrossRef]
- Long, B.; Liao, Y.; Chong, K.T.; Rodriguez, J.; Guerrero, J.M. Enhancement of Frequency Regulation in AC Microgrid: A Fuzzy-MPC Controlled Virtual Synchronous Generator. IEEE Trans. Smart Grid 2021, 12, 3138–3149. [Google Scholar] [CrossRef]
- Abubakr, H.; Guerrero, J.M.; Vasquez, J.C.; Mohamed, T.H.; Mahmoud, K.; Darwish, M.M.; Dahab, Y.A. Adaptive LFC Incorporating Modified Virtual Rotor to Regulate Frequency and Tie-Line Power Flow in Multi-Area Microgrids. IEEE Access 2022, 10, 33248–33268. [Google Scholar] [CrossRef]
- Abubakr, H.; Vasquez, J.C.; Mohamed, T.H.; Guerrero, J.M. The concept of direct adaptive control for improving voltage and frequency regulation loops in several power system applications. Int. J. Electr. Power Energy Syst. 2022, 140, 108068. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Q.; Lin, S.; Bian, X.Y. A Self-Adaptive Inertia and Damping Combination Control of VSG to Support Frequency Stability. IEEE Trans. Energy Convers. 2017, 32, 397–398. [Google Scholar] [CrossRef]
- STyagi, S.; Das, S.; Singh, B. Coordinated Control for Seamless Integration of Wind Energy Conversion System with Small Hydrogenerator Through Modified Notch Filters. IEEE Trans. Energy Convers. 2023, 2023, 1–10. [Google Scholar] [CrossRef]
- Melhem, B.M.; Liu, S. Adaptive approach for primary frequency support by wind turbines based on grid code requirements and turbines limitations. In Proceedings of the 2023 IEEE PES Grid Edge Technologies Conference & Exposition (Grid Edge), San Diego, CA, USA, 10–13 April 2023; pp. 1–5. [Google Scholar]
- Fan, Y.; Qin, C.; Ju, P. Model Simplification and Parameter Identification of Generator Speed Governor System with Dead Zone Counting. In Proceedings of the 2022 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Shanghai, China, 6–9 July 2022. [Google Scholar]
- Huang, X.; Jin, Y.; Yan, P.; Ma, J.; Wang, C.; Ju, P. Integrated Model of DFIG and SFR for Frequency Regulation Control Research of Wind Turbine Generator. In Proceedings of the 2021 International Conference on Power System Technology (POWERCON), Haikou, China, 8–9 December 2021; pp. 57–61. [Google Scholar]
- Yu, L.; Sun, X.; Li, T.; Zhong, H.; Li, M.; Shao, Y. Virtual Inertia Control and Identification Method of Inertia Parameters for Doubly-Fed Units. In Proceedings of the 2022 4th International Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 27–30 October 2022; pp. 958–963. [Google Scholar]
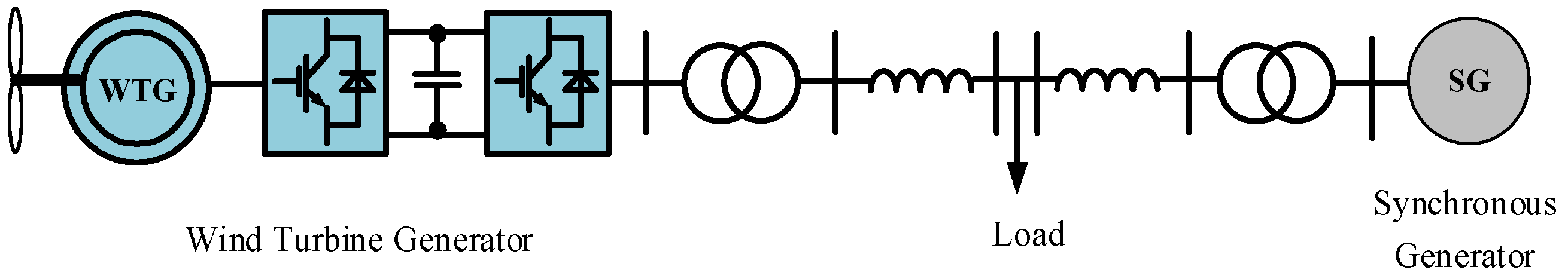



| Parameter | Value |
|---|---|
| Jvsg | 0.98 pu |
| Kvsg | 7.54 pu |
| KG | 20 pu |
| DL | 0 pu |
| Dvsg | 4 pu |
| TG | 5 s |
| H | 2.77 s |
| ∆PL | 0.1 pu |
| Parameter | Trajectory Sensitivity |
|---|---|
| Jvsg | 2.77 × 10−5 |
| Dvsg | 7.59 × 10−4 |
| Kvsg | 4.71 × 10−4 |
| d | 1.41 × 10−4 |
| Parameter | Value |
|---|---|
| Rated power | 2 MW |
| Rated voltage | 690 V |
| Frequency | 50 Hz |
| DC-link voltage | 1200 V |
| Stator resistance | 0.0126 pu |
| Stator d/q-axis inductance | 1.326 pu |
| Parameter | Value |
|---|---|
| Rated power | 5 MW |
| Rated voltage | 10.5 kV |
| Frequency | 50 Hz |
| d axis synchronous reactance | 2.13 pu |
| q axis synchronous reactance | 2.07 pu |
| Stator resistance | 0.005 pu |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Sun, P.; Chen, Z.; Qin, Z. Optimization of a Virtual Synchronous Control Parameter for a Wind Turbine Generator Considering the Physical Constraint Boundary of Primary Frequency Regulation. Appl. Sci. 2023, 13, 5569. https://doi.org/10.3390/app13095569
Cao J, Sun P, Chen Z, Qin Z. Optimization of a Virtual Synchronous Control Parameter for a Wind Turbine Generator Considering the Physical Constraint Boundary of Primary Frequency Regulation. Applied Sciences. 2023; 13(9):5569. https://doi.org/10.3390/app13095569
Chicago/Turabian StyleCao, Junying, Peng Sun, Zhaoyang Chen, and Zhentao Qin. 2023. "Optimization of a Virtual Synchronous Control Parameter for a Wind Turbine Generator Considering the Physical Constraint Boundary of Primary Frequency Regulation" Applied Sciences 13, no. 9: 5569. https://doi.org/10.3390/app13095569
APA StyleCao, J., Sun, P., Chen, Z., & Qin, Z. (2023). Optimization of a Virtual Synchronous Control Parameter for a Wind Turbine Generator Considering the Physical Constraint Boundary of Primary Frequency Regulation. Applied Sciences, 13(9), 5569. https://doi.org/10.3390/app13095569







