1. Introduction
The fundamental principle of seismic base isolation is to modify the structural response by introducing a “soft layer” made of isolation bearings able to decouple the soil motion from that of the structure above, which almost behaves rigidly above the isolation system [
1,
2,
3]. Consequently, the behavior of isolation devices plays a fundamental role in the seismic response of base-isolated structures, and the variability of their properties during the service life significantly influences the seismic response of both the isolation system itself and the superstructure. Thus, this variability cannot be neglected in the analysis and design of base isolated structures and must be properly accounted for to increase the seismic reliability of base-isolated buildings, especially the strategic ones, such as schools and hospitals, whose diffusion is more and more increasing worldwide [
4,
5,
6].
Different sources of variability can be identified, from environmental conditions (such as temperature, ageing, etc.) to behavioral effects specific of each device typology. For example, for high damping rubber bearings (HDRBs), which are the focus of this paper, the behavior significantly depends on the strain amplitude, the strain rate and the load history (i.e., on the maximum strain amplitude attained and the number of experienced cycles) [
7,
8]. This last effect results in a change in the device properties with cycles, and it is known as the Mullins effect [
9] or “scragging” [
7,
8,
10,
11]. For other kinds of bearings, such as lead rubber bearings (LRBs) or concave curved sliders (CSSs), the behavior significantly depends on the temperature increment during the load history, i.e., the heating effect [
12,
13]. Other critical aspects influencing the performance of sliding isolation devices are, for example, the vertical pressure, the sliding velocity affecting the friction coefficient [
12] and the breakaway effect [
14]. Different papers were recently published on the importance of these effects on the actual behavior of base-isolated buildings [
15,
16], as well as for other supplemental damping systems, e.g., [
17].
The international seismic codes all agree in prescribing that the design process cannot be performed by only considering nominal properties of isolation bearings. However, in some cases, such codes provide only some general information or prescribe simplified approaches that are not always complete or clear, making difficult, de facto, the application of such prescriptions. In more detail, focusing on the European context and on HDRBs, Eurocode 8 for buildings [
18] only specifies that the values of physical and mechanical properties of the isolation system should be the most unfavorable ones that can be attained during the lifetime of the structure. Both environmental and behavioral effects should be considered, where relevant. Eurocode 8 for bridges [
19] gives more operative indications by proposing a simplified approach, described in Annex J, based on upper and lower bound coefficients to obtain upper bound design properties (UBDPs) and lower bound design properties (LBDPs) from nominal design properties (NDPs). Consequently, two analyses shall be performed: one using the UBDPs (generally leading to maximum forces and accelerations acting on the superstructure) and another using the LBDPs (generally leading to maximum displacements of the isolation system). This code also specifies that in absence of relevant test results, the upper and lower bound coefficients (also called
λ-factors) given in Annex JJ may be assumed. The same approach is proposed by the European standard on anti-seismic devices (EN 15129) [
20], which is a product standard mainly focused on qualification and control tests that also includes some design indications. In detail, this standard also prescribes the use of
λ-factors values based on the experimental data provided by the specific manufacturer, and, in the case of unavailability of such data, it provides the Annex J with the same
λ-factors values given by Annex JJ of the Eurocode 8 for bridges [
19]. It is important to note that, nowadays, in both the national and international contexts, experimental data are often available only after the qualification tests of the devices, thus, resulting as unknown at the design phase. Moreover, type tests made during the qualification procedure do not always include all the necessary information to correctly evaluate the UBDPs and LBDPs. Consequently, the values of the
λ-factors proposed by codes often become the only reference for structural engineers.
The aim of this paper is to illustrate in detail such factors by making a historical reconstruction of their origin. In more detail, in the first part of the paper, the current European seismic codes are illustrated by highlighting that all the provided
λ-factors derive from the second edition of the AASHTO (AASHTO 1999) [
21]. Thus, such code is illustrated in detail by showing that most of the proposed values of the
λ-factors derive from old and/or limited data that do not reflect the actual production of seismic devices, especially for HDRBs, and that were never updated in the subsequent editions: AASHTO 2010 [
22] and AASHTO 2014 [
23]. Moreover, in some cases, important clerical errors or omissions were made in the European standards, as was also outlined in [
24]. This is the case, for example, for the temperature effect and the so-called “scragging” effect (or repeated cycles effect) of HDRBs. Concerning the temperature effect, indeed, a transcription error was made by passing from the American to the European standard. This error was corrected in the updated version of Eurocode 8-part 2 [
25] but not in the EN15129 [
20]. For the repeated cycles effect, instead, American values were not included in the European standards. In this regard, it is worth noting that the difference between scragged and unscragged properties suggested by the AASHTO code is remarkable, and this aspect has limited the use of this kind of bearings in the USA, especially for strategic structures, such as nuclear power plants and bridges [
26,
27,
28,
29]. For this kind of structure, natural rubber bearings (NRBs) or lead rubber bearings (LRBs) are only allowed as alternative systems to friction pendulum (FP) systems. However, this paper explains that such a remarkable effect refers to old bearings (with incomplete curing) that could differ significantly from the current ones. For this reason, the values of AASHTO were not transposed by the European standards; however, alternative values were not provided, leaving a lack of data regarding this aspect. In the last part of the paper, more recent international regulations orientated towards new approaches [
30,
31,
32,
33] are examined to provide a complete overview and to open new perspectives. In detail, the indications of ASCE 7 seismic standards for new and existing buildings [
30,
31] are illustrated. These codes, which are also taken as a reference by high-risk countries other than the U.S., such as Chile, Turkey, and New Zealand, provide updated values of the
λ-factors, which, however, must be verified by mandatory experimental tests. Finally, the approach of recent international regulations to elastomeric bearings, the ISO 22726 for buildings and bridges [
32,
33], is also reported. However, these documents provide few values only, since, following the Japanese approach described in the design recommendations for seismically isolated buildings [
34], they specify that the ranges of variation for most of the effects should be defined in agreement between the structural engineer and the manufacturers.
2. Behavior of HDRBs
HDRBs are composed by alternating layers of steel and rubber; thus, under horizontal loads, they inherit the shear behavior of the rubber compound adopted in their manufacturing.
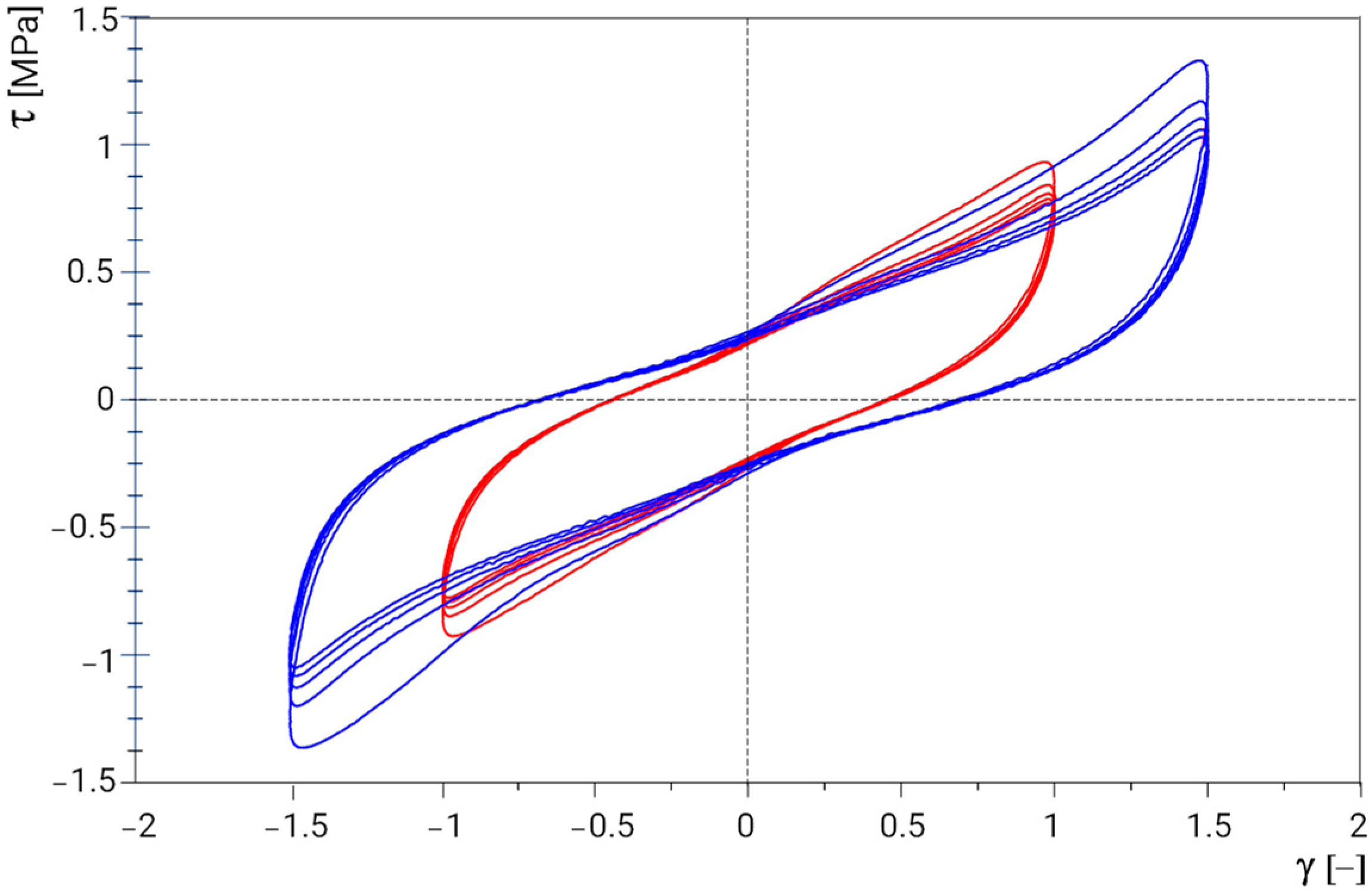
Figure 1 shows the shear behavior of a compound typically used for HDRBs (furnished by FIP MEC) at two different strain amplitudes, i.e., 100% and 150%. As can be observed from the hysteresis loops, the strain amplitude dependence and the repeated cycle effect are not negligible, even though they are limited. Differently, the strain rate dependence is generally negligible in the range of velocities relevant to seismic applications [
7,
8].
These behavioral effects can be accounted for in advanced numerical models [
7,
8,
11,
35,
36]. Alternatively, simplified models can be adopted, such as linear models [
37] (defined in terms of equivalent linear stiffness,
G, and damping,
ξ) or bi-linear equivalent models [
38,
39] (defined in terms of strength at zero displacement,
F0, and post-elastic stiffness,
Kp), by assuming different sets of parameters properly calibrated to simulate these effects. Similarly, for the environmental effects of ageing and temperature, two simplified models can be calibrated to simulate the two extreme conditions (i.e., aged and not-aged conditions or the behaviors under maximum and minimum design temperatures).
In
Figure 2a, a general representation of UBDPs, LBDPs and NDPs is depicted, with reference to the bi-linear model. It is worth noting that the stiffness of the bearings directly influences the isolation period,
Tis, while their dissipation capacity influences the displacements of the bearings themselves. Moreover, both the parameters influence the base shear and the absolute acceleration experienced by the superstructure. Thus, LBDPs usually maximize the isolation system displacements, while UBDPs maximize the isolation system reactions, i.e., the base shear and floor accelerations of the superstructure.
The following sections summarize the code recommendations in the most seismically active counties on the U/L bound approach to account for these sources of variability in the design and analysis of base-isolated structures. The main aim is to illustrate the limits of the current approach of the European codes, which are still based on outdated American standards and present some omissions and transcription errors, and to highlight and promote more modern approaches.
3. Seismic European Standards
Eurocode 8 for bridges [
19] specifies that nominal design properties (DP) of isolator units shall be evaluated according to EN15129 [
20], i.e., for elastomeric bearing 3rd cycle data at the reference condition: a temperature of 23°, a frequency of 0.5 Hz and a shear strain equal to 100%. However, since environmental or behavioral effects (such as temperature, contamination, ageing or repeated cycles) may significantly influence the dynamic properties of the isolator units and, thus, the seismic response of the isolation system, two sets of design properties should be used in the analyses: UBDPs and LBDPs. This variability should be established in accordance with Annex J and Annex JJ unless different indications are derived by performing the appropriate tests. In more detail, the influence of the following phenomena should be evaluated: ageing (
f1), temperature (
f2), contamination (
f3) and cumulative travel (
f4). Moreover, by assuming a bi-linear behavior of the bearings, the design properties influenced by the above-mentioned factors are the post elastic stiffness (
Kp) and the force at zero displacement (
F0), as shown in
Figure 2. The recommended values for the most commonly used isolators, i.e., elastomeric bearings and sliding isolating units, are given. For elastomeric isolators, which are the object of this investigation, the recommended values for ageing and temperature are given (as reported in
Table 1 and
Table 2, respectively), while unitary values are suggested for contamination and cumulative travel. Four categories are considered by this code: low damping rubber bearings (LDRBs) with an equivalent shear modulus at 100% of strain G > 0.5 MPa; HDRBs
1 with an equivalent damping coefficient of ξ ≤ 0.15, and an equivalent shear modulus at 100% of strain G > 0.5 MPa; HDRBs
2 with an equivalent damping coefficient of ξ > 0.15 and an equivalent shear modulus at 100% of strain G > 0.5 MPa and LRBs. Furthermore, combination factors (
λU,fi) are defined to account for the low probability of the simultaneous occurrence of all maximum adverse effects, as shown in
Table 3 for important classes I (bridges of less than average importance), II (bridge of average importance) and III (bridges of critical importance). The effective UBDPs used in the design are estimated as follows:
where modification factors
λU,fi are defined as follow:
For the effective LBDPs and relevant modification factors, λL,fi, a similar format should be used, in conjunction with λmin,fi. However, for the commonly used elastomeric and friction bearings, it may be assumed in general that λmin,fi = 1 and, therefore, that LBDP = min DPnom.
A similar approach is recommended by the European standard on anti-seismic devices [
20] by also considering the variation of the dynamic properties of the bearings within the production supply. Here, again, the code specifies that for all the effects (i.e., the variation in temperature or ageing for elastomeric bearings), UBDPs and LBDPs shall be determined from the type tests carried out before the bearing production. However, when such experimental values are not available, the Annex J provides the same reference factors as Annex JJ of [
19]. For the production variability, a tolerance of ±20 % is allowed unless a lower variability agreed upon for the factory production control tests. In combining these effects, a combination factor equal to
ψfi = 0.7 is suggested for both the production variability and temperature variation, whereas a factor
ψfi = 1.0 is recommended for the ageing variation. In any case, the ratio between the UBDPs and LBDPs should be less than 1.8 for the elastomeric bearings.
As is illustrated in the next section, the
λ-factors currently suggested by both the European codes derive from the second AASHTO edition [
21], whose data are based on the report of Constantinou et al. [
40]. It is highlighted that these documents, dated back to 1999, were never updated for elastomeric bearings.
4. Second Edition of AASHTO Guide Specification (1999)
The upper and lower bound properties of isolation bearings were provided for the first time by the second edition of AASHTO [
21] to increase the reliability of the design of base-isolated bridges. To obtain such bounding values, property modification factors (
λ) were proposed and then used to obtain the adjusted maximum and minimum system property modification factors (accounting for the reduced probability of the occurrence of joint events) by applying the following expressions:
where
a is the adjustment factor. Based on engineering judgment and on the desire to employ a conservative approach for mission-critical bridges, the following adjustment factors (
a) are proposed for bridges: 1.0 for critical bridges, 0.75 for essential bridges and 0.66 for all other bridges. In more detail,
λ-factors are provided for different effects (ageing, contamination, travel, temperature and scragging for sliding and/or elastomeric isolators), based on the experimental and theoretical knowledge of the behavior of seismic isolation bearings at the code drafting time. Furthermore, all the proposed values are based on the report of Constantinou et al. [
40], containing background information that led to the definition of
λ-factor values. In this regard, it is worth noting that, while for sliding bearings, several data are reported and commented, those related to elastomeric devices are limited and briefly reported. In Section 5.6 of [
40], “system property modification factors for elastomeric bearings”, the authors themselves affirm that for elastomeric bearings,
λ-factors strongly depend on the elastomeric compound, that a variety of compounds is used for their manufacturing and that experimental data are scarce. Thus, the values presented in their document and assumed in [
21] are primary based on a “proposal of the Authors”. In the following subsections, the
λ-factors are reported and commented on for each considered effect with reference to elastomeric systems. The proposed values refer to the post-elastic stiffness (
Kd) and the characteristic strength (
Qd), corresponding, respectively, to
Kp and
F0 in the Eurocodes.
4.1. Ageing Effect
Concerning the ageing effect, the authors of the report again affirm that “given the rather recent origin of the seismic isolation technology, there is a complete lack of data on aged isolation bearings. During the research several laboratories and in field data are collected for sliding bearings, while very limited data are collected for elastomeric bearings”. In detail, the
λ-factors for both
Kd and
Qd are assumed equal to 1.1 for LDRBs, 1.2 for HDRBs with small differences between scragged and unscragged properties (smaller than 25%) and 1.3 for HDRBs with large differences between scragged and unscragged properties (larger than 25%, as reported in
Table 4). It can be observed that the values suggested by the European codes (
Table 1) agree with those proposed by AASHTO (
Table 4) by assuming that HDRBs
1 and HDRBs
2 correspond to HDRBs with small and large differences between scragged and unscragged properties, respectively. Nevertheless, it should be noted that the authors themselves write that the first two values are based on limited data and the last one is mainly based on the engineering judgement. In more detail, the authors cite in their report some papers dealing with old natural rubbers that are not provided with sufficient anti-oxidant properties, as opposed to what happens with modern compounds. The most relevant paper considered by the report is the one of Clark et al. [
41], which concerns some tests carried out on some LDRBs and HDRBs in 1983, in conjunction with the construction of the Foothill Communities Law and Justice Center in California. After 12 years of service, some HDRBs were removed from the building and tested again. Although there is uncertainty in the interpretation of the results, since original tests and re-tests were performed with different machine configurations and probably with different rates of loading, the authors conclude that the effective stiffness increment is approximately 25%. Based on this study, they conclude that the mechanical properties modestly increase due to ageing: the increment is in the order of 10% for LDRBs (made by natural rubber) and 20% for HDRBs over a period of approximately 30 years. They also introduce a difference between elastomeric isolators with small or large differences between unscragged and scragged properties. In their opinion, such a large difference is typical of high damping elastomeric isolators characterized by incomplete curing of the elastomer, which implies the continuation of chemical processes in the rubber and, therefore, a potential source for ageing. To account for this aspect, they advanced the proposal of increasing the ageing effect (over the same period) up to 30% for HDRBs with large differences between scragged and unscragged properties.
4.2. Temperature Effect
Concerning the temperature effect, the
λ-factors assumed in the AASHTO code are reported in
Table 5. It is explained in the report that such values are based on results described in [
42,
43], referring to LDRBs and HDRBs with effective damping less than 15% and moderate differences between unscragged and scragged properties, whereas no data are available for HDRBs with effective damping larger than 15%. Thus, as outlined by the authors, the difference between values of these two kinds of HDRBs (see
Table 5) “has been arbitrarily assumed” by the task group writing the code. A further interesting remark of the authors is that all the analyzed studies focus on the effect of low temperature on the properties of elastomeric bearings, neglecting the influence of the duration of exposure to such low temperatures. In more detail, some of them do not report the duration of exposure at all, while others report an approximate exposure time. This aspect introduces a significant source of uncertainty affecting all the proposed data.
Moreover, it should be observed that, differently from the ageing effect, in this case, the suggested values for
Qd and
Kd are different and they coincide with those proposed by the European codes for
F0 and
Kp (
Table 2) (by assuming that HDRBs
1 and HDRBs
2 correspond to HDRBs with small and large differences between scragged and unscragged properties) only if the values referring to
Kp and
F0 in
Table 2 are inverted. This suggests that a transcription error was made when writing the annexes of [
19,
20]. This error was later corrected in the updated version of the Eurocode 8 [
25], but it remains in the EN 15129 [
20].
4.3. Repeated Cycles Effect
Regarding the repeated cycles effect, it is generally recognized that LDRBs do not exhibit much difference between unscragged and scragged properties. Differently, the additives used in the rubber compound to enhance the damping capacity of HDRBs and the curing process are responsible for a significant loading history dependence of the rubber behavior, leading to a bigger difference between the unscragged (virgin) and scragged (stable) properties. It is also known that rubber bearings recover their virgin properties and that significant recovery occurs within a short period of time. Based on these observations, the authors of the report specify that if nominal properties of HDRBs refer to the scragged condition (i.e., stable hysteretic cycles), the
λ-factors may be used to estimate the unscragged (virgin) properties of the isolation bearings. However, at the drafting time of the report, few published results were available in a form that could be suitable for the calibration of the appropriate values of
λ-factors. In [
44], by testing small scale HDRBs with effective damping less than approximately 0.15, it was found that the
λ-factors for both the characteristic strength and the post-yield stiffness were of the order of 1.2 (or even less). However, the authors of the report here again declare that improperly cured bearings may exhibit much higher damping and a much higher ratio between unscragged and scragged properties, as is also confirmed by data reported in [
45], relevant to bearings with effective damping in the range 0.15–0.20. Based on these limited data, the factors shown in
Table 6 were proposed by the task group writing the second edition of the AASHTO code [
21].
It is important to remark that such values of property modification factors for scragging were never adopted by the European codes because they refer to scragged properties, i.e., stable properties, whereas Eurocodes define 3rd cycle data as nominal properties. However, alternative values were not given, thus, in the case where experimental data are unavailable, there are no indications in the European context regarding how to account for the repeated cycles effect.
5. Updated Editions of AASHTO Guide Specification (2010 and 2014)
The 1999 report [
40] first proposed indications to account for the effects of the change in the mechanical properties of isolation bearings, which were implemented in [
21], as well as in other successive seismic codes such as [
19,
20,
46]. In 2007, a new technical report, Constantinou et al. [
12], was developed to update the previous one, i.e., to better predict the behavioral and environmental effects on seismic isolators and dampers. In detail, Section 12 of [
12] focuses on system property modification factors and clearly specifies that the approach based on
λ-factors is a simplified one and that the most probable maximum and minimum values of the mechanical properties of isolation bearings should be established by statistical analysis of the distribution of the properties. However, since the exact approach is challenging, the
λ-factors approach may be used for most of the base-isolated structures. In this case, it is specified that the maximum and minimum values of the mechanical properties presented in the document are default values that should be verified with appropriate test data and that all manufacturers are encouraged to develop these kinds of tests. However, the default values are also maintained in the case of unavailable experimental data, but here, again, for friction bearings (widely used in American applications), the updated values are based on a large experimental campaign carried out at the University of Buffalo and at Queen’s University in Canada and/or on the analyses of the extensive technical literature. Differently, for elastomeric bearings the experimental tests concern LDRBs only (tested at the Buffalo University), while for HDRBs (scarcely used in American applications), few of the new data available in the technical literature are collected and discussed.
5.1. Temperature Effect
For the temperature effect on elastomeric bearings, the same references of the past report [
40] are reported, except for one paper [
47], which was published after 1999 and which investigates the low temperature performance of LDRBs as a function of temperature and duration of exposure for four materials. Based on these studies, the
λ-values collected in
Table 7 are proposed by specifying that the data for HDRBs are for elastomers named as HDRB
a in
Table 5.
However, the task group in charge of updating the AASHTO guide specifications decided to not change values of the previous edition. Thus, in both the 3rd edition [
22] and 4th edition [
23], the values of
Table 5 are maintained.
5.2. Repeated Cycles Effect
For the repeated cycles effect, notably influencing the behavior of HDRBs, two further studies [
10,
48] were analyzed in addition to the references already commented on in the previous section. The first one reports an experimental campaign carried out on 23 moderate-scale rubber bearings with effective damping in the range between 0.05–0.17 and establishes that the scragging effect increases as the shear modulus of rubber decreases and the effective damping increases. The second paper extends the first one and presents results from tests performed on 45 moderate-scale rubber bearings fabricated by six manufacturers using a total of 12 compounds. The outcomes show that the percentage reduction in the effective shear modulus from the first to third cycle strongly depends on the formulation of the rubber compound, the vulcanization procedure used to fabricate the isolator and the imposed strain history. The data reported in these two works suggest that the greater the volume of filler (to obtain high damping and low shear modulus), the greater the potential scragging effect. Furthermore, all rubber bearings recover their virgin properties, but the time to fully recover them depends on the rubber compound, the extent of its curing and the ambient temperature. Finally, experimental cruciform tests also indicate that scragging along one axis significantly influences the response on the perpendicular axis, as was also found in more recent papers [
8,
11], but here, again, the degree of interaction is strongly compound dependent. Based on these considerations, the values reported in
Table 8 are proposed in [
12] as defaults ones to apply to full scragged properties (assumed as nominal properties). Differently. for low damping and low modulus elastomers (usually used in lead-rubber bearings), little-to-no scragging is assumed.
Basically, the two previous papers [
10,
48] deftly advise against the use of HDRBs because their load history dependent behavior (leading to the scragging effect) was too compound-dependent and difficult to predict. This is one of the reasons why
λ-factors have not been updated in AASHTO guide specifications [
22,
23].
5.3. Ageing Effect
The data reported in [
10,
48] are also discussed for the ageing effect. In the 2007 report, it is affirmed that HDRBs are generally not significantly affected by ozone and oxygen because they are fabricated with a layer of cover rubber, including anti-oxidants, to protect the core of the bearing from significant infiltrations and that age-related stiffening or hardening is rather due to the vulcanization process of the elastomer, which continues over time. Thus, the percentage of increase in the effective modulus varies depending on several factors, including the level of the initial curing and the temperature. The ongoing vulcanization of the rubber matrix occurs more rapidly in the first few years after the rubber is compounded, while it slows later. Although the authors recognize in their new report that experimental data on this specific topic do not exist, they confirmed the
λ-factors of
Table 4, including the value of 1.3 for HDRBs with large differences between scragged and unscragged properties. Concerning LRBs, it is confirmed that they generally show an insignificant change in the characteristic strength (which is mainly dictated by the yield strength of the lead core) and a minor (and negligible) increase in the post-elastic stiffness.