Clustering Approach for Reliable Wireless Communication
Abstract
:1. Introduction
2. Materials and Methods
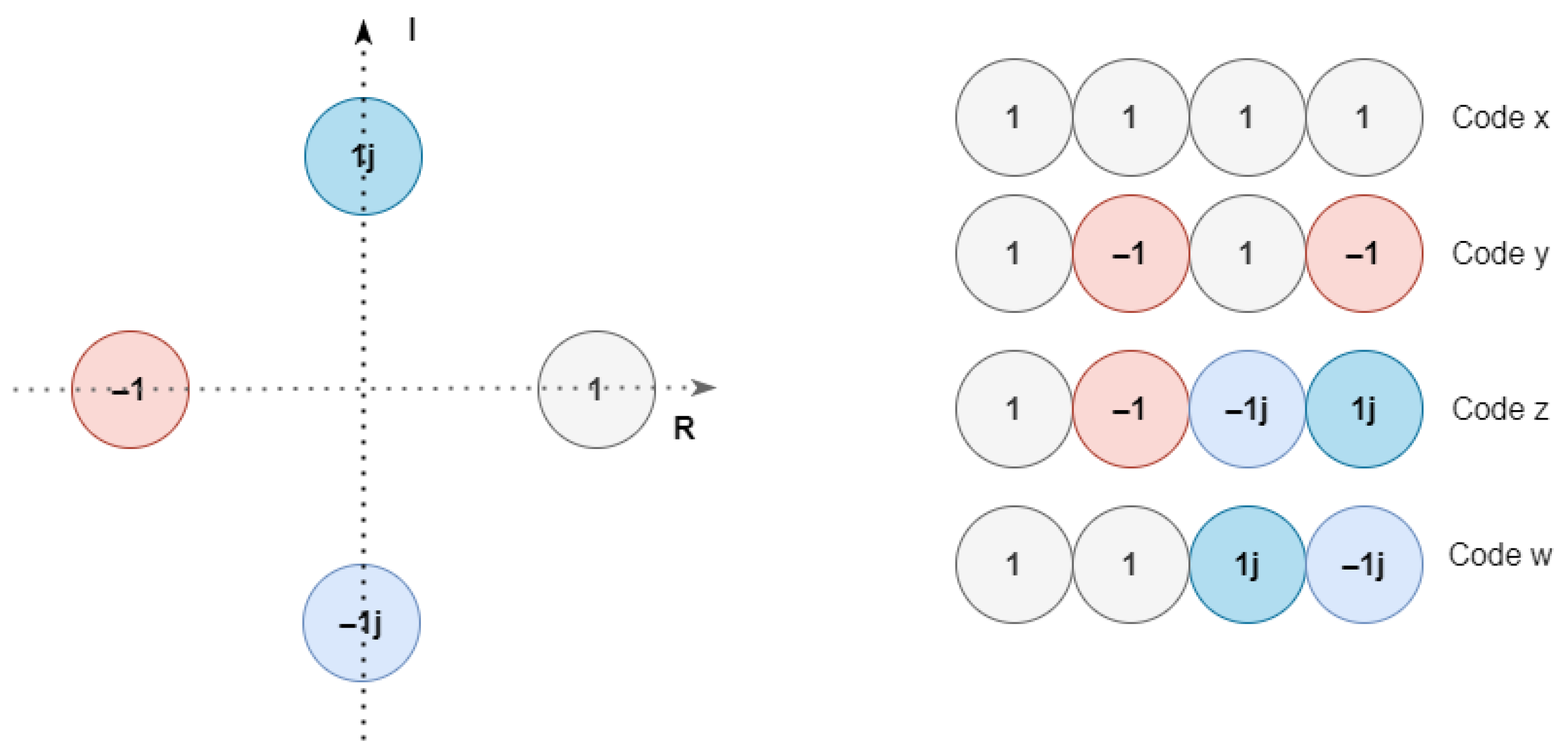
2.1. MUSA Codes Selection
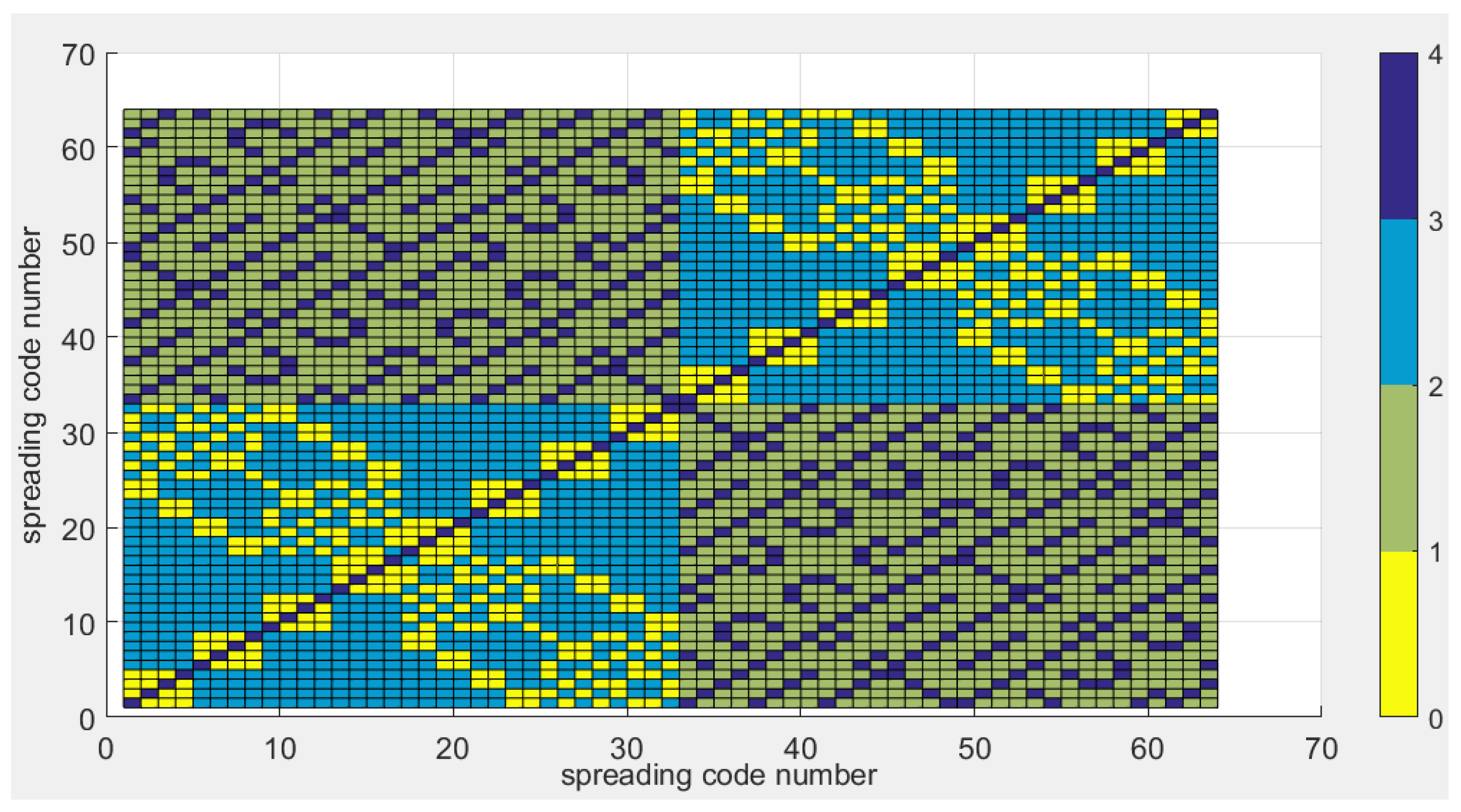
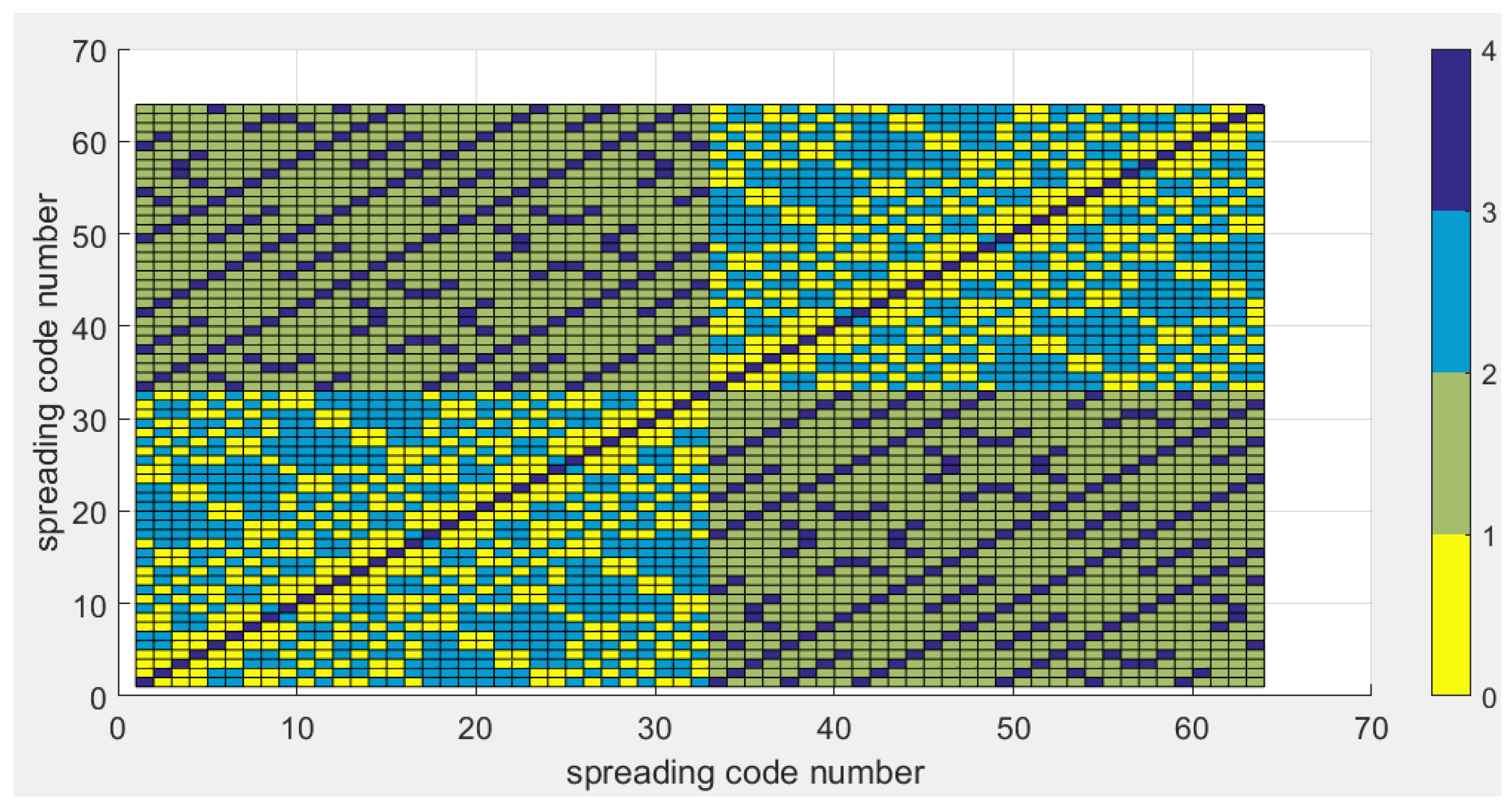
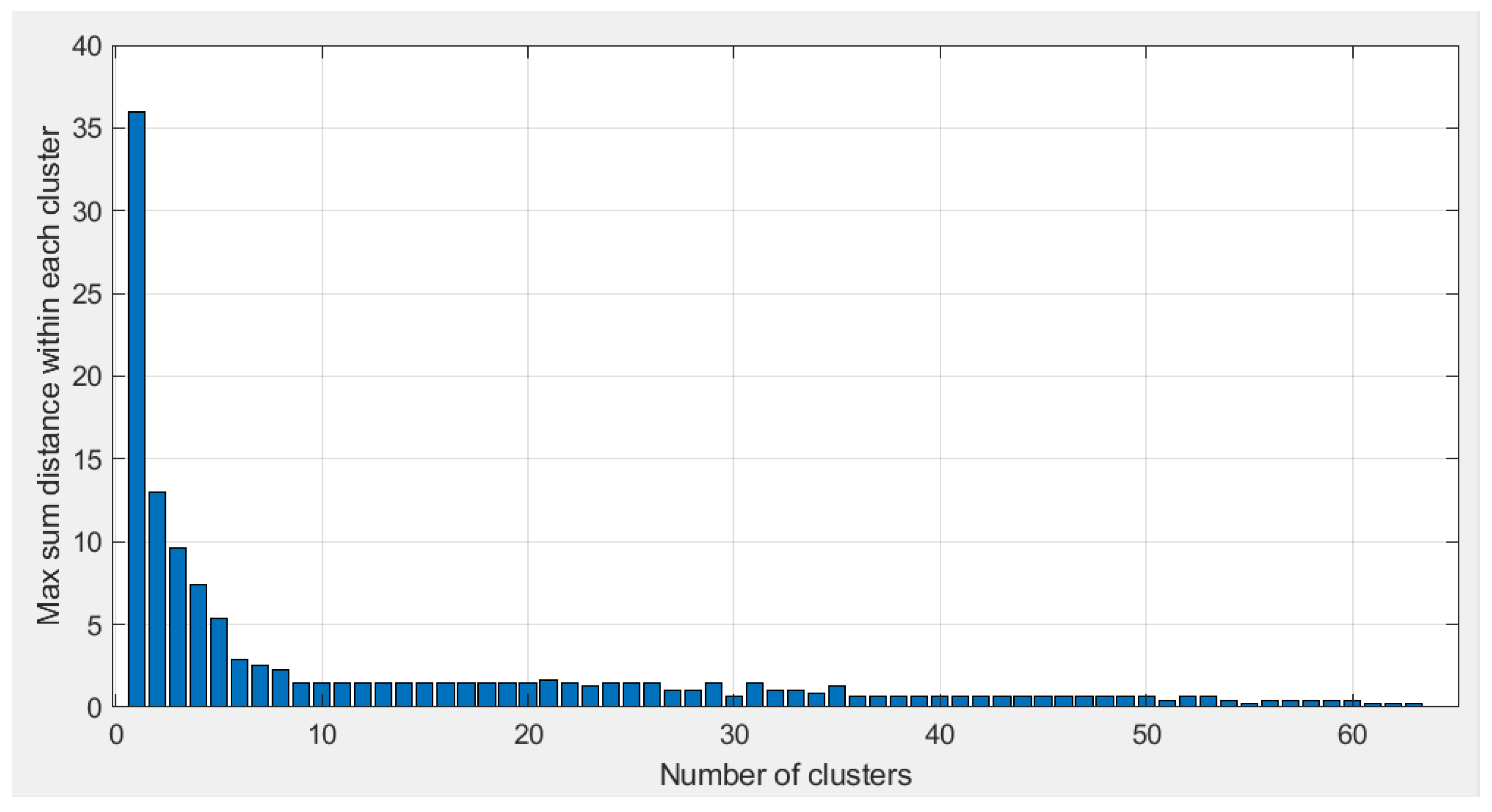
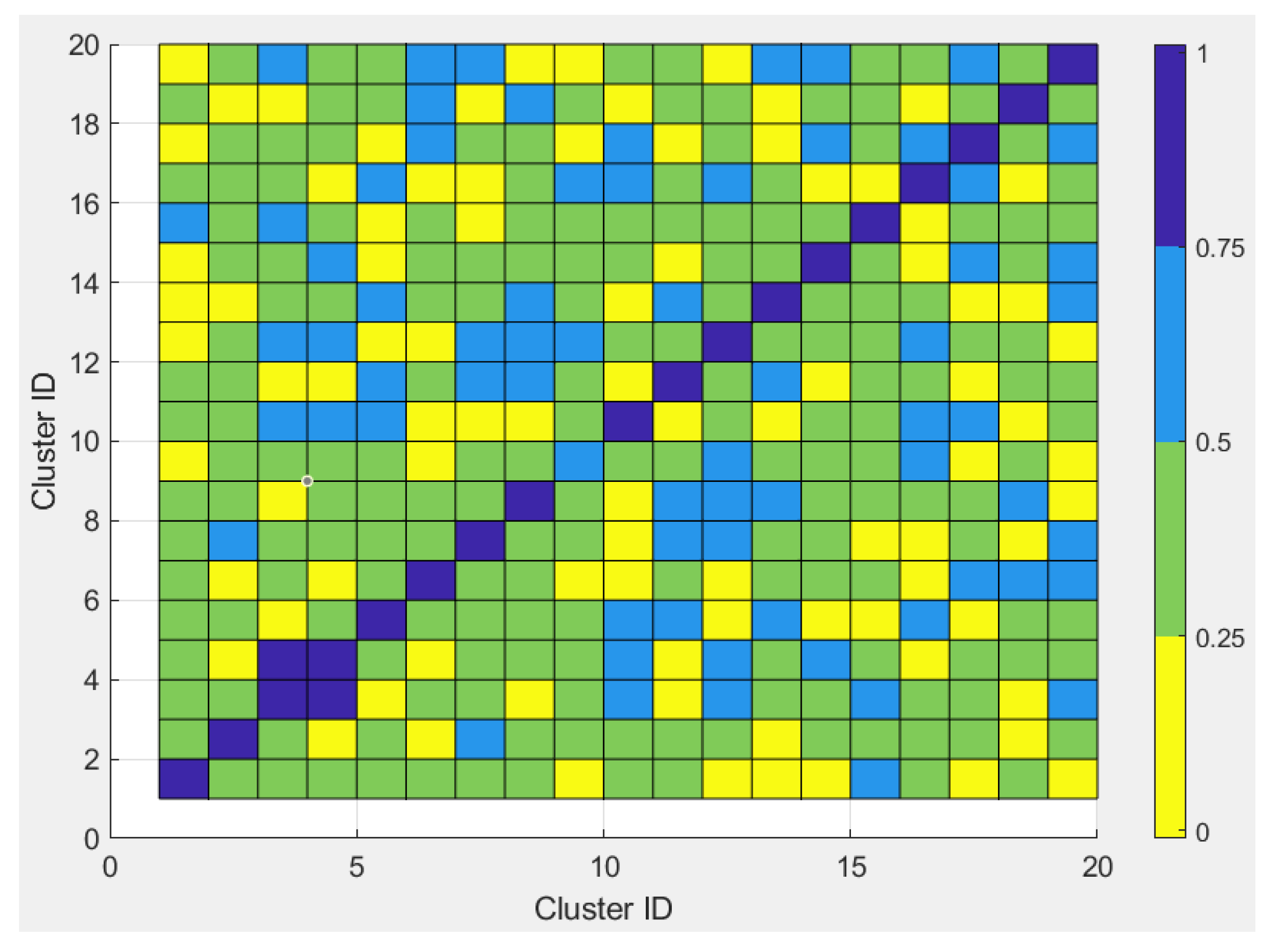
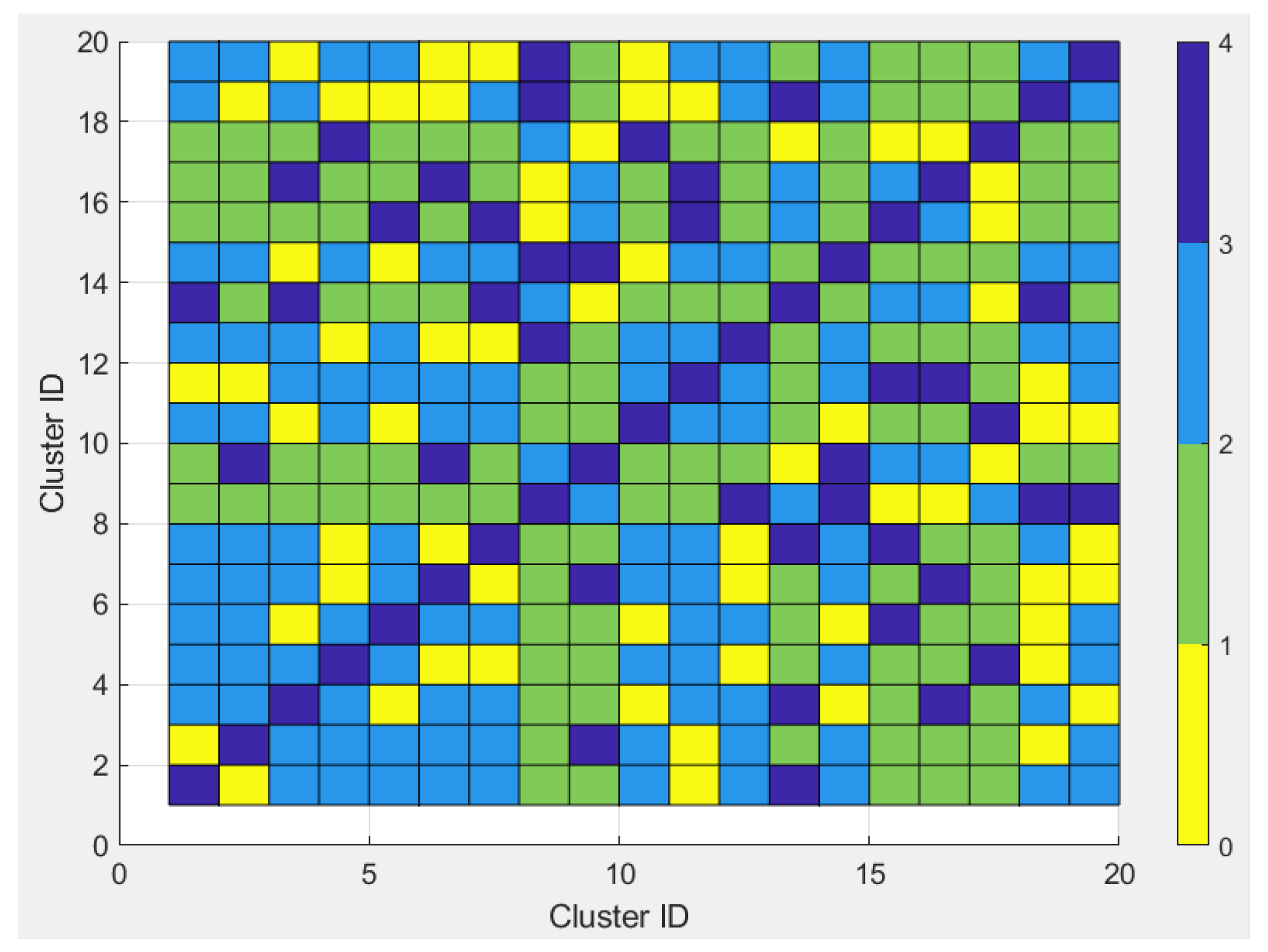
2.2. Cluster Conception and Performance
- The method first creates k groups (clusters) of highly cross-correlated sequences.
- Next, a single sequence is assigned to various users, chosen at random from the group. Users are divided into groups based on a round-robin process. Users using the same cluster can only randomly choose sequences from that corresponding cluster.
- ○
- Squared Euclidean distance:
- ○
- Assumption: The higher the distance d between sequences s and c, the less the cross-correlation.
- ○
- The center sequence of cluster c is the average value of the sequences of the cluster:
- ○
- Sample correlation between sequences:
- ○
- Assumption: The higher the difference of “1 − sample correlation between points” (viewed as sequences of values) is, the smaller the correlation.
- ○
- To determine the sequences of a cluster, they are normalized to have zero mean and unit standard deviation. Next, the center sequence (s) in cluster (c) is computed.
where is a row of L elements of one.are elements of a sequence s and the cluster’s center c.- ○
- One minus the normalized cross-correlation.
- ○
- The clustering algorithm groups highly correlated codes by minimizing the distance between them. Therefore, the distance metric should be smaller for codes with high correlation. Thus, we chose one minus the normalized cross-correlation as a distance metric.
3. System Model and Set-Up
- The number of users varies from 20 to 70.
- The length of data transmitted by each user is 700 or 7000 bits.
- Digital modulation: BPSK and QPSK;
- Noise on the communication channel: AWGN;
- Simulation iterations: 10.
4. Results and Discussion
4.1. Scenario 1: Two Antennas at BS/20 Users/MUSA Codes Length 4
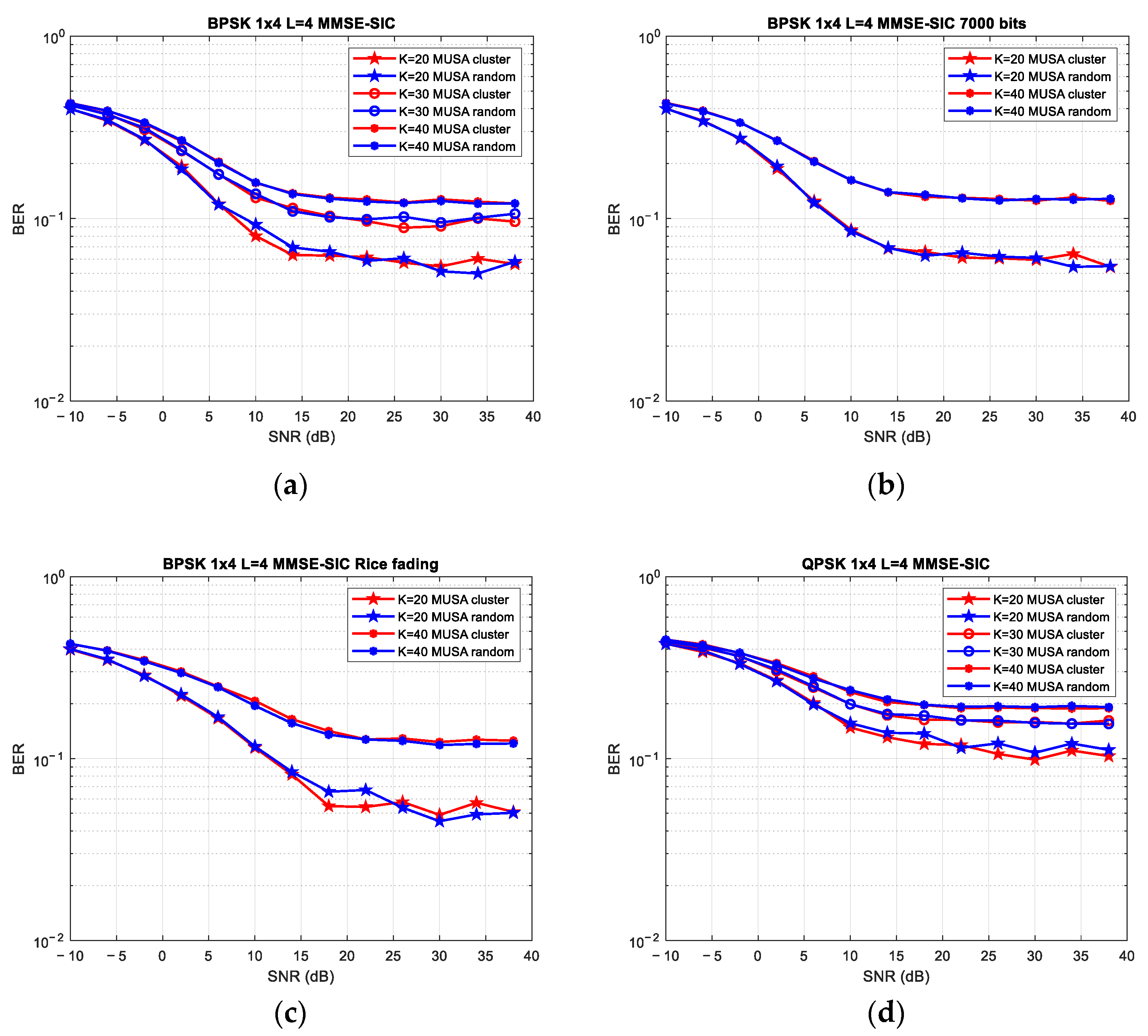
4.2. Scenario 2: Two Antennas at BS/20, 30, and 40 Users/MUSA Code Length of 4
4.3. Scenario 3: Four Antennas at BS/20, 30, and 40 Users/MUSA Code Length of 4
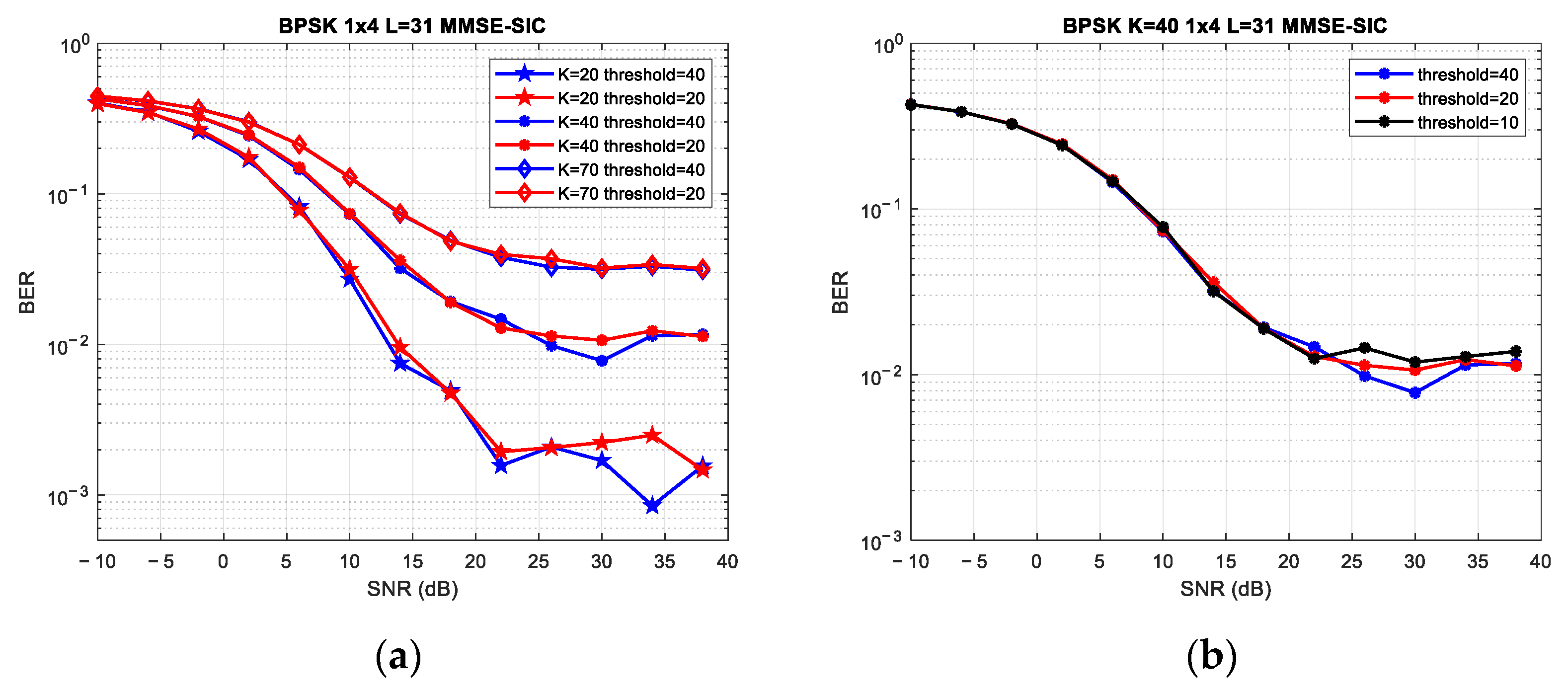
4.4. Scenario 4: Four Antennas at BS/40 and 62 Users/MUSA Code Length of 31
4.5. Scenario 5: Four Antennas at BS/20, 40, and 70 Users/MUSA Code Length of 31
4.6. Scenario 6: Two and Four Antennas at BS/20, 30, and 40 Users/MUSA Code Length of 4
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sinaie, M.; Wing Kwan Ng, D.; Jorswieck, E.A. Resource Allocation in NOMA Virtualized Wireless Networks under Statistical Delay Constraints. IEEE Wirel. Commun. Let. 2018, 7, 954–957. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, H.; Li, Y.; Ding, Z.; Vucetic, B. Antenna selection for MIMO-NOMA networks. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017. [Google Scholar]
- Ding, Z.; Liu, Y.; Choi, J.; Sun, Q.; Elkashlan, M.; Chih-Lin, I.; Poor, H.V. Application of non-orthogonal multiple access in LTE and 5G networks. IEEE Commun. Mag. 2017, 55, 185–191. [Google Scholar] [CrossRef]
- Ding, Z.; Lei, X.; Karagiannidis, G.K.; Schober, R.; Yuan, J.; Bhargava, V. A survey on non-orthogonal multiple access for 5G networks: Research challenges and future trends. IEEE J. Sel. Areas Commun. 2017, 35, 2181–2195. [Google Scholar] [CrossRef]
- Baidas, M.W.; Alsusa, E.; Hamdi, K.A. Performance analysis of downlink NOMA networks over Rayleigh fading channels. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018. [Google Scholar]
- Wan, D.; Wen, M.; Cheng, X.; Mumtaz, S.; Guizani, M. A promising non-orthogonal multiple access-based networking architecture: Motivation, conception, and evolution. IEEE Wirel. Commun. 2019, 26, 152–159. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Yuan, Y.; Han, S.; Chih-Lin, I.; Wang, Z. Nonorthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends. IEEE Commun. Mag. 2015, 53, 74–81. [Google Scholar] [CrossRef]
- Lin, B.; Tang, X.; Ghassemlooy, Z. A Power Domain Sparse Code Multiple Access Scheme for Visible Light Communications. IEEE Wirel. Commun. Lett. 2020, 9, 61–64. [Google Scholar] [CrossRef]
- Balasubramanya, N.M.; Gupta, A.; Sellathurai, M. Combining Code-Domain and Power-Domain NOMA for Supporting Higher Number of Users. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018. [Google Scholar]
- Islam, S.M.R.; Avazov, N.; Dobre, O.A.; Kwak, K.-S. Power domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and challenges. IEEE Commun. Surv. Tutor. 2017, 19, 721–742. [Google Scholar] [CrossRef]
- Ding, Z.; Adachi, F.; Poor, H.V. The application of MIMO to nonorthogonal multiple access. IEEE Trans. Wirel. Commun. 2016, 15, 537–552. [Google Scholar] [CrossRef]
- Ding, Z.; Dai, L.; Poor, H.V. MIMO-NOMA design for small packet transmission in the Internet of Things. IEEE Access 2016, 4, 1393–1405. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, Z.; Elkashlan, M.; Poor, H.V. Cooperative nonorthogonal multiple access with simultaneous wireless information and power transfer. IEEE J. Sel. Areas Commun. 2016, 34, 938–953. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, X.; Lu, L.; Wu, Y.; He, G.; Chen, Y. Sparse code multiple access: An energy efficient uplink approach for 5G wireless systems. In Proceedings of the 2015 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014. [Google Scholar]
- Mathur, H.; Deepa, T. A Survey on Advanced Multiple Access Techniques for 5G and Beyond Wireless Communications. Wirel. Pers. Commun. 2021, 118, 1775–1792. [Google Scholar] [CrossRef]
- Mohammadi, M.; Shi, X.; Chalise, B.K.; Ding, Z.; Suraweera, H.A.; Zhong, C.; Thompson, J.S. Full-duplex non-orthogonal multiple access for next generation wireless systems. IEEE Commun. Mag. 2019, 57, 110–116. [Google Scholar] [CrossRef]
- Jamali, M.V.; Mahdavifar, H. Massive Coded-NOMA for Low-Capacity Channels: A Low-Complexity Recursive Approach. IEEE Trans. Commun. 2021, 69, 3664–3681. [Google Scholar] [CrossRef]
- Yan, C.; Yuan, Z.; Li, W.; Yuan, Y. Non-Orthogonal Multiple Access Schemes for 5G. ZTE Commun. 2016, 14, 11–16. [Google Scholar]
- Shukla, A.; Kumar, M.; Kumar Deolia, V. Code domain non orthogonal multiple access schemes for 5G and beyond communication networks: A review. J. Eng. Res. 2021, 10, 132–152. [Google Scholar] [CrossRef]
- Chauhan, A.; Jaiswal, A. Multidimensional Signal Space Non-Orthogonal Multiple Access with Imperfect SIC: A Novel SIC Reduction Technique. IEEE Trans. Veh. Technol. 2023, 1–15. [Google Scholar] [CrossRef]
- Kusume, K.; Bauch, G.; Utschick, W. IDMA vs. CDMA: Analysis and Comparison of Two Multiple Access Schemes. IEEE Trans. Wirel. Commun. 2012, 11, 78–87. [Google Scholar] [CrossRef]
- Sony, D.; Keerthi, P.; Aditya, O.; Sravya, N. Simulation and Performance Analysis of Interleave Division Multiple Access (IDMA) in Comparison with Code Division Multiple Access (CDMA). Asian J. Appl. Sci. Technol. 2021, 5, 90–94. [Google Scholar] [CrossRef]
- Al-Imari, M.; Imran, M.A. Low density spreading multiple access. In Multiple Access Techniques for 5G Wireless Networks and Beyond; Springer: Cham, Switzerland, 2018; pp. 493–514. [Google Scholar]
- Elsaraf, Z. Performance Analysis of Code Domain NOMA in 5G Systems. In Proceedings of the 2019 Conference: Emerging Technology Conference (EMiT_19), Huddersfield, UK, 9–11 April 2019. [Google Scholar]
- Wang, Q.; Zhang, R.; Yang, L.-L.; Hanzo, L. Non-Orthogonal Multiple Access: A Unified Perspective. IEEE Wirel. Commun. 2018, 25, 10–16. [Google Scholar] [CrossRef]
- Nikopour, H.; Baligh, H. Sparse code multiple access. In Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013. [Google Scholar]
- Tao, Y.; Liu, L.; Liu, S.; Zhang, Z. A Survey: Several Technologies of Non-Orthogonal Transmission for 5G. China Commun. 2015, 12, 1–15. [Google Scholar] [CrossRef]
- Yuan, Z.; Yu, G.; Li, W.; Yuan, Y.; Wang, X.; Xu, J. Multi-User Shared Access for Internet of Things. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016. [Google Scholar]
- Eid, E.M.; Fouda, M.M.; Tag Eldien, A.S.; Tantawy, M.M. Performance analysis of MUSA with different spreading codes using ordered SIC method. In Proceedings of the 2017 12th International Conference on Computer Engineering and Systems (ICCES), Cairo, Egypt, 19–20 December 2017. [Google Scholar]
- Zia, M.F.; Hamamreh, J.M. An advanced non-orthogonal multiple access security technique for future wireless communication networks. RS Open J. Innov. Commun. Technol. 2020, 1, 1–10. [Google Scholar] [CrossRef]
- Hayat, O.; Ngah, R.; Hashim, S.Z.M. Multi-user Shared Access (MUSA) procedure for device discovery in D2D communication. Telecommun. Syst. 2021, 76, 291–297. [Google Scholar] [CrossRef]
- Kim, H.; Kim, H.; Hong, D. Performance of 5G Multiple Access Schemes. In Proceedings of the 2022 International Conference on Electronics, Information, and Communication (ICEIC), Jeju, Republic of Korea, 6–9 February 2022. [Google Scholar]
- Tan, Y.; Li, S.; Su, B.; Xia, Z. MUSA System Based on Extended Sequences Optimization and User Rate Power Allocation. In Proceedings of the 2023 9th International Conference on Control Science and Systems Engineering (ICCSSE), Shenzhen, China, 16–18 June 2023. [Google Scholar]
- Thushan, S.; Ali, S.; Mahmood, N.H.; Rajatheva, N.; Latva-Aho, M. Deep Learning-Based Blind Multiple User Detection for Grant-Free SCMA and MUSA Systems. IEEE Trans. Mach. Learn. Commun. Netw. 2023, 1, 61–77. [Google Scholar] [CrossRef]
- Wu, X.; Lu, L.; Jiang, M. Deep learning aided cyclostationary feature analysis for blind modulation recognition in massive MIMO systems. Digit. Signal Process. 2023, 134, 103890. [Google Scholar] [CrossRef]
- Jhamb, A. Analysis of Various Parameters Used in CDMA and IDMA Techniques. Int. J. Eng. Dev. Res. 2017, 5, 392–394. [Google Scholar]
- Vishvaksenan, K.S.; Rajmohan, R. Performance analysis of multi-carrier IDMA system for co-operative networks. Clust. Comput. 2019, 22, 7695–7703. [Google Scholar] [CrossRef]
- Luo, Q.; Gao, P.; Liu, Z.; Xiao, L.; Mheich, Z.; Xiao, P.; Maaref, A. An Error Rate Comparison of Power Domain Non-Orthogonal Multiple Access and Sparse Code Multiple Access. IEEE Open J. Commun. Soc. 2021, 2, 500–511. [Google Scholar] [CrossRef]
- Jehan, A.; Zeeshan, M. Comparative Performance Analysis of Code-Domain NOMA and Power-Domain NOMA. In Proceedings of the 2022 16th International Conference on Ubiquitous Information Management and Communication (IMCOM), Seoul, Republic of Korea, 3–5 January 2022. [Google Scholar]
- Shukla, A. Comparative analysis of various code domain NOMA schemes for future communication networks. Mater. Today Proc. 2021, 46, 5797–5800. [Google Scholar] [CrossRef]
- Al-Dulaimi, O.M.K.; Al-Dulaimi, A.M.K.; Alexandra, M.O.; Al-Dulaimi, M.K.H. Strategy for Non-Orthogonal Multiple Access and Performance in 5G and 6G Networks. Sensors 2023, 23, 1705. [Google Scholar] [CrossRef]
- Chen, Y.; Bayesteh, A.; Wu, Y.; Ren, B.; Kang, S.; Sun, S.; Xiong, Q.; Qian, C.; Yu, B.; Ding, Z.; et al. Toward the standardization of non-orthogonal multiple access for next generation wireless networks. IEEE Commun. Mag. 2018, 56, 19–27. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, G.; Zheng, L.; Liu, R.; Zhao, D. BER Performance Evaluation of Downlink MUSA over Rayleigh Fading Channel. In Proceedings of the MLICOM 2017: Machine Learning and Intelligent Communications, Weihai, China, 5–6 August 2017. [Google Scholar]
- Prashar, A.; Sood, N. Performance Analysis of MIMO-NOMA and SISO-NOMA in Downlink Communication Systems. In Proceedings of the 2022 2nd International Conference on Intelligent Technologies (CONIT), Hubli, India, 24–26 June 2022. [Google Scholar]
- Umakoglu, I.; Namdar, M.; Basgumus, A. UAV-Assisted Cooperative NOMA System with the nth Best Relay Selection. Adv. Electr. Comput. Eng. 2023, 23, 39–46. [Google Scholar] [CrossRef]
- Budhiraja, I.; Kumar, N.; Tyagi, S.; Tanwar, S.; Han, Z.; Piran, J.; Suh, D.Y. A Systematic Review on NOMA Variants for 5G and beyond. IEEE Access 2021, 9, 85573–85644. [Google Scholar] [CrossRef]
- Wang, B.; Wang, K.; Lu, Z.; Xie, T.; Quan, J. Comparison study of non-orthogonal multiple access schemes for 5G. In Proceedings of the 2015 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, Ghent, Belgium, 17–19 June 2015. [Google Scholar]
- Oyerinde, O.O. Comparative Study of Overloaded and Underloaded NOMA Schemes with Two Multiuser Detectors. In Proceedings of the 2019 IEEE 2nd Wireless Africa Conference (WAC), Pretoria, South Africa, 18–20 August 2019. [Google Scholar]
- Kim, H.; Lim, Y.-G.; Chae, C.-B.; Hong, D. Multiple Access for 5G New Radio: Categorization, Evaluation, and Challenges. arXiv 2017, arXiv:1703.09042. [Google Scholar]
- Eid, E.M.; Fouda, M.M.; Tag Eldien, A.S.; Tantawy, M.M. Performance analysis of 5-ary MUSA and SCMA for uplink transmission. Indones. J. Electr. Eng. Comput. Sci. 2019, 15, 365–372. [Google Scholar]
- ATIS 3GPP SPECIFICATION, 3rd Generation Partnership Project; Technical Specification Group Radio Access Network. Study on Non-Orthogonal Multiple Access (NOMA) for NR (Release 16); 3GPP Support Office: Sophia Antipolis, France, 2018. [Google Scholar]
- 3GPP 38.812 TR. Study on Non-Orthogonal Multiple Access (NOMA) for NR. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3236 (accessed on 20 July 2023).
- Dutta, P.; Ramyasree, J.; Sridhar, V.; Minchula, V.K.; Mohanta, H.C.; Mahfoudh, S.; Shah, S.B.H.; Singh, S.P. Evaluating the Efficiency of Non-Orthogonal MU-MIMO Methods in Smart Cities Technologies & 5G Communication. Sustainability 2023, 15, 236. [Google Scholar] [CrossRef]
- Andrew, G.J. A Primer on Zadoff Chu Sequences. arXiv 2023, arXiv:2211.05702v2. [Google Scholar]
- Matlab Documentation for K-Means. Available online: https://www.mathworks.com/help/stats/kmeans.html (accessed on 1 November 2023).
- Domathoti, B.; Ch, C.; Madala, S.; Berhanu, A.A.; Rao, Y.N. Simulation Analysis of 4G/5G OFDM Systems by Optimal Wavelets with BPSK Modulator. J. Sens. 2022, 2022, 8070428. [Google Scholar] [CrossRef]





| Codeword No. | Codeword No. | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 33 | 1 | 1 | 1 | −j |
| 2 | 1 | 1 | −1 | −1 | 34 | 1 | 1 | −1 | j |
| 3 | 1 | −1 | 1 | −1 | 35 | 1 | −1 | 1 | j |
| 4 | 1 | −1 | −1 | 1 | 36 | 1 | −1 | −1 | −j |
| 5 | 1 | 1 | −j | j | 37 | 1 | 1 | −j | 1 |
| 6 | 1 | 1 | j | −j | 38 | 1 | 1 | j | −1 |
| 7 | 1 | −1 | −j | −j | 39 | 1 | −1 | −j | −1 |
| 8 | 1 | −1 | j | j | 40 | 1 | −1 | j | 1 |
| 9 | 1 | −j | 1 | j | 41 | 1 | −j | 1 | 1 |
| 10 | 1 | −j | −1 | −j | 42 | 1 | −j | −1 | −1 |
| 11 | 1 | j | 1 | −j | 43 | 1 | j | 1 | −1 |
| 12 | 1 | j | −1 | j | 44 | 1 | j | −1 | 1 |
| 13 | 1 | −j | −j | −1 | 45 | 1 | −j | −j | j |
| 14 | 1 | −j | j | 1 | 46 | 1 | −j | j | −j |
| 15 | 1 | j | −j | 1 | 47 | 1 | j | −j | −j |
| 16 | 1 | j | j | −1 | 48 | 1 | j | j | j |
| 17 | 1 | 1 | 1 | −1 | 49 | 1 | 1 | 1 | j |
| 18 | 1 | 1 | −1 | 1 | 50 | 1 | 1 | −1 | −j |
| 19 | 1 | −1 | 1 | 1 | 51 | 1 | −1 | 1 | −j |
| 20 | 1 | −1 | −1 | −1 | 52 | 1 | −1 | −1 | j |
| 21 | 1 | 1 | −j | −j | 53 | 1 | 1 | −j | −1 |
| 22 | 1 | 1 | j | j | 54 | 1 | 1 | j | 1 |
| 23 | 1 | −1 | −j | j | 55 | 1 | −1 | −j | 1 |
| 24 | 1 | −1 | j | −j | 56 | 1 | −1 | j | −1 |
| 25 | 1 | −j | 1 | −j | 57 | 1 | −j | 1 | −1 |
| 26 | 1 | −j | −1 | j | 58 | 1 | −j | −1 | 1 |
| 27 | 1 | j | 1 | j | 59 | 1 | j | 1 | 1 |
| 28 | 1 | j | −1 | −j | 60 | 1 | j | −1 | −1 |
| 29 | 1 | −j | −j | 1 | 61 | 1 | −j | −j | −j |
| 30 | 1 | −j | j | −1 | 62 | 1 | −j | j | j |
| 31 | 1 | j | −j | −1 | 63 | 1 | j | −j | j |
| 32 | 1 | j | j | 1 | 64 | 1 | j | −j | |
| Parameter | Value |
|---|---|
| FFT length | 128 |
| Data subcarriers | 72 |
| SC spacing | 15 kHz |
| FFT sampling frequency | 15 kHz × 128 = 1.92 MHz |
| Subcarrier indexes | −36 to −1 and 1 to 36 |
| OFDM symbol duration | 1/15 kHz = 66.7 µs |
| CP duration | 4.76 µs |
| Total symbol duration | 71.43 µs |
| Scenario No. | Features |
|---|---|
| 1 | 2 antennas at BS/K = 20/MUSA code length of 4/Rayleigh fading/BPSK |
| 2 | 2 antennas at BS/K = 20, 30, 40/MUSA code length of 4/Rayleigh and Rice fading/BPSK and QPSK |
| 3 | 4 antennas at BS/K = 20, 30, 40/MUSA code length of 4/Rayleigh and Rice fading/BPSK and QPSK |
| 4 | 4 antennas at BS/K = 40 and 62/MUSA code length of 31 |
| 5 | 4 antennas at BS/K = 20, 40, and 70/MUSA code length of 31 |
| 6 | 2 and 4 antennas at BS/K = 20, 30, and 40/MUSA code length of 4 |
| Scenario No. | Method Type | MUSA Code Length | SNR (dB) | Variation | Discussions |
|---|---|---|---|---|---|
| 1 | No clustering | 2 | 30 | MMSE | The combination of the clustering method and MMSE-SIC leads to better results in BER terms than the classic approach for low-length MUSA codes. |
| Clustering | MMSE-SIC | ||||
| 2 | K = 20 | 4 | 30 | Random vs. Cluster | Since performance is similar, it can be stated that the clustering approach cannot be efficient for an overloaded system with users having limited resources which transmit large data. When comparing the outcomes of Rayleigh and Rice fading, Rice performs better because it emulates LoS communication. Furthermore, by analyzing BPSK and QPSK performance in this system, it was shown that a BPSK modulation scheme produces better BER values; however, the clustering benefits can be at a lower SNR for QPSK. |
| K = 30 | |||||
| K = 40 | |||||
| 3 | No clustering vs. clustering | 4 | 30 | K= 20 vs. K = 30 vs. K = 40 | |
| 4 | No clustering | 31 | - | K = 40 vs. K = 62 and random vs. PN codes | Overlapping high-length MUSA codewords (random/PN) and an increased number of users does not lead to improvement. The clustering approach performs well for a reduced number of users. |
| Clustering | |||||
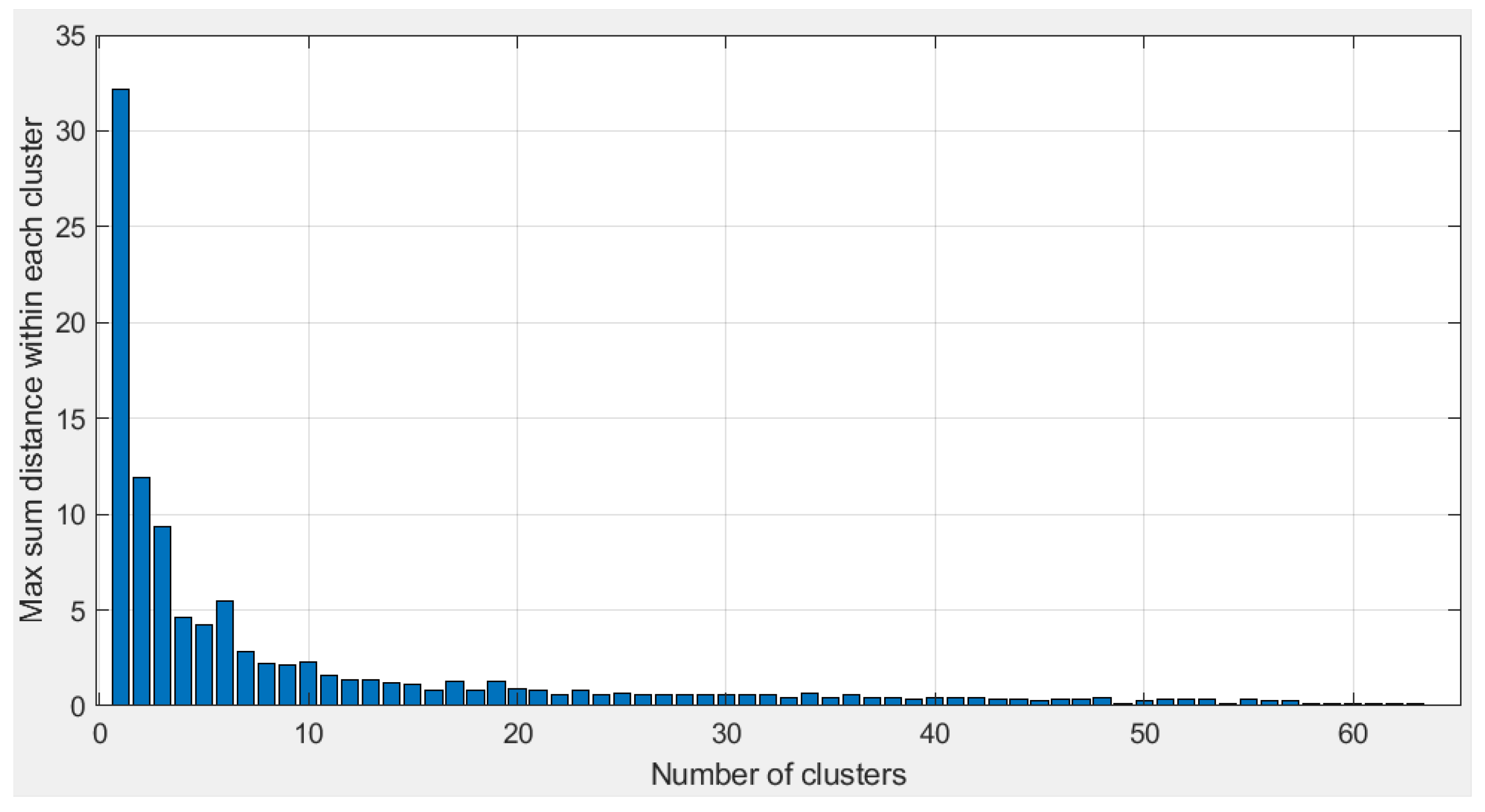
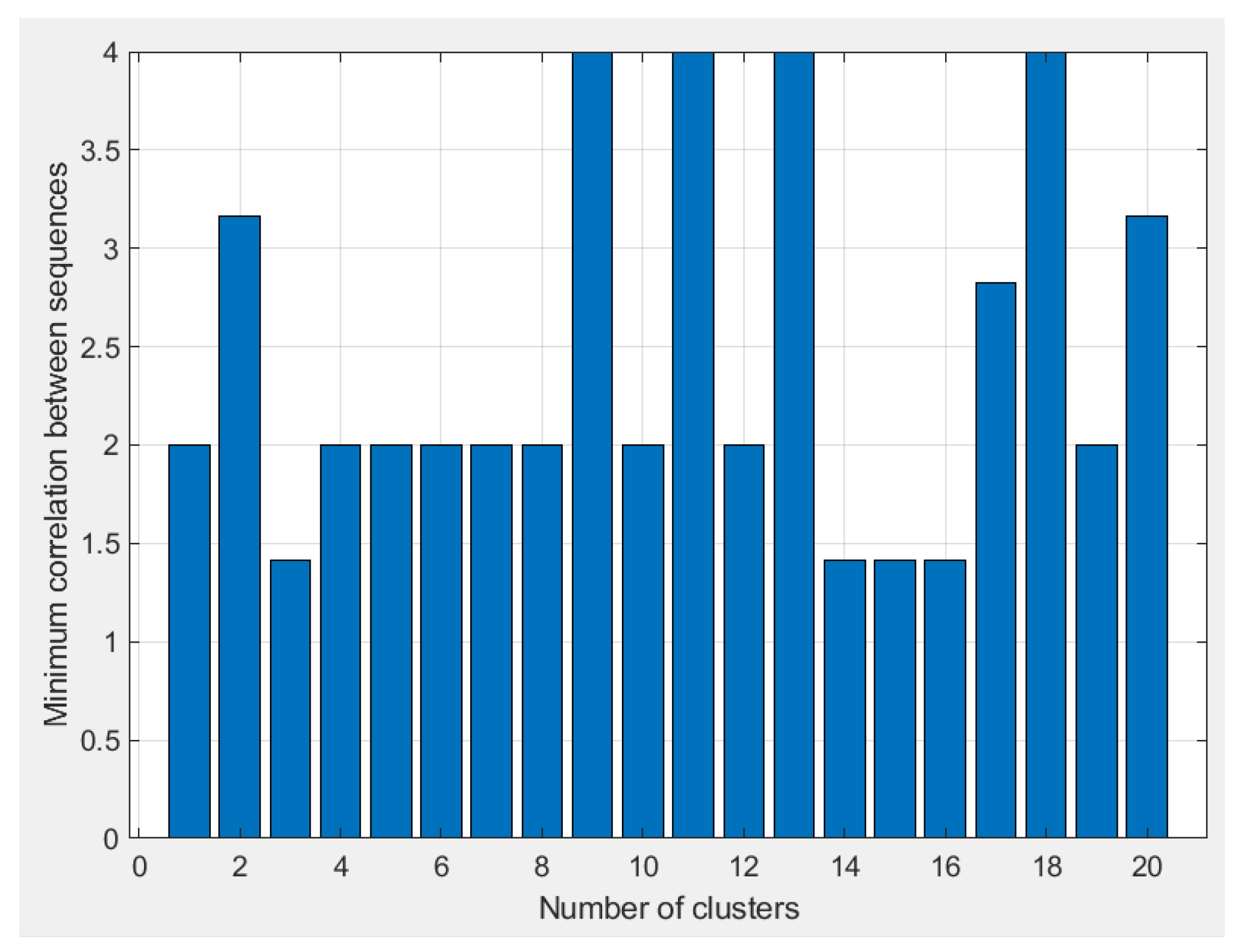
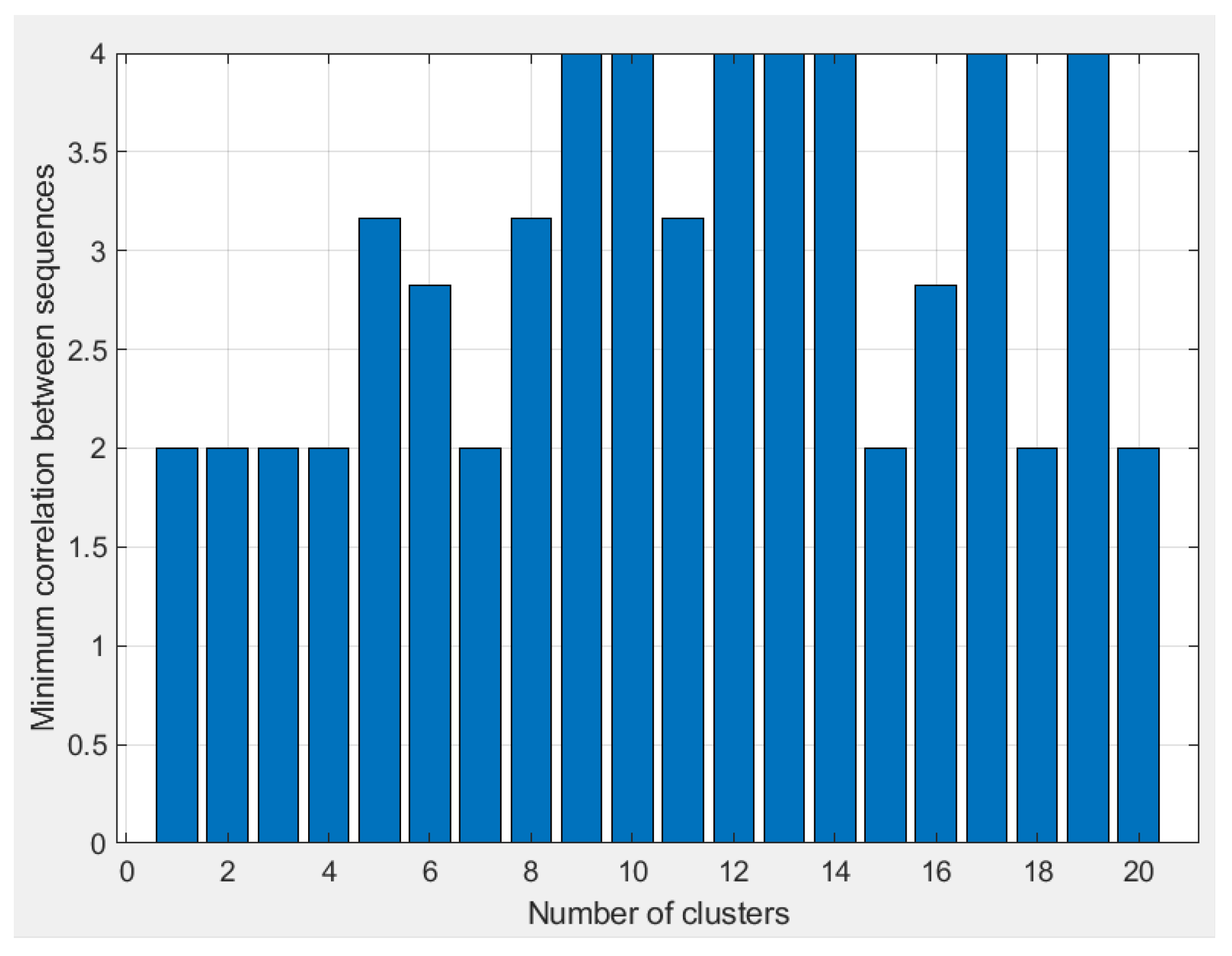
| 5 | 20 clusters vs. 40 clusters | - | 40 | - | Without using a sequence allocation mechanism that evaluates the correlation between clusters, it is efficient to group the code sequences into a higher number of clusters. Creating more clusters with fewer, but highly correlated, codewords leads to marginally better BER values. |
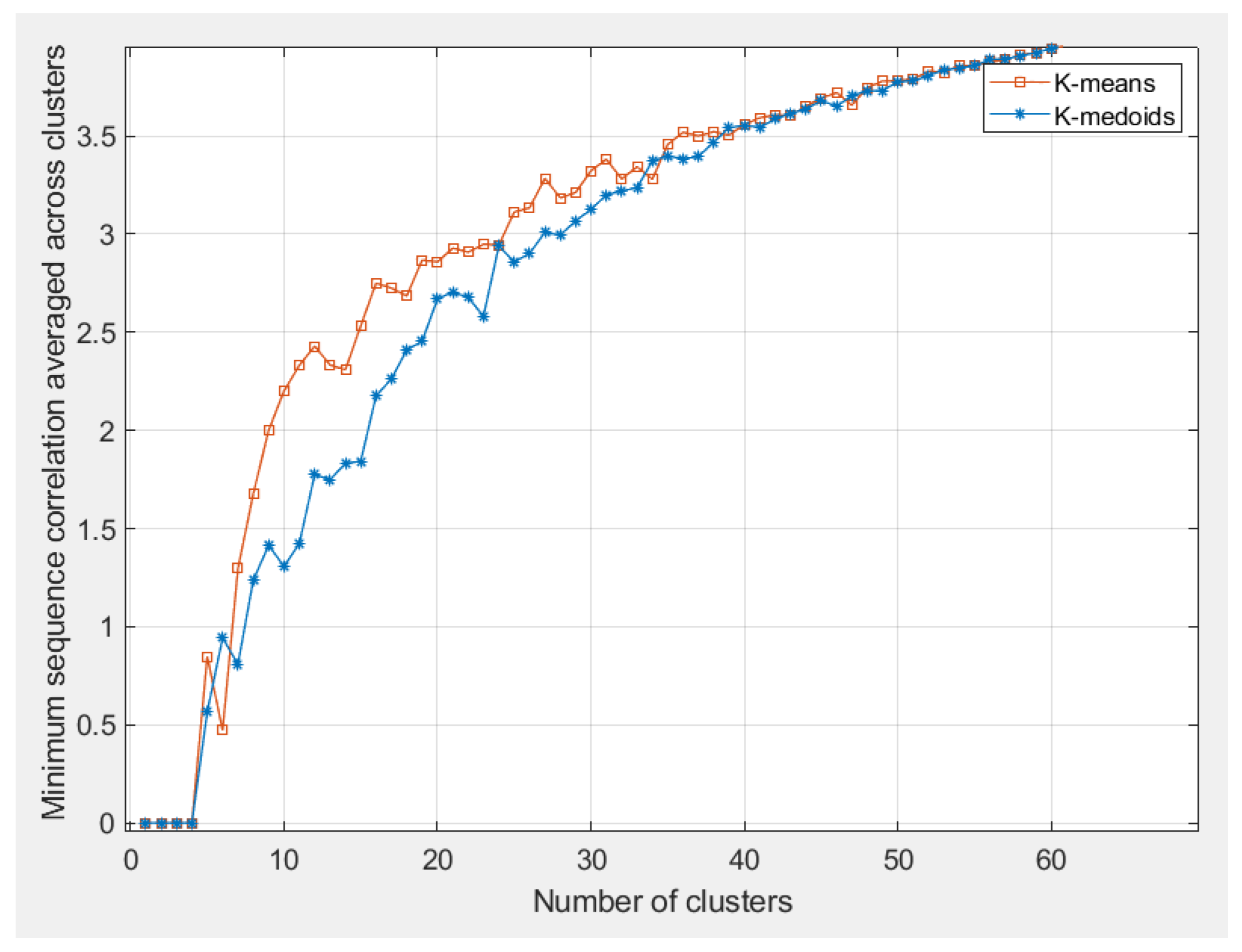
| 6 | k-means vs. k-medoids algorithms | 4 | - | - | Both clustering algorithms (k-means and k-medoids) lead to acceptable and comparable results only for a small number of users. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Florea, C.; Berceanu, M.-G.; Trifan, R.-F.; Marcu, I.-M. Clustering Approach for Reliable Wireless Communication. Appl. Sci. 2024, 14, 13. https://doi.org/10.3390/app14010013
Florea C, Berceanu M-G, Trifan R-F, Marcu I-M. Clustering Approach for Reliable Wireless Communication. Applied Sciences. 2024; 14(1):13. https://doi.org/10.3390/app14010013
Chicago/Turabian StyleFlorea, Carmen, Mădălina-Georgiana Berceanu, Răzvan-Florentin Trifan, and Ioana-Manuela Marcu. 2024. "Clustering Approach for Reliable Wireless Communication" Applied Sciences 14, no. 1: 13. https://doi.org/10.3390/app14010013
APA StyleFlorea, C., Berceanu, M.-G., Trifan, R.-F., & Marcu, I.-M. (2024). Clustering Approach for Reliable Wireless Communication. Applied Sciences, 14(1), 13. https://doi.org/10.3390/app14010013







