Designing Sustainable Flexible Manufacturing Cells with Multi-Objective Optimization Models †
Abstract
:1. Introduction
2. Literature Review
3. Material and Methods
3.1. Problem Formulation
- In the system, the routing flexibility for each part is taken into account. Only one alternative route of each part can be chosen.
- The system has machine flexibility. Multiple part types can be processed on different machines.
- The capacities of the cells are limited, and there are upper and lower limits for the number of machines to be taken into account.
- The part demands are fixed and known values. The processing time of a part on its route is known.
- The amount of power that machines consume during production is considered. Indirect and energy-related carbon emissions arising from the operation of the machines are considered. Machine idle times are ignored.
- The movements of parts between cells are considered.
- The carbon emission conversion factor is a constant coefficient.
- The time required for the addition of machines to cells and the removal of machines from the cells is ignored.
- The system has worker flexibility, and different workers may have different skills.
- In addition, worker skills are assumed constant in each period.
3.2. Developed Goal Programming Model
| Indices: | |
| W | Set of part types (w W). |
| R | Set of alternative routes (r R). |
| Q | Set of cells (q Q). |
| S | Set of machine types (s S). |
| I | Set of worker types (I I). |
| L | Set of skills (l L). |
| E | Set of periods (e E). |
| Parameters: | |
| The demand of part w in period e. | |
| The time capacity of machine s in period e. | |
| The machining time of part w on machine s in cell q using alternative route r. | |
| The amount of power consumed while machining part w on machine s in cell q using alternative route r. | |
| The cost of moving part w between cells in a period e. | |
| The machine s carbon emission cost per period e. | |
| The machine s processing/operation cost per period e. | |
| The cost of adding machine s to cells per period e. | |
| The cost of removing machine s from cells per period e. | |
| The training cost of worker i in cell q in period e. | |
| The time that worker i spends on an operation of skill l. | |
| The limit value of skill l in cell q in period e. | |
| The limit time that workers with skill l in cell q in period e can spend. | |
| The maximum number of workers of cell q in period e. | |
| The lower bound for the number of machines in cell q in period e. | |
| The upper limit for the number of machines in cell q in period e. | |
| The carbon emission conversion factor. | |
| The carbon emission limit value of cell q in period e. | |
| The bonus wage to be received by l skilled worker. | |
| The training time received by worker i in the skill l in period e. | |
| Decision Variables | |
| The number of machine s assigned to cell q in period e. | |
| The number of machine s added to cell q in period e. | |
| The number of machine s removed from cell q in period e. | |
| The number of workers in cell q in period e. | |
| The total number of workers in the system in period e. | |
| The total training time that worker i will receive during all periods according to the worker’s abilities. |
Linearization of the Model
3.3. Developed ε-Constraint Model
3.4. Developed Augmented ε-Constraint Model (AUGMECON)
4. Results and Discussion
Sensitivity Analyses
5. Conclusions and Future Studies
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Part | Route | Cell–Machine (Operating Time)/(Machine Power Amount) |
|---|---|---|
| 1 | 1 | Q1-S1(9)/PW(14) Q2-S4(4)/PW(15) Q3-S7(6)/PW(13) Q4-S11(3)/PW(14)-S12(7)/PW(17) Q5-S14(7)/PW(18)-S15(5)/PW(14) Q6-S20(8)/PW(18) |
| 2 | Q1-S2(6)/PW(13)-S3(5)/PW(15) Q2-S5(7)/PW(17) Q4-S11(7)/PW(19)-S12(8)/PW(17)-S13(4)/PW(15) Q5-S14(9)/PW(18)-S15(4)/PW(14) Q6-S18(5)/PW(14) Q6-S20(7)/PW(18) | |
| 3 | Q1-S1(6)/PW(16)-S2(9)/PW(19)-S3(4)/PW(14) Q3-S8(2)/PW(22) Q4-S12(9)/PW(19)-S13(6)/PW(26) Q5-S14(8)/PW(18)-S15(4)/PW(24) Q6-S18(9)/PW(19)-S20(8)/PW(18) | |
| 4 | Q1-S1(11)/PW(19)-S2(6)/PW(18)-S3(5)PW(25) Q2-S5(5)/PW(25) Q4-S11(8)/PW(19)-S12(5)/PW(24)-S13(5)/PW(15) Q5-S14(5)/PW(23) Q5-S15(4)/PW(24) Q6-S20(8)/PW(18) | |
| 5 | Q1-S1(8)/PW(16)-S2(5)/PW(19)-S3(4)/PW(24) Q3-S8(8)/PW(16) Q4-S12(9)/PW(19)-S13(6)/PW(16) Q5-S14(7)/PW(18)-S15(4)/PW(24) Q6-S18(8)/PW(19)-S20(5)/PW(18) | |
| 2 | 1 | Q1-S3(8)/PW(18) Q2-S6(5)/PW(15) Q3-S7(4)/PW(14) Q4-S9(8)PW(14)-S10(6)/PW(15) Q5-S13(7)/PW(18)-S14(9)/PW(19) Q6-S19(4)/PW(24) |
| 2 | Q1-S1(6)/PW(20) Q2-S6(7)/PW(18) Q4-S11(8)/PW(18)-S13(5)/PW(23) Q5-S14(6)/PW(27) Q6-S18(8)/PW(18)-S19(3)/PW(22) | |
| 3 | Q1-S2(5)/PW(25)-S3(3)/PW(23) Q2-S6(6)/PW(16) Q3-S7(4)/PW(24)-S8(7)/PW(17) Q4-S8(8)/PW(8) Q5-S16(4)/PW(14) Q6-S20(7)/PW(17) | |
| 4 | Q1-S1(8)/PW(18)-S2(9)/PW(17)-S3(3)/PW(23) Q2-S6(8)/PW(8) Q4-S11(8)/PW(8)-S13(3)/PW(23) Q5-S14(7)/PW(17) Q6-S18(8)/PW(18)-S19(3)/PW(22) | |
| 5 | Q1-S2(5)/PW(15)-S3(3)/PW(23) Q3-S7(5)/PW(24)-S8(7)/PW(17) Q4-S8(7)/PW(18) Q5-S15(5)/PW(25)-S16(4)/PW(24) Q6-S20(9)/PW(17) | |
| 3 | 1 | Q1-S1(9)/PW(12)-S3(4)/PW(14) Q2-S6(6)/PW(17) Q4-S10(5)/PW(17)-S12(4)/PW(22) Q5-S15(5)/PW(18) Q6-S19(7)/PW(14)-S20(6)/PW(15) |
| 2 | Q1-S1(2)/PW(23) Q2-S4(5)/PW(15)-S5(7)/PW(18) Q3-S8(6)/PW(26) Q5-S16(4)/PW(24) Q6-S19(3)/PW(23)-S20(4)/PW(24) | |
| 3 | Q1-S1(7)/PW(17)-S2(5)/PW(21)-S3(3)/PW(13) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(5)/PW(23)-S2(7)/PW(17) Q2-S4(1)/PW(19)-S5(6)/PW(18) Q3-S8(5)/PW(16)-S9(6)/PW(16) Q6-S20(7)/PW(27) | |
| 5 | Q1-S1(8)/PW(11)-S2(1)/PW(17) Q2-S5(8)/PW(18) Q3-S8(2)/PW(14)-S9(6)/PW(16) Q6-S20(7)/PW(17) | |
| 4 | 1 | Q1-S1(5)/PW(21)-S2(7)/PW(22)-S3(3)/PW(14) Q2-S4(5)/PW(15)-S6(8)/PW(17) Q4-S10(7)/PW(17)-S12(4)/PW(12) Q5-S15(6)/PW(18) Q6-S19(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(16) Q5-S16(4)/PW(14) Q6-S19(3)/PW(23)-S20(4)/PW(24) | |
| 3 | Q1-S1(6)/PW(17)-S2(9)/PW(22)-S3(3)/PW(23) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(3)/PW(23)-S2(4)/PW(17) Q2-S4(6)/PW(21)-S5(1)7PW(18) Q3-S8(5)/PW(16)-S9(6)/PW(26) Q6-S20(7)/PW(17) | |
| 5 | Q1-S1(4)/PW(21)-S2(6)/PW(17) Q2-S5(7)/PW(18) Q3-S8(8)/PW(24)-S9(6)/PW(26) Q6-S20(3)/PW(27) | |
| 5 | 1 | Q1-S1(2)/PW(14)-S2(5)/PW(15)-S3(4)/PW(19) Q2-S6(8)/PW(18)-S7(10)/PW(19) Q4-S10(5)/PW(15)-S12(2)/PW(12) Q5-S15(6)/PW(16)-S16(5)/PW(15) Q6-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23)-S2(11)/PW(17) Q2-S4(9)/PW(19)-S5(8)/PW(18)-S6(6)/PW(16) Q3-S8(6)/PW(16)-S9(7)/PW(7) Q5-S16(4)/PW(24)-S17(5)/PW(25) Q6-S18(5)/PW(15)-S19(3)/PW(23)-S20(4)/PW(14) | |
| 3 | Q1-S1(8)/PW(18)-S3(3)/PW(23) Q2-S5(9)/PW(19) Q3-S7(7)/PW(17) Q4-S15(9)/PW(19)-S16(8)/PW(18) | |
| 4 | Q1-S1(6)/PW(16)-S2(8)/PW(18)-S3(5)/PW(25) Q2-S4(4)/PW(24)-S5(7)/PW(17)-S6(6)/PW(26) Q3-S8(6)/PW(16)-S9(5)/PW(25) Q6-S19(4)/PW(24)-S20(7)/PW(17) | |
| 5 | Q1-S1(5)/PW(15)-S2(6)/PW(16) Q2-S5(8)/PW(18) Q3-S8(8)/PW(18)-S9(6)/PW(16) Q6-S19(6)/PW(19) | |
| 6 | 1 | Q1-S1(9)/PW(17)-S2(6)/PW(15)-S3(8)/PW(18) Q2-S6(7)/PW(17)-S7(6)/PW(26) Q4-S10(7)/PW(17)-S12(2)/PW(22) Q5-S15(8)/PW(28) Q6-S19(4)/PW(24)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(9)/PW(15)-S5(8)/PW(8) Q3-S8(6)/PW(16) Q5-S16(4)/PW(14) Q6-S19(3)/PW(23)-S20(4)/PW(24) | |
| 3 | Q1-S1(8)/PW(17)-S2(2)/PW(22)-S3(1)/PW(23) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(5)/PW(13)-S2(7)/PW(17) Q2-S4(2)/PW(19)-S5(4)/PW(18) Q3-S8(5)/PW(16)-S9(6)/PW(16) Q6-S20(3)/PW(17) | |
| 5 | Q1-S1(6)/PW(18)-S2(3)/PW(17) Q2-S5(8)/PW(8) Q3-S8(2)/PW(4)-S9(6)/PW(6) Q6-S20(6)/PW(7) | |
| 7 | 1 | Q1-S3(8)/PW(24) Q2-S5(5)/PW(8)-S6(7)/PW(17) Q4-S10(7)/PW(17)-S12(8)/PW(12) Q5-S15(8)/PW(8) Q6-S19(4)/PW(4)-S20(5)/PW(5) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(7)/PW(5)-S5(8)/PW(8) Q3-S8(6)/PW(6) Q5-S16(5)/PW(14) Q6-S19(3)/PW(13)-S20(4)/PW(4) | |
| 3 | Q1-S1(7)/PW(7)-S2(1)/PW(18)-S3(3)/PW(13) Q2-S5(5)/PW(5) Q3-S7(6)/PW(6) Q4-S15(6)/PW(7) | |
| 4 | Q1-S1(4)/PW(3)-S2(7)/PW(7) Q2-S4(3)/PW(11)-S5(8)/PW(8) Q3-S8(9)/PW(6)-S9(6)/PW(6) Q6-S20(7)/PW(7) | |
| 5 | Q1-S1(5)/PW(12)-S2(6)/PW(17) Q2-S5(8)/PW(18) Q3-S8(4)/PW(14)-S9(5)/PW(16) Q6-S20(6)/PW(7) | |
| 8 | 1 | Q1-S1(9)/PW(9)-S3(8)/PW(8) Q2-S6(8)/PW(7) Q4-S10(5)/PW(7)-S12(3)/PW(12) Q5-S15(6)/PW(8) Q6-S19(5)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(9)/PW(9) Q2-S4(6)/PW(16)-S5(8)/PW(8) Q3-S8(6)/PW(6) Q5-S16(4)/PW(14) Q6-S19(3)/PW(13)-S20(4)/PW(14) | |
| 3 | Q1-S1(7)/PW(17)-S2(5)/PW(15)-S3(3)/PW(13) Q2-S5(5)/PW(5) Q3-S7(6)/PW(16) Q4-S15(7)/PW(7) | |
| 4 | Q1-S1(7)PW(13)-S2(7)/PW(7) Q2-S4(9)/PW(11)-S5(8)/PW(8) Q3-S8(10)/PW(16)-S9(6)/PW(16) Q6-S20(7)/PW(7) | |
| 5 | Q1-S1(4)/PW(14)-S2(7)/PW(7) Q2-S5(8)/PW(8) Q3-S8(5)/PW(14)-S9(6)/PW(16) Q6-S20(2)/PW(7) | |
| 9 | 1 | Q1-S3(8)/PW(8) Q2-S5(8)/PW(18)-S6(3)/PW(17)-S7(12)/PW(19) Q4-S11(7)/PW(9)-S12(2)/PW(12) Q5-S15(8)/PW(18) Q6-S19(4)/PW(4)-S20(5)/PW(5) |
| 2 | Q1-S1(5)/PW(8)-S2(9/PW(9) Q2-S4(6)/PW(15)-S5(8)/PW(8) Q3-S7(7)/PW(7)-S8(6)/PW(6) Q5-S16(4)/PW(14)-S17(6)/PW(6) Q6-S20(4)/PW(4) | |
| 3 | Q1-S1(9)/PW(7)-S3(7)/PW(13) Q2-S5(6)/PW(5)-S6(8)/PW(8) Q3-S7(6)/PW(6)-S8(8)/PW(8) Q4-S15(7)/PW(17)-S16(9)/PW(9) | |
| 4 | Q1-S1(3)/PW(13)-S2(7)/PW(7)-S3(4)/PW(14) Q2-S4(6)/PW(11)-S5(8)/PW(18) Q3-S8(6)/PW(16)-S9(6)/PW(6) Q6-S20(2)/PW(7) | |
| 5 | Q1-S1(3)/PW(15)-S2(5)/PW(7)-S3(7)/PW(7) Q2-S5(8)/PW(8) Q3-S8(4)/PW(14)-S9(6)/PW(16) Q6-S19(3)/PW(18)-S20(6)/PW(17) | |
| 10 | 1 | Q2-S5(4)/PW(14)-S6(4)/PW(15) Q4-S10(7)/PW(17)-S11(8)/PW(18)-S12(5)/PW(22) Q5-S15(8)/PW(8)-S17(9)/PW(9) Q6-S19(1)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23)-S2(5)/PW(25) Q2-S4(5)/PW(25)-S5(8)/PW(28)-S6(4)/PW(24) Q3-S8(6)/PW(6) Q5-S16(4)/PW(14)-S17(5)/PW(15) Q6-S19(3)/PW(13)-S20(4)/PW(14) | |
| 3 | Q1-S1(9)/PW(16)-S2(8)/PW(18)-S3(3)/PW(13) Q2-S5(5)/PW(15)-S6(6)/PW(17) Q3-S7(6)/PW(16)-S8(8)/PW(18) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(5)/PW(15)-S2(7)/PW(17) Q2-S4(4)/PW(14)-S5(8)/PW(8) Q3-S8(6)/PW(16)-S9(6)/PW(16) Q6-S18(8)/PW(18)-S20(7)/PW(17) | |
| 5 | Q1-S1(3)/PW(14)-S2(7)/PW(17)-S3(8)/PW(18) Q2-S5(8)/PW(18) Q3-S8(4)/PW(14)-S9(6)/PW(26) Q6-S19(4)/PW(17) | |
| 11 | 1 | Q1-S2(8)/PW(18) Q2-S5(4)/PW(14)-S6(7)7PW(17) Q4-S10(4)/PW(14)-S11(8)/PW(18)-S12(5)/PW(15) Q5-S15(8)/PW(8)-S16(7)/PW(7) Q6-S18(6)/PW(16)-S19(6)/PW(18)-S20(9)/PW(9) |
| 2 | Q1-S1(8)/PW(18)-S2(6)/PW(8) Q2-S4(5)/PW(15)-S5(4)/PW(8)-S6(9)/PW(9) Q3-S8(6)/PW(16) Q5-S16(4)/PW(14) Q6-S19(3)/PW(11)-S20(4)/PW(14) | |
| 3 | Q1-S2(5)/PW(15) Q2-S6(7)/PW(17)-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(10)/PW(19)-S2(7)/PW(17)-S3(9)/PW(9) Q2-S4(3)/PW(8)-S5(8)/PW(8) Q3-S8(5)/PW(15)-S9(6)/PW(16) Q6-S18(4)/PW(14)-S19(8)/PW(18)-S20(7)/PW(17) | |
| 5 | Q1-S1(9)/PW(16)-S2(7)/PW(17) Q2-S4(7)/PW(17)-S5(8)/PW(8) Q3-S7(5)/PW(15)-S8(4)/PW(24)-S9(6)/PW(16) Q6-S19(4)/PW(18)-S20(6)/PW(16) | |
| 12 | 1 | Q1-S3(8)/PW(13) Q2-S6(6)/PW(16)-S7(5)/PW(15) Q4-S10(4)/PW(14)-S11(3)/PW(13)-S12(2)/PW(12) Q5-S15(8)/PW(18) Q6-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(13)-S2(7)/PW(17) Q2-S4(7)/PW(26)-S5(7)/PW(17) Q3-S8(7)/PW(14) Q5-S16(5)/PW(15)-S17(4)/PW(14) Q6-S19(7)/PW(17)-S20(8)/PW(18) | |
| 3 | Q1-S1(2)/PW(22)-S2(8)/PW(18) Q2-S5(7)/PW(17)-S6(4)/PW(24) Q3-S7(6)/PW(6)-S8(5)/PW(5) Q4-S15(7)/PW(19)-S16(8)/PW(18) | |
| 4 | Q1-S1(6)/PW(7)-S2(6)/PW(16) Q2-S4(5)/PW(15)-S5(4)/PW(24) Q3-S8(4)/PW(24) Q6-S20(7)/PW(17) | |
| 5 | Q1-S2(1)/PW(8) Q2-S5(11)/PW(18) Q3-S8(2)/PW(24)-S9(6)/PW(16) Q6-S19(8)/PW(18) | |
| 13 | 1 | Q1-S2(7)/PW(18)-S3(5)/PW(12) Q2-S4(3)/PW(16)-S6(7)/PW(17) Q4-S10(6)/PW(17)-S11(3)/PW(18)-S12(2)/PW(22) Q5-S15(8)/PW(18)-S16(9)/PW(9) Q6-S18(7)/PW(17)-S19(6)/PW(16)-S20(5)/PW(25) |
| 2 | Q1-S1(5)/PW(15)-S2(7)/PW(26) Q2-S4(5)/PW(15)-S5(4)/PW(18)-S6(7)/PW(17) Q3-S8(6)/PW(6)-S9(7)/PW(7) Q5-S16(4)/PW(24)-S17(5)/PW(15) Q6-S19(6)/PW(16) | |
| 3 | Q1-S3(3)/PW(13) Q2-S5(3)/PW(15)-S6(7)/PW(17) Q3-S7(6)/PW(16)-S8(7)/PW(17) Q4-S15(7)/PW(17)-S16(6)/PW(16) | |
| 4 | Q1-S2(10)/PW(17) Q2-S5(8)/PW(18) Q3-S8(9)/PW(15)-S9(6)/PW(16)-S10(4)/PW(24) Q6-S19(8)/PW(18) | |
| 5 | Q1-S1(6)/PW(24)-S2(7)/PW(17) Q2-S5(1)/PW(21) Q3-S8(4)/PW(24)-S9(6)/PW(16) Q6-S18(9)/PW(9)-S19(8)/PW(18) | |
| 14 | 1 | Q2-S6(9)/PW(17) Q4-S10(5)/PW(21)-S12(2)/PW(22) Q5-S15(8)/PW(18) Q6-S19(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(16) Q5-S16(4)/PW(24) Q6-S19(3)/PW(23)-S20(4)/PW(24) | |
| 3 | Q1-S1(8)/PW(17)-S2(1)/PW(22)-S3(3)/PW(13) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(4)/PW(13)-S2(7)(PW(17) Q2-S4(1)/PW(21)-S5(5)/PW(28) Q3-S8(6)/PW(26)-S9(6)/PW(16) Q6-S20(7)/PW(17) | |
| 5 | Q1-S1(11)/PW(21)-S2(3)/PW(17) Q2-S5(8)/PW(18) Q3-S8(4)/PW(14)-S9(6)/PW(16) Q6-S20(4)/PW(17) | |
| 15 | 1 | Q1-S1(11)/PW(18) Q2-S6(7)/PW(17)-S7(5)/PW(15) Q3-S15(8)/PW(8) Q4-S10(3)/PW(17)-S11(5)/PW(15)-S12(2)/PW(23) Q5-S15(8)/PW(8) Q6-S18(9)/PW(19)-S19(4)/PW(24)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23)-S2(7)/PW(17) Q3-S8(6)/PW(16) Q5-S16(4)/PW(14) Q6-S19(3)/PW(13)-S20(4)/PW(14) | |
| 3 | Q1-S1(10)/PW(19)-S3(3)/PW(23) Q2-S5(5)/PW(25) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(3)/PW(23)-S2(7)/PW(17)-S3(8)/PW(18) Q2-S4(9)/PW(19)-S5(8)/PW(18) Q3-S8(6)/PW(16)-S9(3)/PW(16)-S10(7)/PW(17) Q6-S19(6)/PW(16) S20(9)/PW(19) | |
| 5 | Q1-S2(7)/PW(17) Q2-S5(8)/PW(8) Q3-S9(6)/PW(16) Q6-S19(3)/PW(18)-S20(7)/PW(17) | |
| 16 | 1 | Q4-S10(7)/PW(17)-S12(5)/PW(20) Q5-S15(8)/PW(18) |
| 2 | Q2-S4(12)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(16) Q5-S16(2)/PW(24) Q6-S19(3)/PW(23)-S20(4)/PW(24) | |
| 3 | Q1-S1(4)/PW(17)-S2(8)/PW(22)-S3(3)/PW(23) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(3)/PW(13)-S2(7)/PW(17) Q2-S4(6)/PW(18)-S5(3)/PW(18) Q3-S8(7)/PW(16)-S9(6)/PW(16) Q6-S20(7)/PW(17) | |
| 5 | Q1-S1(7)/PW(17)-S2(3)/PW(19)-S3(5)/PW(15) Q2-S5(8)/PW(18) Q3-S6(4)/PW(14)-S8(4)/PW(14)-S9(6)/PW(16) Q6-S19(5)/PW(15)-S20(2)/PW(17) | |
| 17 | 1 | Q1-S2(6)/PW(17)-S3(5)/PW(15) Q2-S6(7)/PW(17) Q4-S10(1)/PW(17)-S12(2)/PW(22) Q5-S15(6)/PW(18)-S16(5)/PW(25) Q6-S18(6)/PW(26)-S20(5)/PW(25) |
| 2 | Q1-S1(3)/PW(23)-S2(8)/PW(18) Q2-S4(5)/PW(15) Q3-S7(4)/PW(14)-S8(6)/PW(16) Q5-S16(11)/PW(24)-S17(7)/PW(17) Q6-S20(9)/PW(19) | |
| 3 | Q1-S1(8)/PW(19)-S3(7)/PW(14) Q2-S5(5)/PW(15)-S6(7)/PW(17) Q3-S7(6)/PW(26)-S8(5)/PW(15) Q4-S15(7)/PW(17)-S16(8)/PW(18) Q5-S18(9)/PW(19) | |
| 4 | Q1-S1(6)/PW(23)-S2(7)/PW(27) Q2-S4(1)/PW(21)-S5(8)/PW(18) Q3-S8(4)/PW(16)-S9(6)/PW(16) Q6-S20(7)/PW(17) | |
| 5 | Q1-S2(4)/PW(17) Q2-S5(8)/PW(18) Q3-S8(4)/PW(14)-S9(6)/PW(16) | |
| 18 | 1 | Q1-S2(9)/PW(19)-S3(4)/PW(24) Q2-S6(7)/PW(17) Q4-S10(7)/PW(27)-S12(9)/PW(19) Q5-S15(8)/PW(18)-S19(4)/PW(24)-S20(5)/PW(25) Q6-S18(5)PW(15) |
| 2 | Q1-S1(9)/PW(19)-S2(5)/PW(25) Q2-S4(4)/PW(24) Q3-S8(6)/PW(16)-S9(6)/PW(16) Q5-S16(6)/PW(16)-S17(7)/PW(17) Q6-S19(8)/PW(18)-S20(4)/PW(24) | |
| 3 | Q1-S1(9)/PW(19)-S3(7)/PW(17) Q2-S5(5)PW(15) Q3-S7(6)/PW(16)-S8(5)/PW(15) Q4-S15(9)/PW(19)-S16(4)/PW(24) | |
| 4 | Q1-S2(9)/PW(9)-S3(4)/PW(14) Q2-S5(3)/PW(13)-S6(5)/PW(15) Q3-S8(6)/PW(16) Q6-S18(3)/PW(13)-S19(8)/PW(8)-S20(4)/PW(14) | |
| 5 | Q1-S1(6)/PW(16)-S2(7)/PW(17)-S3(5)/PW(25) Q2-S5(8)/PW(8)-S8(4)/PW(14) Q3-S8(4)/PW(14)-S9(6)/PW(16)-S10(5)/PW(15) Q6-S19(5)/PW(15)-S20(7)/PW(17) | |
| 19 | 1 | Q2-S6(4)/PW(14)-S7(8)/PW(18) Q4-S10(7)/PW(17)-S11(5)/PW(25)-S12(2)/PW(22) Q5-S15(8)/PW(18) Q6-S19(4)/PW(24)-S20(5)/PW(15) |
| 2 | Q1-S1(6)/PW(16) Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(26) Q5-S16(6)/PW(26) Q6-S19(13)/PW(13)-S20(4)/PW(14) | |
| 3 | Q1-S2(9)/PW(9)-S3(8)/PW(18) Q2-S5(5)/PW(15) Q3-S7(11)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S2(9)/PW(19) Q2-S4(7)/PW(11)-S5(8)/PW(18) Q3-S8(7)/PW(7)-S9(6)/PW(16) Q6-S19(2)/PW(22)-S20(3)/PW(3) | |
| 5 | Q2-S5(8)/PW(8) Q3-S8(4)/PW(24)-S9(6)/PW(16) Q6-S19(9)/PW(15)-S20(6)/PW(16) | |
| 20 | 1 | Q2-S6(11)/PW(9)-S7(9)/PW(9) Q3-S9(5)PW(15) Q4-S10(6)/PW(16)-S11(8)/PW(18)-S12(2)/PW(22) Q5-S15(9)/PW(9) Q6-S18(6)/PW(16)-S19(4)/PW(24)-S20(5)/PW(25) |
| 2 | Q1-S1(3)/PW(13)-S2(8)/PW(18) Q2-S4(9)/PW(9)-S5(6)/PW(16) Q3-S7(7)/PW(17)-S8(6)/PW(16) Q6-S20(4)/PW(14) | |
| 3 | Q1-S2(12)/PW(12) Q2-S5(9)/PW(9) Q3-S7(6)/PW(16)-S8(7)/PW(17) Q4-S15(8)/PW(8)-S16(9)/PW(9) Q6-S19(8)/PW(8) | |
| 4 | Q1-S2(7)/PW(17)-S3(8)/PW(18) Q3-S8(3)/PW(16)-S9(6)/PW(16)-S10(5)/PW(25) Q5-S17(9)/PW(9) Q6-S19(5)/PW(25)-S20(8)/PW(18) | |
| 5 | Q2-S5(8)/PW(8) Q3-S8(7)/PW(9)-S9(10)/PW(6) | |
| 21 | 1 | Q1-S1(9)/PW(8)-S2(5)/PW(9)-S3(4)/PW(14) Q4-S10(8)/PW(15)-S11(6)/PW(16)-S12(2)/PW(22) Q6-S19(4)/PW(24)-S20(5)/PW(25) |
| 2 | Q2-S4(9)/PW(15)-S5(8)/PW(18) Q3-S8(8)/PW(16)-S9(7)/PW(17) Q6-S19(9)/PW(9) | |
| 3 | Q1-S3(9)/PW(9) Q2-S5(5)/PW(25)-S6(7)/PW(17) Q3-S7(6)/PW(26) Q4-S15(7)/PW(17) Q6-S18(8)/PW(18)-S19(9)/PW(19) | |
| 4 | Q1-S2(7)/PW(17) Q2-S4(13)/PW(11)-S5(4)/PW(18) Q3-S8(6)/PW(16)-S9(6)/PW(16) Q6-S20(7)/PW(17) | |
| 5 | Q1-S1(4)/PW(24)-S2(6)/PW(16) Q2-S5(5)/PW(17) Q3-S8(4)/PW(14)-S9(6)/PW(16) Q4-S11(7)/PW(17) | |
| 22 | 1 | Q1-S1(5)/PW(16)-S3(2)/PW(24) Q2-S5(5)/PW(18) Q4-S10(7)/PW(17)-S11(9)/PW(9)-S12(7)/PW(17) Q5-S15(8)/PW(8)-S16(5)/PW(15) Q6-S20(9)/PW(9) |
| 2 | Q1-S1(5)/PW(3)-S2(9)/PW(9) Q3-S8(6)/PW(16)-S9(8)/PW(8) Q5-S16(4)/PW(14)-S17(5)/PW(15) Q6-S19(9)/PW(9) | |
| 3 | Q1-S1(8)/PW(18)-S2(2)/PW(12) Q2-S5(9)/PW(9) Q3-S7(7)/PW(16)-S8(7)/PW(17) Q4-S15(7)/PW(17)-S16(8)/PW(18) | |
| 4 | Q2-S5(8)/PW(8)-S6(7)/PW(7) Q3-S8(6)/PW(6)-S9(8)/PW(9) Q6-S18(3)/PW(3)-S20(9)/PW(9) | |
| 5 | Q1-S1(7)/PW(17)-S2(9)/PW(9) Q2-S4(2)/PW(20)-S5(8)/PW(18) Q3-S8(4)/PW(14)-S9(6)/PW(16)-S10(3)/PW(23) Q4-S16(4)/PW(14) Q5-S17(6)/PW(16)-S18(5)/PW(15) Q6-S20(7)/PW(17) | |
| 23 | 1 | Q1-S3(3)/PW(14) Q2-S6(7)/PW(14) Q5-S15(8)/PW(18)-S16(9)/PW(9) |
| 2 | Q1-S1(3)/PW(23)-S2(8)/PW(18) Q2-S4(5)/PW(15)-S5(6)/PW(18)-S6(7)/PW(17) Q3-S8(6)/PW(16) Q4-S15(6)/PW(16) Q6-S20(9)/PW(9) | |
| 3 | Q1-S1(9)/PW(9)-S2(8)/PW(8) Q2-S4(4)/PW(24)-S5(5)/PW(25) Q3-S7(6)/PW(26)-S8(7)/PW(17) | |
| 4 | Q2-S4(2)/PW(21)-S5(5)/PW(17)-S6(8)/PW(18) Q6-S19(3)/PW(23)-S20(9)/PW(9) | |
| 5 | Q2-S5(6)/PW(16) Q3-S9(6)/PW(6) Q6-S18(11)/PW(9)-S20(3)/PW(15) | |
| 24 | 1 | Q1-S1(9)/PW(8)-S2(2)/PW(13)-S3(1)/PW(14) Q2-S5(6)/PW(16)-S6(7)/PW(17) Q4-S10(6)/PW(14)-S11(8)/PW(18) Q5-S14(6)/PW(16)-S15(8)/PW(18) Q6-S19(6)/PW(16)-S20(3)/PW(13) |
| 2 | Q2-S5(7)/PW(16)-S6(7)/PW(17) Q3-S8(9)/PW(19)-S9(5)/PW(15) Q5-S16(3)/PW(23)-S17(2)/PW(22) Q6-S20(4)/PW(12) | |
| 3 | Q1-S1(6)/PW(16)-S3(8)/PW(9) Q4-S15(4)/PW(4)-S16(5)/PW(5) Q6-S19(8)/PW(8) | |
| 4 | Q1-S1(3)/PW(23)-S2(7)/PW(17)-S3(6)/PW(16) Q2-S5(8)/PW(8)-S6(5)/PW(15) Q6-S19(8)/PW(18)-S20(9)/PW(9) | |
| 5 | Q1-S2(7)/PW(17) Q2-S5(8)/PW(18)-S6(5)/PW(15) Q3-S8(4)/PW(14) | |
| 25 | 1 | Q1-S1(5)/PW(15)-S2(6)/PW(16)-S3(5)/PW(14) Q2-S5(8)PW(18)-S6(7)/PW(17)-S7(5)/PW(15) Q3-S8(5)/PW(23) Q4-S12(9)/PW(9) Q5-S15(8)/PW(18) |
| 2 | Q1-S1(3)/PW(3)-S2(1)/PW(5) Q2-S4(4)/PW(24)-S5(7)/PW(17) Q3-S8(5)/PW(15)-S9(4)PW(24) Q5-S16(3)/PW(8) Q6-S19(9)/PW(9)-S20(6)/PW(6) | |
| 3 | Q1-S2(8)/PW(18)-S3(9)/PW(9) Q2-S5(5)/PW(15) Q3-S6(4)/PW(10)-S7(6)/PW(16) | |
| 4 | Q1-S1(6)/PW(16)-S2(7)/PW(17)-S3(8)/PW(18) Q2-S4(2)/PW(12)-S5(8)/PW(18)-S6(3)/PW(11) Q3-S8(6)/PW(16)-S9(6)/PW(16) Q6-S19(8)/PW(18)-S20(7)/PW(17) | |
| 5 | Q1-S2(9)/PW(17) Q2-S4(4)/PW(14)-S5(8)/PW(8) Q3-S8(4)/PW(14)-S9(6)/PW(16) Q6-S19(9)/PW(16)-S20(7)/PW(17) | |
| 26 | 1 | Q1-S3(4)/PW(14) Q2-S6(10)/PW(17)-S7(8)/PW(18) Q4-S10(7)/PW(17) Q5-S15(8)/PW(8)-S16(8)/PW(8) Q6-S18(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(7)/PW(17)-S2(8)/PW(18) Q2-S4(2)/PW(21)-S5(3)/PW(13)-S6(4)/PW(24) Q3-S7(5)/PW(15)-S8(6)/PW(16)-S9(7)/PW(17) Q5-S16(4)/PW(14)-S17(5)/PW(15) Q6-S18(7)/PW(17)S20(4)/PW(24) | |
| 3 | Q1-S1(10)/PW(18)-S2(9)/PW(19) Q2-S5(5)/PW(15)-S6(6)/PW(16) Q3-S7(6)/PW(16)-S8(7)/PW(17) Q4-S14(7)/PW(17)-S15(8)/PW(18) | |
| 4 | Q2-S4(8)/PW(18)-S5(8)/PW(18) Q3-S8(9)/PW(19) | |
| 5 | Q1-S2(4)/PW(14) Q2-S5(6)/PW(16)-S6(7)/PW(17) Q3-S8(5)/PW(15)-S9(7)/PW(17) Q5-S16(6)/PW(16)-S17(3)/PW(23) Q6-S18(2)/PW(14)-S19(8)/PW(18) | |
| 27 | 1 | Q1-S1(7)/PW(9)-S2(1)/PW(21)-S3(4)/PW(14) Q2-S4(3)/PW(23)-S6(5)/PW(15) Q4-S10(5)/PW(15)-S11(6)/PW(16)-S12(2)/PW(12) Q6-S19(7)/PW(17) |
| 2 | Q1-S1(15)/PW(13)-S2(5)/PW(15)-S3(1)/PW(16) Q2-S5(5)/PW(15)-S6(2)/PW(2) Q3-S7(3)/PW(17)-S8(6)/PW(16) Q5-S6(4)/PW(4)-S17(5)PW(5) | |
| 3 | Q1-S1(6)/PW(16)-S3(3)/PW(23) Q2-S5(8)/PW(18)-S6(9)/PW(9) Q3-S7(7)/PW(17)-S8(5)/PW(15) Q4-S14(6)/PW(26)-S15(7)/PW(7) Q6-S19(8)/PW(18)-S20(4)/PW(14) | |
| 4 | Q1-S1(3)/PW(3)-S2(8)/PW(6)-S3(4)/PW(4) Q4-S5(7)/PW(8) Q6-S20(7)/PW(7) | |
| 5 | Q1-S1(4)/PW(24)-S2(7)/PW(17)-S3(8)/PW(18) Q2-S4(5)/PW(25)-S5(8)/PW(18) Q3-S8(4)/PW(24)-S9(6)/PW(16) Q5-S17(6)/PW(16) Q6-S19(5)/PW(17)-S20(7)/PW(17) | |
| 28 | 1 | Q1-S1(4)/PW(15)-S3(6)/PW(16) Q2-S6(9)/PW(9) Q4-S10(6)/PW(16)-S12(3)/PW(13) Q5-S15(8)/PW(18) Q6-S19(6)/PW(16)-S20(8)/PW(18) |
| 2 | Q1-S1(3)/PW(16) Q2-S4(12)/PW(22)-S5(8)/PW(18) Q3-S8(7)/PW(17) Q5-S16(6)/PW(6) Q6-S19(5)/PW(15)-S20(1)/PW(23) | |
| 3 | Q1-S1(9)/PW(19)-S3(6)/PW(26) Q2-S5(5)/PW(5) Q3-S7(7)/PW(7) Q4-S15(8)/PW(8) | |
| 4 | Q1-S1(4)/PW(14)-S2(8)/PW(18) Q2-S4(3)/PW(13)-S5(7)/PW(11) Q3-S8(9)PW(19)-S9(6)/PW(26) Q6-S19(4)/PW(14)-S20(8)/PW(18) | |
| 5 | Q1-S1(6)/PW(16)-S2(8)/PW(18) Q2-S5(8)(PW(18) Q3-S8(9)/PW(19)-S9(5)/PW(15) Q6-S19(3)/PW(23)-S20(6)/PW(16) | |
| 29 | 1 | Q1-S1(3)/PW(15)-S3(3)/PW(13) Q2-S6(8)/PW(8) Q4-S12(9)/PW(9) Q6-S20(6)/PW(16) |
| 2 | Q2-S4(5)/PW(9)-S5(6)/PW(16)-S6(5)/PW(15) Q3-S7(7)/PW(17)-S8(8)/PW(8) Q4-S9(9)/PW(9) Q5-S16(3)/PW(23)-S17(2)/PW(20) Q6-S20(4)/PW(14) | |
| 3 | Q1-S2(6)/PW(9)-S3(3)/PW(13) Q3-S7(7)/PW(17)-S8(8)/PW(18) Q6-S18(9)/PW(9) | |
| 4 | Q1-S2(7)/PW(17) Q2-S5(8)/PW(18)-S6(4)/PW(14) Q3-S7(5)/PW(15)-S8(4)/PW(16)-S9(6)/PW(16) Q6-S19(5)/PW(15)-S20(6)/PW(16) | |
| 5 | Q1-S2(7)/PW(17) Q2-S5(8)/PW(18) Q3-S8(4)/PW(14)-S9(6)/PW(16) Q5-S16(4)/PW(14)-S17(5)PW(15) Q6-S19(3)/PW(13)-S20(6)/PW(9) | |
| 30 | 1 | Q1-S1(9)/PW(9)-S2(1)/PW(13)-S3(5)/PW(15) Q2-S5(6)/PW(16)-S7(7)/PW(17) Q3-S8(5)/PW(15)-S9(4)/PW(24) Q5-S15(6)/PW(16) Q6-S20(9)/PW(19) |
| 2 | Q1-S1(9)/PW(13)-S2(5)/PW(15)-S3(8)/PW(18) Q2-S4(7)/PW(14)-S5(3)/PW(13) Q3-S7(9)/PW(13)-S8(9)/PW(9) Q5-S16(6)/PW(6)-S17(7)/PW(7) | |
| 3 | Q1-S2(7)/PW(17)-S3(3)PW(13) Q2-S5(6)/PW(16)-S6(7)/PW(17) Q3-S7(11)/PW(11) Q4-S15(3)/PW(23)-S16(4)/PW(14) Q6-S18(5)/PW(15)-S19(6)/PW(16) | |
| 4 | Q1-S1(9)/PW(9)-S2(7)/PW(17) Q2-S5(8)/PW(8) Q3-S8(5)/PW(15)-S9(4)/PW(14) Q6-S19(8)/PW(8)-S20(9)/PW(9) | |
| 5 | Q1-S2(9)/PW(9)-S3(7)/PW(17) Q2-S4(6)/PW(16)-S5(5)/PW(15) Q3-S8(4)/PW(14)-S9(6)/PW(16) Q4-S11(6)/PW(16)-S12(8)/PW(8) Q5-S16(9)/PW(9)-S17(8)/PW(8) | |
| 31 | 1 | Q1-S1(5)/PW(18)-S3(5)PW(15) Q2-S6(6)/PW(16) Q4-S10(6)/PW(16)-S12(3)/PW(23) Q5-S15(9)/PW(19) Q6-S19(7)-S20(3) |
| 2 | Q1-S1(6)/PW(16) Q2-S4(7)/PW(17)-S5(8)/PW(18) Q3-S8(9)/PW(19) Q5-S16(5)/PW(25) Q6-S19(4)/PW(24)-S20(5)/PW(15) | |
| 3 | Q1-S1(6)/PW(16)-S2(3)/PW(13)-S3(5)/PW(15) Q2-S5(9)/PW(19) Q3-S7(7)/PW(17) Q4-S15(9)/PW(19) | |
| 4 | Q1-S1(9)/PW(17)-S2(3)/PW(23) Q2-S4(2)/PW(20)-S5(4)/PW(14) Q3-S8(9)/PW(19)-S9(3)/PW(23) Q6-S20(8)/PW(18) | |
| 5 | Q1-S1(3)/PW(25)-S2(9)/PW(19) Q2-S5(4)/PW(24) Q3-S8(6)/PW(23)-S9(2)/PW(17) Q6-S20(8)/PW(18) | |
| 32 | 1 | Q3-S7(6)/PW(16) Q4-S10(8)/PW(18)-S11(7)/PW(17)-S12(1)/PW(23) Q5-S15(4)/PW(14) Q6-S20(5)/PW(15) |
| 2 | Q1-S1(13)/PW(13)-S2(8)/PW(18)-S3(4)/PW(24) Q2-S5(3)/PW(13) Q3-S7(5)/PW(13)-S8(7)/PW(18) Q5-S16(6)/PW(16)-S17(7)/PW(17) Q6-S19(8)/PW(18) | |
| 3 | Q1-S1(9)/PW(9) Q3-S7(6)/PW(16)-S8(9)/PW(9) Q4-S14(6)/PW(16)-S15(7)/PW(17) Q5-S16(9)/PW(9)-S17(3)/PW(13) Q6-S18(8)/PW(8)-S19(9)/PW(9) | |
| 4 | Q1-S1(6)/PW(16)-S2(10)/PW(17)-S3(5)/PW(10) Q2-S4(2)/PW(5) Q3-S8(3)/PW(13)-S9(7)/PW(7) Q5-S16(5)/PW(15) Q6-S18(5)/PW(15)-S19(9)/PW(9) | |
| 5 | Q1-S2(9)/PW(9) Q3-S8(6)/PW(13)-S9(2)/PW(21) Q6-S19(3)/PW(16)-S20(7)/PW(7) | |
| 33 | 1 | Q1-S1(3)/PW(9)-S2(3)/PW(12)-S3(9)/PW(23) Q2-S5(9)/PW(15)-S6(7)/PW(17) Q3-S7(6)/PW(16)-S8(5)/PW(20) Q4-S10(7)/PW(17)-S11(3)/PW(13)-S12(2)/PW(21) Q5-S15(8)/PW(18)-S16(4)/PW(18) Q6-S18(6)/PW(16)-S19(4)/PW(24)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(13)-S2(8)/PW(18) Q2-S4(5)/PW(13)-S5(8)/PW(18) Q3-S8(6)/PW(16)-S9(7)/PW(17) Q5-S16(4)/PW(14)-S17(5)/PW(23) Q6-S18(5)/PW(15)-S20(4)/PW(14) | |
| 3 | Q1-S1(7)/PW(16)-S3(10)/PW(23) Q2-S5(6)/PW(16) Q3-S7(3)/PW(19) Q4-S15(8)/PW(18)-S16(9)/PW(19) | |
| 4 | Q1-S2(9)/PW(19)-S3(5)/PW(15) Q2-S4(3)/PW(11)-S5(3)/PW(9) Q3-S7(4)/PW(14) Q4-S10(5)/PW(15)-S11(3)/PW(16) | |
| 5 | Q1-S2(8)/PW(18)-S3(9)/PW(19) Q2-S4(4)/PW(24)-S5(5)/PW(12) Q3-S8(3)PW(13)-S9(6)/PW(16)-S10(2)/PW(14) Q5-S16(2)/PW(20)-S17(3)/PW(13) Q6-S18(4)/PW(15)-S19(3)/PW(16)-S20(7)/PW(17) | |
| 34 | 1 | Q4-S10(6)/PW(16)-S11(5)/PW(18)-S12(2)PW(22) Q5-S15(6)/PW(18)-S16(8)/PW(18) Q6-S19(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23)-S2(8)/PW(18) Q2-S5(6)/PW(18)-S6(7)/PW(21) Q3-S8(5)/PW(22)-S9(4)/PW(18)-S10(3)/PW(13) Q5-S16(4)/PW(14)-S17(5) Q6-S18(7)/PW(17)-S20(4)/PW(20) | |
| 3 | Q1-S1(8)/PW(9)-S3(5)/PW(15) Q2-S5(5)/PW(15)-S6(6)/PW(16) Q3-S7(6)/PW(16)-S8(8)/PW(18) Q4-S15(7)/PW(17)-S16(8)/PW(18) | |
| 4 | Q1-S1(3)/PW(23)-S2(7)/PW(17)-S3(4)/PW(24) Q2-S5(8)/PW(18) Q3-S8(6)/PW(16)-S9(5)/PW(15) Q6-S19(8)/PW(8) | |
| 5 | Q1-S1(6)/PW(16)-S2(3)/PW(23)-S3(5)/PW(15) Q2-S5(8)/PW(18)-S6(4)/PW(24) Q3-S8(9)/PW(14)-S9(6)/PW(15)-S10(3)/PW(23) Q6-S18(6)/PW(14)-S19(5)/PW(15)-S20(7)/PW(17) | |
| 35 | 1 | Q2-S6(8)/PW(18)-S7(9)/PW(19) Q4-S10(7)/PW(17)-S12(2)/PW(22) Q5-S15(8)/PW(18) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(6)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(16) Q5-S16(4)/PW(14) Q6-S19(3)/PW(23)-S20(4)/PW(14) | |
| 3 | Q1-S1(7)/PW(17)-S2(2)/PW(20)-S3(3)/PW(15) Q2-S5(5)/PW(5) Q3-S7(6)/PW(6) Q4-S15(7)/PW(7) | |
| 4 | Q1-S1(10)/PW(23)-S2(7)/PW(17) Q2-S4(3)/PW(21)-S5(9)/PW(18) Q3-S8(6)/PW(6)-S9(6)/PW(6) Q6-S20(7)/PW(17) | |
| 5 | Q1-S1(6)/PW(11)-S2(7)/PW(17) Q2-S5(8)/PW(8) Q3-S8(1)/PW(15)-S9(6)/PW(16) Q6-S20(2)/PW(17) | |
| 36 | 1 | Q1-S1(3)/PW(12) Q2-S4(5)/PW(17) Q3-S7(3)/PW(13) Q4-S11(3)/PW(14)-S12(7)/PW(17) Q5-S14(8)/PW(18)-S15(4)/PW(14) Q6-S20(8)/PW(18) |
| 2 | Q1-S2(3)/PW(23)-S3(5)/PW(18) Q2-S5(7)/PW(17) Q4-S11(9)/PW(19)-S12(6)/PW(17)-S13(5)/PW(15) Q5-S14(8)/PW(18)-S15(4)/PW(14) Q6-S18(4)/PW(14)-S20(8)/PW(18) | |
| 3 | Q1-S1(6)/PW(16)-S2(9)/PW(19)-S3(1)/PW(14) Q3-S8(2)/PW(22) Q4-S12(9)/PW(19)-S13(6)/PW(26) Q5-S14(8)/PW(18)-S15(4)/PW(24) Q6-S18(9)/PW(19)-S20(8)/PW(18) | |
| 4 | Q1-S1(9)/PW(21)-S2(7)/PW(18)-S3(5)/PW(25) Q2-S5(5)/PW(25) Q4-S11(9)/PW(19)-S12(4)/PW(24)-S13(5)/PW(15) Q5-S14(3)/PW(23)-S15(4)/PW(24) Q6-S20(8)/PW(18) | |
| 5 | Q1-S1(9)/PW(20)-S2(9)/PW(23)-S3(4)/PW(24) Q3-S8(6)/PW(14) Q4-S12(9)/PW(15)-S13(6)/PW(16) Q5-S14(4)/PW(11)-S15(4)/PW(24) Q6-S18(3)/PW(17)-S20(8)/PW(16) | |
| 37 | 1 | Q1-S3(8)/PW(15) Q2-S6(5)/PW(24) Q3-S7(4)/PW(14) Q4-S9(4)PW(20)-S10(5)/PW(18) Q5-S13(8)/PW(18)-S14(9)/PW(19) Q6-S19(4)/PW(24) |
| 2 | Q1-S1(2)/PW(20) Q2-S6(8)/PW(28) Q4-S11(8)/PW(18)-S13(3)/PW(23) Q5-S14(7)/PW(27) Q6-S18(8)/PW(18)-S19(2)/PW(22) | |
| 3 | Q1-S2(9)/PW(25)-S3(3)/PW(23) Q2-S6(6)/PW(16) Q3-S7(4)/PW(24)-S8(7)/PW(17) Q4-S8(3)/PW(8) Q5-S16(4)/PW(14) Q6-S20(7)/PW(17) | |
| 4 | Q1-S1(5)/PW(18)-S2(7)/PW(17)-S3(3)/PW(23) Q2-S6(8)/PW(8) Q4-S11(8)/PW(8)-S13(3)/PW(23) Q5-S14(7)/PW(17) Q6-S18(8)/PW(18)-S19(2)/PW(22) | |
| 5 | Q1-S2(5)/PW(25)-S3(3)/PW(23) Q3-S7(4)/PW(24)-S8(7)/PW(17) Q4-S8(8)/PW(20) Q5-S15(5)/PW(22)-S16(4)/PW(24) Q6-S20(7)/PW(27) | |
| 38 | 1 | Q1-S1(2)/PW(19)-S3(14)/PW(17) Q2-S6(7)/PW(19) Q4-S10(7)/PW(20)-S12(2)/PW(22) Q5-S15(8)/PW(18) Q6-S19(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(5)/PW(25)-S5(8)/PW(18) Q3-S8(6)/PW(16) Q5-S16(4)/PW(24) Q6-S19(3)/PW(13)-S20(4)/PW(24) | |
| 3 | Q1-S1(3)/PW(19)-S2(2)/PW(11)-S3(13)/PW(13) Q2-S5(5)/PW(15) Q3-S7(6)/PW(17) Q4-S15(7)/PW(19) | |
| 4 | Q1-S1(3)/PW(23)-S2(7)/PW(17) Q2-S4(1)/PW(19)-S5(8)/PW(18) Q3-S8(6)/PW(16)-S9(6)/PW(19) Q6-S20(7)/PW(24) | |
| 5 | Q1-S1(3)/PW(10)-S2(7)/PW(17) Q2-S5(8)/PW(18) Q3-S8(4)/PW(19)-S9(6)/PW(16) Q6-S20(10)/PW(21) | |
| 39 | 1 | Q1-S1(1)/PW(24)-S2(8)/PW(26)-S3(4)/PW(14) Q2-S4(5)/PW(18)-S6(7)/PW(17) Q4-S10(7)/PW(17)-S12(2)/PW(18) Q5-S15(8)/PW(18) Q6-S19(4)/PW(19)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(5)/PW(22)-S5(8)/PW(18) Q3-S8(6)/PW(16) Q5-S16(4)/PW(14) Q6-S19(3)/PW(23)-S20(4)/PW(24) | |
| 3 | Q1-S1(3)/PW(17)-S2(2)/PW(22)-S3(3)/PW(23) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(3)/PW(23)-S2(7)/PW(17) Q2-S4(3)/PW(21)-S5(5)7PW(18) Q3-S8(6)/PW(16)-S9(6)/PW(26) Q6-S20(7)/PW(17) | |
| 5 | Q1-S1(4)/PW(21)-S2(9)/PW(27) Q2-S5(8)/PW(18) Q3-S8(4)/PW(24)-S9(6)/PW(26) Q6-S20(5)/PW(27) | |
| 40 | 1 | Q1-S1(2)/PW(14)-S2(5)/PW(15)-S3(4)/PW(19) Q2-S6(8)/PW(18)-S7(9)/PW(19) Q4-S10(5)/PW(15)-S12(2)/PW(12) Q5-S15(6)/PW(16)-S16(5)/PW(15) Q6-S20(5)/PW(15) |
| 2 | Q1-S1(13)/PW(23)-S2(7)/PW(27) Q2-S4(9)/PW(19)-S5(8)/PW(18)-S6(6)/PW(16) Q3-S8(6)/PW(26)-S9(7)/PW(7) Q5-S16(4)/PW(24)-S17(5)/PW(25) Q6-S18(5)/PW(15)-S19(3)/PW(23) S20(4)/PW(14) | |
| 3 | Q1-S1(8)/PW(18)-S3(3)/PW(28) Q2-S5(9)/PW(19) Q3-S7(7)/PW(17) Q4-S15(9)/PW(19)-S16(8)/PW(18) | |
| 4 | Q1-S1(3)/PW(19)-S2(8)/PW(18)-S3(5)/PW(25) Q2-S4(4)/PW(21)-S5(7)/PW(17)-S6(6)/PW(26) Q3-S8(4)/PW(16)-S9(5)/PW(25) Q6-S19(4)/PW(24)-S20(7)/PW(17) | |
| 5 | Q1-S1(5)/PW(15)-S2(6)/PW(16) Q2-S5(8)/PW(28) Q3-S8(8)/PW(18)-S9(6)/PW(16) Q6-S19(9)/PW(17) | |
| 41 | 1 | Q1-S1(8)/PW(16) Q2-S4(5)/PW(18) Q3-S7(3)/PW(13) Q4-S11(4)/PW(14)-S12(7)/PW(17) Q5-S14(8)/PW(18)-S15(4)/PW(14) Q6-S20(8)/PW(18) |
| 2 | Q1-S2(3)/PW(23)-S3(5)/PW(15) Q2-S5(7)/PW(17) Q4-S11(9)/PW(19)-S12(7)/PW(19)-S13(5)/PW(15) Q5-S14(8)/PW(18)-S15(4)/PW(14) Q6-S18(4)/PW(24) Q6-S20(8)/PW(18) | |
| 3 | Q1-S1(6)/PW(16)-S2(5)/PW(19)-S3(4)/PW(14) Q3-S8(2)/PW(22) Q4-S12(9)/PW(17)-S13(6)/PW(26) Q5-S14(8)/PW(18)-S15(4)/PW(21) Q6-S18(9)/PW(19)-S20(8)/PW(18) | |
| 4 | Q1-S1(9)/PW(19)-S2(8)/PW(18)-S3(5)PW(25) Q2-S5(5)/PW(25) Q4-S11(9)/PW(18)-S12(4)/PW(24)-S13(5)/PW(15) Q5-S14(13)/PW(23)-S15(4)/PW(24) Q6-S20(8)/PW(18) | |
| 5 | Q1-S1(6)/PW(19)-S2(9)/PW(19)-S3(4)/PW(24) Q3-S8(6)/PW(26) Q4-S12(11)/PW(19)-S13(6)/PW(16) Q5-S14(8)/PW(18)-S15(4)/PW(24) Q6-S18(3)/PW(14)-S20(8)/PW(18) | |
| 42 | 1 | Q1-S3(8)/PW(19) Q2-S6(5)/PW(25) Q3-S7(4)/PW(14) Q4-S9(4)PW(14)-S10(5)/PW(15) Q5-S13(8)/PW(18)-S14(7)/PW(19) Q6-S19(4)/PW(24) |
| 2 | Q1-S1(8)/PW(20) Q2-S6(8)/PW(18) Q4-S11(8)/PW(18)-S13(3)/PW(23) Q5-S14(7)/PW(27) Q6-S18(8)/PW(18)-S19(2)/PW(22 | |
| 3 | Q1-S2(7)/PW(25)-S3(3)/PW(23) Q2-S6(3)/PW(16) Q3-S7(4)/PW(24)-S8(7)/PW(17) Q4-S8(8)/PW(8) Q5-S16(4)/PW(14) Q6-S20(7)/PW(17) | |
| 4 | Q1-S1(6)/PW(18)-S2(7)/PW(17)-S3(3)/PW(23) Q2-S6(8)/PW(8) Q4-S11(8)/PW(8)-S13(3)/PW(23) Q5-S14(7)/PW(17) Q6-S18(8)/PW(18)-S19(2)/PW(22) | |
| 5 | Q1-S2(5)/PW(15)-S3(3)/PW(23) Q3-S7(4)/PW(24)-S8(7)/PW(17) Q4-S8(8)/PW(18) Q5-S15(5)/PW(25)-S16(4)/PW(24) Q6-S20(5)/PW(17) | |
| 43 | 1 | Q1-S1(8)/PW(19)-S3(4)/PW(14) Q2-S6(7)/PW(17) Q4-S10(7)/PW(17)-S12(1)/PW(22) Q5-S15(8)/PW(18) Q6-S19(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(13) Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(26) Q5-S16(4)/PW(14) Q6-S19(3)/PW(23)-S20(4)/PW(24) | |
| 3 | Q1-S1(2)/PW(17)-S2(2)/PW(21)-S3(3)/PW(15) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(3)/PW(23)-S2(7)/PW(17) Q2-S4(5)/PW(19)-S5(3)/PW(18) Q3-S8(3)/PW(19)-S9(6)/PW(16) Q6-S20(7)/PW(27) | |
| 5 | Q1-S1(4)/PW(21)-S2(2)/PW(17) Q2-S5(8)/PW(18) Q3-S8(3)/PW(15)-S9(9)/PW(16) Q6-S20(2)/PW(27) | |
| 44 | 1 | Q1-S1(1)/PW(20)-S2(5)/PW(22)-S3(4)/PW(14) Q2-S4(5)/PW(15)-S6(7)/PW(27) Q4-S10(7)/PW(17)-S12(2)/PW(12) Q5-S15(8)/PW(18) Q6-S19(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(16) Q5-S16(4)/PW(14) Q6-S19(3)/PW(13)-S20(4)/PW(24) | |
| 3 | Q1-S1(4)/PW(17)-S2(2)/PW(12)-S3(3)/PW(23) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(3)/PW(25)-S2(5)/PW(17) Q2-S4(1)/PW(21)-S5(3)PW(18) Q3-S8(6)/PW(16)-S9(6)/PW(26) Q6-S20(7)/PW(17) | |
| 5 | Q1-S1(3)/PW(16)-S2(5)/PW(17) Q2-S5(8)/PW(18) Q3-S8(3)/PW(24)-S9(6)/PW(26) Q6-S20(3)/PW(17) | |
| 45 | 1 | Q1-S1(9)/PW(14)-S2(5)/PW(15)-S3(4)/PW(13) Q2-S6(8)/PW(18)-S7(6)/PW(12) Q4-S10(5)/PW(15)-S12(2)/PW(12) Q5-S15(6)/PW(16)-S16(5)/PW(15) Q6-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23)-S2(7)/PW(17) Q2-S4(6)/PW(19)-S5(8)/PW(18)-S6(6)/PW(16) Q3-S8(6)/PW(16)-S9(9)/PW(7) Q5-S16(4)/PW(24)-S17(5)/PW(25) Q6-S18(5)/PW(15)-S19(3)/PW(23)-S20(4)/PW(14) | |
| 3 | Q1-S1(8)/PW(18)-S3(3)/PW(23) Q2-S5(6)/PW(19) Q3-S7(7)/PW(17) Q4-S15(9)/PW(19)-S16(8)/PW(18) | |
| 4 | Q1-S1(6)/PW(16)-S2(8)/PW(18)-S3(5)/PW(25) Q2-S4(4)/PW(24)-S5(3)/PW(17)-S6(6)/PW(26) Q3-S8(6)/PW(16)-S9(5)/PW(25) Q6-S19(4)/PW(24)-S20(5)/PW(17) | |
| 5 | Q1-S1(5)/PW(15)-S2(6)/PW(16) Q2-S5(8)/PW(18) Q3-S8(8)/PW(21)-S9(6)/PW(16) Q6-S19(9)/PW(20) | |
| 46 | 1 | Q1-S1(4)/PW(17)-S2(2)/PW(15)-S3(8)/PW(18) Q2-S6(7)/PW(17)-S7(5)/PW(26) Q4-S10(7)/PW(17)-S12(2)/PW(22) Q5-S15(8)/PW(28) Q6-S19(4)/PW(24)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(16) Q5-S16(4)/PW(14) Q6-S19(3)/PW(23)-S20(4)/PW(24) | |
| 3 | Q1-S1(5)/PW(19)-S2(2)/PW(22)-S3(3)/PW(23) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(14) | |
| 4 | Q1-S1(4)/PW(19)-S2(7)/PW(17) Q2-S4(2)/PW(19)-S5(8)/PW(18) Q3-S8(3)/PW(16)-S9(6)/PW(16) Q6-S20(7)/PW(17) | |
| 5 | Q1-S1(3)/PW(18)-S2(7)/PW(17) Q2-S5(8)/PW(8) Q3-S8(12)/PW(4)-S9(6)/PW(6) Q6-S20(3)/PW(16) | |
| 47 | 1 | Q1-S3(4)/PW(24) Q2-S5(8)/PW(8)-S6(7)/PW(17) Q4-S10(7)/PW(17)-S12(2)/PW(12) Q5-S15(8)/PW(18) Q6-S19(14)/PW(4)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(5)/PW(5)-S5(8)/PW(8) Q3-S8(6)/PW(6) Q5-S16(4)/PW(14) Q6-S19(3)/PW(13)-S20(4)/PW(14) | |
| 3 | Q1-S1(7)/PW(17)-S2(9)/PW(18)-S3(3)/PW(13) Q2-S5(5)/PW(5) Q3-S7(6)/PW(6) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(6)/PW(13)-S2(7)/PW(17) Q2-S4(1)/PW(11)-S5(5)/PW(8) Q3-S8(3)/PW(16)-S9(6)/PW(21) Q6-S20(7)/PW(22) | |
| 5 | Q1-S1(3)/PW(12)-S2(7)/PW(17) Q2-S5(9)/PW(18) Q3-S8(4)/PW(14)-S9(6)/PW(16) Q6-S20(4)/PW(11) | |
| 48 | 1 | Q1-S1(6)/PW(19)-S3(8)/PW(18) Q2-S6(4)/PW(14) Q4-S10(7)/PW(17)-S12(2)/PW(12) Q5-S15(8)/PW(8) Q6-S19(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(6)/PW(21) Q2-S4(6)/PW(16)-S5(8)/PW(18) Q3-S8(6)/PW(19) Q5-S16(4)/PW(14) Q6-S19(3)/PW(13)-S20(4)/PW(14) | |
| 3 | Q1-S1(7)/PW(17)-S2(5)/PW(15)-S3(3)/PW(23) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(3)PW(13)-S2(7)/PW(17) Q2-S4(10)/PW(11)-S5(8)/PW(19) Q3-S8(4)/PW(16)-S9(6)/PW(16) Q6-S20(11)/PW(16) | |
| 5 | Q1-S1(4)/PW(14)-S2(7)/PW(17) Q2-S5(8)/PW(22) Q3-S8(6)/PW(14)-S9(3)/PW(16) Q6-S20(8)/PW(21) | |
| 49 | 1 | Q1-S3(6)/PW(11) Q2-S5(8)/PW(18)-S6(7)/PW(17)-S7(9)/PW(19) Q4-S11(6)/PW(9)-S12(4)/PW(12) Q5-S15(8)/PW(18) Q6-S19(5)/PW(13)-S20(5)/PW(11) |
| 2 | Q1-S1(6)/PW(8)-S2(9)/PW(9) Q2-S4(5)/PW(15)-S5(8)/PW(8) Q3-S7(7)/PW(7)-S8(6)/PW(6) Q5-S16(4)/PW(14)-S17(6)/PW(6) Q6-S20(4)/PW(14) | |
| 3 | Q1-S1(6)/PW(17)-S3(3)/PW(13) Q2-S5(5)/PW(15)-S6(8)/PW(18) Q3-S7(6)/PW(22)-S8(8)/PW(8) Q4-S15(7)/PW(17)-S16(9)/PW(9) | |
| 4 | Q1-S1(3)/PW(21)-S2(7)/PW(17)-S3(4)/PW(18) Q2-S4(3)/PW(11)-S5(6)/PW(18) Q3-S8(6)/PW(14)-S9(6)/PW(13) Q6-S20(7)/PW(17) | |
| 5 | Q1-S1(1)/PW(15)-S2(7)/PW(11)-S3(7)/PW(17) Q2-S5(8)/PW(8) Q3-S8(4)/PW(22)-S9(6)/PW(16) Q6-S19(8)/PW(18)-S20(7)/PW(21) | |
| 50 | 1 | Q2-S5(4)/PW(14)-S6(5)/PW(15) Q4-S10(7)/PW(17)-S11(8)/PW(18)-S12(2)/PW(22) Q5-S15(8)/PW(21)-S17(9)/PW(19) Q6-S19(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(7)/PW(23)-S2(5)/PW(25) Q2-S4(5)/PW(25)-S5(7)/PW(28)-S6(4)/PW(24) Q3-S8(4)/PW(14) Q5-S16(2)/PW(14)-S17(5)/PW(15) Q6-S19(3)/PW(13)-S20(4)/PW(14) | |
| 3 | Q1-S1(6)/PW(16)-S2(8)/PW(18)-S3(3)/PW(13) Q2-S5(5)/PW(15)-S6(7)/PW(17) Q3-S7(6)/PW(16)-S8(8)/PW(18) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(4)/PW(15)-S2(7)/PW(17) Q2-S4(4)/PW(14)-S5(8)/PW(21) Q3-S8(5)/PW(16)-S9(6)/PW(16) Q6-S18(5)/PW(18)-S20(7)/PW(17) | |
| 5 | Q1-S1(4)/PW(14)-S2(6)/PW(17)-S3(8)/PW(18) Q2-S5(8)/PW(18) Q3-S8(5)/PW(14)-S9(6)/PW(26) Q6-S19(7)/PW(17) | |
| 51 | 1 | Q1-S2(9)/PW(18) Q2-S5(4)/PW(14)-S6(7)7PW(17) Q4-S10(4)/PW(14)-S11(8)/PW(18)-S12(5)/PW(15) Q5-S15(8)/PW(8)-S16(7)/PW(7) Q6-S18(6)/PW(16)-S19(8)/PW(18)-S20(9)/PW(21) |
| 2 | Q1-S1(8)/PW(10)-S2(8)/PW(12) Q2-S4(5)/PW(17)-S5(8)/PW(20)-S6(9)/PW(19) Q3-S8(6)/PW(16) Q5-S16(3)/PW(14) Q6-S19(3)/PW(11)-S20(4)/PW(14) | |
| 3 | Q1-S2(5)/PW(15) Q2-S6(6)/PW(15)-S7(7)/PW(17) Q4-S15(7)/PW(16) | |
| 4 | Q1-S1(8)/PW(17)-S2(4)/PW(19)-S3(9)/PW(9) Q2-S4(8)/PW(21)-S5(5)/PW(10) Q3-S8(5)/PW(15)-S9(6)/PW(16) Q5-S18(4)/PW(14) Q6-S19(8)/PW(18)-S20(7)/PW(17) | |
| 5 | Q1-S1(5)/PW(16)-S2(7)/PW(17) Q2-S4(7)/PW(17)-S5(8)/PW(12) Q3-S7(5)/PW(15)-S8(4)/PW(24)-S9(6)/PW(16) Q6-S19(8)/PW(20)-S20(6)/PW(16) | |
| 52 | 1 | Q1-S3(8)/PW(23) Q2-S6(6)/PW(16)-S7(5)/PW(15) Q4-S10(3)/PW(14)-S11(3)/PW(13)-S12(2)/PW(12) Q5-S15(8)/PW(18) Q6-S20(5)/PW(15) |
| 2 | Q1-S1(5)/PW(21)-S2(6)/PW(18) Q2-S4(6)/PW(24)-S5(7)/PW(17) Q3-S8(7)/PW(14) Q5-S16(5)/PW(15)-S17(4)/PW(14) Q6-S19(7)/PW(17)-S20(8)/PW(18) | |
| 3 | Q1-S1(4)/PW(22)-S2(6)/PW(18) Q2-S5(7)/PW(17)-S6(5)/PW(24) Q3-S7(6)/PW(11)-S8(5)/PW(15) Q4-S15(7)/PW(19)-S16(8)/PW(18) | |
| 4 | Q1-S1(4)/PW(18)-S2(6)/PW(16) Q2-S4(5)/PW(15)-S5(4)/PW(24) Q3-S8(7)/PW(24) Q6-S20(7)/PW(21) | |
| 5 | Q1-S2(8)/PW(8) Q2-S5(7)/PW(18) Q3-S8(4)/PW(24)-S9(6)/PW(16) Q6-S19(9)/PW(19) | |
| 53 | 1 | Q1-S2(9)/PW(18)-S3(3)/PW(12) Q2-S4(6)/PW(16)-S6(7)/PW(17) Q4-S10(6)/PW(20)-S11(8)/PW(18)-S12(2)/PW(12) Q5-S15(7)/PW(18)-S16(9)/PW(9) Q6-S18(7)/PW(17)-S19(6)/PW(16)-S20(5)/PW(20) |
| 2 | Q1-S1(8)/PW(15)-S2(6)/PW(26) Q2-S4(5)/PW(15)-S5(8)/PW(18)-S6(7)/PW(17) Q3-S8(6)/PW(24)-S9(7)/PW(17) Q5-S16(4)/PW(24)-S17(5)/PW(15) Q6-S19(6)/PW(16) | |
| 3 | Q1-S3(3)/PW(13) Q2-S5(5)/PW(15)-S6(7)/PW(17) Q3-S7(6)/PW(16)-S8(7)/PW(17) Q4-S15(7)/PW(17)-S16(6)/PW(16) | |
| 4 | Q1-S2(7)/PW(17) Q2-S5(8)/PW(18) Q3-S8(5)/PW(15)-S9(6)/PW(16)-S10(4)/PW(24) Q6-S19(8)/PW(18) | |
| 5 | Q1-S1(1)/PW(24)-S2(7)/PW(17) Q2-S5(3)/PW(21) Q3-S8(4)/PW(24)-S9(6)/PW(16) Q6-S18(4)/PW(22)-S19(8)/PW(19) | |
| 54 | 1 | Q2-S6(9)/PW(17) Q4-S10(7)/PW(21)-S12(1)/PW(22) Q5-S15(10)/PW(18) Q6-S19(11)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(16) Q5-S16(4)/PW(24) Q6-S19(3)/PW(23)-S20(4)/PW(24) | |
| 3 | Q1-S1(4)/PW(17)-S2(2)/PW(22)-S3(3)/PW(13) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(3)/PW(12)-S2(6)(PW(14) Q2-S4(2)/PW(11)-S5(8)/PW(18) Q3-S8(6)/PW(23)-S9(6)/PW(16) Q6-S20(7)/PW(17) | |
| 5 | Q1-S1(1)/PW(21)-S2(5)/PW(17) Q2-S5(3)/PW(18) Q3-S8(4)/PW(14)-S9(6)/PW(16) Q6-S20(7)/PW(22) | |
| 55 | 1 | Q1-S1(5)/PW(18) Q2-S6(7)/PW(17)-S7(5)/PW(15) Q3-S15(8)/PW(8) Q4-S10(4)/PW(17)-S11(5)/PW(15)-S12(2)/PW(23) Q5-S15(8)/PW(8) Q6-S18(9)/PW(19)-S19(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23)-S2(7)/PW(17) Q3-S8(6)/PW(16) Q5-S16(4)/PW(14) Q6-S19(3)/PW(13)-S20(4)/PW(14) | |
| 3 | Q1-S1(11)/PW(19)-S3(3)/PW(23) Q2-S5(5)/PW(25) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(6)/PW(26)-S2(7)/PW(11)-S3(8)/PW(18) Q2-S4(9)/PW(15)-S5(8)/PW(18) Q3-S8(8)/PW(16)-S9(6)/PW(19)-S10(7)/PW(17) Q6-S19(6)/PW(16)-S20(9)/PW(16) | |
| 5 | Q1-S2(7)/PW(17) Q2-S5(8)/PW(8) Q3-S9(6)/PW(16) Q6-S19(9)/PW(24)-S20(7)/PW(17) | |
| 56 | 1 | Q4-S10(7)/PW(15)-S12(9)/PW(20) Q5-S15(8)/PW(18) |
| 2 | Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(16) Q5-S16(5)/PW(24) Q6-S19(3)/PW(13)-S20(4)/PW(24) | |
| 3 | Q1-S1(9)/PW(18)-S2(2)/PW(24)-S3(3)/PW(23) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(3)/PW(18)-S2(7)/PW(17) Q2-S4(3)/PW(19)-S5(8)/PW(21) Q3-S8(10)/PW(21)-S9(6)/PW(15) Q6-S20(7)/PW(18) | |
| 5 | Q1-S1(4)/PW(13)-S2(9)/PW(20)-S3(9)/PW(15) Q2-S5(8)/PW(19) Q3-S6(4)/PW(16)-S8(7)/PW(18)-S9(6)/PW(16) Q6-S19(5)/PW(17)-S20(4)/PW(21) | |
| 57 | 1 | Q1-S2(9)/PW(21)-S3(5)/PW(15) Q2-S6(4)/PW(17) Q4-S10(7)/PW(17)-S12(5)/PW(22) Q5-S15(8)/PW(18)-S16(5)/PW(25) Q6-S18(6)/PW(26)-S20(5)/PW(25) |
| 2 | Q1-S1(3)/PW(23)-S2(8)/PW(18) Q2-S4(5)/PW(15) Q3-S7(4)/PW(14)-S8(6)/PW(16) Q5-S16(4)/PW(24)-S17(3)/PW(17) Q6-S20(9)/PW(19) | |
| 3 | Q1-S1(8)/PW(19)-S3(4)/PW(14) Q2-S5(5)/PW(15)-S6(7)/PW(17) Q3-S7(6)/PW(26)-S8(5)/PW(15) Q4-S15(7)/PW(17)-S16(8)/PW(18) Q5-S18(9)/PW(19) | |
| 4 | Q1-S1(3)/PW(23)-S2(7)/PW(17) Q2-S4(1)/PW(21)-S5(4)/PW(8) Q3-S8(6)/PW(13)-S9(6)/PW(19) Q6-S20(7)/PW(22) | |
| 5 | Q1-S2(9)/PW(21) Q2-S5(8)/PW(18) Q3-S8(4)/PW(14)-S9(6)/PW(16) | |
| 58 | 1 | Q1-S2(9)/PW(18)-S3(4)/PW(14) Q2-S6(7)/PW(17) Q4-S10(7)/PW(27)-S12(9)/PW(19) Q5-S15(8)/PW(18) Q6-S18(5)PW(15)-S19(4)/PW(24)-S20(5)/PW(25) |
| 2 | Q1-S1(8)/PW(19)-S2(5)/PW(25) Q2-S4(9)/PW(24) Q3-S8(6)/PW(26)-S9(6)/PW(16) Q5-S16(6)/PW(16)-S17(7)/PW(17) Q6-S19(8)/PW(18)-S20(4)/PW(24) | |
| 3 | Q1-S1(9)/PW(19)-S3(7)/PW(17) Q2-S5(5)PW(15) Q3-S7(6)/PW(16)-S8(5)/PW(15) Q4-S15(9)/PW(19)-S16(4)/PW(24) | |
| 4 | Q1-S2(9)/PW(9)-S3(4)/PW(14) Q2-S5(3)/PW(13)-S6(5)/PW(15) Q3-S8(6)/PW(16) Q6-S18(3)/PW(13)-S19(8)/PW(18)-S20(4)/PW(14) | |
| 5 | Q1-S1(6)/PW(19)-S2(7)/PW(16)-S3(5)/PW(15) Q2-S5(8)/PW(8)-S8(4)/PW(14) Q3-S8(4)/PW(14)-S9(6)/PW(26)-S10(5)/PW(15) Q6-S19(9)/PW(18)-S20(7)/PW(13) | |
| 59 | 1 | Q2-S6(3)/PW(14)-S7(8)/PW(18) Q4-S10(7)/PW(17)-S11(5)/PW(25)-S12(2)/PW(22) Q5-S15(8)/PW(18) Q6-S19(4)/PW(24)-S20(5)/PW(15) |
| 2 | Q1-S1(6)/PW(16) Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(26) Q5-S16(5)/PW(26) Q6-S19(13)/PW(13)-S20(4)/PW(14) | |
| 3 | Q1-S2(9)/PW(9)-S3(7)/PW(18) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S2(9)/PW(19) Q2-S4(11)/PW(11)-S5(8)/PW(18) Q3-S8(4)/PW(7)-S9(6)/PW(16) Q6-S19(2)/PW(22)-S20(3)/PW(14) | |
| 5 | Q2-S5(8)/PW(8) Q3-S8(4)/PW(24)-S9(6)/PW(16) Q6-S19(5)/PW(15)-S20(6)/PW(19) | |
| 60 | 1 | Q2-S6(7)/PW(11)-S7(9)/PW(9) Q3-S9(8)PW(15) Q4-S10(3)/PW(19)-S11(8)/PW(18)-S12(2)/PW(22) Q5-S15(9)/PW(9) Q6-S18(6)/PW(16)-S19(4)/PW(14)-S20(5)/PW(25) |
| 2 | Q1-S1(3)/PW(23)-S2(8)/PW(18) Q2-S4(9)/PW(9)-S5(6)/PW(16) Q3-S7(7)/PW(17)-S8(6)/PW(16) Q6-S20(4)/PW(14) | |
| 3 | Q1-S2(12)/PW(12) Q2-S5(8)/PW(9) Q3-S7(6)/PW(16)-S8(7)/PW(17) Q4-S15(8)/PW(19)-S16(9)/PW(9) Q6-S19(8)/PW(18) | |
| 4 | Q1-S2(7)/PW(17)-S3(8)/PW(18) Q3-S8(6)/PW(16)-S9(6)/PW(16)-S10(5)/PW(25) Q5-S17(9)/PW(19) Q6-S19(5)/PW(25)-S20(8)/PW(18) | |
| 5 | Q2-S5(3)/PW(18) Q3-S8(5)/PW(21)-S9(6)/PW(16) | |
| 61 | 1 | Q1-S1(6)/PW(21)-S2(5)/PW(19)-S3(4)/PW(14) Q4-S10(5)/PW(15)-S11(7)/PW(16)-S12(8)/PW(22) Q6-S19(4)/PW(24)-S20(5)/PW(15) |
| 2 | Q2-S4(5)/PW(25)-S5(8)/PW(18) Q3-S8(6)/PW(26)-S9(7)/PW(17) Q6-S19(9)/PW(9) | |
| 3 | Q1-S3(5)/PW(9) Q2-S5(5)/PW(25)-S6(7)/PW(17) Q3-S7(6)/PW(26) Q4-S15(7)/PW(17) Q6-S18(8)/PW(18)-S19(9)/PW(19) | |
| 4 | Q1-S2(7)/PW(17) Q2-S4(11)/PW(11)-S5(8)/PW(18) Q3-S8(6)/PW(19)-S9(6)/PW(18) Q6-S20(7)/PW(20) | |
| 5 | Q1-S1(4)/PW(24)-S2(5)/PW(16) Q2-S5(8)/PW(27) Q3-S8(4)/PW(22)-S9(6)/PW(16) Q4-S11(4)/PW(17) | |
| 62 | 1 | Q1-S1(8)/PW(18)-S3(7)/PW(24) Q2-S5(6)/PW(18) Q4-S10(7)/PW(17)-S11(8)/PW(9)-S12(5)/PW(17) Q5-S15(9)/PW(8)-S16(3)/PW(15) Q6-S20(7)/PW(9) |
| 2 | Q1-S1(6)/PW(3)-S2(8)/PW(9) Q3-S8(4)/PW(16)-S9(5)/PW(8) Q5-S16(8)/PW(14)-S17(5)/PW(15) Q6-S19(7)/PW(9) | |
| 3 | Q1-S1(6)/PW(18)-S2(7)/PW(12) Q2-S5(7)/PW(9) Q3-S7(8)/PW(16)-S8(4)/PW(19) Q4-S15(7)/PW(27)-S16(6)/PW(18) | |
| 4 | Q2-S5(9)/PW(8)-S6(3)/PW(7) Q3-S8(9)/PW(6)-S9(5)/PW(9) Q6-S18(3)/PW(3)-S20(9)/PW(9) | |
| 5 | Q1-S2(5)/PW(17)-S3(9)/PW(9) Q2-S4(2)/PW(20)-S5(8)/PW(18) Q3-S8(5)/PW(21)-S9(6)/PW(16)-S10(3)/PW(13) Q4-S16(4)/PW(14) Q5-S17(3)/PW(18)-S18(5)/PW(15) Q6-S20(9)/PW(21) | |
| 63 | 1 | Q1-S3(9)/PW(24) Q2-S6(7)/PW(17) Q5-S15(8)/PW(18)-S16(9)/PW(9) |
| 2 | Q1-S1(7)/PW(23)-S2(3)/PW(18) Q2-S4(5)/PW(15)-S5(8)/PW(18)-S6(7)/PW(17) Q3-S8(6)/PW(16) Q4-S15(6)/PW(16) Q6-S20(9)/PW(19) | |
| 3 | Q1-S1(7)/PW(9)-S2(8)/PW(8) Q2-S4(4)/PW(24)-S5(5)/PW(25) Q3-S7(6)/PW(26)-S8(9)/PW(17) | |
| 4 | Q2-S4(3)/PW(23)-S5(7)/PW(17)-S6(3)/PW(18) Q6-S19(9)/PW(23)-S20(7)/PW(11) | |
| 5 | Q2-S5(7)/PW(19) Q3-S9(6)/PW(6) Q6-S18(8)/PW(9)-S20(5)/PW(15) | |
| 64 | 1 | Q1-S1(9)/PW(14)-S2(3)/PW(20)-S3(2)/PW(14) Q2-S5(9)/PW(16)-S6(7)/PW(17) Q4-S10(2)/PW(19)-S11(8)/PW(18) Q5-S14(6)/PW(16)-S15(8)/PW(18) Q6-S19(6)/PW(16)-S20(3)/PW(13) |
| 2 | Q2-S5(6)/PW(16)-S6(7)/PW(17) Q3-S8(9)/PW(19)-S9(5)/PW(15) Q5-S16(7)/PW(23)-S17(2)/PW(22) Q6-S20(4)/PW(12) | |
| 3 | Q1-S1(6)/PW(16)-S3(9)/PW(9) Q4-S15(7)/PW(21)-S16(5)/PW(15) Q6-S19(8)/PW(18) | |
| 4 | Q1-S1(3)/PW(13)-S2(7)/PW(17)-S3(6)/PW(16) Q2-S5(8)/PW(8)-S6(5)/PW(15) Q6-S19(8)/PW(18)-S20(9)/PW(9) | |
| 5 | Q1-S2(3)/PW(17) Q2-S5(9)/PW(14)-S6(5)/PW(15) Q3-S8(7)/PW(21) | |
| 65 | 1 | Q1-S1(7)/PW(15)-S2(4)/PW(16)-S3(5)/PW(14) Q2-S5(8)PW(18)-S6(7)/PW(17)-S7(5)/PW(15) Q3-S8(3)/PW(23) Q4-S12(9)/PW(9) Q5-S15(8)/PW(18) |
| 2 | Q1-S1(9)/PW(9)-S2(5)/PW(15) Q2-S4(4)/PW(24)-S5(7)/PW(17) Q3-S8(5)/PW(15)-S9(4)PW(24) Q5-S16(8)/PW(8) Q6-S19(9)/PW(9)-S20(6)/PW(6) | |
| 3 | Q1-S2(7)/PW(18)-S3(9)/PW(9) Q2-S5(5)/PW(15) Q3-S6(4)/PW(10)-S7(6)/PW(16) | |
| 4 | Q1-S1(5)/PW(16)-S2(7)/PW(17)-S3(8)/PW(18) Q2-S4(9)/PW(12)-S5(8)/PW(18)-S6(3)/PW(11) Q3-S8(6)/PW(16)-S9(6)/PW(16) Q6-S19(8)/PW(18)-S20(7)/PW(17) | |
| 5 | Q1-S2(8)/PW(17) Q2-S4(5)/PW(14)-S5(3)/PW(8) Q3-S8(7)/PW(14)-S9(6)/PW(16) Q6-S19(6)/PW(16)-S20(7)/PW(17) | |
| 66 | 1 | Q1-S3(4)/PW(14) Q2-S6(7)/PW(17)-S7(8)/PW(18) Q4-S10(7)/PW(17) Q5-S15(8)/PW(8)-S16(8)/PW(8) Q6-S18(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(7)/PW(17)-S2(8)/PW(18) Q2-S4(2)/PW(21)-S5(3)/PW(13)-S6(4)/PW(24) Q3-S7(5)/PW(15)-S8(6)/PW(16)-S9(7)/PW(17) Q5-S16(4)/PW(14)-S17(5)/PW(15) Q6-S18(7)/PW(17)-S20(4)/PW(24) | |
| 3 | Q1-S1(8)/PW(18)-S2(9)/PW(19) Q2-S5(5)/PW(15)-S6(6)/PW(16) Q3-S7(6)/PW(16)-S8(7)/PW(17) Q4-S14(7)/PW(17)-S15(8)/PW(18) | |
| 4 | Q2-S4(7)/PW(18)-S5(8)/PW(18) Q3-S8(9)/PW(19) | |
| 5 | Q1-S2(5)/PW(14) Q2-S5(8)/PW(16)-S6(7)/PW(17) Q3-S8(5)/PW(15)-S9(7)/PW(17) Q5-S16(6)/PW(16)-S17(3)/PW(23) Q6-S18(4)/PW(14)-S19(8)/PW(18) | |
| 67 | 1 | Q1-S1(7)/PW(19)-S2(1)/PW(21)-S3(4)/PW(14) Q2-S4(3)/PW(23)-S6(5)/PW(15) Q4-S10(7)/PW(15)-S11(6)/PW(16)-S12(2)/PW(12) Q6-S19(7)/PW(17) |
| 2 | Q1-S1(11)/PW(13)-S2(5)/PW(15)-S3(5)/PW(16) Q2-S5(9)/PW(15)-S6(7)/PW(8) Q3-S7(4)/PW(17)-S8(5)/PW(16) Q5-S6(6)/PW(4)-S17(8)PW(5) | |
| 3 | Q1-S1(6)/PW(16)-S3(8)/PW(23) Q2-S5(8)/PW(18)-S6(9)/PW(9) Q3-S7(7)/PW(17)-S8(8)/PW(19) Q4-S14(6)/PW(26)-S15(7)/PW(7) Q6-S19(8)/PW(18)-S20(6)/PW(14) | |
| 4 | Q1-S1(3)/PW(3)-S2(6)/PW(6)-S3(4)/PW(4) Q4-S5(8)/PW(8) Q6-S20(7)/PW(7) | |
| 5 | Q1-S1(6)/PW(24)-S2(7)/PW(17)-S3(8)/PW(18) Q2-S4(5)/PW(25)-S5(8)/PW(18) Q3-S8(3)/PW(24)-S9(6)/PW(16) Q5-S17(6)/PW(16) Q6-S19(4)/PW(21)-S20(7)/PW(17) | |
| 68 | 1 | Q1-S1(7)/PW(22)-S3(6)/PW(14) Q2-S6(9)/PW(9) Q4-S10(6)/PW(16)-S12(3)/PW(13) Q5-S15(8)/PW(18) Q6-S19(6)/PW(16)-S20(8)/PW(18) |
| 2 | Q1-S1(6)/PW(16) Q2-S4(6)/PW(22)-S5(8)/PW(18) Q3-S8(9)/PW(17) Q5-S16(6)/PW(6) Q6-S19(7)/PW(15)-S20(3)/PW(23) | |
| 3 | Q1-S1(9)/PW(19)-S3(6)/PW(26) Q2-S5(5)/PW(5) Q3-S7(7)/PW(7) Q4-S15(8)/PW(8) | |
| 4 | Q1-S1(4)/PW(14)-S2(8)/PW(18) Q2-S4(3)/PW(16)-S5(11)/PW(11) Q3-S8(9)PW(19)-S9(6)/PW(26) Q6-S19(4)/PW(14)-S20(8)/PW(18) | |
| 5 | Q1-S1(6)/PW(16)-S2(8)/PW(18) Q2-S5(8)(PW(18) Q3-S8(9)/PW(11)-S9(5)/PW(15) Q6-S19(3)/PW(23)-S20(6)/PW(16) | |
| 69 | 1 | Q1-S1(7)/PW(17)-S3(5)/PW(13) Q2-S6(9)/PW(8) Q4-S12(9)/PW(9) Q6-S20(6)/PW(16) |
| 2 | Q2-S4(9)/PW(11)-S5(6)/PW(16)-S6(5)/PW(15) Q3-S7(7)/PW(17)-S8(8)/PW(8) Q4-S9(9)/PW(9) Q5-S16(3)/PW(23)-S17(2)/PW(20) Q6-S20(4)/PW(9) | |
| 3 | Q1-S2(6)/PW(9)-S3(3)/PW(13) Q3-S7(7)/PW(17)-S8(8)/PW(18) Q6-S18(9)/PW(9) | |
| 4 | Q1-S2(9)/PW(17) Q2-S5(7)/PW(18)-S6(4)/PW(14) Q3-S7(6)/PW(15)-S8(6)/PW(16)-S9(6)/PW(16) Q6-S19(5)/PW(15)-S20(6)/PW(16) | |
| 5 | Q1-S2(7)/PW(17) Q2-S5(8)/PW(18) Q3-S8(4)/PW(14)-S9(6)/PW(16) Q5-S16(4)/PW(14)-S17(5)PW(15) Q6-S19(3)/PW(13)-S20(8)/PW(19) | |
| 70 | 1 | Q1-S1(10)/PW(17)-S2(2)/PW(11)-S3(4)/PW(15) Q2-S5(6)/PW(16)-S7(7)/PW(17) Q3-S8(5)/PW(15)-S9(4)/PW(24) Q5-S15(6)/PW(16) Q6-S20(9)/PW(19) |
| 2 | Q1-S1(3)/PW(14)-S2(5)/PW(15)-S3(8)/PW(18) Q2-S4(4)/PW(19)-S5(3)/PW(13) Q3-S7(3)/PW(23)-S8(9)/PW(9) Q5-S16(6)/PW(16)-S17(7)/PW(17) | |
| 3 | Q1-S2(13)/PW(17)-S3(3)PW(13) Q2-S5(6)/PW(16)-S6(7)/PW(17) Q3-S7(11)/PW(11) Q4-S15(3)/PW(23)-S16(4)/PW(14) Q6-S18(5)/PW(15)-S19(6)/PW(16) | |
| 4 | Q1-S1(9)/PW(9)-S2(7)/PW(17) Q2-S5(8)/PW(8) Q3-S8(5)/PW(15)-S9(4)/PW(14) Q6-S19(8)/PW(8)-S20(9)/PW(9) | |
| 5 | Q1-S2(8)/PW(9)-S3(7)/PW(17) Q2-S4(6)/PW(16)-S5(5)/PW(15) Q3-S8(4)/PW(24)-S9(3)/PW(16) Q4-S11(7)/PW(16)-S12(8)/PW(8) Q5-S16(10)/PW(19)-S17(8)/PW(18) | |
| 71 | 1 | Q1-S1(7)/PW(18)-S3(5)PW(25) Q2-S6(6)/PW(16) Q4-S10(6)/PW(16)-S12(3)/PW(23) Q5-S15(9)/PW(19) Q6-S19/PW(17)-S20(3)/PW(13) |
| 2 | Q1-S1(6)/PW(16) Q2-S4(9)/PW(17)-S5(8)/PW(18) Q3-S8(5)/PW(19) Q5-S16(5)/PW(25) Q6-S19(4)/PW(24)-S20(5)/PW(15) | |
| 3 | Q1-S1(6)/PW(16)-S2(3)/PW(13)-S3(5)/PW(15) Q2-S5(8)/PW(19) Q3-S7(3)/PW(17) Q4-S15(9)/PW(19) | |
| 4 | Q1-S1(7)/PW(17)-S2(3)/PW(23) Q2-S4(2)/PW(20)-S5(4)/PW(14) Q3-S8(7)/PW(22)-S9(3)/PW(23) Q6-S20(10)/PW(18) | |
| 5 | Q1-S1(3)/PW(25)-S2(3)/PW(19) Q2-S5(5)/PW(24) Q3-S8(6)/PW(23)-S9(8)/PW(17) Q6-S20(8)/PW(26) | |
| 72 | 1 | Q3-S7(9)/PW(16) Q4-S10(8)/PW(18)-S11(6)/PW(17)-S12(3)/PW(23) Q5-S15(5)/PW(14) Q6-S20(5)/PW(15) |
| 2 | Q1-S1(8)/PW(19)-S2(8)/PW(18)-S3(4)/PW(24) Q2-S5(3)/PW(13) Q3-S7(5)/PW(23)-S8(7)/PW(18) Q5-S16(6)/PW(16)-S17(7)/PW(17) Q6-S19(8)/PW(18) | |
| 3 | Q1-S1(7)/PW(9) Q3-S7(6)/PW(16)-S8(9)/PW(19) Q4-S14(6)/PW(26)-S15(7)/PW(17) Q5-S16(9)/PW(9)-S17(3)/PW(13) Q6-S18(8)/PW(8)-S19(9)/PW(9) | |
| 4 | Q1-S1(10)/PW(16)-S2(3)/PW(17)-S3(5)/PW(10) Q2-S4(2)/PW(5) Q3-S8(3)/PW(13)-S9(7)/PW(7) Q5-S16(5)/PW(15) Q6-S18(5)/PW(15)-S19(9)/PW(9) | |
| 5 | Q1-S2(9)/PW(9) Q3-S8(3)/PW(13)-S9(2)/PW(21) Q6-S19(5)/PW(16)-S20(3)/PW(27) | |
| 73 | 1 | Q1-S1(6)/PW(23)-S2(2)/PW(19)-S3(4)/PW(13) Q2-S5(5)/PW(15)-S6(7)/PW(17) Q3-S7(3)/PW(16)-S8(5)/PW(20) Q4-S10(4)/PW(17)-S11(3)/PW(13)-S12(2)/PW(21) Q5-S15(8)/PW(18)-S16(4)/PW(24) Q6-S18(6)/PW(16)-S19(4)/PW(24)-S20(5)/PW(15) |
| 2 | Q1-S1(5)/PW(13)-S2(8)/PW(18) Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(16)-S9(7)/PW(17) Q5-S16(4)/PW(14)-S17(5)/PW(23) Q6-S18(5)/PW(15)-S20(4)/PW(24) | |
| 3 | Q1-S1(7)/PW(16)-S3(13)/PW(23) Q2-S5(6)/PW(16) Q3-S7(9)/PW(19) Q4-S15(8)/PW(18)-S16(9)/PW(19) | |
| 4 | Q1-S2(9)/PW(19)-S3(5)/PW(15) Q2-S4(3)/PW(11)-S5(9)/PW(9) Q3-S7(4)/PW(14) Q4-S10(5)/PW(15)-S11(6)/PW(16) | |
| 5 | Q1-S2(8)/PW(19)-S3(8)/PW(19) Q2-S4(4)/PW(22)-S5(8)/PW(12) Q3-S8(3)PW(13)-S9(9)/PW(16)-S10(2)/PW(14) Q5-S16(8)/PW(20)-S17(3)/PW(13) Q6-S18(7)/PW(15)-S19(6)/PW(11)-S20(3)/PW(27) | |
| 74 | 1 | Q4-S10(8)/PW(16)-S11(8)/PW(18)-S12(2)PW(22) Q5-S15(9)/PW(18)-S16(3)/PW(18) Q6-S19(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23)-S2(8)/PW(18) Q2-S5(8)/PW(18)-S6(7)/PW(21) Q3-S8(5)/PW(22)-S9(4)/PW(18)-S10(3)/PW(13) Q5-S16(4)/PW(14)-S17(5) Q6-S18(5)/PW(17)-S20(4)/PW(20) | |
| 3 | Q1-S1(9)/PW(9)-S3(5)/PW(15) Q2-S5(5)/PW(15)-S6(6)/PW(16) Q3-S7(6)/PW(16)-S8(8)/PW(18) Q4-S15(7)/PW(17)-S16(8)/PW(18) | |
| 4 | Q1-S1(8)/PW(23)-S2(7)/PW(17)-S3(4)/PW(24) Q2-S5(8)/PW(18) Q3-S8(6)/PW(16)-S9(5)/PW(15) Q6-S19(9)/PW(8 | |
| 5 | Q1-S1(6)/PW(16)-S2(7)/PW(23)-S3(6)/PW(15) Q2-S5(7)/PW(18)-S6(8)/PW(24) Q3-S8(4)/PW(14)-S9(6)/PW(25)-S10(8)/PW(23) Q6-S18(4)/PW(14)-S19(6)/PW(15)-S20(8)/PW(17) | |
| 75 | 1 | Q2-S6(4)/PW(18)-S7(9)/PW(19) Q4-S10(6)/PW(17)-S12(5)/PW(22) Q5-S15(8)/PW(18) |
| 2 | Q1-S1(7)/PW(23) Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(16) Q5-S16(5)/PW(14) Q6-S19(6)/PW(23)-S20(4)/PW(14) | |
| 3 | Q1-S1(6)/PW(17)-S2(2)/PW(22)-S3(5)/PW(15) Q2-S5(4)/PW(5) Q3-S7(3)/PW(6) Q4-S15(5)/PW(7) | |
| 4 | Q1-S1(4)/PW(23)-S2(7)/PW(17) Q2-S4(5)/PW(21)-S5(6)/PW(18) Q3-S8(8)/PW(6)-S9(6)/PW(6) Q6-S20(6)/PW(17) | |
| 5 | Q1-S1(1)/PW(11)-S2(4)/PW(17) Q2-S5(3)/PW(18) Q3-S8(5)/PW(15)-S9(6)/PW(16) Q6-S20(9)/PW(25) | |
| 76 | 1 | Q1-S1(7)/PW(24) Q2-S4(7)/PW(15) Q3-S7(4)/PW(13) Q4-S11(6)/PW(14)-S12(7)/PW(17) Q5-S14(5)/PW(18)-S15(4)/PW(14) Q6-S20(8)/PW(18) |
| 2 | Q1-S2(3)/PW(13)-S3(5)/PW(15) Q2-S5(7)/PW(17) Q4-S11(5)/PW(19)-S12(4)/PW(17)-S13(3)/PW(15) Q5-S14(8)/PW(18)-S15(4)/PW(14) Q6-S18(4)/PW(14)-S20(8)/PW(18) | |
| 3 | Q1-S1(5)/PW(16)-S2(7)/PW(19)-S3(4)/PW(14) Q3-S8(8)/PW(22) Q4-S12(9)/PW(19)-S13(8)/PW(26) Q5-S14(8)/PW(18)-S15(4)/PW(24). Q6-S18(9)/PW(19)-S20(8)/PW(18) | |
| 4 | Q1-S1(9)/PW(19)-S2(8)/PW(18)-S3(5)/PW(25) Q2-S5(5)/PW(25) Q4-S11(9)/PW(19)-S12(4)/PW(24)-S13(5)/PW(15) Q5-S14(3)/PW(23)-S15(4)/PW(24) Q6-S20(8)/PW(28) | |
| 5 | Q1-S1(7)/PW(16)-S2(8)/PW(19)-S3(4)/PW(24) Q3-S8(6)/PW(16) Q4-S12(7)/PW(19)-S13(6)/PW(16) Q5-S14(8)/PW(18)-S15(4)/PW(24) Q6-S18(10)/PW(19)-S20(6)/PW(28) | |
| 77 | 1 | Q1-S3(7)/PW(18) Q2-S6(5)/PW(15) Q3-S7(4)/PW(14) Q4-S9(6)PW(24)-S10(5)/PW(15) Q5-S13(7)/PW(18)-S14(9)/PW(19) Q6-S19(6)/PW(24) |
| 2 | Q1-S1(5)/PW(20) Q2-S6(8)/PW(18) Q4-S11(8)/PW(18)-S13(3)/PW(23) Q5-S14(7)/PW(27) Q6-S18(8)/PW(18)-S19(5)/PW(22) | |
| 3 | Q1-S2(3)/PW(25)-S3(6)/PW(23) Q2-S6(4)/PW(19) Q3-S7(7)/PW(24)-S8(8)/PW(17) Q4-S8(5)/PW(8) Q5-S16(5)/PW(14) Q6-S20(7)/PW(17) | |
| 4 | Q1-S1(8)/PW(21)-S2(7)/PW(17)-S3(3)/PW(23) Q2-S6(8)/PW(8) Q4-S11(9)/PW(8)-S13(2)/PW(23) Q5-S14(7)/PW(17) Q6-S18(8)/PW(28)-S19(2)/PW(22) | |
| 5 | Q1-S2(5)/PW(15)-S3(3)/PW(23) Q3-S7(7)/PW(24)-S8(7)/PW(17) Q4-S8(8)/PW(18) Q5-S15(3)/PW(25)-S16(6)/PW(24) Q6-S20(7)/PW(24) | |
| 78 | 1 | Q1-S1(8)/PW(22)-S3(4)/PW(14) Q2-S6(6)/PW(17) Q4-S10(8)/PW(17)-S12(2)/PW(22) Q5-S15(8)/PW(18) Q6-S19(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(5)/PW(15)-S5(8)/PW(18) Q3-S8(6)/PW(26) Q5-S16(4)/PW(18) Q6-S19(3)/PW(23)-S20(4)/PW(24) | |
| 3 | Q1-S1(6)/PW(17)-S2(2)/PW(21)-S3(3)/PW(13) Q2-S5(5)/PW(15) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(8)/PW(23)-S2(7)/PW(17) Q2-S4(6)/PW(19)-S5(6)/PW(18) Q3-S8(5)/PW(16)-S9(6)/PW(16) Q6-S20(3)/PW(17) | |
| 5 | Q1-S1(3)/PW(11)-S2(7)/PW(17) Q2-S5(8)/PW(18) Q3-S8(8)/PW(24)-S9(6)/PW(16) Q6-S20(5)/PW(26) | |
| 79 | 1 | Q1-S1(5)/PW(11)-S2(2)/PW(22)-S3(4)/PW(14) Q2-S4(1)/PW(25)-S6(7)/PW(17) Q4-S10(7)/PW(17)-S12(2)/PW(12) Q5-S15(8)/PW(18) Q6-S19(4)/PW(14)-S20(5)/PW(15) |
| 2 | Q1-S1(3)/PW(23) Q2-S4(5)/PW(19)-S5(8)/PW(18) Q3-S8(6)/PW(26) Q5-S16(5)/PW(14) Q6-S19(3)/PW(23)-S20(4)/PW(24) | |
| 3 | Q1-S1(7)/PW(17)-S2(6)/PW(22)-S3(3)/PW(23) Q2-S5(4)/PW(19) Q3-S7(6)/PW(16) Q4-S15(7)/PW(17) | |
| 4 | Q1-S1(3)/PW(23)-S2(7)/PW(17) Q2-S4(3)/PW(21)-S5(8)7PW(18) Q3-S8(2)/PW(16)-S9(6)/PW(26) Q6-S20(11)/PW(17) | |
| 5 | Q1-S1(4)/PW(21)-S2(6)/PW(17) Q2-S5(8)/PW(18) Q3-S8(5)/PW(24)-S9(6)/PW(26) Q6-S20(8)/PW(27) | |
| 80 | 1 | Q1-S1(8)/PW(19)-S2(5)/PW(25)-S3(4)/PW(19) Q2-S6(8)/PW(18)-S7(9)/PW(19) Q4-S10(5)/PW(15)-S12(2)/PW(12) Q5-S15(6)/PW(16)-S16(5)/PW(15) Q6-S20(5)/PW(15) |
| 2 | Q1-S1(7)/PW(23)-S2(4)/PW(17) Q2-S4(5)/PW(19)-S5(7)/PW(18)-S6(6)/PW(16) Q3-S8(5)/PW(16)-S9(7)/PW(7) Q5-S16(4)/PW(24)-S17(3)/PW(25) Q6-S18(5)/PW(25)-S19(6)/PW(23)-S20(4)/PW(14) | |
| 3 | Q1-S1(6)/PW(18)-S3(7)/PW(23) Q2-S5(7)/PW(19) Q3-S7(5)/PW(17) Q4-S15(6)/PW(25)-S16(8)/PW(18) | |
| 4 | Q1-S1(6)/PW(16)-S2(8)/PW(18)-S3(5)/PW(25) Q2-S4(4)/PW(24)-S5(7)/PW(17)-S6(6)/PW(26) Q3-S8(6)/PW(16)-S9(5)/PW(25) Q6-S19(5)/PW(24)-S20(7)/PW(19) | |
| 5 | Q1-S1(7)/PW(15)-S2(6)/PW(20) Q2-S5(7)/PW(21) Q3-S8(4)/PW(18)-S9(6)/PW(16) Q6-S19(8)/PW(19) |
| Part | Part Demands | Movement Costs between Cells | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1. Period | 2. Period | 3. Period | 4. Period | 5. Period | 1. Period | 2. Period | 3. Period | 4. Period | 5. Period | |
| 1 | 150 | 90 | 80 | 70 | 65 | 45 | 40 | 35 | 30 | 40 |
| 2 | 80 | 75 | 70 | 75 | 70 | 35 | 50 | 45 | 40 | 45 |
| 3 | 40 | 35 | 30 | 50 | 45 | 30 | 47 | 40 | 37 | 47 |
| 4 | 75 | 70 | 65 | 85 | 80 | 34 | 48 | 40 | 38 | 48 |
| 5 | 80 | 75 | 70 | 100 | 95 | 52 | 40 | 55 | 40 | 45 |
| 6 | 120 | 100 | 90 | 85 | 80 | 55 | 50 | 55 | 50 | 55 |
| 7 | 60 | 55 | 50 | 65 | 60 | 37 | 45 | 40 | 35 | 45 |
| 8 | 50 | 45 | 40 | 55 | 50 | 36 | 45 | 35 | 35 | 40 |
| 9 | 85 | 75 | 70 | 85 | 75 | 33 | 50 | 44 | 40 | 45 |
| 10 | 90 | 70 | 65 | 90 | 85 | 40 | 35 | 30 | 30 | 35 |
| 11 | 90 | 75 | 70 | 45 | 40 | 55 | 43 | 40 | 33 | 38 |
| 12 | 60 | 55 | 50 | 50 | 45 | 32 | 52 | 50 | 36 | 42 |
| 13 | 50 | 45 | 40 | 40 | 35 | 35 | 45 | 45 | 40 | 45 |
| 14 | 55 | 50 | 45 | 55 | 50 | 38 | 40 | 50 | 48 | 55 |
| 15 | 70 | 60 | 55 | 65 | 60 | 45 | 45 | 40 | 39 | 49 |
| 16 | 110 | 90 | 85 | 70 | 65 | 47 | 42 | 40 | 32 | 45 |
| 17 | 100 | 80 | 75 | 55 | 50 | 45 | 55 | 50 | 45 | 48 |
| 18 | 50 | 45 | 40 | 40 | 38 | 40 | 38 | 35 | 32 | 38 |
| 19 | 65 | 50 | 45 | 55 | 50 | 33 | 45 | 40 | 39 | 42 |
| 20 | 80 | 75 | 70 | 80 | 75 | 52 | 45 | 40 | 35 | 45 |
| 21 | 70 | 65 | 60 | 60 | 55 | 40 | 50 | 55 | 50 | 55 |
| 22 | 100 | 95 | 85 | 90 | 75 | 45 | 55 | 50 | 50 | 55 |
| 23 | 60 | 55 | 50 | 50 | 45 | 40 | 37 | 35 | 33 | 38 |
| 24 | 55 | 50 | 45 | 55 | 50 | 43 | 38 | 35 | 30 | 35 |
| 25 | 70 | 60 | 55 | 65 | 60 | 40 | 30 | 35 | 32 | 38 |
| 26 | 50 | 45 | 40 | 40 | 35 | 45 | 45 | 40 | 36 | 40 |
| 27 | 90 | 85 | 80 | 90 | 80 | 55 | 55 | 50 | 48 | 55 |
| 28 | 45 | 40 | 35 | 70 | 65 | 40 | 45 | 45 | 43 | 53 |
| 29 | 55 | 50 | 45 | 80 | 75 | 33 | 40 | 40 | 38 | 45 |
| 30 | 90 | 80 | 75 | 90 | 85 | 40 | 45 | 45 | 40 | 45 |
| 31 | 120 | 85 | 80 | 60 | 55 | 45 | 38 | 30 | 29 | 45 |
| 32 | 90 | 85 | 80 | 100 | 95 | 46 | 55 | 50 | 48 | 52 |
| 33 | 100 | 75 | 70 | 85 | 80 | 32 | 52 | 50 | 45 | 55 |
| 34 | 85 | 70 | 65 | 80 | 70 | 35 | 48 | 45 | 40 | 45 |
| 35 | 80 | 70 | 65 | 80 | 70 | 52 | 45 | 35 | 30 | 40 |
| 36 | 150 | 125 | 115 | 105 | 100 | 41 | 38 | 50 | 45 | 55 |
| 37 | 90 | 85 | 80 | 80 | 75 | 37 | 52 | 40 | 35 | 45 |
| 38 | 40 | 35 | 30 | 65 | 60 | 33 | 45 | 45 | 40 | 45 |
| 39 | 45 | 40 | 35 | 40 | 35 | 43 | 40 | 40 | 35 | 48 |
| 40 | 90 | 80 | 75 | 60 | 55 | 40 | 43 | 40 | 39 | 42 |
| 41 | 90 | 65 | 60 | 60 | 50 | 47 | 38 | 35 | 30 | 35 |
| 42 | 70 | 65 | 60 | 65 | 60 | 45 | 43 | 40 | 35 | 38 |
| 43 | 60 | 55 | 50 | 75 | 70 | 40 | 45 | 40 | 35 | 40 |
| 44 | 95 | 60 | 55 | 65 | 60 | 42 | 48 | 45 | 40 | 45 |
| 45 | 70 | 60 | 50 | 65 | 60 | 51 | 50 | 55 | 50 | 55 |
| 46 | 150 | 115 | 105 | 75 | 70 | 43 | 35 | 35 | 30 | 39 |
| 47 | 70 | 65 | 55 | 80 | 70 | 37 | 40 | 40 | 35 | 42 |
| 48 | 60 | 55 | 45 | 75 | 65 | 33 | 42 | 45 | 42 | 45 |
| 49 | 75 | 70 | 60 | 80 | 70 | 35 | 46 | 50 | 46 | 50 |
| 50 | 80 | 70 | 50 | 90 | 80 | 48 | 43 | 45 | 43 | 53 |
| 51 | 120 | 115 | 95 | 75 | 70 | 43 | 35 | 30 | 30 | 45 |
| 52 | 70 | 65 | 60 | 60 | 55 | 37 | 53 | 55 | 53 | 55 |
| 53 | 50 | 45 | 40 | 40 | 35 | 30 | 45 | 45 | 40 | 45 |
| 54 | 65 | 60 | 55 | 55 | 50 | 34 | 40 | 40 | 35 | 45 |
| 55 | 70 | 60 | 55 | 55 | 55 | 52 | 45 | 55 | 45 | 50 |
| 56 | 50 | 45 | 40 | 40 | 37 | 45 | 48 | 40 | 38 | 40 |
| 57 | 90 | 70 | 60 | 80 | 75 | 34 | 48 | 45 | 44 | 45 |
| 58 | 70 | 65 | 60 | 75 | 73 | 40 | 45 | 55 | 45 | 48 |
| 59 | 65 | 60 | 55 | 65 | 64 | 38 | 40 | 35 | 30 | 35 |
| 60 | 70 | 65 | 60 | 60 | 58 | 52 | 45 | 40 | 38 | 42 |
| 61 | 130 | 105 | 100 | 95 | 90 | 47 | 36 | 40 | 36 | 40 |
| 62 | 80 | 65 | 60 | 60 | 55 | 30 | 47 | 45 | 43 | 45 |
| 63 | 80 | 70 | 60 | 75 | 70 | 35 | 39 | 35 | 33 | 35 |
| 64 | 70 | 60 | 55 | 70 | 65 | 30 | 41 | 40 | 31 | 35 |
| 65 | 85 | 70 | 65 | 75 | 70 | 50 | 45 | 45 | 40 | 45 |
| 66 | 130 | 85 | 80 | 80 | 75 | 40 | 52 | 50 | 42 | 48 |
| 67 | 80 | 75 | 65 | 70 | 65 | 38 | 55 | 55 | 50 | 55 |
| 68 | 70 | 65 | 60 | 85 | 80 | 37 | 45 | 40 | 38 | 42 |
| 69 | 85 | 80 | 70 | 90 | 85 | 40 | 40 | 45 | 40 | 45 |
| 70 | 90 | 80 | 70 | 75 | 70 | 45 | 50 | 55 | 50 | 55 |
| 71 | 110 | 95 | 90 | 70 | 65 | 40 | 45 | 50 | 45 | 48 |
| 72 | 90 | 85 | 80 | 65 | 60 | 35 | 52 | 55 | 52 | 55 |
| 73 | 70 | 65 | 60 | 60 | 55 | 30 | 45 | 40 | 38 | 42 |
| 74 | 85 | 50 | 45 | 40 | 35 | 38 | 44 | 45 | 40 | 45 |
| 75 | 80 | 70 | 60 | 60 | 55 | 55 | 43 | 40 | 38 | 42 |
| 76 | 60 | 55 | 50 | 65 | 60 | 40 | 50 | 50 | 45 | 55 |
| 77 | 70 | 65 | 60 | 95 | 90 | 30 | 55 | 55 | 50 | 55 |
| 78 | 80 | 75 | 70 | 105 | 100 | 40 | 39 | 35 | 36 | 40 |
| 79 | 65 | 60 | 55 | 70 | 65 | 35 | 49 | 45 | 42 | 45 |
| 80 | 70 | 55 | 50 | 55 | 45 | 40 | 50 | 50 | 45 | 55 |
Appendix B
| Parts | Optimal Route for Goal Programming | Optimal Route for ε-Constraint | Optimal Route for AUGMECON |
|---|---|---|---|
| 1 | x111, x211, x311, x411, x511 | x111, x211, x311, x411, x511 | x111, x211, x311, x411, x511 |
| 2 | x123, x222, x323, x422, x523 | x122, x222, x323, x422, x523 | x122, x222, x323, x423, x523 |
| 3 | x135, x235, x335, x435, x535 | x135, x235, x335, x435, x535 | x135, x235, x335, x435, x535 |
| 4 | x142, x242, x342, x443, x542 | x142, x242, x342, x443, x542 | x142, x242, x342, x443, x542 |
| 5 | x155, x255, x355, x455, x555 | x155, x255, x355, x455, x555 | x155, x255, x355, x455, x555 |
| 6 | x165, x265, x365, x465, x565 | x165, x265, x365, x465, x565 | x165, x265, x365, x465, x565 |
| 7 | x173, x273, x373, x473, x573 | x173, x273, x373, x473, x573 | x173, x273, x373, x473, x573 |
| 8 | x185, x285, x385, x483, x585 | x185, x285, x385, x483, x585 | x185, x285, x385, x483, x585 |
| 9 | x192, x295, x395, x492, x592 | x195, x295, x395, x494, x592 | x195, x295, x395, x494, x592 |
| 10 | x1,10,4, x2,10,1, x3,10,1, x4,10,1, x5,10,5 | x1,10,5, x2,10,5, x3,10,1, x4,10,1, x5,10,5 | x1,10,5, x2,10,5, x3,10,1, x4,10,1, x5,10,5 |
| 11 | x1,11,3, x2,11,3, x3,11,3, x4,11,3, x5,11,3 | x1,11,3, x2,11,3, x3,11,3, x4,11,3, x5,11,3 | x1,11,3, x2,11,3, x3,11,3, x4,11,3, x5,11,3 |
| 12 | x1,12,5, x2,12,5, x3,12,5, x4,12,5, x5,12,5 | x1,12,5, x2,12,5, x3,12,5, x4,12,5, x5,12,5 | x1,12,5, x2,12,5, x3,12,5, x4,12,5, x5,12,5 |
| 13 | x1,13,5, x2,13,5, x3,13,5, x4,13,5, x5,13,5 | x1,13,5, x2,13,5, x3,13,5, x4,13,5, x5,13,5 | x1,13,5, x2,13,5, x3,13,5, x4,13,5, x5,13,5 |
| 14 | x1,14,3, x2,14,3, x3,14,3, x4,14,3, x5,14,3 | x1,14,3, x2,14,3, x3,14,3, x4,14,3, x5,14,3 | x1,14,3, x2,14,3, x3,14,3, x4,14,3, x5,14,3 |
| 15 | x1,15,5, x2,15,5, x3,15,2, x4,15,2, x5,15,2 | x1,15,5, x2,15,5, x3,15,2, x4,15,2, x5,15,2 | x1,15,5, x2,15,5, x3,15,2, x4,15,2, x5,15,2 |
| 16 | x1,16,2, x2,16,1, x3,16,1, x4,16,1, x5,16,3 | x1,16,2, x2,16,1, x3,16,1, x4,16,1, x5,16,3 | x1,16,2, x2,16,1, x3,16,1, x4,16,1, x5,16,3 |
| 17 | x1,17,5, x2,17,5, x3,17,5, x4,17,5, x5,17,5 | x1,17,5, x2,17,5, x3,17,5, x4,17,5, x5,17,5 | x1,17,5, x2,17,5, x3,17,5, x4,17,5, x5,17,5 |
| 18 | x1,18,4, x2,18,4, x3,18,4, x4,18,4, x5,18,4 | x1,18,4, x2,18,4, x3,18,4, x4,18,4, x5,18,4 | x1,18,4, x2,18,4, x3,18,4, x4,18,4, x5,18,4 |
| 19 | x1,19,5, x2,19,5, x3,19,5, x4,19,5, x5,19,5 | x1,19,5, x2,19,5, x3,19,5, x4,19,5, x5,19,5 | x1,19,5, x2,19,5, x3,19,5, x4,19,5, x5,19,5 |
| 20 | x1,20,5, x2,20,5, x3,20,5, x4,20,5, x5,20,5 | x1,20,5, x2,20,5, x3,20,5, x4,20,5, x5,20,5 | x1,20,5, x2,20,5, x3,20,5, x4,20,5, x5,20,5 |
| 21 | x1,21,5, x2,21,5, x3,21,5, x4,21,5, x5,21,5 | x1,21,5, x2,21,5, x3,21,5, x4,21,5, x5,21,5 | x1,21,5, x2,21,5, x3,21,5, x4,21,5, x5,21,5 |
| 22 | x1,22,4, x2,22,4, x3,22,4, x4,22,4, x5,22,4 | x1,22,4, x2,22,4, x3,22,4, x4,22,4, x5,22,4 | x1,22,4, x2,22,4, x3,22,4, x4,22,4, x5,22,4 |
| 23 | x1,23,5, x2,23,5, x3,23,5, x4,23,5, x5,23,5 | x1,23,5, x2,23,5, x3,23,5, x4,23,5, x5,23,5 | x1,23,5, x2,23,5, x3,23,5, x4,23,5, x5,23,5 |
| 24 | x1,24,5, x2,24,5, x3,24,5, x4,24,5, x5,24,5 | x1,24,5, x2,24,5, x3,24,5, x4,24,5, x5,24,5 | x1,24,5, x2,24,5, x3,24,5, x4,24,5, x5,24,5 |
| 25 | x1,25,3, x2,25,3, x3,25,3, x4,25,3, x5,25,3 | x1,25,3, x2,25,3, x3,25,3, x4,25,3, x5,25,3 | x1,25,3, x2,25,3, x3,25,3, x4,25,3, x5,25,3 |
| 26 | x1,26,4, x2,26,4, x3,26,4, x4,26,4, x5,26,4 | x1,26,4, x2,26,4, x3,26,4, x4,26,4, x5,26,4 | x1,26,4, x2,26,4, x3,26,4, x4,26,4, x5,26,4 |
| 27 | x1,27,4, x2,27,4, x3,27,4, x4,27,4, x5,27,4 | x1,27,4, x2,27,4, x3,27,4, x4,27,4, x5,27,4 | x1,27,4, x2,27,4, x3,27,4, x4,27,4, x5,27,4 |
| 28 | x1,28,3, x2,28,3, x3,28,3, x4,28,3, x5,28,3 | x1,28,3, x2,28,3, x3,28,3, x4,28,3, x5,28,3 | x1,28,3, x2,28,3, x3,28,3, x4,28,3, x5,28,3 |
| 29 | x1,29,1, x2,29,1, x3,29,1, x4,29,1, x5,29,1 | x1,29,1, x2,29,1, x3,29,1, x4,29,1, x5,29,1 | x1,29,1, x2,29,1, x3,29,1, x4,29,1, x5,29,1 |
| 30 | x1,30,4, x2,30,4, x3,30,4, x4,30,4, x5,30,4 | x1,30,4, x2,30,4, x3,30,4, x4,30,4, x5,30,4 | x1,30,4, x2,30,4, x3,30,4, x4,30,4, x5,30,4 |
| 31 | x1,31,5, x2,31,3, x3,31,3, x4,31,3, x5,31,5 | x1,31,5, x2,31,3, x3,31,3, x4,31,3, x5,31,5 | x1,31,5, x2,31,3, x3,31,3, x4,31,3, x5,31,5 |
| 32 | x1,32,5, x2,32,5, x3,32,5, x4,32,5, x5,32,5 | x1,32,5, x2,32,5, x3,32,5, x4,32,5, x5,32,5 | x1,32,5, x2,32,5, x3,32,5, x4,32,5, x5,32,5 |
| 33 | x1,33,2, x2,33,4, x3,33,4, x4,33,4, x5,33,2 | x1,33,2, x2,33,4, x3,33,4, x4,33,4, x5,33,2 | x1,33,2, x2,33,4, x3,33,4, x4,33,4, x5,33,2 |
| 34 | x1,34,4, x2,34,1, x3,34,1, x4,34,1, x5,34,4 | x1,34,4, x2,34,1, x3,34,1, x4,34,1, x5,34,4 | x1,34,4, x2,34,1, x3,34,1, x4,34,1, x5,34,4 |
| 35 | x1,35,3, x2,35,3, x3,35,3, x4,35,3, x5,35,3 | x1,35,3, x2,35,3, x3,35,3, x4,35,3, x5,35,3 | x1,35,3, x2,35,3, x3,35,3, x4,35,3, x5,35,3 |
| 36 | x1,36,1, x2,36,1, x3,36,1, x4,36,1, x5,36,1 | x1,36,1, x2,36,1, x3,36,1, x4,36,1, x5,36,1 | x1,36,1, x2,36,1, x3,36,1, x4,36,1, x5,36,1 |
| 37 | x1,37,2, x2,37,4, x3,37,3, x4,37,4, x5,37,3 | x1,37,2, x2,37,2, x3,37,3, x4,37,2, x5,37,3 | x1,37,2, x2,37,2, x3,37,3, x4,37,3, x5,37,3 |
| 38 | x1,38,3, x2,38,3, x3,38,3, x4,38,3, x5,38,3 | x1,38,3, x2,38,3, x3,38,3, x4,38,3, x5,38,3 | x1,38,3, x2,38,3, x3,38,3, x4,38,3, x5,38,3 |
| 39 | x1,39,3, x2,39,3, x3,39,3, x4,39,3, x5,39,3 | x1,39,3, x2,39,3, x3,39,3, x4,39,3, x5,39,3 | x1,39,3, x2,39,3, x3,39,3, x4,39,3, x5,39,3 |
| 40 | x1,40,5, x2,40,5, x3,40,5, x4,40,1, x5,40,5 | x1,40,5, x2,40,5, x3,40,5, x4,40,5, x5,40,5 | x1,40,5, x2,40,5, x3,40,5, x4,40,5, x5,40,5 |
| 41 | x1,41,1, x2,41,1, x3,41,1, x4,41,1, x5,41,1 | x1,41,1, x2,41,1, x3,41,1, x4,41,1, x5,41,1 | x1,41,1, x2,41,1, x3,41,1, x4,41,1, x5,41,1 |
| 42 | x1,42,3, x2,42,4, x3,42,3, x4,42,4, x5,42,3 | x1,42,4, x2,42,4, x3,42,3, x4,42,4, x5,42,3 | x1,42,4, x2,42,4, x3,42,3, x4,42,3, x5,42,3 |
| 43 | x1,43,3, x2,43,3, x3,43,3, x4,43,3, x5,43,3 | x1,43,3, x2,43,3, x3,43,3, x4,43,3, x5,43,3 | x1,43,3, x2,43,3, x3,43,3, x4,43,3, x5,43,3 |
| 44 | x1,44,3, x2,44,3, x3,44,3, x4,44,3, x5,44,3 | x1,44,3, x2,44,3, x3,44,3, x4,44,3, x5,44,3 | x1,44,3, x2,44,3, x3,44,3, x4,44,3, x5,44,3 |
| 45 | x1,45,5, x2,45,5, x3,45,5, x4,45,1, x5,45,5 | x1,45,5, x2,45,5, x3,45,5, x4,45,5, x5,45,5 | x1,45,5, x2,45,5, x3,45,5, x4,45,5, x5,45,5 |
| 46 | x1,46,5, x2,46,5, x3,46,5, x4,46,5, x5,46,5 | x1,46,5, x2,46,3, x3,46,5, x4,46,5, x5,46,5 | x1,46,5, x2,46,3, x3,46,5, x4,46,5, x5,46,5 |
| 47 | x1,47,2, x2,47,2, x3,47,2, x4,47,2, x5,47,2 | x1,47,2, x2,47,2, x3,47,2, x4,47,2, x5,47,2 | x1,47,2, x2,47,2, x3,47,2, x4,47,2, x5,47,2 |
| 48 | x1,48,3, x2,48,3, x3,48,3, x4,48,3, x5,48,3 | x1,48,3, x2,48,3, x3,48,3, x4,48,3, x5,48,3 | x1,48,3, x2,48,3, x3,48,3, x4,48,3, x5,48,3 |
| 49 | x1,49,2, x2,49,2, x3,49,2, x4,49,2, x5,49,2 | x1,49,2, x2,49,2, x3,49,2, x4,49,2, x5,49,2 | x1,49,2, x2,49,2, x3,49,2, x4,49,2, x5,49,2 |
| 50 | x1,50,4, x2,50,4, x3,50,4, x4,50,3, x5,50,4 | x1,50,4, x2,50,5, x3,50,4, x4,50,3, x5,50,4 | x1,50,4, x2,50,5, x3,50,4, x4,50,3, x5,50,4 |
| 51 | x1,51,3, x2,51,3, x3,51,3, x4,51,3, x5,51,3 | x1,51,3, x2,51,3, x3,51,3, x4,51,3, x5,51,3 | x1,51,3, x2,51,3, x3,51,3, x4,51,3, x5,51,3 |
| 52 | x1,52,5, x2,52,5, x3,52,5, x4,52,5, x5,52,5 | x1,52,5, x2,52,5, x3,52,5, x4,52,5, x5,52,5 | x1,52,5, x2,52,5, x3,52,5, x4,52,5, x5,52,5 |
| 53 | x1,53,5, x2,53,5, x3,53,5, x4,53,5, x5,53,5 | x1,53,5, x2,53,5, x3,53,5, x4,53,5, x5,53,5 | x1,53,5, x2,53,5, x3,53,5, x4,53,5, x5,53,5 |
| 54 | x1,54,5, x2,54,3, x3,54,3, x4,54,3, x5,54,3 | x1,54,5, x2,54,3, x3,54,3, x4,54,3, x5,54,3 | x1,54,5, x2,54,3, x3,54,3, x4,54,3, x5,54,3 |
| 55 | x1,55,2, x2,55,2, x3,55,2, x4,55,2, x5,55,2 | x1,55,2, x2,55,2, x3,55,2, x4,55,2, x5,55,2 | x1,55,2, x2,55,2, x3,55,2, x4,55,2, x5,55,2 |
| 56 | x1,56,2, x2,56,1, x3,56,1, x4,56,1, x5,56,2 | x1,56,2, x2,56,1, x3,56,1, x4,56,1, x5,56,3 | x1,56,2, x2,56,1, x3,56,1, x4,56,1, x5,56,3 |
| 57 | x1,57,5, x2,57,5, x3,57,5, x4,57,5, x5,57,5 | x1,57,5, x2,57,5, x3,57,5, x4,57,5, x5,57,5 | x1,57,5, x2,57,5, x3,57,5, x4,57,5, x5,57,5 |
| 58 | x1,58,4, x2,58,4, x3,58,4, x4,58,4, x5,58,4 | x1,58,4, x2,58,4, x3,58,4, x4,58,4, x5,58,4 | x1,58,4, x2,58,4, x3,58,4, x4,58,4, x5,58,4 |
| 59 | x1,59,5, x2,59,5, x3,59,5, x4,59,5, x5,59,5 | x1,59,5, x2,59,5, x3,59,5, x4,59,5, x5,59,5 | x1,59,5, x2,59,5, x3,59,5, x4,59,5, x5,59,5 |
| 60 | x1,60,5, x2,60,5, x3,60,5, x4,60,5, x5,60,5 | x1,60,5, x2,60,5, x3,60,5, x4,60,5, x5,60,5 | x1,60,5, x2,60,5, x3,60,5, x4,60,5, x5,60,5 |
| 61 | x1,61,2, x2,61,2, x3,61,5, x4,61,5, x5,61,5 | x1,61,5, x2,61,2, x3,61,5, x4,61,5, x5,61,5 | x1,61,5, x2,61,2, x3,61,5, x4,61,5, x5,61,5 |
| 62 | x1,62,4, x2,62,4, x3,62,4, x4,62,4, x5,62,4 | x1,62,4, x2,62,4, x3,62,4, x4,62,4, x5,62,4 | x1,62,4, x2,62,4, x3,62,4, x4,62,4, x5,62,4 |
| 63 | x1,63,5, x2,63,5, x3,63,5, x4,63,5, x5,63,5 | x1,63,5, x2,63,5, x3,63,5, x4,63,5, x5,63,5 | x1,63,5, x2,63,5, x3,63,5, x4,63,5, x5,63,5 |
| 64 | x1,64,5, x2,64,5, x3,64,5, x4,64,5, x5,64,5 | x1,64,5, x2,64,5, x3,64,5, x4,64,5, x5,64,5 | x1,64,5, x2,64,5, x3,64,5, x4,64,5, x5,64,5 |
| 65 | x1,65,3, x2,65,3, x3,65,3, x4,65,3, x5,65,3 | x1,65,3, x2,65,3, x3,65,3, x4,65,3, x5,65,3 | x1,65,3, x2,65,3, x3,65,3, x4,65,3, x5,65,3 |
| 66 | x1,66,4, x2,66,4, x3,66,4, x4,66,4, x5,66,4 | x1,66,4, x2,66,4, x3,66,4, x4,66,4, x5,66,4 | x1,66,4, x2,66,4, x3,66,4, x4,66,4, x5,66,4 |
| 67 | x1,67,4, x2,67,4, x3,67,4, x4,67,4, x5,67,4 | x1,67,4, x2,67,4, x3,67,4, x4,67,4, x5,67,4 | x1,67,4, x2,67,4, x3,67,4, x4,67,4, x5,67,4 |
| 68 | x1,68,3, x2,68,3, x3,68,3, x4,68,3, x5,68,3 | x1,68,3, x2,68,3, x3,68,3, x4,68,3, x5,68,3 | x1,68,3, x2,68,3, x3,68,3, x4,68,3, x5,68,3 |
| 69 | x1,69,3, x2,69,1, x3,69,3, x4,69,1, x5,69,3 | x1,69,3, x2,69,1, x3,69,3, x4,69,1, x5,69,3 | x1,69,3, x2,69,1, x3,69,3, x4,69,1, x5,69,3 |
| 70 | x1,70,4, x2,70,4, x3,70,4, x4,70,4, x5,70,4 | x1,70,4, x2,70,4, x3,70,4, x4,70,4, x5,70,4 | x1,70,4, x2,70,4, x3,70,4, x4,70,4, x5,70,4 |
| 71 | x1,71,3, x2,71,3, x3,71,3, x4,71,3, x5,71,3 | x1,71,3, x2,71,3, x3,71,3, x4,71,3, x5,71,3 | x1,71,3, x2,71,3, x3,71,3, x4,71,3, x5,71,3 |
| 72 | x1,72,5, x2,72,5, x3,72,5, x4,72,5, x5,72,5 | x1,72,5, x2,72,5, x3,72,5, x4,72,5, x5,72,5 | x1,72,5, x2,72,5, x3,72,5, x4,72,5, x5,72,5 |
| 73 | x1,73,2, x2,73,4, x3,73,4, x4,73,4, x5,73,2 | x1,73,2, x2,73,4, x3,73,4, x4,73,4, x5,73,2 | x1,73,2, x2,73,4, x3,73,4, x4,73,4, x5,73,2 |
| 74 | x1,74,4, x2,74,1, x3,74,1, x4,74,1, x5,74,4 | x1,74,4, x2,74,1, x3,74,1, x4,74,1, x5,74,4 | x1,74,4, x2,74,1, x3,74,1, x4,74,1, x5,74,4 |
| 75 | x1,75,3, x2,75,3, x3,75,3, x4,75,3, x5,75,3 | x1,75,3, x2,75,3, x3,75,3, x4,75,3, x5,75,3 | x1,75,3, x2,75,3, x3,75,3, x4,75,3, x5,75,3 |
| 76 | x1,76,1, x2,76,1, x3,76,1, x4,76,1, x5,76,1 | x1,76,2, x2,76,1, x3,76,1, x4,76,1, x5,76,1 | x1,76,2, x2,76,1, x3,76,1, x4,76,1, x5,76,1 |
| 77 | x1,77,3, x2,77,2, x3,77,3, x4,77,2, x5,77,3 | x1,77,2, x2,77,2, x3,77,3, x4,77,2, x5,77,3 | x1,77,2, x2,77,2, x3,77,3, x4,77,3, x5,77,3 |
| 78 | x1,78,3, x2,78,3, x3,78,3, x4,78,3, x5,78,3 | x1,78,3, x2,78,3, x3,78,3, x4,78,3, x5,78,3 | x1,78,3, x2,78,3, x3,78,3, x4,78,3, x5,78,3 |
| 79 | x1,79,3, x2,79,3, x3,79,3, x4,79,3, x5,79,3 | x1,79,3, x2,79,3, x3,79,3, x4,79,3, x5,79,3 | x1,79,3, x2,79,3, x3,79,3, x4,79,3, x5,79,3 |
| 80 | x1,80,5, x2,80,5, x3,80,5, x4,80,5, x5,80,5 | x1,80,5, x2,80,5, x3,80,5, x4,80,5, x5,80,5 | x1,80,5, x2,80,5, x3,80,5, x4,80,5, x5,80,5 |
References
- Coca, G.; Castrillón, O.D.; Ruiz, S.; Mateo-Sanz, J.M.; Jiménez, L. Sustainable evaluation of environmental and occupational risks scheduling flexible job shop manufacturing systems. J. Clean. Prod. 2019, 209, 146–168. [Google Scholar] [CrossRef]
- Singh, S.; Olugu, E.U.; Musa, S.N. Development of sustainable manufacturing performance evaluation expert system for small and medium enterprises. Procedia CIRP 2016, 40, 608–613. [Google Scholar] [CrossRef]
- Ahmad, S.; Wong, K.Y.; Rajoo, S. Sustainability indicators for manufacturing sectors A literature survey and maturity analysis from the triple-bottom line perspective. J. Manuf. Technol. Manag. 2019, 30, 312–334. [Google Scholar] [CrossRef]
- Sutherland, J.W.; Richter, J.S.; Hutchins, M.J.; Dornfeld, D.; Dzombak, R.; Mangold, J.; Robinson, S.; Hauschild, M.Z.; Bonou, A.; Schönsleben, P.; et al. The role of manufacturing in affecting the social dimension of sustainability. CIRP Ann. Manuf. Technol. 2016, 65, 689–712. [Google Scholar] [CrossRef]
- Galal, N.M.; Moneim, A.F.A. A mathematical programming approach to the optimal sustainable product mix for the process industry. Sustainability 2015, 7, 13085–13103. [Google Scholar] [CrossRef]
- Rajak, S.; Vinodh, S. Application of fuzzy logic for social sustainability performance evaluation: A case study of an Indian automotive component manufacturing organization. J. Clean. Prod. 2015, 108, 1184–1192. [Google Scholar] [CrossRef]
- Vimal, K.E.K.; Vinodh, S.; Raja, A. Modelling, assessment and deployment of strategies for ensuring sustainable shielded metal arc welding process-a case study. J. Clean. Prod. 2015, 93, 364–377. [Google Scholar] [CrossRef]
- Lin, C.J.; Belis, T.T.; Kuo, T.C. Ergonomics-based factors or criteria for the evaluation of sustainable product manufacturing. Sustainability 2019, 11, 4955. [Google Scholar] [CrossRef]
- Mengistu, A.T.; Panizzolo, R. Tailoring sustainability indicators to small and medium enterprises for measuring industrial sustainability performance. Meas. Bus. Excell. 2023, 27, 54–70. [Google Scholar] [CrossRef]
- Giret, A.; Trentesaux, D.; Prabhu, V. Sustainability in manufacturing operations scheduling: A state of the art review. J. Manuf. Syst. 2015, 37, 126–140. [Google Scholar] [CrossRef]
- Niakan, F.; Baboli, A.; Moyaux, T.; Botta-Genoulaz, V. A bi-objective model in sustainable dynamic cell formation problem with skill-based worker assignment. J. Manuf. Syst. 2016, 38, 46–62. [Google Scholar] [CrossRef]
- Jain, A.K.; Kasilingam, R.G.; Bhole, S.D. Joint consideration of cell formation and tool provisioning problems in flexible manufacturing systems. Comput. Ind. Eng. 1991, 20, 271–277. [Google Scholar] [CrossRef]
- Alhourani, F. Cellular manufacturing system design considering machines reliability and parts alternative process routings. Int. J. Prod. Res. 2016, 54, 846–863. [Google Scholar] [CrossRef]
- Ghodsi, R.; Mostafayi, S.; Mansouri, Z.; Bakhtiari, M. Designing a bi-objective integrating mathematical model for dynamic sustainable cellular manufacturing systems considering production planning. J. Appl. Mech. Eng. 2015, 4, 184. [Google Scholar]
- Aljuneidi, T.; Bulgak, A.A. A mathematical model for designing reconfigurable cellular hybrid manufacturing-remanufacturing systems. Int. J. Adv. Manuf. Technol. 2016, 87, 1585–1596. [Google Scholar] [CrossRef]
- Mehdizadeh, E.; Niaki, S.V.D.; Rahimi, V. A vibration damping optimization algorithm for solving a new multi-objective dynamic cell formation problem with workers training. Comput. Ind. Eng. 2016, 101, 35–52. [Google Scholar] [CrossRef]
- Niakan, F.; Baboli, A.; Moyaux, T.; Botta-Genoulaz, V. A new multi-objective mathematical model for dynamic cell formation under demand and cost uncertainty considering social criteria. Appl. Math. Model. 2016, 40, 2674–2691. [Google Scholar] [CrossRef]
- Imran, M.; Kang, C.; Lee, Y.H.; Jahanzaib, M.; Aziz, H. Cell formation in a cellular manufacturing system using simulation integrated hybrid genetic algorithm. Comput. Ind. Eng. 2017, 105, 123–135. [Google Scholar] [CrossRef]
- Arghish, O.; Tavakkoli-Moghaddam, R.; Shahandeh-Nookabadi, A.; Rezaeian, J. Comparison among four calibrated meta-heuristic algorithms for solving a type-2 fuzzy cell formation problem considering economic and environmental criteria. Adv. Prod. Eng. Manag. 2018, 13, 5–17. [Google Scholar] [CrossRef]
- Iqbal, A.; Al-Ghamdi, K.A. Energy-efficient cellular manufacturing system: Eco-friendly revamping of machine shop configuration. Energy 2018, 163, 863–872. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.P. Simulated annealing-based embedded meta-heuristic approach to solve bi-objective robust stochastic sustainable cellular layout. Glob. J. Flex. Syst. Manag. 2018, 19, 69–93. [Google Scholar] [CrossRef]
- Raoofpanah, H.; Ghezavati, V.; Tavakkoli-Moghaddam, R. Solving a new robust green cellular manufacturing problem with environmental issues under uncertainty using Benders decomposition. Eng. Optim. 2019, 51, 1229–1250. [Google Scholar] [CrossRef]
- Telegraphi, A.H.; Bulgak, A.A. A mathematical model for designing sustainable cellular remanufacturing systems. J. Ind. Syst. Eng. 2021, 13, 98–123. [Google Scholar]
- Forghani, K.; Fatemi Ghomi, S.M.T.; Kia, R. Group layout design of manufacturing cells incorporating assembly and energy aspects. Eng. Optim. 2022, 54, 770–785. [Google Scholar] [CrossRef]
- Jafarzadeh, J.; Khalili, H.A.; Shoja, N. A multiobjective optimization model for a dynamic and sustainable cellular manufacturing system under uncertainty. Comput. Intell. Neurosci. 2022, 2022, 1334081. [Google Scholar] [CrossRef] [PubMed]
- Aryanezhad, M.B.; Deljoo, V.; Mirzapour Al-e-hashem, S.M.J. Dynamic cell formation and the worker assignment problem: A new model. Int. J. Adv. Manuf. Technol. 2009, 41, 329–342. [Google Scholar] [CrossRef]
- Fan, J.; Feng, D. Design of cellular manufacturing system with quasi-dynamic dual resource using multi-objective GA. Int. J. Prod. Res. 2013, 51, 4134–4154. [Google Scholar] [CrossRef]
- Bagheri, M.; Bashiri, M. A new mathematical model towards the integration of cell formation with operator assignment and inter-cell layout problems in a dynamic environment. Appl. Math. Model. 2014, 38, 1237–1254. [Google Scholar] [CrossRef]
- Azadeh, A.; Pashapour, S.; Zadeh, S.A. Designing a cellular manufacturing system considering decision style, skill and job security by NSGA-II and response surface methodology. Int. J. Prod. Res. 2016, 54, 6825–6847. [Google Scholar] [CrossRef]
- Mehdizadeh, E.; Rahimi, V. An integrated mathematical model for solving dynamic cell formation problem considering operator assignment and inter/intra cell layouts. Appl. Soft Comput. 2016, 42, 325–341. [Google Scholar] [CrossRef]
- Nouri, H. Development of a comprehensive model and BFO algorithm for a dynamic cellular manufacturing system. Appl. Math. Model. 2016, 40, 1514–1531. [Google Scholar] [CrossRef]
- Zohrevand, A.M.; Rafiei, H.; Zohrevand, A.H. Multi-objective dynamic cell formation problem: A stochastic programming approach. Comput. Ind. Eng. 2016, 98, 323–332. [Google Scholar] [CrossRef]
- Sadeghi, S.; Forghani, M.A.; Seidi, M. Integrated dynamic cell formation with operator assignment and inter-cell layout problems: A mathematical model. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 1658–1669. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, B. Design an incremental cell formation problem considering human factor. In Proceedings of the 2017 IEEE 3rd Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 3–5 October 2017; pp. 559–563. [Google Scholar]
- Delgoshaei, A.; Mirzazadeh, A.; Ali, A. A hybrid ant colony system and tabu search algorithm for the production planning of dynamic cellular manufacturing systems while confronting uncertain costs. Braz. J. Oper. Prod. Manag. 2018, 15, 499–516. [Google Scholar] [CrossRef]
- Fahmy, S.A. MILP model and a genetic algorithm for the integrated cell formation, layout and worker assignment problem. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Intelligent Manufacturing Technologies (ICMIMT), Cape Town, South Africa, 15–17 February 2019; pp. 117–121. [Google Scholar]
- Sakhaii, M.; Tavakkoli-Moghaddam, R.; Bagheri, M.; Vatani, B. A robust optimization approach for an integrated dynamic cellular manufacturing system and production planning with unreliable machines. Appl. Math. Model. 2016, 40, 169–191. [Google Scholar] [CrossRef]
- Feng, H.; Da, W.; Xi, L.; Pan, E.; Xia, T. Solving the integrated cell formation and worker assignment problem using particle swarm optimization and linear programming. Comput. Ind. Eng. 2017, 110, 126–137. [Google Scholar] [CrossRef]
- Shafiee-Gol, S.; Kia, R.; Kazemi, M.; Tavakkoli-Moghaddam, R.; Darmian, S.M. A mathematical model to design dynamic cellular manufacturing systems in multiple plants with production planning and location–allocation decisions. Soft Comput. 2021, 25, 3931–3954. [Google Scholar] [CrossRef]
- Felfel, H.; Ayadi, O.; Masmoudi, F. A decision-making approach for a multi-objective multisite supply network planning problem. Int. J. Comput. Integr. Manuf. 2016, 29, 754–767. [Google Scholar] [CrossRef]
- Mavrotas, G. Effective implementation of the ε-constraint method in multi-objective mathematical programming problems. Appl. Math. Comput. 2009, 213, 455–465. [Google Scholar] [CrossRef]
- Mahdavi, I.; Teymourian, E.; Baher, N.T.; Kayvanfar, V. An integrated model for solving cell formation and cell layout problem simultaneously considering new situations. J. Manuf. Syst. 2013, 32, 655–663. [Google Scholar] [CrossRef]
- Yadollahi, M.S.; Mahdavi, I.; Paydar, M.M.; Jouzdani, J. Design a bi-objective mathematical model for cellular manufacturing systems considering variable failure rate of machines. Int. J. Prod. Res. 2014, 52, 7401–7415. [Google Scholar] [CrossRef]
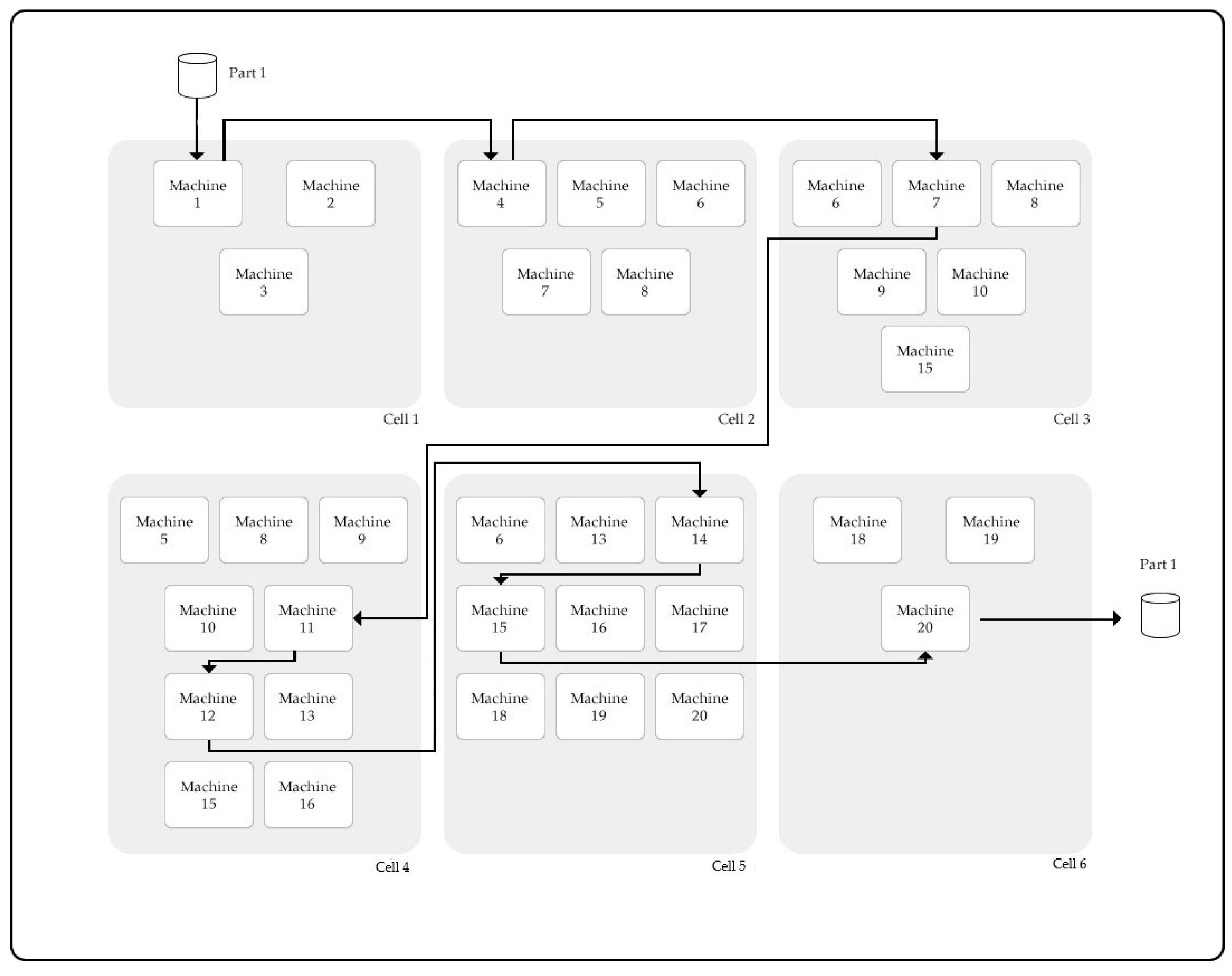
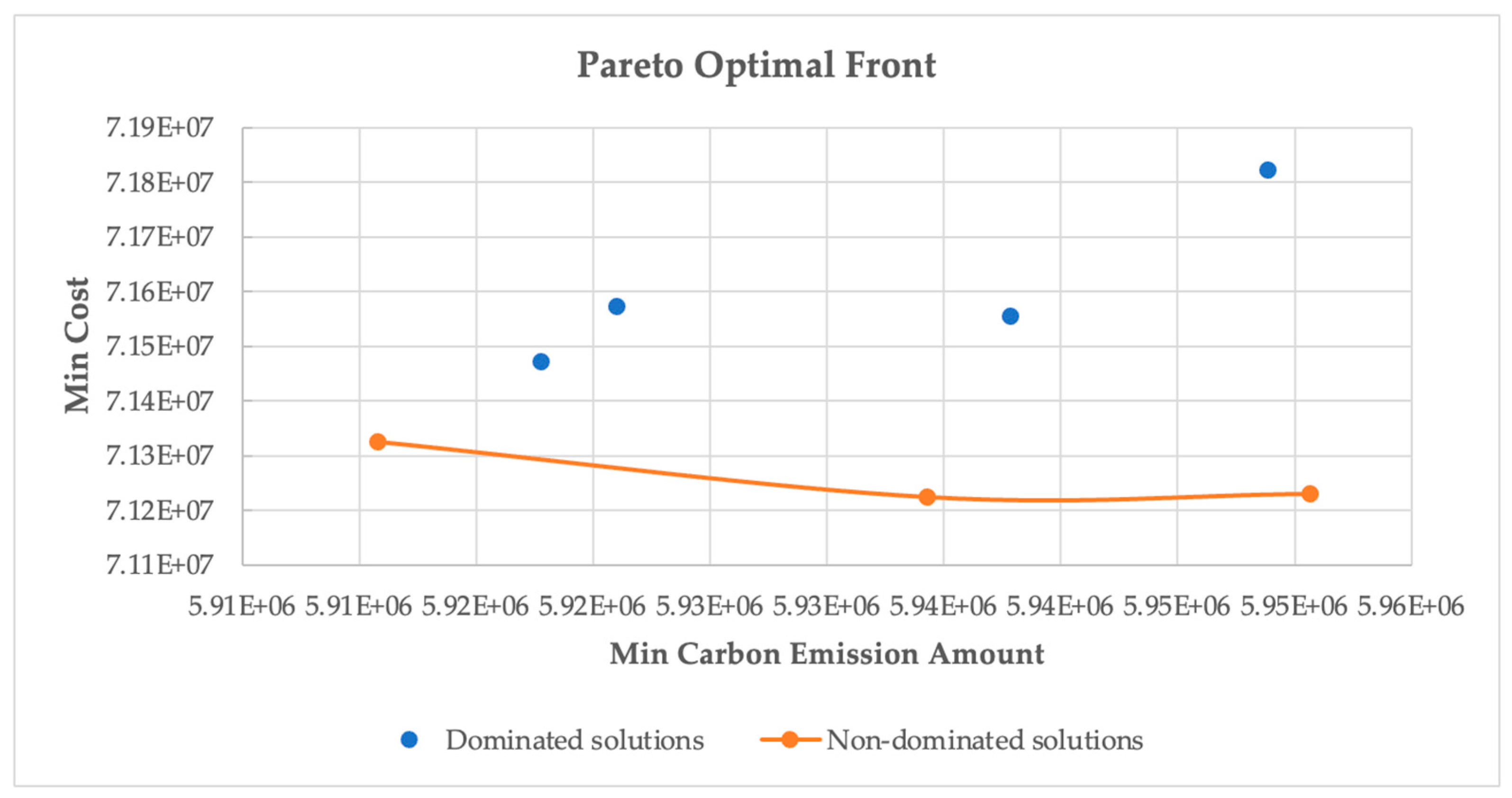
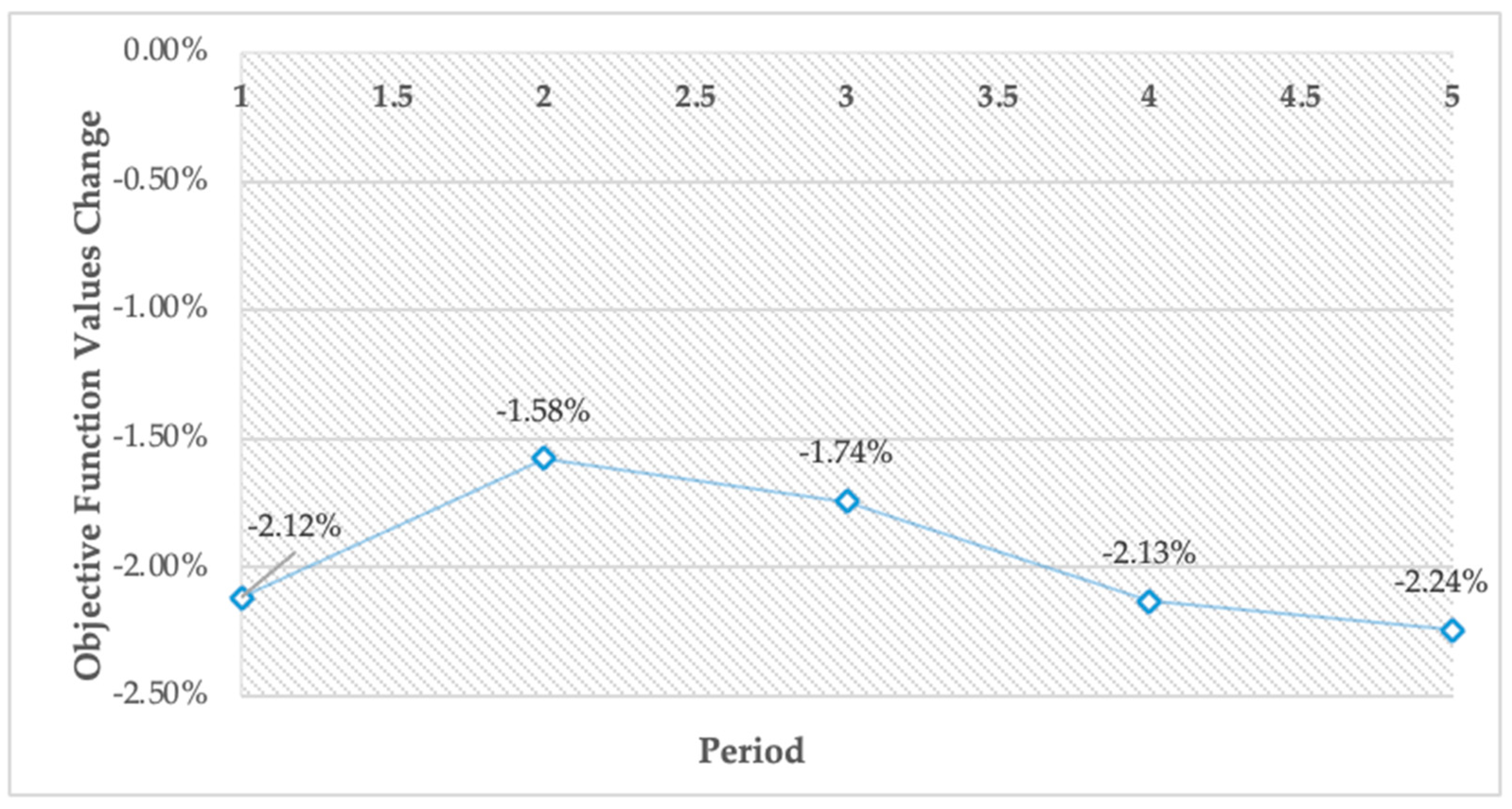

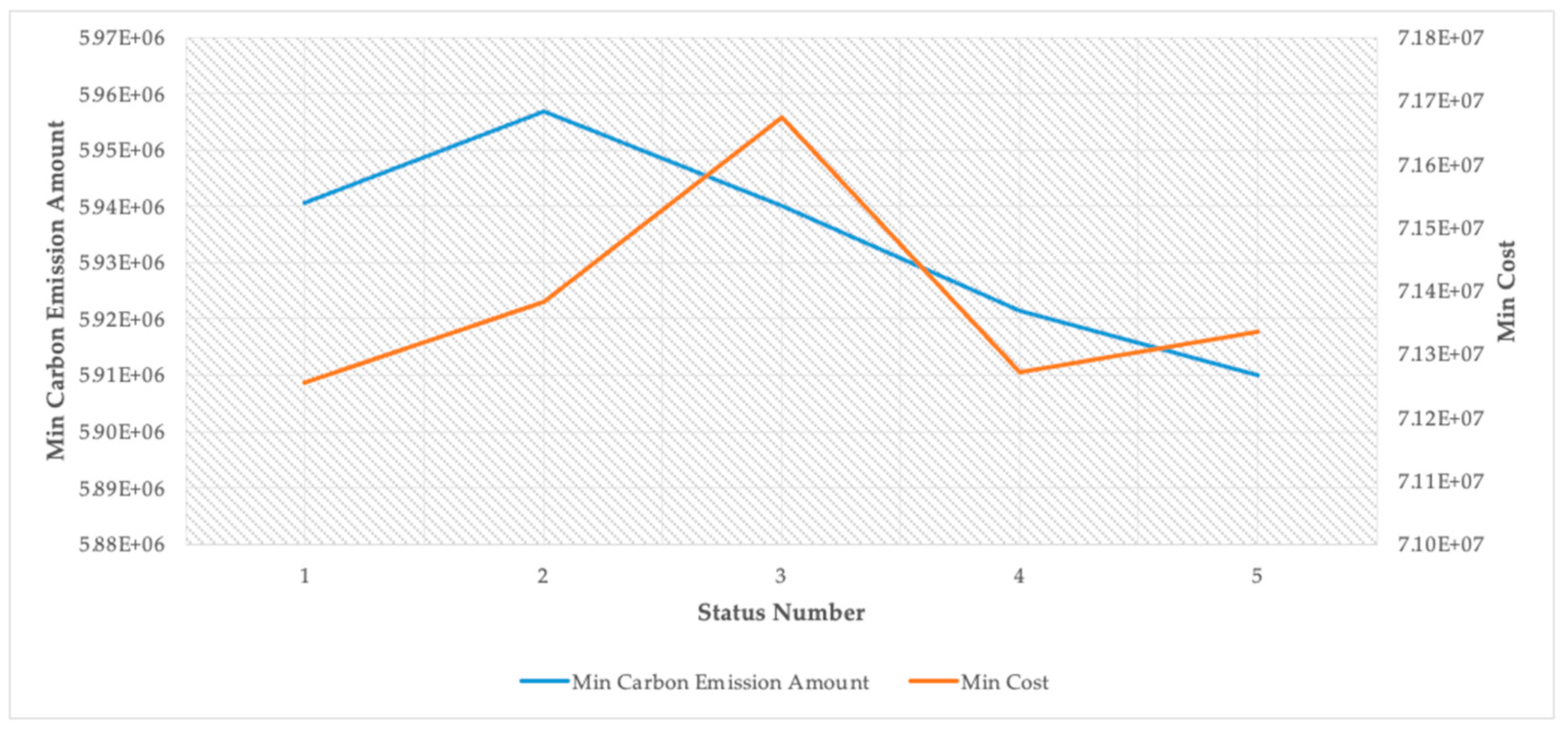
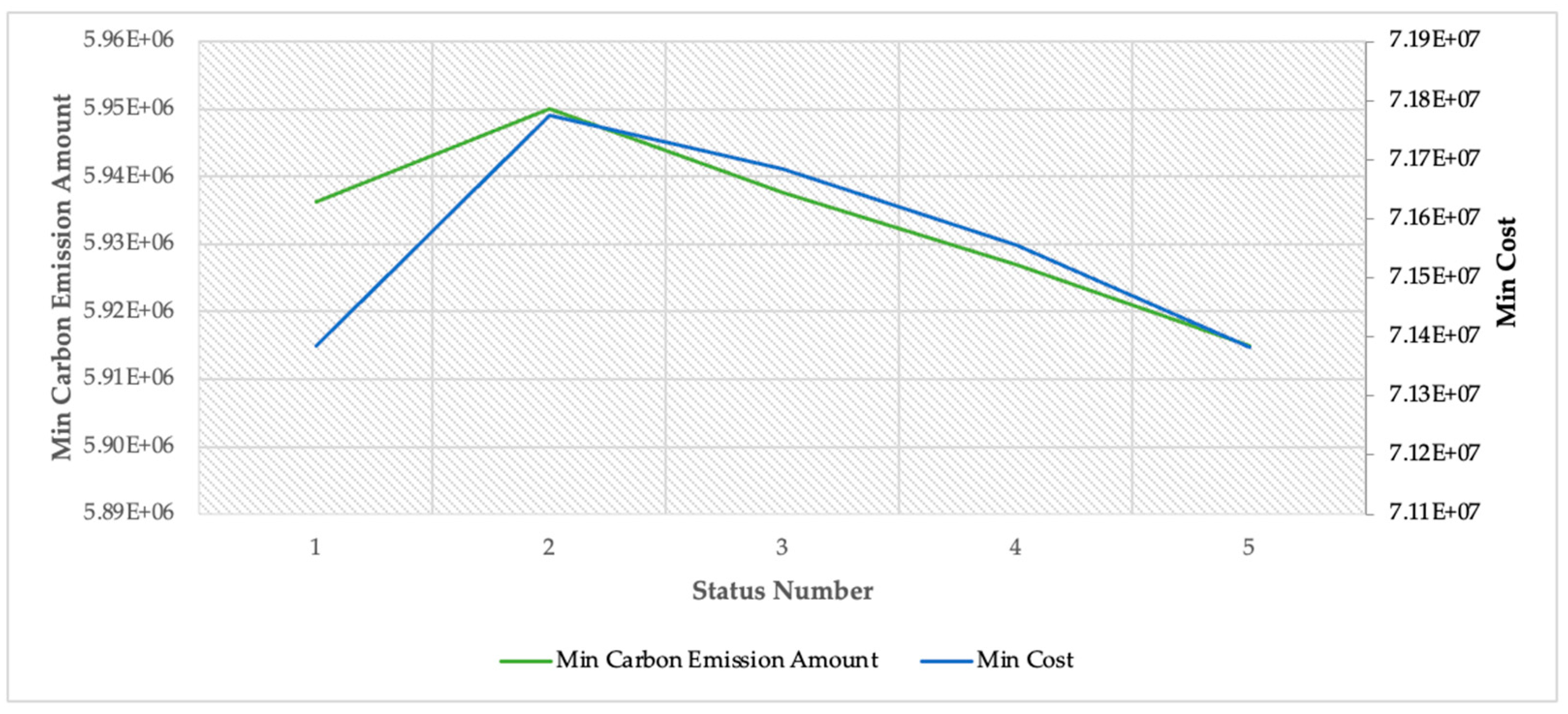
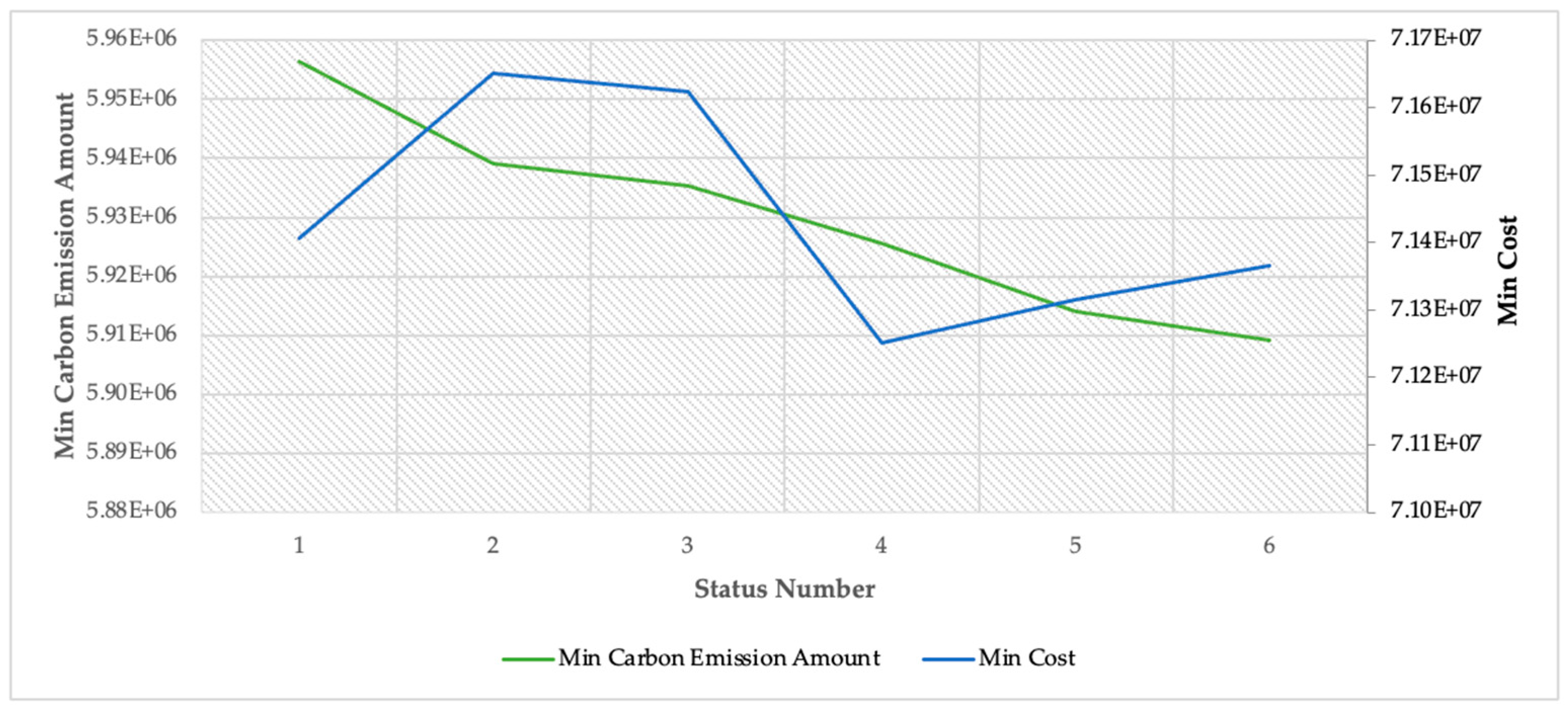


| Authors | Movement Costs | Machine Relocation-Related Cost | Worker Training Cost | Hiring and Firing Cost | Salary Cost | Energy Cost | Remanufacturing Cost | Pollution Cost | |
|---|---|---|---|---|---|---|---|---|---|
| Intra-Cellular | Inter-Cellular | ||||||||
| Aryanezhad et al. [26] | √ | √ | √ | √ | √ | ||||
| Fan and Feng [27] | √ | √ | √ | √ | |||||
| Bagheri and Bashiri [28] | √ | √ | √ | √ | |||||
| Aljuneidi and Bulgak [15] | √ | √ | |||||||
| Azadeh et al. [29] | √ | √ | √ | ||||||
| Mehdizadeh and Rahimi [30] | √ | √ | √ | ||||||
| Mehdizadeh et al. [16] | √ | √ | √ | √ | √ | √ | |||
| Niakan et al. [11] | √ | √ | √ | √ | √ | √ | |||
| Nouri [31] | √ | √ | √ | √ | √ | ||||
| Zohrevand et al. [32] | √ | √ | √ | ||||||
| Sadeghi et al. [33] | √ | √ | √ | √ | √ | √ | |||
| Zhang and Zhou [34] | √ | √ | √ | ||||||
| Arghish et al. [19] | √ | √ | √ | ||||||
| Delgoshaei et al. [35] | √ | √ | √ | ||||||
| Fahmy [36] | √ | √ | √ | ||||||
| Raoofpanah et al. [22] | √ | √ | √ | ||||||
| Authors | Economical | Environmental | Social |
|---|---|---|---|
| Fan and Feng [27] | √ | √ | |
| Ghodsi et al. [14] | √ | √ | √ |
| Aljuneidi and Bulgak [15] | √ | √ | |
| Mehdizadeh and Rahimi [30] | √ | ||
| Niakan et al. [11] | √ | √ | √ |
| Niakan et al. [17] | √ | √ | |
| Nouri [31] | √ | ||
| Imran et al. [18] | √ | ||
| Sadeghi et al. [33] | √ | ||
| Zhang and Zhou [34] | √ | √ | |
| Arghish et al. [19] | √ | √ | |
| Delgoshaei et al. [35] | √ | ||
| Iqbal and Al-Ghamdi [20] | √ | ||
| Kumar and Singh [21] | √ | √ | |
| Raoofpanah et al. [22] | √ | √ | |
| Forghani et al. [24] | √ | ||
| Jafarzadeh et al. [25] | √ | √ | √ |
| This article | √ | √ | √ |
| Authors | Worker Assignment | Skill | Route Flexibility | Period |
|---|---|---|---|---|
| Aryanezhad et al. [26] | √ | √ | √ | √ |
| Fan and Feng [27] | √ | √ | √ | √ |
| Bagheri and Bashiri [28] | √ | √ | ||
| Azadeh et al. [29] | √ | √ | √ | |
| Mehdizadeh and Rahimi [30] | √ | √ | ||
| Niakan et al. [11] | √ | √ | √ | |
| Nouri [31] | √ | √ | √ | |
| Sakhaii et al. [37] | √ | √ | √ | |
| Feng et al. [38] | √ | √ | √ | |
| Raoofpanah et al. [22] | √ | |||
| Shafiee-Gol et al. [39] | √ | √ | ||
| This article | √ | √ | √ | √ |
| Machine | Capacity | ||||
|---|---|---|---|---|---|
| 1. Period | 2. Period | 3. Period | 4. Period | 5. Period | |
| 1 | 55,200 | 51,900 | 48,800 | 45,400 | 35,400 |
| 2 | 48,900 | 45,400 | 44,200 | 43,900 | 42,900 |
| 3 | 50,100 | 46,300 | 44,100 | 43,300 | 42,300 |
| 4 | 49,200 | 48,100 | 47,100 | 45,100 | 44,100 |
| 5 | 48,900 | 46,800 | 45,500 | 44,800 | 43,800 |
| 6 | 46,200 | 45,000 | 44,000 | 43,500 | 41,000 |
| 7 | 47,500 | 45,900 | 42,000 | 40,900 | 38,900 |
| 8 | 44,850 | 42,750 | 41,800 | 40,750 | 38,750 |
| 9 | 47,200 | 46,900 | 45,800 | 43,900 | 37,900 |
| 10 | 48,900 | 44,400 | 43,700 | 38,900 | 35,900 |
| 11 | 51,100 | 50,300 | 48,800 | 45,300 | 42,900 |
| 12 | 58,200 | 55,100 | 53,500 | 50,400 | 48,900 |
| 13 | 47,900 | 45,800 | 44,800 | 43,800 | 41,800 |
| 14 | 48,200 | 47,000 | 45,800 | 45,000 | 43,900 |
| 15 | 54,500 | 52,900 | 50,500 | 48,900 | 46,900 |
| 16 | 52,850 | 50,750 | 48,200 | 46,750 | 41,750 |
| 17 | 48,900 | 45,800 | 43,220 | 42,800 | 40,800 |
| 18 | 48,200 | 45,000 | 43,400 | 42,000 | 41,500 |
| 19 | 45,500 | 43,900 | 42,000 | 41,600 | 40,300 |
| 20 | 47,850 | 45,750 | 43,500 | 42,750 | 41,750 |
| Machine | Operation Costs | Carbon Emission Costs | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1. Period | 2. Period | 3. Period | 4. Period | 5. Period | 1. Period | 2. Period | 3. Period | 4. Period | 5. Period | |
| 1 | 9 | 10 | 12 | 13 | 15 | 7 | 8 | 9 | 8 | 12 |
| 2 | 8 | 10 | 13 | 16 | 17 | 6 | 9 | 10 | 9 | 11 |
| 3 | 10 | 11 | 14 | 15 | 19 | 7 | 8 | 9 | 9 | 14 |
| 4 | 11 | 12 | 16 | 18 | 20 | 9 | 7 | 9 | 10 | 13 |
| 5 | 13 | 13 | 18 | 19 | 23 | 7 | 7 | 7 | 9 | 12 |
| 6 | 14 | 15 | 16 | 16 | 22 | 6 | 6 | 9 | 8 | 13 |
| 7 | 15 | 17 | 12 | 13 | 18 | 8 | 7 | 8 | 9 | 12 |
| 8 | 13 | 15 | 16 | 17 | 19 | 7 | 9 | 9 | 11 | 13 |
| 9 | 15 | 18 | 19 | 20 | 21 | 7 | 8 | 10 | 12 | 14 |
| 10 | 9 | 12 | 14 | 18 | 19 | 6 | 9 | 8 | 7 | 13 |
| 11 | 10 | 13 | 13 | 13 | 19 | 7 | 8 | 6 | 7 | 12 |
| 12 | 12 | 15 | 19 | 20 | 24 | 9 | 7 | 9 | 8 | 11 |
| 13 | 12 | 13 | 16 | 17 | 20 | 7 | 7 | 7 | 9 | 12 |
| 14 | 16 | 18 | 19 | 17 | 18 | 5 | 6 | 10 | 10 | 14 |
| 15 | 13 | 15 | 16 | 18 | 22 | 8 | 6 | 9 | 10 | 12 |
| 16 | 12 | 15 | 16 | 17 | 20 | 7 | 9 | 8 | 9 | 10 |
| 17 | 14 | 18 | 18 | 20 | 23 | 6 | 7 | 9 | 8 | 11 |
| 18 | 16 | 17 | 21 | 23 | 26 | 6 | 8 | 9 | 8 | 12 |
| 19 | 13 | 15 | 14 | 17 | 22 | 7 | 6 | 9 | 12 | 13 |
| 20 | 12 | 16 | 15 | 18 | 20 | 8 | 9 | 9 | 10 | 11 |
| Machine | Machine Addition Costs | Machine Removal Costs | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1. Period | 2. Period | 3. Period | 4. Period | 5. Period | 1. Period | 2. Period | 3. Period | 4. Period | 5. Period | |
| 1 | 25 | 45 | 30 | 40 | 49 | 55 | 46 | 40 | 45 | 55 |
| 2 | 55 | 30 | 35 | 38 | 48 | 75 | 55 | 50 | 55 | 58 |
| 3 | 45 | 35 | 30 | 38 | 51 | 45 | 55 | 50 | 55 | 59 |
| 4 | 65 | 62 | 45 | 49 | 59 | 65 | 62 | 65 | 75 | 78 |
| 5 | 48 | 63 | 50 | 59 | 65 | 48 | 75 | 70 | 75 | 79 |
| 6 | 55 | 55 | 55 | 60 | 63 | 65 | 55 | 55 | 65 | 75 |
| 7 | 40 | 56 | 50 | 55 | 65 | 60 | 65 | 60 | 65 | 69 |
| 8 | 50 | 63 | 60 | 60 | 66 | 45 | 50 | 55 | 65 | 70 |
| 9 | 25 | 45 | 45 | 55 | 58 | 55 | 46 | 40 | 45 | 55 |
| 10 | 55 | 30 | 35 | 38 | 48 | 75 | 55 | 50 | 55 | 58 |
| 11 | 45 | 35 | 42 | 43 | 53 | 45 | 55 | 55 | 58 | 65 |
| 12 | 65 | 62 | 40 | 60 | 65 | 65 | 62 | 60 | 65 | 70 |
| 13 | 48 | 63 | 45 | 65 | 68 | 48 | 75 | 70 | 73 | 75 |
| 14 | 55 | 55 | 50 | 50 | 55 | 65 | 55 | 50 | 54 | 60 |
| 15 | 40 | 56 | 55 | 59 | 63 | 60 | 65 | 60 | 63 | 65 |
| 16 | 50 | 63 | 60 | 63 | 65 | 45 | 50 | 70 | 74 | 75 |
| 17 | 48 | 63 | 60 | 65 | 68 | 48 | 75 | 45 | 48 | 55 |
| 18 | 55 | 55 | 50 | 55 | 65 | 65 | 55 | 55 | 58 | 60 |
| 19 | 40 | 56 | 55 | 55 | 65 | 60 | 65 | 60 | 65 | 70 |
| 20 | 50 | 63 | 60 | 65 | 70 | 45 | 50 | 55 | 58 | 70 |
| Period | Cell Machine Upper Limit | Cell Machine Lower Limit | Cell Worker Upper Limit | Cell Carbon Emission Upper Limit | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cell | Cell | Cell | Cell | |||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 5 | 5 | 4 | 4 | 4 | 5 | 1 | 1 | 1 | 1 | 1 | 1 | 4 | 4 | 4 | 4 | 4 | 4 | 365,100 | 376,400 | 397,500 | 425,100 | 376,400 | 377,500 |
| 2 | 5 | 5 | 4 | 5 | 5 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | 4 | 4 | 4 | 4 | 4 | 4 | 375,000 | 388,500 | 387,000 | 395,000 | 438,500 | 377,000 |
| 3 | 5 | 5 | 4 | 5 | 5 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | 4 | 4 | 4 | 4 | 4 | 4 | 385,000 | 354,000 | 350,000 | 405,000 | 415,000 | 357,800 |
| 4 | 5 | 5 | 4 | 5 | 5 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | 4 | 4 | 4 | 4 | 4 | 4 | 395,000 | 364,000 | 390,000 | 425,000 | 435,000 | 387,800 |
| 5 | 4 | 4 | 5 | 4 | 5 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | 4 | 4 | 4 | 4 | 4 | 4 | 355,000 | 334,000 | 370,000 | 405,000 | 405,000 | 357,800 |
| Skill | Worker | |||||
| I1 | I2 | I3 | I4 | I5 | I6 | |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 2 | 1 | 1 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 |
| Skill | Worker | |||||
| I1 | I2 | I3 | I4 | I5 | I6 | |
| 1 | 5 | 0 | 2 | 0 | 0 | 3 |
| 2 | 4 | 8 | 0 | 0 | 7 | 0 |
| 3 | 0 | 0 | 3 | 9 | 0 | 0 |
| The Limit Value of Workers with Skills | The Limit Time of Workers with Skills | Training Cost of Workers | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Skill | Skill | Workers | ||||||||||
| 1. Period | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | 6 |
| Cell 1 | 1 | 2 | 0 | 25 | 20 | 0 | 50 | 65 | 75 | 45 | 35 | 70 |
| Cell 2 | 2 | 2 | 1 | 15 | 30 | 25 | 30 | 80 | 55 | 65 | 35 | 25 |
| Cell 3 | 2 | 0 | 3 | 35 | 0 | 30 | 33 | 65 | 78 | 40 | 25 | 30 |
| Cell 4 | 1 | 2 | 0 | 25 | 20 | 0 | 40 | 75 | 45 | 35 | 35 | 70 |
| Cell 5 | 2 | 2 | 1 | 15 | 30 | 25 | 30 | 80 | 65 | 55 | 35 | 25 |
| Cell 6 | 2 | 0 | 3 | 35 | 0 | 30 | 38 | 65 | 78 | 40 | 25 | 30 |
| 2. Period | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | 6 |
| Cell 1 | 3 | 2 | 0 | 20 | 15 | 0 | 50 | 65 | 75 | 45 | 35 | 70 |
| Cell 2 | 1 | 3 | 0 | 40 | 25 | 0 | 30 | 80 | 55 | 65 | 35 | 25 |
| Cell 3 | 2 | 1 | 2 | 35 | 40 | 25 | 33 | 65 | 78 | 40 | 25 | 30 |
| Cell 4 | 3 | 2 | 0 | 20 | 15 | 0 | 40 | 75 | 45 | 35 | 35 | 70 |
| Cell 5 | 1 | 3 | 0 | 40 | 25 | 0 | 30 | 80 | 65 | 55 | 35 | 25 |
| Cell 6 | 2 | 1 | 2 | 35 | 40 | 25 | 38 | 65 | 78 | 40 | 25 | 30 |
| 3. Period | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | 6 |
| Cell 1 | 3 | 2 | 0 | 20 | 15 | 0 | 50 | 65 | 75 | 45 | 35 | 70 |
| Cell 2 | 1 | 3 | 0 | 40 | 25 | 0 | 30 | 80 | 55 | 65 | 35 | 25 |
| Cell 3 | 2 | 1 | 2 | 35 | 40 | 25 | 33 | 65 | 78 | 40 | 25 | 30 |
| Cell 4 | 3 | 2 | 0 | 20 | 15 | 0 | 40 | 75 | 45 | 35 | 35 | 70 |
| Cell 5 | 1 | 3 | 0 | 40 | 25 | 0 | 30 | 80 | 65 | 55 | 35 | 25 |
| Cell 6 | 2 | 1 | 2 | 55 | 45 | 35 | 38 | 65 | 78 | 40 | 25 | 30 |
| 4. Period | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | 6 |
| Cell 1 | 4 | 3 | 0 | 30 | 35 | 0 | 60 | 75 | 85 | 55 | 45 | 75 |
| Cell 2 | 2 | 3 | 0 | 50 | 35 | 0 | 35 | 70 | 65 | 75 | 55 | 35 |
| Cell 3 | 3 | 2 | 3 | 45 | 40 | 25 | 39 | 65 | 75 | 45 | 35 | 35 |
| Cell 4 | 4 | 2 | 0 | 30 | 35 | 0 | 45 | 78 | 48 | 55 | 45 | 80 |
| Cell 5 | 3 | 3 | 0 | 45 | 35 | 0 | 35 | 85 | 75 | 59 | 45 | 35 |
| Cell 6 | 4 | 2 | 3 | 40 | 50 | 35 | 40 | 75 | 80 | 50 | 30 | 40 |
| 5. Period | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | 6 |
| Cell 1 | 1 | 1 | 0 | 22 | 17 | 0 | 40 | 55 | 70 | 40 | 30 | 65 |
| Cell 2 | 2 | 2 | 1 | 13 | 20 | 20 | 25 | 70 | 50 | 60 | 30 | 20 |
| Cell 3 | 2 | 0 | 3 | 30 | 0 | 25 | 30 | 60 | 70 | 35 | 20 | 25 |
| Cell 4 | 1 | 2 | 0 | 20 | 20 | 0 | 38 | 65 | 40 | 30 | 33 | 68 |
| Cell 5 | 2 | 2 | 1 | 13 | 25 | 27 | 28 | 70 | 60 | 50 | 30 | 23 |
| Cell 6 | 2 | 0 | 2 | 30 | 0 | 25 | 35 | 60 | 75 | 35 | 20 | 28 |
| Training Time According to Skill | ||||
|---|---|---|---|---|
| 1. Period | Worker | Skill 1 | Skill 2 | Skill 3 |
| 1 | 15 | 10 | 0 | |
| 2 | 0 | 15 | 0 | |
| 3 | 17 | 0 | 15 | |
| 4 | 0 | 0 | 11 | |
| 5 | 0 | 18 | 10 | |
| 6 | 18 | 0 | 0 | |
| 2. Period | Worker | Skill 1 | Skill 2 | Skill 3 |
| 1 | 10 | 8 | 0 | |
| 2 | 0 | 18 | 0 | |
| 3 | 17 | 0 | 13 | |
| 4 | 0 | 0 | 11 | |
| 5 | 0 | 13 | 0 | |
| 6 | 17 | 0 | 0 | |
| 3.Period | Worker | Skill 1 | Skill 2 | Skill 3 |
| 1 | 10 | 8 | 0 | |
| 2 | 0 | 13 | 0 | |
| 3 | 15 | 0 | 18 | |
| 4 | 0 | 0 | 12 | |
| 5 | 0 | 12 | 0 | |
| 6 | 23 | 0 | 0 | |
| 4.Period | Worker | Skill 1 | Skill 2 | Skill 3 |
| 1 | 15 | 17 | 0 | |
| 2 | 0 | 18 | 0 | |
| 3 | 22 | 0 | 13 | |
| 4 | 0 | 0 | 16 | |
| 5 | 0 | 16 | 0 | |
| 6 | 20 | 0 | 0 | |
| 5.Period | Worker | Skill 1 | Skill 2 | Skill 3 |
| 1 | 11 | 7 | 0 | |
| 2 | 0 | 16 | 0 | |
| 3 | 15 | 0 | 14 | |
| 4 | 0 | 0 | 10 | |
| 5 | 0 | 23 | 0 | |
| 6 | 15 | 0 | 0 | |
| Period | Cell | Optimal Machine Assignments | Optimal Machine Addition | Optimal Machine Removal |
|---|---|---|---|---|
| 1 | 1 | N111(1), N112(1), N113(1) | ||
| 2 | N124(1), N125(1), N126(1) | |||
| 3 | N136(1), N137(1), N138(1), N139(1) | |||
| 4 | N148(1), N1,4,11(1), N1,4,12(1), N1,4,15(1) | |||
| 5 | N1,5,14(1), N1,5,15(1), N1,5,16(1), N1,5,17(1) | |||
| 6 | N1,6,18(1), N1,6,19(1), N1,6,20(1) | |||
| 2 | 1 | N211(1), N212(1), N213(1) | ||
| 2 | N224(1), N225(1), N226(1) | |||
| 3 | N236(1), N237(1), N238(1), N239(1) | |||
| 4 | N2,4,10(1), N2,4,11(1), N2,4,12(1), N2,4,13(1), N2,4,15(1) | NA2,4,10(1) NA2,4,13(1) | NR248(1) | |
| 5 | N2,5,14(1), N2,5,15(1), N2,5,16(1), N2,5,17(1) | |||
| 6 | N2,6,18(1), N2,6,19(1), N2,6,20(1) | |||
| 3 | 1 | N311(1), N312(1), N313(1) | ||
| 2 | N324(1), N325(1), N326(1) | |||
| 3 | N336(1), N337(1), N338(1), N339(1) | |||
| 4 | N3,4,8(1), N3,4,10(1), N3,4,11(1), N3,4,12(1), N3,4,15(1) | NA348(1) | NR3,4,13(1) | |
| 5 | N3,5,14(1), N3,5,15(1), N3,5,16(1), N3,5,17(1) | |||
| 6 | N3,6,18(1), N3,6,19(1), N3,6,20(1) | NA3,6,13(1) | ||
| 4 | 1 | N411(1), N412(1), N413(1) | ||
| 2 | N424(1), N425(1), N426(1), N427(1) | NA427(1) | ||
| 3 | N436(1), N437(1), N438(1), N439(1) | |||
| 4 | N4,4,10(1), N4,4,11(1), N4,4,12(1), N4,4,13(1), N4,4,15(1) | NA4,4,13(1) | NR448(1) | |
| 5 | N4,5,14(1), N4,5,15(1), N4,5,16(1), N4,5,17(1), N4,5,18(1) | NA4,5,18(1) | ||
| 6 | N4,6,18(1), N4,6,19(1), N4,6,20(1) | |||
| 5 | 1 | N511(1), N512(1), N513(1), N5,1,14(1) | NA5,1,14(1) | |
| 2 | N524(1), N525(1), N526(1) | NR527(1) | ||
| 3 | N536(1), N537(1), N538(1), N539(1) | |||
| 4 | N548(1), N5,4,11(1), N5,4,12(1), N5,4,15(1) | NA548(1) | NR5,4,10(1) NR5,4,13(1) | |
| 5 | N5,5,14(1), N5,5,15(1), N5,5,16(1), N5,5,17(1), N5,5,18(1) | |||
| 6 | N5,6,13(1), N5,6,18(1), N5,6,19(1), N5,6,20(1) |
| Period | Cell | Optimal Machine Assignments | Optimal Machine Addition | Optimal Machine Removal |
|---|---|---|---|---|
| 1 | 1 | N111(1), N112(1), N113(1) | ||
| 2 | N124(1), N125(1), N126(1), N127(1) | |||
| 3 | N136(1), N137(1), N138(1), N139(1) | |||
| 4 | N1,4,11(1), N1,4,12(1), N1,4,13(1), N1,4,15(1) | |||
| 5 | N1,5,14(1), N1,5,15(1), N1,5,16(1), N1,5,17(1) | |||
| 6 | N1,6,18(1), N1,6,19(1), N1,6,20(1) | |||
| 2 | 1 | N211(1), N212(1), N213(1) | ||
| 2 | N224(1), N225(1), N226(1), N227(1) | |||
| 3 | N236(1), N237(1), N238(1), N239(1) | |||
| 4 | N2,4,10(1), N2,4,11(1), N2,4,12(1), N2,4,13(1), N2,4,15(1) | NA2,4,10(1) | ||
| 5 | N2,5,14(1), N2,5,15(1), N2,5,16(1), N2,5,17(1) | |||
| 6 | N2,6,18(1), N2,6,19(1), N2,6,20(1) | |||
| 3 | 1 | N311(1), N312(1), N313(1) | ||
| 2 | N324(1), N325(1), N326(1), N327(1) | |||
| 3 | N336(1), N337(1), N338(1), N339(1) | |||
| 4 | N3,4,8(1), N3,4,10(1), N3,4,11(1), N3,4,12(1), N3,4,15(1) | NA3,4,8(1) | NR3,4,13(1) | |
| 5 | N3,5,14(1), N3,5,15(1), N3,5,16(1), N3,5,17(1) | |||
| 6 | N3,6,18(1), N3,6,19(1), N3,6,20(1) | |||
| 4 | 1 | N411(1), N412(1), N413(1) | ||
| 2 | N424(1), N425(1), N426(1), N427(1) | |||
| 3 | N436(1), N437(1), N438(1), N439(1) | |||
| 4 | N4,4,10(1), N4,4,11(1), N4,4,12(1), N4,4,13(1), N4,4,15(1) | NA4,4,13(1) | NR4,4,8(1) | |
| 5 | N4,5,14(1), N4,5,15(1), N4,5,16(1), N4,5,17(1) | |||
| 6 | N4,6,18(1), N4,6,19(1), N4,6,20(1) | |||
| 5 | 1 | N511(1), N512(1), N513(1) | ||
| 2 | N524(1), N525(1), N526(1), N527(1) | |||
| 3 | N536(1), N537(1), N538(1), N539(1) | |||
| 4 | N548(1), N5,4,11(1), N5,4,12(1), N5,4,15(1) | NA548(1) | NR5,4,10(1) NR5,4,13(1) | |
| 5 | N5,5,14(1), N5,5,15(1), N5,5,16(1), N5,5,17(1) | |||
| 6 | N5,6,18(1), N5,6,19(1), N5,6,20(1) |
| Period | Cell | Optimal Machine Assignments | Optimal Machine Addition | Optimal Machine Removal |
|---|---|---|---|---|
| 1 | 1 | N111(1), N112(1), N113(1) | ||
| 2 | N124(1), N125(1), N126(1) | |||
| 3 | N136(1), N137(1), N138(1), N139(1) | |||
| 4 | N1,4,11(1), N1,4,12(1), N1,4,13(1), N1,4,15(1) | |||
| 5 | N1,5,14(1), N1,5,15(1), N1,5,16(1), N1,5,17(1) | |||
| 6 | N1,6,18(1), N1,6,19(1), N1,6,20(1) | |||
| 2 | 1 | N211(1), N212(1), N213(1) | ||
| 2 | N224(1), N225(1), N226(1) | |||
| 3 | N236(1), N237(1), N238(1), N239(1) | |||
| 4 | N2,4,10(1), N2,4,11(1), N2,4,12(1), N2,4,13(1), N2,4,15(1) | NA2,4,10(1) | ||
| 5 | N2,5,14(1), N2,5,15(1), N2,5,16(1), N2,5,17(1) | |||
| 6 | N2,6,18(1), N2,6,19(1), N2,6,20(1) | |||
| 3 | 1 | N311(1), N312(1), N313(1) | ||
| 2 | N324(1), N325(1), N326(1) | |||
| 3 | N336(1), N337(1), N338(1), N339(1) | |||
| 4 | N3,4,8(1), N3,4,10(1), N3,4,11(1), N3,4,12(1), N3,4,15(1) | NA3,4,8(1) | NR3,4,13(1) | |
| 5 | N3,5,14(1), N3,5,15(1), N3,5,16(1), N3,5,17(1) | |||
| 6 | N3,6,18(1), N3,6,19(1), N3,6,20(1) | |||
| 4 | 1 | N411(1), N412(1), N413(1) | ||
| 2 | N424(1), N425(1), N426(1) | |||
| 3 | N436(1), N437(1), N438(1), N439(1) | |||
| 4 | N4,4,8(1), N4,4,10(1), N4,4,11(1), N4,4,12(1), N4,4,15(1) | |||
| 5 | N4,5,14(1), N4,5,15(1), N4,5,16(1), N4,5,17(1) | |||
| 6 | N4,6,18(1), N4,6,19(1), N4,6,20(1) | |||
| 5 | 1 | N511(1), N512(1), N513(1) | ||
| 2 | N524(1), N525(1), N526(1) | |||
| 3 | N536(1), N537(1), N538(1), N539(1) | |||
| 4 | N5,4,8(1), N5,4,11(1), N5,4,12(1), N5,4,15(1) | NR5,4,10(1) | ||
| 5 | N5,5,14(1), N5,5,15(1), N5,5,16(1), N5,5,17(1) | |||
| 6 | N5,6,18(1), N5,6,19(1), N5,6,20(1) |
| Period | Optimal Worker Assignment for Goal Programming | Optimal Worker Assignment for ε-Constraint | Optimal Worker Assignment for AUGMECON |
|---|---|---|---|
| 1 | V111, V112, V146, V155, V163, V164 | V112, V121, V123,V155, V156, V164 | V112, V121, V123,V155, V156, V164 |
| 2 | V241, V233,V234, V246, V252, V255 | V226, V232, V233, V234, V251, V265 | V226, V232, V233, V234, V251, V265 |
| 3 | V333, V334, V341, V346, V352, V355 | V326, V332, V333, V334, V351, V365 | V326, V332, V333, V334, V351, V365 |
| 4 | V421, V422, V425, V426, V433, V434 | V421, V426, V432, V433, V434, V465 | V421, V426, V432, V433, V434, V465 |
| 5 | V512, V521, V525, V563, V564, V566 | V512, V521, V523, V525, V556, V564 | V512, V521, V523, V525, V556, V564 |
| Period | Optimal Total Worker for Goal Programming | Optimal Total Worker for ε-Constraint | Optimal Total Worker for AUGMECON |
|---|---|---|---|
| 1 | IS11(2), IS12(0), IS13(0), IS14(1), IS15(1), IS16(2) | IS11(1), IS12(2), IS13(0), IS14(0), IS15(2), IS16(1) | IS11(1), IS12(2), IS13(0), IS14(0), IS15(2), IS16(1) |
| 2 | IS21(0), IS22(0), IS23(2), IS24(2), IS25(2), IS26(0) | IS21(0), IS22(1), IS23(3), IS24(0), IS25(1), IS26(1) | IS21(0), IS22(1), IS23(3), IS24(0), IS25(1), IS26(1) |
| 3 | IS31(0), IS32(0), IS33(2), IS34(2), IS35(2), IS36(0) | IS31(0), IS32(1), IS33(3), IS34(0), IS35(1), IS36(1) | IS31(0), IS32(1), IS33(3), IS34(0), IS35(1), IS36(1) |
| 4 | IS41(0), IS42(4), IS43(2), IS44(0), IS45(0) IS46(0) | IS41(0), IS42(2), IS43(3), IS44(0), IS45(0), IS46(1) | IS41(0), IS42(2), IS43(3), IS44(0), IS45(0), IS46(1) |
| 5 | IS51(1), IS52(2), IS53(0), IS54(0), IS55(0) IS56(3) | IS51(1), IS52(3), IS53(0), IS54(0), IS55(1), IS56(1) | IS51(1), IS52(3), IS53(0), IS54(0), IS55(1), IS56(1) |
| SNC1 | SNC2 | |
|---|---|---|
| Min SNC1 | 5,902,903 | 72,492,480 |
| Min SNC2 | 5,974,220 | 71,788,790 |
| SNC1 | SNC2 | |
|---|---|---|
| Min SNC1 | 5,929,063 | 71,788,790 |
| Min SNC2 | 5,974,220 | 71,788,790 |
| Status Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Epsilon Value | 5,977,181 | 5,958,612 | 5,940,043 | 5,921,474 | 5,902,905 |
| Status Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Epsilon Value | 5,963,143 | 5,951,103 | 5,939,063 | 5,927,023 | 5,914,983 |
| Status Number | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Epsilon Value | 5,959,367 | 5,948,075 | 5,936,783 | 5,925,491 | 5,914,199 | 5,909,193 |
| Status Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Epsilon Value | 5,962,379 | 5,953,925 | 5,945,771 | 5,937,417 | 5,929,064 |
| Status Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Epsilon Value | 5,965,359 | 5,955,535 | 5,945,711 | 5,935,887 | 5,929,064 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bozoklar, E.; Yılmaz, E. Designing Sustainable Flexible Manufacturing Cells with Multi-Objective Optimization Models. Appl. Sci. 2024, 14, 203. https://doi.org/10.3390/app14010203
Bozoklar E, Yılmaz E. Designing Sustainable Flexible Manufacturing Cells with Multi-Objective Optimization Models. Applied Sciences. 2024; 14(1):203. https://doi.org/10.3390/app14010203
Chicago/Turabian StyleBozoklar, Emine, and Ebru Yılmaz. 2024. "Designing Sustainable Flexible Manufacturing Cells with Multi-Objective Optimization Models" Applied Sciences 14, no. 1: 203. https://doi.org/10.3390/app14010203
APA StyleBozoklar, E., & Yılmaz, E. (2024). Designing Sustainable Flexible Manufacturing Cells with Multi-Objective Optimization Models. Applied Sciences, 14(1), 203. https://doi.org/10.3390/app14010203








