Stand-Up Time Dependence on Protective Roof–Pillar Bearing Structure of Bauxite

Abstract

The immediate roof of Shanxi sedimentary bauxite is hard clay rock, which maintain stable difficultly in goaf. It is necessary to ensure the stability of the goaf during the mine production period. The relevant research objects did not involve soft rock mass such as bauxite and hard clay and did not pay attention to the weakening characteristics of load-bearing structures under the action of weathering and rheology. This paper provides theoretical support for the safety production of bauxite and similar mines. In order to study the relationship between the stability of the protective roof-pillar bearing structure and time, this paper uses elastic thin plates and rheological theory to build the physical model of the bauxite protective roof-pillar bearing structure, and gives the calculation formula of the stand-up time of the bearing structure. The influence of factors such as the thickness of the protective roof, the uniform surface force coefficient of pillar, the span of the goaf and the thickness of the overlying rock layer on the stand-up time of the bearing structure is analyzed. The relationship between the ultimate bearing capacity and stand-up time of the bearing structure is quantified. The results show that the bearing capacity of the bearing structure is affected by the mechanical properties of the rock mass and the structural parameters of the goaf. Under the condition that the influencing factors of the mechanical parameters of the rock mass remain unchanged, the stand-up time T, which represents the bearing capacity of the bearing structure, is positively correlated with the thickness of the protective roof, positively correlated with the uniform surface force coefficient of the pillar, negatively correlated with the span of the goaf and negatively correlated with the thickness of the overlying rock layer. The engineering example verifies the rationality of theoretical calculation and provides a new idea for mining safety.

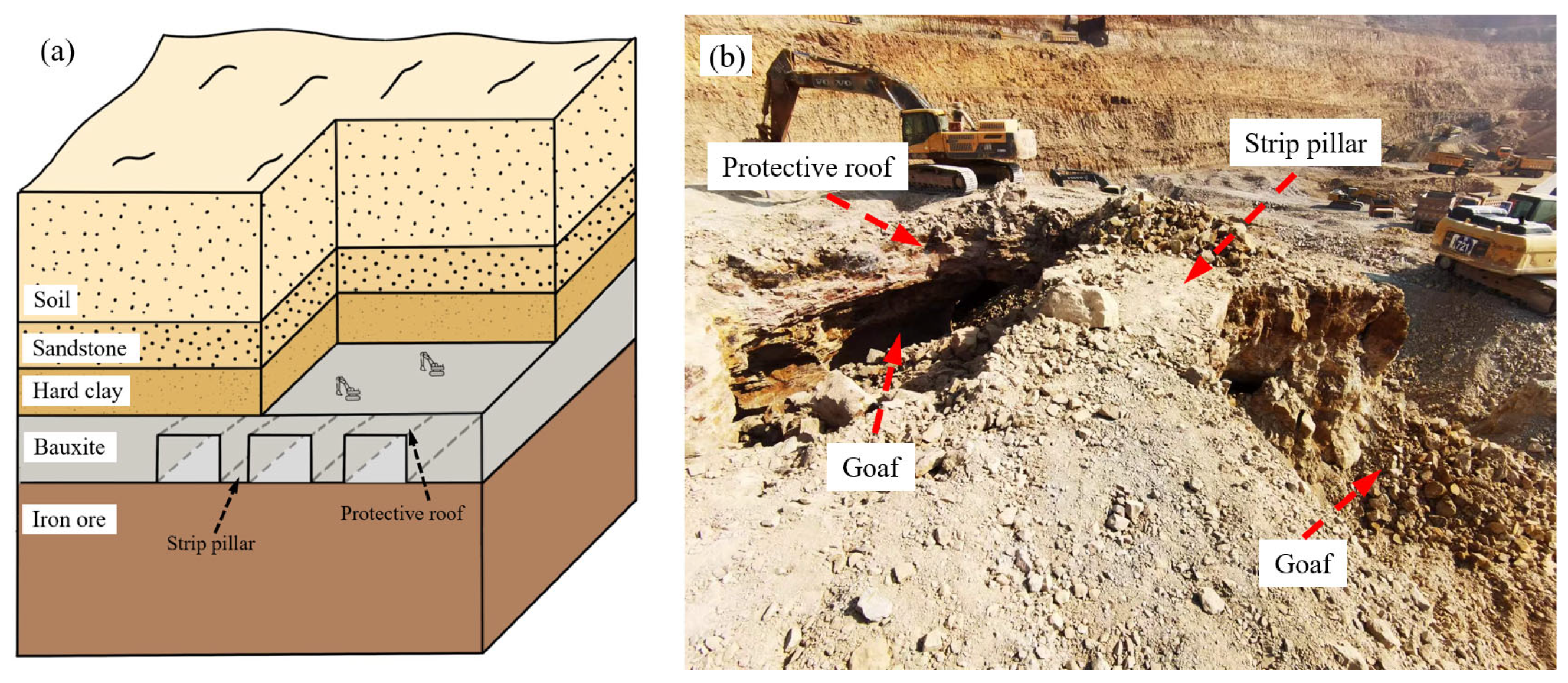
1. Introduction

The average thickness of Shanxi sedimentary bauxite is thin. The direct roof is mostly unstable clay rock and the contact boundary between the two is interleaved [1]. In order to ensure the safety of the mining goaf, the combination of a dotted pillar, strip pillar and bauxite protective roof with a certain thickness is usually adopted in the mine, which forms the goaf bearing structure to resist the gravity of the overlying surrounding rock and weakening of surrounding rock in goaf [1,2,3,4]. With the development of underground mining, there are a large number of mined-out areas, residual pillars and low-grade orebody affected by mining. With the increase of the exposure time of goaf, the bauxite layer and hard clay layer in the goaf bearing structure are prone to weathering and fragmentation and the rheological phenomenon occurs at the same time, resulting in a rapid decline in the compressive and tensile strength of the goaf bearing structure and a sharp decline in the bearing capacity. The instability of the goaf bearing structure may pose a threat to open-pit mining activities. Bauxite goaf usually uses wood support and waste rock filling to maintain the stability of the goaf and control the subsidence of the surface [5,6,7].

To sum up, there is a close correlation between the self-stability of bearing structures and time [2,8,9]. It is beneficial to the safety of mine production to study how to quantify the relationship between the stability of bearing structures and the stand-up time.

At present, relevant studies on goaf bearing structures at home and abroad such as [10,11,12,13,14,15,16] mainly describe the bearing structure characteristics by establishing a hard rock beam model, and carry out static analysis of the structure by using structural mechanics and elastic mechanics methods. The most common mechanical model of load-bearing structures is the rock-beam model. Qin (2005) [10] studied the evolutionary instability process of the bearing structure by establishing the “coal pillar-hard roof” bearing structure, analyzed the factors affecting the instability of the narrow pillar bearing structure and provided the mechanical criteria of the necessary and sufficient conditions of the bearing structure’s instability. Xu (2018) [11] constructed a “pillar-rock beam” bearing structure of gypsum mine, used the energy theory to establish a bearing structure mutation model, studied the relationship between the energy dissipation and release of the bearing structure and the deformation of the bearing structure and qualitatively analyzed the sensitivity ranking of factors affecting the stability of the bearing structure. Chen (2018) [12] built a mechanical model of the roof bearing structure at the boundary of the elastic foundation with long side caving and calculated the law of the influence of pillar width, supporting coefficient and basic roof thickness on the instability of the bearing structure by using the finite difference method. Zhao (2018) [13] established a mechanical model of the roof rock beam for the problem of roof fractures in shallow mining. The relationship between deflection and vertical displacement is determined by means of theoretical analysis and numerical simulation. The result shows, for the roof rock beam, when the vertical load keeps constant, the horizontal thrust fluctuating rises with increasing deflection. Wang (2021) [14] established a mechanical model of UMO rock beam-column structure, studied the instability mechanism and evolution process and determined the criteria for the instability of the bearing structure and the evolution path of energy during the process. Li (2023) [15] gave the bending stress–strain curves, and the cumulative ringing counts were obtained by a three-point bending test and acoustic emission (AE) monitoring of limestone beams which study the characteristics of tensile cracking by rock-bending damage. The numerical simulation based on the criterion of rock damaged fracture reflect the bending process of rock beams under three-point bending stress. Qin (2023) [16] established a stope spatial model considering the influence of horizontal stress. Through theoretical analysis and numerical simulation, the migration law of overlying strata in deep goaf was studied. On this basis, the technical system of “migration control” of surrounding rock in deep mining area was proposed and three support schemes were designed. The research results provide theoretical and technical support for the deformation control of mining roadways in the deep mining process.

In the same way, rheological properties are widely used in research at home and abroad [17,18,19,20,21,22,23] and has rich research achievements in the fields of polymer material manufacturing [17], architectural engineering [18], food science & technology [19], geoscience [20] and so on. Applications in the field of geoscience are mainly concentrated in slope stability research, paste filling, surface subsidence research, etc., [20,21,22,23]. There are some gaps in the study of goaf stability, especially the few studies that consider the goaf stability under the condition of weak ore bodies such as bauxite [24,25].

Based on the site investigation of a sedimentary bauxite mine in Shanxi Province, this paper uses elastic thin plates and rheological theory to build a physical model of the bearing structure of bauxite goaf, deduced the calculation formula of stand-up time, analyzed the influence of factors such as the thickness of the protective roof, the uniform surface force coefficient of the pillar, the span of the goaf and the thickness of the overlying rock layer. Engineering examples are used to verify the reliability of the theoretical calculation method.

In the existing studies, the relevant research objects did not involve soft rock mass such as bauxite and hard clay [26,27,28,29] and did not pay attention to the weakening characteristics of load-bearing structures under the action of weathering and rheology. This paper provides theoretical support for the safety production of bauxite and similar mines.

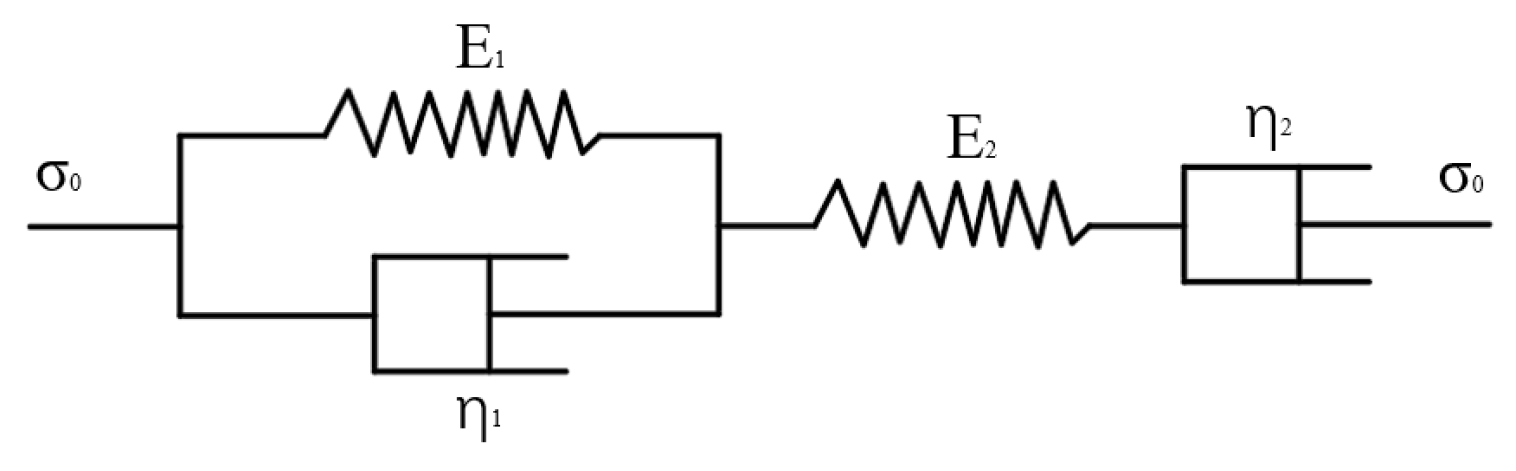
2. Rheological Model of Bearing Structure

Under the action of mining stress, the internal stress field of the goaf bearing structure will be redistributed and the goaf bearing structure will have local deformation, exposing the whole goaf to potential collapse and instability. The instability and collapse of the goaf in bauxite mining is attributed to two factors. First, the inadequate design of the stope span, protective roof, pillars and other structural parameters cannot withstand the impact of strong mining disturbances. Second, after the formation of goaf, the physical and mechanical properties of ore rock are deteriorated which reduces the ultimate bearing capacity of the goaf bearing structure. As a result, it cannot withstand prolonged action of overburden pressure from overlying rock layer.

2.1. Selection of Ore-Rock Failure Constitutive Relation

At present, there is mainly the Maxwell model, generalized Kelvin model, Bingham model, Burgers model and Nishihara model to describe the rheological properties of rock mass [30]. Burgers’ model can reflect the physical and mechanical properties of rock and soil mass such as instantaneous deformation, constant velocity creep and relaxation, and can better describe the after-effects of elastic deformation of rock and soil mass. After the formation of the bauxite goaf, under the action of gravity load of the overlying rock layer, the pillar’s own bearing capacity is weak which is manifested as the characteristics of soft rock. Longitudinal and transverse cracks constantly appear in the pillar which gradually increase over time and continue to expand and penetrate, eventually leading to the plastic deformation of the pillar [31]. Therefore, the deformation characteristics of bauxite pillar rock mass were described using Burgers’ body (Figure 1). In Figure 1, E₁ and E₂ represent elastic elements in the Burgers’ body, and η₁ and η₂ represent damping elements for energy loss.

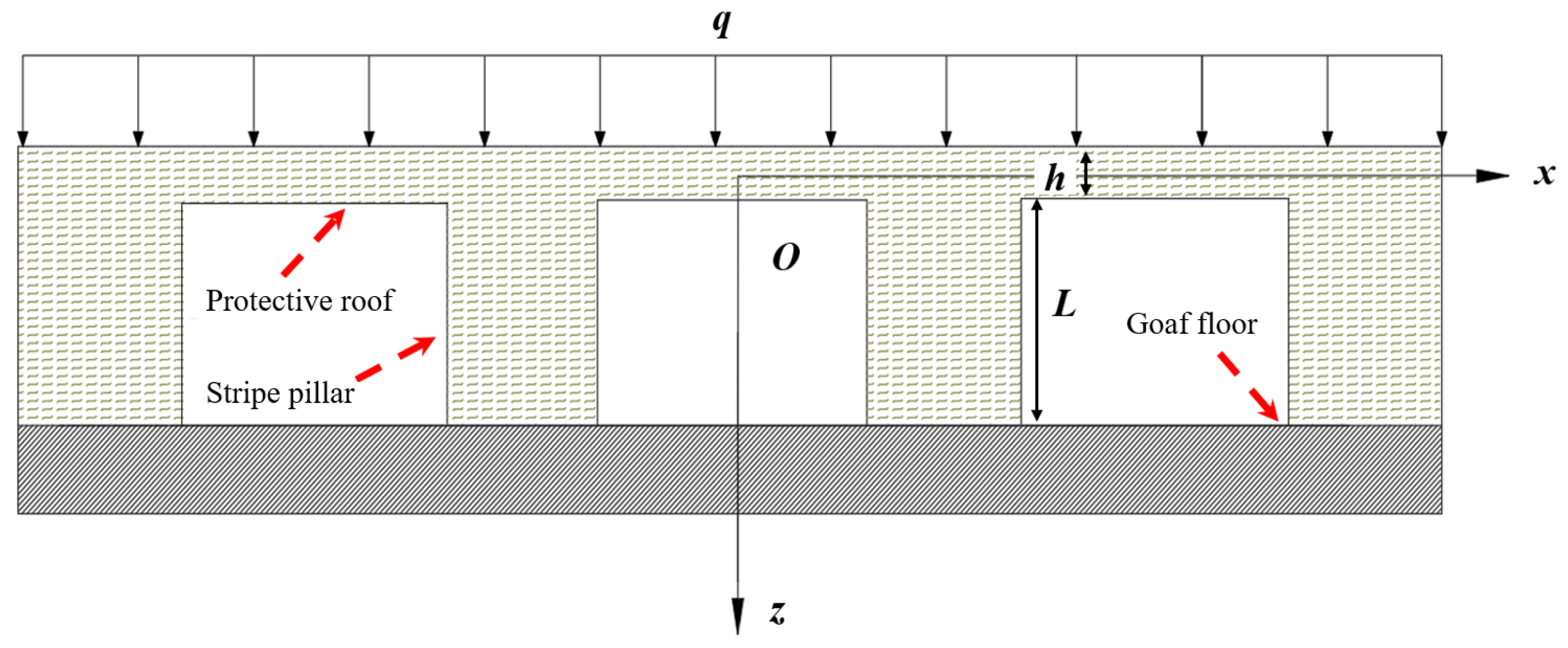
2.2. Mechanical Model and Solution of Protective Roof—Pillar Bearing Structure

Bauxite buried depth is relatively shallow, usually between 10 m to 100 m. Bauxite body usually has a few-meter-thick hard clay layer and 10- to 100-m-thick soil layer. The excavation section of the goaf is usually approximately rectangular or arched, and the thickness of the protective roof is usually 0.5–1.0 m. The hard clay layer above the bauxite is weak, easy to break and collapses under weathering, meaning that it does not have much bearing capacity and is difficult to be used as the direct roof of the bauxite goaf. The goaf bearing structure of Shanxi sedimentary bauxite is usually composed of a protective roof with a certain thickness and reserved pillars [32] (Figure 2).

In order to simplify the theoretical calculation of the bearing structure. There are three basic assumptions in the theoretical model of this paper:

(1)

The difference of occurrence of rock mass in bearing structures is not considered;

(2)

The pillar is regarded as a regular rectangular body and the top layer is regarded as a thin plate structure of equal thickness, without considering the occurrence of special shape pillar and the protective roof;

(3)

The gravity load of the overlying rock layer on the bearing structure is regarded as a uniform load and the influence of mechanical load and blasting load on the bearing structure is not considered.

Because of bauxite is stratified, stopes and pillars are equally spaced in a panel unit during mining (Figure 3). Set the number of pillars as R, height as L and average area as A. The thickness of the overlying rock layer is H and the gravity load q is uniformly applied to the protective roof of the goaf. The center point of the protective roof is the origin of the 3D coordinate system in which the direction of the long side of the protective roof is the x axis, the direction of the short side of the protective roof is the y axis and the vertical downward direction is the z axis. The protective roof is simplified into the elastic rectangular thin plate. The roof plate has a dimension of 2m × 2n × h, where 2m ≥ 2n, and is characterized by Young’s modulus, E, Poisson’s ratio, μ and tensile strength [σ_t]. The pillar rock mass is regarded as a Burgers body model.

Based on the elastic plate theory, the governing equation of the protective roof of goaf can be expressed by:

$$D{\nabla }^4\omega +\lambda \sigma =\mathrm{q}$$

(1)

where ω is the flexural deformation of the protective roof, D is its bending stiffness i.e., $D=Eh/[12(1-{\mu }^2)]$, ∇⁴ is the Laplace operator, λ is the equivalent uniform surface force coefficient of pillar i.e., $\lambda =\frac{RA}{2m\times 2n}$, where R is the number of pillars, A is the average section area of pillars in the goaf where 2m is the radial length of the protective roof, 2n is the transverse width of the protective roof, namely the span of the goaf, σ is the normal stress of the pillar and q is the gravity load of the overlying layer.

The deformation of the bearing structure includes the flexural deformation of the protective roof and the compression deformation of the pillar. Due to the co-deformation relationship between the roof and pillar, there exists a correlation between the strain and displacement of the pillar.

$$\epsilon =\frac{\omega }{L}$$

(2)

where ω is the compression deformation of pillar, as well as the flexural deformation of the protective roof, L is the height of the pillar.

The stress–strain relation of Burgers’ model is given as

$$\frac{1}{E_2}{\sigma }^{″}+(\frac{1}{{\eta }_1}+\frac{1}{{\eta }_2}+\frac{E_1}{E_2{\eta }_1}){\sigma }^{\prime }+\frac{E_1}{E_2{\eta }_1{\eta }_2}\sigma ={\epsilon }^{″}+\frac{E_1}{{\eta }_1}{\epsilon }^{\prime }$$

(3)

where η₁ and η₂ are the viscosity coefficients of Burgers. E₁ and E₂ are the elastic coefficients of Burgers body (Figure 1). ${\sigma }^{\prime }$ and ${\epsilon }^{\prime }$ are the first derivative of stress and strain with respect to time t, ${\sigma }^{″}$ and ${\epsilon }^{″}$ are the second derivative of stress and strain with respect to time t.

As a result of substituting the strain-displacement relation equation of pillar (2) and the stress–strain constitutive relation equation of pillar (3) into the governing Equation (1), the governing equation of the protective roof-pillar bearing structure can be obtained as

$$D{\nabla }^4[\frac{E_1}{E_2{\eta }_1{\eta }_2}\omega +(\frac{1}{{\eta }_1}+\frac{1}{{\eta }_2}+\frac{E_1}{E_2{\eta }_1}){\omega }^{\prime }+\frac{1}{E_2}{\omega }^{″}]+\frac{\lambda }{L}({\omega }^{″}+\frac{E_1}{{\eta }_1}{\omega }^{\prime })=\frac{E_1}{E_2{\eta }_1{\eta }_2}q$$

(4)

where ${\omega }^{\prime }$ and ${\omega }^{″}$ are the first and second derivative of the deformation function with respect to time.

Bearing structure deformation is closely related to time. The deformation function of the bearing structure can be expressed analytically in the following for:

$$\omega (x,y,t)={\omega }_0(t)f(x,y)$$

(5)

where ω₀(t) is the function of bearing structure deformation with respect to time t, and f (x, y) is the function of bearing structure deformation with respect to position distribution.

After full integration, Equation (4) is obtained as following form [33]:

$${\displaystyle \iint \begin{array}{l}[(D{\nabla }^4\frac{1}{E_2}f+\frac{\lambda f}{H}){{\omega }_0}^{″}+[D{\nabla }^4(\frac{1}{{\eta }_1}+\frac{1}{{\eta }_2}+\frac{E_1}{E_2{\eta }_1})f+\frac{\lambda f{E}_1}{{\eta }_{1}H}]{{\omega }_0}^{\prime }\\ +D{\nabla }^4\frac{E_1}{E_2{\eta }_1{\eta }_2}{\omega }_{0}f-\frac{E_{1}q}{E_2{\eta }_1{\eta }_2}]\end{array}}fdxdy=0$$

(6)

where ${\displaystyle \iint f^{2}dxdy={\beta }_1}$; ${\displaystyle \iint {\nabla }^{4}f\cdot fdxdy={\beta }_2}$; ${\displaystyle \iint fdxdy={\beta }_3}$. Equation (6) can be organized in the following form:

$${{\omega }_0}^{″}+j{{\omega }_0}^{\prime }+k{\omega }_0=l$$

(7)

j, k and l are general constants that can be obtained from the basic principles of nonhomogeneous linear equations, where $j=\frac{D{a}_2{\beta }_{2}L+\lambda a_4{\beta }_1}{D{a}_1{\beta }_{2}L+\lambda {\beta }_1}$, $k=\frac{D{a}_3{\beta }_{2}L}{D{a}_1{\beta }_{2}L+\lambda {\beta }_1}$ and $l=\frac{a_{3}Lq{\beta }_3}{D{a}_1{\beta }_{2}L+\lambda {\beta }_1}$.

Equation (7) is the differential equation of the relation between deformation and time of the bearing structure. By combining Equations (5) and (7), the deflection expression of any point on the sheath of the bearing structure can be obtained and then the stress state of any point can be obtained.

If the boundary conditions and initial conditions are given, the problem of Equation (7) can be transformed into a second-order linear nonhomogeneous differential equation problem. Then the analytical solution of the deflection of the protective roof is written as:

$${\omega }_0=C_1{e}^{r_{1}t}+C_2{e}^{r_{2}t}+\frac{l}{k}$$

(8)

where $r_{1,2}=\left(-j\pm \sqrt{j^2-4k}\right)/2$, C₁ and C₂ are integral constants, which are determined by initial conditions.

In order to solve the integral constant of the deflection expression (8), the initial conditions need to be determined. According to [34], when the bearing structure is in the initial stable state, the initial conditions for the deformation of the protective roof in the first stage include the deformation amount of the protective roof ω₀ and the sinking velocity of the protective roof v₀ can be expressed as follows:

$$\{\begin{array}{l}{{\omega }_0|}_{t=0}=\frac{441q}{129\left[2\lambda E_2+9D\frac{(7m^4+4m^2{n}^2+7n^4)}{m^4{n}^4}\right]}\\ {{{\omega }_0}^{\prime }|}_{t=0}=v_0={\sigma }_0(\frac{1}{{\eta }_1}+\frac{1}{{\eta }_2})\end{array}$$

(9)

where ${\sigma }_0={\omega }_0\lambda E_2$ [34], σ₀ is the initial stress of pillar.

By substituting the initial condition Formula (9) into the analytical Formula (8), the integral constants C₁ and C₂ of the deflection control formula of the first stage of the protective roof can be solved. The integral constant of the deflection distribution function of different stages is different. The critical point of each stage can be obtained by the ultimate strength condition of the protective roof and the boundary condition of each stage respectively. The initial deformation conditions of the second stage, the deformation of the protective roof ω₁ and the sinking velocity of the protective roof v₁ are obtained from the state at the end of the first stage. By the same token, ω₂ and v₂ of the initial deformation conditions of the third stage sheath can be obtained.

The failure of bauxite protective roofs is usually tensile failure [18], so the ultimate tensile strength of bauxite rock is selected as the failure criterion in this paper.

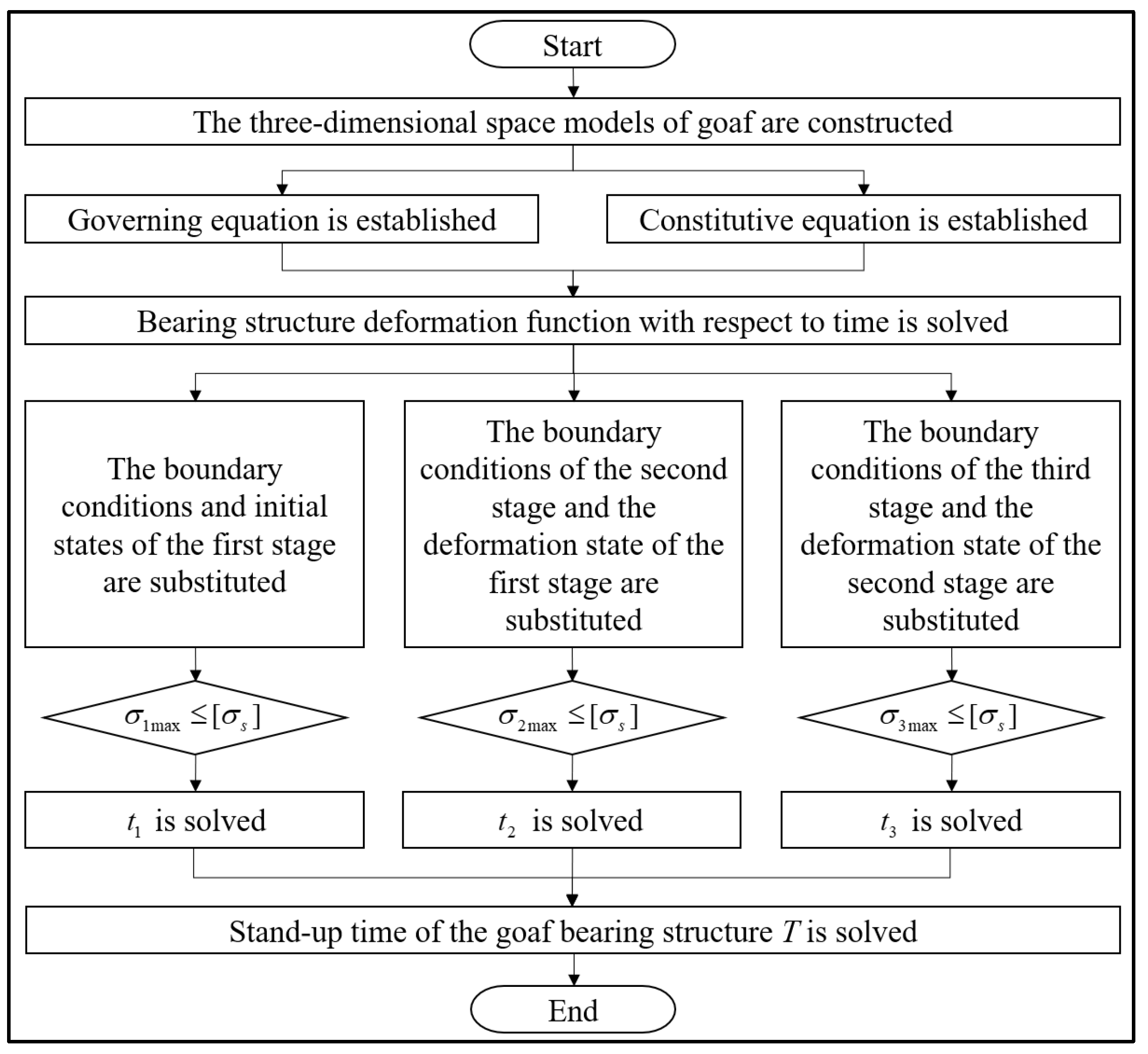
3. Computation of Stand-Up Time of Bearing Structure

The failure of goaf bearing structure is usually a gradual process, which is closely related to time. The failure forms of the bearing structure (pillar, protective roof) in the goaf of bauxite are usually local deformation, collapse, etc.

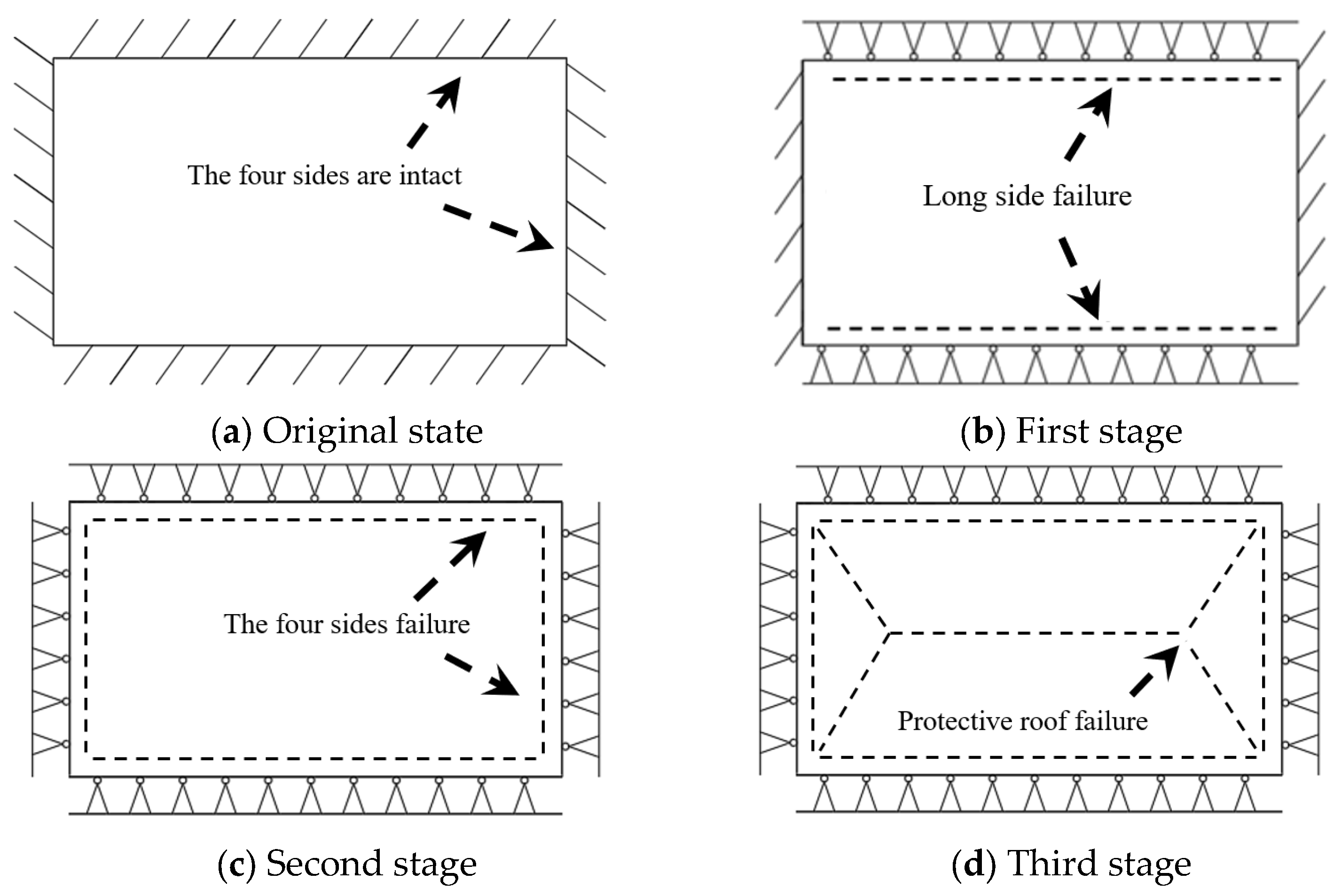
3.1. Pillar Failure Process

After the goaf is formed, under the action of gravity, mining stress and weathering, longitudinal and transverse cracks will continuously appear in the rock mass of bauxite pillars. With the gradual increase of time, cracks will develop continuously, resulting in local deformation, fragmentation, spalling and other phenomena. The supporting force decreases continuously, the hanging area of the protective roof expands and the goaf collapse is induced.

3.2. Protective Roof Failure Process

Failure of the protective roof of protection roughly experienced three stages, namely, the first, the second and the third, corresponding to three states, namely, longside failure, quadrangle failure and overall collapse failure (Figure 4).

In order to study the boundary conditions and failure states of the protective roof in different failure stages in detail, the plane coordinate system of the protective roof is given based on the 3D coordinate system described in Section 2.2. This section states that where the center point O of the protective roof is taken as the origin, the direction of the long side of the protective roof is the x axis and the direction of the short side is the y axis (Figure 5).

3.2.1. Original State

At the end of the stope construction, the goaf will form a structure of complete protective roof and the overall state of the protective roof rock mass is intact. It can be regarded as a thin plate model with four sides fixed. The boundary deflection angle of the protective roof is zero, and the boundary conditions of the protective roof can be expressed as:

$$\{\begin{array}{l}\omega |{}_{x=\pm m}=0,\omega |{}_{y=\pm n}=0\\ \frac{\partial \omega }{\partial x}|{}_{x=\pm m}=0,\frac{\partial \omega }{\partial y}|{}_{y=\pm n}=0\end{array}$$

(10)

3.2.2. First Stage

Under the action of gravity and other external forces, the protective roof of goaf begins to display signs of gradual failure and the boundary condition is same as the initial state Equation (10). At this time, the deflection distribution function of the protective roof can be approximately expressed as:

$$f(x,y)=\frac{{(x^2-m^2)}^2{(y^2-n^2)}^2}{m^4{n}^4}$$

(11)

According to the Equation (11) of the deflection function of the protective roof, the maximum bending moment value |M_x|_max will appear at the middle point of the long edge boundary of the protective roof in the first stage and the maximum stress value σ_xmax will appear here. The maximum stress value σ_xmax can be given as follows:

$${\sigma }_{\mathrm{x}\max }=\frac{6{\left|M_x\right|}_{\max }}{h^2}=\frac{48D{\omega }_0(t_1)}{n^2{h}^2}\le \left[{\sigma }_t\right]$$

(12)

where [σ_t] is the ultimate tensile strength of bauxite.

In combination with Equations (8) and (12), the stand-up time t₁ of the bearing structure in the first stage is:

$$t_1={\omega }^{-1}(\frac{\left[{\sigma }_s\right]n^2{h}^2}{48D})$$

(13)

where ω⁻¹ is the inverse function of ω.

According to the calculation Formula (13), the stand-up time of the bearing structure at the first stage is mainly affected by the span of the goaf, the thickness of the protective roof, the ultimate tensile strength of bauxite and the main control parameters of ω⁻¹. Further classification analysis shows that the stand-up time of the bearing structure is mainly affected by (1) structural parameters such as the thickness of the protective roof, pillar uniform surface force coefficient, goaf span, etc. and (2) the influence of the thickness of overlying rock layer and the ultimate tensile strength of bauxite rock.

3.2.3. Second Stage

Under the action of gravity and external force, the long edge boundary of the protective roof will be destroyed first. At this time, the constraint condition of the long edge of the protective roof will change from fixed support to hinged support, and the short edge will be a fixed support boundary. The boundary condition of the protective roof in this stage is expressed as:

$$\{\begin{array}{l}\omega |{}_{x=\pm m}=0,\omega |{}_{y=\pm n}=0\\ \frac{{\partial }^2\omega }{\partial x^2}|{}_{x=\pm m}=0,\frac{\partial \omega }{\partial y}|{}_{y=\pm n}=0\end{array}$$

(14)

At this stage, the deflection distribution function of the protective roof can be approximately expressed as:

$$f(x,y)=\cos \frac{\pi x}{2m}\frac{{(y^2-n^2)}^2}{n^4}$$

(15)

After the damage of the long edge boundary of the protective roof, the internal stress will gradually transfer. According to Equation (15) of the deflection function of the protective roof, the maximum bending moment value |M_x|_max appears at the location of $(\pm m,0)$. At the same time, the maximum stress value σ_xmax will appear here:

$$\{\begin{array}{l}{\sigma }_{x\max }=\frac{6{\left|M_x\right|}_{\max }}{h^2}=24D{\omega }_1(t_2)\left(\frac{1}{m^2{h}^2}+\frac{{\pi }^2\mu }{n^2{h}^2}\right)\le \left[{\sigma }_t\right]\\ {\sigma }_{y\max }=\frac{6{\left|M_y\right|}_{\max }}{h^2}=24D{\omega }_1(t_2)\left(\frac{\mu }{m^2{h}^2}+\frac{{\pi }^2}{16n^2{h}^2}\right)\le \left[{\sigma }_t\right]\end{array}$$

(16)

where μ is Poisson’s ratio of bauxite protective roof rock mass.

In combination with Equations (8) and (16), the stand-up time t₂ of the bearing structure in the second stage is given as follows:

$$t_2={\omega }^{-1}(\frac{\left[{\sigma }_s\right]2m^2{n}^2{h}^2}{3D(16\mu n^2+{\pi }^2{m}^2)})$$

(17)

Similarly, according to the calculation Formula (17) of the stand-up time of the second stage, the stand-up time of the bearing structure in the second stage is mainly affected by the span of the goaf, the radial length of the protective roof, the thickness of the protective roof, the Poisson’s ratio of the protective roof, the ultimate tensile strength of the bauxite rock and the main control parameters of the ω⁻¹.

3.2.4. Third Stage

At this time, both the long side and the short side of the protective roof have been damaged, and the constraint condition of the contact surface between the protective roof and the surrounding rock has been changed into four hinged sides. The overall damage of the protective roof will further occur and its boundary condition can be expressed as:

$$\{\begin{array}{l}\omega |{}_{x=\pm m}=0,\omega |{}_{y=\pm n}=0\\ \frac{{\partial }^2\omega }{\partial x^2}|{}_{x=\pm m}=0,\frac{{\partial }^2\omega }{\partial y^2}|{}_{y=\pm n}=0\end{array}$$

(18)

At this stage, the deflection distribution function of the protective roof can be approximately expressed as:

$$f(x,y)=\cos \frac{\pi x}{2m}\cos \frac{\pi y}{2n}$$

(19)

At this time, the boundary conditions of the four sides of the fixed support are all broken, the stress is further transferred to the center of the protective roof and the failure of the protective roof continues to extend which is manifested as the rock collapse of the protective roof. Finally, the stress state of the protective roof reaches the limit state.

The bending moment of any section of the protective roof can be obtained by differentiating the Equation (19) of the deflection distribution function of the protective roof, and the maximum stress value σ_max on the protective roof can be calculated after taking the extreme value. Then, the maximum stress σ_max on the protective roof can be expressed as

$$\{\begin{array}{l}{\sigma }_{x\max }=\frac{6{\left|M_x\right|}_{\max }}{h^2}=\frac{3{\pi }^{2}D}{2h^2}(\frac{1}{m^2}+\frac{\mu }{n^2}){\omega }_2(t_3)\le \left[{\sigma }_{\mathrm{t}}\right]\\ {\sigma }_{y\max }=\frac{6{\left|M_y\right|}_{\max }}{h^2}=\frac{3{\pi }^{2}D}{2h^2}(\frac{\mu }{m^2}+\frac{1}{n^2}){\omega }_2(t_3)\le \left[{\sigma }_t\right]\end{array}$$

(20)

In combination with (8) and (20), the stand-up time t₃ of the bearing structure in the third stage is:

$$t_3={\omega }^{-1}(\frac{\left[{\sigma }_s\right]2m^2{n}^2{h}^2}{3{\pi }^{2}D(\mu n^2+m^2)})$$

(21)

Similarly, according to the Formula (24) for calculating the stand-up time of the third stage, it can be seen that the influencing factors of the stand-up time of the bearing structure are the same as t₁ and t₂ (Figure 6).

In conclusion, when the bearing structure in the third stage reaches its limit state, a large area of fracture will occur on the protective roof, resulting in multiple lumpiness bodies, overall dismemberment and destruction. Large area collapse may be formed at any time. At this time, it can be considered that the bearing structure has lost its bearing capacity and the goaf will be in a dangerous state.

Based on the above Equations (13), (17) and (21), the stand-up time T of bearing structure can be expressed as:

$$T=t_1+t_2+t_3$$

(22)

For the goaf bearing structure of a specific bauxite mine, the composition of the overlying rock layer is determined by the physical properties of each layer of rock and soil. Therefore, when analyzing the stand-up time factors of the goaf bearing structure, the influencing factors such as the thickness of the protective roof, the coefficient of pillar uniform surface force, the span of the goaf and the thickness of the overlying rock layer are mainly selected for analysis.

4. Influencing Factors of Bearing Structure Stand-Up Time

4.1. Engineering Characteristics

The underground mine of a bauxite mine in Shanxi Province is located in the western margin of Lvliang Mountain system and Loess Plateau, and the bauxite body occurs on the erosion surface of Ordovician system and under the Benxi Formation of the middle Carboniferous system. The deposit is stratified as a whole, with an average thickness of less than 5.0 m and a general strike of about 33° northeast. The inclination is NW, 5.0–12.0°, with an average of less than 10.0°. Bauxite is usually mined by shallow blasting. The overlying rock layer consists of loess, metamorphic sandstone, bauxite and Shanxi type iron ore from top to bottom. The physical and mechanical parameters are shown in

Table 1. Physical and mechanical parameters.

Lithology	Test Weight γ/KN·m−3	Young’s Modulus E/GPa	Poisson’s Ratio μ	Cohesion c/kPa	Internal Friction Angle φ/(°)	Tensile Strength [σt]/MPa	Thickness H/m
Surface soil	24.6	3.25	0.25	0.56	35.6	0.002	20–60
Metasandstone	25.1	8.02	0.27	4.23	38.9	1.51	5–20
Clay rock	22.5	3.50	0.24	1.29	31.7	1.42	5–20
Sedimentary bauxite	25.7	4.50	0.27	12.72	44.2	2.27	2–10
Iron ore deposit	30.2	10.91	0.29	13.19	41.8	3.84	5–20

.

According to mine data and field investigation, the structural parameters and other parameters of different goaf are sorted out for each calculation example. The specific structural parameters are shown in

Table 2. Structural parameters of goaf.

Case	Thickness of Protective Roof h/m	Equivalent Uniform Surface Force Coefficient of Pillar λ	Goaf Span 2n/m	Length of Protective Roof 2m/m	Thickness of Overlying Soil Layer H/m	Pillar Height L/m
Case 1 (Region 1)	0.5	0.45	20.0	50.0	50.0	3.0
Case 2 (Region 2)	0.5	0.45	35.0	75.0	50.0	3.0

. The rheological parameters [35,36,37] are shown in

Table 3. Rheological parameter of rock mass.

	E1/MPa	E2/MPa	η1/(MPa·h)	η2/(MPa·h)
Pillar	3.69 × 103	2.25 × 103	1.499 × 104	4.686 × 105

. The goaf parameters in Example 1 are taken as an example to calculate and analyze the relationship between the stand-up time of the bearing structure and the influencing factors such as the thickness of the protective roof, the uniform surface force coefficient of pillar, the span of the goaf and the thickness of the overlying rock and soil layer.

According to mine production statistics, cycle operation time of the disk area [T] is about six months, so [T] = 180 is selected in this paper. Here, the stand-up time T of the bearing structure is selected as the index.

To consider the bearing capacity of the goaf, when T is greater than [T], the bearing capacity of the bearing structure can meet the requirements of safe production. On the contrary, when T is less than [T], it cannot be satisfied. The goaf would be damaged during the production window-time.

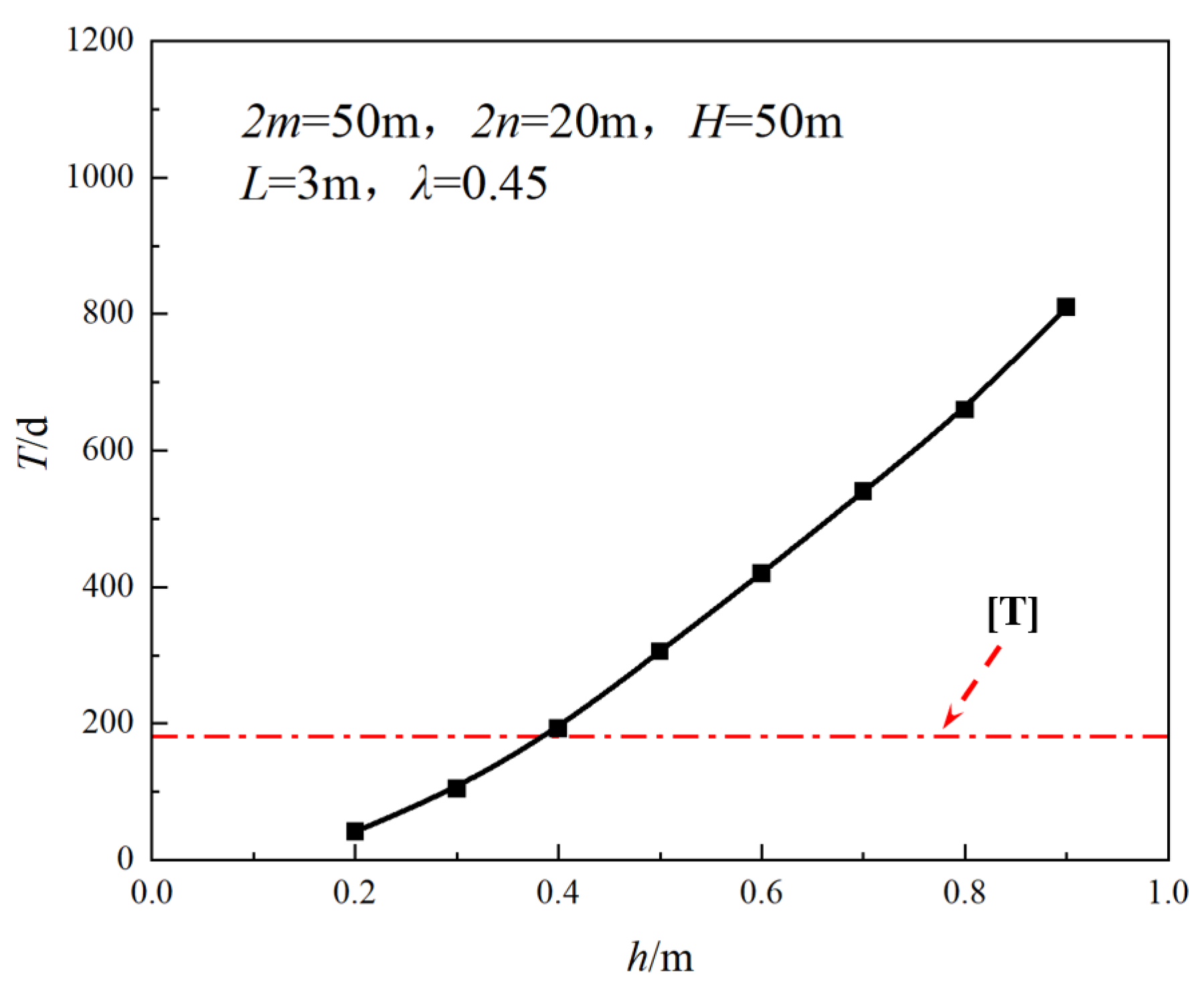
4.2. Thickness of Protective Roof

When the other three parameters (the equivalent uniform surface force coefficient of pillar, the thickness of the overlying soil layer and the span of the goaf) are unchanged, the thickness of the protective roof (h) is calculated from 0.1 m to 0.9 m for analysis. After trial calculation, the relationship between h and the stand-up time T is directly shown here in the range between 0.1 m and 0.9 m for the thickness of the protective roof (Figure 7).

As can be seen from Figure 7, T is positively correlated with the thickness of the protective roof (h). As h increases, it increases, and the growth rate increases gradually.

As a tensile structure in the bearing structure, the greater the thickness of the protective roof, the greater the stiffness of the protective roof as a plate structure, and the greater the tensile strength is. When the thickness of the protective roof is more than 0.4 m, the stand-up time of the bearing structure can meet the needs of safe production. When h is in the range of 0.3–0.4 m, the bearing structure will reach the limit state.

It is worth noting that when the thickness of the protective roof is less than 0.3 m, the change of the data is non-linear, which may be caused by the limitations of the theoretical calculation method. For example, when the thickness of the protective roof is 0.2 m, the stand-up time of the bearing structure is very short. In the actual situation of the mining, the thickness of the protective roof is too thin, which makes it difficult to support the load of the overlying rock and soil layer and goaf collapse will occur directly. However, it is difficult to obtain the result that the stand-up time is zero in theoretical calculation.

4.3. Equivalent Uniform Surface Force Coefficient of Pillar

When the other three parameters (the thickness of the protective roof, the thickness of the overlying soil layer and the span of the goaf) are unchanged, the equivalent uniform surface force coefficient of pillar (λ) is calculated from 0.1 to 0.9 for analysis. After trial calculation, the relationship between λ and the stand-up time T is directly given in the range between 0.1 and 0.9 for the equivalent uniform surface force coefficient of pillar (Figure 8).

As can be seen from Figure 8, T is positively correlated with the equivalent uniform surface force coefficient of pillar (λ) and increases with the increase of λ. The increment is gradually accelerated. The equivalent uniform surface force coefficient of the pillar means the relative ratio of the pillar support area to the total area of the bearing structure. While it comes bigger, the value of λ is closer to 1. With the increase of λ, the stand-up time of the bearing structure increases rapidly which means that the supporting capacity of the bearing structure is greatly enhanced. When the value of λ approaches 1, the stand-up time of the bearing structure approaches infinity and the ore and rock show an approximate stress state of the original rock before excavation.

However, it has no practical significance for mine engineering due to the fact that the value of λ is greater than 0.6, which means that the mine recovery rate may be very low and usually the mine benefit has reached unacceptable status. When the value of λ is less than 0.6, the relationship between stand-up time and λ is approximately linear. When λ ranges from 0.3 to 0.4, the bearing structure reaches its limit state. Therefore, for this mine, when other conditions remain unchanged, the range from 0.4 to 0.6 of λ is recommended.

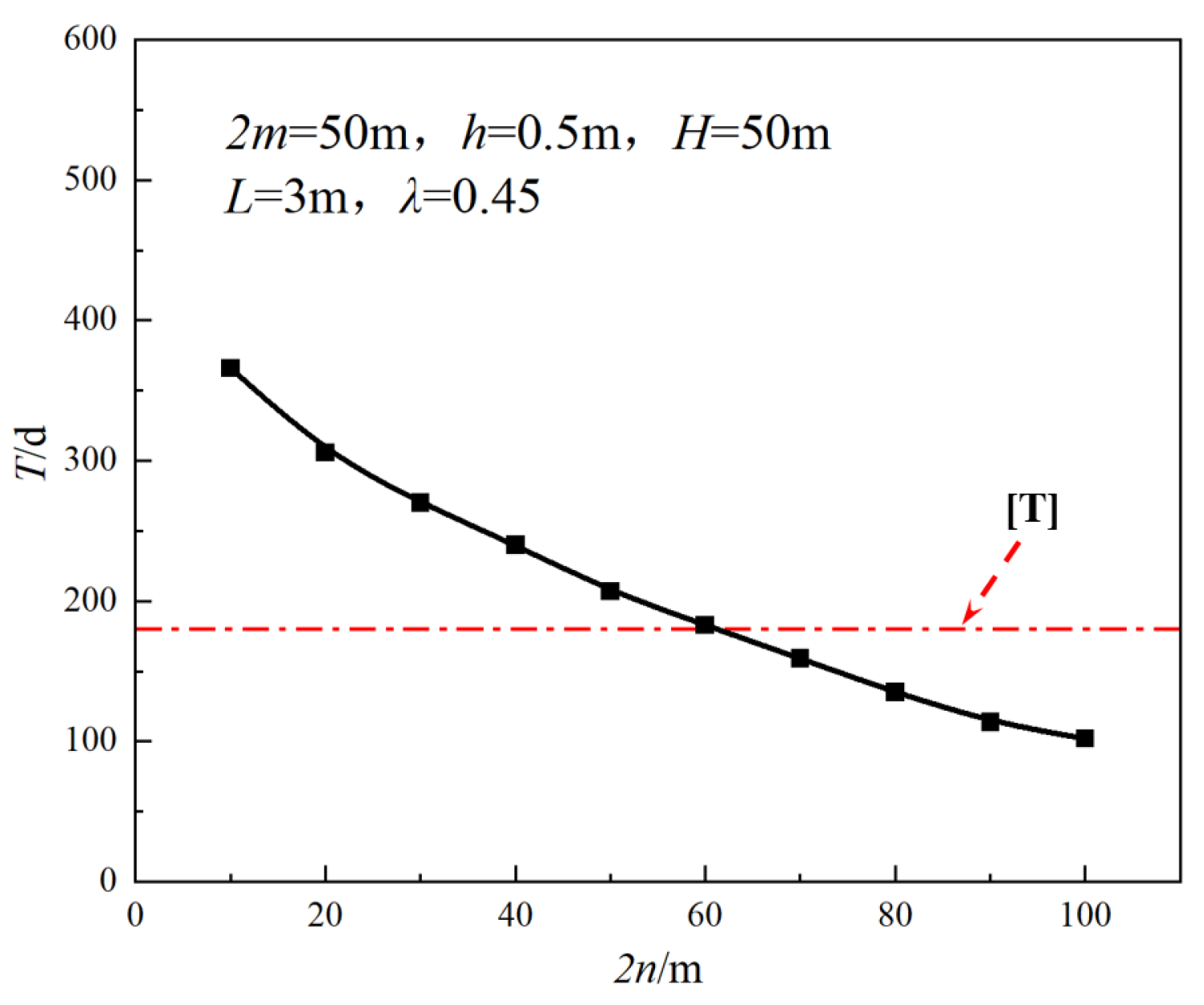
4.4. Goaf Span

When the other three parameters (the thickness of the protective roof, the thickness of the overlying soil layer and the equivalent uniform surface force coefficient of pillar) are unchanged, the span of the goaf (2n) is calculated from 10.0 to 100.0 m for analysis. Through trial calculation, the relation between 2n and stand-up time T is directly given in the range between 10.0 and 100.0 m for span of goaf (Figure 9).

As can be seen from Figure 9, T is negatively correlated with goaf span (2n), decreasing with the increase of 2n and the deceleration slows down gradually. With the goaf span increasing from 10.0 m to 100.0 m, the stand-up time of the bearing structure decreases from 380 days to 100 days. When the goaf span reaches 60.0 m, the bearing structure reaches the limit state.

It should be pointed out that when the land is unchanged, increasing the span of the goaf is equivalent to increasing the total area of the bearing structure and increasing the number of goafs in the bearing structure. Under the condition of a goaf span that is too small, the supporting capacity of the bearing structure is strong, which can meet the needs of safe production. After a period of time, the collapse will still occur due to the influence of rock rheological behavior. When other conditions remain unchanged and the span of the goaf reaches more than 60 m, the stand-up time of the bearing structure cannot meet the needs of safe production.

With the increase of the span of the goaf, the stand-up time decreases rapidly, mainly because with the increase of the number of goafs, the mutual stress arch effect [38] between adjacent goafs become more and more obvious and the phenomenon of stress concentration is prone to occur, leading to the collapse of the goaf.

4.5. Thickness of the Overlying Soil Layer

When the other three parameters (the thickness of the protective roof, the equivalent uniform surface force coefficient of pillar and the span of the goaf) are unchanged, the thickness of the overlying soil layer (H) is calculated from 10.0 m to 100.0 m for analysis. Through trial calculation, the relation between H and stand-up time T is directly given here when the thickness of the overlying soil layer ranges from 10.0 m to 100.0 m (Figure 10).

As can be seen from Figure 10, T is negatively correlated with the thickness of the overlying soil layer (H), which decreases with the increase of H and the decreasing speed slows down gradually.

The influence of the thickness of the overlying rock layer on the stand-up time of the bearing structure is mainly studied because the surface of the mining area is loess gully landform, and the thickness of overlying rock layers in different goaf areas in the same bauxite mining may be different, resulting in the formation of differently-sized gravity loads of overlying rock layer, which affects the stand-up time of the bearing structure.

It can be seen that when the thickness of the overlying rock layer is too small, the stand-up time is very large, which is because the load of the overlying rock layer is very small at this time, and the rock mass is affected by weathering and can still bear the load of the overlying rock layer after the reduction of the physical and mechanical parameters of the rock mass. When H is 10.0–40.0 m, the stand-up time of the bearing structure decreases rapidly. When H is 40.0–100.0 m, the change rate of stand-up time gradually slows down, showing an approximate linear relationship with the thickness of the overlying soil layer. When other conditions remain unchanged and H reaches more than 80 m, the bearing structure reaches the limit state and the structural parameters of the goaf can hardly meet the needs of safe production. It is easy to find that the overall change trend of the curve corresponds to the creep characteristics of the rock mass, the change rate of the rock mass stress with time is first fast and then slow and the yield failure point is reached after a certain time.

5. Engineering Verification

In order to verify the above theoretical calculation results, the goaf under a bauxite mine in Section 4.1 is taken as an example, and two typical bearing structures—region 1 and region 2—are selected for analysis according to the site investigation (Figure 11).

5.1. Case 1 (Region 1)

According to the field investigation results, in region 1, the direct roof of the goaf is the reserved bauxite protective roof. The physical and mechanical parameters of the bauxite rock and the thickness of the overlying rock layer are shown in Table 1, and the structural parameters of the goaf are shown in Table 2.

According to the initial condition Formula (9), through calculation, the flexural deformation control formula of the protective roof in the first stage can be obtained by:

$${\omega }_0=-2.1334e^{-1.994\times {10}^{-5}t}-5.957\times {10}^{-4}{e}^{-0.2466t}+2.1353$$

(23)

According to Formula (13), the stand-up time of the bearing structure in the first stage t₁ is 122d. In this stage, the bearing capacity of the structure and the integrity and the rock mass are complete.

Similarly, the flexural deformation control formula of the protective roof in the second stage can be obtained by:

$${\omega }_1=-4.127e^{-1.424\times {10}^{-4}t}-3.781\times {10}^{-7}{e}^{-0.2465t}+4.219$$

(24)

According to Formula (17), the stand-up time of the bearing structure in the second stage t₂ is 12d. At this stage, the boundary conditions of the bearing structure changed, the lateral extrusion occurred in the radial direction of the protective roof, the rock mass collapsed in a small area and the carrying capacity of the goaf decreased, but the bearing structure was stable as a whole.

In the same way, the flexural deformation control formula of the protective roof in the third stage can be obtained by:

$${\omega }_2=-10.317e^{-2.074\times {10}^{-7}t}-1.495\times {10}^{-7}{e}^{-0.2462t}+10.666$$

(25)

According to Formula (21), the stand-up time of the bearing structure at the second stage t₃ is 204d. The bearing capacity of the protective roof of the bearing structure is further weakened and the stress is concentrated to the center of the protective roof of the bearing structure, which is manifested as the collapse of the protective roof rock mass and the large-scale collapse may occur at any time. It is considered that the bearing structure has been damaged but still capable. Therefore, the stand-up time of the goaf in region 1 is 388 days, or about 13 months, which reaches the needs of mine production (Figure 12).

Engineering verification shows that the formation time of the goaf is about 7 months in region 1. There is a small area of rock mass extrusion and collapse phenomenon in this region, and the bearing structure is stable as a whole, which is roughly consistent with the theoretical calculation results.

5.2. Case 2 (Region 2)

According to the field investigation results, in region 2, the direct roof of the goaf is the reserved protective roof. The physical and mechanical parameters of the bauxite rock and the thickness of the overlying rock layer are shown in Table 1, and the structural and mechanical parameters of the goaf are shown in Table 2.

Similarly, according to the calculation Formulas (13), (17) and (21), the stand-up time of each stage is obtained, and the stand-up time of the goaf is 264 days in region 2, about 9 months, which reaches the needs of mine production. Field investigation shows that the formation time of the goaf is about 14 months in region 2. The bearing structure of this region loses its bearing capacity and goaf collapse accidents occur several times (Figure 13). It is roughly consistent with the theoretical calculation results, which verifies the rationality of the theoretical calculation results.

6. Discussion

Many complex factors affect the self-stability of goaf bearing structures. For the goaf of bauxite, it is affected by the form of goaf, rock mass composition and mining disturbance, as well as the combined action of gravity, weathering and rock mass rheological weakening. The weight of each factor is still to be clarified. There may be some deviation between the failure model and the real state. In order to serve mine production, this paper has made the corresponding simplified treatment as follows. There may be some limitations and deficiencies.

(1)

There may be other factors in the paper that have an impact on the stand-up time, for example, (a) when analyzing the influence of one factor on the stand-up time of bauxite bearing structure, it is assumed that other factors are established and the effect of only one factor is considered instead of multi-factor coupling effect which may be different from the actual project. (b) The research object of this paper is the underground bauxite mine in the Loess Plateau landform. The rock layer is dry, surface water and cracks are not developed and the effect of groundwater is not considered. In the karst water development area in the south, the influence of groundwater should be considered. The influence of groundwater on the stability of the gob should be considered in the gob developed by underground water. The theoretical results in this paper may not be applicable.

(2)

The theoretical model and basic assumptions in this paper are simplified. For example, (a) the difference in occurrence of rock mass in bearing structure is not considered. (b) In the theoretical calculation in this paper, the protective roof-pillar bearing structure is regarded as a regular rectangular body, but the shape of pillar, protective roof and goaf in actual engineering is irregular. (c) The gravity load of the overlying rock layer on the bearing structure is regarded as a uniform load, and the influence of mechanical load and blasting load on the bearing structure is not considered. These assumptions may differ from the actual engineering situation, and our future research will be more suitable for the actual engineering situation.

(3)

In this paper, Galerkin algorithm and nonhomogeneous linear equations are used for theoretical calculations. Galerkin method is a common method for approximate calculation of elastic plate structures, especially when there is no analytical solution as it is difficult to modify and solve. The use of Galerkin’s method can usually transform the problem into a function weighted integral involving the calculation of the physical domain of the problem from the equilibrium equation or the equation of motion, but there may be a large error between the theoretical results and the actual results, and the accuracy of the theoretical results may need to be further improved.

7. Conclusions

This paper uses elastic thin plates and rheological theory to build the physical model of the bauxite protective roof-pillar bearing structure and gives the calculation formula of the stand-up time of the bearing structure. The following conclusions can be obtained from this study:

(1)

Taking the protective roof-pillar bearing structure in the goaf of bauxite mine as the research object, based on the elastic sheet theory and rheological theory and considering the interaction of roof or pillar, a physical model of the protective roof-pillar bearing structure is constructed to solve the problem. The stand-up time T is used as the index to consider the bearing capacity of the goaf bearing structure and the calculation method of the stand-up time of the bearing structure is given.

(2)

The stand-up time (T) of the bearing structure in the goaf of bauxite is mainly affected by the thickness of the protective roof (h), the uniform surface force coefficient (λ) of pillar, the span of the goaf (2n) and the thickness of the overlying rock layer (H).

(a)

When other factors remain unchanged, T is positively correlated with h, which increases with the increase of h. When h is within the range of 0.3–0.4 m, the bearing capacity of the bearing structure reaches the limit state.

(b)

When other factors remain unchanged, T is positively correlated with λ which increases with the increase of λ and the increasing speed is gradually accelerated. When λ is in the range of 0.3–0.4, the bearing capacity of the bearing structure reaches the limit state.

(c)

When other factors remain unchanged, T is negatively correlated with 2n which decreases with the increase of 2n and the decreasing speed slows down gradually. When 2n is greater than 60.0 m, the bearing capacity of the bearing structure reaches the limit state.

(d)

When other factors remain unchanged, T is negatively correlated with H and decreases with H increasing and the decreasing speed slows down gradually. When H comes 90.0 m, the bearing capacity of the structure reaches the limit state.

(3)

The engineering application shows that the goaf bearing structure in case 1 is within stand-up time range and the goaf is basically stable. In case 2, the goaf bearing structure loses its bearing capacity and the goaf has become unstable and collapsed. The results of theoretical calculation are basically consistent with those of engineering examples, which verifies the scientific nature of the calculation results of load-bearing mechanics model.

(4)

Taking the bauxite mine in Shanxi Province studied in this paper as an example, a proposed range of goaf structural parameters is given in consideration of economic benefits and production safety. Under the condition that the thickness of the overlaying rock and soil layer is 50 m, the thickness of the protective roof is 0.5 m, the uniform surface force coefficient of pillars is 0.5 and the goaf span is 30 m. Such a scheme is relatively safe and reliable.