An Assessment of Stability and Strength of a Container Ship for Safety Compliance in Cargo Loading Plans
Abstract
:1. Introduction
- ⚜
- The criterion for areas under the righting arm curve. The area found under the righting arm curve shall not be less than 0.055 m⋅rad, calculated from 0° to 30° of the heel, not less than 0.090 m⋅rad, calculated from 0° to 40° of the heel or up to the angle of flooding (the angle of flooding, in this case, being the angle of heel at which the inner spaces of the ship are flooded with seawater through openings) if the angle of flooding is less than 40°, and not less than 0.030 m⋅rad, calculated for 30° to 40° of the heel, or from 30° to the angle of flooding if the angle of flooding is less than 40° [17].
- ⚜
- Righting arm curve, where the righting arm is at least 0.2 m at an angle of heel equal to or greater than 30°. The maximum righting arm must occur at an angle of the heel of not less than 25°. The righting arm of the vessel in the upright position must increase sufficiently rapidly (the vessel must be sufficiently ‘tough’—it must ‘hold’ sufficiently firmly its equilibrium position). The greatest value of the righting arm (the greatest ability of the ship to return to the equilibrium position) will not occur if the heel angle is too small [17,20].
- ⚜
- The criterion of initial metacentric height—metacentric height is a measure of the ship’s initial stability at small angles of the heel. When its value is high, the ship is considered stiff and will come rapidly to the equilibrium. If the value is low, the rolling will be gentler, but in the event of failure, the ship may lose stability and capsize [21].
- ⚜
- The weather criterion, taking into account the effect of wind and ship motions. According to the weather criterion, the ship’s stability is considered to be sufficient when the conventional wind, under conventional conditions, including wave rolling, does not cause exceeding of the heeling angle of 50° immersion of openings considered to be open, and ship capsizing. These requirements are deemed to be met when the ship’s heeling angle does not exceed 50°, the angle of flooding, or the angle of capsizing. Detailed requirements for this criterion are contained in the Rules for the Classification and Construction of Sea-going Ships, Part IV, Chapter 2 “Stability—Basic Requirements and Criteria” (point 2.1.2) [17,20].
2. Literature Review
3. Research Material and Methodology
4. Analysis of the Loading Status of an Example Container Ship (Results and Discussion)
5. Conclusions
- -
- In the case under consideration, the weight of 4% of the loaded containers was changed by 0.5 t, which was sufficient for one of the most important parameters, the metacentric height, not to meet the requirement. For this reason, it would be advisable to improve and standardize the process of weighing containers before loading. It is also evident that an attempt should be made to minimize the measurement error since even a slight change in the weight of a container can affect stability.
- -
- The container weight verification process should be independent of third parties. In addition, to avoid inaccuracies, it should take place just before the container is loaded onto the ship. One way of doing this would be to use a flat scale that first weighs the container with the truck carrying it and then, after the container has been lifted by crane, the truck itself. The resulting container weight seems to be the most reliable, and weighing alone would not affect the loading rate.
- -
- An update to the loading plan after routine container weighing—the terminals start to weigh containers again on their own, but these data are not always compared to the ones declared. Although the IMO, MCA, and WCS guidance are clear about it, the importance of this practice must be highlighted.
- -
- No information is available about the distribution of cargo in the container space, which necessitates the estimated center of gravity to be assumed through mathematical calculations.
- -
- Containers loaded onto a ship are not always placed in the positions specified in the loading plan, and plans are often updated after the ship’s departure.
- -
- Cargo Securing Manuals are in many cases impractical, as the capacity, number of rows, bays, possible stowing configuration, and loading conditions cannot be inserted in a single paper document. The lashing calculations are now often done using a computer. However, there are no general mandatory requirements or performance criteria.
- -
- Decision support tools in bad weather conditions should be spread onboard ships, making the crew more aware of parametric rolling and whipping effects.
- -
- Bureau International des Containers, appointed by the IMO, formed two databases, containing technical details for individual containers. Both databases are incomplete, hence, it is not possible to assess all the containers before loading. Such databases should be developed as stack collapses are also connected with structural failures of containers.
- -
- Ishikawa’s analysis can easily contribute to estimating the effect of individual causes, as well as the elements contributing to these causes, and can rank the importance of their effect on the damage to the ship (in the case in question, human error in loading containers on the MSC Napoli).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goicoechea, N.; Abadie, L.M. Optimal Slow Steaming Speed for Container Ships under the EU Emission Trading System. Energies 2021, 14, 7487. [Google Scholar] [CrossRef]
- Marlantes, K.E.; Kim, S.; Hurt, L.A. Implementation of the IMO Second Generation Intact Stability Guidelines. J. Mar. Sci. Eng. 2021, 10, 41. [Google Scholar] [CrossRef]
- Oniszczuk-Jastrząbek, A.; Czermański, E. Te Evolution of the Ship Owner Profile in Global Container Shipping. Sci. J. Marit. Univ. Szczec. 2019, 58, 105112. [Google Scholar]
- Szyszko, M. Historia Kontenerowych Przewozów Morskich na Świecie; Świat Morskich Publikacji: Szczecin, Poland, 2010. [Google Scholar]
- Park, N.K.; Suh, S.C. Tendency toward Mega Containerships and the Constraints of Container Terminals. J. Mar. Sci. Eng. 2019, 7, 131. [Google Scholar] [CrossRef]
- He, G.; Xie, B.; Wang, W.; Liu, S.; Jing, P. Ship Loading Influence on the Slamming Impact of Typical Sections of an S-175 Container Ship. J. Mar. Sci. Eng. 2020, 8, 163. [Google Scholar] [CrossRef]
- Imai, A.; Nishimura, E.; Papadimitriou, S.; Sasaki, K. The Containership Loading Problem. Int. J. Marit. Econ. 2002, 4, 126–148. [Google Scholar] [CrossRef]
- van Zwijnsvoorde, T.; Vantorre, M.; Eloot, K.; Ides, S. Safety of Container Ship (Un)Loading Operations in the Port of Antwerp. Marit. Bus. Rev. 2019, 4, 106–127. [Google Scholar] [CrossRef]
- European Maritime Safety Agency. Safety Analysis of EMCIP Data. Analysis of Marine Casualties and Incidents Involving Container Vessels; European Maritime Safety Agency: Lisbon, Portugal, 2020. [Google Scholar]
- Hanzu-Pazara, R.; Duse; Varsami, C.; Andrei, C.; Dumitrache, R. The Influence of Ship’s Stability on Safety of Navigation. IOP Conf. Ser. Mater. Sci. Eng. 2016, 145, 082019. [Google Scholar] [CrossRef]
- Szelangiewicz, T.; Żelazny, K. An Approximate Method for Calculating the Mean Statistical Service Speed of Container Ships on a given Shipping Line and Its Application in Preliminary Design. Sci. J. Zesz. Nauk. Marit. Univ. Szczec. 2015, 44, 34–42. [Google Scholar]
- Wu, P.-C.; Lin, C.-Y. Strategies for the Low Sulfur Policy of IMO—An Example of a Container Vessel Sailing through a European Route. J. Mar. Sci. Eng. 2021, 9, 1383. [Google Scholar] [CrossRef]
- Acanfora, M.; Montewka, J.; Hinz, T.; Matusiak, J. On the Estimation of the Design Loads on Container Stacks Due to Excessive Acceleration in Adverse Weather Conditions. Mar. Struct. 2017, 53, 105–123. [Google Scholar] [CrossRef]
- Stanca, C.; Acomi, N.; Ancuta, C.; Georgescu, S. Comparative Analysis of Different Loading Conditions on Large Container Ships from the Perspective of the Stability Requirement. IOP Conf. Ser. Mater. Sci. Eng. 2015, 95, 012072. [Google Scholar] [CrossRef]
- IMO. International Convention for the Safety of Life at Sea; International Maritime Organization: London, UK, 1974. [Google Scholar]
- IMO. Resolution MSC/Circ.608/Rev.1, Interim Guidelines for Open-Top Container Ships; International Maritime Organization: London, UK, 1994. [Google Scholar]
- Szozda, Z. Stateczność Statku Morskiego; Wydawnictwo Naukowe Akademii Morskiej w Szczecinie: Szczecin, Poland, 2016. [Google Scholar]
- Petacco, N.; Pitardi, D.; Podenzana Bonvino, C.; Gualeni, P. Application of the IMO Second Generation Intact Stability Criteria to a Ballast-Free Containership. J. Mar. Sci. Eng. 2021, 9, 1416. [Google Scholar] [CrossRef]
- Pacino, D.; Delgado, A.; Jensen, R.M.; Bebbington, T. An Accurate Model for Seaworthy Container Vessel Stowage Planning with Ballast Tanks. In Computational Logistics: Third International Conference, ICCL 2012, Shanghai, China, 24–26 September 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 17–32. [Google Scholar]
- Polish Register of Shipping. Rules for the Classification and Construction of Sea-Going Ships. Part IV Stability and Subdivision; Polish Register of Shipping: Gdańsk, Poland, 2018. [Google Scholar]
- Gajewski, I.; Wójcicki, J. Mały Leksykon Morski; Wydawnictwo Ministerstwa Obrony Narodowej: Warszawa, Poland, 1981. [Google Scholar]
- The Danish Maritime Accident Investigation Board. Eugen Maersk Fire on 18 June 2013 Summary Report; The Danish Maritime Accident Investigation Board: Copenhagen, Denmark, 2014. [Google Scholar]
- The Danish Maritime Accident Investigation Board. Svendborg Maersk Heavy Weather Damage on 14 February 2014; The Danish Maritime Accident Investigation Board: Copenhagen, Denmark, 2014. [Google Scholar]
- Marine Accident Investigation Branch. Report on the Investigation into the Loss of 137 Containers from the Container Ship CMA CGM G. Washigton in the North Pacific Ocean on 20 January 2018; Marine Accident Investigation Branch: Southampton, UK, 2020. [Google Scholar]
- Panama Maritime Authority; Federal Bureau of Maritime Casualty Investigation of Germany. Loss of Containers Overboard from MSC Zoe 1–2 January 2019; Panama Maritime Authority: Panama City, Panama; Federal Bureau of Maritime Casualty Investigation of Germany: Hamburg, Germany, 2020. [Google Scholar]
- World Shipping Council. The SOLAS Container Weight Verification Requirement; World Shipping Council: Washington, DC, USA, 2015. [Google Scholar]
- Shipping and Freight Resource. Understanding Container Weight Misdeclaration. Available online: www.shippingandfreightresource.com/understanding-container-weight-misdeclaration (accessed on 5 December 2022).
- Nautilus International. MAIB Questions IMO Cargo Misdeclarations Measures Following Ever Smart Investigation. Available online: https://www.nautilusint.org/en/news-insight/news/maib-questions-imo-cargo-misdeclarations-measures-following-ever-smart-investigation (accessed on 28 April 2022).
- Antonis Karamalegkos. Container News. VGM Losses Are Approximately US$6bn, But Who’s Counting? Available online: https://www.container-news.com/vgm-losses-are-approximately-us6bn-but-whos-counting (accessed on 30 April 2022).
- Perrault, D.E. Probability of Sea Condition for Ship Strength, Stability, and Motion Studies. J. Ship Res. 2021, 65, 1–14. [Google Scholar] [CrossRef]
- Barrass, B.; Derrett, D.R. Ship Stability for Masters and Mates; Elsevier: Amsterdam, The Netherlands, 2012; ISBN 9780080970936. [Google Scholar]
- Yongming, S.; Shuhong, S. The Study of Ships Ballast Water Replacement Monitoring at Sea Based on MCU. Procedia Environ. Sci. 2012, 12, 199–205. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, J.; Ma, L. Modelling and Implementation of an Intelligent Stowage Simulator for Container Ships. Int. J. Simul. Process Model. 2020, 15, 201. [Google Scholar] [CrossRef]
- Caibula, M.N. The Study of a Jib Crane from a Cargo Ship. J. Mar. Technol. Environ. 2022, 2022, 11–14. [Google Scholar] [CrossRef]
- Koning, J.; Grin, R.; Pauw, W. TopTier, Seakeeping and Container Cargo Securing Safety. In Proceedings of the 18th International Ship Stability Workshop, Gdańsk, Poland, 13–15 June 2022. [Google Scholar]
- Perkovic, M.; Gucma, M.; Luin, B.; Gucma, L.; Brcko, T. Accommodating Larger Container Vessels Using an Integrated Laser System for Approach and Berthing. Microprocess Microsyst. 2017, 52, 106–116. [Google Scholar] [CrossRef]
- Wu, Q.; Xia, Q.; Wu, M. Research on Intelligent Loading System for Container Ships. IOP Conf Ser Earth Environ Sci 2021, 632, 022074. [Google Scholar] [CrossRef]
- Tan, H.-S.; Huang, J.; Bu, F.; Song, H.; Warf, G.K. Method of Automatic Positioning for Loading and Unloading of Container Ships in Container Terminals. U.S. Patent 8,452,527, 28 May 2013. [Google Scholar]
- World Shipping Council. Containers Lost at Sea. 2022 Update; World Shipping Council: Washington, DC, USA, 2022. [Google Scholar]
- Fremantle ports. A Guide to Container Weight Declarations. Fremantle Port Sea Freight Container Supply Chain (Loaded Containers) Version I; Fremantle Ports: Fremantle, Australia, 2014. [Google Scholar]
- King, M. The Problem of Misdeclared Container Weight. In Llm Seminar Paper Laws 538: Maritime and Transport Law; Te Herenga Waka—Victoria University of Wellington: Wellington, New Zealand, 2014. [Google Scholar]
- Rahmatika; Putri, R.A.; Sirait, D.P.; Setyawati, A. The Impact of VGM (Verified Gorss Mass) Implementation as SOLAS’s New Regulation—Case Study at Port of Tg.Priok. In Advances in Engineering Research (AER), Conference on Global Research on Sustainable Transport; Atlantis Press: Dordrecht, The Netherlands, 2017. [Google Scholar]
- Tai, S.K. The Application of the Verified Gross Mass Rules in Hong Kong. Marit. Buisness Rev. 2016, 1, 225–230. [Google Scholar] [CrossRef]
- Aras, E.; Chen, P.-L. The Effect of the Verified Gross Mass (VGM) Implementation in Australia. In Proceedings of the 4th Belt and Road Initiative Conference, Bangkok, Thailand, 1–3 August 2019; pp. 1–20. [Google Scholar]
- Hartati, S.R.I.; Nurhayati, I. Implication of Safety of Law at Sea (SOLAS) Amendment 1972-Chapter VI Part A Regulation 2 Related to Verified Gross Mass (VGM) on the Implementation of Plywood Exports (Case Study of Pt. Albasia); Batang Sejahtera: Batang, Indonesia, 2018. [Google Scholar]
- Phor, T.L. The Study of the Impact and Solutions of Verified Gross Mass (VGM) Measures on Thai Import-Export Business in Freight/Forwarder’s Perspective. Panyapiwat J. 2020, 12, 109–123. [Google Scholar]
- Marine Accident Investigation Branch. Report on the Investigatioon of the Loss of 42 Containers from the Container Ship Ever Smart 700 Miles East of Japan, North Pacific Ocean 30 October 2017; Marine Accident Investigation Branch: Southampton, UK, 2020. [Google Scholar]
- Marine Accident Investigation Branch. Report on the Investigation of the Structural Failure of MSC Napoli English Channel on 18 January 2007; Marine Accident Investigation Branch: Southampton, UK, 2008. [Google Scholar]

| Criterion | Requirement |
|---|---|
| Area (A) under the righting arm curve | A0–30° ≥ 0.055 m⋅rad A0–40° ≥ 0.090 m⋅rad A30–40° ≥ 0.030 m⋅rad |
| Righting arm (GZ) | GZφ ≥ 30° ≥ 0.20 m |
| Angle corresponding to the maximum of the righting arms | φGZmax ≥ 25° |
| Initial metacentric height (GM) | GM ≥ 0.15 m |
The weather criterion, where a and b are surface areas in the figure below, is based on: [17]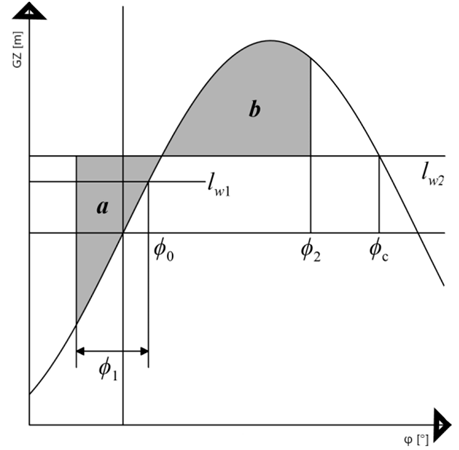 | b ≥ a |
| List of the ship under static wind pressure perpendicular to the plane of symmetry | φ0 ≤ 16° or φ0 ≤ 0.8° φdeck edge entering the water |
| Name of the Tank | Weight [t] | Volume [m3] | Filling [%] | Free Surface [mt] |
|---|---|---|---|---|
| Fore peak TK | 0.0 | 0.0 | 0.0 | 0.0 |
| BW TK 4.01 | 0.0 | 0.0 | 0.0 | 0.0 |
| BW TK 4.03 | 677.4 | 660.9 | 100.0 | 0.0 |
| BW TK 4.04 | 614.0 | 599.0 | 100.0 | 0.0 |
| BW TK 4.05 | 467.0 | 455.6 | 100.0 | 0.0 |
| BW TK 4.06 | 435.6 | 425.0 | 100.0 | 0.0 |
| BW TK 4.07 | 707.4 | 690.1 | 100.0 | 0.0 |
| BW TK 4.08 | 629.9 | 614.5 | 100.0 | 0.0 |
| BW TK 4.09 | 574.2 | 560.2 | 100.0 | 0.0 |
| BW TK 4.10 | 549.8 | 536.4 | 100.0 | 0.0 |
| BW TK 4.15 | 876.5 | 855.1 | 100.0 | 0.0 |
| BW TK 4.16 | 817.4 | 797.5 | 100.0 | 0.0 |
| BW TK 4.17 | 514.5 | 502.0 | 100.0 | 0.0 |
| BW TK 4.18 | 513.7 | 501.2 | 100.0 | 0.0 |
| Heeling TK 4.19 | 327.3 | 319.3 | 70.0 | 0.0 |
| Heeling TK 4.20 | 139.9 | 136.5 | 30.0 | 0.0 |
| BW TK 4.21 | 569.6 | 555.7 | 100.0 | 0.0 |
| BW TK 4.22 | 567.7 | 553.9 | 100.0 | 0.0 |
| REEFER TK 4.24 | 56.7 | 55.3 | 100.0 | 0.0 |
| Aft peak TK | 0.0 | 0.0 | 0.0 | 0.0 |
| Stability Results/without d. Cont.—SeeBG | |||
|---|---|---|---|
| Lever Balance—OK! | Actual | Limit | |
| GM’ (corrected) | 0.421 | 0.421 | m |
| Angle due to transverse Moment | 0.016 | 3.000 | degr. |
| Angle due to Wind + transverse Moment | 0.016 | 18.000 | degr. |
| GZ Lever at 30 Degrees | 0.463 | 0.455 | m |
| Statical Stability Range | 53.962 | 50.000 | degr. |
| Area up to 30 Degrees | 0.100 | 0.055 | mrad |
| Area up to 40 Degrees | 0.191 | 0.090 | mrad |
| Area between 30 and 40 Degrees | 0.091 | 0.030 | mrad |
| Frame No. | Shear Forces | Bending Moments | Torsion | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sea | |||||||||
| Existing [kN] | Limits [kN] | rel. [%] | Existing [kN] | Limits [kN] | rel. [%] | rel. [%] | |||
| 35 | 25,600 | 29,850 | 86 | 345,456 | 454,300 | 76 | max. Mom. | Limit | |
| 52 | 30,532 | 35,000 | * 87 | 722,320 | 1,021,200 | 71 | (kNm) | (kNm) | |
| 77 | 8763 | 27,850 | 31 | 1,111,023 | 1,313,300 | 85 | 41,690 | 79,900 | 52 |
| 94 | 8468 | 50,900 | 17 | 1,213,676 | 1,882,500 | 64 | Area of T. | Limit | |
| 110 | 5746 | 50,900 | 11 | 1,261,864 | 1,891,500 | 67 | (kNm2) | (kNm2) | |
| 131 | −2449 | −50,900 | 5 | 1,226,878 | 1,891,500 | 65 | 2,449,933 | 7,801,000 | 31 |
| 148 | −8431 | −50,850 | 17 | 1,098,927 | 1,809,600 | 61 | |||
| 168 | −17,293 | −50,200 | 34 | 825,294 | 1,271,900 | 65 | |||
| 185 | −17,072 | −47,650 | 36 | 524,022 | 805,400 | 65 | |||
| 204 | −7947 | −23,300 | 34 | 241,115 | 420,200 | 57 | |||
| 222 | 7541 | 18,900 | 40 | 144,461 | 148,000 | * 98 | |||
| Stability Results/Without d. Cont.—SeeBG | ||||
|---|---|---|---|---|
| Lever Balance—OK! | GM not OK! | Actual | Limit | |
| GM’ (corrected) | 0.416 | 0.425 | m | |
| Angle due to transverse Moment | 0.016 | 3.000 | degr. | |
| Angle due to Wind + transverse Moment | 0.016 | 18.000 | degr. | |
| GZ Lever at 30 Degrees | 0.459 | 0.456 | m | |
| Statical Stability Range | 53,859 | 50,000 | degr. | |
| Area up to 30 Degrees | 0.099 | 0.055 | mrad | |
| Area up to 40 Degrees | 0.190 | 0.090 | mrad | |
| Area between 30 and 40 Degrees | 0.091 | 0.030 | mrad | |
| Frame No. | Shear Forces | Bending Moments | Torsion | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sea | |||||||||
| Existing [kN] | Limits [kN] | rel. [%] | Existing [kN] | Limits [kN] | rel. [%] | rel. [%] | |||
| 35 | 25,627 | 29,850 | 86 | 345,864 | 454,300 | 76 | max. Mom. | Limit | |
| 52 | 30,560 | 35,000 | * 87 | 723,082 | 1,021,200 | 71 | (kNm) | (kNm) | |
| 77 | 8741 | 27,850 | 31 | 1,111,843 | 1,313,300 | 85 | 41,852 | 79,900 | 52 |
| 94 | 8460 | 50,900 | 17 | 1,214,300 | 1,882,500 | 65 | Area of T. | Limit | |
| 110 | 5749 | 50,900 | 11 | 1,262,429 | 1,891,500 | 67 | (kNm2) | (kNm2) | |
| 131 | −2466 | −50,900 | 5 | 1,227,304 | 1,891,500 | 65 | 2,466,056 | 7,801,000 | 32 |
| 148 | −8441 | −50,850 | 17 | 1,099,119 | 1,809,600 | 61 | |||
| 168 | −17,299 | −50,200 | 34 | 825,336 | 1,271,900 | 65 | |||
| 185 | −17,065 | −47,650 | 36 | 524,069 | 805,400 | 65 | |||
| 204 | −7958 | −23,300 | 34 | 241,033 | 420,200 | 57 | |||
| 222 | 7552 | 18,900 | 40 | 144,324 | 148,000 | * 98 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaup, M.; Łozowicka, D.; Baszak, K.; Ślączka, W. An Assessment of Stability and Strength of a Container Ship for Safety Compliance in Cargo Loading Plans. Appl. Sci. 2024, 14, 345. https://doi.org/10.3390/app14010345
Kaup M, Łozowicka D, Baszak K, Ślączka W. An Assessment of Stability and Strength of a Container Ship for Safety Compliance in Cargo Loading Plans. Applied Sciences. 2024; 14(1):345. https://doi.org/10.3390/app14010345
Chicago/Turabian StyleKaup, Magdalena, Dorota Łozowicka, Karolina Baszak, and Wojciech Ślączka. 2024. "An Assessment of Stability and Strength of a Container Ship for Safety Compliance in Cargo Loading Plans" Applied Sciences 14, no. 1: 345. https://doi.org/10.3390/app14010345
APA StyleKaup, M., Łozowicka, D., Baszak, K., & Ślączka, W. (2024). An Assessment of Stability and Strength of a Container Ship for Safety Compliance in Cargo Loading Plans. Applied Sciences, 14(1), 345. https://doi.org/10.3390/app14010345





