Analysis of Cost Functions for Reinforcement Learning of Reaching Tasks in Humanoid Robots
Abstract
:1. Introduction
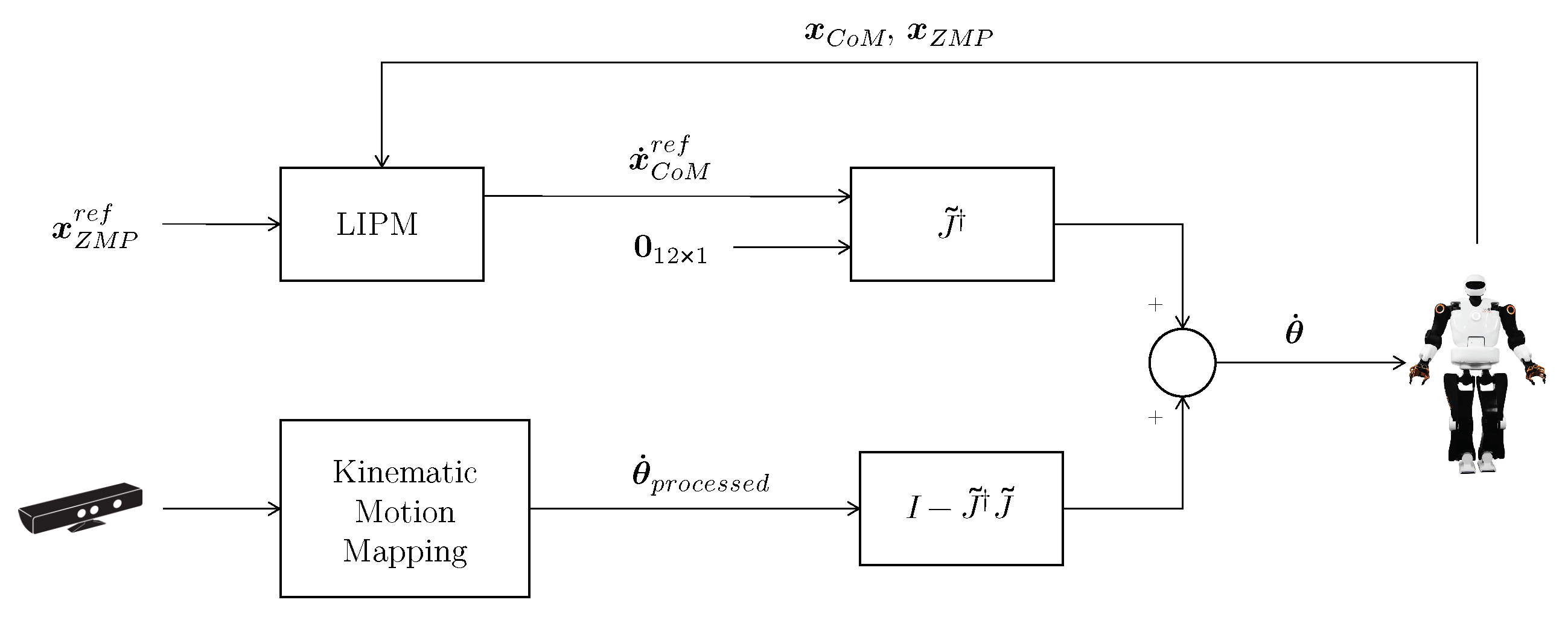
2. Stable Motion Imitation Framework
2.1. Kinematic Motion Mapping
2.2. Stability Control and Motion Mapping
3. Motion Adaptation by Reinforcement Learning
3.1. Cost Function
4. Analysis of Influence of Different Cost Function Terms on the Learnt Motions
4.1. Experimental Setting
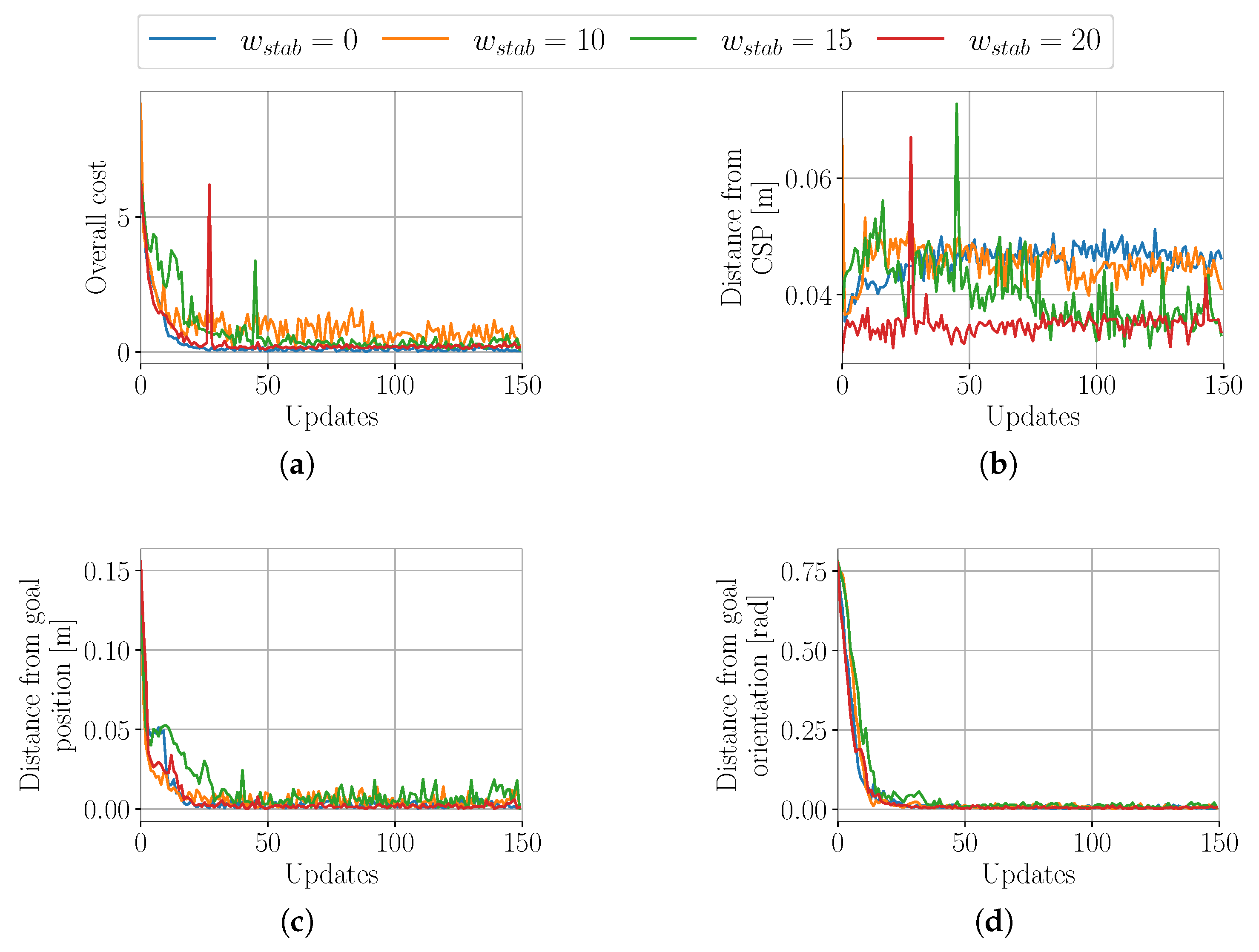
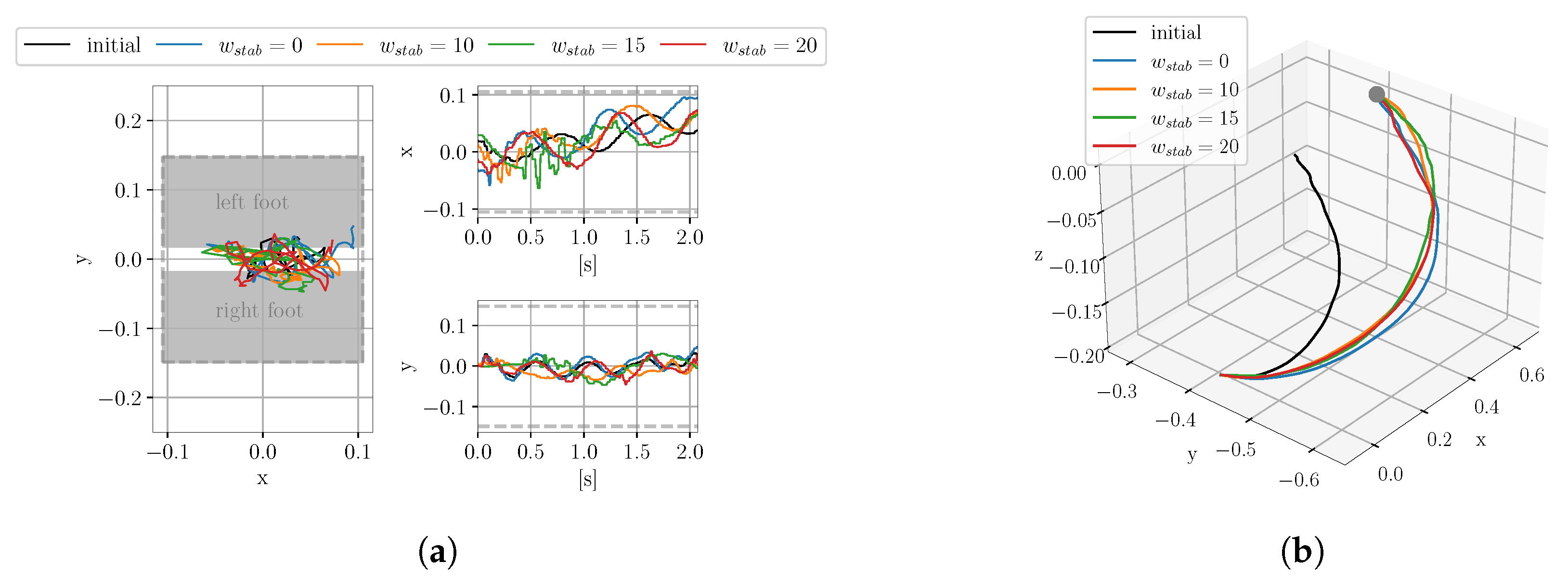
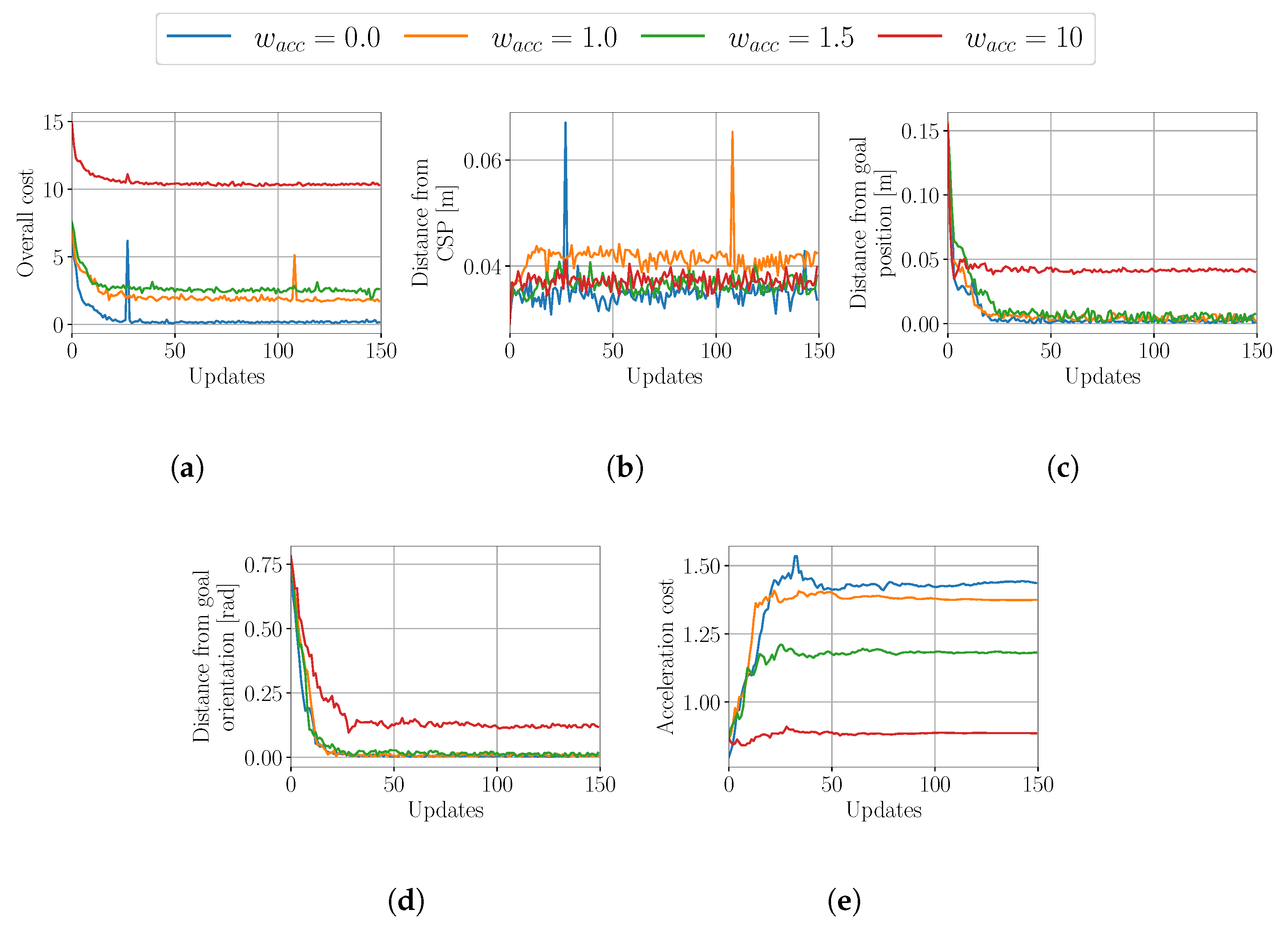
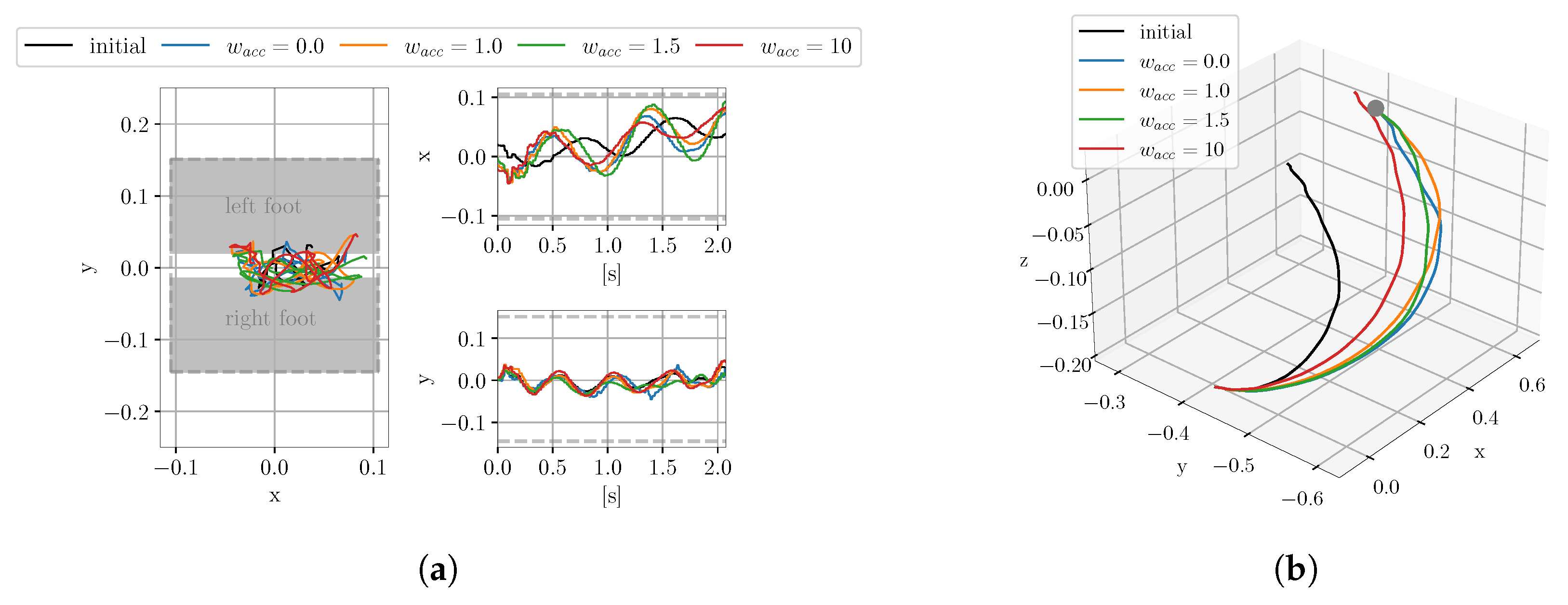
4.1.1. Evaluation of the Influence of the Stability Cost
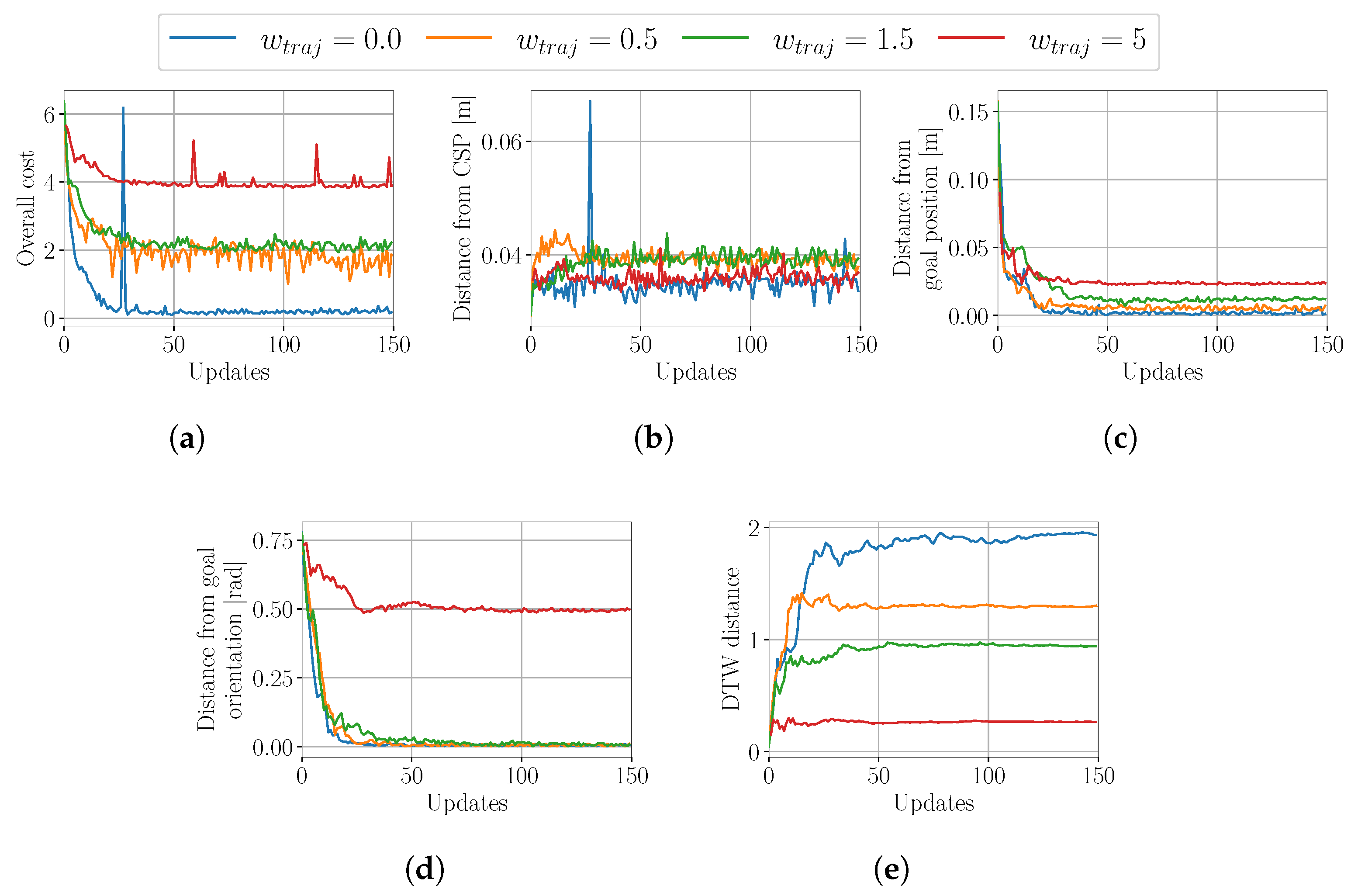
4.1.2. Evaluation of the Influence of the Trajectory Similarity Cost
4.1.3. Evaluation of the Influence of the Smoothing Cost
4.1.4. Systematic Search for the Optimal Weights of the Stability Cost Term
5. Execution of Trajectories Learnt in Simulation on the Real Robot
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kajita, S.; Hirukawa, H.; Harada, K.; Yokoi, K. Introduction to Humanoid Robotics; Springer Tracts in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Hua, J.; Zeng, L.; Li, G.; Ju, Z. Learning for a Robot: Deep Reinforcement Learning, Imitation Learning, Transfer Learning. Sensors 2021, 21, 1278. [Google Scholar] [CrossRef] [PubMed]
- Billard, A.; Calinon, S.; Dillmann, R.; Schaal, S. Robot Programming by Demonstration. In Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1371–1394. [Google Scholar]
- Schaal, S. Learning from Demonstration. In Proceedings of the 9th International Conference on Neural Information Processing Systems, Denver, CO, USA, 3–5 December 1996; pp. 1040–1046. [Google Scholar]
- Argall, B.D.; Chernova, S.; Veloso, M.; Browning, B. A survey of robot learning from demonstration. Robot. Auton. Syst. 2009, 57, 469–483. [Google Scholar] [CrossRef]
- Ude, A.; Riley, M.; Atkeson, C.G. Planning of joint trajectories for humanoid robots using B-spline wavelets. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), San Francisco, CA, USA, 24–28 April 2000; pp. 2223–2228. [Google Scholar]
- Ude, A.; Atkeson, C.G.; Riley, M. Programming full-body movements for humanoid robots by observation. Robot. Auton. Syst. 2004, 47, 93–108. [Google Scholar] [CrossRef]
- Koenemann, J.; Burget, F.; Bennewitz, M. Real-time imitation of human whole-body motions by humanoids. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2806–2812. [Google Scholar]
- Zhang, L.; Cheng, Z.; Gan, Y.; Zhu, G.; Shen, P.; Song, J. Fast human whole body motion imitation algorithm for humanoid robots. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 1430–1435. [Google Scholar]
- Zhang, Z.; Niu, Y.; Yan, Z.; Lin, S. Real-Time Whole-Body Imitation by Humanoid Robots and Task-Oriented Teleoperation Using an Analytical Mapping Method and Quantitative Evaluation. Appl. Sci. 2018, 8, 2005. [Google Scholar] [CrossRef]
- Mi, J.; Takahashi, Y. Whole-Body Joint Angle Estimation for Real-Time Humanoid Robot Imitation Based on Gaussian Process Dynamical Model and Particle Filter. Appl. Sci. 2020, 10, 5. [Google Scholar] [CrossRef]
- Savevska, K.; Simonič, M.; Ude, A. Modular Real-Time System for Upper-Body Motion Imitation on Humanoid Robot Talos. In Advances in Service and Industrial Robotics, RAAD 2021; Zeghloul, S., Laribi, M.A., Sandoval, J., Eds.; Springer: Cham, Switzerland, 2021; pp. 229–239. [Google Scholar]
- Vuga, R.; Ogrinc, M.; Gams, A.; Petrič, T.; Sugimoto, N.; Ude, A.; Morimoto, J. Motion capture and reinforcement learning of dynamically stable humanoid movement primitives. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 5284–5290. [Google Scholar]
- Savevska, K.; Ude, A. Teaching Humanoid Robot Reaching Motion by Imitation and Reinforcement Learning. In Advances in Service and Industrial Robotics, RAAD2023; Petrič, T., Ude, A., Žlajpah, L., Eds.; Springer: Cham, Switzerland, 2023; pp. 53–61. [Google Scholar]
- Theodorou, E.; Buchli, J.; Schaal, S. Learning Policy Improvements with Path Integrals. J. Mach. Learn. Res. 2010, 9, 828–835. [Google Scholar]
- Stulp, F.; Buchli, J.; Theodorou, E.; Schaal, S. Reinforcement learning of full-body humanoid motor skills. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Nashville, TN, USA, 6–8 December 2010; pp. 405–410. [Google Scholar]
- Theodorou, E.; Stulp, F.; Buchli, J.; Schaal, S. An Iterative Path Integral Stochastic Optimal Control Approach for Learning Robotic Tasks. IFAC Proc. Vol. 2011, 44, 11594–11601. [Google Scholar] [CrossRef]
- Theodorou, E.; Buchli, J.; Schaal, S. Reinforcement learning of motor skills in high dimensions: A path integral approach. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 2397–2403. [Google Scholar]
- Stulp, F.; Sigaud, O. Path Integral Policy Improvement with Covariance Matrix Adaptation. In Proceedings of the 29th International Conference on Machine Learning (ICML), Edinburgh, UK, 26 June–1 July 2012. [Google Scholar]
- Fu, J.; Li, C.; Teng, X.; Luo, F.; Li, B. Compound Heuristic Information Guided Policy Improvement for Robot Motor Skill Acquisition. Appl. Sci. 2020, 10, 5346. [Google Scholar] [CrossRef]
- Kober, J.; Peters, J. Policy search for motor primitives in robotics. Mach. Learn. 2010, 84, 171–203. [Google Scholar] [CrossRef]
- Peters, J.; Schaal, S. Natural Actor-Critic. Neurocomputing 2008, 71, 1180–1190. [Google Scholar] [CrossRef]
- Williams, R.J. Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Peters, J.; Schaal, S. Policy Gradient Methods for Robotics. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Beijing, China, 9–15 October 2006; pp. 2219–2225. [Google Scholar]
- Mannor, S.; Rubinstein, R.; Gat, Y. The Cross Entropy method for Fast Policy Search. In Proceedings of the Twentieth International Conference on Machine Learning (ICML), Washington, DC, USA, 21–24 August 2003; pp. 512–519. [Google Scholar]
- Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef] [PubMed]
- Vukobratović, M.; Stepanenko, J. On the stability of anthropomorphic systems. Math. Biosci. 1972, 15, 1–37. [Google Scholar] [CrossRef]
- Kajita, S.; Tani, K. Study of dynamic biped locomotion on rugged terrain-derivation and application of the linear inverted pendulum mode. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Sacramento, CA, USA, 9–11 April 1991; pp. 1405–1411. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Yokoi, K.; Hirukawa, H. The 3D linear inverted pendulum mode: A simple modeling for a biped walking pattern generation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Maui, HI, USA, 30 October–3 November 2001; pp. 239–246. [Google Scholar]
- Yamamoto, K.; Kamioka, T.; Sugihara, T. Survey on model-based biped motion control for humanoid robots. Adv. Robot. 2020, 34, 1353–1369. [Google Scholar] [CrossRef]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Biped walking pattern generation by using preview control of zero-moment point. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Taipei, Taiwan, 14–19 September 2003; pp. 1620–1626. [Google Scholar]
- Kajita, S.; Morisawa, M.; Miura, K.; Nakaoka, S.; Harada, K.; Kaneko, K.; Kanehiro, F.; Yokoi, K. Biped walking stabilization based on linear inverted pendulum tracking. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4489–4496. [Google Scholar]
- Sugihara, T.; Nakamura, Y.; Inoue, H. Real-time humanoid motion generation through ZMP manipulation based on inverted pendulum control. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Washington, DC, USA, 11–15 May 2002; pp. 1404–1409. [Google Scholar]
- Sugihara, T. Standing stabilizability and stepping maneuver in planar bipedalism based on the best COM-ZMP regulator. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Kobe, Japan, 12–17 May 2009; pp. 1966–1971. [Google Scholar]
- Sugihara, T.; Morisawa, M. A survey: Dynamics of humanoid robots. Advanced Robotics 2020, 34, 1338–1352. [Google Scholar] [CrossRef]
- Stulp, F. Adaptive exploration for continual reinforcement learning. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 1631–1636. [Google Scholar]
- Ijspeert, A.J.; Nakanishi, J.; Hoffmann, H.; Pastor, P.; Schaal, S. Dynamical Movement Primitives: Learning Attractor Models for Motor Behaviors. Neural Comput. 2013, 25, 328–373. [Google Scholar] [CrossRef]
- Ude, A.; Gams, A.; Asfour, T.; Morimoto, J. Task-Specific Generalization of Discrete and Periodic Dynamic Movement Primitives. IEEE Trans. Robot. 2010, 26, 800–815. [Google Scholar] [CrossRef]
- Ude, A. Filtering in a unit quaternion space for model-based object tracking. Robot. Auton. Syst. 1999, 28, 163–172. [Google Scholar] [CrossRef]
- Stulp, F.; Sigaud, O. Robot Skill Learning: From Reinforcement Learning to Evolution Strategies. Paladyn, J. Behav. Robot. 2013, 4, 49–61. [Google Scholar] [CrossRef]
- Stulp, F.; Raiola, G. DmpBbo: A versatile Python/C++ library for Function Approximation, Dynamical Movement Primitives, and Black-Box Optimization. J. Open Source Softw. 2019, 4, 1225. [Google Scholar] [CrossRef]
- Stasse, O.; Flayols, T.; Budhiraja, R.; Giraud-Esclasse, K.; Carpentier, J.; Mirabel, J.; Del Prete, A.; Souéres, P.; Mansard, N.; Lamiraux, F.; et al. TALOS: A new humanoid research platform targeted for industrial applications. In Proceedings of the IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids), Birmingham, UK, 15–17 November 2017; pp. 689–695. [Google Scholar]



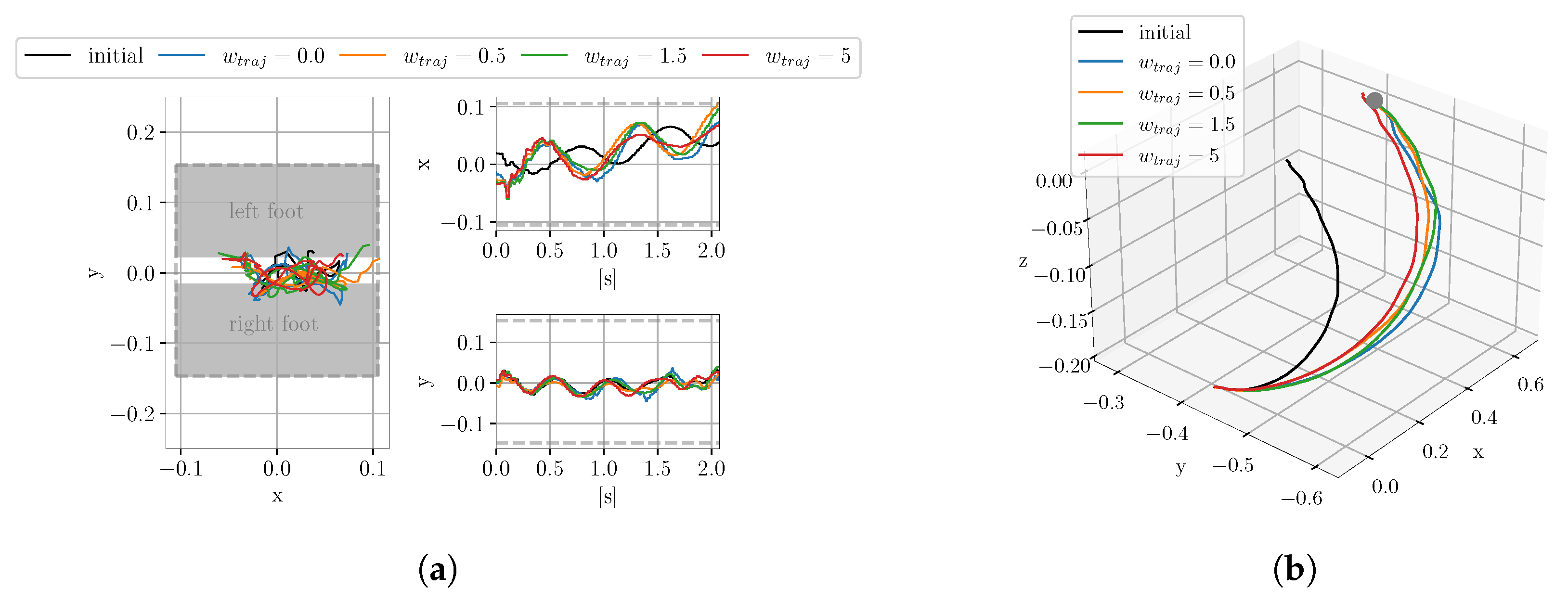




| Position [m] | Orientation [rad] | Distance from CSP [m] | ||||
|---|---|---|---|---|---|---|
| Avg | Min | Avg | Min | Avg | Min | |
| 0.0031 | 0.0003 | 0.0059 | 0.0015 | 0.0469 | 0.0440 | |
| 0.0069 | 0.0011 | 0.0152 | 0.0039 | 0.0494 | 0.0426 | |
| 0.0079 | 0.0003 | 0.0103 | 0.0015 | 0.0364 | 0.0308 | |
| 0.0020 | 0.0003 | 0.0047 | 0.0008 | 0.0352 | 0.0302 | |
| Position [m] | Orientation [rad] | DTW Distance | ||||
|---|---|---|---|---|---|---|
| Avg | Min | Avg | Min | Avg | Min | |
| 0.0020 | 0.0003 | 0.0047 | 0.0008 | 1.9202 | 1.8585 | |
| 0.0053 | 0.0035 | 0.0055 | 0.0003 | 1.2956 | 1.2847 | |
| 0.0120 | 0.0102 | 0.0086 | 0.0005 | 0.9465 | 0.9375 | |
| 0.0234 | 0.0227 | 0.4946 | 0.4868 | 0.2672 | 0.2653 | |
| Position [m] | Orientation [rad] | Smoothing Cost | ||||
|---|---|---|---|---|---|---|
| Avg | Min | Avg | Min | Avg | Min | |
| 0.0020 | 0.0003 | 0.0047 | 0.0008 | 1.4340 | 1.4215 | |
| 0.0041 | 0.0015 | 0.0077 | 0.0024 | 1.3749 | 1.3733 | |
| 0.0047 | 0.0005 | 0.0109 | 0.0021 | 1.1814 | 1.1779 | |
| 0.0414 | 0.0402 | 0.1195 | 0.1114 | 0.8862 | 0.8851 | |
| Position (m) | Orientation (rad) | Distance from CSP (m) | |||
|---|---|---|---|---|---|
| Simulation | Robot | Simulation | Robot | Simulation | Robot |
| 0.0012 | 0.0056 | 0.0061 | 0.0114 | 0.0337 | 0.0441 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savevska, K.; Ude, A. Analysis of Cost Functions for Reinforcement Learning of Reaching Tasks in Humanoid Robots. Appl. Sci. 2024, 14, 39. https://doi.org/10.3390/app14010039
Savevska K, Ude A. Analysis of Cost Functions for Reinforcement Learning of Reaching Tasks in Humanoid Robots. Applied Sciences. 2024; 14(1):39. https://doi.org/10.3390/app14010039
Chicago/Turabian StyleSavevska, Kristina, and Aleš Ude. 2024. "Analysis of Cost Functions for Reinforcement Learning of Reaching Tasks in Humanoid Robots" Applied Sciences 14, no. 1: 39. https://doi.org/10.3390/app14010039
APA StyleSavevska, K., & Ude, A. (2024). Analysis of Cost Functions for Reinforcement Learning of Reaching Tasks in Humanoid Robots. Applied Sciences, 14(1), 39. https://doi.org/10.3390/app14010039





