Numerical Study on the Flow Characteristics of High Attack Angle around the Submarine’s Vertical Plane
Abstract
:1. Introduction
2. Materials and Methods
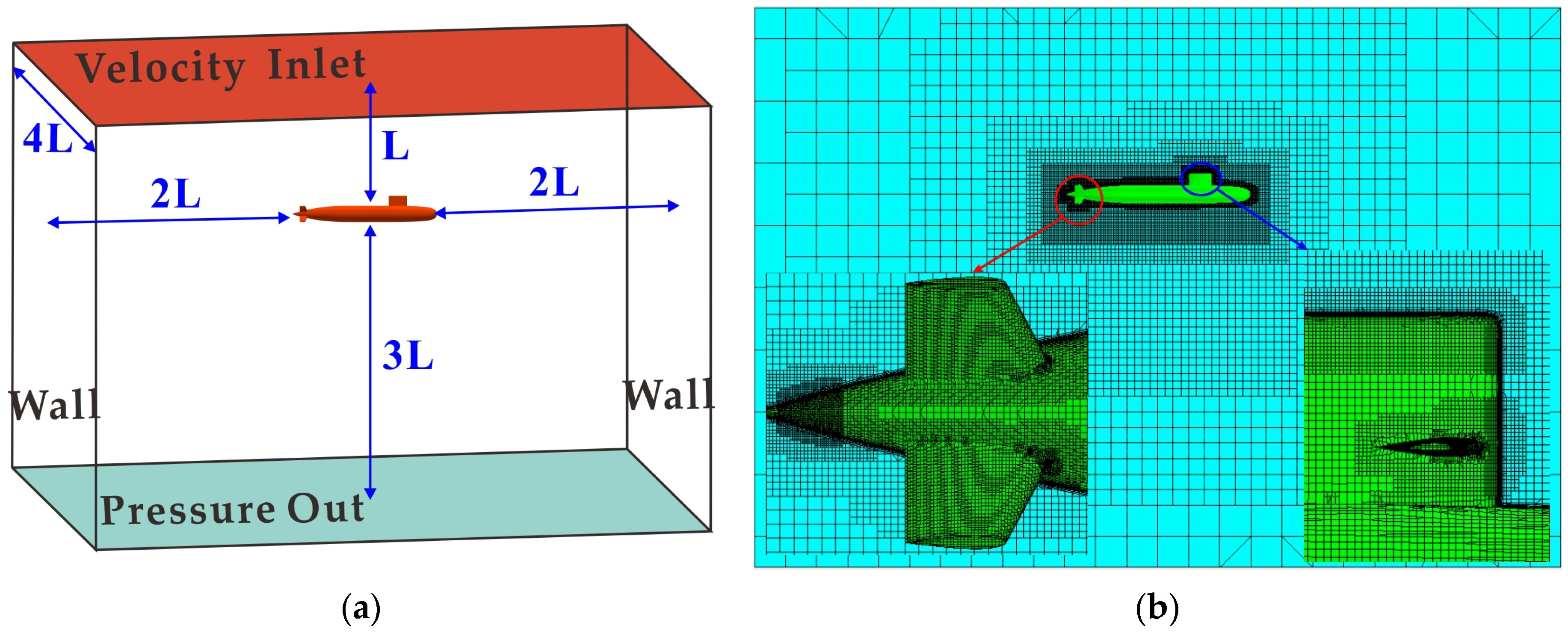
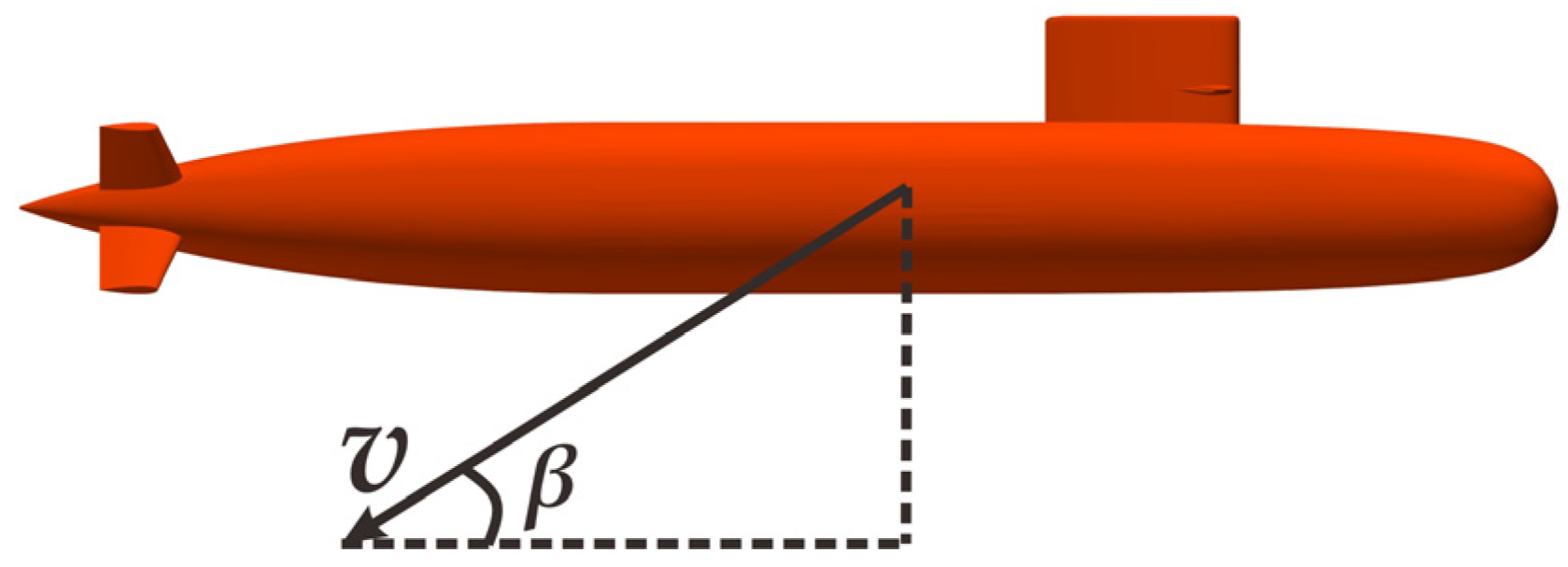
2.1. Development of a Model
2.2. Numerical Approach
2.2.1. Governing Equation Viscous Flow
2.2.2. The SST-Based Model
2.2.3. Establishment of the DDES Model
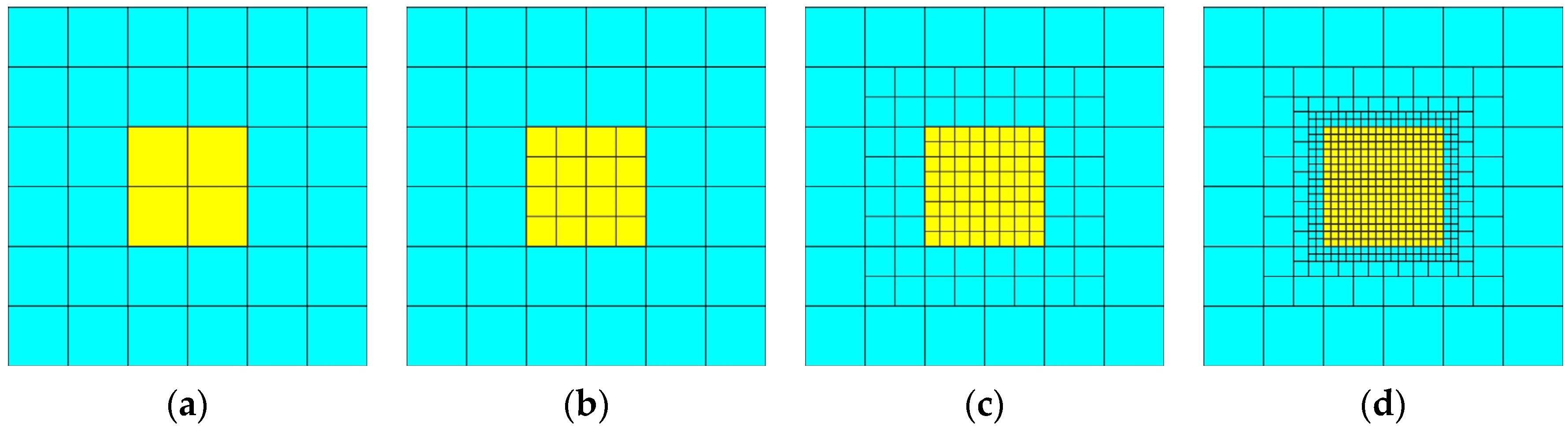
2.2.4. Mesh Adaptation Criteria
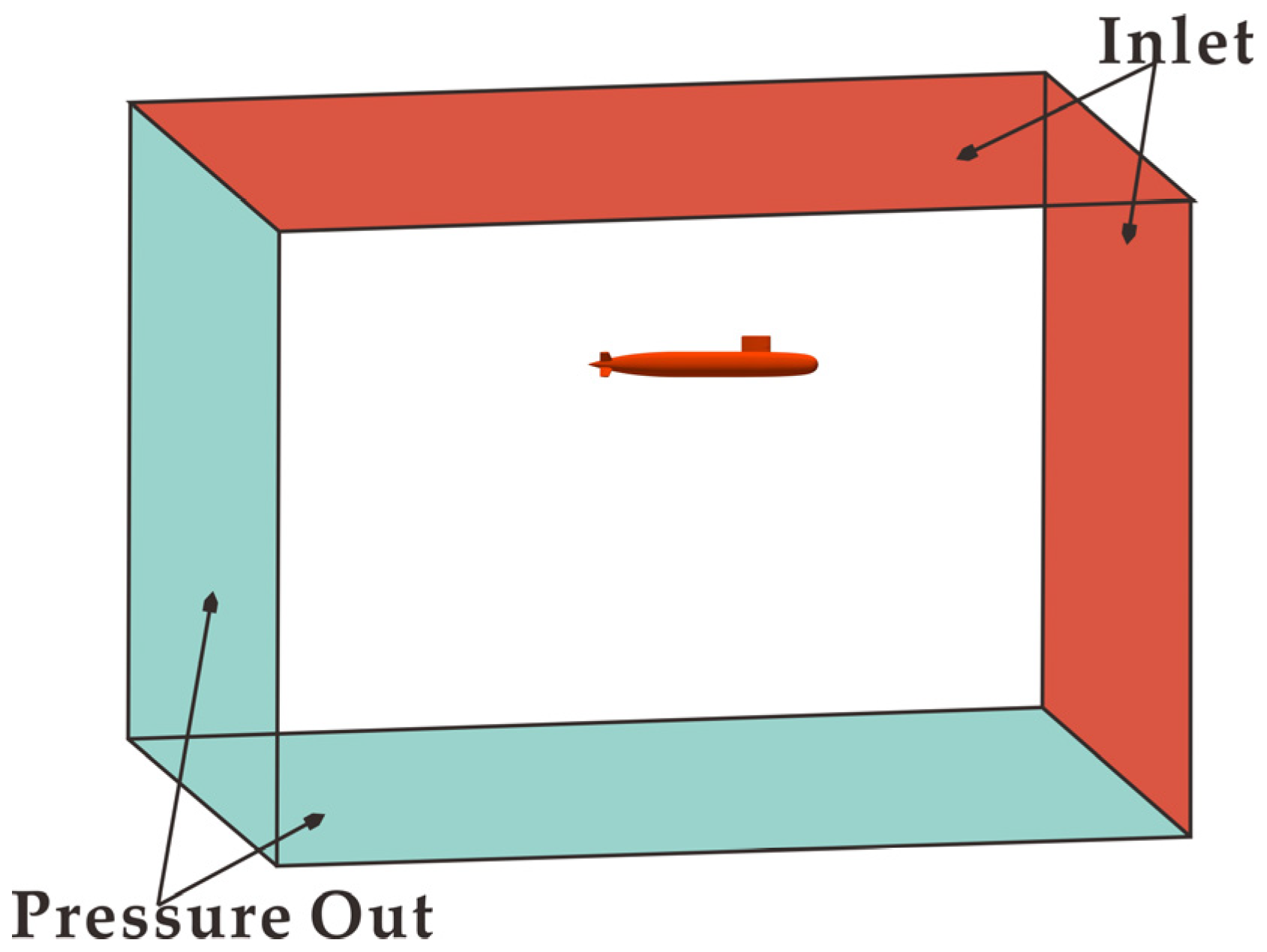
2.2.5. Boundary Conditions and Grid
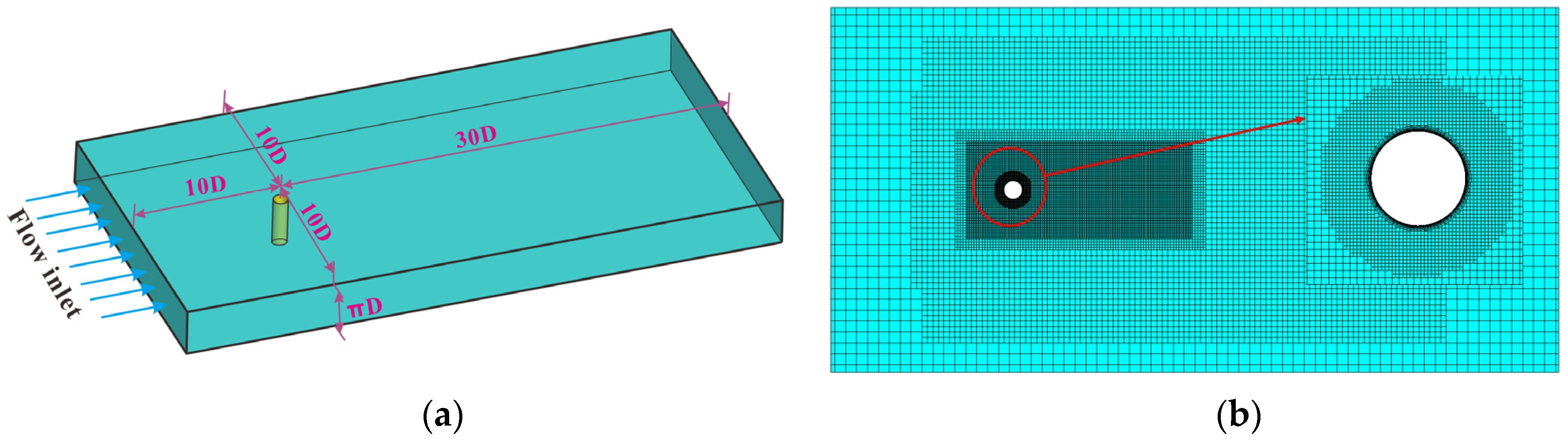
2.3. Experiment
3. Validation of the Proposed Numerical Methods
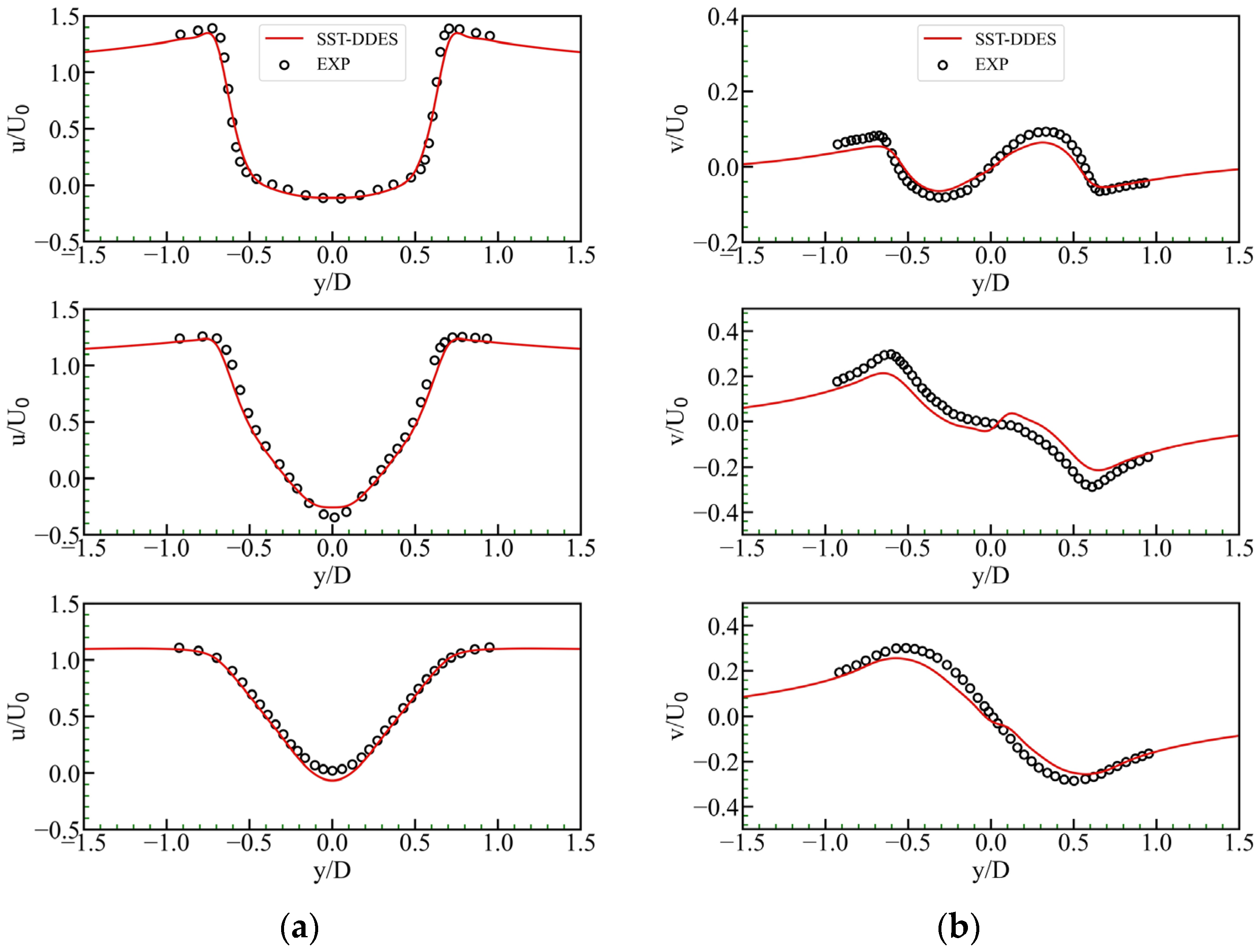
3.1. Preliminary Tests
3.2. Experimental Results of the Flow around a Vertical Plane
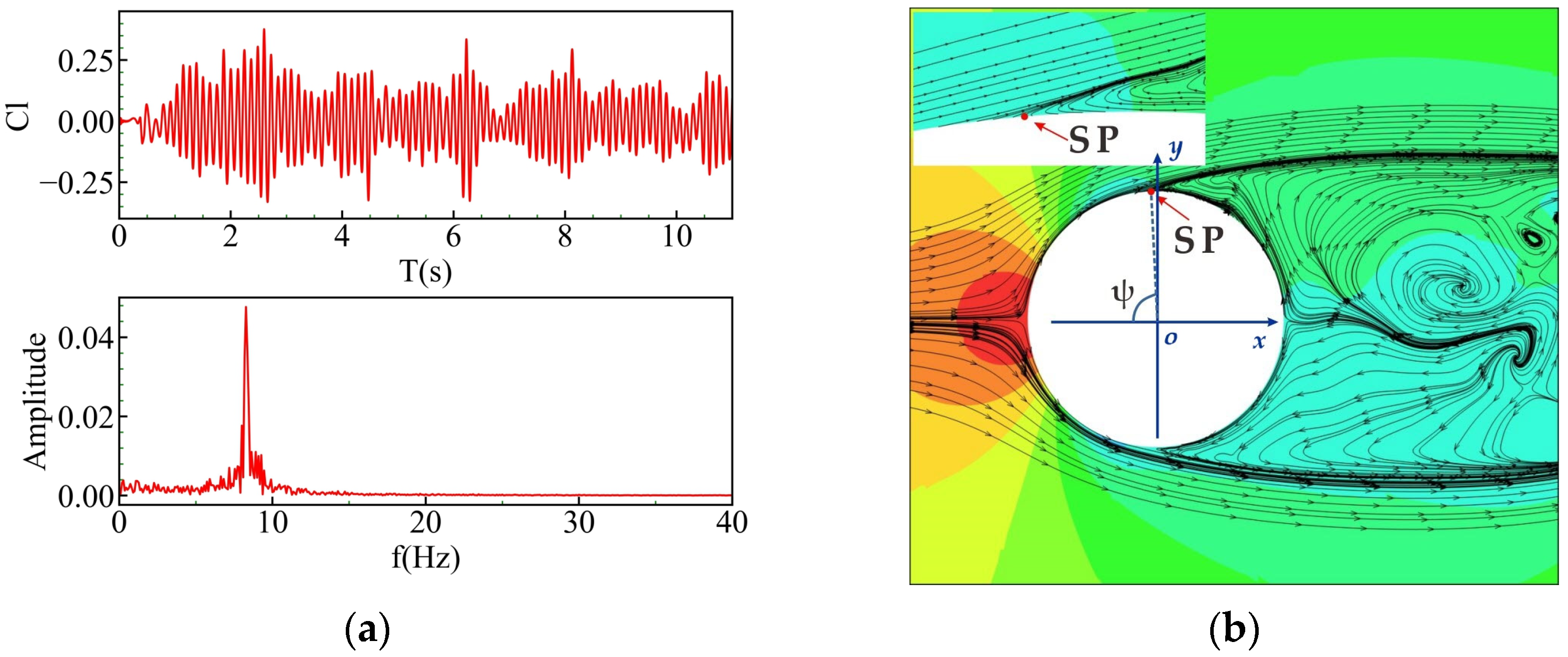
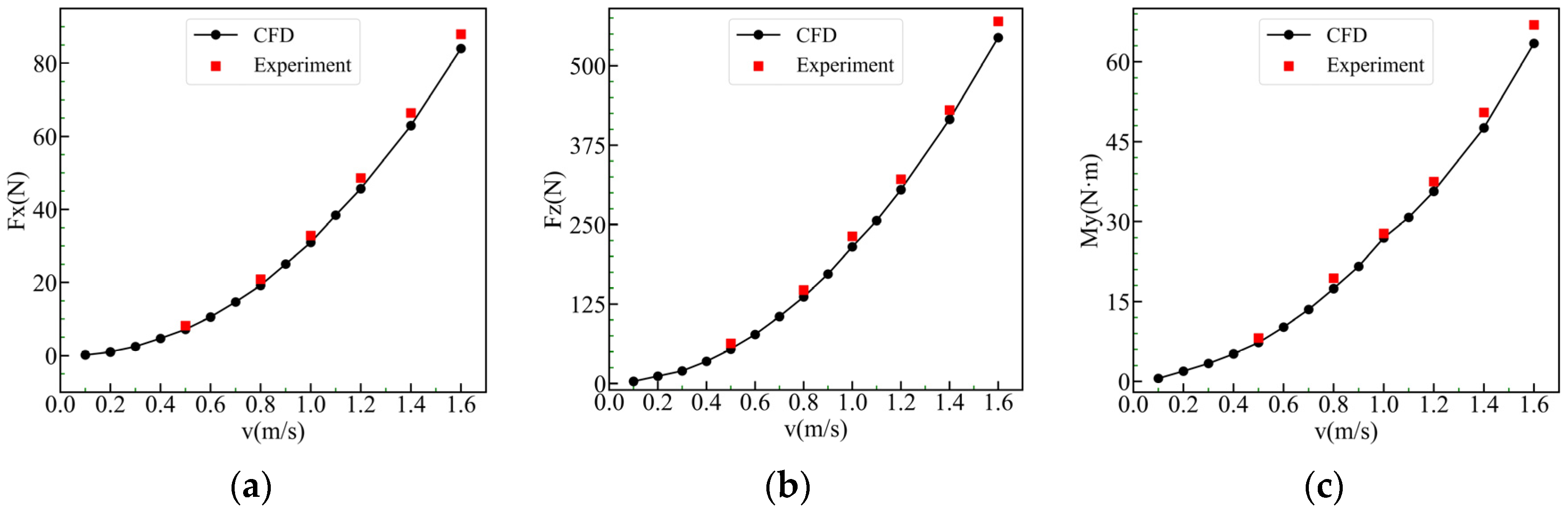
3.2.1. Comparison of the Mean Forces and Moments
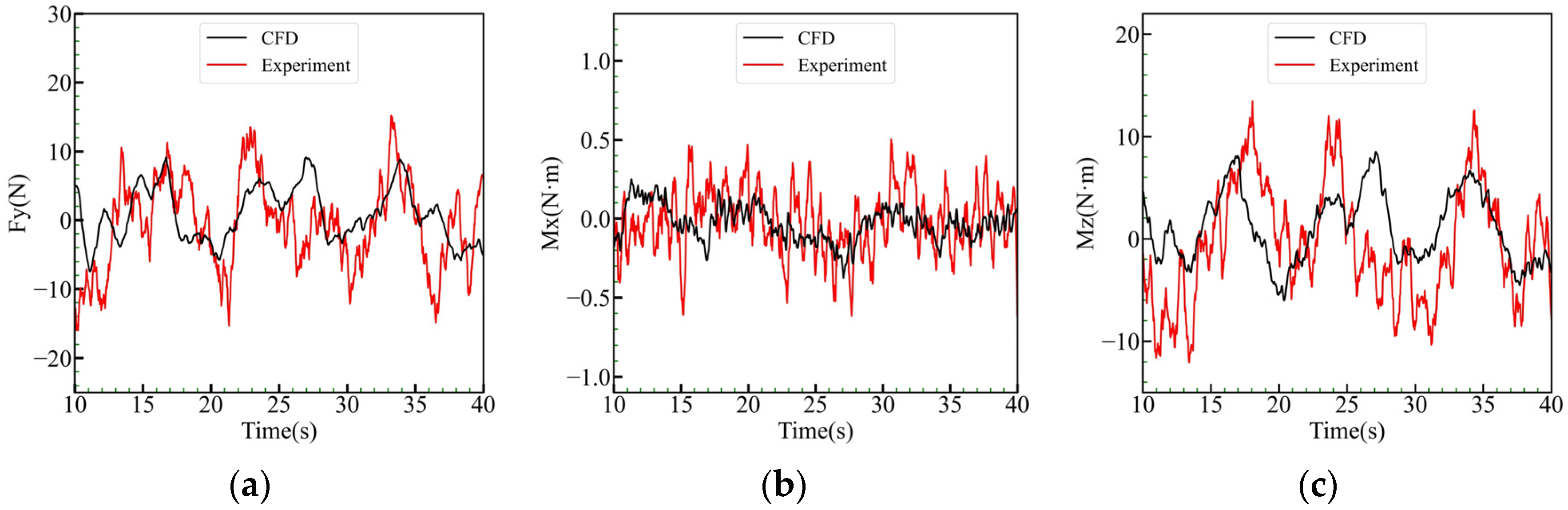
3.2.2. Comparison of the Time-History Forces and Moments
4. Analysis
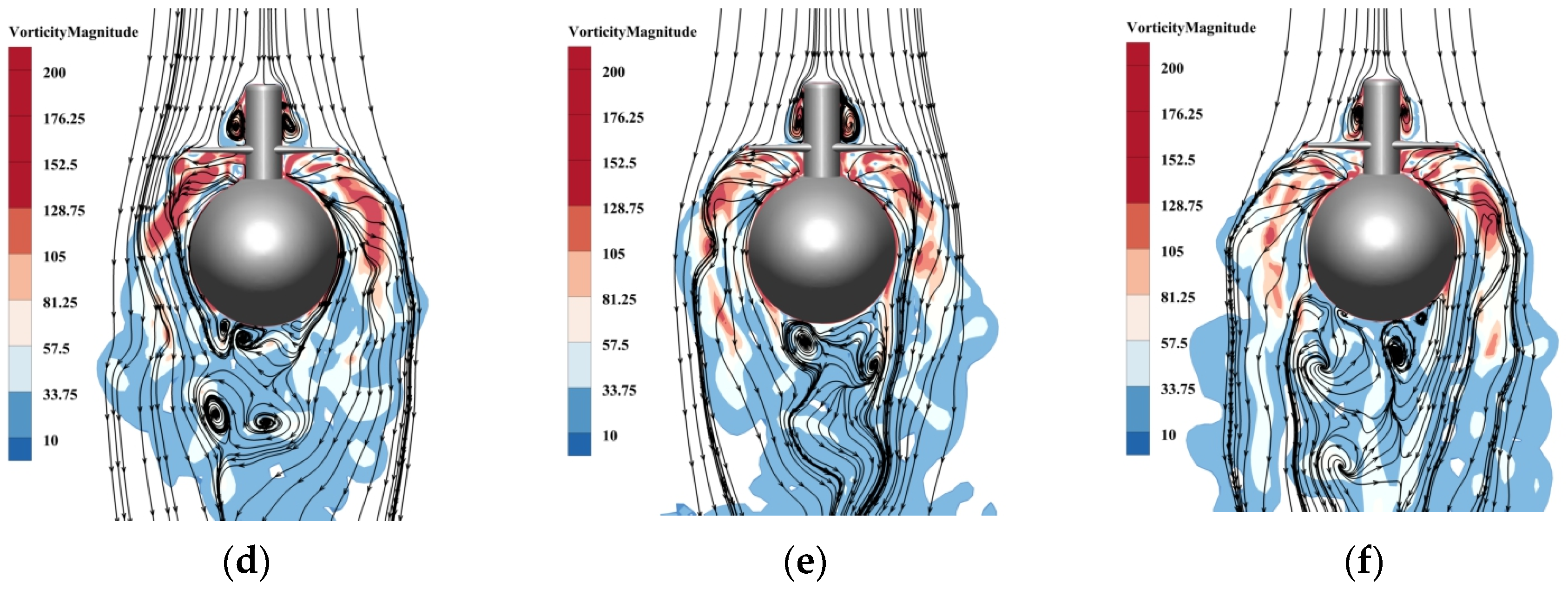
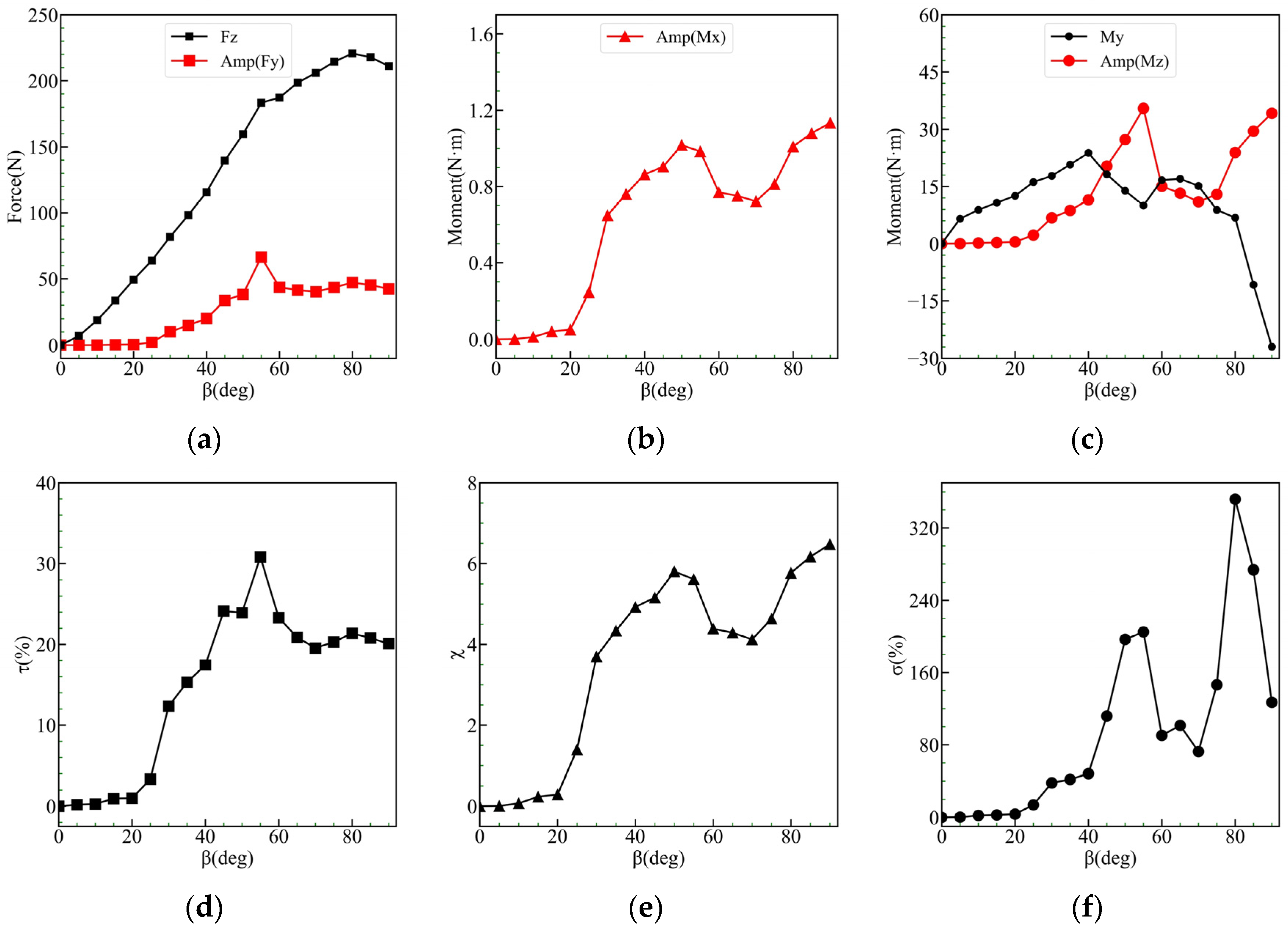
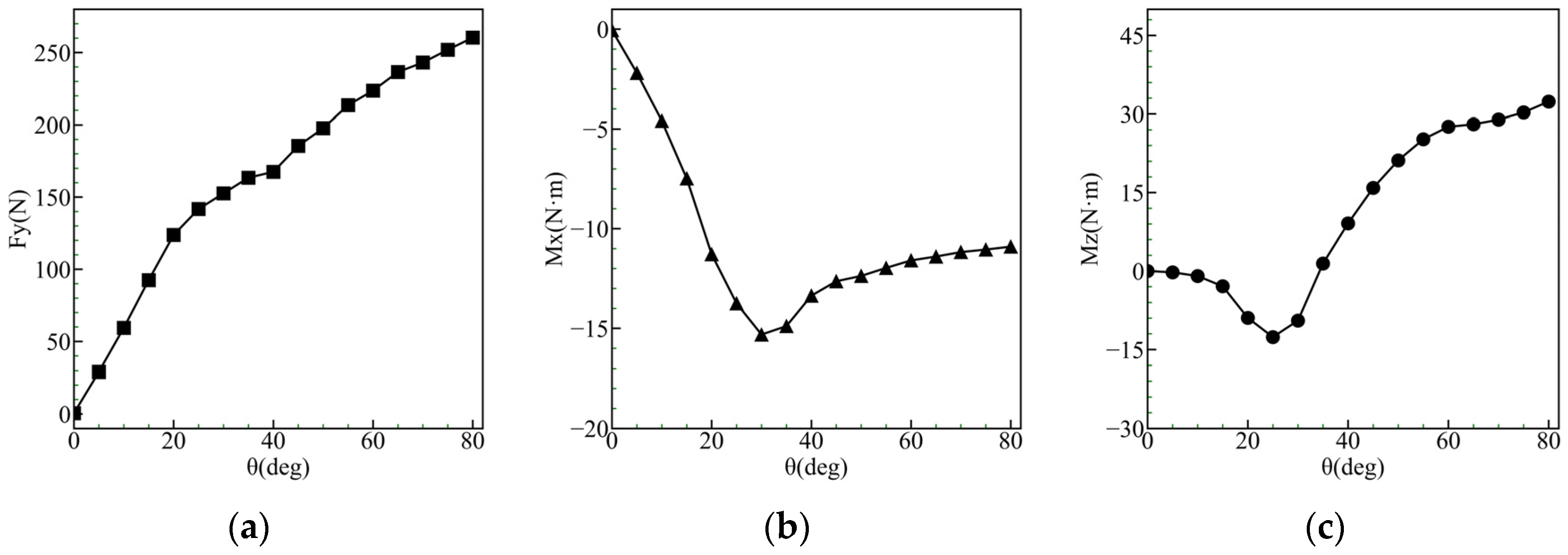
4.1. Analysis of Forces Induced by Flow around the Vertical Plane
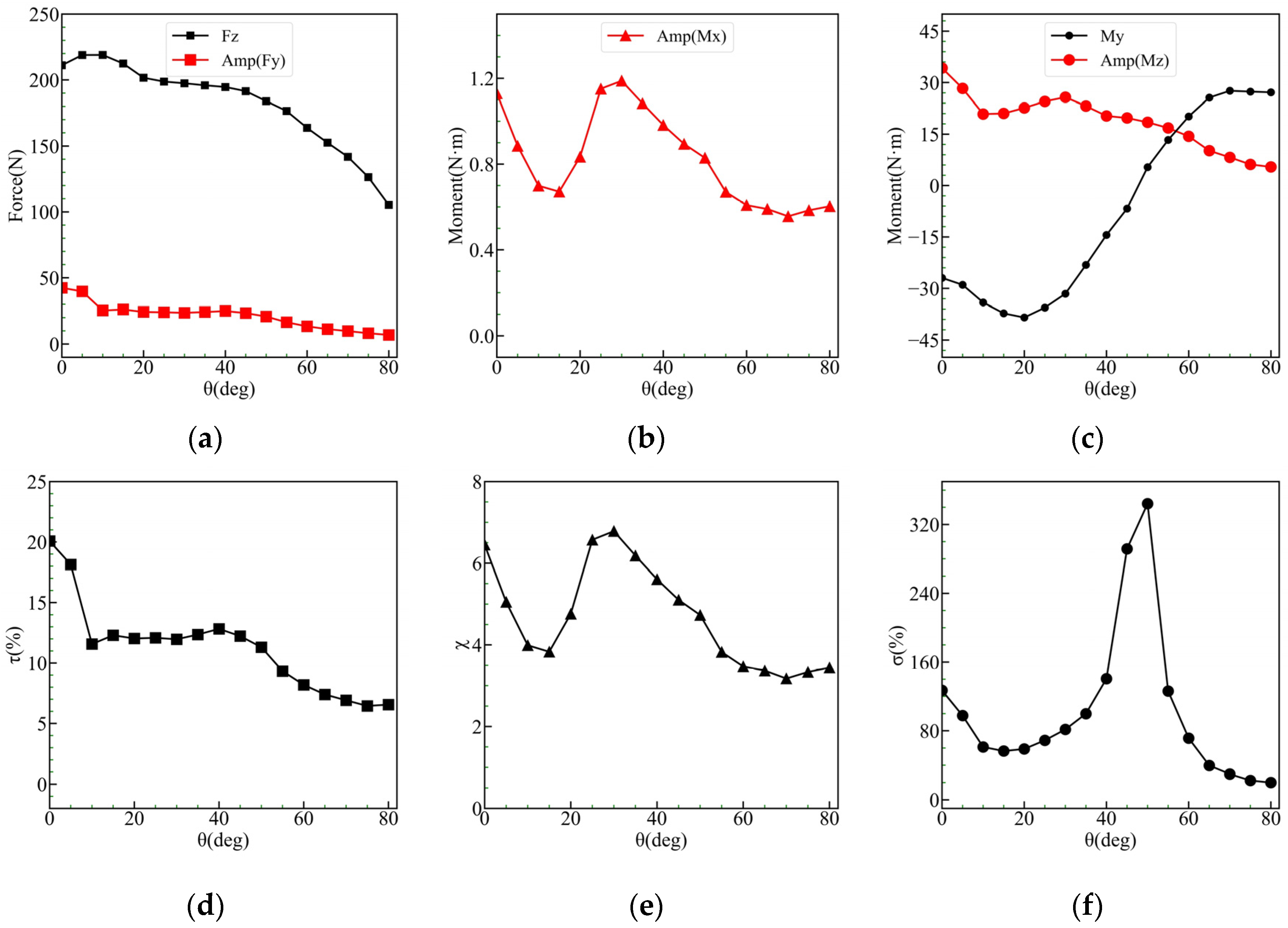
4.2. Impact of the Angle of Attack on the Vertical Plane
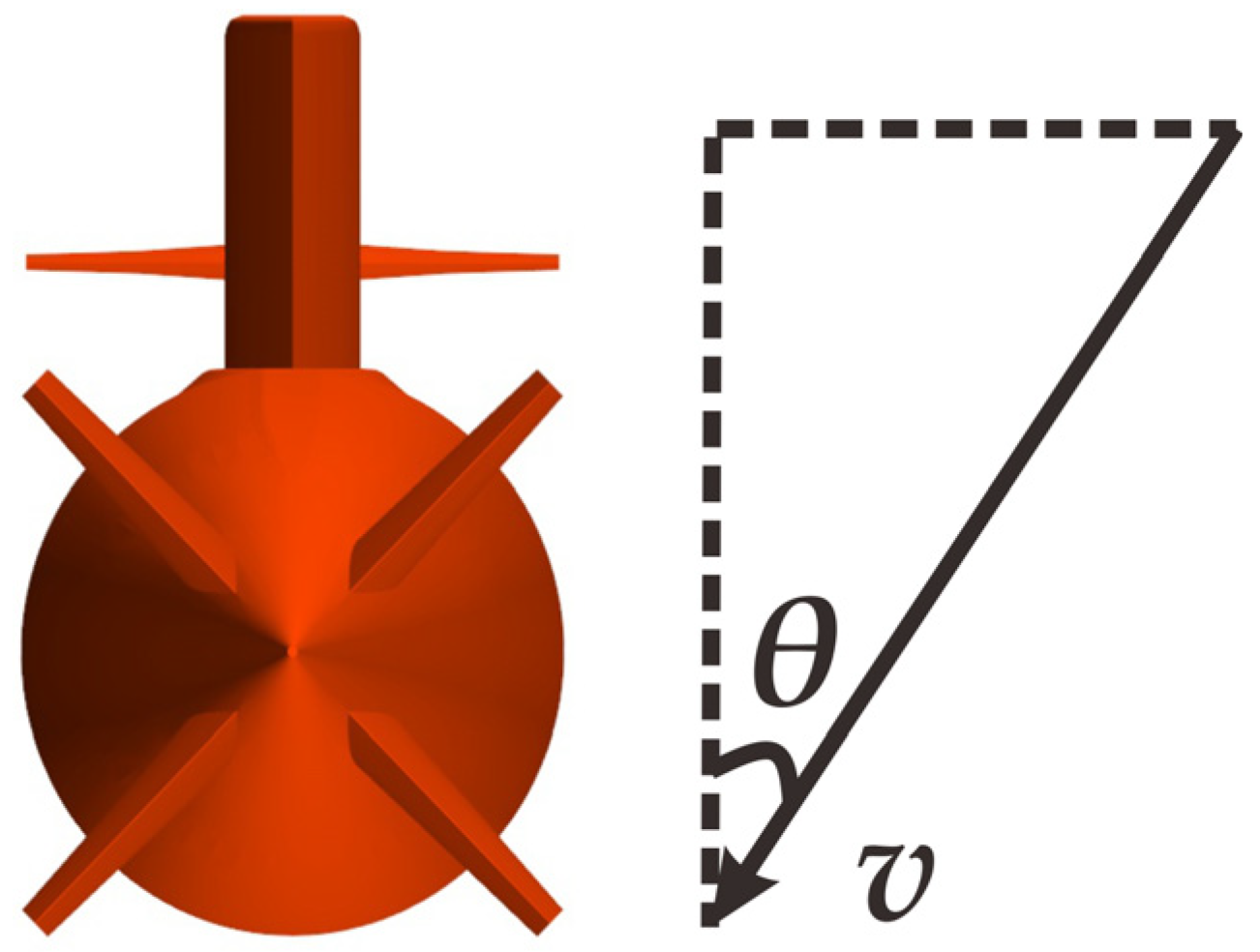
4.3. Impact of the Heel Angle
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schreur, B.G.J.W. The Motion of Buoyant Bodies. Ph.D. Thesis, Trinity College, Cambridge, UK, 1990. [Google Scholar]
- Itard, X. Recovery procedure in case of flooding. In Proceedings of the Warship-International Symposium Then Conference, Brisbane, Australia, 22–25 August 1999. [Google Scholar]
- Watt, G.D.; Bohlmann, H.J. Submarine rising stability: Quasi-steady theory and unsteady effects. In Proceedings of the 25th Symposium on Naval Hydrodynamics, St. John, NL, Canada, 8–13 August 2004. [Google Scholar]
- Bettle, M.C.; Gerber, A.G.; Watt, G.D. Unsteady analysis of the six DOF motion of a buoyantly rising submarine. Comput. Fluids 2009, 38, 1833–1849. [Google Scholar] [CrossRef]
- Chen, Q.; Li, H.; Pang, Y.; Zhang, S.; Chang, W. Investigation of the excess roll problem of an emergent buoyantly rising submarine. J. Fluids Struct. 2019, 91, 102720. [Google Scholar] [CrossRef]
- Watt, G.D. Modelling and Simulating Unsteady Six Degrees-of-Freedom Submarine Rising Maneuvers; Defence R&D Canada-Atlantic: Dartmouth, NS, Canada, 2007. [Google Scholar]
- Liang, X.; Ma, N.; Liu, H.; Gu, X. Experimental study on the maneuvering derivatives of a half-scale SUBOFF model in the vertical plane. Ocean Eng. 2021, 233, 109052. [Google Scholar] [CrossRef]
- Sohail, M.; Chao, Y.; Ullah, R.; Yamin, M. Computational challenges in high angle of attack flow. World Acad. Sci. Eng. Technol. 2011, 80, 1148–1155. [Google Scholar]
- Ma, B.; Huang, Y.; Liu, T. Low-frequency unsteadiness of vortex wakes over slender bodies at high angle of attack. Chin. J. Aeronaut. 2014, 27, 772–780. [Google Scholar] [CrossRef]
- Le Clainche, S.; Li, J.I.; Theofilis, V.; Soria, J. Flow around a hemisphere-cylinder at high angle of attack and low Reynolds number. Part I: Experimental and numerical investigation. Aerosp. Sci. Technol. 2015, 44, 77–87. [Google Scholar] [CrossRef]
- Le Clainche, S.; Rodríguez, D.; Theofilis, V.; Soria, J. Flow around a hemisphere-cylinder at high angle of attack and low Reynolds number. Part II: POD and DMD applied to reduced domains. Aerosp. Sci. Technol. 2015, 44, 88–100. [Google Scholar] [CrossRef]
- de Moraes, P.G.; de Oliveira, M.A.; de Andrade, C.L.; Bimbato, A.M.; Alcântara Pereira, L.A. Effects of surface roughness and wall confinement on bluff body aerodynamics at large-gap regime. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 397. [Google Scholar] [CrossRef]
- Han, X.; Tang, Y.; Meng, Z.; Fu, F.; Qiu, A.; Gu, J.; Wu, J. Surface roughness effect on cylinder vortex-induced vibration at moderate Re regimes. Ocean Eng. 2021, 224, 108690. [Google Scholar] [CrossRef]
- Strelets, M. Detached Eddy Simulation of Massively Separated Flows. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar]
- Spalart, P.; Jou, W.H.; Strelets, M.; Allmaras, S. Comments on the Feasibility of LES for Wings, and on a Hybrid RANS/LES Approach. In Proceedings of the First AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Weiwen, Z.; Decheng, W. Detached Eddy Simulation of Flow Past Tandem Cylinders. Appl. Math. Mech. 2016, 37, 1272. [Google Scholar]
- Nguyen, V.T.; Nguyun, H.H. Detached eddy simulations of flow induced vibrations of circular cylinders at high Reynolds numbers. J. Fluids Struct. 2016, 63, 103–119. [Google Scholar] [CrossRef]
- Yao, J.; Jinsheng, C.; Fei, L. Comparative Numerical Studies of Flow Past Cylinder at Reynolds Number 3900. Appl. Math. Mech. 2016, 37, 1282. [Google Scholar]
- Liu, Z.; Yang, Y.; Zhou, W.; Gong, A. Study of Unsteady Separation Flow Around Airfoil at High Angle of Attack Using Hybrid RANS-LES Method. Acta Aeronaut. Astronaut. Sin. 2014, 35, 372–380. [Google Scholar]
- Oliger, B.J. Adaptive mesh refinement for hyperbolic partial differential equations. J. Comput. Phys. 1984, 52, 484–512. [Google Scholar]
- Bao, G.; Chen, Z.; Wu, H. Adaptive finite-element method for diffraction gratings. J. Opt. Soc. Am. A 2005, 22, 1106–1114. [Google Scholar] [CrossRef] [PubMed]
- Golay, F.; Ersoy, M.; Yushchenko, L.; Sous, D. Block-based adaptive mesh refinement scheme using numerical density ofentropy production for three-dimensional two-fluid flows. Int. J. Comput. Fluid Dyn. 2015, 29, 67–81. [Google Scholar] [CrossRef]
- Gou, J.; Su, X.; Yuan, X. Adaptive mesh refinement method-based large eddy simulation for the flow over circular cylinder at ReD = 3900. Int. J. Comput. Fluid Dyn. 2018, 32, 1–8. [Google Scholar] [CrossRef]
- Mozaffari, S.; Guilmineau, E.; Visonneau, M.; Wackers, J. Average-based mesh adaptation for hybrid RANS/LES simulation of complex flows. Comput. Fluids 2022, 232, 105202. [Google Scholar] [CrossRef]
- Liu, C.Q.; Wang, Y.Q.; Yang, Y.; Duan, Z.W. New omega vortex identification method. Sci. China 2016, 59, 684711. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Transport Turbulence Model for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A New Version of Detached-eddy Simulation, Resistant to Ambiguous Grid Densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Dong, X.; Wang, Y.; Chen, X.; Dong, Y.; Zhang, Y.; Liu, C. Determination of epsilon for Omega vortex identification method. J. Hydrodyn. 2018, 30, 541–548. [Google Scholar] [CrossRef]
- Parnaudeau, P.; Carlier, J.; Heitz, D.; Lamballais, E. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 2008, 20, 085101. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]














| Parameter | Unit | Value |
|---|---|---|
| Total length L | m | 3.0 |
| Diameter DL | m | 0.3 |
| Displacement Δ | kg | 170.5 |
| Height of CB above CG BG | m | 0.006 |
| Roll moment per degree Mθ | N·m | 0.175 |
| Parameter | Unit | Value |
|---|---|---|
| Towing tank dimensions | m | 510 × 6.5 × 5 |
| Effective working length | m | 450 |
| Depth | m | 2.5 |
| Towing speed | m/s | 0.5~12 |
| Towing speed error | - | <1.5% |
| St | ψ | Umin/U0 | |
|---|---|---|---|
| Experiment | 0.208 ± 0.002 | 86.0° ± 2 | −0.340 |
| SST-DDES | 0.213 | 87.2 | −0.312 |
| w (m/s) | Fx (N) | Fz (N) | My (N·m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EXP. | CFD | Error | EXP. | CFD | Error | EXP. | CFD | Error | |
| 0.5 | 8.20 | 7.17 | 12.6% | 63.04 | 54.25 | 14.0% | 8.14 | 7.27 | 10.7% |
| 0.8 | 20.89 | 19.21 | 8.0% | 147.11 | 136.40 | 7.3% | 19.37 | 17.43 | 10.0% |
| 1 | 32.85 | 30.95 | 5.8% | 231.58 | 215.07 | 7.1% | 27.80 | 26.95 | 3.0% |
| 1.2 | 48.59 | 45.70 | 6.0% | 321.33 | 305.04 | 5.1% | 37.50 | 35.68 | 4.9% |
| 1.4 | 66.43 | 62.94 | 5.3% | 430.21 | 415.49 | 3.4% | 50.49 | 47.59 | 5.7% |
| 1.6 | 87.95 | 84.04 | 4.4% | 569.68 | 544.34 | 4.4% | 66.93 | 63.46 | 5.2% |
| w (m/s) | Amplitude of Fy (N) | Amplitude of Mx (N·m) | Amplitude of Mz (N·m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EXP. | CFD | Error | EXP. | CFD | Error | EXP. | CFD | Error | |
| 0.5 | 15.47 | 9.14 | 40.9% | 0.62 | 0.38 | 39.3% | 13.41 | 8.50 | 36.7% |
| 1.0 | 55.34 | 44.73 | 19.2% | 1.58 | 1.32 | 16.6% | 52.93 | 42.96 | 18.8% |
| 1.6 | 112.24 | 127.89 | 13.9% | 3.51 | 3.77 | 7.4% | 116.73 | 102.79 | 11.9% |
| w (m/s) | Fundamental Frequency of Fy | Fundamental Frequency of Mx | Fundamental Frequency of Mz | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EXP. | CFD | Error | EXP. | CFD | Error | EXP. | CFD | Error | |
| 0.5 | 0.133 | 0.100 | 25.0% | 0.143 | 0.100 | 30.2% | 0.127 | 0.100 | 21.5% |
| 1.0 | 0.219 | 0.200 | 8.7% | 0.231 | 0.200 | 13.4% | 0.212 | 0.200 | 5.6% |
| 1.6 | 0.351 | 0.349 | 0.6% | 0.347 | 0.350 | 0.9% | 0.353 | 0.350 | 0.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, G.; Ou, Y.; Chen, J.; Wang, W.; Wu, H. Numerical Study on the Flow Characteristics of High Attack Angle around the Submarine’s Vertical Plane. Appl. Sci. 2024, 14, 395. https://doi.org/10.3390/app14010395
Xiang G, Ou Y, Chen J, Wang W, Wu H. Numerical Study on the Flow Characteristics of High Attack Angle around the Submarine’s Vertical Plane. Applied Sciences. 2024; 14(1):395. https://doi.org/10.3390/app14010395
Chicago/Turabian StyleXiang, Guo, Yongpeng Ou, Junjie Chen, Wei Wang, and Hao Wu. 2024. "Numerical Study on the Flow Characteristics of High Attack Angle around the Submarine’s Vertical Plane" Applied Sciences 14, no. 1: 395. https://doi.org/10.3390/app14010395
APA StyleXiang, G., Ou, Y., Chen, J., Wang, W., & Wu, H. (2024). Numerical Study on the Flow Characteristics of High Attack Angle around the Submarine’s Vertical Plane. Applied Sciences, 14(1), 395. https://doi.org/10.3390/app14010395




