Genetic Multi-Objective Optimization of Sensor Placement for SHM of Composite Structures
Abstract
:1. Introduction
2. Tested Structure and Experiments
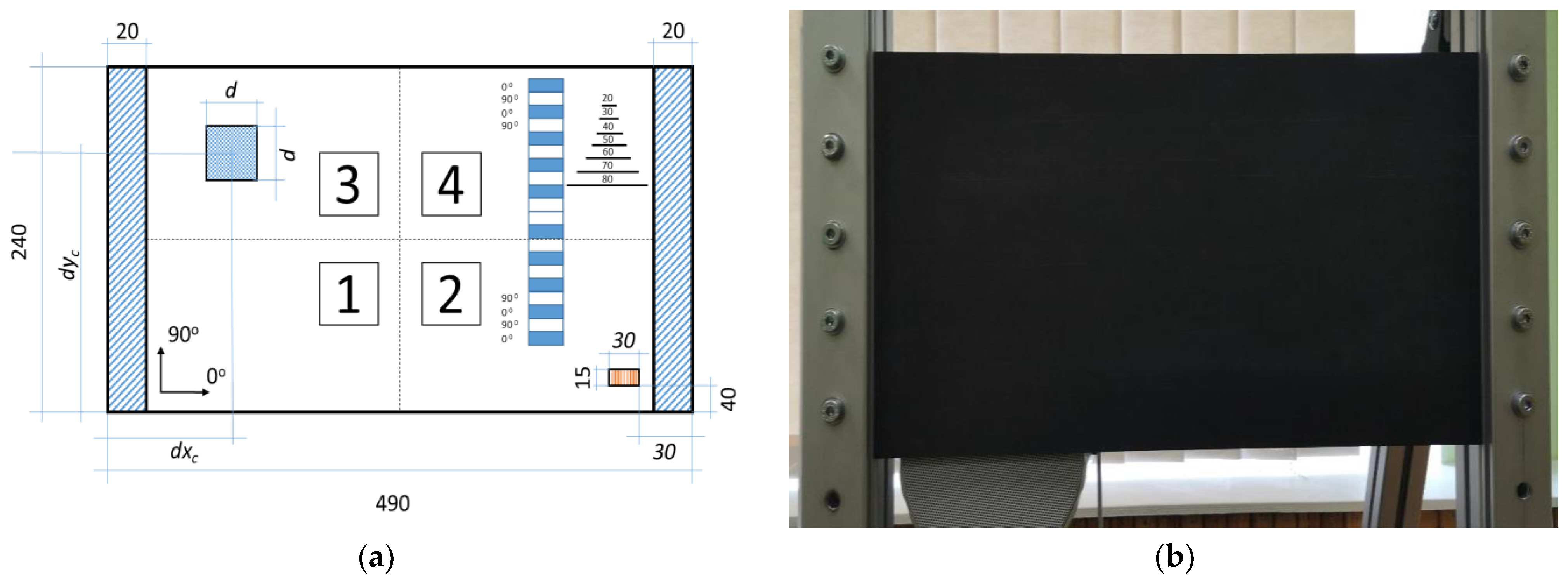
2.1. Parameters of the Tested Structure
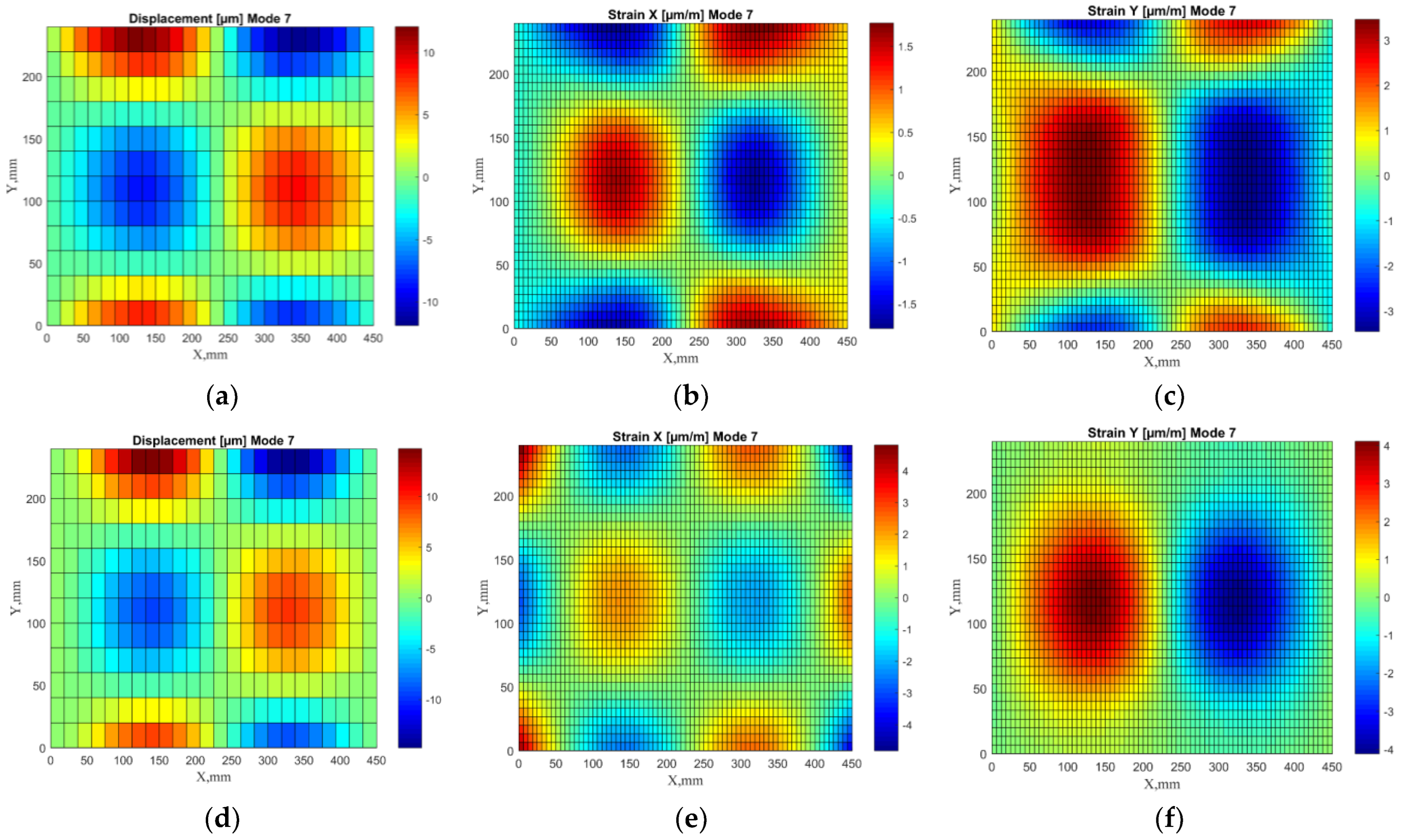
2.2. Numerical Experiments
3. Multi-Objective Optimization
3.1. OSP Problem
3.2. General Optimization Procedure
3.3. Data Preparation
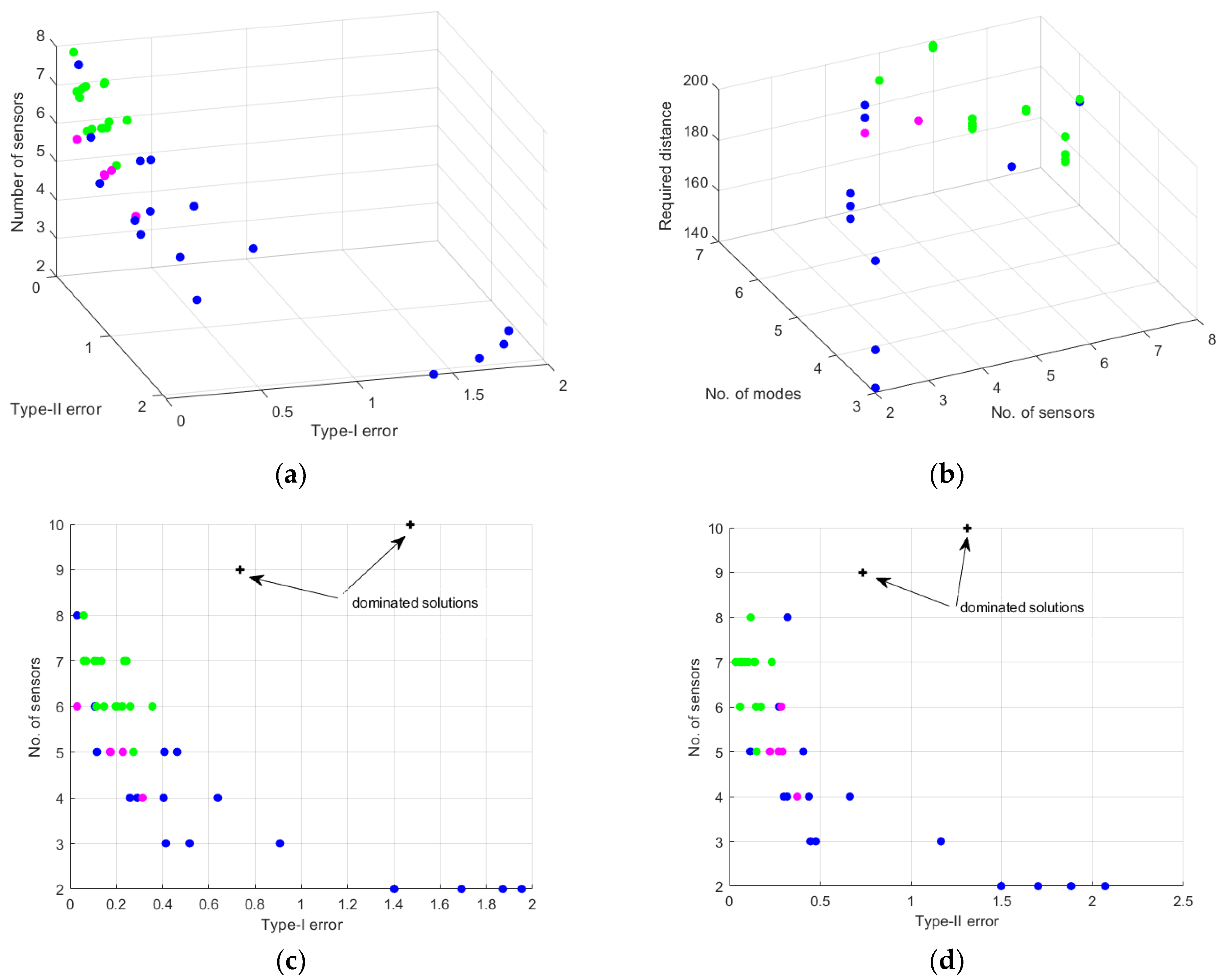
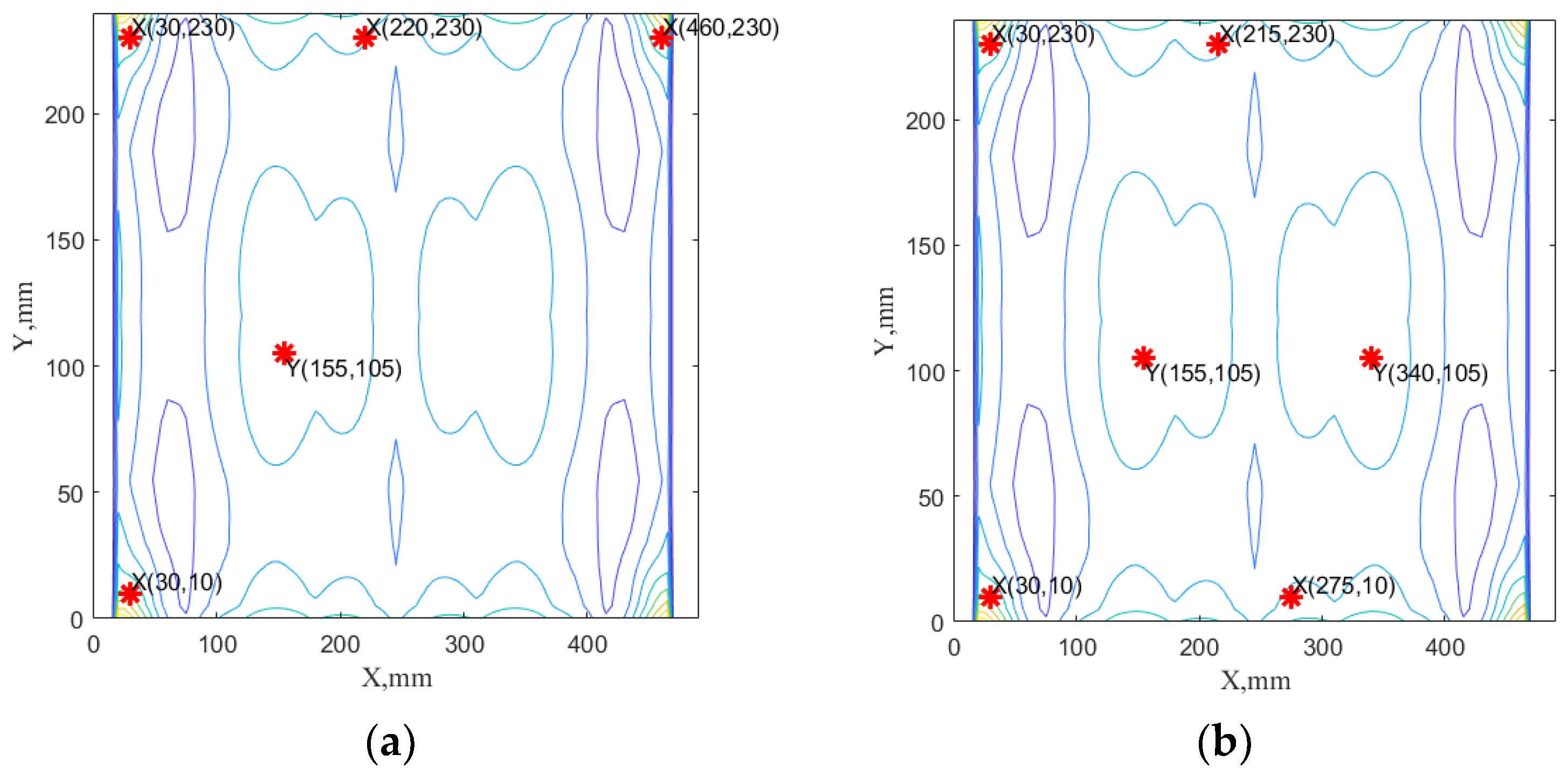
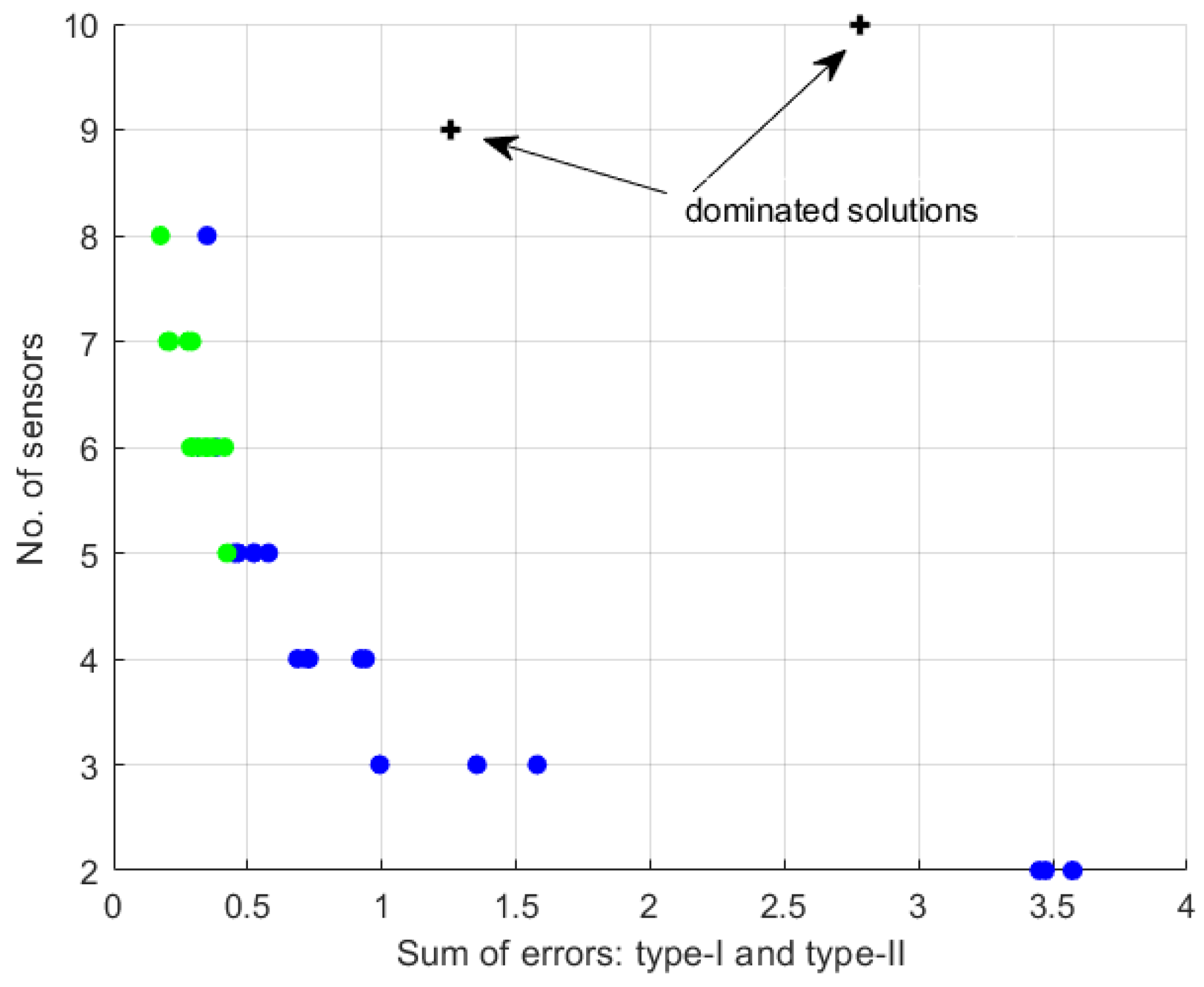
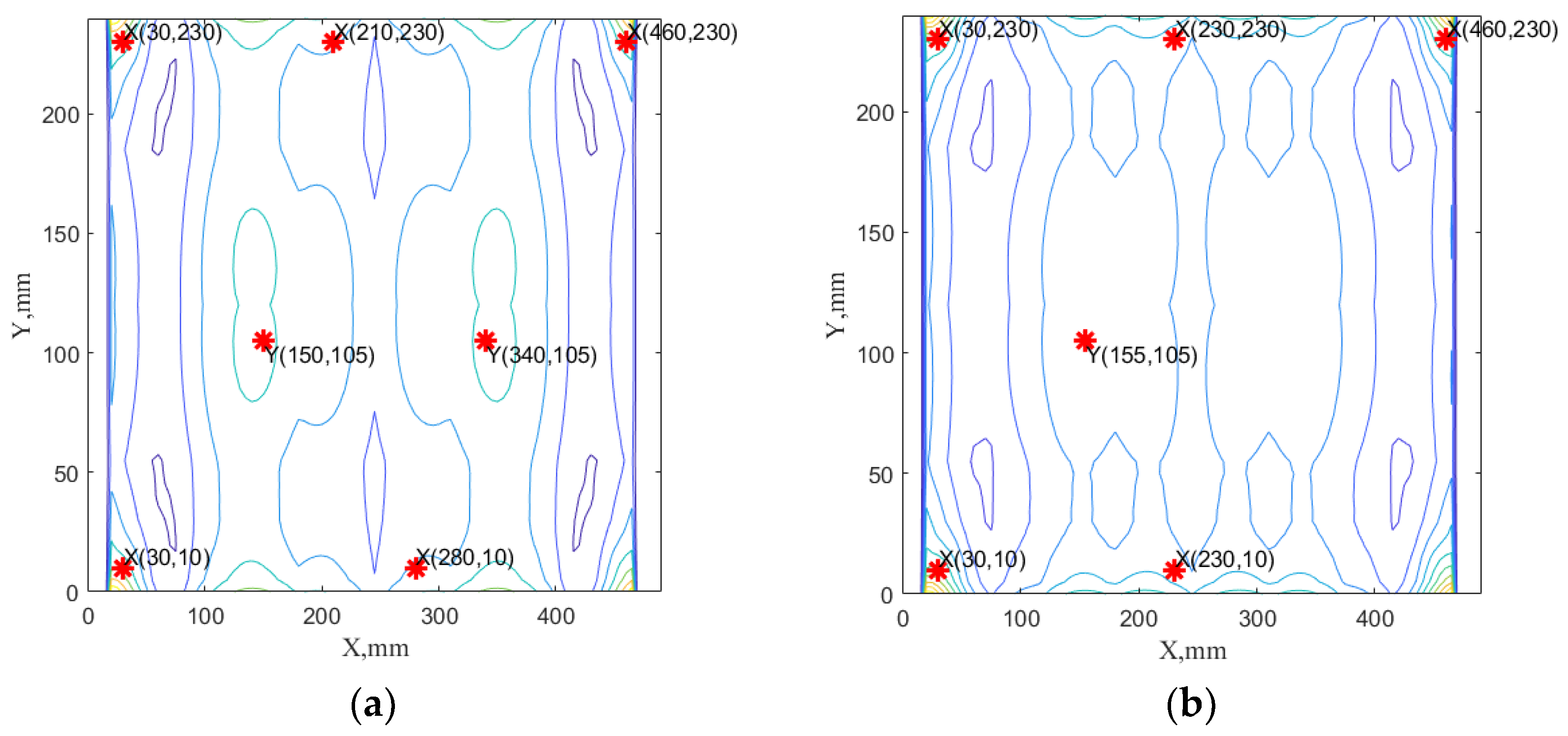
3.4. Optimization Results
4. Analysis and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tinga, T.; Loendersloot, R. Aligning PHM, SHM and CBM by understanding the physical system failure behaviour. In Proceedings of the PHM Society European Conference, Nantes, France, 8–10 July 2014. [Google Scholar]
- Broer, A.A.R.; Benedictus, R.; Zarouchas, D. The need for multi-sensor data fusion in structural health monitoring of composite aircraft structures. Aerospace 2022, 9, 183. [Google Scholar] [CrossRef]
- Sadhu, A.; Peplinski, J.E.; Mohammadkhorasani, A.; Moreu, F. A review of data management and visualization techniques for structural health monitoring using BIM and virtual or augmented reality. J. Stuct. Eng. 2022, 149, 03122006. [Google Scholar] [CrossRef]
- Fawad, M.; Salamak, M.; Poprawa, G.; Koris, K.; Jasinski, M.; Lazinski, P.; Piotrowski, D.; Hasnain, M.; Gerges, M. Automation of structural health monitoring (SHM) system of a bridge using BIMification approach and BIM-based finite element model development. Sci. Rep. 2023, 13, 13215. [Google Scholar] [CrossRef] [PubMed]
- Bado, F.M.; Tonelli, D.; Poli, F.; Zonta, D.; Casas, J.R. Digital twin for civil engineering systems: An exploratory review for distributed sensing updating. Sensors 2022, 22, 3168. [Google Scholar] [CrossRef]
- Janeliukstis, R.; Mironovs, D.; Safronovs, A. Statistical structural integrity control of composite structures based on an automatic operational modal analysis—A review. Mech. Compos. Mater. 2022, 58, 181–208. [Google Scholar] [CrossRef]
- Ručevskis, S.; Rogala, T.; Katunin, A. Optimal sensor placement for modal-based health monitoring of a composite structure. Sensors 2022, 22, 3867. [Google Scholar] [CrossRef]
- Ručevskis, S.; Rogala, T.; Katunin, A. Monitoring of damage in composite structures using an optimized sensor network: A data-driven experimental approach. Sensors 2023, 23, 2290. [Google Scholar] [CrossRef] [PubMed]
- Barthorpe, R.J.; Worden, K. Emerging Trends in Optimal Structural Health Monitoring System Design: From Sensor Placement to System Evaluation. J. Sens. Actuator Netw. 2020, 9, 31. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U. A Systematic Review of Optimization Algorithms for Structural Health Monitoring and Optimal Sensor Placement. Sensors 2023, 23, 3293. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Yao, Y.; Ou, J. Advancements in Optimal Sensor Placement for Enhanced Structural Health Monitoring: Current Insights and Future Prospects. Buildings 2023, 13, 3129. [Google Scholar] [CrossRef]
- Kammer, D.C. Sensor placement for on-orbit modal identification and correlation of large space structures. J. Guid. Control Dyn. 1991, 14, 251–259. [Google Scholar] [CrossRef]
- Azin Mehrjoo, B.; Moaveni, B.; Papadimitriou, C.; Khan, U.; Rife, J. Iterative optimal sensor placement for adaptive structural identification using mobile sensors: Numerical application to a footbridge. Mech. Syst. Signal Process. 2023, 200, 110556. [Google Scholar]
- Zhang, B.-Y.; Ni, Y.-Q. A data-driven sensor placement strategy for reconstruction of mode shapes by using recurrent Gaussian process regression. Eng. Struct. 2023, 284, 115998. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Tao, J.; Huang, H.-H. A Multiobjective Perspective to Optimal Sensor Placement by Using a Decomposition-Based Evolutionary Algorithm in Structural Health Monitoring. Appl. Sci. 2020, 10, 7710. [Google Scholar] [CrossRef]
- Civera, M.; Pecoreelli, M.L.; Ceravolo, R.; Surace, C.; Fragonara, L.Z. A multi-objective genetic algorithm strategy for robust optimal sensor placement. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 1185–1202. [Google Scholar] [CrossRef]
- de Souza Mello, F.M.; Pereira, J.L.J.; Gomes, G.F. Multi-objective sensor placement optimization in SHM systems with Kriging-based mode shape interpolation. J. Sound Vib. 2024, 568, 118050. [Google Scholar] [CrossRef]
- Yang, C.; Xia, Y. Interval Pareto front-based multi-objective robust optimization for sensor placement in structural modal identification. Reliab. Eng. Syst. Saf. 2024, 242, 109703. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons, Ltd.: Chichester, UK, 2001. [Google Scholar]
- Zhang, Z.; Peng, C.; Wang, G.; Ju, Z.; Ma, L. A new optimal sensor placement method for virtual sensing of composite laminate. Mech. Syst. Signal Process. 2023, 195, 110319. [Google Scholar] [CrossRef]
- Guratzsch, R.F.; Mahadevan, S. Structural health monitoring sensor placement optimization under uncertainty. AIAA J. 2010, 48, 1281. [Google Scholar] [CrossRef]
- Downey, A.; Hu, C.; Laflamme, S. Optimal sensor placement within a hybrid dense sensor network using an adaptive genetic algorithm with learning gene pool. Struct. Health Monit. 2018, 17, 450–460. [Google Scholar] [CrossRef]
- Gomes, G.F.; de Almeida, F.A.; da Silva Lopes Alexandrino, P.; da Cunha, S.S.; de Sousa, B.S.; Ancelotti, A.C. A multi-objective sensor placement optimization for SHM systems considering Fisher information matrix and mode shape interpolation. Eng. Comput. 2019, 35, 519–535. [Google Scholar] [CrossRef]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2021, 17, 168–192. [Google Scholar] [CrossRef]
- Nong, S.-X.; Yang, D.-H.; Yi, T.-H. Pareto-Based Bi-Objective Optimization Method of Sensor Placement in Structural Health Monitoring. Buildings 2021, 11, 549. [Google Scholar] [CrossRef]
- Yang, Y.; Chadha, M.; Hu, Z.; Todd, M.D. An optimal sensor design framework accounting for sensor reliability over the structural life cycle. Mech. Syst. Signal Process. 2023, 202, 110673. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- An, H.; Youn, B.D.; Kim, H.S. A methodology for sensor number and placement optimization for vibration-based damage detection of composite structures under model uncertainty. Compos. Struct. 2022, 279, 114863. [Google Scholar] [CrossRef]
- An, H.; Youn, B.D.; Kim, H.S. Optimal placement of non-redundant sensors for structural health monitoring under model uncertainty and measurement noise. Measurement 2022, 204, 112102. [Google Scholar] [CrossRef]
- Mendler, A.; Döhler, M.; Ventura, C.E. Sensor placement with optimal damage detectability for statistical damage detection. Mech. Syst. Signal Process. 2022, 170, 108767. [Google Scholar] [CrossRef]
- Deep, K.; Singh, K.P.; Kansal, M.L.; Mohan, C. A real coded genetic algorithm for solving integer and mixed integer optimization problems. Appl. Math. Comput. 2009, 212, 505–518. [Google Scholar] [CrossRef]

| Mode No. | Frequency, Hz | Vibration Velocity, 10−4 m/s |
|---|---|---|
| 1 | 58.20 | 0.2 |
| 2 | 67.58 | 0.17 |
| 3 | 159.76 | 0.31 |
| 4 | 174.22 | 0.48 |
| 5 | 232.81 | 1.1 |
| 6 | 294.92 | 0.66 |
| 7 | 299.61 | 1.37 |
| 8 | 339.45 | 0.41 |
| 9 | 434.76 | 0.53 |
| 10 | 543.36 | 0.47 |
| 11 | 562.11 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rogala, T.; Ścieszka, M.; Katunin, A.; Ručevskis, S. Genetic Multi-Objective Optimization of Sensor Placement for SHM of Composite Structures. Appl. Sci. 2024, 14, 456. https://doi.org/10.3390/app14010456
Rogala T, Ścieszka M, Katunin A, Ručevskis S. Genetic Multi-Objective Optimization of Sensor Placement for SHM of Composite Structures. Applied Sciences. 2024; 14(1):456. https://doi.org/10.3390/app14010456
Chicago/Turabian StyleRogala, Tomasz, Mateusz Ścieszka, Andrzej Katunin, and Sandris Ručevskis. 2024. "Genetic Multi-Objective Optimization of Sensor Placement for SHM of Composite Structures" Applied Sciences 14, no. 1: 456. https://doi.org/10.3390/app14010456
APA StyleRogala, T., Ścieszka, M., Katunin, A., & Ručevskis, S. (2024). Genetic Multi-Objective Optimization of Sensor Placement for SHM of Composite Structures. Applied Sciences, 14(1), 456. https://doi.org/10.3390/app14010456








