A 3D-0D Computational Model of the Left Ventricle for Investigating Blood Flow Patterns for Cases of Systolic Anterior Motion and after Anterior Mitral Leaflet Splitting
Abstract
1. Introduction
2. Materials and Methods
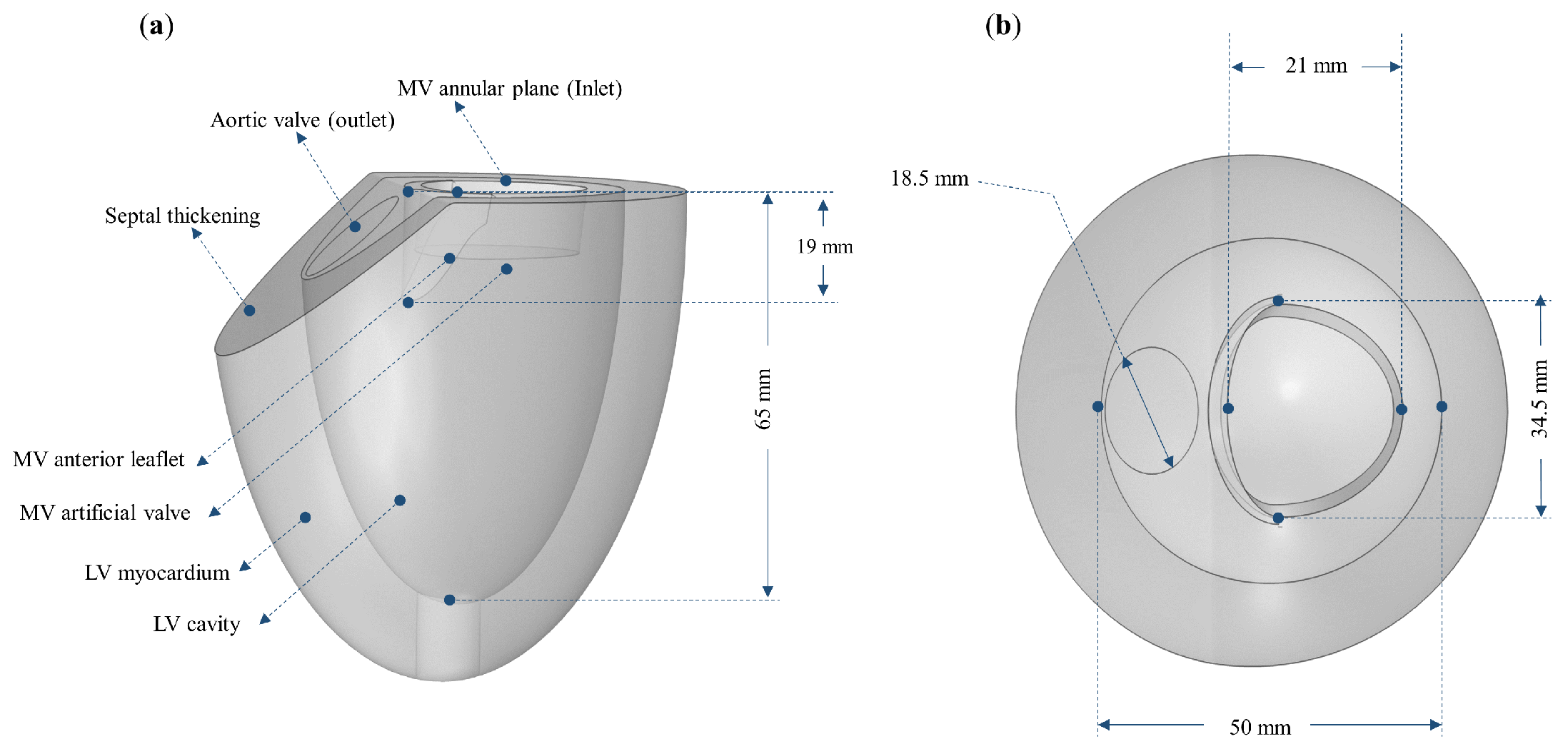
2.1. Model Geometry
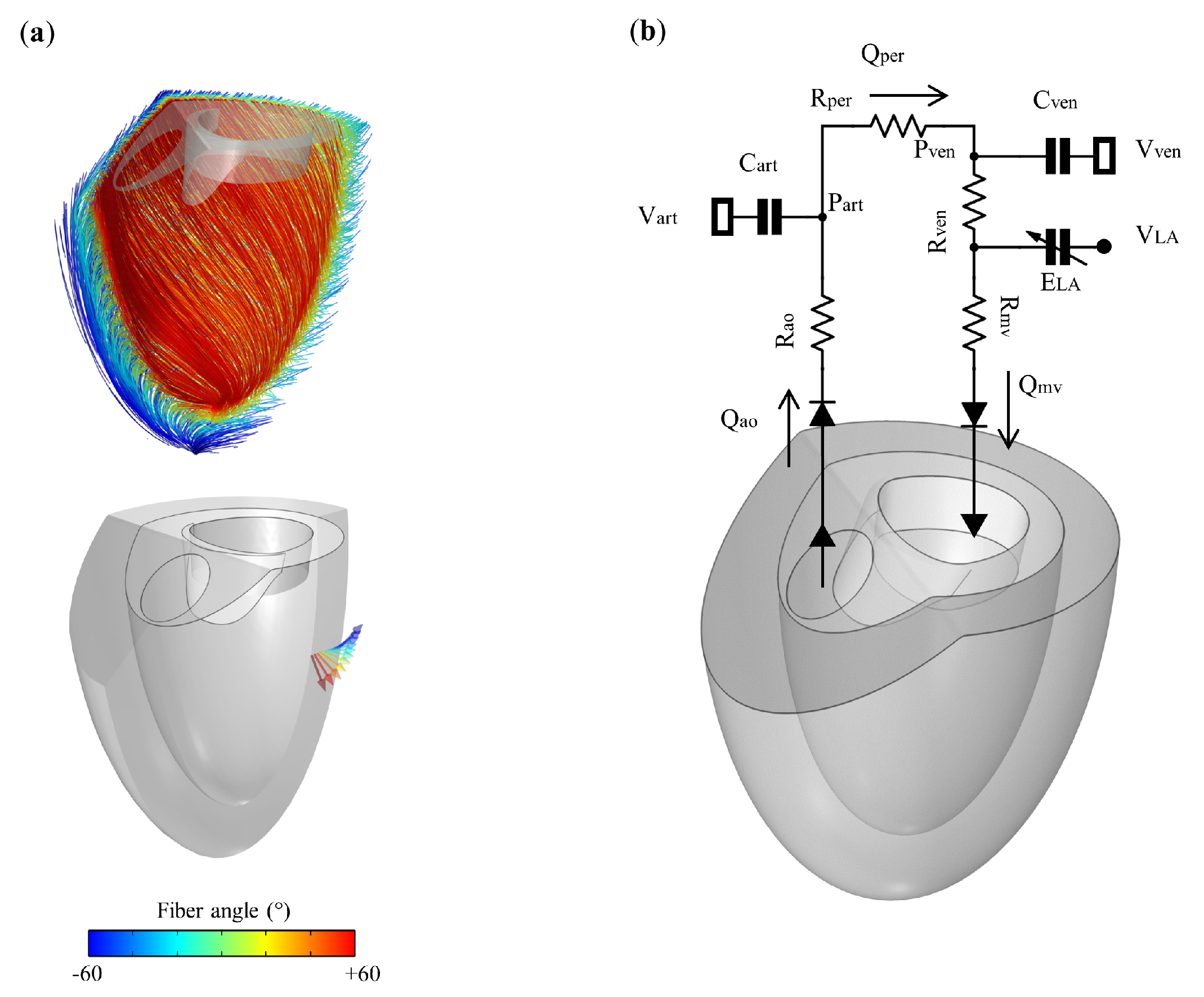
2.2. LV Mechanics and Fluid Formulation
2.3. 0D Closed-Loop Windkessel Circulatory
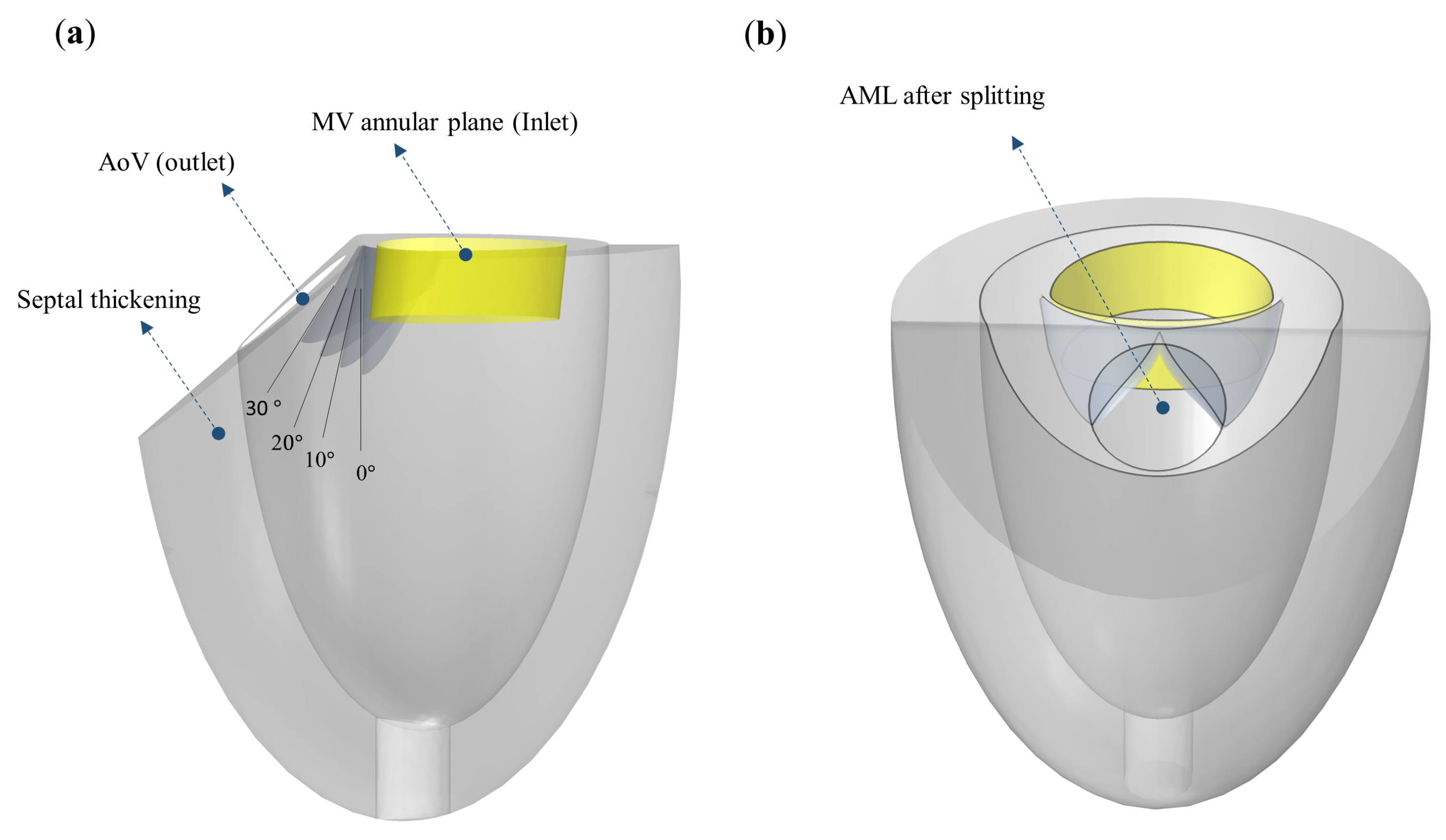
2.4. Model Setting for SAM Simulations
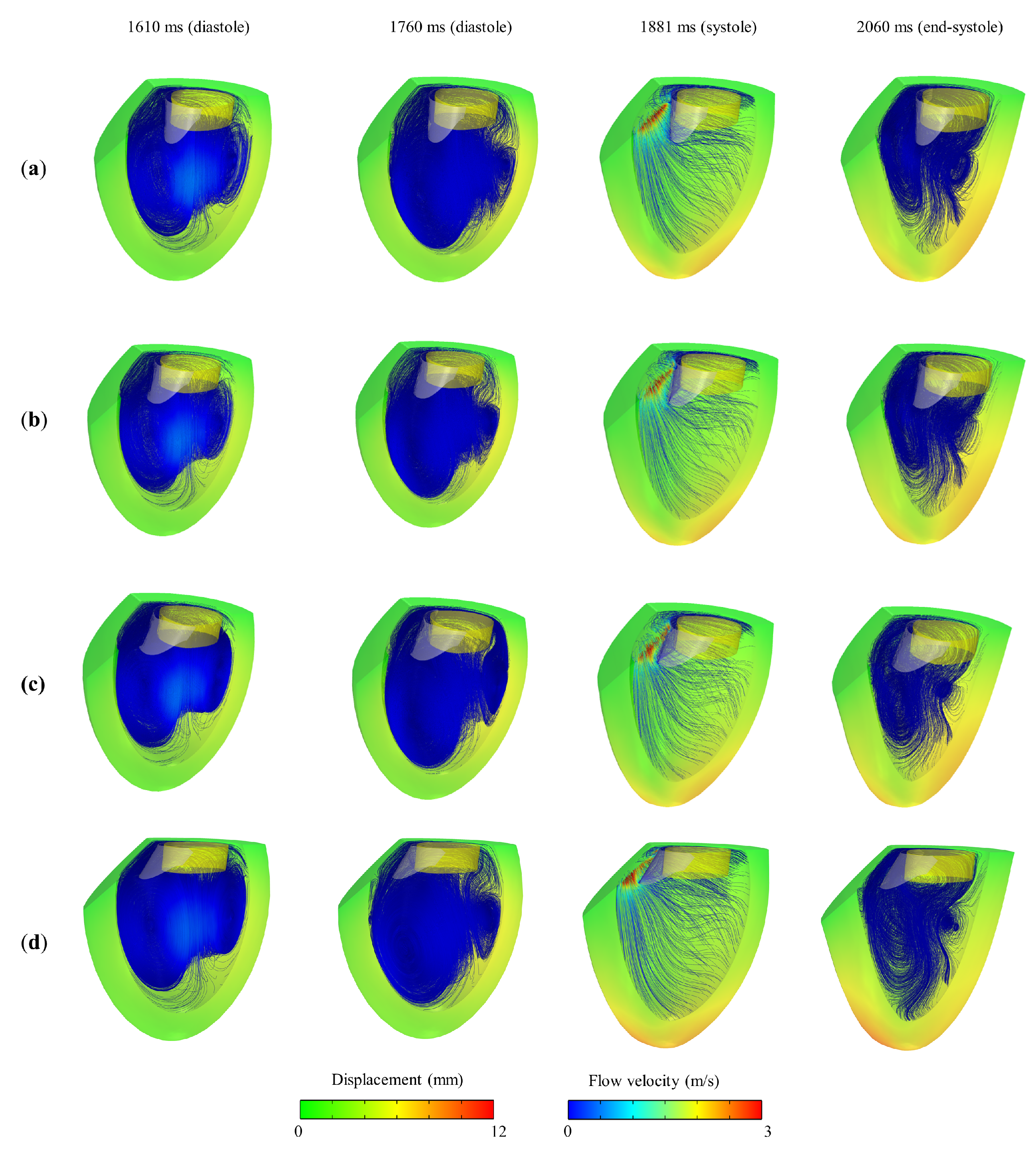
3. Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nkomo, V.T.; Gardin, J.M.; Skelton, T.N.; Gottdiener, J.S.; Scott, C.G.; Enriquez-Sarano, M. Burden of valvular heart diseases: A population-based study. Lancet 2006, 368, 1005–1011. [Google Scholar] [CrossRef] [PubMed]
- Butzner, M.; Leslie, D.L.; Cuffee, Y.; Hollenbeak, C.S.; Sciamanna, C.; Abraham, T. Stable Rates of Obstructive Hypertrophic Cardiomyopathy in a Contemporary Era. Front. Cardiovasc. Med. 2021, 8, 765876. [Google Scholar] [CrossRef] [PubMed]
- Maron, B.J.; Gardin, J.M.; Flack, J.M.; Gidding, S.S.; Kurosaki, T.T.; Bild, D.E. Prevalence of hypertrophic cardiomyopathy in a general population of young adults. Echocardiographic analysis of 4111 subjects in the CARDIA Study. Coronary Artery Risk Development in (Young) Adults. Circulation 1995, 92, 785–789. [Google Scholar] [CrossRef]
- Veselka, J.; Anavekar, N.S.; Charron, P. Hypertrophic obstructive cardiomyopathy. Lancet 2017, 389, 1253–1267. [Google Scholar] [CrossRef] [PubMed]
- Czimbalmos, C.; Csecs, I.; Toth, A.; Kiss, O.; Suhai, F.I.; Sydo, N.; Dohy, Z.; Apor, A.; Merkely, B.; Vago, H. The demanding grey zone: Sport indices by cardiac magnetic resonance imaging differentiate hypertrophic cardiomyopathy from athlete’s heart. PLoS ONE 2019, 14, e0211624. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Wang, S.; Guo, Y.; Zheng, X.; Lu, J.; Fang, X.; Wang, S.; Huang, X. Preoperative NT-proBNP Predicts Midterm Outcome After Septal Myectomy. J. Am. Heart Assoc. 2019, 8, e011075. [Google Scholar] [CrossRef]
- Guigui, S.A.; Torres, C.; Escolar, E.; Mihos, C.G. Systolic anterior motion of the mitral valve in hypertrophic cardiomyopathy: A narrative review. J. Thorac. Dis. 2022, 14, 2309–2325. [Google Scholar] [CrossRef] [PubMed]
- Saccocci, M.; Taramasso, M.; Maisano, F. Mitral Valve Interventions in Structural Heart Disease. Curr. Cardiol. Rep. 2018, 20, 49. [Google Scholar] [CrossRef]
- Regueiro, A.; Granada, J.F.; Dagenais, F.; Rodés-Cabau, J. Transcatheter mitral valve replacement: Insights from early clinical experience and future challenges. J. Am. Coll. Cardiol. 2017, 69, 2175–2192. [Google Scholar] [CrossRef]
- Bapat, V.; Pirone, F.; Kapetanakis, S.; Rajani, R.; Niederer, S. Factors influencing left ventricular outflow tract obstruction following a mitral valve-in-valve or valve-in-ring procedure, part 1. Catheter. Cardiovasc. Interv. 2015, 86, 747–760. [Google Scholar] [CrossRef]
- Blanke, P.; Naoum, C.; Webb, J.; Dvir, D.; Hahn, R.T.; Grayburn, P.; Moss, R.R.; Reisman, M.; Piazza, N.; Leipsic, J. Multimodality Imaging in the Context of Transcatheter Mitral Valve Replacement: Establishing Consensus Among Modalities and Disciplines. JACC Cardiovasc. Imaging 2015, 8, 1191–1208. [Google Scholar] [CrossRef] [PubMed]
- Murphy, D.J.; Ge, Y.; Don, C.W.; Keraliya, A.; Aghayev, A.; Morgan, R.; Galper, B.; Bhatt, D.L.; Kaneko, T.; Di Carli, M.; et al. Use of Cardiac Computerized Tomography to Predict Neo–Left Ventricular Outflow Tract Obstruction Before Transcatheter Mitral Valve Replacement. J. Am. Heart Assoc. 2017, 6, e007353. [Google Scholar] [CrossRef] [PubMed]
- Babaliaros, V.C.; Greenbaum, A.B.; Khan, J.M.; Rogers, T.; Wang, D.D.; Eng, M.H.; O’Neill, W.W.; Paone, G.; Thourani, V.H.; Lerakis, S.; et al. Intentional percutaneous laceration of the anterior mitral leaflet to prevent outflow obstruction during transcatheter mitral valve replacement: First-in-human experience. Cardiovasc. Interv. 2017, 10, 798–809. [Google Scholar] [CrossRef] [PubMed]
- Russell, H.M.; Guerrero, M.E.; Salinger, M.H.; Manzuk, M.A.; Pursnani, A.K.; Wang, D.; Nemeh, H.; Sakhuja, R.; Melnitchouk, S.; Pershad, A.; et al. Open atrial transcatheter mitral valve replacement in patients with mitral annular calcification. J. Am. Coll. Cardiol. 2018, 72, 1437–1448. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Huang, X.; Yang, C.; Lyu, B.; Duan, F.; Tang, D.; Song, Y. Numerical simulation study on systolic anterior motion of the mitral valve in hypertrophic obstructive cardiomyopathy. Int. J. Cardiol. 2018, 266, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, S.; Kalbacher, D.; Waldschmidt, L.; Schaefer, A.; Modine, T.; Dvir, D.; Carasso, S.; Denti, P.; Schofer, N.; Conradi, L. Prevention of LVOT Obstruction by Device-Mediated Laceration of the Anterior Mitral Valve Leaflet During TMVR. Case Rep. 2023, 16, 101873. [Google Scholar] [CrossRef] [PubMed]
- Eleid, M.F.; Cabalka, A.K.; Williams, M.R.; Whisenant, B.K.; Alli, O.O.; Fam, N.; Pollak, P.M.; Barrow, F.; Malouf, J.F.; Nishimura, R.A.; et al. Percutaneous Transvenous Transseptal Transcatheter Valve Implantation in Failed Bioprosthetic Mitral Valves, Ring Annuloplasty, and Severe Mitral Annular Calcification. JACC Cardiovasc. Interv. 2016, 9, 1161–1174. [Google Scholar] [CrossRef] [PubMed]
- Descoutures, F.; Himbert, D.; Maisano, F.; Casselman, F.; de Weger, A.; Bodea, O.; Van der Kley, F.; Colombo, A.; Giannini, C.; Rein, K.A.; et al. Transcatheter valve-in-ring implantation after failure of surgical mitral repair. Eur. J. Cardio Thorac. Surg. 2013, 44, e8–e15. [Google Scholar] [CrossRef][Green Version]
- Kohli, K.; Wei, Z.A.; Yoganathan, A.P.; Oshinski, J.N.; Leipsic, J.; Blanke, P. Transcatheter mitral valve planning and the neo-LVOT: Utilization of virtual simulation models and 3D printing. Curr. Treat. Options Cardiovasc. Med. 2018, 20, 1–14. [Google Scholar] [CrossRef]
- Seo, J.H.; Vedula, V.; Abraham, T.; Lardo, A.C.; Dawoud, F.; Luo, H.; Mittal, R. Effect of the mitral valve on diastolic flow patterns. Phys. Fluids 2014, 26, 121901. [Google Scholar] [CrossRef]
- Schnittger, I.; Gordon, E.P.; Fitzgerald, P.J.; Popp, R.L. Standardized intracardiac measurements of two-dimensional echocardiography. J. Am. Coll. Cardiol. 1983, 2, 934–938. [Google Scholar] [CrossRef] [PubMed]
- Kunzelman, K.S.; Cochran, R.P.; Verrier, E.D.; Eberhart, R.C. Anatomic basis for mitral valve modelling. J. Heart Valve Dis. 1994, 3, 491–496. [Google Scholar] [PubMed]
- Tsang, W.; Meineri, M.; Hahn, R.T.; Veronesi, F.; Shah, A.P.; Osten, M.; Nathan, S.; Russo, M.; Lang, R.M.; Horlick, E.M. A three-dimensional echocardiographic study on aortic-mitral coupling in transcatheter aortic valve replacement. Eur. Heart J. Cardiovasc. Imaging 2013, 14, 950–956. [Google Scholar] [CrossRef] [PubMed]
- Legrice, I.J.; Hunter, P.J.; Smaill, B.H. Laminar structure of the heart: A mathematical model. Am. J. Physiol. Heart Circ. Physiol. 1997, 272, H2466–H2476. [Google Scholar] [CrossRef] [PubMed]
- Ahmad Bakir, A.; Al Abed, A.; Stevens, M.C.; Lovell, N.H.; Dokos, S. A Multiphysics Biventricular Cardiac Model: Simulations With a Left-Ventricular Assist Device. Front. Physiol. 2018, 9, 1259. [Google Scholar] [CrossRef]
- Alharbi, Y.; Al Abed, A.; Bakir, A.A.; Lovell, N.H.; Muller, D.W.; Otton, J.; Dokos, S. Fluid structure computational model of simulating mitral valve motion in a contracting left ventricle. Comput. Biol. Med. 2022, 148, 105834. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of passive myocardium: A structurally based framework for material characterization. Philos. Trans. R. Soc. A 2009, 367, 3445–3475. [Google Scholar] [CrossRef]
- Cai, L.; Wang, Y.; Gao, H.; Li, Y.; Luo, X. A mathematical model for active contraction in healthy and failing myocytes and left ventricles. PLoS ONE 2017, 12, e0174834. [Google Scholar] [CrossRef]
- Usyk, T.P.; LeGrice, I.J.; McCulloch, A.D. Computational model of three-dimensional cardiac electromechanics. Comput. Vis. Sci. 2002, 4, 249–257. [Google Scholar] [CrossRef]
- Shavik, S.M.; Wall, S.T.; Sundnes, J.; Burkhoff, D.; Lee, L.C. Organ-level validation of a cross-bridge cycling descriptor in a left ventricular finite element model: Effects of ventricular loading on myocardial strains. Physiol. Rep. 2017, 5, e13392. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Nithiarasu, P. Convection-Dominated Problems: Finite Element Approximations to the Convection-Diffusion-Reaction Equation. In The Finite Element Method for Fluid Dynamics, 7th ed.; Zienkiewicz, O.C., Taylor, R.L., Nithiarasu, P., Eds.; Butterworth-Heinemann: Oxford, UK, 2014; Chapter 2; pp. 31–85. [Google Scholar]
- Wang, D.D.; Eng, M.H.; Greenbaum, A.B.; Myers, E.; Forbes, M.; Karabon, P.; Pantelic, M.; Song, T.; Nadig, J.; Guerrero, M.; et al. Validating a prediction modeling tool for left ventricular outflow tract (LVOT) obstruction after transcatheter mitral valve replacement (TMVR). Catheter. Cardiovasc. Interv. 2018, 92, 379–387. [Google Scholar] [CrossRef] [PubMed]
- Pasipoularides, A.; Murgo, J.P.; Miller, J.W.; Craig, W.E. Nonobstructive left ventricular ejection pressure gradients in man. Circ. Res. 1987, 61, 220–227. [Google Scholar] [CrossRef] [PubMed]
- Khan, J.M.; Babaliaros, V.C.; Greenbaum, A.B.; Foerst, J.R.; Yazdani, S.; McCabe, J.M.; Paone, G.; Eng, M.H.; Leshnower, B.G.; Gleason, P.T.; et al. Anterior Leaflet Laceration to Prevent Ventricular Outflow Tract Obstruction During Transcatheter Mitral Valve Replacement. J. Am. Coll. Cardiol. 2019, 73, 2521–2534. [Google Scholar] [CrossRef] [PubMed]
- Khan, J.M.; Rogers, T.; Schenke, W.H.; Mazal, J.R.; Faranesh, A.Z.; Greenbaum, A.B.; Babaliaros, V.C.; Chen, M.Y.; Lederman, R.J. Intentional Laceration of the Anterior Mitral Valve Leaflet to Prevent Left Ventricular Outflow Tract Obstruction During Transcatheter Mitral Valve Replacement: Pre-Clinical Findings. JACC Cardiovasc. Interv. 2016, 9, 1835–1843. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, J.D.Z.; Bateman, M.G.; Iaizzo, P.A. Engineering and technologies associated with cardiac valve repair and replacement therapies. Eng. Med. 2019, 219–254. [Google Scholar]
- Geske, J.B.; Sorajja, P.; Ommen, S.R.; Nishimura, R.A. Variability of left ventricular outflow tract gradient during cardiac catheterization in patients with hypertrophic cardiomyopathy. JACC Cardiovasc. Interv. 2011, 4, 704–709. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.M.; Shapiro, L.M.; Wells, F.C. Importance of subvalvular preservation and early operation in mitral valve surgery. Circulation 1996, 94, 2117–2123. [Google Scholar] [CrossRef]
- Fu, G.; Zhou, Z.; Huang, S.; Chen, G.; Liang, M.; Huang, L.; Wu, Z. Mitral valve surgery in patients with rheumatic heart disease: Repair vs. replacement. Front. Cardiovasc. Med. 2021, 8, 685746. [Google Scholar] [CrossRef]
- Toma, M.; Krdey, A.; Takagi, S.; Oshima, M. Strongly Coupled Fluid-Structure Interaction Cardiovascular Analysis with the Effect of Peripheral Network. Seisan Kenkyu 2011, 63, 339–344. [Google Scholar]
- Taelman, L.; Degroote, J.; Verdonck, P.; Vierendeels, J.; Segers, P. Modeling hemodynamics in vascular networks using a geometrical multiscale approach: Numerical aspects. Ann. Biomed. Eng. 2013, 41, 1445–1458. [Google Scholar] [CrossRef]
- Espino, D.M.; Shepherd, D.E.; Hukins, D.W. Evaluation of a transient, simultaneous, arbitrary Lagrange-Euler based multi-physics method for simulating the mitral heart valve. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 450–458. [Google Scholar] [CrossRef] [PubMed]
- Hassani, K.; Karimi, A.; Dehghani, A.; Tavakoli Golpaygani, A.; Abdi, H.; Espino, D.M. Development of a fluid-structure interaction model to simulate mitral valve malcoaptation. Perfusion 2018, 34, 267659118811045. [Google Scholar] [CrossRef] [PubMed]
- Govindarajan, V.; Mousel, J.; Udaykumar, H.S.; Vigmostad, S.C.; McPherson, D.D.; Kim, H.; Chandran, K.B. Synergy between Diastolic Mitral Valve Function and Left Ventricular Flow Aids in Valve Closure and Blood Transport during Systole. Sci. Rep. 2018, 8, 6187. [Google Scholar] [CrossRef] [PubMed]
- Lau, K.D.; Diaz, V.; Scambler, P.; Burriesci, G. Mitral valve dynamics in structural and fluid-structure interaction models. Med. Eng. Phys. 2010, 32, 1057–1064. [Google Scholar] [CrossRef] [PubMed]
- Domenichini, F.; Pedrizzetti, G. Asymptotic Model of Fluid-Tissue Interaction for Mitral Valve Dynamics. Cardiovasc. Eng. Technol. 2015, 6, 95–104. [Google Scholar] [CrossRef]
- Dokos, S.; Smaill, B.H.; Young, A.A.; LeGrice, I.J. Shear properties of passive ventricular myocardium. Am. J. Physiol. Heart Circ. Physiol. 2002, 283, H2650–H2659. [Google Scholar] [CrossRef]
- Demer, L.L.; Yin, F.C. Passive biaxial mechanical properties of isolated canine myocardium. J. Physiol. 1983, 339, 615–630. [Google Scholar] [CrossRef]
- Watanabe, H.; Sugiura, S.; Kafuku, H.; Hisada, T. Multiphysics simulation of left ventricular filling dynamics using fluid-structure interaction finite element method. Biophys. J. 2004, 87, 2074–2085. [Google Scholar] [CrossRef]

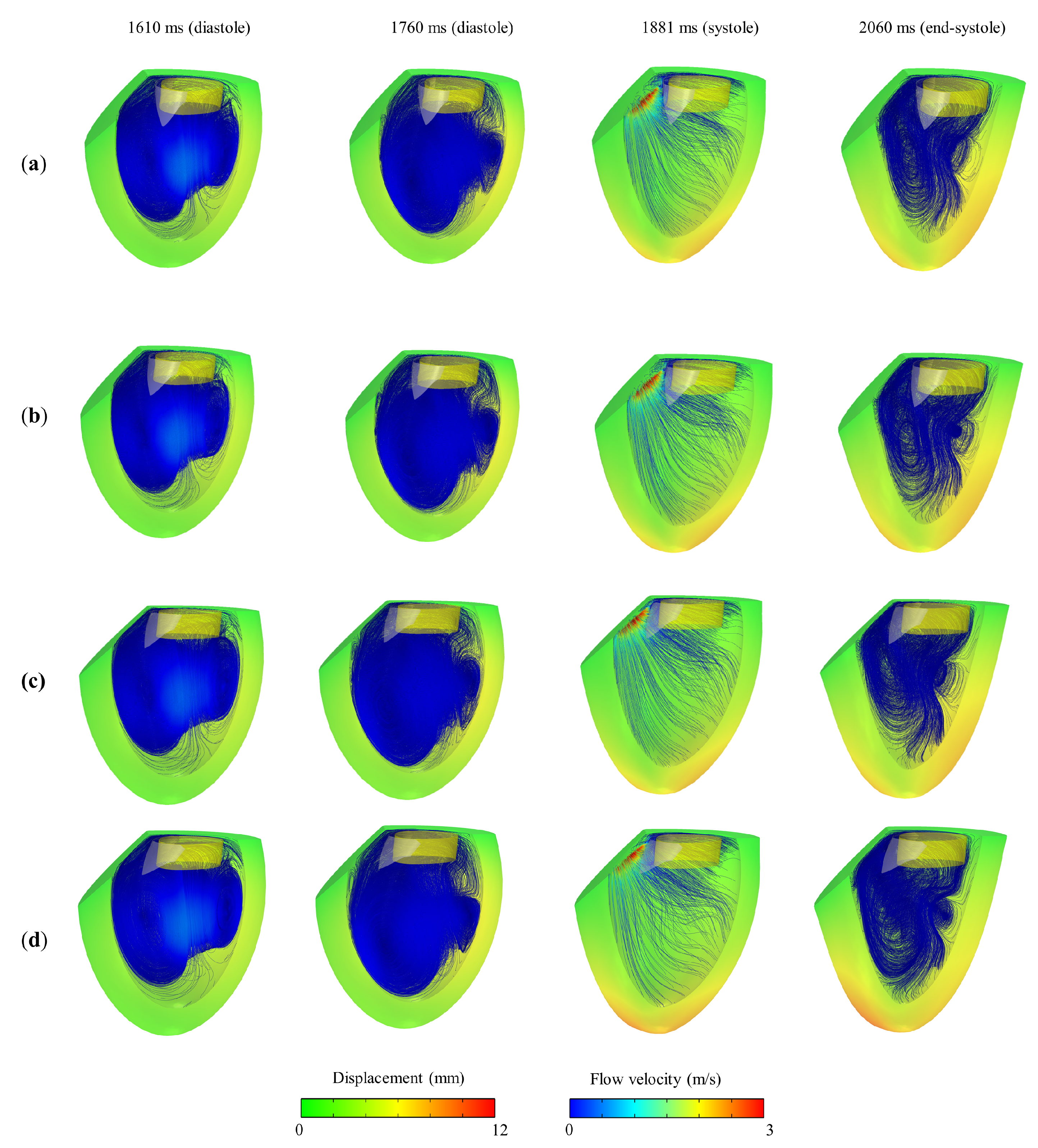
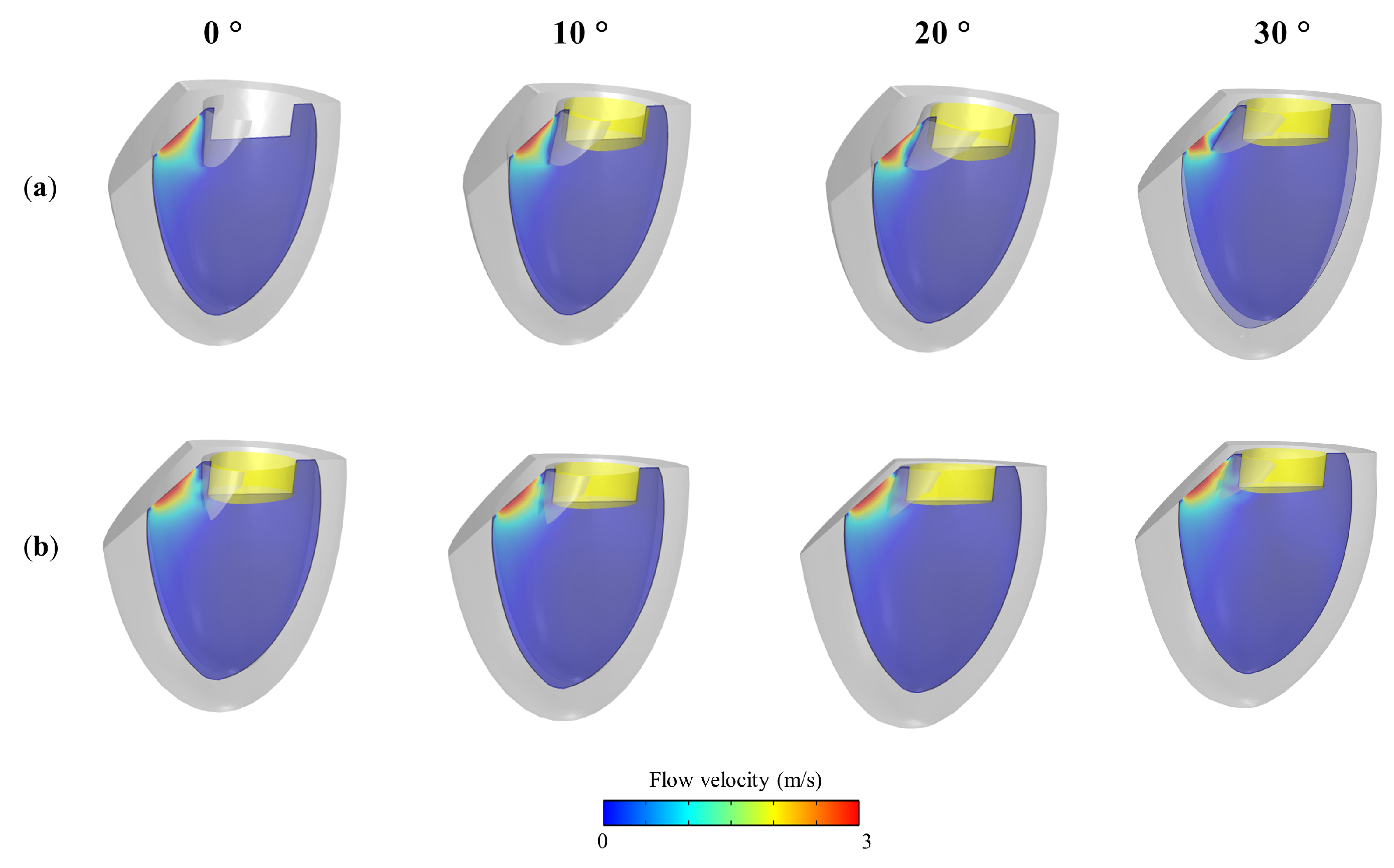

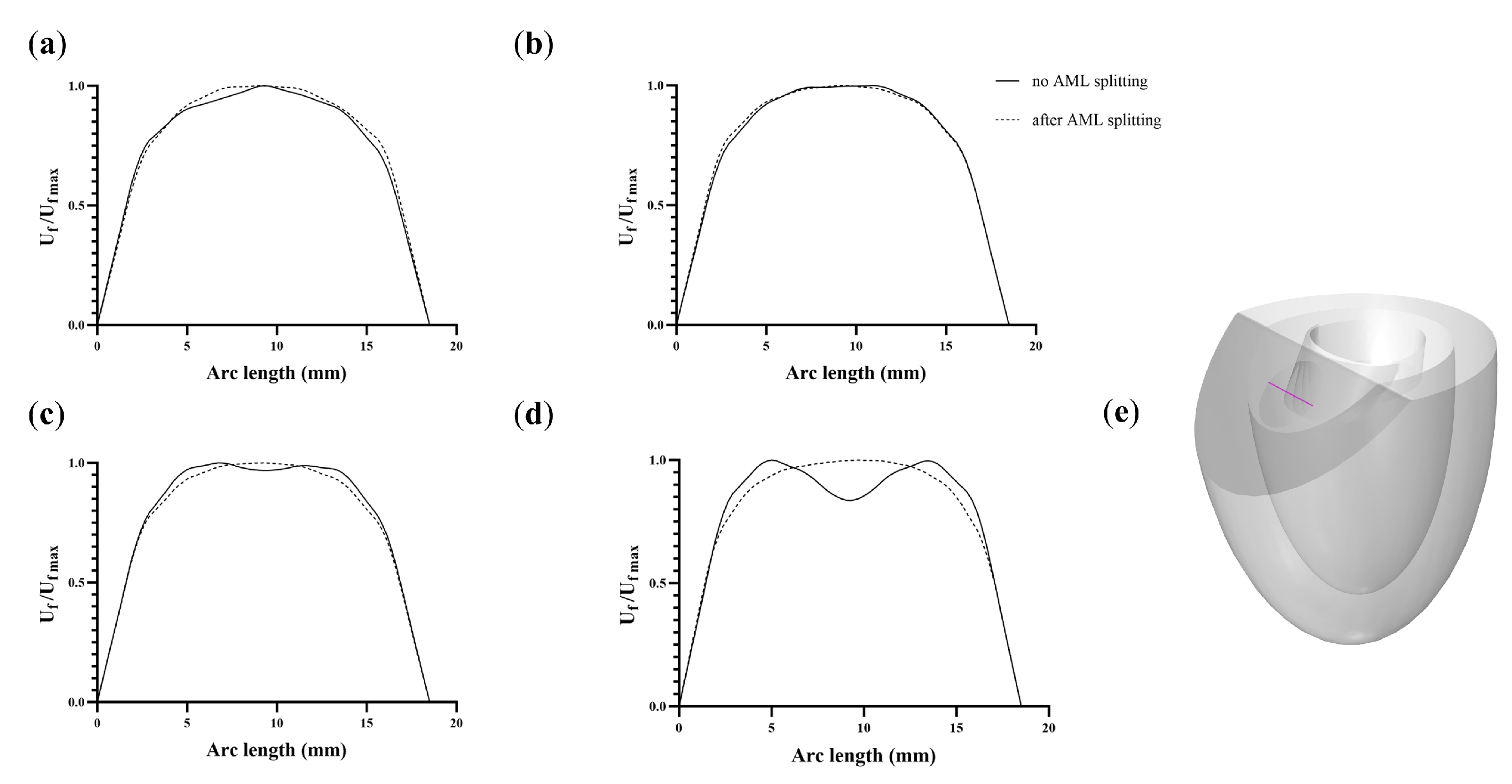
| Parameter | Value | Unit | Description |
|---|---|---|---|
| mmHg s mL | Systematic resistance | ||
| mL mmHg | Systematic compliance | ||
| mmHg s mL | Aortic valve resistance | ||
| mmHg s mL | Peripheral resistance | ||
| mmHg s mL | Venous resistance | ||
| 65 | mL mmHg | Venous compliance | |
| 3200 | mL | Resting volume for vein | |
| 400 | mL | Resting volume for artery | |
| 4 | mL | Resting volume for LA | |
| 1 | mmHg | Resting pressure for LA | |
| mmHg mL | End-systolic elastance | ||
| mmHg mL | End-diastolic elastance | ||
| s | Cardiac cycle | ||
| Initial values | |||
| mL | |||
| 641 | mL | ||
| 4082 | mL |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alharbi, Y. A 3D-0D Computational Model of the Left Ventricle for Investigating Blood Flow Patterns for Cases of Systolic Anterior Motion and after Anterior Mitral Leaflet Splitting. Appl. Sci. 2024, 14, 466. https://doi.org/10.3390/app14010466
Alharbi Y. A 3D-0D Computational Model of the Left Ventricle for Investigating Blood Flow Patterns for Cases of Systolic Anterior Motion and after Anterior Mitral Leaflet Splitting. Applied Sciences. 2024; 14(1):466. https://doi.org/10.3390/app14010466
Chicago/Turabian StyleAlharbi, Yousef. 2024. "A 3D-0D Computational Model of the Left Ventricle for Investigating Blood Flow Patterns for Cases of Systolic Anterior Motion and after Anterior Mitral Leaflet Splitting" Applied Sciences 14, no. 1: 466. https://doi.org/10.3390/app14010466
APA StyleAlharbi, Y. (2024). A 3D-0D Computational Model of the Left Ventricle for Investigating Blood Flow Patterns for Cases of Systolic Anterior Motion and after Anterior Mitral Leaflet Splitting. Applied Sciences, 14(1), 466. https://doi.org/10.3390/app14010466






