Research on Multi-Objective Flexible Job Shop Scheduling Problem with Setup and Handling Based on an Improved Shuffled Frog Leaping Algorithm
Abstract
1. Introduction
- (a)
- Multi-variety and small-batch order type:
- (b)
- Production system of multi-equipment work center:
- (c)
- Taking into account the machine setup time:
- (d)
- Taking into account the job handling time
- (e)
- Adopting parallel sequential movement mode
2. Problem Formulation
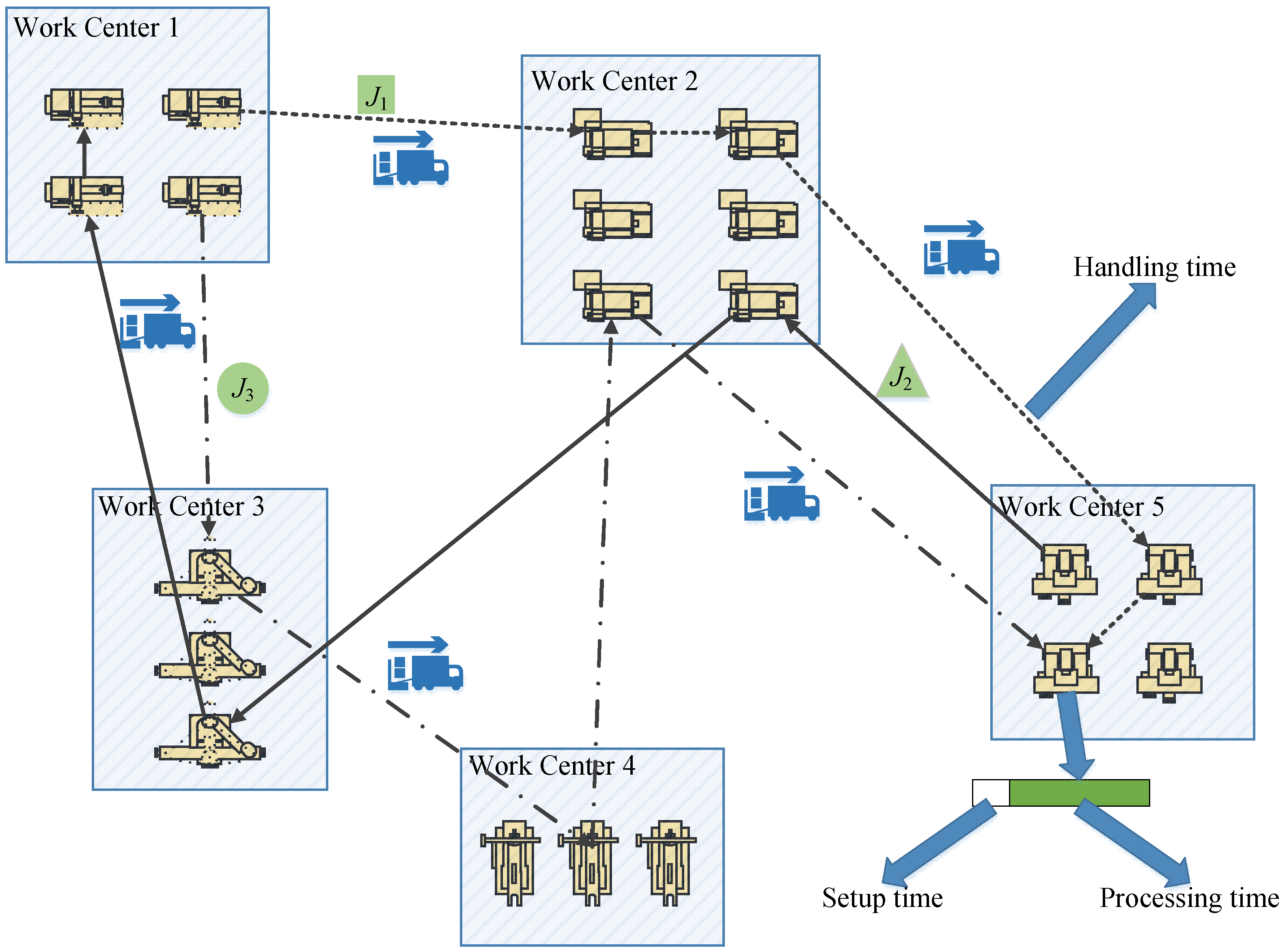
2.1. Problem Description
2.2. Assumptions
- (1)
- All jobs can be processed at time 0.
- (2)
- All machines are available at time 0.
- (3)
- One machine can only process one operation at a time.
- (4)
- The same operation can only be processed on one machine in one work center at the same time and can only be processed once.
- (5)
- The constraint of operation processing order is only considered within the same type of jobs, and the operation processing order cannot be altered.
- (6)
- Jobs are independent and all types of jobs have the same priority.
- (7)
- The interruption of a job during processing is not considered.
- (8)
- Machine breakdowns are not considered.
- (9)
- When the same machine successively processes two different types of jobs that are different, it needs to have a setup time before processing.
- (10)
- The handling capacity of each handling equipment is not limited, and the number of handling equipment is not limited.
2.3. Notations
2.4. Objectives
2.5. Constraints
3. Optimization Algorithm for FJSP-cSH
3.1. Shuffled Frog Leaping Algorithm
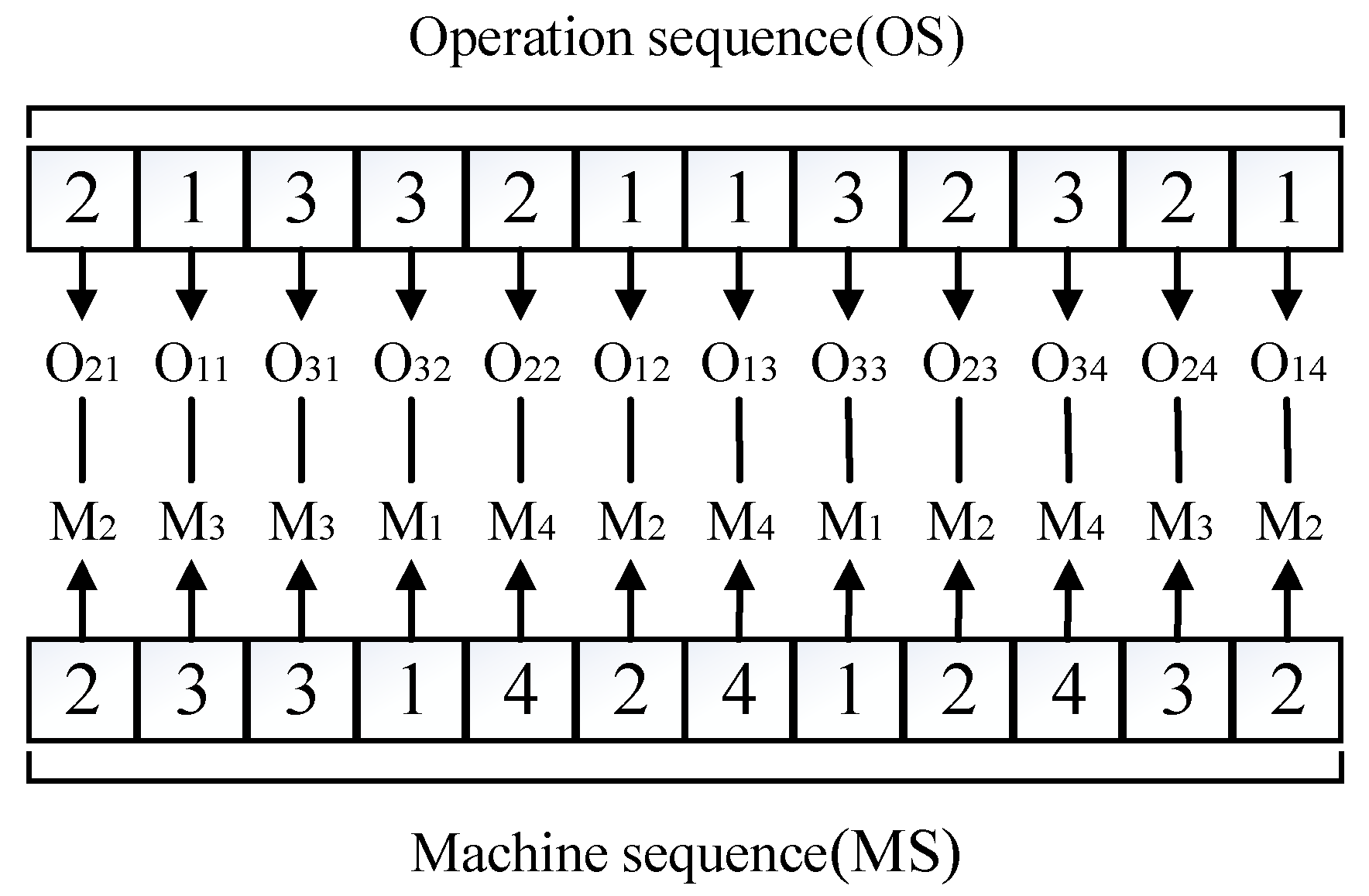
3.2. Solution Representation
3.3. Population Initialization
3.3.1. The Machine with the Earliest Idle Time for the Job That Arrives First
3.3.2. The Machine with the Shortest Processing Time for the Job That Arrives First
3.3.3. Simple Randomly Generated Solution
3.4. Population Division
3.5. Local Evolutionary Process
3.5.1. The Jump Size of the FJSP-cSH Based on Gravity Search Algorithm
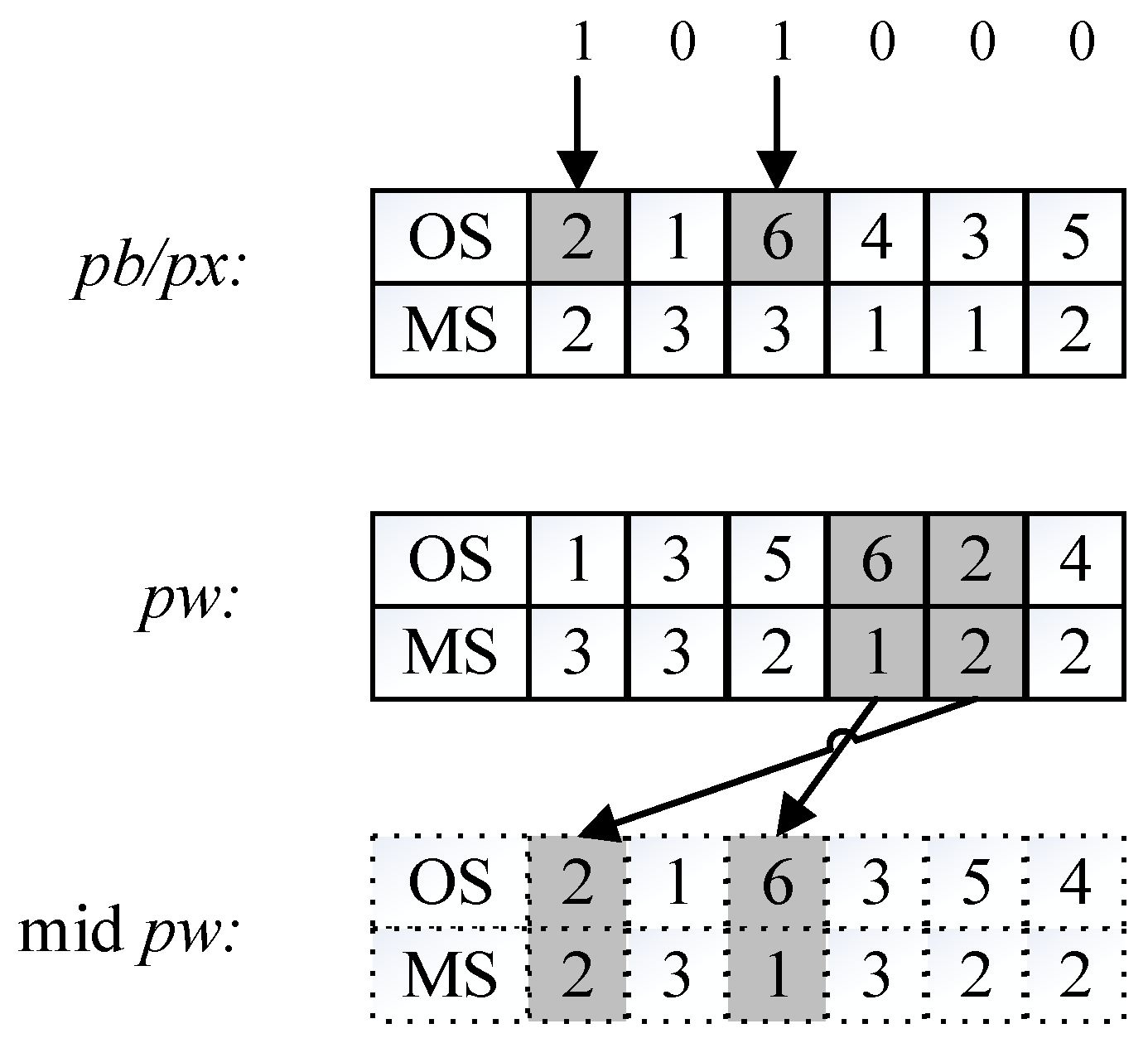
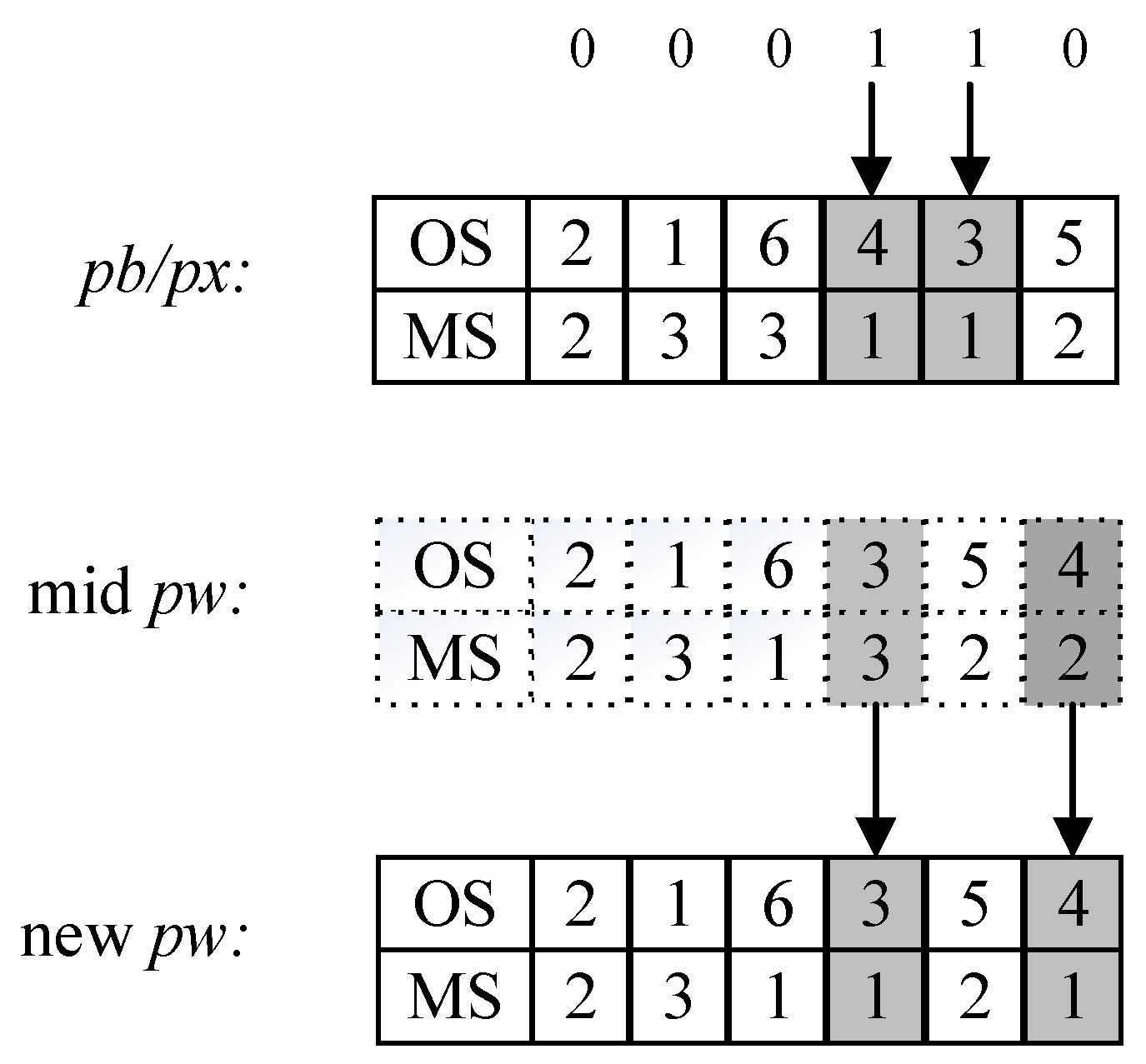
3.5.2. The Jump Rules of the FJSP-cSH
3.6. Population Shuffling
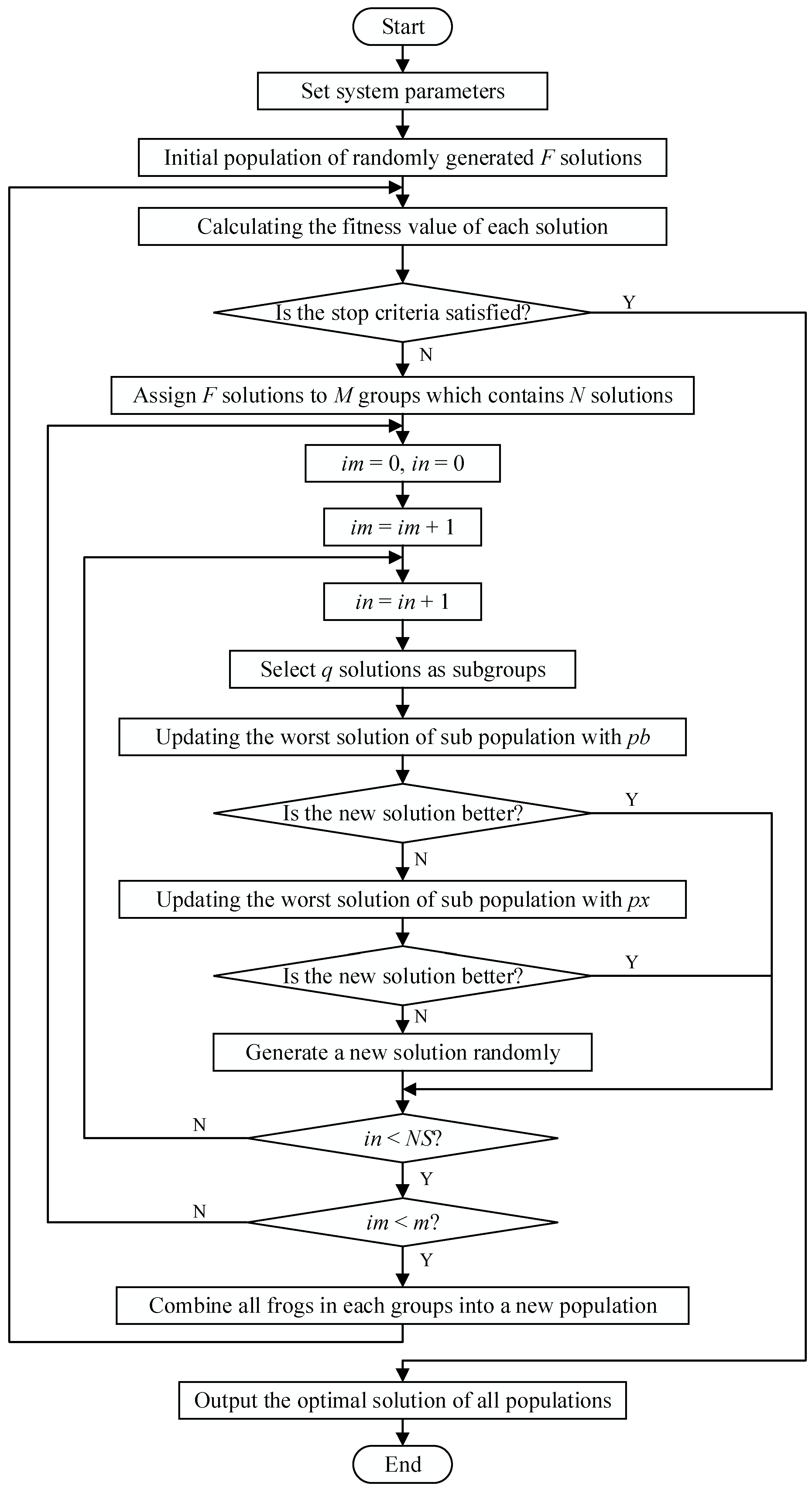
3.7. Algorithm Description
| Algorithm 1 Step description of improvd SFLA-uGSA |
| Step 1: Initialization phase. Step 1.1: Set the system parameters, such as the population size F, the number of groups m and the number of local evolution NS. Step 1.2: Read the file data, such as the number of jobs, the number of machines, the processing time, the handing time and the setup time. Step 2: Generate the initial population according to three different rules that are established in Section 3.3, calculate the fitness of each frog, and determine the global optimal solution px. Step 3: If the termination criterion is satisfied, output the global optimal solution px; otherwise, perform step 4. Step 4: Divide the population F into m groups according to the rules of population division, and calculate the value of G of this generation of population. Step 5: For each group i, i = 1, 2,…, m, perform local evolution process for NS times. Step 5.1: Determine the best solution pb and the worst solution pw in the group i. Step 5.2: Update the worst solution pw with the best solution pb according to the local updating evolution formula (Equation (17)), and a new solution is generated through gravitational calculation and renewal evolution. If the fitness of new solution is better than old solution pw, then let the new solution replace the old solution pw, perform step 5.5; otherwise, perform step 5.3. Step 5.3: Update the worst solution pw with the population best solution px according to the local updating evolution formula (Equation (18)), and a new solution is generated through gravitational calculation and renewal evolution. If the fitness of new solution is better than old solution pw, then let the new solution replace the old solution pw, perform step 5.5; otherwise, perform step 5.4. Step 5.4: Use individual mutation method to transform the worst solution pw, if the fitness of the new solution after transformation is better than that of the old solution before transformation, let the new solution replace the old solution pw, perform step 5.5; otherwise, randomly generate a new solution to replace the worst solution pw, perform step 5.5. Step 5.5: Update the group i. Step 6: Shuffle the evolved groups, perform step 3. |
4. Multi-Objective Optimization: Model Rules and Algorithm Design
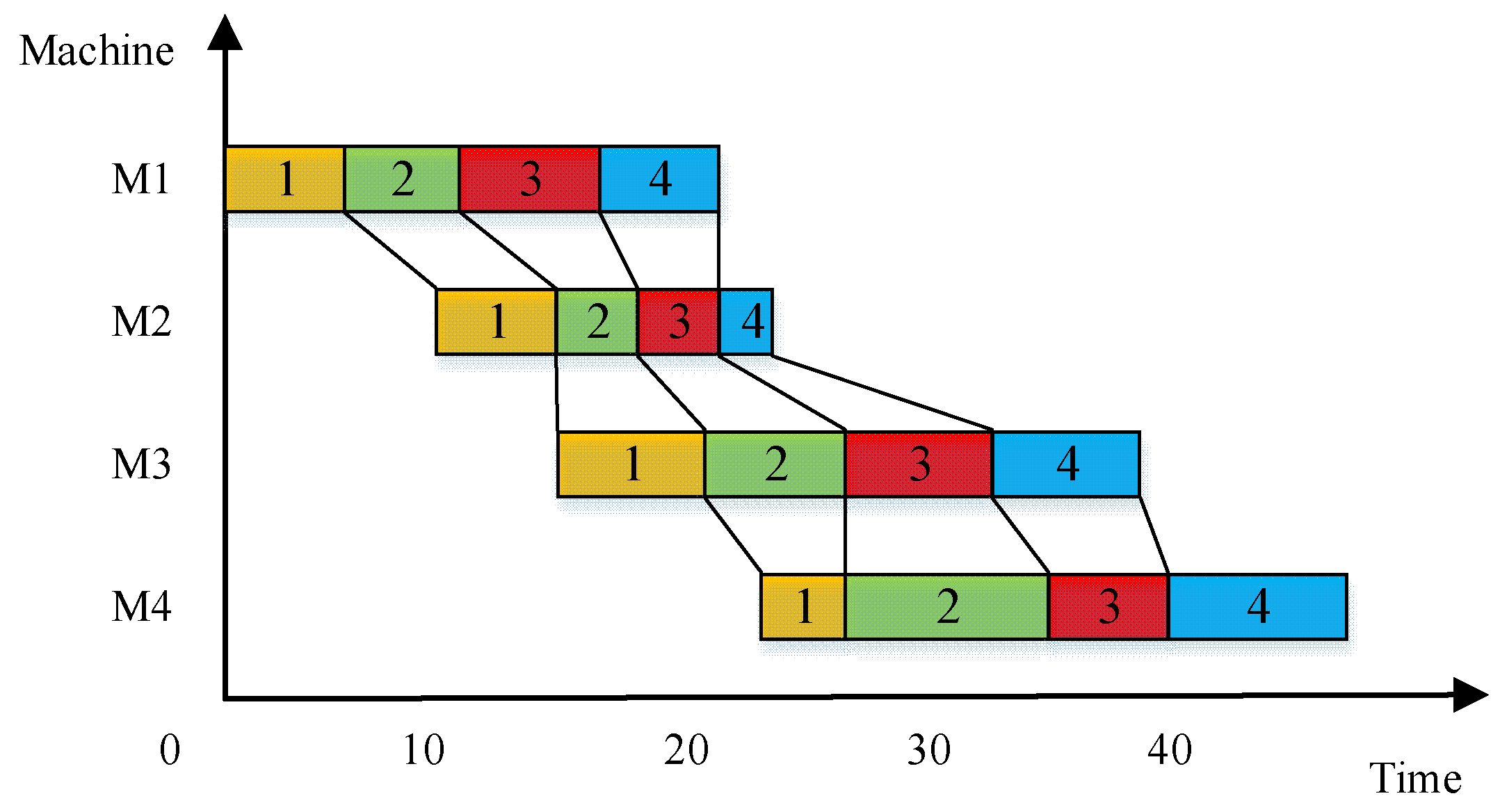
4.1. Parallel Sequential Movement Mode
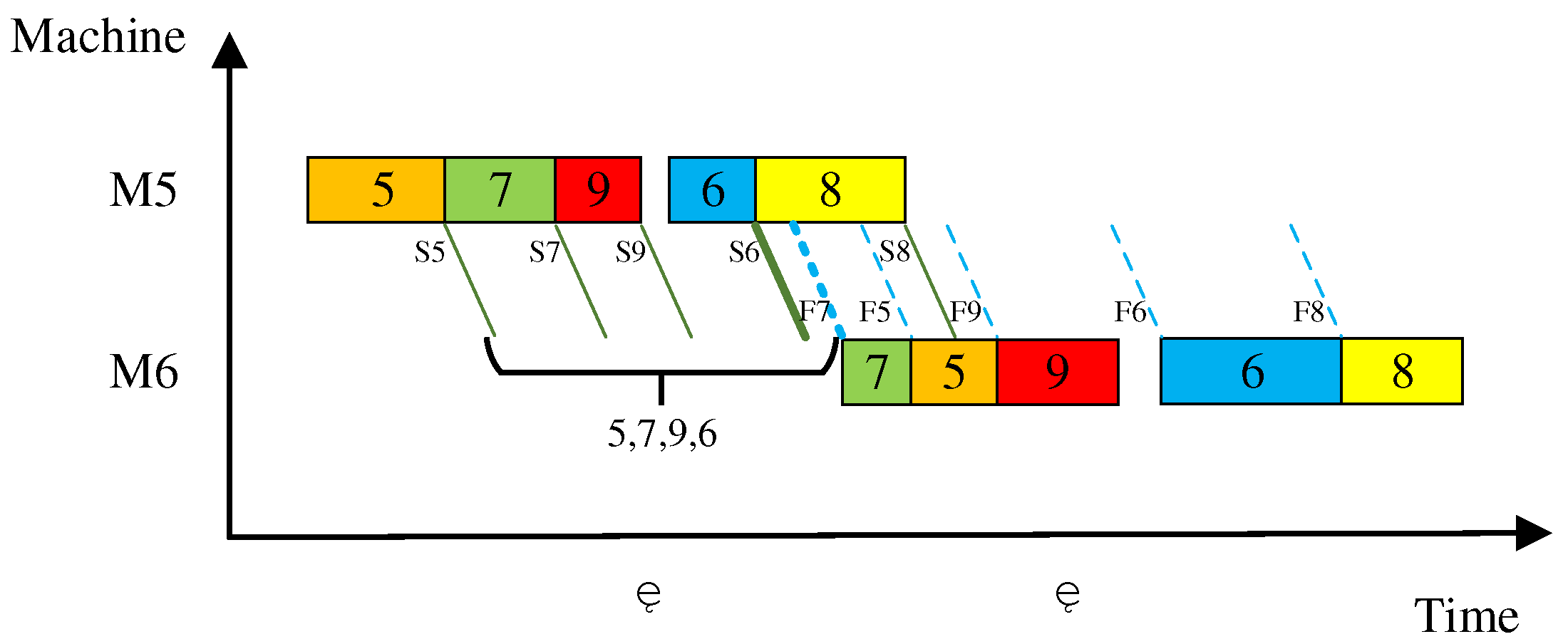
4.2. Batch Handling Mode Design
4.3. Pareto Ranking Method
5. Experimental Results
5.1. Algorithm Parameter Setting
5.2. Algorithm Effectiveness Analysis
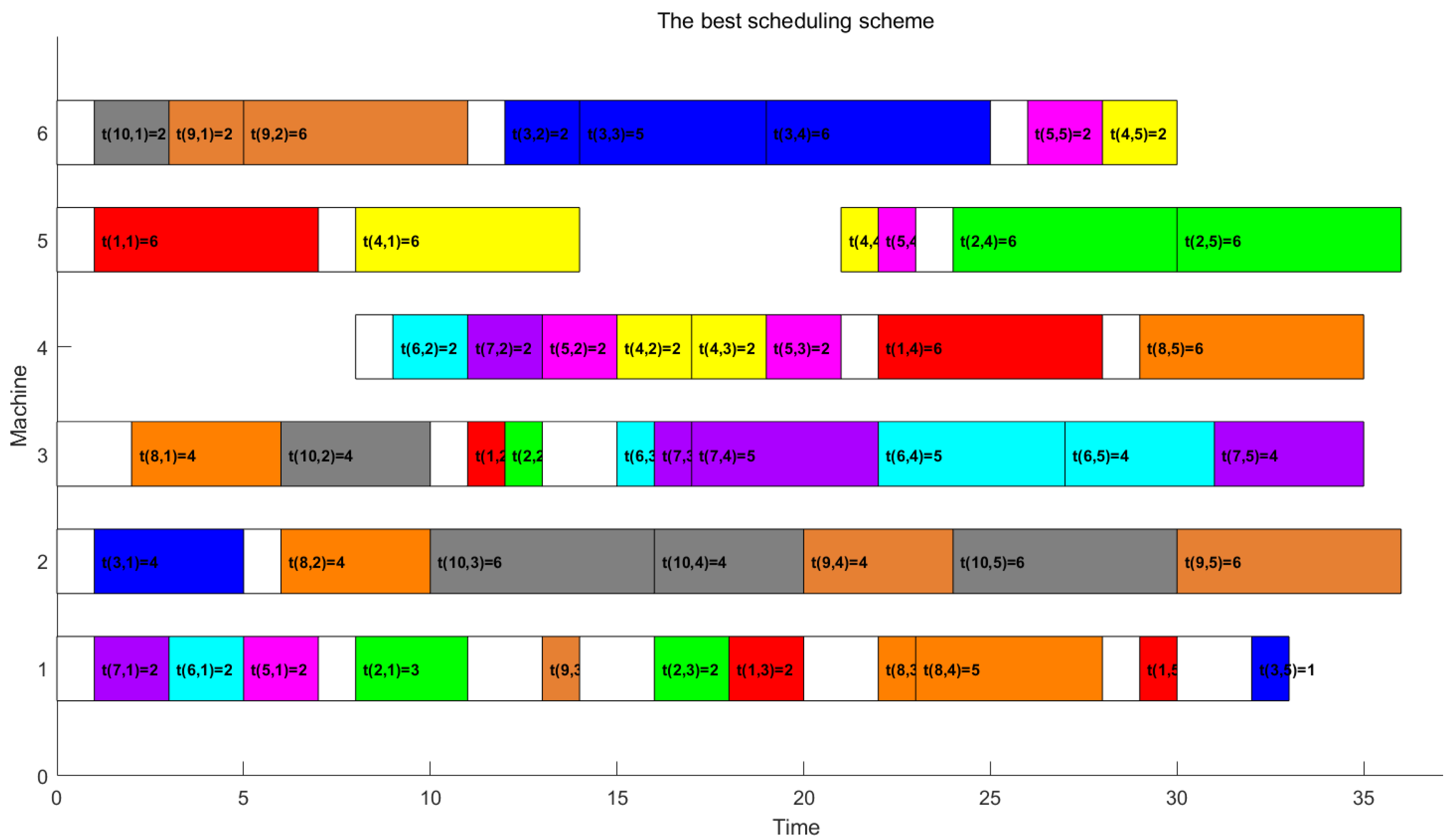
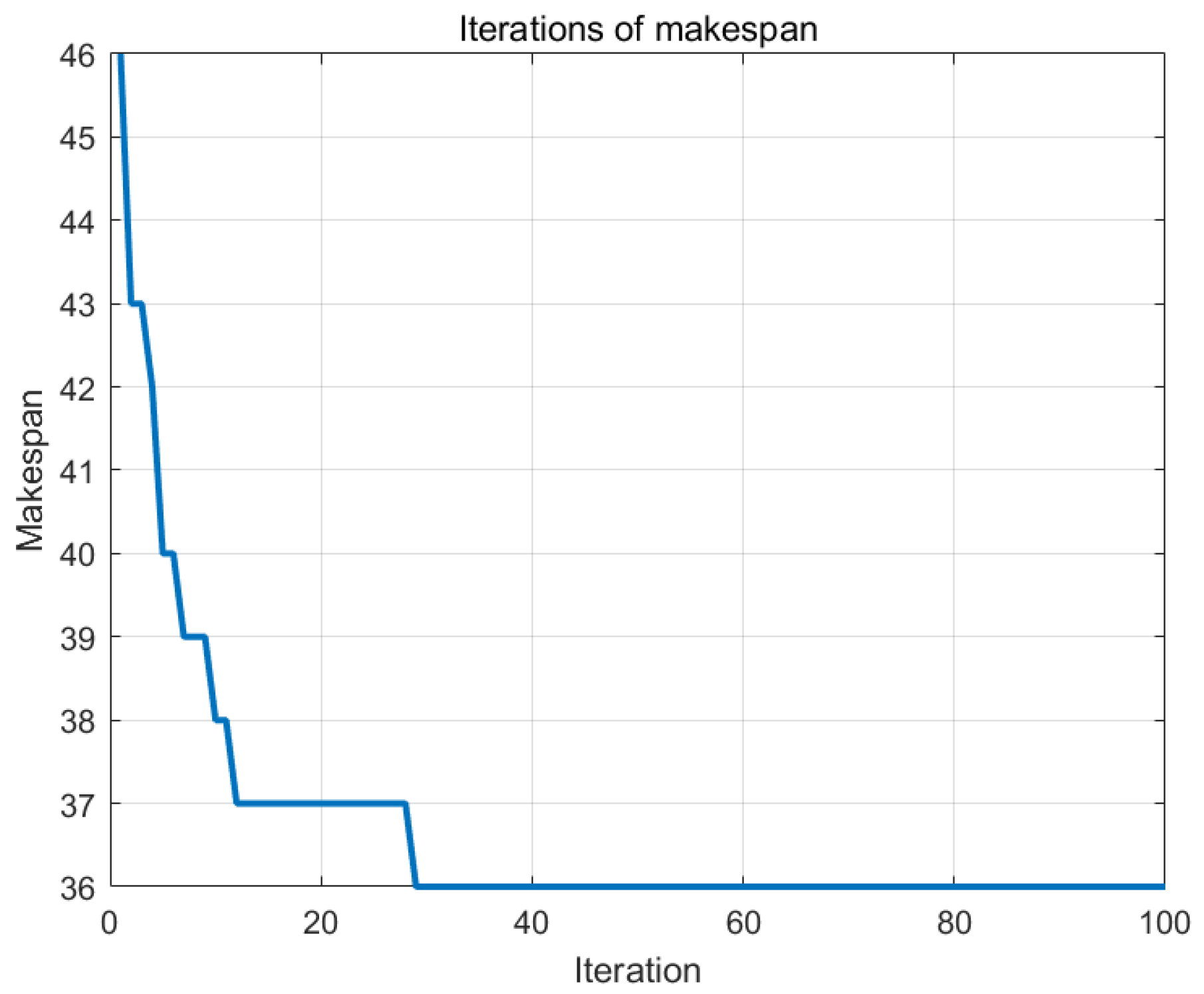
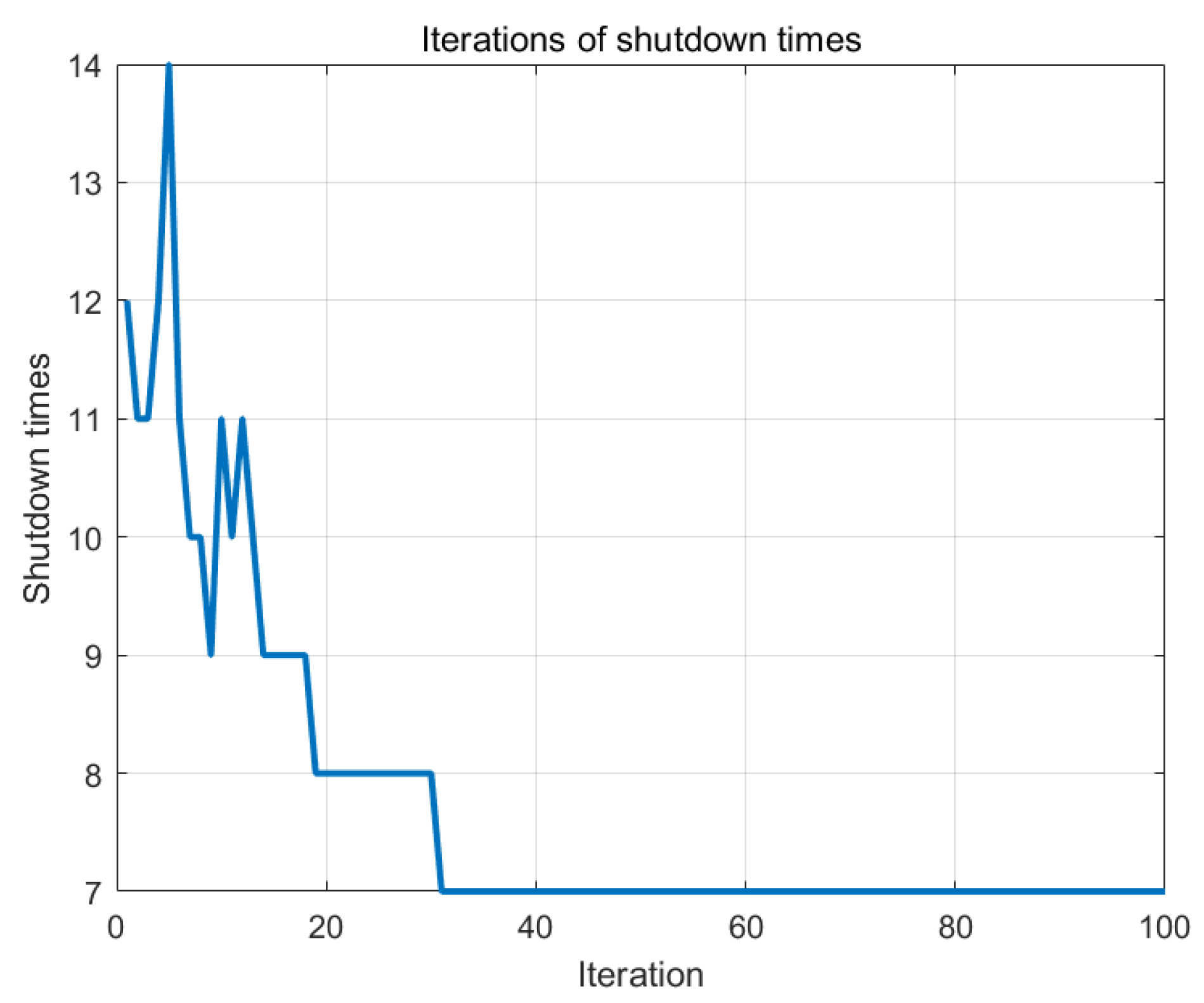
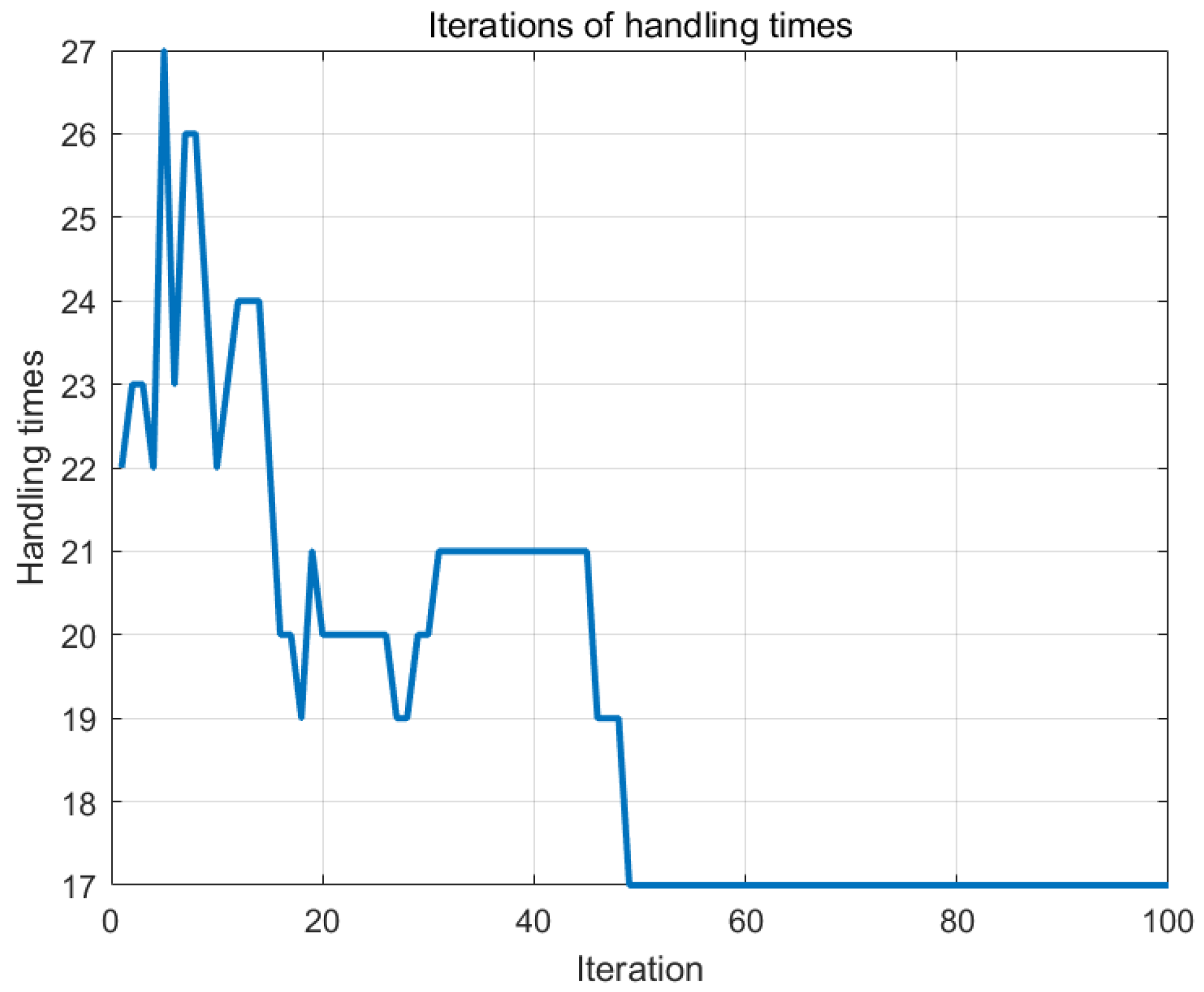
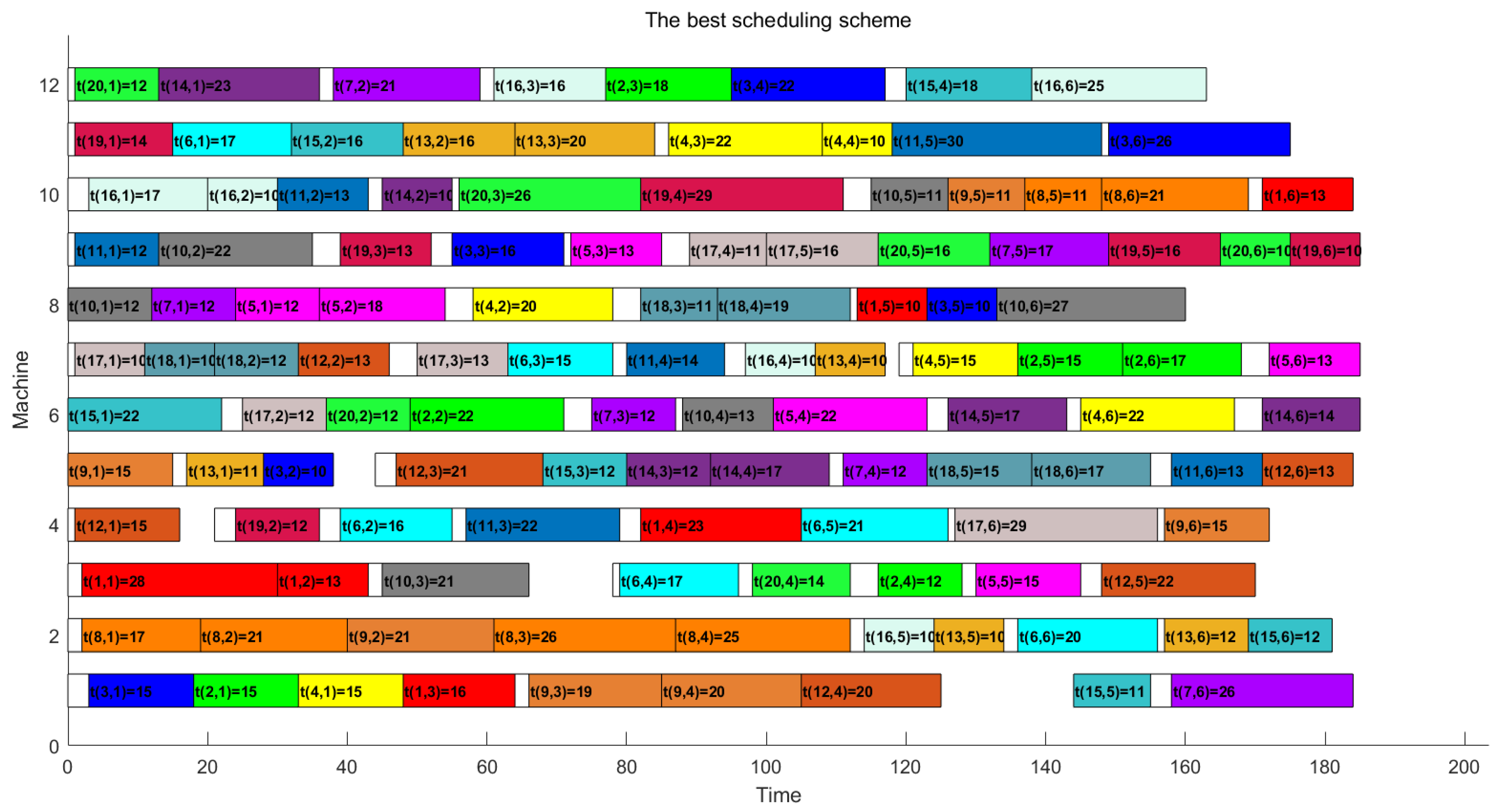
5.3. Example Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | Definitions |
| Ji | the set of jobs (i = 1, 2,…, n) |
| Oij | the set of operations (i = 1, 2,…, n; j = 1, 2,…, w; Oij represents the j-th operation of job i) |
| Mk | the set of machines (k = 1, 2,…, m) |
| MUij | the set of work centers, that is, the optional machines’ set of the operation Oij |
| TPijk | the processing time of operation Oij on machine Mk |
| TSijk | the setup time of operation Oij on machine Mk |
| TCk1k2 | handling time from machine Mk1 to machine Mk2 |
| L | a sufficiently large positive number (or constraint) |
| Ci | the completion time of job Ji |
| Cmax | the makespan of order task |
| the start processing time of operation Oij on machine Mk | |
| the completion processing time of operation Oij on machine Mk | |
| the start setup time of operation Oij on machine Mk | |
| the completion setup time of operation Oij on machine Mk | |
| start handling time after operation Oij | |
| completion handling time after operation Oij | |
| NOH | the number of handling tasks |
| Th | the set of handling tasks (h = 1, 2,…, NOH) |
| the start handling time of the handling task h | |
| the completion handling time of the handling task h |
References
- Chaudhry, A.I.; Khan, A.A. A research survey: Review of flexible job shop scheduling techniques. Int. Trans. Oper. Res. A J. Int. Fed. Oper. Res. Soc. 2016, 23, 551–591. [Google Scholar] [CrossRef]
- Andy, H. Transfer-robot task scheduling in job shop. Int. J. Prod. Res. 2021, 59, 813–823. [Google Scholar]
- Yige, S.; Sai-Ho, C.; Xin, W.; Hoi-Lam, M. Novel robotic job-shop scheduling models with deadlock and robot movement considerations. Transp. Res. Part E 2021, 149, 102273. [Google Scholar]
- Soroush, F.; Reza, T.; Mehdi, F.; Behdin, V. Scheduling of Multi-Robot Job Shop Systems in Dynamic Environments: Mixed-Integer Linear Programming and Constraint Programming Approaches. Omega 2023, 115, 102770. [Google Scholar]
- Allahverdi, A.; Ng, C.; Cheng, T.; Kovalyov, M. A survey of scheduling problems with setup times or costs. Eur. J. Oper. Res. 2006, 187, 985–1032. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, Y.; Peng, K.; Li, X.; Lian, K.; Zhang, S. Dynamic flexible job shop scheduling method based on improved gene expression programming. Meas. Control 2020, 54, 002029402094635. [Google Scholar] [CrossRef]
- Behnke, D.; Geiger, M.J. Test Instances for the Flexible Job Shop Scheduling Problem with Work Centers. Logist.-Manag. 2012. [Google Scholar] [CrossRef]
- Govi, D.; Rizzuto, A.; Schipani, F.; Lazzeri, A. A Two-stage Genetic Algorithm for a Novel FJSP with Working Centers in a Real-world Industrial Application. In Proceedings of the 2nd International Conference on Innovative Intelligent Industrial Production and Logistics, Online, 25–27 October 2021; pp. 75–83. [Google Scholar]
- Pal, M.; Mittal, M.L.; Soni, G.; Chouhan, S.S.; Kumar, M. A multi-agent system for FJSP with setup and transportation times. Expert Syst. Appl. 2023, 216, 119474. [Google Scholar] [CrossRef]
- Feng, Y.J.; Kong, J.L. Multi-Objective Hybrid Flow Shop Scheduling in Parallel Sequential Mode While Considering Handling Time and Setup Time. Appl. Sci. 2023, 13, 3563. [Google Scholar] [CrossRef]
- Wu, Q.; Ji, Z.; Wu, D. Cooperative hybrid particle swarm optimization algorithm for job-shop scheduling problems. Comput. Eng. Appl. 2016, 52, 266–270. [Google Scholar]
- Vital-Soto, A.; Azab, A.; Baki, F.M. Mathematical modeling and a hybridized bacterial foraging optimization algorithm for the flexible job-shop scheduling problem with sequencing flexibility. J. Manuf. Syst. 2020, 54, 74–93. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, J.; Zhang, C.; Chu, H.; Ding, G.; Zhang, L. A hybrid genetic-particle swarm algorithm based on multilevel neighbourhood structure for flexible job shop scheduling problem. Comput. Oper. Res. 2021, 135, 105431. [Google Scholar] [CrossRef]
- Alzaqebah, M.; Jawarneh, S.; Alwohaibi, M.; Alsmadi, M.K.; Almarashdeh, I.; Mohammad, R. Hybrid Brain Storm Optimization algorithm and Late Acceptance Hill Climbing to solve the Flexible Job-Shop Scheduling Problem. J. King Saud Univ.-Comput. Inf. Sci. 2020, 34, 2926–2937. [Google Scholar] [CrossRef]
- Liu, X. Improved Multi-Objective Composed Optimization Algorithm Studying for Flexible Job-Shop Scheduling Problems. Master’s Thesis, Jilin University, Changchun, China, 2020. [Google Scholar]
- Yan, S.; Zhang, G.; Sun, J.; Zhang, W. An improved ant colony optimization for solving the flexible job shop scheduling problem with multiple time constraints. Math. Biosci. Eng. MBE 2023, 20, 7519–7547. [Google Scholar] [CrossRef]
- Teekeng, W.; Thammano, A. A Combination of Shuffled Frog Leaping and Fuzzy Logic for Flexible Job-Shop Scheduling Problems. Procedia Comput. Sci. 2011, 6, 69–75. [Google Scholar] [CrossRef]
- Ramya, G.; Chandrasekaran, D.M. Shuffled frog leaping algorithm approach to employee timetabling and job shop scheduling. Int. J. Internet Manuf. Serv. 2014, 3, 178–203. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, D.; Wang, B.; Chen, W. Research on Improved Strategy of Shuffled Frog Leaping Algorithm. In Proceedings of the 2019 34th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Jinzhou, China, 6–8 June 2019. [Google Scholar]
- Lei, D.; Guo, X. A shuffled frog-leaping algorithm for job shop scheduling with outsourcing options. Int. J. Prod. Res. 2015, 54, 4793–4804. [Google Scholar] [CrossRef]
- Meng, L.; Ren, Y.; Zhang, B.; Li, J.Q.; Sang, H.; Zhang, C. MILP Modeling and Optimization of Energy-Efficient Distributed Flexible Job Shop Scheduling Problem. IEEE Access 2020, 8, 191191–191203. [Google Scholar] [CrossRef]
- Karakoyun, M.; Ozkis, A.; Kodaz, H. A new algorithm based on gray wolf optimizer and shuffled frog leaping algorithm to solve the multi-objective optimization problems. Appl. Soft Comput. J. 2020, 96, 106560. [Google Scholar] [CrossRef]
- Ramya, G.; Chandrasekaran, M.; Arulmozhi, P. Optimization of production cost for integrating job shop scheduling with production resources. Mater. Today Proc. 2020, 37, 1839–1844. [Google Scholar] [CrossRef]
- Brandimarte, P. Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar] [CrossRef]
- Kacem, I.; Hammadi, S.; Borne, P. Approach by localization and multi-objective evolutionary optimization for flexible job-shop scheduling problems. IEEE Trans. Syst. Man Cybern. Part C 2002, 32, 1–13. [Google Scholar] [CrossRef]
- Rou, L.Y.; Asmuni, H. A study of cooperative co-evolutionary genetic algorithm for solving flexible job shop scheduling problem. Int. J. Comput. Inf. Eng. 2010, 4, 1849–1854. [Google Scholar]
- Kemmoé-Tchomté, S.; Lamy, D.; Tchernev, N. An effective multi-start multi-level evolutionary local search for the flexible job-shop problem. Eng. Appl. Artif. Intell. 2017, 62, 80–95. [Google Scholar] [CrossRef]
- Chen, R.; Yang, B.; Li, S.; Wang, S. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem. Comput. Ind. Eng. 2020, 149, 106778. [Google Scholar] [CrossRef]
- Ding, H.; Gu, X. Improved particle swarm optimization algorithm based novel encoding and decoding schemes for flexible job shop scheduling problem. Comput. Oper. Res. 2020, 121, 104951. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Li, X. Solving flexible job shop scheduling problem by a multi-swarm collaborative genetic algorithm. J. Syst. Eng. Electron. 2021, 32, 261–271. [Google Scholar]
- Hurink, J.; Jurisch, B.; Thole, M. Tabu search for the job-shop scheduling problem with multi-purpose machines. Oper. Res. Spektrum 1994, 15, 205–215. [Google Scholar] [CrossRef]
- Kong, J.; Yuan, C.; Yang, F.; Jia, G. Multi-objective flow shop batch scheduling with separable processing time and setup time under parallel-sequence-transfer mode. Syst. Eng.-Theory Pract. 2017, 37, 2882–2896. [Google Scholar]
- Zeng, Q.; Chang, M.; Wang, M.; Zhang, J. Multi-objective optimization method for FJSP under mixed work calendars. J. Chongqing Univ. 2019, 42, 10–26. [Google Scholar]
- Tian, M.; Zhang, G.; Liu, R. Solve FJSP Considering Transport Time via Particle Swarm Genetic Hybrid Algorithm. Oper. Res. Manag. Sci. 2019, 28, 78–88. [Google Scholar]

| FJSP | Transportation | Preparation | Work Center | Model | Algorithm | |
|---|---|---|---|---|---|---|
| Andy [2] | √ 1 | √ | CP | LNS | ||
| Yige et al. [3] | √ | √ | RJSPDT | |||
| Soroush et al. [4] | √ | √ | MILP, CP | |||
| Allahverdi et al. [5] | √ | √ | FSP, JSP | |||
| Zhang et al. [6] | √ | √ | DFJSP | GEP | ||
| Behnke and Geiger [7] | √ | √ | ||||
| Govi et al. [8] | √ | √ | FJSP | GA | ||
| Pal et al. [9] | √ | √ | √ | FJSP | hGWO | |
| Feng and Kong [10] | √ | √ | √ | HFSP-PSMM | NSGA-II-V | |
| This paper | √ | √ | √ | √ | FJSP-cSH | SFLA-uGSA |
| Problem | α × β | Size | LB | CCGA | GRASP | SLGA | PSO | MSCGA | SFLA-uGSA | SD |
|---|---|---|---|---|---|---|---|---|---|---|
| MK03 | 15 × 8 | 150 | 204 | 204 | 204 | 204 | 204 | 204 | 204 | 0 |
| MK06 | 15 × 10 | 150 | 57 | 64 | 58 | 69 | 77 | 57 | 63 | 1.8 |
| MK07 | 20 × 5 | 100 | 139 | 140 | 139 | 144 | 145 | 139 | 144 | 2.1 |
| Kacem 01 | 4 × 5 | 20 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 0 |
| Kacem 02 | 8 × 8 | 64 | 14 | 17 | 15 | 15 | 14 | 15 | 14 | 0 |
| Kacem 03 | 10 × 7 | 70 | 11 | 13 | 13 | 11 | 11 | 12 | 11 | 0.32 |
| Kacem 04 | 10 × 10 | 100 | 7 | 8 | 7 | 7 | 7 | 7 | 7 | 0 |
| Kacem 05 | 15 × 10 | 150 | 11 | 12 | 13 | 12 | 11 | 11 | 12 | 0.54 |
| Optimal proportion | - | - | - | 25% | 37.5% | 37.5% | 75% | 62.5% | 62.5% | - |
| Problem | α × β | Size | LB | SFLA-uGSA | SFLA | ||||
|---|---|---|---|---|---|---|---|---|---|
| Best | Average | SD | Best | Average | SD | ||||
| LA01 | 10 × 5 | 50 | 570 | 575 | 577.9 | 1.88 | 575 | 579.2 | 2.61 |
| LA02 | 10 × 5 | 50 | 529 | 535 | 541.2 | 2.40 | 541 | 543.4 | 1.55 |
| LA03 | 10 × 5 | 50 | 477 | 477 | 481.7 | 3.16 | 482 | 487.0 | 4.39 |
| LA04 | 10 × 5 | 50 | 502 | 510 | 513.9 | 2.10 | 510 | 516.5 | 3.94 |
| LA05 | 10 × 5 | 50 | 457 | 506 | 514.5 | 5.10 | 514 | 520.7 | 4.63 |
| LA06 | 15 × 5 | 75 | 799 | 799 | 802.3 | 1.96 | 801 | 807.1 | 4.79 |
| LA07 | 15 × 5 | 75 | 749 | 753 | 756.9 | 2.70 | 755 | 760.3 | 3.11 |
| LA08 | 15 × 5 | 75 | 765 | 766 | 769 | 1.80 | 768 | 770 | 1.25 |
| LA09 | 15 × 5 | 75 | 853 | 856 | 858.8 | 1.64 | 858 | 863.9 | 3.37 |
| LA10 | 15 × 5 | 75 | 804 | 855 | 858 | 2.20 | 867 | 873 | 3.85 |
| LA11 | 20 × 5 | 100 | 1071 | 1072 | 1077.3 | 2.76 | 1079 | 1084.1 | 3.24 |
| LA12 | 20 × 5 | 100 | 936 | 937 | 938.6 | 1.40 | 937 | 940.8 | 2.15 |
| LA13 | 20 × 5 | 100 | 1038 | 1040 | 1042.7 | 1.64 | 1044 | 1046.2 | 1.78 |
| LA14 | 20 × 5 | 100 | 1070 | 1071 | 1073.7 | 1.24 | 1071 | 1074.4 | 2.08 |
| LA15 | 20 × 5 | 100 | 1089 | 1094 | 1096.7 | 2.38 | 1099 | 1102.9 | 2.46 |
| LA16 | 10 × 10 | 100 | 717 | 728 | 737.1 | 9.32 | 735 | 746.2 | 8.94 |
| LA17 | 10 × 10 | 100 | 646 | 652 | 657.6 | 5.60 | 655 | 661.4 | 5.35 |
| LA18 | 10 × 10 | 100 | 663 | 700 | 710 | 5.80 | 723 | 730.2 | 4.39 |
| LA19 | 10 × 10 | 100 | 617 | 771 | 801.7 | 10.16 | 779 | 805.3 | 13.85 |
| LA20 | 10 × 10 | 100 | 756 | 800 | 809 | 7.20 | 803 | 814.1 | 8.32 |
| Single | Pareto | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| Target 1 | 204 | 219 | 234 | 209 | 221 | 237 | 213 | 206 | 217 | 204 | 220 |
| Target 2 | 36 | 23 | 20 | 21 | 21 | 17 | 27 | 25 | 24 | 39 | 24 |
| Target 3 | 114 | 106 | 97 | 107 | 102 | 98 | 86 | 89 | 91 | 90 | 86 |
| Job number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Job type | 1 | 1 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 4 |
| Machine number | 1 | 2 | 3 | 4 | 5 | 6 |
| Work center | 1 | 2 | 2 | 3 | 4 | 4 |
| Processing Times | Machine 1 | Machine 2 | Machine 3 | Machine 4 | Machine 5 | Machine 6 | |
|---|---|---|---|---|---|---|---|
| Job type 1 | Operation 1 | 3 | - 2 | - | - | 6 | - |
| Operation 2 | - | - | 1 | - | - | - | |
| Operation 3 | 2 | - | - | - | - | - | |
| Operation 4 | - | - | - | 6 | 6 | - | |
| Operation 5 | 1 | - | - | - | 6 | 5 | |
| Job type 2 | Operation 1 | - | 4 | - | - | 6 | - |
| Operation 2 | - | - | 4 | - | - | 2 | |
| Operation 3 | 1 | - | - | - | 6 | 5 | |
| Operation 4 | 5 | - | 4 | - | 6 | 6 | |
| Operation 5 | 1 | 5 | - | - | - | - | |
| Job type 3 | Operation 1 | 2 | - | - | - | 6 | 5 |
| Operation 2 | - | - | - | 2 | 6 | - | |
| Operation 3 | - | - | 1 | 2 | - | - | |
| Operation 4 | - | 3 | 5 | - | 1 | - | |
| Operation 5 | - | - | 4 | - | - | 2 | |
| Job type 4 | Operation 1 | - | - | 4 | - | - | 2 |
| Operation 2 | - | 4 | 4 | - | - | 6 | |
| Operation 3 | 1 | 6 | - | - | - | 5 | |
| Operation 4 | 5 | 4 | - | - | - | - | |
| Operation 5 | - | 6 | - | 6 | - | - | |
| Setup Times | Machine 1 | Machine 2 | Machine 3 | Machine 4 | Machine 5 | Machine 6 | |
|---|---|---|---|---|---|---|---|
| Job type 1 | Operation 1 | 1 | - | - | - | 1 | - |
| Operation 2 | - | - | 1 | - | - | - | |
| Operation 3 | 2 | - | - | - | - | - | |
| Operation 4 | - | - | - | 1 | 1 | - | |
| Operation 5 | 1 | - | - | - | 1 | 1 | |
| Job type 2 | Operation 1 | - | 1 | - | - | 1 | - |
| Operation 2 | - | - | 1 | - | - | 1 | |
| Operation 3 | 2 | - | - | - | 1 | 2 | |
| Operation 4 | 1 | - | 1 | - | 1 | 1 | |
| Operation 5 | 2 | 1 | - | - | - | - | |
| Job type 3 | Operation 1 | 1 | - | - | - | 1 | 1 |
| Operation 2 | - | - | - | 1 | 1 | - | |
| Operation 3 | - | - | 2 | 1 | - | - | |
| Operation 4 | - | 1 | 1 | - | 2 | - | |
| Operation 5 | - | - | 1 | - | - | 1 | |
| Job type 4 | Operation 1 | - | - | 2 | - | - | 1 |
| Operation 2 | - | 1 | 1 | - | - | 1 | |
| Operation 3 | 2 | 1 | - | - | - | 1 | |
| Operation 4 | 1 | 1 | - | - | - | - | |
| Operation 5 | - | 1 | - | 1 | - | - | |
| Handling Times | Work Center 1 | Work Center 2 | Work Center 3 | Work Center 4 |
|---|---|---|---|---|
| Work center 1 | - 3 | 1 | 1 | 2 |
| Work center 2 | 1 | - | 1 | 1 |
| Work center 3 | 1 | 1 | - | 1 |
| Work center 4 | 2 | 1 | 1 | - |
| Job(i) | Operation(ij) | Machine(k) | Work Center | |||||
|---|---|---|---|---|---|---|---|---|
| J1 | O11 | M5 | WC4 | 0 | 1 | 1 | 6 | 7 |
| O12 | M3 | WC2 | 10 | 1 | 11 | 1 | 12 | |
| O13 | M1 | WC1 | 18 | 0 | 18 | 2 | 20 | |
| O14 | M4 | WC3 | 21 | 1 | 22 | 6 | 28 | |
| O15 | M1 | WC1 | 28 | 1 | 29 | 1 | 30 | |
| J2 | O21 | M1 | WC1 | 7 | 1 | 8 | 3 | 11 |
| O22 | M3 | WC2 | 12 | 0 | 12 | 1 | 13 | |
| O23 | M1 | WC1 | 14 | 2 | 16 | 2 | 18 | |
| O24 | M5 | WC4 | 23 | 1 | 24 | 6 | 30 | |
| O25 | M5 | WC4 | 30 | 0 | 30 | 6 | 36 | |
| J3 | O31 | M2 | WC2 | 0 | 1 | 1 | 4 | 5 |
| O32 | M6 | WC4 | 11 | 1 | 12 | 2 | 14 | |
| O33 | M6 | WC4 | 14 | 0 | 14 | 5 | 19 | |
| O34 | M6 | WC4 | 19 | 0 | 19 | 6 | 25 | |
| O35 | M1 | WC1 | 30 | 2 | 32 | 1 | 33 | |
| J4 | O41 | M5 | WC4 | 7 | 1 | 8 | 6 | 14 |
| O42 | M4 | WC3 | 15 | 0 | 15 | 2 | 17 | |
| O43 | M4 | WC3 | 17 | 0 | 17 | 2 | 19 | |
| O44 | M5 | WC4 | 21 | 0 | 21 | 1 | 22 | |
| O45 | M6 | WC4 | 28 | 0 | 28 | 2 | 30 | |
| J5 | O51 | M1 | WC1 | 5 | 0 | 5 | 2 | 7 |
| O52 | M4 | WC3 | 13 | 0 | 13 | 2 | 15 | |
| O53 | M4 | WC3 | 19 | 0 | 19 | 2 | 21 | |
| O54 | M5 | WC4 | 22 | 0 | 22 | 1 | 23 | |
| O55 | M6 | WC4 | 25 | 1 | 26 | 2 | 28 | |
| J6 | O61 | M1 | WC1 | 3 | 0 | 3 | 2 | 5 |
| O62 | M4 | WC3 | 8 | 1 | 9 | 2 | 11 | |
| O63 | M3 | WC2 | 13 | 2 | 15 | 1 | 16 | |
| O64 | M3 | WC2 | 22 | 0 | 22 | 5 | 27 | |
| O65 | M3 | WC2 | 27 | 0 | 27 | 4 | 31 | |
| J7 | O71 | M1 | WC1 | 0 | 1 | 1 | 2 | 3 |
| O72 | M4 | WC3 | 11 | 0 | 11 | 2 | 13 | |
| O73 | M3 | WC2 | 16 | 0 | 16 | 1 | 17 | |
| O74 | M3 | WC2 | 17 | 0 | 17 | 5 | 22 | |
| O75 | M3 | WC2 | 31 | 0 | 31 | 4 | 35 | |
| J8 | O81 | M3 | WC2 | 0 | 2 | 2 | 4 | 6 |
| O82 | M2 | WC2 | 5 | 1 | 6 | 4 | 10 | |
| O83 | M1 | WC1 | 20 | 2 | 22 | 1 | 23 | |
| O84 | M1 | WC1 | 23 | 0 | 23 | 5 | 28 | |
| O85 | M4 | WC3 | 28 | 1 | 29 | 6 | 35 | |
| J9 | O91 | M6 | WC4 | 3 | 0 | 3 | 2 | 5 |
| O92 | M6 | WC4 | 5 | 0 | 5 | 6 | 11 | |
| O93 | M1 | WC1 | 11 | 2 | 13 | 1 | 14 | |
| O94 | M2 | WC2 | 20 | 0 | 20 | 4 | 24 | |
| O95 | M2 | WC2 | 30 | 0 | 30 | 6 | 36 | |
| J10 | O10,1 | M6 | WC4 | 0 | 1 | 1 | 2 | 3 |
| O10,2 | M3 | WC2 | 6 | 0 | 6 | 4 | 10 | |
| O10,3 | M2 | WC2 | 10 | 0 | 10 | 6 | 16 | |
| O10,4 | M2 | WC2 | 16 | 0 | 16 | 4 | 20 | |
| O10,5 | M2 | WC2 | 24 | 0 | 24 | 6 | 30 |
| Serial Number | Machine | Start Time of Shutdown 3 | Time of Shutdown | Completion Time of Shutdown /Start Time of Processing | Time of Processing | Completion Time of Processing |
|---|---|---|---|---|---|---|
| 1 | M1 | 0 | 0 | 0 | 33 | 33 |
| 2 | M2 | 0 | 0 | 0 | 36 | 36 |
| 3 | M3 | 0 | 0 | 0 | 35 | 35 |
| 4 | M4 | 0 | 8 | 8 | 27 | 35 |
| 5 | M5 | 0 | 0 | 0 | 14 | 14 |
| 6 | M6 | 14 | 7 | 21 | 15 | 36 |
| 7 | M6 | 0 | 0 | 0 | 30 | 30 |
| Serial Number | From Work Center | To Work Center | Jobs | Time of Handling | Earliest Start Time | Earliest Completion Time | Latest Start Time | Latest Completion Time |
|---|---|---|---|---|---|---|---|---|
| 1 | WC1 | WC2 | J2 | 1 | 11 | 12 | 11 | 12 |
| 2 | WC1 | WC2 | J9 | 1 | 14 | 15 | 19 | 20 |
| 3 | WC1 | WC3 | J5, J6, J7 | 1 | 7 | 8 | 8 | 9 |
| 4 | WC1 | WC3 | J1 | 1 | 20 | 21 | 21 | 22 |
| 5 | WC1 | WC3 | J8 | 1 | 28 | 29 | 28 | 29 |
| 6 | WC1 | WC4 | J2 | 2 | 18 | 20 | 22 | 24 |
| 7 | WC2 | WC1 | J1, J2, J8 | 1 | 13 | 14 | 15 | 16 |
| 8 | WC2 | WC4 | J3 | 1 | 5 | 6 | 11 | 12 |
| 9 | WC3 | WC1 | J1 | 1 | 28 | 29 | 28 | 29 |
| 10 | WC3 | WC2 | J6, J7 | 1 | 13 | 14 | 14 | 15 |
| 11 | WC3 | WC4 | J4 | 1 | 19 | 20 | 20 | 21 |
| 12 | WC3 | WC4 | J5 | 1 | 21 | 22 | 21 | 22 |
| 13 | WC4 | WC1 | J9 | 2 | 11 | 13 | 11 | 13 |
| 14 | WC4 | WC1 | J3 | 2 | 25 | 27 | 30 | 32 |
| 15 | WC4 | WC2 | J10 | 1 | 3 | 4 | 5 | 6 |
| 16 | WC4 | WC2 | J1 | 1 | 7 | 8 | 10 | 11 |
| 17 | WC4 | WC3 | J4 | 1 | 14 | 15 | 14 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, J.; Yang, Y. Research on Multi-Objective Flexible Job Shop Scheduling Problem with Setup and Handling Based on an Improved Shuffled Frog Leaping Algorithm. Appl. Sci. 2024, 14, 4029. https://doi.org/10.3390/app14104029
Kong J, Yang Y. Research on Multi-Objective Flexible Job Shop Scheduling Problem with Setup and Handling Based on an Improved Shuffled Frog Leaping Algorithm. Applied Sciences. 2024; 14(10):4029. https://doi.org/10.3390/app14104029
Chicago/Turabian StyleKong, Jili, and Yi Yang. 2024. "Research on Multi-Objective Flexible Job Shop Scheduling Problem with Setup and Handling Based on an Improved Shuffled Frog Leaping Algorithm" Applied Sciences 14, no. 10: 4029. https://doi.org/10.3390/app14104029
APA StyleKong, J., & Yang, Y. (2024). Research on Multi-Objective Flexible Job Shop Scheduling Problem with Setup and Handling Based on an Improved Shuffled Frog Leaping Algorithm. Applied Sciences, 14(10), 4029. https://doi.org/10.3390/app14104029






