Study on Shear Failure Process and Zonal Disintegration Mechanism of Roadway under High Ground Stress: A Numerical Simulation via a Strain-Softening Plastic Model and the Discrete Element Method

Abstract

Fracture expansion in rock masses can be observed by monitoring the break of contacts between the bounding particles via the discrete element method. The latter’s realization in this study via the PFC^2D program tracked the evolution process of the zonal disintegration in an exemplary roadway-surrounding rock affected by mining. Besides, the damage evolution pattern in a high-stress soft rock roadway was simulated by the FLAC^2D program using a strain-softening plastic model, revealing the effects of rock mass strength, stress state, and anchor support on the zonal disintegration of the roadway. Numerical simulation results show that in a roadway with high-level stress, the obvious fractures spread from the roadway surface to the depth of the surrounding rock along a series of geometric planes and cut the surrounding rock into rock mass blocks. Under high crustal stress, conjugate shear fractures occur near the roadway surfaces and form a closed-loop fractured zone after intersecting the conjugate fracture faces. The closed fractured zone becomes a free face, from which conjugate shear fractures develop, forming new closed fractured zones in the deep surrounding rock. By repeatedly generating the closed fracture zones, a fracture network appears in the roadway-surrounding rock. The development of zonal disintegration of roadway-surrounding rock mainly depends on the rock mass strength and its stress state. Zonal disintegration only occurs when the crustal stress of the roadway-surrounding rock exceeds its strength. When the horizontal stress is low and the vertical stress exceeds the rock mass strength, zonal disintegration only occurs on two sides of the roadway. When the vertical stress is low and the horizontal stress exceeds the rock’s mass strength, it only appears on the roof and floor. When the values of cohesion, internal friction angle, and tensile strength are reduced in the same proportion, cohesion has the greatest impact on the expansion of the zonal disintegration zone, followed by the internal friction angle, while the tensile strength effect is the least. In anchor-supported roadways undergoing zonal disintegration processes, the intact zone blocks slide relatively along the fracture surface during the process of loosening and deformation of the surrounding rock, making the anchor rods susceptible to tensile, shear, and bending actions.

1. Introduction

The surrounding rocks in the roadway may show zonal disintegration characteristics at a great burial depth or under high stress, i.e., obviously fractured zones and complete zones appear alternately in shallow and deep surrounding rocks [1]. This phenomenon was revealed as early as 1972 by Borisovets [2]. Scholars from South Africa and China also observed zonal disintegration phenomena later in deep mining [3,4,5,6]. Zonal disintegration is currently recognized as a common phenomenon in deep roadways [7] and has become a hotspot in rock mechanics and rock engineering. In general, zonal integration is the key feature of roadway damage in deep mining. Gaining in-depth knowledge on its formation mechanisms and patterns can provide insightful references for addressing the control problems of the surrounding rocks in deep roadways [7,8,9].

Scholars have first investigated zonal integration based on field borehole measurements. By arranging the drilling holes along the periphery of the roadway in a cross-section, the alternate appearance of disintegration and complete zones was confirmed in the drilling holes via borehole TV survey and ultrasonic perspective examination. It was thus derived that the disintegration zone and the complete zones appeared alternately around the roadway, approximately in a circular-ring pattern [4,5,6]. The related studies were mainly focused on the reproduction of alternate distribution characteristics in the laboratory. Some scholars conducted physical experiments but failed to obtain the obvious zonal disintegration phenomenon [10,11,12]; others did not obtain annularly-distributed disintegration in the roadway-surrounding rocks from physical analog experiments but found the distribution of the fractures in the section parallel to the roadway [13]. Accordingly, they deduced that the spatial distribution of conjugated shear zones can explain zonal disintegration. Afterward, scholars placed their research emphasis on annular zonal disintegration. They concluded that the approximately annularly zonal disintegration effect was due to the nonuniform settings of the mechanical parameters of the surrounding rocks in the roadway [14]. Gao et al. simulated the development characteristics of the fractures in homogeneous surrounding rocks based on a bilinear strain-softening ubiquitous-joint model in FLAC^2D. Nevertheless, they did not observe annular disintegration zones in alternate patterns [15].

Investigating the zonal disintegration patterns of the surrounding rocks in the roadway via physical experiments or numerical simulation was crucial for validating field measurement results and provided the foundation for further analyzing the mechanisms and related influencing factors. Since fractures in the surrounding rocks involved the rock fracturing process, the latter was successfully simulated by the discrete element method. Based on the research results in roadway support engineering, this study first conducted a numerical simulation of the development of zonal disintegration in the surrounding rocks during deformation and fracture processes in high-stress and deep high-stress roadways via PFC^2D 5.00 and FLAC^2D 7.00 software packages. The performed numerical simulation clarified the effects of the surrounding rock’s mechanical parameters, the distribution of stress fields, and the roadway’s sectional shape/pattern on zonal disintegration.

2. Zonal Rupture Modeling of Roadway Perimeter Rock under High Stress

2.1. Base Range Modeling of Roadway Perimeter Rock Fragmentation Based on Discrete Element Approach

This study is focused on a belt conveyance haulage way in the working face of the Chahasu mine in Erdos, China, with a burial depth of approximately 650 m and a coal seam depth of 6.0 m. The immediate roof and floor were made up of mudstone with depths of 3.2 and 5.4 m, respectively, while the upper roof and floor were made up of medium-grained sandstone. The rectangular roadway cross-section was 5.8 m in width and 4.0 m in height. The surrounding rocks’ deformation and failure process after the roadway’s excavation was simulated using the PFC^2D (particle flow code in two dimensions) software produced by Itasca Consulting Group, Inc. (Minneapolis, MN, USA), via the established discrete element model shown in Figure 1. The model dimensions were 36.0 m × 24.0 m. In the numerical simulation, the radii of particles in the coal seam, immediate roof/floor, and upper roof/floor were set at 0.05, 0.1, and 0.2 m, respectively.

A parallel bonding model is used between particles, and bonding bonds are set between adjacent particles. The parallel bonding model is one of the bonding models built into the software, the core implementation of which is to generate a bonding material of a certain size between neighboring particles. When the bonding material is broken, the broken surface of the particles will become a linear stiffness model. In this model, the particles can be similar to springs with constant normal and tangential stiffness, uniformly distributed in a rectangular cross-section on the contact plane centered at the point of contact. These springs act in parallel with the springs of the linear assembly to produce a parallel bond, and then contact occurs where the bond breaks if the maximum stress exceeds the bond strength. It is possible to model the contact forces ${\overline{F}}_{\mathrm{p}}$ and moments ${\overline{M}}_{\mathrm{p}}$ expressed as follows:

$${\overline{F}}_{\mathrm{p}}=F_{\mathrm{n}}{\overline{\mathrm{n}}}_{\mathrm{p}}+F_{\mathrm{s}}{\overline{\mathrm{t}}}_{\mathrm{p}}$$

(1)

$${\overline{M}}_{\mathrm{p}}=M_{\mathrm{n}}{\overline{\mathrm{n}}}_{\mathrm{p}}+M_{\mathrm{s}}{\overline{\mathrm{t}}}_{\mathrm{p}}$$

(2)

In models made using the parallel bonding ontological relationship, a large number of particles are usually bonded to form constructs of multiple shapes, while the mechanical properties of the constructs are described using the holistic approach. The fact that the constructs are composed of multiple particles also allows the constructs to be modeled with tensile, shear, and torsional mechanical characteristics. When the stress on the construct exceeds its corresponding bond strength, the bond relationship between particles will be broken, the bond relationship at the corresponding particle contact will be degraded to a linear relationship, and the construct as a whole becomes multiple smaller constructs that continue to move, as shown in Figure 2 [16].

The model parameters were verified with reference to the simulation data from the literature [17], which is based on the experimental results of the mechanical parameters of the surrounding rock in the roadway of the Chahasu mine. The specific parameters are listed in

Table 1. Statistical table of mechanical experiment results for the coal rock body.

Stratum	Normal Stiffness, GPa	Tensile Strength, MPa	Tangential Stiffness, GPa	Shear Strength, MPa	Frictional Coefficient
Upper roof/floor	2.4	1.0	2.4	5.0	0.35
Immediate roof/floor	1.2	0.3	1.2	2.5	0.25
Coal seam	0.8	0.15	0.8	1.0	0.2

.

Both sides and the floor obeyed the following displacement boundary conditions: the horizontal displacements were fixed at both sides, while the vertical displacement was fixed at the floor.

At this stage, the load on the roof plate will increase from the original rock stress to the situation of over-head support pressure affected by mining. Combined with the actual data measured in the field, we set the original rock stress of the roof slab to 18 MPa and the over-support pressure to 30 MPa. The original rock stress load was applied when the roadway in the model had not yet been excavated and the model reached an initial equilibrium, and the over-support pressure was applied when the roadway was further excavated.

We monitored the fracture of the bonding bonds between particles in the model, as shown in Figure 3, and used it to represent the fracture process of the roadway perimeter rock.

After the rectangular roadway was excavated, the stress concentration was observed at four angular points [18], where fractures also began to appear, as shown in Figure 3a. Next, the fractures extended along two conjugate shear planes to the depth between the two sides and the roof, forming the conjugate fracture planes within two sides, depicted by OA, OB, O’A’, and O’B’ in Figure 3b. On both sides of the roadway, when the conjugate failure surfaces intersected at points O and O’, these surfaces stopped extending forward and started to develop vertically toward the floor (see Figure 3c). After reaching the floor, the fracture planes underwent two different development processes on two sides: the first one implied the development from the intersection point O’ to the roof until the coal-rock interface was reached, forming a vertical failure plane penetrating through the coal seam (see the plane CD in Figure 3d). The second process involved a continued development to the depth via a conjugate failure pattern (see the OF and EF fracture planes in Figure 3d), generating a vertical failure plane at the intersection point F that penetrated through the coal seam (see HI in Figure 3e). After forming the vertical failure plane from the coal seam to the roof/floor, the fractures continued developing toward both sides via a conjugate failure pattern towards the depth of the two sides (see Figure 3f). Besides, upward conjugate failures appeared on the roof (see the IJ and MN fracture planes in Figure 3f).

2.2. Perimeter Rock Damage Model of a Deep, High-Stress Soft Rock Tunnel Based on the Finite Difference Method

2.2.1. Modeling

The destruction process of the surrounding rock in the deep, high-stress soft rock roadway was adopted from the basic geological conditions of the belt transportation roadway in the mining area of the Quandian coal mine in Xuchang City, China. The section size of this roadway is 5.2 m × 4.0 m, the burial depth is about 600 m, and the top and bottom plates of the rock formation consist of low-strength mudstone and sandy mudstone.

Our model parameters were adopted from the data obtained from physical tests. As shown in Figure 4, the researcher collected core samples of the surrounding rock from the belt transportation roadway of the mining area at the Quandian coal mine. The uniaxial compressive test, the Brazilian splitting method tensile test, and the shear test were carried out on these samples using the MTS servo tester and the SYNS pressure shear machine, respectively. The mechanical parameters of the perimeter rock of this roadway were obtained as shown in

Table 2. Test results of the mechanical parameters of the surrounding rock.

Stratum	Densities, kg/m3	Bulk Modulus, GPa	Shear Modulus, GPa	Cohesion, MPa	Internal Friction Angle, °
Mudstone	2300	1.2	0.3	1.0	16

.

The deformation and fracture processes after roadway excavation were numerically simulated in this study by a model with a size of 80.0 m × 64.0 m, as shown in Figure 5, which was realized via the commercial FLAC^2D software package. The roadway vicinity was represented by a refined mesh with a size of 0.2 m × 0.2 m.

In the simulations, we used a strain softening model for the reduction. The rock density was set at 2300 kg/m³, while the bulk and shear moduli were set at 1.2 and 0.3 GPa, respectively. The strain softening model is a commonly used simulation method based on the Moore–Coulomb model that is not associated with the shear flow law but with the tensile flow law, the difference being that the cohesion, friction angle, shear expansion and dilatation, and tensile strength may change after the onset of plastic yielding. In the Moore–Coulomb model, such properties are assumed to remain constant. Users can define their own softening parameters, such as cohesion and friction angle, and set them as segmented linear functions (Figure 6). They can then use these softening parameters to measure plastic shear strains. In this model, we use data obtained from physical tests. This model calculates the total plastic shear and tensile strains by increasing the softening parameter at each time step and, in this way, drives the material properties to be consistent with the user-defined functions. For yield and potential functions, the plastic flow law and stress corrections are identical to the Moore–Coulomb model.

Both vertical and horizontal in-situ stresses in the surrounding rock were set at 15.0 MPa. The horizontal displacement of both sides and the vertical displacement of the floor were fixed. The upper boundary was under a pressure of 15.0 MPa.

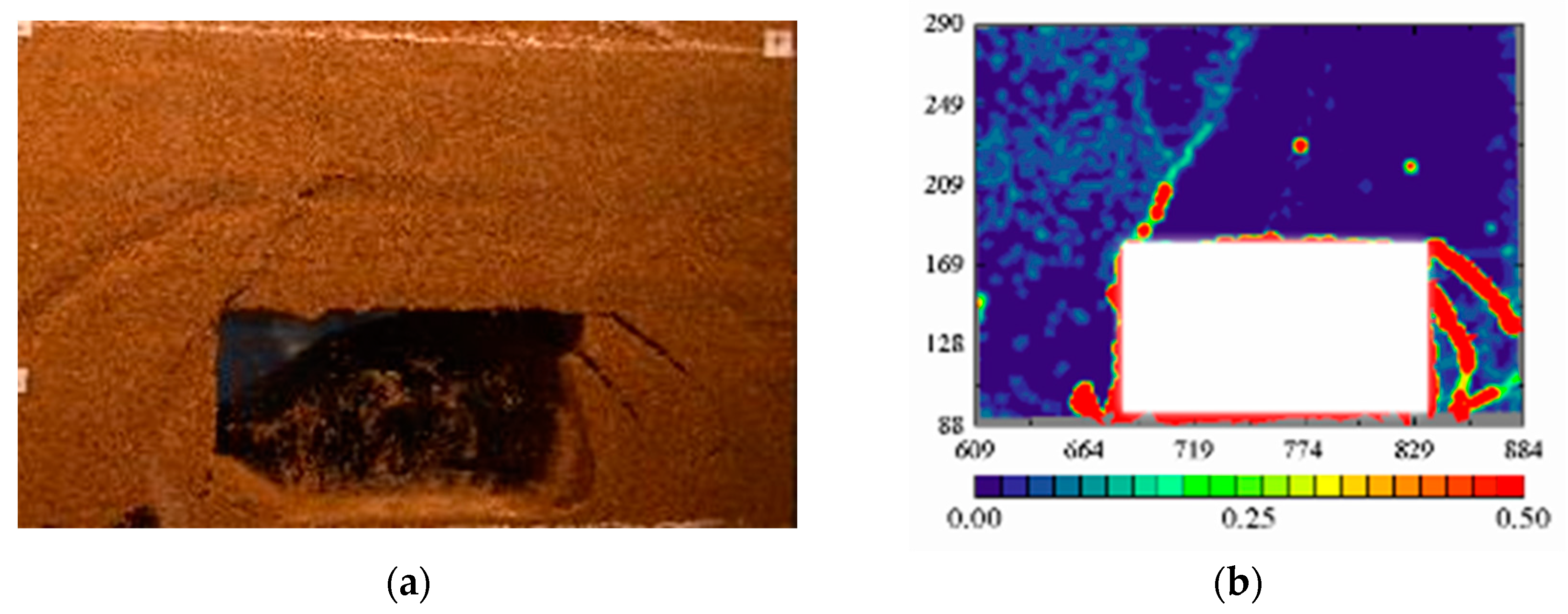
2.2.2. Simulation Results

Firstly, the calculation was made to bring the model to the initial equilibrium, then the roadway was excavated, and the calculation was continued for the new equilibrium state. The deformation and damage degrees of the surrounding rock were evaluated via the shear strain increment (Δγ). A larger shear strain increment indicates more serious deformation and damage to the rock [14]. Figure 7 shows the evolution of the shear strain increment of the surrounding rock in the roadway, which was calculated via the proposed model.

According to the discrete element analysis predictions, the fracturing of the surrounding rocks in the roadway first occurred at four angular points (see Figure 7a) and developed in the form of compression–shear conjugate damage deep into the two sides, the roof, and the floor, until the fractures became intersected (see Figure 7b), thereby forming a tilted rectangular fracture loop. After the conjugate fracture planes intersected, the fractures developed from the intersection point toward the deep surrounding rocks along vertical and horizontal directions (see Figure 7c) until they intersected (see Figure 7d). Accordingly, a new rectangular fracture loop was formed outside the first layer of the fracture loop. Next, the fracture planes developed from the four angular points of the second layer of rectangular fracture loop deep towards the sides, the roof, and the floor in a shear fracture mode (see Figure 7e).

3. Analysis of Results

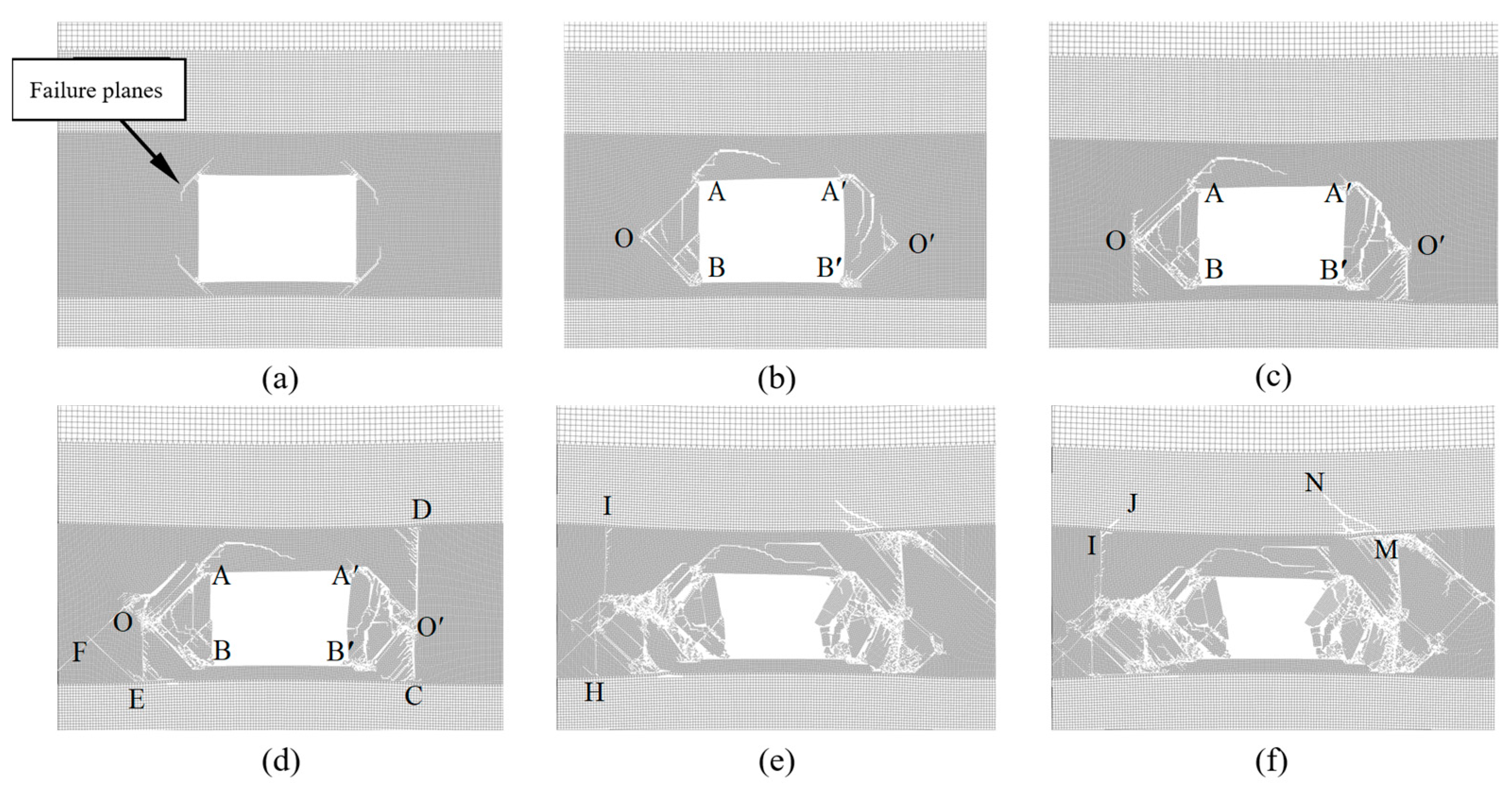
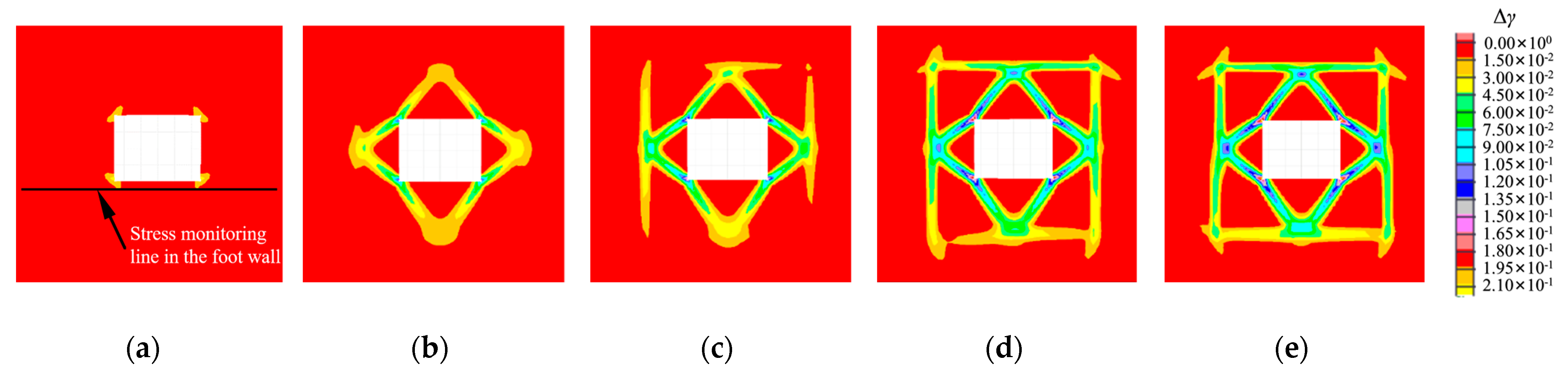
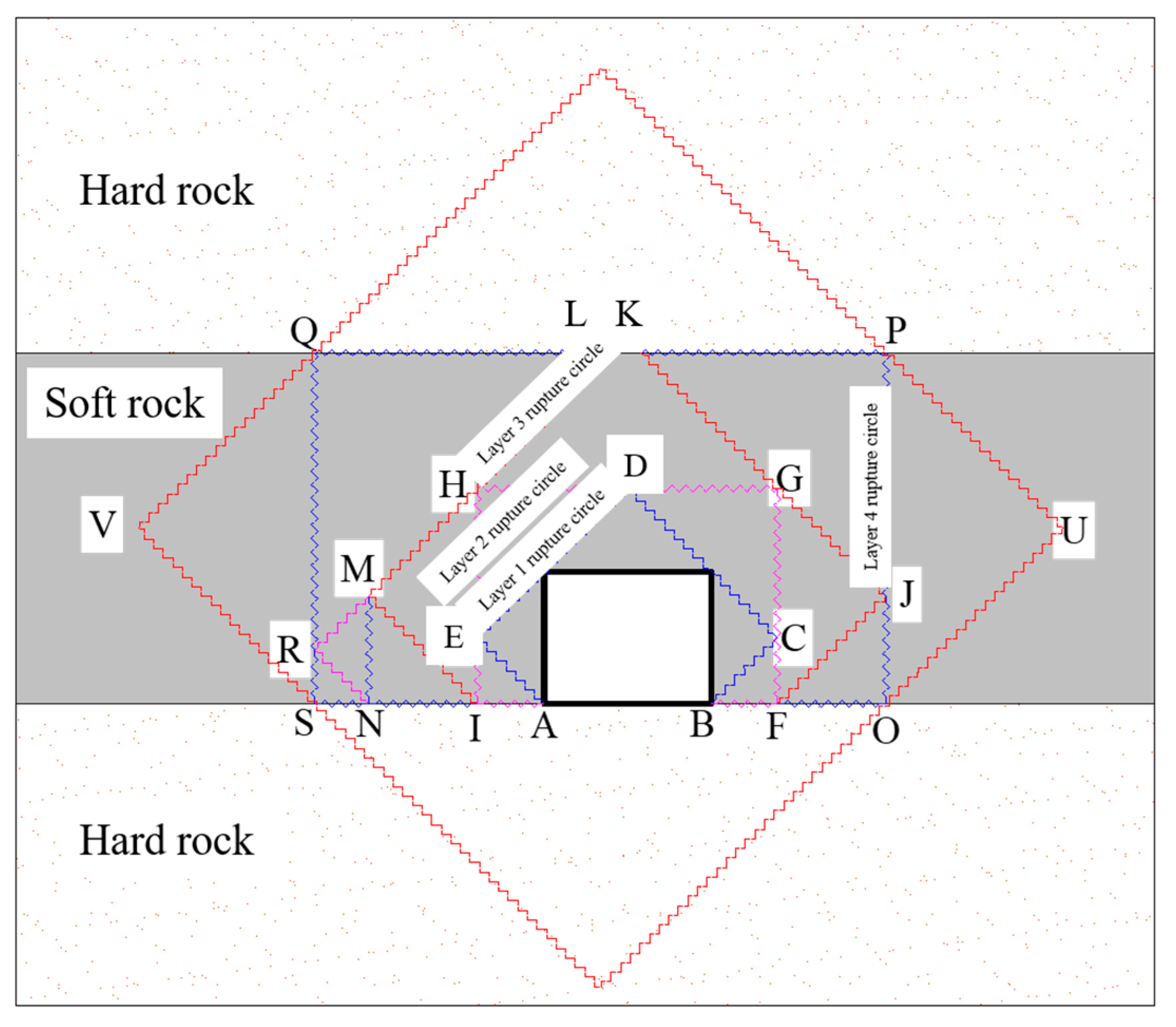
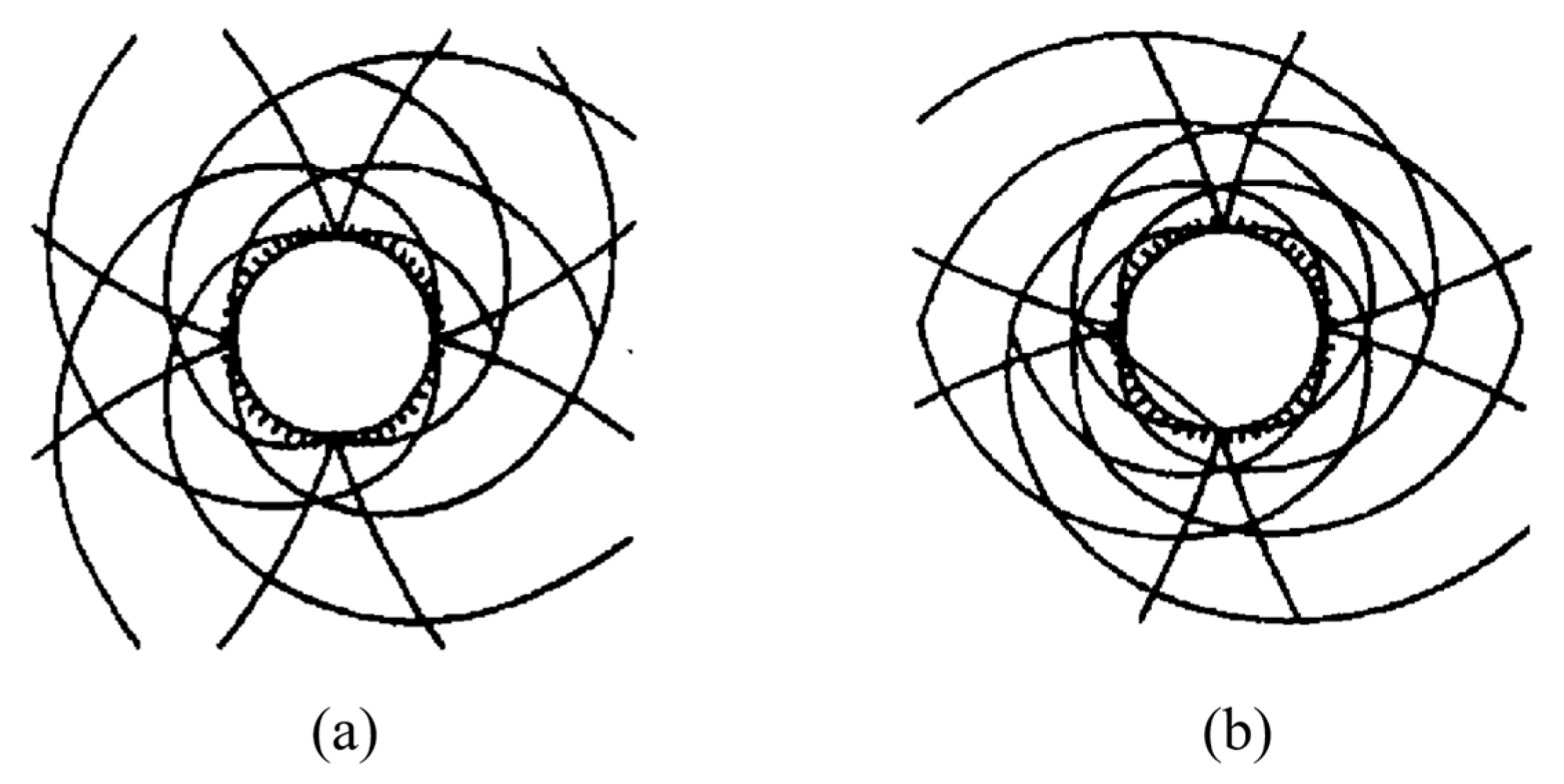
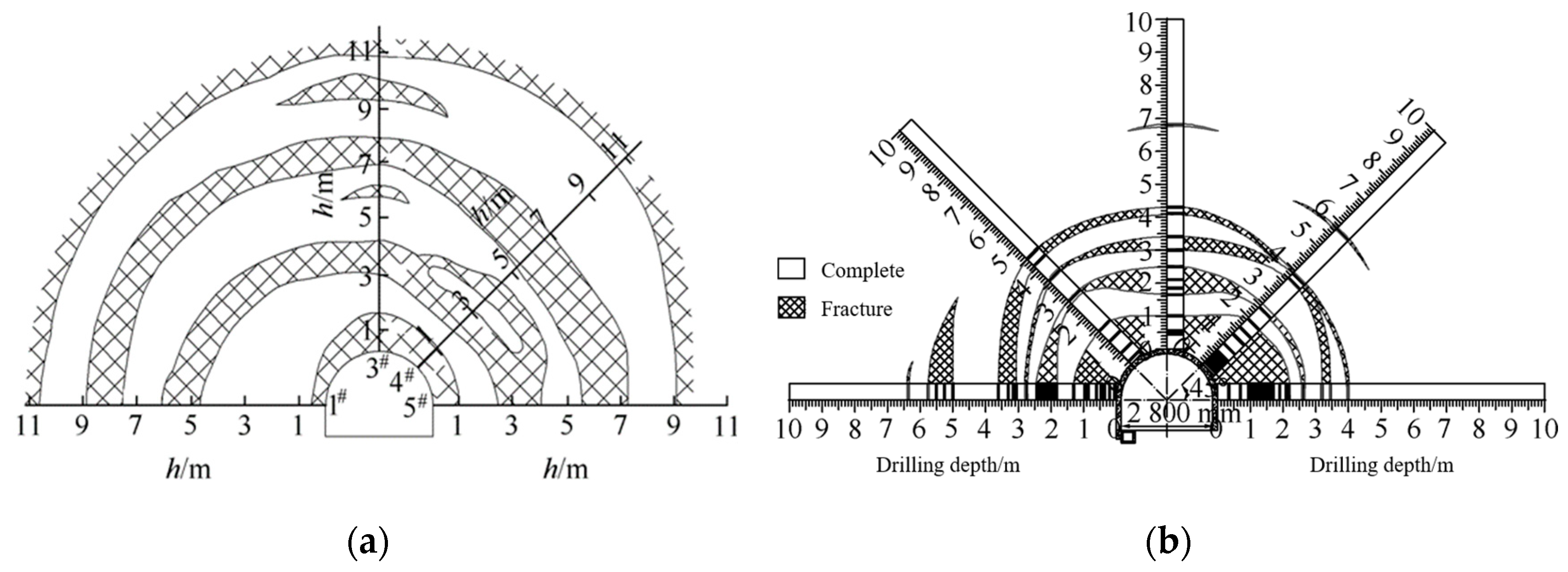
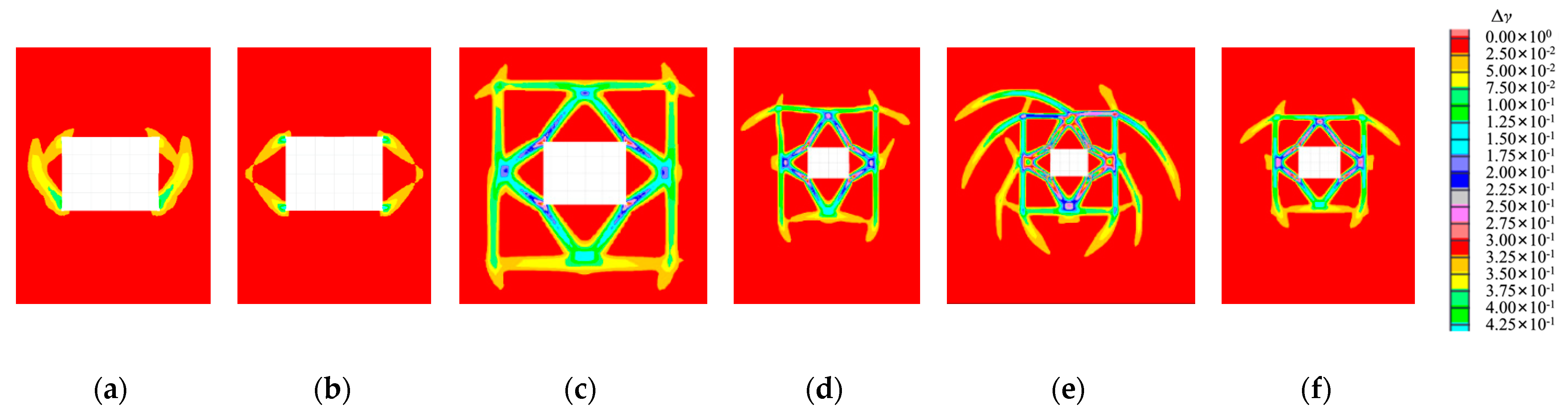
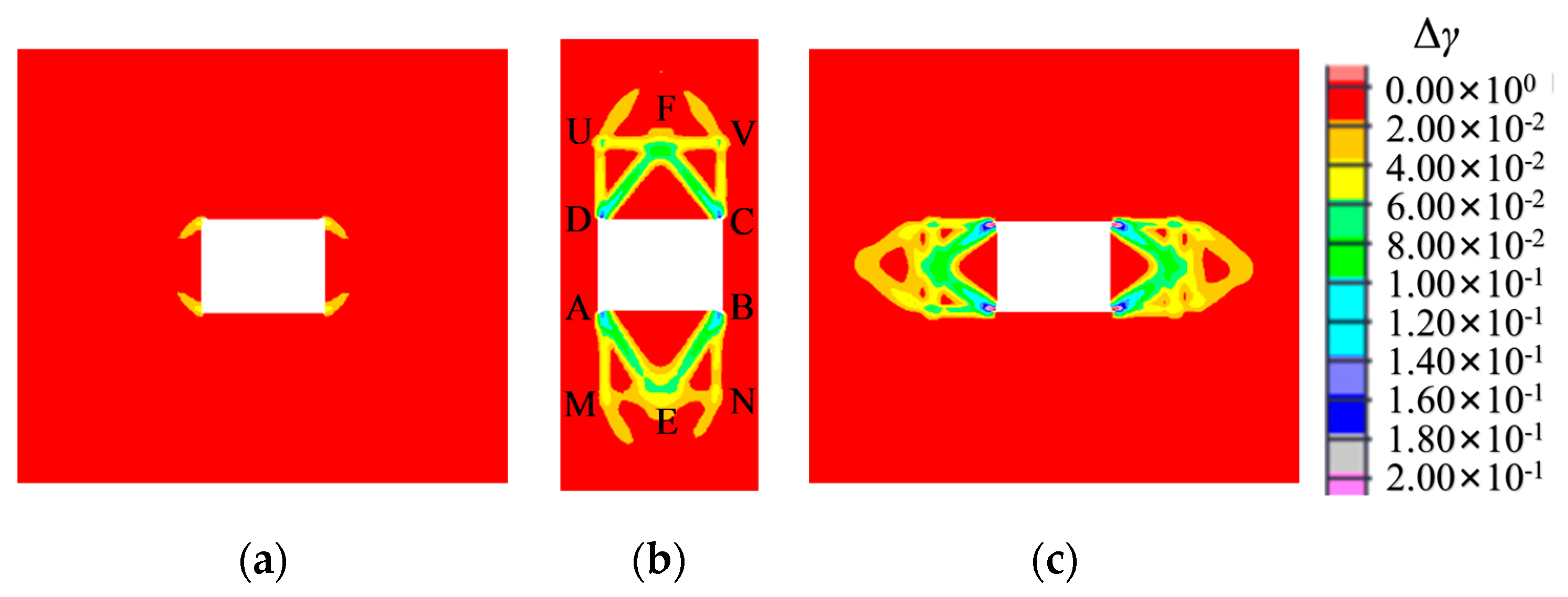
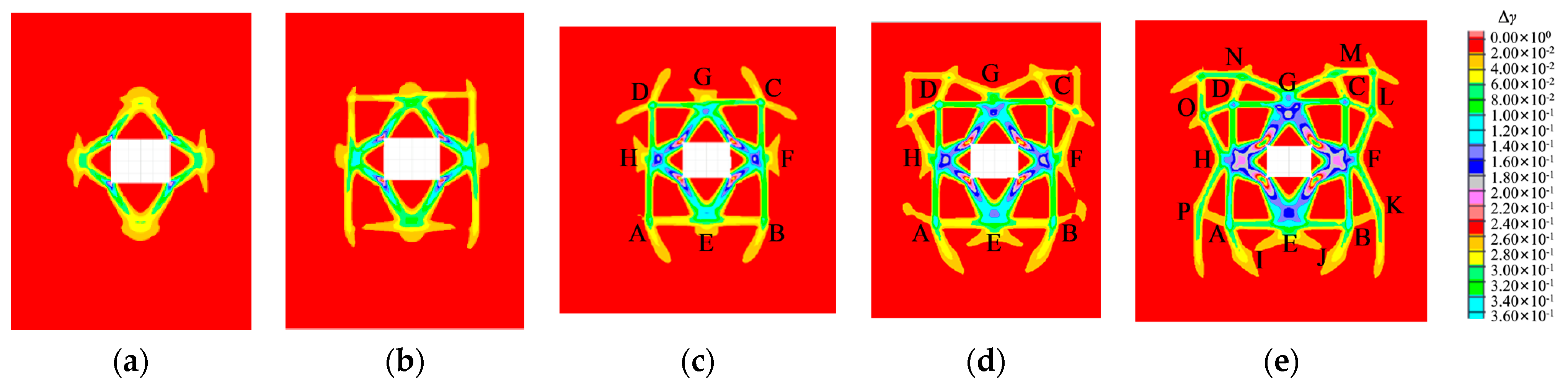
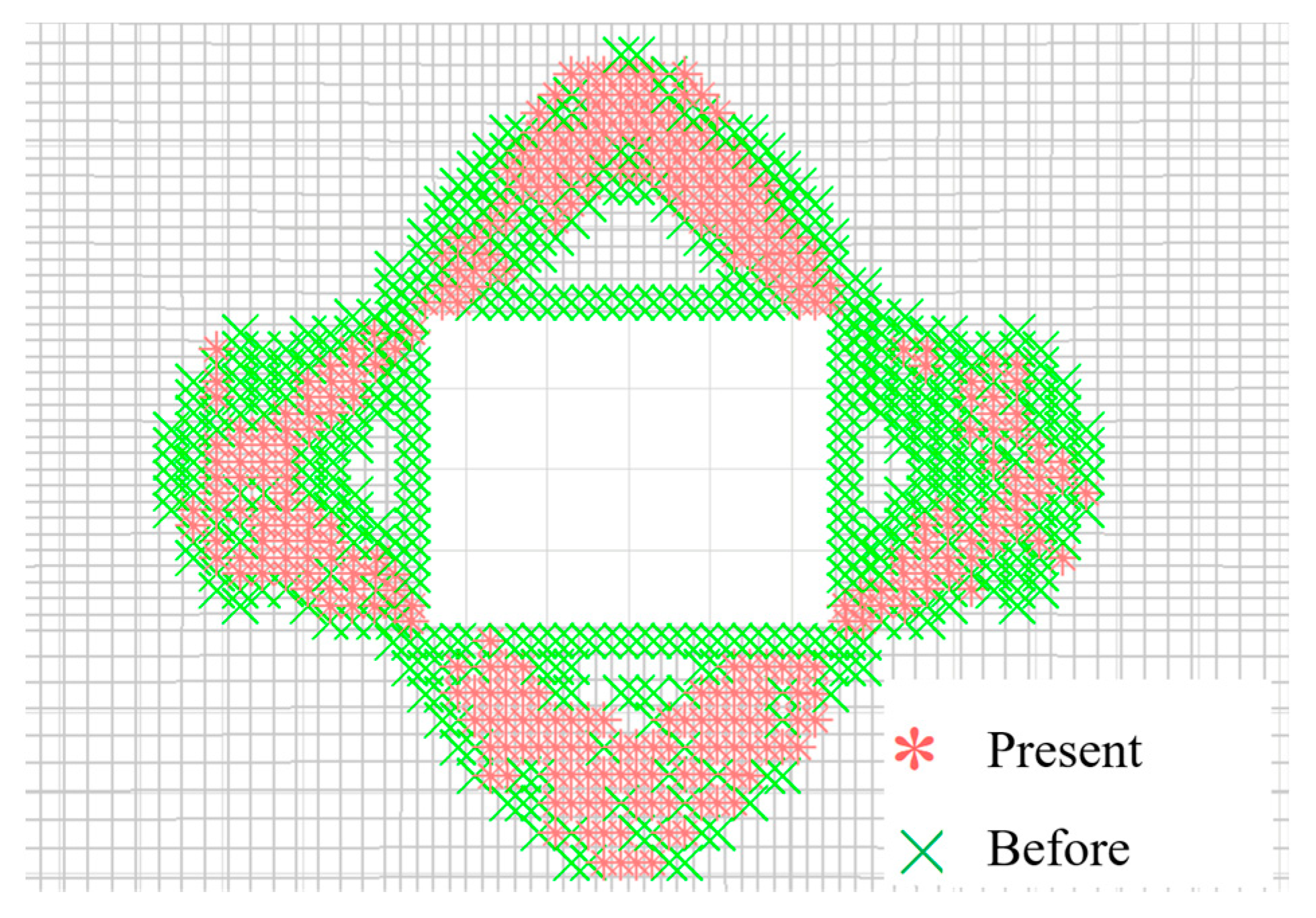
3.1. Zonal Rupture Pattern of the Roadway Enclosure

According to numerical simulation results, the development of the fracture planes of the surrounding rocks in the roadway followed the compression–shear conjugate fracture patterns of rock mechanics [18]. In the rectangular roadway after excavation, as shown in Figure 8, the shallow surrounding rocks became loose toward the roadway, and the stresses perpendicular to the roadway surface were gradually released. Accordingly, the shallow surrounding rocks underwent bidirectional compression. Therefore, the stress condition of the roadway could be reduced to a plane strain state. The stress conditions on the roof and the floor are shown in Figure 8 by ABCD, while AEFG corresponds to the stress conditions on both sides. When the horizontal σ_H and vertical σ_V stresses in the surrounding rocks exceeded the compressive strength value, conjugate failure occurred along the AM, GM, AN, and DN lines. After the conjugate fracture planes intersected, they formed an enclosed fracture loop MNOP in the surrounding rocks. The shallow surrounding rocks in the roadway were fractured and cut into wedge-shaped blocks by the fracture loop MNOP, as shown by the triangle AMG in Figure 8. Under high-stress conditions, the surrounding rocks could easily slip toward the roadway. After this loosening, the MNOP acted as a new roadway boundary: the stressed body under plane strain conditions (such as MUVN) continued to be isolated along each side of the MNOP. When the pressure σ_s exceeded the strength of the surrounding rocks, the conjugate shear fracture occurred, and a new fracture loop was formed outside the MNOP.

According to the simulation results depicted in Figure 4, the nonuniform strength of the surrounding rocks can affect the development of the fracturing process. As shown in Figure 9, the roadway was located in soft rock strata, while its roof and floor were in hard rock strata.

A comprehensive analysis of the simulation results presented in Figure 4 and the above fracture patterns revealed that the first and fourth layers of the fracture loops developed only in soft strata without penetrating the hard strata. With the expanding boundary of the loosening loop, the vertical pressures acting on the roof and floor gradually dropped. For example, during the process shown in Figure 6, the vertical stress variation along the preset stress-monitoring line (Figure 7a) set up in the roadway floor occurred, as shown in Figure 10. After forming the second layer of the fracture loop, the mean vertical stress on the floor between the left and right boundaries dropped by approximately 40% compared with the value reached after the formation of the first layer of the fracture loop. After forming the first layer of the fracture loop, as shown in Figure 8, the stress on the floor within the range AB was close to zero, while both sides AI and BF were located in the stress-reduction zone. After forming the second layer of the fracture loop, the stresses within the AI and BF ranges further decreased. Accompanied by the decline in vertical pressure, the floor became prone to compression–shear failure. It was assumed that the roof and the floor reached their ultimate condition when the loosening fractured zones developed into OPQS. Afterward, the fractures developed towards the deep roof, the floor, and both sides in a compression–shear conjugate failure pattern.

It can be inferred from the failure processes depicted in Figure 4d,e that the development patterns of the fracture planes on the two sides were not completely symmetrical, even in the strata with identical lithological properties. For example, after forming the third layer of the fracture loop, as shown in Figure 9, the JO, FO, JP, and KP fracture planes could develop on the right side. Meanwhile, after forming the NI and MN fracture planes on the left side, the NR and MR fracture planes were next to appear, with a further gradual development of the RS, NS, RQ, and LQ fracture planes.

Overall, on account of the difference in lithology and stress states, the development of the fracture planes in the surrounding rocks shows a certain complexity; however, after repeated compression–shear conjugate damage, the intact and fractured zones with varying fracture degrees are systematically obtained.

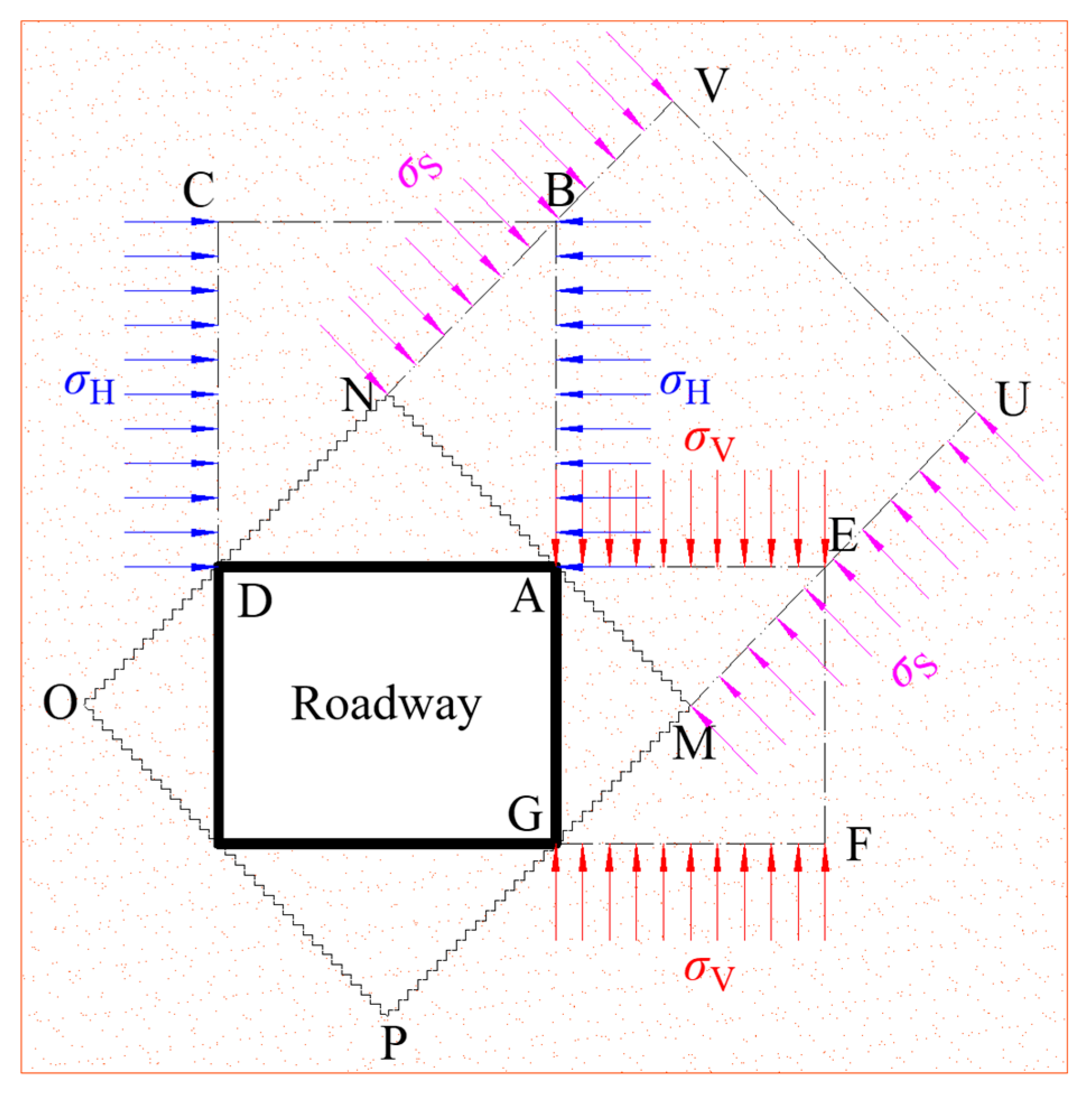
3.2. Mechanical Principle of Zonal Disintegration

Besides the physical analog modeling and numerical analysis of zonal disintegration, its mechanical mechanisms were also widely explored. Zhu et al. revealed the existence of unloading waves in deep strata after the excavation of high-stress strata, thereby inducing discontinuous fracturing of the surrounding rocks in the roadway [19]. Qi et al. analyzed the stress field evolution of the surrounding rock based on the pressure fluctuation at the inner wall of the roadway to explore the alternate manifestation patterns of fractured and intact zones [20,21]. Based on the energy conversion characteristics of deep rocks, some scholars have analyzed the mechanical principle of zonal disintegration by modifying the conventional elastoplastic model [22,23]. Chanyshev et al. performed a theoretical exploration of fractured and intact zones in the roadway based on damage mechanics and non-Euclidean geometry [24]. Other studies mostly focused on the heterogeneity and discontinuity of rock masses. Thus, using the rock strength-related parameters that obeyed the Weibull distribution law, Wang et al. designed a nonuniform strain-softening model of rocks and obtained annular zonal disintegration results via numerical simulation [14]. The factors of interest in each mechanical mechanism or model can lead to non-homogeneous rock mass damage. Accordingly, scholars hold different opinions regarding zonal disintegration mechanisms.

The disputes on the zonal disintegration mechanism essentially lie in the fact that the alternate appearance of disintegration and intact zones in the annular pattern was speculated based on limited measurement results. Despite the alternate occurrence of fractured and intact zones that could be observed in multiple drilling holes of the same roadway section, the stressed state of these zones between boreholes was unknown. The existing empirical model was obtained by collocating them in the order of their occurrence [8]. At the same time, the scientific validity of this data-processing method has not been effectively confirmed in the laboratory.

Wang et al. constructed the characteristic lines of the roadway perimeter based on the elastoplastic flow theory and pointed out that the zonal disintegration can be obtained by reproducing the cave shape using a family of characteristic lines [24], as shown in Figure 11. Based on the actual measurement results of Meng [25], Shemyakin et al. reported that the zonal disintegration occurred in a circular damage zone, with a certain distance (spacing) between damaged zones and a circular intact zone between adjacent damaged zones. Moreover, the neighboring disintegration regions were separated by annular intact ones, while slip or failure lines intersected to a certain degree, which was not consistent with the actual condition of zonal disintegration. According to field measurements, not all disintegration zones were annular or completely separated from each other. Figure 12a shows the measured results in [25], where different numbers of disintegration zones can be observed in the drilling holes 2, 3, 4, and 5, suggesting fairly complex spatial relationships between fractured zones. The data in [5] can also validate the measured results (see Figure 12b).

The following conclusions can be drawn from the above numerical simulation results: Firstly, the fractures in the surrounding rocks gradually developed from the roadway surface to deeper parts. Secondly, the fracture planes developed towards the deep surrounding rocks from the free plane (the roadway surface), forming an enclosed fracture loop around the roadway. Thirdly, at sufficiently high stress, the fractures developed toward the depth of the surrounding rock from the boundary (i.e., the outermost failure loop) in a compression–shear conjugate failure pattern. According to the numerical simulation results, various fracture loops were connected, while the finally formed fractured zone was no longer a closed ring but an interconnected network structure. It can be concluded that the compression–shear conjugate damage surface was the result of the damage development along the slip line based on elastoplastic theory, which was consistent with the theoretical predictions depicted in Figure 11.

Figure 13 shows the failure mode of the surrounding rocks in the roadway obtained via physical analog modeling in the study [26]. Specifically, Figure 13a is the physical image, while Figure 13b is a digital photograph depicting shear deformation in the surrounding rocks. The conjugate failure in the physical analog test and the fracture planes in the numerical simulation results reflect similar development processes, confirming the rationality of interpreting zonal disintegration via the compression–shear conjugate failure pattern.

3.3. Factors Influencing the Roadway Zonal Disintegration

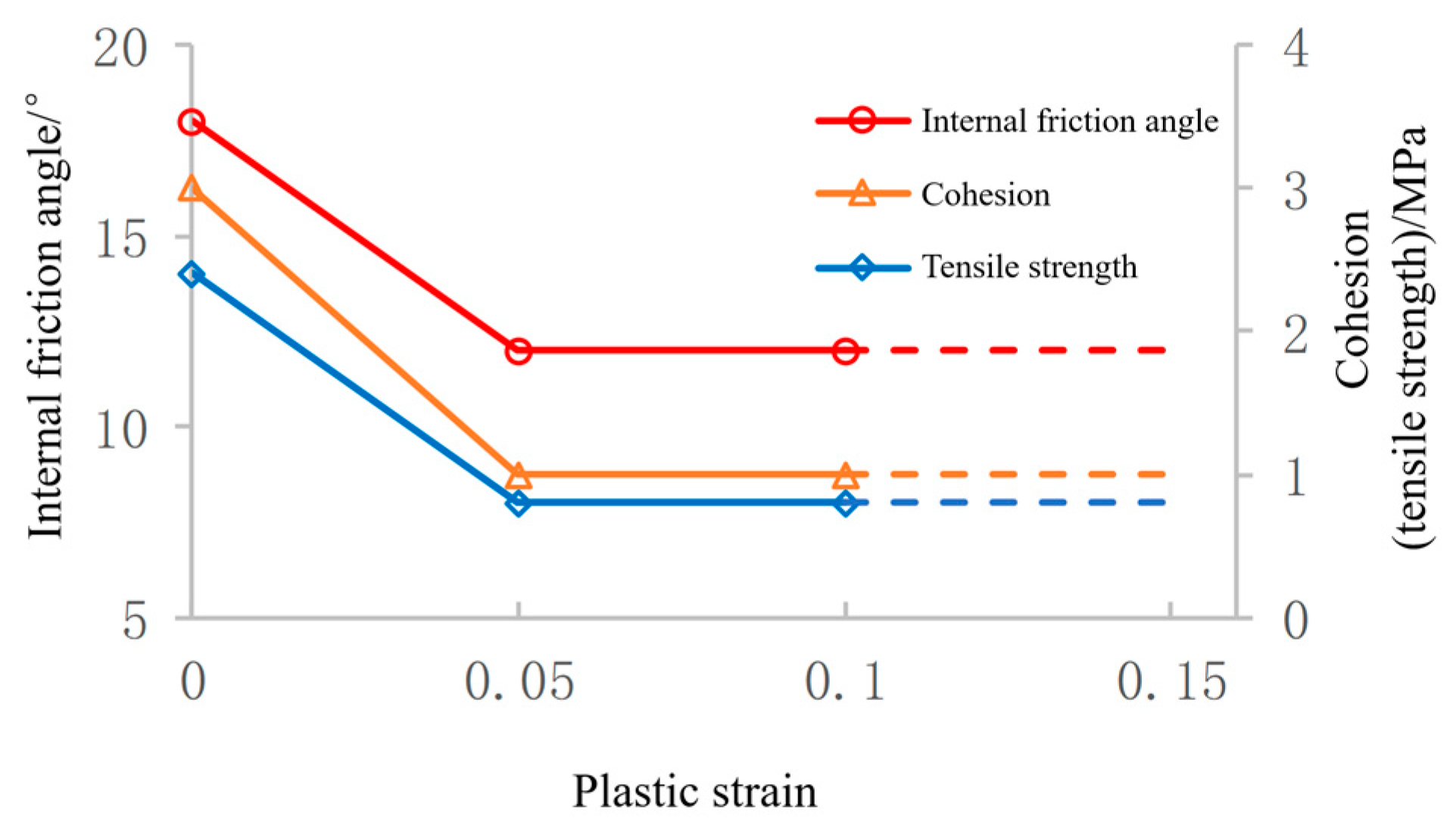
3.3.1. Effect of the Surrounding Rock Strength

Based on the parameter settings depicted in Figure 6, new simulation schemes were designed by varying the surrounding rocks’ internal friction angle, the cohesive force, and the uniaxial tensile strength, respectively, as shown in

Table 3. Strength parameters of rock mass in the designed schemes.

Scheme No.	Initial Strength			Residual Strength
	Internal Friction angle, °	Cohesive Force, MPa	Tensile Strength, MPa	Internal Friction Angle, °	Cohesive Force, MPa	Tensile Strength, MPa
1	36	3	2.4	24	1	0.8
2	18	6	2.4	12	2	0.8
3	18	3	4.8	12	1	1.6
4	18	2	2.4	12	0.8	0.8
5	12	3	2.4	9	1	0.8
6	18	3	1.6	12	1	0.5

. In schemes 1–3, both the initial and residual values of the internal friction angle, cohesive force, and uniaxial tensile strength were doubled, respectively. In schemes 4~6, the above parameters were reduced by 1/3, respectively. The remaining physical and mechanical parameters in all schemes, such as density and bulk modulus, remained unchanged.

Figure 14 shows the distribution pattern of the significantly fractured zones in the roadway-surrounding rocks for the strength parameters in schemes 1–6. As seen in Figure 14, the increased rock strength parameters hindered the development of the disintegration zones and vice versa. After the internal friction angle was doubled, significant fractured zones developed only on both sides (see Figure 14a), and the maximum shear strain increment of 0.06 appeared at two footings, reaching about 29% of the value in the original scheme (see Figure 7e). After the cohesive force was doubled, significantly fractured zones also developed on two sides (Figure 14b). The maximum shear strain increment appeared on two shoulders and footings and approximately equaled 0.105, which was 50% of the original scheme’s value. After the tensile strength was doubled, the distribution pattern and range of the fractured zones (see Figure 14c) were similar to those in the original scheme, while the maximum shear strain increment remained unchanged (0.21). Therefore, the effect of tensile strength on the development of fractured zones was weaker than that of the internal friction angle and cohesive force.

When the original scheme’s values of the internal frictional angle and tensile strength were reduced by 2/3, the distribution pattern of significant fractured zones showed a slight difference (see Figure 14e,f). Nevertheless, the maximum fracturing depths in the surrounding rocks increased by approximately 52 and 39%, respectively. The maximum shear strain increments increased by approximately 43 and 64% compared to the original scheme’s values. After the cohesive force was reduced by 2/3, the fracture planes pointed toward deeper parts of the surrounding rocks appeared at the angular points of the second layer of the fracture loop and the first/second layer intersection points of the fracture loop in the conjugate fracture plane direction (see Figure 14d). The maximum depth for the fractured zone was doubled, and the maximum shear strain increment increased by 107% compared to the original scheme’s value (see Figure 6e). Conclusively, the cohesive force imposed the most significant effect on the degree of zonal disintegration.

3.3.2. Effect of the Stress Environment

Based on the stress settings in the primary rock, as shown in Figure 7, the simulation was performed under new stress conditions by varying the vertical and horizontal stress settings.

Table 4. Stress levels in designed schemes.

Design scheme	Scheme 7	Scheme 8	Scheme 9	Scheme 10
Vertical stress, MPa	10.0	10.0	17.0	25.0
Horizontal stress, MPa	10	15.0	12.0	25.0

shows the designed simulation schemes under different stress conditions.

Figure 15 and Figure 16 show the simulation results under different stress conditions. The zonal disintegration morphology was closely related to the stress state. When both vertical and horizontal stresses were 10.0 MPa, the significant fractures only occurred at four corners of the roadway (at two shoulders and two footings), despite plastic failure on two sides, the roof, and the floor of the roadway (see Figure 17). At a vertical stress of 10.0 MPa and a horizontal stress of 15.0 MPa, the fractured zones were observed only within the roof and the floor (see Figure 15b). The conjugate failure first started from the free surfaces (i.e., the roof and the floor) such as the AE, BE, CF, and DF fracture planes; next, conjugate failures occurred with the AE, BE, CF, and DF fracture planes as the boundaries; finally, the MN and UV fracture planes developed to form conjugate failures in the deep roof and floor. At a vertical stress of 17.0 MPa and a horizontal stress of 12.0 MPa (i.e., at high vertical but low horizontal stress), fractured zones only occurred on two sides (Figure 15c). The development of the fracture planes on two sides was similar to that in the roof and the floor (see Figure 15b).

Figure 16 shows the development of the fractured zones at identical vertical and horizontal stresses of 25.0 MPa. The first layer of the fracture loop was first formed in the surrounding rocks (see Figure 16a), which then developed to form the second layer of the fracture loop (see Figure 16b,c). After forming the AEBFCGDH fracture loop (see Figure 16c), the fracture planes developed from the AE, EB, BF, FC, CG, GD, DH, and DA boundaries toward the deep surrounding rocks via the compression–shear conjugate failure pattern (see Figure 16d). Finally, the AI, IE, EJ, JB, BK, KF, FL, LC, CM, MG, GN, ND, DO, OH, HP, and PA fracture planes were formed in the third layer of the fracture loop. The fractures outside the third layer of the fracture loop continued their outward development along LCM, NGM, and NDO boundaries in a conjugate failure pattern.

3.4. Effect of the Roadway Cross-Section

Previous theoretical studies on zonal disintegration of the roadway-surrounding rocks were mainly focused on circular roadways and derived the annular distribution pattern of the zonal fracturing zones around the roadway [20,21,22,23,24,25,26,27,28,29,30]. Based on elastoplastic theory and numerical simulation results, it can be observed that failures were not always centrosymmetric and mostly presented a large damage depth near the two shoulders and two footings, while the damage depth at the roof, floor, and two sides was small [31,32].

In this study, the roadway with a circular cross-section was simulated using the PFC^2D and FLAC^2D software packages, with the results shown in Figure 18. The wedge-shaped shear deformation failures first appeared on the roadway wall at the beginning of the failure in the circular roadway. The discrete finite simulation results showed that the initial failures were concentrated around two shoulders and two footings. As shown in Figure 18a, the wedge-shaped failures appeared at points A, B, C, and D, while the boundary of the ABCD failure zone can be approximated by a rectangle. According to finite difference simulation results, the significant compression–shear deformation also showed wedge-shaped failure at the beginning, with uniform distribution around the roadway perimeter (see Figure 18c). As the deformation increased, the shear strain increment near the two shoulders and two footings began to increase. Therefore, the significant failure zone boundary can be approximated by a rectangle (see Figure 18d).

After the formation of the initial failure boundary, which was approximately rectangular in shape, the initially formed boundaries comprised the free surface for the subsequent damage development of the roadway, and a significant failure developed towards the deep surrounding rocks in the compression–shear failure pattern (see the AE and DE fracture planes in Figure 18b and the DE and CF fracture planes in Figure 18d).

The initial position of the zonal disintegration development in the surrounding rocks of the circular roadway was subjected to the effect of the initial failure boundary. In contrast, the shape of the initial failure boundary was related to the physical and mechanical properties of the surrounding rocks and the stress state [33,34]. This inevitably increased the complexity of zonal disintegration in the circular roadway.

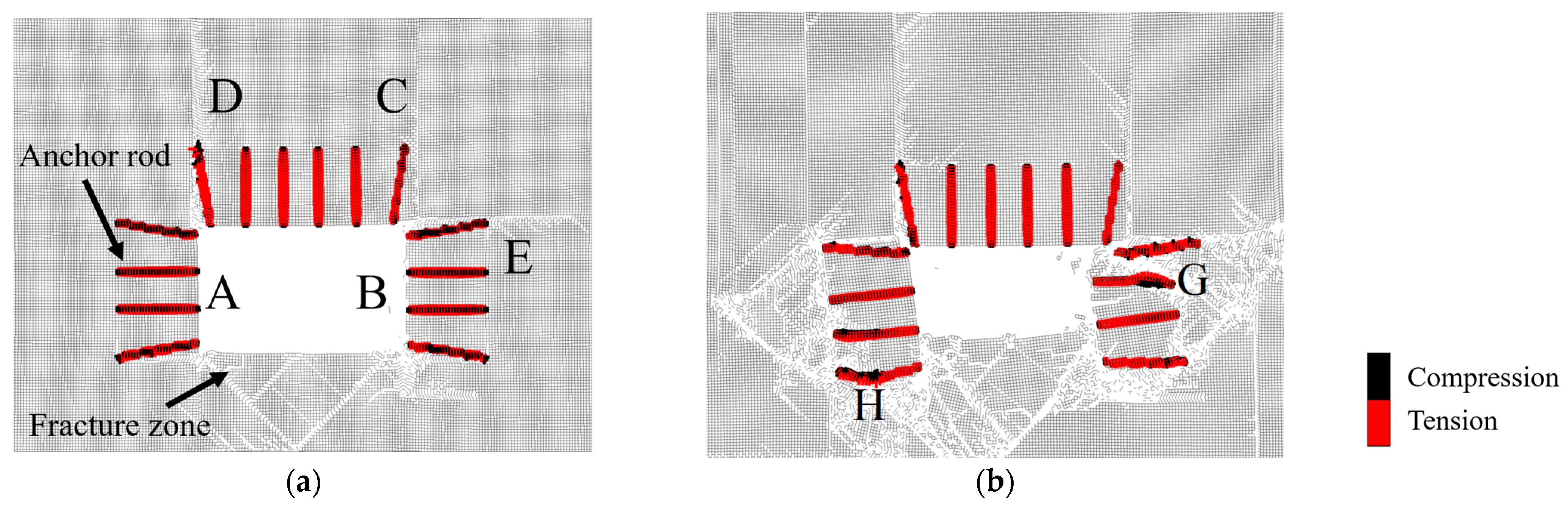
3.5. Compression Mechanisms of Anchor Rods

Fang et al. measured the force condition on the anchor rods and found that many anchor rods were under extension; additionally, tension and compression segments co-existed on some anchor rods [28]. Wang et al. concluded that tension and compression alternately appeared in the surrounding rocks based on field-measured results [29]. Li et al. also conducted field measurements and found that both loosening and compression zones existed in the roadway-surrounding rocks; moreover, they derived that the co-existence of loosening and compression regions was tightly related to the appearance of zonal disintegration in the surrounding rocks [8]. Explaining the alternate appearance of tension and compression in the roadway-surrounding rocks has become a basic problem that should be addressed in investigating zonal disintegration mechanisms.

Figure 19 shows the numerical simulation results obtained via the discrete element method for the failure of the surrounding rocks in the roadway reinforced by anchor rods and the forces acting on the anchor rods of 2.2 m in length and a 100.0 kN bearing capacity.

After the reinforcement of the roof and two sides by the anchor rods, the initial failure of the surrounding rocks occurred on the floor. The conjugate failure plane was formed and extended from two shoulders of the roadway in the vertical or horizontal directions, as illustrated by the AD, BC, and BE fracture planes in Figure 19a. As the stress in the roof increased, the compression–shear failure began to appear on two sides and developed deeper toward the surrounding rocks in a conjugate-failure pattern (see Figure 19b). By monitoring the forces acting on the anchor rods, it can be concluded that the anchor rods were mainly subjected to tension. This occurred because the radial displacement of the shallow surrounding rocks was larger than that of the deep rocks when the surrounding rocks at different depths underwent deformation and movement toward the roadway, thus putting each anchor rod as a whole in a tensile state. When the surrounding rocks were fractured, the integrated rocks moved along the shear-fractured zones, and the anchor rods were subjected to bending moments. In the bending deformation of the anchor rods, the bulk of the bent segment was under compression, as shown by stress conditions near points H and G in Figure 19b. Therefore, the compression of the anchor rods in the roadway-surrounding rocks in the zonal disintegration state could be measured via strain gauges attached to the anchor rod surface.

The compression phenomenon in the roadway-surrounding rocks was closely related to zonal disintegration. However, the compression state was not the result of radial compression of the surrounding rocks but was induced by the bending of the anchor rods or the testing devices when the integrated rocks after compression–shear cutting were loosened toward the roadway.

4. Discussion

There are the following elements of this study that need to be discussed in order to provide hints for further research:

• The results discussed in this paper are based on the simulation effect of numerical simulation software, so the conclusions may have idealized results. Including the homogenization and isotropy of the surrounding rock of the roadway, these are conditions that are difficult to exist in the real environment.
• The geological conditions of the mine are certain, and there is a risk of distortion by reducing a certain rock mechanical parameter one by one in the simulation test.
• In the process of excavation, the surrounding rock of the tunnel may be damaged, and this damage is usually shown on a three-dimensional scale, which is ignored in the two-dimensional direction of the simulation conducted in this paper.

5. Conclusions

The development of fractures in the rock can be judged by intermittent zonal fracturing via the discrete element method. The damage to roadway-surrounding rocks can be subdivided into distinct fractured and intact zones. The zonal disintegration characteristics were obtained in this study by numerical simulation using the FLAC^2D software. The development of fractured zones and the appearance of intact ones exhibited a certain regularity. The main conclusions were drawn as follows:

(1)

Under high-stress conditions, the damage to a rectangular roadway started at its four corners. The fractured zones extended towards the deeper parts of surrounding rocks in a compression–shear conjugate fracture mode, forming a nearly rectangular fracture loop, whereas the four edges (the roof, the floor, and two sides) served as free surfaces. The rock masses within the fracture loop were extruded and loosened into the roadway, and the boundary stress of the fracture loop dropped, thereby forming a new free surface. Under high stress, the fractures developed toward the deep parts of the surrounding rocks in a compression–shear conjugate fracture mode along various sides of the fracture loop to form a new fracture loop. For a circular roadway, the loosening failure first appeared near the two shoulders and footings, accompanied by the formation of a nearly rectangular failure boundary. Next, zonal disintegration evolved and developed in the surrounding rocks. Thus, the rectangular and circular roadways showed similar development patterns of zonal disintegration.

(2)

Rock strength is a crucial factor in influencing zonal disintegration. Under fixed stress conditions, significantly fractured zones appeared only in shallow surrounding rocks and could not develop deep when rock strength was high. According to the Mohr–Coulomb model, the main factors controlling the development of zonal disintegration could be ranked in decreasing order as follows: cohesive force, internal friction angle, and tensile strength.

(3)

The stressed state is a key factor controlling the development of zonal disintegration. At low vertical and horizontal stresses, significantly fractured zones appeared only near the roadway perimeter surfaces. At high vertical stresses and low horizontal ones, zonal disintegration appeared on the roadway’s two sides. At high horizontal stresses and low vertical ones, zonal disintegration developed only in the roof and the floor. When both vertical and horizontal stresses increased, the extension range of the fractured zone grew steadily, while its structure became increasingly complex.

(4)

The fractured zones in the surrounding rocks formed under the compression–shear conjugate fracture mode originated from the roadway surface. Various layers of fracture loops were interconnected, forming a network, which was consistent with the elastoplastic slip line theory prediction.

(5)

In anchor-supported roadways undergoing zonal disintegration processes, the intact zone blocks slid relatively along the fracture surface during the process of loosening and deformation of the surrounding rock, making the anchor rods susceptible to tensile, shear, and bending actions.