Abstract
Group recommender systems aim to provide recommendations to a group of users as a whole rather than to individual users. Nonetheless, prevailing methodologies predominantly aggregate user preferences without adequately accounting for the unique individual intents influencing item selection. This oversight becomes particularly problematic in the context of ephemeral groups formed by users with limited shared historical interactions, which exacerbates the data sparsity challenge. In this paper, we introduce a novel Disentangled Self-Attention Group Recommendation framework with auto-regressive contrastive learning method, termed DAGA. This framework not only employs disentangled neural architectures to reconstruct the multi-head self-attention network but also incorporates modules for mutual information optimization via auto-regressive contrastive learning to better leverage the context information of user–item and group–item historical interactions, obtaining group representations and further executing recommendations. Specifically, we develop a disentangled model comprising multiple components to individually assess and interpret the diverse intents of users and their impacts on collective group preferences towards items. Building upon this model, we apply the principle of contrastive mutual information maximization to train our framework, aligning the group representations with the corresponding user representations derived from each factor of the disentangled model, thereby enriching the contextual understanding required to effectively address the challenges posed by ephemeral groups. Empirical evaluations conducted on three real-world benchmark datasets substantiate the superior performance of our proposed framework over existing state-of-the-art group recommendation approaches.
1. Introduction
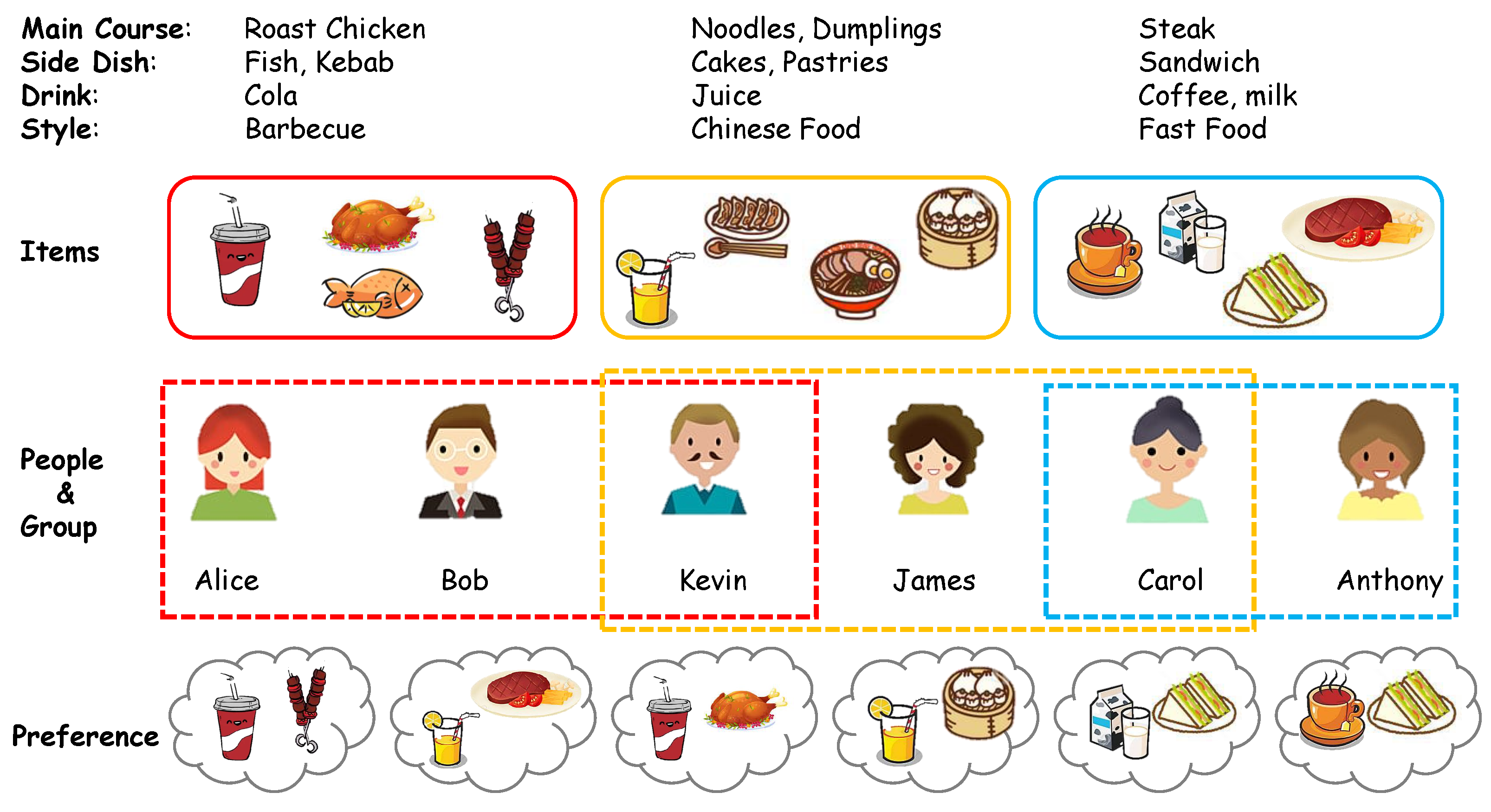
Human interactions frequently involve group activities. The advent and proliferation of social media platforms [1,2] alongside e-commerce websites [3,4] have catalyzed a shift from personalized recommendations, which prioritize individual preferences, towards group-oriented recommendations. The objective of group recommendation systems is to identify items that foster consensus among group members. However, the diverse preferences inherent to different groups pose significant challenges for decision-making processes, rendering traditional individual-focused recommendation strategies inadequate for group settings. Consequently, there is a pressing necessity to develop methodologies tailored to the group recommendation domain. The complexities of this domain are exemplified by the following scenario (refer to Figure 1): When Kevin dines with friends Alice and Bob, they might opt for barbecue, reflecting their majority preference. Conversely, a dining arrangement involving Kevin, his colleague Carol and their superior James might favor Chinese cuisine, illustrating the group’s deference to hierarchical influence. In contrast, the mutual preference of Carol and Anthony may lead them to choose fast food for convenience. In addition, there are many application domains that would benefit from group recommender systems. For example, on some e-commerce platforms like pinduoduo, in order to sell goods in bulk, it is necessary to recommend items for a temporary user group who is willing to buy at a slightly lower price. In another academic scenario, an institution needs to recommend a journal for a group of scholars attending a famous conference to improve the impact of this journal. Accordingly, understanding the intricate dynamics within and across groups, as well as their contributions to collective decision-making, is crucial for enhancing group recommendation systems.
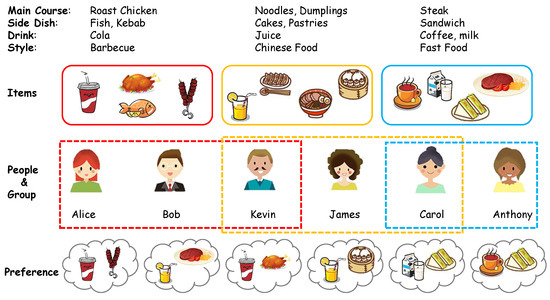
Figure 1.
An example of group recommendation.
The existing literature [3,4,5,6,7,8,9] has predominantly concentrated on personalized recommendations, with a significant emphasis on methodologies grounded in collaborative filtering. However, the domain of group recommendation [10,11,12] has been garnering escalating interest in recent scholarly endeavors. A considerable segment of this research is dedicated to elucidating methodologies for the derivation of group representations, which are subsequently utilized for inferential purposes. These methodologies frequently resort to heuristic rules for the aggregation of individual user features into a cohesive group representation, with prevalent approaches including mean pooling [13,14], the maximum principle [15] and the least misery strategy [16].
Parallel to the ascent of deep learning paradigms and attention mechanisms, a number of innovative approaches [17,18,19] have emerged, incorporating attention-based modules within user–item bipartite graphs to effectively harness user interactions for the formulation of group preference representations. The recent discourse has progressively shifted towards an examination of the representational capacities of these frameworks. In this vein, GroupIM [12] has emerged as a pioneering initiative aimed at augmenting performance through architectural innovations and refined optimization objectives. Subsequently, the HHGR model [20] was introduced, utilizing a hypergraph framework to encapsulate the intricate higher-order relationships among users, both within and external to group contexts. Furthermore, CubeRec [21] ventured into employing a hypercube structure for articulating group preferences within the embedding space, thereby imbuing the model with enhanced flexibility and the capability to navigate the complex dynamics of user–group interactions. Recently, SGGCF [22] was proposed to capture the high-order interactions between users, items and groups by modeling with a user-centered heterogeneous graph and a self-supervised learning framework.
Despite the remarkable achievements of existing methodologies such as the aforementioned CF-based methods, GroupIM, HHGR, CubeReC and SGGCF, they are often encumbered by certain limitations as follows. Predominantly, when delineating user or group preferences and underlying intentions, they resort to a hybrid modeling approach utilizing conventional neural networks like MLP, attention layers or GNNs, resulting in a lack of fine-grained modeling of relationships between the factor elements of the user/group interest preferences. This means that they are not applicable for inherently complex and multifactorial recommendation tasks, which demand a more fine-grained representation for the modeling approach to adequately represent user and group preferences. To be more specific, we illustrate this with the example in Figure 1. The figure shows a typical traditional model which constructs a neural network that translates input features—reflecting the original culinary preferences of users or groups—into embeddings that signify a synthesized decision-making probability distribution for potential meal options. This approach tends to oversimplify by directly targeting the gastronomic preferences of users or groups without accounting for detailed attributes such as the selection of main courses, side dishes or beverages. Furthermore, the ephemeral nature of certain group recommendations exacerbates the issue of data sparsity. Given that ephemeral groups often comprise individuals with minimal shared historical activities, there is a paucity of meaningful group–item interaction data to accurately reflect the preferences and intentions of such groups, leading to diminished recommendation performance. This lack of historical data particularly hampers neural-network-based group recommendation architectures as the scarcity of supervised signals hinders optimal network training.
According to these challenges, i.e., the lack of effective methodologies to represent user/group preferences with fine-grained modeling and data sparsity issues, we propose a disentangled self-attention-based neural framework to adequately model user/group potential factors of preferences with more fine-grained representations and propose auto-regressive user preferences and mutual information optimization objectives. Specifically, we introduce a novel Disentangled Self-Attention Group Recommendation framework with an auto-regressive contrastive learning method (DAGA), designed to derive nuanced user and group representations and facilitate item suggestions based on historical user–item and group–item interactions and group-related mutual information. To address the limitations of synthetic modeling, we establish distinct factors, each represented by a separate neural network module, to encapsulate potential user/group factors. These modules allow attribute-specific input features to be processed accordingly, with the resulting representations integrated for inferential purposes. On this basis, a disentangled multi-head self-attention module is designed to better encode the user preferences assisted by the preference features of the other individuals of the same group so as to produce more accurate group representations via an attention-based aggregator and further execute group recommendation. Moreover, to mitigate the detrimental impact of data sparsity, we first leverage the auto-regressive user preferences to train the disentangled multi-head self-attention encoder and then employ the mutual information between user representations and group representations, ensuring congruence within groups while maintaining distinctiveness from other groups, unfolding contrastive learning to fine-tune our framework and assisting with the sparse supervised signal of group–item historical interactions. To the best of our knowledge, this is the first work that has designed a disentangled multi-head self-attention module to encode users and groups with finer granularity coupled with auto-regressive and contrastive mutual information optimization that is specifically tailored for ephemeral group recommendations.
The principal contributions of this work are delineated as follows:
- We combine disentangled neural networks with a multi-head self-attention mechanism and propose a disentangled multi-head self-attention module to generate precise group and user representations, dissecting user intents for preference encoding from multiple dimensions;
- We introduce optimization objectives based on auto-regressive user preference information and group-related mutual information maximization to counteract information scarcity in group data, thus facilitating network training and enhancing the fidelity of representations;
- Comprehensive experiments conducted across three public benchmark datasets for group recommendations corroborate the efficacy of our framework, showcasing its superiority over state-of-the-art baselines.
The structure of this paper is as follows: Section 2 delves into the pertinent literature. Section 3 elucidates the foundational concepts of ephemeral group recommendations. The architecture, components and theoretical underpinnings of our DAGA framework are explicated in Section 4. Section 5 presents an empirical evaluation of the performance of our framework on real-world datasets. Section 6 concludes with a summation and an outline of prospective research directions.
2. Scientific Method
This section delineates the contributions relevant to the present study, categorically segmented based on the targeted problems, the proposed framework and the adopted optimization objectives.
2.1. Group Recommendation
Group recommendation methodologies have been conceptualized from dual perspectives to cater to two distinct audience types: ephemeral [12,23] and persistent [19] groups. The latter category, characterized by dense group–item interaction records, readily lends itself to the application of collaborative filtering techniques directly to group–item interactions [10,24]. The focus of this paper, however, is on the more pragmatically challenging domain of ephemeral group recommendations, a subject that has received considerable attention in the recent literature [12,20,21]. Within this domain, the primary challenge lies in the paucity of group–item interaction data [12,25]. Consequently, this review is bifurcated into two streams: methods for group preference aggregation and strategies to counteract data sparsity.
Preference Aggregation: In the realm of ephemeral group recommendations, the synthesis of group preferences is achieved by amalgamating individual member preferences, which can be executed either at an early or late stage. Late-stage aggregation involves deriving group–item recommendation scores after the individual preference processing, employing strategies such as the maximum pleasure, least misery and average satisfaction strategies [13,16,23]. These traditional approaches, however, are heavily heuristics dependent, which compromises their adaptability and expressive capabilities [26,27]. Early aggregation, conversely, entails the initial consolidation of individual preferences to formulate a collective group preference, which is subsequently utilized for recommendation generation. Probabilistic models [28,29,30] form the basis of several such methodologies, assuming uniform significance across members while accounting for individual preferences and their contributions to the group dynamic. Advanced latent factor models [31,32] facilitate group embedding within a vectorial space, enhancing representational granularity. Further sophistication is achieved through the adoption of attention-based neural networks [11,26], enabling nuanced aggregation of biased user embeddings within a group context. Additionally, a model capable of delineating the intricate inter-member relationships via attention mechanisms has been introduced [18]. Contemporary studies have extended these methodologies by integrating ancillary information sources such as social networks [33] and knowledge graphs [34], thereby enriching the learning paradigms for group representation. Innovations such as hypercube-based representations [21] and hypergraph convolutional neural networks [20] have been explored to encapsulate complex relational dynamics within and beyond group entities. Moreover, the group identification (GI) task, aiming to recommend the potential group to users, has recently attracted more attention from researchers. As a representative work among them, CFAG [35] was the first to propose using GNNs with factorized attention block to aggregate contextual information among the items, groups and users so as to perform ranking-based GI tasks. GTGS [36] designed a transitional hypergraph convolution-layer-based framework and leveraged the cross-view SSL method to predict the preferences of users for groups based on the users’ previous group participation and coordinated interests in items.
Data Sparsity Issue: Addressing the challenge of sparse data, the influence of user social networks on group decision-making [19] has been leveraged to augment the available dataset. Innovations such as self-attention mechanisms [37] have been employed in intra-group voting models [26] to concurrently assess user interactions and social influences. Additionally, methodologies that construct heterogeneous graphs from multifaceted relationships among users, items and groups have been proposed [17,22]. The efficacy of self-supervised learning (SSL) in ameliorating recommendation tasks [38,39,40] has prompted the derivation of SSL-based optimization objectives to address data scarcity in ephemeral group recommendation contexts. For instance, the double-scale contrastive learning framework [20] has been designed to refine user and group representations through common membership patterns. The mutual information optimization mechanism [12], focusing on the cohesive embedding of user and group representations, has been developed to enhance preference learning. Moreover, SSL objectives exploiting the geometric properties of hypercubes [21] aim to mitigate the data sparsity issue by enriching group representations with more comprehensive informational content.
2.2. Disentangled Neural Networks
The pursuit of disentangled neural networks and representation learning revolves around the extraction of factorized representations that isolate and reflect the latent, intrinsic factors embedded within data [41]. The bulk of the research on disentanglement has originated from the field of computer vision [42,43,44], with recent burgeoning interest in its application to graph learning [45,46]. Additionally, generative models, particularly Variational Autoencoders (VAEs), have been leveraged for disentanglement purposes [47,48]. In the research field of group recommendation, IGRec [49] was the first work that used a disentanglement-based method to disentangle the representations of user interests, providing for the subsequent group preference aggregation. However, DAGA, the framework proposed in our work, can be distinguished from IGRec by the following aspects:
- Encoder: IGRec considers the embedding of the disentanglement factors for the same user when producing the representations of user disentangled interests. However, our framework is realized by two MLP encoders and a multi-head disentangled self-attention block which additionally considers the relationships between different user representations within the same group when producing the representations of user disentangled interests;
- Aggregator: IGRec depends on Gumbel-SoftMax among the disentangled factors to aggregate the user interests. In our framework, the multi-factor representations are jointly projected for group preference prediction by an MLP, which can automatically extract and utilize the relevance between each factor and the group representation;
- Optimization Objectives: IGRec leverages user–item and group–item historical interactions to construct supervised signals for dual training. In our work, to alleviate the data sparsity issue, we leverage auto-regressive user preferences to train the disentangled multi-head self-attention encoder and employ the mutual information between user representations and group representations.
An illustration of our framework will be unfolded with more details in Section 4.
2.3. Mutual Information Optimization
The paradigm of mutual information (MI) has significantly propelled the advancements in SSL, particularly within the ambit of contrastive learning (CL). In recent years, CL has emerged as a formidable approach, achieving unparalleled success across various domains. Notably, in the realm of computer vision, CL-based methodologies have ascended to the forefront, establishing new benchmarks [50,51,52]. A quintessential illustration of this is found in [51], where CL techniques were innovatively applied to embed local image features into a latent vector space with the objective of maximizing the MI between local and global representations.
This successful application of SSL and CL paradigms precipitated their widespread adoption across diverse fields, extending notably to graph learning [53,54,55,56]. An exemplary instance of this cross-disciplinary migration is seen in [53], which extrapolates the foundational principles laid out in [51] to the domain of graph learning. In this domain, the focus shifts to optimizing the MI between localized patch embeddings and overarching graph summaries, thereby facilitating the learning of more nuanced node representations.
3. Problem Statement
For clarity and ease of comprehension, this section elucidates the ephemeral group recommendation task and delineates the notational conventions adopted throughout this paper.
Table 1 presents a summary of the principal notations utilized in this paper. Let represent the set of users, denote the set of items and signify the set of groups, where identifies the n-th group. These sets underpin the formulation of user–item, group–item and user–group interaction records, reflecting historical preferences and affiliations. The binary interaction matrices and encapsulate user–item and group–item interactions, respectively, where indicates an interaction between user u and item i, and, similarly, represents an interaction between group g and item i.

Table 1.
Summary of notations.
Group encompasses a subset of users characterized by sparse interaction records , a row vector in matrix Q. The matrices R and Q serve as the raw features for users and groups, respectively, and are embedded into a latent space of dimension d. The resultant user and group embeddings (produced from MLP Encoder2) and , respectively, are concatenated from disentangled embedding matrices and , corresponding to the k factors within our framework. Each one of the factor-specific embedding matrices and resides in a subspace of dimension .
The primary objective in this work is to address the challenges inherent in ephemeral group recommendations characterized by minimal historical interactions among group members. Our framework aims to harness limited historical group–item interactions to predict item preference rankings for ephemeral groups composed of loosely connected members. The user and group representations and , derived from the input feature matrix R, underpin the prediction of group preference distributions, denoted by Y.
4. The Proposed Framework
This section describes the architecture and operational details of our neural group recommendation framework DAGA. Our demonstration commences with an overview of the architecture, highlighting the disentanglement strategy employed by the multi-head self-attention mechanism to capture the nuanced intents of users and groups. Subsequently, the discussion transitions to the optimization objectives crafted to navigate the challenges posed by data sparsity, culminating in a detailed examination of the constituent modules, regularization strategies and optimization pipelines integral to DAGA.
4.1. Overview
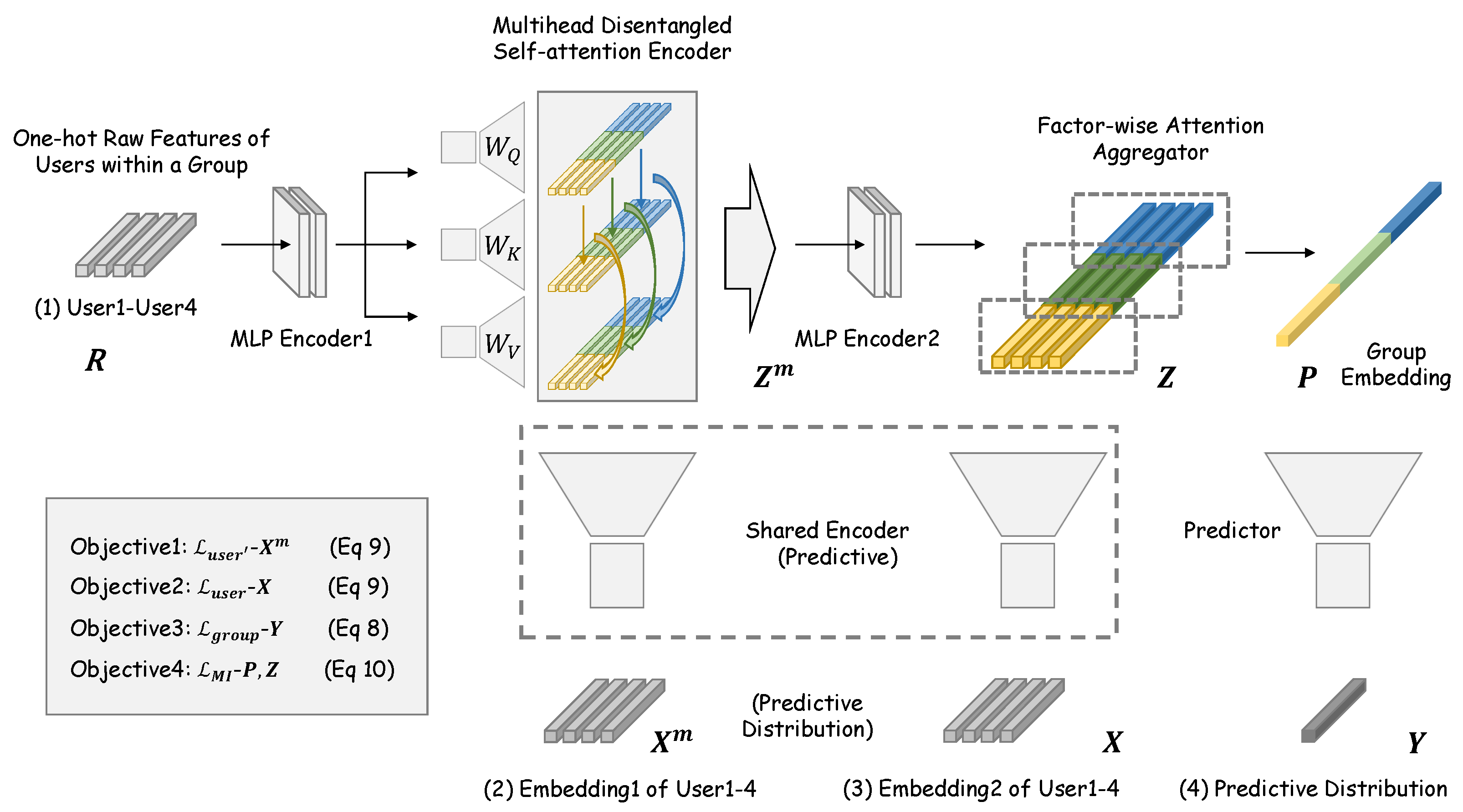
Firstly, we introduce the building blocks of DAGA, designed to distill user and group intents with enhanced granularity for better item recommendation, which are visually encapsulated in Figure 2, exemplified through the processing of a group of users.

Figure 2.
Schematic overview of the proposed DAGA framework illustrating its constituent components and associated loss functions.
MLP Encoder: Serving as the cornerstone of DAGA, the encoder (MLP Encoder1) leverages the user–item interaction matrix R as the input, facilitating the derivation of embedded user representations Z with our multi-head disentangled self-attention encoder. Moreover, the disentangled MLP encoder (MLP Encoder2) is utilized to embed the features obtained from the aforementioned disentangled self-attention encoder to further facilitate the derivation of embedded group representations P with the subsequent attention-based aggregator.
Disentangled Self-Attention Encoder: Subsequently, the user representations are encoded with the group’s prior information, drawing inspiration from [37]. That is to say, the derivation of user representations can utilize similar preference context information from the other group members to enhance the encoding process. To be specific, the embeddings produced from MLP Encoder1 are transformed by three independent encoders with the same structure, K, Q and V, for preparation of the attention mechanism. These K, Q and V encoders consist of a layer that is a dimensional invariance embedding network and a layer that is an embedding network to complete higher-dimension mapping (from to d), which is followed by a strategic disentanglement of (the intermediate variable produced by our disentangled self-attention mechanism before obtaining Z) into k distinct factors, represented as .
This disentanglement process is predicated on the premise of isolating and elucidating the latent intents embedded within the users’ original preferences. The encoder’s pivotal function is to coalesce user features, latent within the raw interaction data R, and intrinsically associated with specific factors, into their respective disentangled representations and . This mechanism effectively transitions the raw user–item interaction data, reflective of generalized item preferences, to the more nuanced, intent-driven representations associated with distinct attributes. Drawing from the illustrative scenario shown in Figure 1, the encoder’s adept utilization facilitates the extraction of user intents pertaining to underlying attributes (e.g., food categories such as main courses, side dishes and beverages, or more complex attributes like flavor profiles, temperature preferences, etc.) from the broader spectrum of user preferences for various food items (e.g., roast chicken, fish, dumplings, steak, sandwiches, cola, etc.).
Subsequent to generating disentangled user representations, we employ a distinct multi-head self-attention calculation process with independent encoder networks for each factor, facilitating their embedding into another hidden space for further processing. In the illustrative case of food attributes, these disentangled operations yield refined representations that encapsulate the nuanced attributes of potential food selections.
Aggregator: The objective of the aggregation process is to synthesize disentangled group representations within the hidden space through a meticulous aggregation of the disentangled user representations corresponding to each factor. This phase incorporates an attention aggregator to assign a set of trainable weights to individual group members within each factor. This facilitates a weighted aggregation approach to generate the factor-specific group representations from the constituent member representations. The culmination of this process is the construction of comprehensive group representations by concatenating the representations across all factors, thus reflecting the collective group intents pertaining to various attributes.
Predictor: With the disentangled group representations at our disposal, we proceed to predict the group preference distribution. This entails employing a predictor that effectively maps the group intents associated with specific attributes to the overarching group preferences for the items, thereby completing the inference process. This operation is essentially the converse of the initial encoding step and aims to recombine the disentangled factors into coherent inference outcomes (from d to ). Reflecting on the food attribute example, this predictor translates the group’s attribute-based intents into concrete preferences for the available food options. Similarly, the user preference distribution is predicted via an auto-regressive behavior to regularize the training process. As illustrated in Figure 2, Embedding1 and Embedding2 are the regressive preference distributions which are predicted by a shared dimensionality reduction encoder (from d to ).
Optimization Objectives: The DAGA framework integrates all the aforementioned modules and is trained utilizing a set of optimization objectives that encompass both supervised learning (Objectives 1, 2 and 3 in Figure 2) and SSL loss functions (Objective 4 in Figure 2). These are designed to leverage historical interactions and the mutual information inherent within the contextual data. The supervised loss components are derived by quantifying the congruence between the predicted preference distributions and the historical preference data for both users and groups, employing KL divergence as a measure due to its efficacy in comparing probability distributions. In parallel, a contrastive SSL loss function is formulated to identify and differentiate between positive and negative samples intra- and inter-group, where the group with its members is regarded as a set of positive samples while different groups with their members constitute the negative samples. This is achieved by adhering to the principle of mutual information maximization, ensuring that the disentangled representations align with positive samples while diverging from negative ones. The intricacies of these optimization strategies are expounded in subsequent sections.
4.2. Supervised Learning
Training our framework for ephemeral group recommendations necessitates the utilization of supervised signals. The most direct form of supervision in this context is derived from the group–item interaction matrix Q. Given the sparse nature of group–item interactions, the user–item interaction matrix R is employed as an auxiliary supervised signal to augment the training process. To encapsulate the preference distributions inferred by the predictor, we introduce the following formulation:
when P, Z and are input variables, and the output variables correspond to Y, X and , where Y and X represent the preference distributions of groups and users, respectively. represents the user preference distribution obtained from the intermediate variable produced by our disentangled self-attention mechanism. It is important to note that Equation (1) is applied on a per-row basis, enabling the computation of individual preference probabilities for each group and user.
To align these inferred distributions with their historical counterparts, we define normalized distributions and for the supervised signals Q and R, respectively, as follows:
where and denote the normalized historical preference distributions of groups and users, respectively, choosing among candidate items.
To quantify the congruence between these distributions, we employ the KL divergence, defined as
which can be decomposed into
where
represents the information entropy, and
represents the entropy of distribution A, and denotes the cross-entropy between distributions A and B. Given that encapsulates the dissimilarity between A and B within the context of KL divergence, we adopt the cross-entropy form to articulate the loss functions, assessing the alignment between and Y, and X and and , respectively. These are expressed as:
while can also be represented by Equation (9) by replacing the input with , where , , , and correspond to the elements within , , , and , respectively. Equation (8) encapsulates the loss function associated with group–item interactions, pivotal in the principal training phase of DAGA, while and pertain to the user–item interaction loss. Actually, in order to train our framework more efficiently, in practice, a pre-training phase is conducted to train the disentangled multi-head self-attention encoder with in an auto-regressive manner. In the subsequent training phase (called fine-tuning and primary training in this paper), the loss function and are applied to train the end-to-end framework. Our experiments indicate that this method can produce the model with the best performance.
4.3. Contrastive Leaning
To tackle the challenge of sparse supervised signals in ephemeral group recommendations we introduce a contrastive SSL loss function underpinned by the principle of mutual information (MI) maximization [50,51,52,53,54,55,56]. The crux of this approach is to maximize the MI between the disentangled representations of a group and its constituent members for each factor and for every member .
To augment the sparse data, members of a group are treated as positive samples, while members from other groups serve as negative samples. A parameterized discriminator D assesses the similarity between groups and users, assigning higher scores to intra-group pairings and lower scores to inter-group pairings.
This methodology is encapsulated in the following SSL loss function, which employs a binary cross-entropy (BCE) format to discriminate between positive and negative samples for each group:
where
represents the total number of samples considered, is the count of negative samples per group and denotes a user not belonging to group g. The notations , and retain their aforementioned meanings, referring to the discriminator, user embeddings and group embeddings within the i-th disentangled factor, respectively.
The essence of this loss function is to reinforce the alignment of group embeddings with those of their constituent members while ensuring divergence from non-members through the maximization and minimization of discriminator-generated similarity scores. This approach generates a plethora of self-supervised signals, thereby mitigating the impact of sparse historical group–item interactions.
4.4. Framework Details
This section elucidates the structural intricacies and operational dynamics of the DAGA framework, emphasizing the synergy between supervised and SSL loss functions in enhancing the model’s efficacy. Following a procedural overview of the training regimen, we delve into the specifics of the model architecture.
4.4.1. Training Procedure
The training paradigm of DAGA, as delineated in Algorithm 1, employs a mini-batch strategy to expedite computational efficiency, alongside a pre-training and fine-tuning sequence designed to optimize recommendation performance. The core objective encompasses the refinement of model parameters and the accurate prediction of group preference distributions Y. According to Figure 2, denote the model parameters of MLP Encoder1, the multi-head disentangled self-attention encoder, MLP Encoder2, the Factor-Wise Attention Aggregator, the Predictor of Group Embedding and the Shared Encoder (predictor of user embeddings), respectively, while denote the discriminator parameters of Equations (10) and (11).
Initiated with the stochastic initialization of parameters , the model undergoes pre-training with , which instills foundational user representation learning and predictive capabilities. Subsequent fine-tuning, leveraging and , refines the discriminative prowess of our framework, particularly in discerning complex user–group dynamics. The primary training involves a comprehensive optimization of , and , ensuring the model’s adeptness in capturing and predicting nuanced group preferences.
| Algorithm 1 Training procedure of DAGA. |
|
4.4.2. Model Architecture
The framework architecture of DAGA comprises several key components: encoders, disentangled multi-head self-attention encoders, aggregators, predictors and a discriminator. Each component plays a pivotal role in processing user preferences, disentangling user intents, aggregating group preferences and predicting group–item interactions.
Encoder (MLP Encoder1): The foundation of user preference encoding lies in a two-layer Multi-Layer Perceptron (MLP). This encoder transforms the original user preference matrix R into hidden representations , employing nonlinear activation functions and distinct learnable weight matrices and alongside biases and as follows:
Disentangled Self-Attention Encoder: According to the conventional attention mechanism [37], to represent the user preference with the other members within a group, the hidden representation is embedded into as follows:
where and , and and and with related and , and and and are used to encode the Q, K and V of the attention mechanism and perform the mapping of the dimensionality increase, respectively. Moreover, the disentanglement is realized by , and . Subsequently, the factor-wise self-attention mechanism is applied to calculate the attention matrix and related encoded representations as follows:
where H denotes the number of heads to average the results from different heads of our disentangled self-attention module.
Disentangled Encoders (MLP Encoder2): To further process the disentangled representations , a two-layer MLP is utilized, equipped with a unique parameter matrix to cater to each factor, thus facilitating the embedding into another factor-specific feature space as follows:
Aggregators: The framework incorporates three aggregation mechanisms—Maxpooling, Meanpooling and Attention—to synthesize group representations from user embeddings. The Maxpooling and Meanpooling operations perform element-wise maximum and mean calculations, respectively, across each factor of the disentangled representations. The Attention mechanism, primarily employed within DAGA, computes a weighted summation of member representations for each factor with weights derived from attention networks and disentangled encoder outputs as follows:
where the weight for each user u in group g is determined by the attention mechanism [37]
Predictor: The predictor component, comprising two fully connected layers followed by a softmax function, is responsible for translating the aggregated disentangled group representations or disentangled user representations into preference distributions for group–item interactions or user–item interactions. The expressions, whose first layer performs dimensionality reduction from d to and whose second layer is a normal fully connected layer, are formally similar to Equation (1).
Discriminator: A parameterized bilinear layer functions as the discriminator D, differentiating users based on group membership by calculating similarity scores. This is essential for optimizing as follows:
where is a learnable weight matrix, and denotes the logistic sigmoid function, facilitating the generation of scores indicative of user–group affiliations.
This comprehensive model architecture enables DAGA to adeptly navigate the complexities of ephemeral group recommendation by leveraging disentangled representations, attentive aggregation and discriminative prediction to understand and cater to group preferences effectively.
5. Experiments
This section delineates the comprehensive experimental evaluation conducted to assess the efficacy of the proposed neural group recommendation framework (DAGA). We commence with the experimental setup, including dataset descriptions, baseline comparisons and other pertinent settings. Subsequent sections present our main findings, highlighting the performance of DAGA in ephemeral group recommendation scenarios and analyzing the influence of key framework parameters on the recommendation outcomes.
5.1. Experimental Settings
Datasets: To rigorously evaluate DAGA’s performance, we employ three public benchmark datasets, Weeplaces, CAMRa2011 and Douban, each offering unique challenges and insights into ephemeral group recommendation dynamics. Table 2 summarizes key statistics of these datasets.

Table 2.
Statistics of the evaluated datasets. # represents the number of the indicators.
- Weeplaces captures point-of-interest (POI) interactions within major US cities, offering rich categorical data ranging from entertainment data to dining data. Groups are constructed based on simultaneous check-ins, aligning with previous methodologies [12];
- CAMRa2011, a movie rating dataset, is adapted to the group recommendation context by focusing on households as implicit groups, with ratings transformed into binary interaction data for compatibility with our framework [11];
- Douban, sourced from a versatile social platform, facilitates the exploration of group dynamics within cultural contexts. Group interactions are inferred from shared participation in activities, following a strategy similar to that in [20].
For experimental rigor, each dataset is partitioned into training, validation and test sets in a 70:10:20 ratio, ensuring a comprehensive evaluation across diverse group recommendation scenarios.
Baselines: The effectiveness of the proposed DAGA framework is evaluated against a diverse array of baseline methods, encompassing traditional popularity-based approaches, neural collaborative filtering techniques and advanced group recommendation models incorporating attention mechanisms and graph embeddings. The following selected baselines are included:
- Popular: A rudimentary yet widely applied method that recommends items based solely on their overall popularity, disregarding personalized preferences or group dynamics;
- NeuMF [57]: NeuMF represents the integration of neural network architectures into collaborative filtering, enhancing recommendation performance by directly leveraging group–item interactions as the supervisory signal. NeuMF exemplifies the advancements in neural collaborative filtering by predicting group preferences with heightened accuracy;
- AGREE [11]: AGREE innovates by incorporating an attention mechanism to deduce group preferences from individual member preferences. It computes weights for each group member and aggregates them to obtain a unified group preference vector, employing a neural collaborative filtering framework to model group–item interactions;
- MoSAN [18]: An advanced group recommendation model that utilizes a neural network structure with multiple sub-attention modules. These modules are tasked with capturing nuanced user preferences and effectively modeling the intricate dynamics of user–item and group–item interactions;
- SIGR [19]: SIGR introduces an attention-based model augmented with latent variables to capture both global and local social influences among users. It conceptualizes interactions within a bipartite graph structure, applying graph embedding techniques to mitigate issues related to data sparsity;
- GroupIM [12]: A cutting-edge group recommendation model that aggregates individual member preferences through attention networks to forecast group preferences. It distinguishes itself by optimizing the mutual information between group and member representations, addressing the challenge of sparse data;
- HHGR [20]: HHGR utilizes a hypergraph neural network to encapsulate the complex high-order relationships among users, groups and items. It is particularly noted for its innovative double-scale self-supervised learning objective, designed to complement traditional supervised learning signals and enhance the training process;
- HHGR [20]: An extension of the HHGR model, this self-supervised variant represents the state of the art in group recommendation. It leverages self-supervised learning techniques to further refine the model’s ability to discern and predict group preferences;
- SGGCF [22]: SGGCF captures the high-order interactions between users, items and groups by modeling with a user-centered heterogeneous graph and a self-supervised learning framework. SGGCF realizes a state-of-the-art performance for ephemeral group recommendation.
Each baseline is selected for its relevance and contribution to the field of group recommendation, providing a comprehensive benchmark against which the performance of DAGA is evaluated. Official implementations of these models, where available, are utilized to ensure fidelity to the original methodologies.
Evaluation Metrics: The efficacy of DAGA and the compared baseline models is quantified using two widely recognized metrics in the domain of recommendation systems: Normalized Discounted Cumulative Gain at K (NDCG@K) and Recall at K (Recall@K) for . These metrics are selected for their ability to provide a comprehensive assessment of the models’ performance from different perspectives.
- NDCG@K is a metric that measures the quality of the ranked recommendation list up to the K-th position, taking into account the position of relevant items. It is particularly well suited for evaluating recommendation systems where the order of recommendations is of importance. The computation of NDCG@K involves the gain of each item (with more weight given to items at higher ranks) and a normalization factor to ensure that the perfect ranking has a score of 1. This makes NDCG@K an effective measure for understanding how well a model can rank truly relevant items higher in the recommendation list;
- Recall@K, on the other hand, assesses the model’s ability to retrieve relevant items within the top K recommendations, regardless of their order. It is calculated as the fraction of relevant items that are successfully included in the top K recommended items out of all relevant items. Recall@K is particularly useful in scenarios where the goal is to capture as many relevant items as possible in the top K recommendations without an emphasis on the ranking order among these items.
Both NDCG@K and Recall@K provide valuable insights into the model performance, with NDCG@K focusing on the ranking quality of the recommendations and Recall@K emphasizing the model’s ability to identify relevant items. Employing both metrics allows for a balanced evaluation of the recommendation models, catering to different aspects of recommendation quality that are crucial in real-world applications.
Parameter Settings: The configuration of hyperparameters plays a pivotal role in the performance and efficiency of the DAGA framework. To establish a robust experimental foundation, we meticulously select and fine-tune the following hyperparameters:
- Learning Rate: Set at , the learning rate determines the step size during the gradient descent optimization process. This value is chosen to balance the trade-off between convergence speed and stability;
- Weight Decay: A regularization parameter employed to prevent overfitting by penalizing large weights. For our experiments, weight decay is set to 0, emphasizing model flexibility in learning from the data;
- Dropout Ratio: Applied within the MLPs to mitigate overfitting through the random omission of neurons during training. A dropout ratio of 0.4 is found to provide an optimal balance between regularization and model complexity;
- Batch Size: The number of samples processed before the internal parameters of the model are updated. A batch size of 256 is selected to leverage computational efficiency while maintaining sufficient gradient approximation;
- Epochs: Both the pre-training and fine-tuning phases are conducted over 100 epochs, ensuring ample opportunity for the model to learn and adapt to the training data;
- Factor Number: Our disentangled network architecture incorporates eight factors, allowing the model to capture a diverse array of latent user and group preferences;
- Embedded Size: The dimensionality of the user and group representations in the latent space is set to 192, with each factor contributing a 24-dimensional sub-representation. This configuration facilitates a comprehensive yet computationally efficient representation scheme;
- Number of Negative Samples (): In the mutual information maximization process (Section 4.3), five negative samples are used for each positive instance, balancing the learning signal derived from both positive and negative interactions;
- SSL Loss Weight (λ): The weight assigned to the SSL loss function during the fine-tuning phase is set to 1, underscoring its equal importance alongside the supervised loss components in model optimization.
These parameter settings are uniformly applied across all datasets and experiments presented in Section 5.2, ensuring consistency and comparability in our evaluation. Additionally, Section 5.4 will explore the impact of varying some of the hyperparameters, providing deeper insights into their influence on the recommendation performance of DAGA.
5.2. Experimental Results
Comparative Analysis of Performance
The empirical evaluation underscores the preeminence of DAGA across three benchmark datasets, as delineated in Table 3 and Table 4. This section expounds on the comparative performance analysis, highlighting the salient findings and their implications.

Table 3.
The recommendation (NDCG) performance comparison on three datasets.

Table 4.
The recommendation (Recall) performance comparison on three datasets.
Enhanced Performance of Attention-Based Models: Among the evaluated baselines, models incorporating attention mechanisms, namely AGREE and MoSAN, consistently outshine conventional heuristic and collaborative filtering approaches such as Popular and NeuMF. This observation corroborates the pivotal role of attention mechanisms in adeptly capturing and aggregating individual preferences within groups.
Superiority of Graph-Based Representations: The SIGR model, leveraging a bipartite graph structure, exhibits superior performance compared to AGREE and MoSAN in the majority of scenarios. This enhancement is attributed to SIGR’s nuanced representation of user–group–item interactions, facilitated by the graph-based approach, underscoring the efficacy of graph embeddings in capturing complex relational dynamics. Moreover, the state-of-the-art method SGGCF, leveraging the heterogeneous graph, realizes more sufficient modeling to capture the relationships between users, groups and items, outperforming the aforementioned baselines.
Advantages of Mutual Information Optimization: The GroupIM and SGGCF models, apart from harnessing attention-based aggregation, integrate mutual information (MI) SSL optimization objectives, endowing them with a distinct advantage over their counterparts. The MI objectives enrich the representation learning process, furthering the models’ predictive accuracy.
Contribution of Hypergraph Neural Networks: Diverging from the MI optimization strategy, the HHGR model employs SSL objectives within a hypergraph neural network framework. This approach enables HHGR to intricately model high-order relationships between groups, users and items, thereby yielding notable performance gains over other baselines.
Empirical Validation of DAGA: Central to our findings is the exceptional performance of DAGA, which surpasses all baseline models across the evaluated metrics and datasets. Notably, DAGA achieves this with a relatively simpler architecture, employing a disentangled multi-head self-attention encoder in conjunction with SSL objectives and an attention-based aggregation mechanism. This configuration not only simplifies the model but also accentuates the effectiveness of disentangled representations in group recommendation tasks.
In summary, the empirical insights gleaned from the performance comparison validate the efficacy of attention mechanisms, graph-based representations and, particularly, the novel disentangled representation approach adopted by the self-attention mechanism in DAGA. The findings underscore the potential of disentanglement and SSL in advancing the state of the art in group recommendation.
5.3. Analysis of Parameter Complexity
While the empirical efficacy of our DAGA framework is evident from the experimental outcomes, an equally significant advantage lies in its computational efficiency, particularly in terms of parameter complexity. The innovative disentanglement design intrinsic to DAGA significantly mitigates the parameter complexity, transitioning from an exponential to a linear growth pattern. This section elucidates the underlying mechanisms and implications of this design choice.
Consider a conventional single-layer perceptron utilized as an encoder within a group recommendation model. In such a scenario, embedding user representations from an original dimension s into a hidden dimension d necessitates a trainable matrix of dimensions . The complexity and resource requirements for this model scale with the product of the input and output dimensions, potentially leading to computational inefficiency, especially for high-dimensional data.
In contrast, the disentanglement approach employed by DAGA and its self-attention/MLP encoders restructures this model into k distinct factors, each responsible for capturing a specific aspect of the user or group preferences. This architectural modification implies that, instead of a single large matrix, the model now comprises k smaller matrices, each with dimensions . Consequently, the total parameter count is significantly reduced to , thereby alleviating the computational burden.
This reduction in parameter complexity does not compromise the performance; rather, it enhances the DAGA framework’s efficiency, making it a compelling choice for scenarios where computational resources are limited. The disentangled representation not only streamlines the learning process by focusing on distinct latent factors but also ensures that the model remains scalable and adaptable to various group recommendation contexts.
In summary, the disentanglement design within DAGA serves a dual purpose: it bolsters the recommendation capabilities of the model while simultaneously ensuring computational parsimony. This approach marks a significant advancement in the design of recommendation methods, marrying effectiveness with efficiency in a manner that sets a new precedent for future research in the field.
5.4. Ablation Studies and Parameter Studies
This section delves into a comprehensive examination of the DAGA framework focusing on the impact of the different aggregation mechanisms and key hyperparameters on the performance of group recommendations.
5.4.1. Ablation Studies
To elucidate the significance of various aggregation modules within DAGA, ablation experiments are conducted on the Weeplaces dataset utilizing variants of DAGA with distinct aggregation strategies: Maxpooling and Meanpooling in lieu of the default Attention mechanism. The performance metrics for the DAGA variants, namely, DAGA-Max, DAGA-Mean and the standard DAGA-Attention, are summarized in Table 5.

Table 5.
Ablation study: performance of DAGA variants on Weeplaces dataset.
The empirical results reveal that DAGA-Attention, incorporating the attention aggregator, consistently outperforms the other variants. This finding underscores the superior capability of the attention aggregator in effectively synthesizing individual member preferences into a cohesive group representation, thereby enhancing recommendation accuracy. In contrast, DAGA-Max, which solely relies on the maximal elements within the member representations, exhibits the lowest performance, highlighting the limitations of such an approach in capturing the full spectrum of group preferences. DAGA-Mean demonstrates moderate performance, indicating that averaging member representations, while more comprehensive than Maxpooling, still lacks the nuanced adaptability afforded by the attention aggregation.
In order to dissect the performance of our proposed multi-head disentangled self-attention module, we further conduct experiments with different structure settings. To be specific, multi-head disentangled self-attention encoders with 1–3 layers and with 2, 4 and 8 heads, respectively, are verified. When we test one of them, the other structure settings are kept as default (two layers, four heads with attention aggregator).
The experimental results demonstrate that the effect of the layer setting is less important than that of the head setting. The multi-head disentangled self-attention module with two attention layers and four heads can produce the best performance, which indicates that the preference relationships between users are relatively easy to capture, and the more complex model structures are not necessary.
5.4.2. Parameter Studies
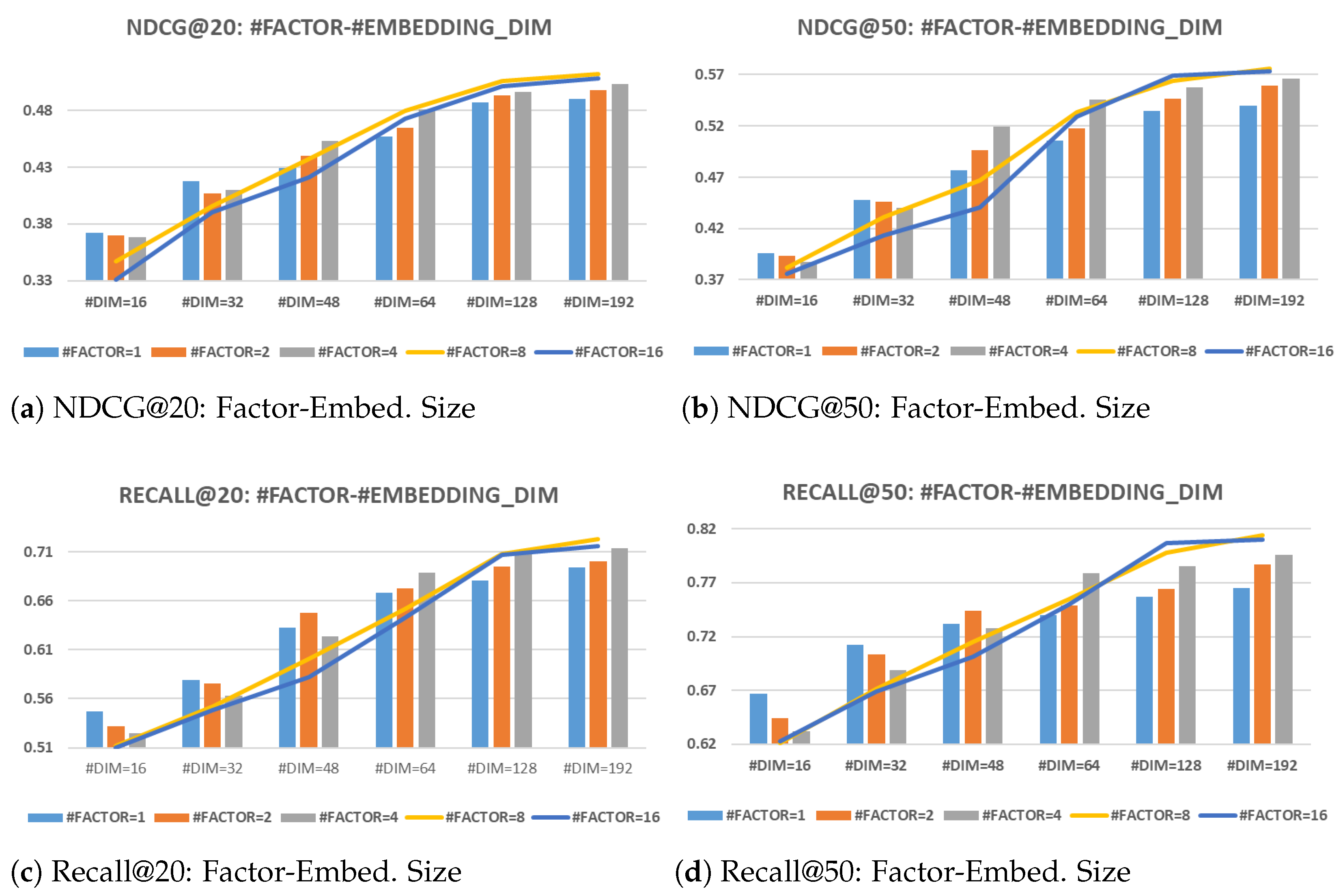
Subsequent to the ablation studies, a series of parameter sensitivity analyses are undertaken to assess the influence of key hyperparameters, including the factor number and embedded size of user and group representations, on the framework performance. The variations in performance metrics across different configurations of factor numbers and embedding dimensions are depicted in Figure 3.
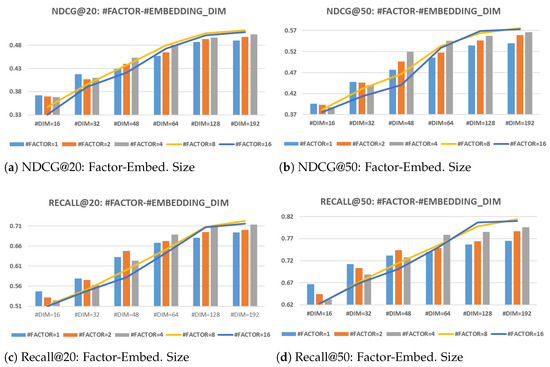
Figure 3.
Performance of variations of DAGA across embedding dimension sizes (16 to 192) and factor numbers (1 to 16) on the Weeplaces dataset.
The analysis illustrated in Figure 3 demonstrates that increasing the embedded size generally enhances the framework performance, which is attributable to the enriched representational capacity of the neural networks. However, the performance gains tend to plateau at higher dimensions, suggesting diminishing returns with excessively large embedding sizes.
Interestingly, the optimal number of factors varies with the embedding size. Larger embedding dimensions benefit from a higher number of factors, leveraging the finer granularity afforded by the disentangled representations. Conversely, smaller embedding sizes exhibit optimal performance with fewer factors, indicating that overly granular disentanglement may be counterproductive when representational capacity is limited.
The comprehensive ablation and parameter studies elucidate the effectiveness of our design and the hyperparameter configurations in optimizing the performance of DAGA for group recommendations. These insights not only affirm the framework robustness but also pave the way for future enhancements in disentangled representation learning for recommendation methods.
6. Conclusions
In this work, we introduce a novel ephemeral group recommendation framework, termed DAGA, which employs disentangled neural networks for self-attention-based and MLP-based encoder design in conjunction with a self-supervised learning strategy predicated on mutual information to intricately model user intents and address issues of data sparsity.
- Theoretical Contributions: The innovative disentanglement approach allows for the independent transfer of user and group representations across distinct factors in the self-attention mechanism and MLP encoders, effectively mitigating the amalgamation of unrelated factor information. To facilitate the training of this framework, we formulate both supervised and self-supervised loss functions. These functions capitalize on the preference probability distributions at the input and output stages of DAGA, as well as on the contextual insights gleaned through the maximization of mutual information pertaining to group representations;
- Applied Contributions: Comprehensive empirical analyses conducted on three publicly available benchmark datasets substantiate the superior performance of DAGA in comparison to the state-of-the-art methodologies. Given the demonstrated efficacy of collaborative filtering (CF) in recommendation systems, our future endeavors will focus on the exploration of group recommendation models predicated on CF techniques and the development of more nuanced objective functions to further enhance model performance;
- Main Limitations: Additionally, there are also some limitations to our proposed framework. For example, DAGA performs best when the training flow follows the training procedure as shown in Algorithm 1. However, when it comes to an end-to-end training procedure, there will be some performance degradation. In our future work, we will explore the more efficient end-to-end training framework for group recommendation and also want to discover more applicable scenarios for the multi-head disentangled self-attention encoder, including a variety of recommended and non-recommended tasks.
Author Contributions
Conceptualization, L.G., H.Z. and L.F.; methodology, L.G., H.Z. and L.F.; software, L.G. and H.Z.; validation, L.G. and H.Z.; formal analysis, L.G., H.Z. and L.F.; investigation, L.G.; resources, H.Z.; data curation, L.G.; writing—original draft preparation, L.G., H.Z. and L.F.; writing—review and editing, L.G., H.Z. and L.F.; visualization, L.G.; supervision, L.F. All authors have read and agreed to the published version of the manuscript.
Funding
This paper is supported in part by the National Natural Science Foundation of China (62371290, U20A20185) and 111 project (BP0719010).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors sincerely acknowledge Shanghai Jiao Tong University for supporting steps of this work.
Conflicts of Interest
Author Haonan Zhang was employed by the company Huawei Technologies Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zheng, K.; Zhang, J.; Liu, X.; Fu, L.; Wang, X.; Jiang, X.; Zhang, W. Secrecy Capacity Scaling of Large-Scale Networks With Social Relationships. IEEE Trans. Veh. Technol. 2017, 66, 2688–2702. [Google Scholar] [CrossRef]
- Zheng, K.; Jia, X.; Chi, K.; Liu, X. DDPG-Based Joint Time and Energy Management in Ambient Backscatter-Assisted Hybrid Underlay CRNs. IEEE Trans. Commun. 2023, 71, 441–456. [Google Scholar] [CrossRef]
- Kabbur, S.; Ning, X.; Karypis, G. FISM: Factored item similarity models for top-N recommender systems. In Proceedings of the KDD ’13: Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 659–667. [Google Scholar]
- Wang, X.; He, X.; Wang, M.; Feng, F.; Chua, T.-S. Neural Graph Collaborative Filtering. In Proceedings of the SIGIR’19: Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, 21–25 July 2019. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian Personalized Ranking from Implicit Feedback. arXiv 2009, arXiv:1205.2618. [Google Scholar]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation. In Proceedings of the SIGIR ’20: Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 25–30 July 2020. [Google Scholar]
- He, X.; He, Z.; Song, J.; Liu, Z.; Jiang, Y.; Chua, T.-S. NAIS: Neural Attentive Item Similarity Model for Recommendation. IEEE Trans. Knowl. Data Eng. 2018, 30, 2354–2366. [Google Scholar] [CrossRef]
- Koren, Y. Factorization meets the neighborhood: A multifaceted collaborative fltering model. In Proceedings of the KDD ’08: Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 426–434. [Google Scholar]
- Liang, D.; Krishnan, R.G.; Hoffman, M.D.; Jebara, T. Variational Autoencoders for Collaborative Filtering. In Proceedings of the WWW ’18: Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 689–698. [Google Scholar]
- Hu, L.; Cao, J.; Xu, G.; Cao, L.; Gu, Z.; Cao, W. Deep modeling of group preferences for group-based recommendation. Proc. AAAI Conf. Artif. Intell. 2014, 28, 1861–1867. [Google Scholar] [CrossRef]
- Cao, D.; He, X.; Miao, L.; An, Y.; Yang, C.; Hong, R. Attentive group recommendation. In Proceedings of the SIGIR ’18: The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 645–654. [Google Scholar]
- Sankar, A.; Wu, Y.; Wu, Y.; Zhang, W.; Yang, H.; Sundaram, H. GroupIM: A mutual information maximization framework for neural group recommendation. In Proceedings of the SIGIR ’20: Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 25–30 July 2020; pp. 1279–1288. [Google Scholar]
- Baltrunas, L.; Makcinskas, T.; Ricci, F. Group recommendations with rank aggregation and collaborative fltering. In Proceedings of the RecSys ’10: Proceedings of the Fourth ACM Conference on Recommender Systems, Barcelona, Spain, 26–30 September 2010; pp. 119–126. [Google Scholar]
- Berkovsky, S.; Freyne, J. Group-based recipe recommendations: Analysis of data aggregation strategies. In Proceedings of the RecSys ’10: Proceedings of the fourth ACM conference on Recommender systems, Barcelona, Spain, 26–30 September 2010; pp. 111–118. [Google Scholar]
- Boratto, L.; Carta, S. State-of-the-Art in Group Recommendation and New Approaches for Automatic Identifcation of Groups. In Information Retrieval and Mining in Distributed Environments; Springer: Berlin/Heidelberg, Germany, 2011; Volume 324, pp. 1–20. [Google Scholar]
- Amer-Yahia, S.; Roy, S.B.; Chawla, A.; Das, G.; Yu, C. Group Recommendation: Semantics and Efciency. Proc. VLDB Endow. 2009, 2, 754–765. [Google Scholar] [CrossRef]
- He, Z.; Chow, C.-Y.; Zhang, J.-D. GAME: Learning Graphical and Attentive Multi-view Embeddings for Occasional Group Recommendation. In Proceedings of the SIGIR ’20: Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 25–30 July 2020; pp. 649–658. [Google Scholar]
- Tran, L.V.; Pham, T.-A.N.; Tay, Y.; Liu, Y.; Cong, G.; Li, X. Interact and Decide: Medley of Sub-Attention Networks for Effective Group Recommendation. In Proceedings of the SIGIR’19: Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, 21–25 July 2019; pp. 255–264. [Google Scholar]
- Yin, H.; Wang, Q.; Zheng, K.; Li, Z.; Yang, J.; Zhou, X. Social Influence-Based Group Representation Learning for Group Recommendation. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macao, China, 8–11 April 2019; pp. 566–577. [Google Scholar]
- Zhang, J.; Gao, M.; Yu, J.; Guo, L.; Li, J.; Yin, H. Double-Scale Self-Supervised Hypergraph Learning for Group Recommendation. In Proceedings of the CIKM ’21: Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Virtual Event, 1–5 November 2021; pp. 2557–2567. [Google Scholar]
- Chen, T.; Yin, H.; Long, J.; Nguyen, Q.V.H.; Wang, Y.; Wang, M. Thinking inside The Box: Learning Hypercube Representations for Group Recommendation. In Proceedings of the SIGIR ’22: Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, 11–15 July 2022; pp. 1664–1673. [Google Scholar]
- Li, K.; Wang, C.-D.; Lai, J.; Yuan, H. Self-Supervised Group Graph Collaborative Filtering for Group Recommendation. In Proceedings of the WSDM ’23: Proceedings of the Sixteenth ACM International Conference on Web Search and Data Mining, Singapore, 27 February–3 March 2023; pp. 69–77. [Google Scholar]
- Quintarelli, E.; Rabosio, E.; Tanca, L. Recommending new items to ephemeral groups using contextual user influence. In Proceedings of the RecSys ’16: Proceedings of the 10th ACM Conference on Recommender Systems, Boston, MA, USA, 15–19 September 2016; pp. 285–292. [Google Scholar]
- Seko, S.; Yagi, T.; Motegi, M.; Muto, S. Group recommendation using feature space representing behavioral tendency and power balance among members. In Proceedings of the RecSys ’11: Proceedings of the Fifth ACM Conference on Recommender Systems, Chicago, IL, USA, 23–27 October 2011; pp. 101–108. [Google Scholar]
- Yin, H.; Wang, Q.; Zheng, K.; Li, Z.; Zhou, X. Overcoming data sparsity in group recommendation. IEEE Trans. Knowl. Data Eng. 2020, 34, 3447–3460. [Google Scholar] [CrossRef]
- Guo, L.; Yin, H.; Wang, Q.; Cui, B.; Huang, Z.; Cui, L. Group recommendation with latent voting mechanism. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 121–132. [Google Scholar]
- Jia, R.; Zhou, X.; Dong, L.; Pan, S. Hypergraph Convolutional Network for Group Recommendation. In Proceedings of the 2021 IEEE International Conference on Data Mining (ICDM), Auckland, New Zealand, 7–10 December 2021; pp. 260–269. [Google Scholar]
- Gorla, J.; Lathia, N.; Robertson, S.; Wang, J. Probabilistic group recommendation via information matching. In Proceedings of the WWW ’13: Proceedings of the 22nd international conference on World Wide Web, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 495–504. [Google Scholar]
- Liu, X.; Tian, Y.; Ye, M.; Lee, W.-C. Exploring personal impact for group recommendation. In Proceedings of the CIKM ’12: Proceedings of the 21st ACM International Conference on Information and Knowledge Management, Maui, HI, USA, 29 October–2 November 2012; pp. 674–683. [Google Scholar]
- Yuan, Q.; Cong, G.; Lin, C.-Y. COM: A generative model for group recommendation. In Proceedings of the KDD ’14: Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 163–172. [Google Scholar]
- Huang, Z.; Xu, X.; Zhu, H.; Zhou, M. An efcient group recommendation model with multiattention-based neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4461–4474. [Google Scholar] [CrossRef]
- Ghaemmaghami, S.S.; Salehi-Abari, A. DeepGroup: Group Recommendation with Implicit Feedback. In Proceedings of the CIKM ’21: Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Virtual Event, 1–5 November 2021; pp. 3408–3412. [Google Scholar]
- Cao, D.; He, X.; Miao, L.; Xiao, G.; Chen, H.; Xu, J. Social-Enhanced Attentive Group Recommendation. IEEE Trans. Knowl. Data Eng. 2021, 33, 1195–1209. [Google Scholar] [CrossRef]
- Deng, Z.; Li, C.; Liu, S.; Ali, W.; Shao, J. KnowledgeAware Group Representation Learning for Group Recommendation. In Proceedings of the 2021 IEEE 37th International Conference on Data Engineering (ICDE), Chania, Greece, 19–22 April 2021; pp. 1571–1582. [Google Scholar]
- Yang, M.; Liu, Z.; Yang, L.; Liu, X.; Wang, C.; Peng, H.; Yu, P.S. Ranking-based Group Identification via Factorized Attention on Social Tripartite Graph. In Proceedings of the WSDM ’23: Proceedings of the Sixteenth ACM International Conference on Web Search and Data Mining, Singapore, 27 February–3 March 2023; pp. 769–777. [Google Scholar]
- Yang, M.; Liu, Z.; Yang, L.; Liu, X.; Wang, C.; Peng, H.; Yu, P.S. Group Identification via Transitional Hypergraph Convolution with Cross-view Self-supervised Learning. In Proceedings of the CIKM ’23: Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023; pp. 2969–2979. [Google Scholar]
- Vaswani; Ashish; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Wu, J.; Wang, X.; Feng, F.; He, X.; Chen, L.; Lian, J.; Xie, X. Self-supervised graph learning for recommendation. In Proceedings of the SIGIR ’21: Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 11–15 July 2021; pp. 726–735. [Google Scholar]
- Yu, J.; Yin, H.; Xia, X.; Chen, T.; Li, J.; Huang, Z. Self-Supervised Learning for Recommender Systems: A Survey. arXiv 2022, arXiv:2203.15876. [Google Scholar] [CrossRef]
- Zhou, Y.; Dou, Z.; Zhu, Y.; Wen, J.-R. PSSL: Selfsupervised Learning for Personalized Search with Contrastive Sampling. In Proceedings of the CIKM ’21: Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Virtual Event, 1–5 November 2021; pp. 2749–2758. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, J.T.; Liu, B.; Huang, D.A.; Fei-Fei, L.F.; Niebles, J.C. Learning to decompose and disentangle representations for video prediction. Adv. Neural Inf. Process. Syst. 2018, 31, 517–526. [Google Scholar]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. Infogan: Interpretable representation learning by information maximizing generative adversarial nets. Adv. Neural Inf. Process. Syst. 2016, 29, 2180–2188. [Google Scholar]
- Ma, L.; Sun, Q.; Georgoulis, S.; Gool, L.V.; Schiele, B.; Fritz, M. Disentangled person image generation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 99–108. [Google Scholar]
- Ma, J.; Cui, P.; Kuang, K.; Wang, X.; Zhu, W. Disentangled graph convolutional networks. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 4212–4221. [Google Scholar]
- Li, H.; Wang, X.; Zhang, Z.; Yuan, Z.; Li, H.; Zhu, W. Disentangled Contrastive Learning on Graphs. Adv. Neural Inf. Process. Syst. 2021, 34, 21872–21884. [Google Scholar]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. beta-vae: Learning basic visual concepts with a constrained variational framework. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Burgess, C.P.; Higgins, I.; Pal, A.; Matthey, L.; Watters, N.; Desjardins, G.; Lerchner, A. Understanding disentangling in β-vae. In Proceedings of the NeurIPS Workshop on Learning Disentangled Representations, Long Beach, CA, USA, 9 December 2017. [Google Scholar]
- Liu, X.; Yang, L.; Liu, Z.; Li, X.; Yang, M.; Wang, C.; Yu, P.S. Group-Aware Interest Disentangled Dual-Training for Personalized Recommendation. In Proceedings of the 2023 IEEE International Conference on Big Data (BigData), Sorrento, Italy, 15–18 December 2023; pp. 393–402. [Google Scholar]
- Oord, A.v.; Li, Y.; Vinyals, O. Representation learning with contrastive predictive coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Hjelm, R.D.; Fedorov, A.; Lavoie-Marchildon, S.; Grewal, K.; Bachman, P.; Trischler, A.; Bengio, Y. Learning deep representations by mutual information estimation and maximization. arXiv 2018, arXiv:1808.06670. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the 37th International Conference on Machine Learning, Virtual Event, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Veličković, P.; Fedus, W.; Hamilton, W.L.; Liò, P.; Bengio, Y.; Hjelm, R.D. Deep graph infomax. arXiv 2018, arXiv:1809.10341. [Google Scholar]
- Hassani, K.; Khasahmadi, A.H. Contrastive multi-view representation learning on graphs. In Proceedings of the 37th International Conference on Machine Learning, Virtual Event, 13–18 July 2020; pp. 4116–4126. [Google Scholar]
- Peng, Z.; Huang, W.; Luo, M.; Zheng, Q.; Rong, Y.; Xu, T.; Huang, J. Graph representation learning via graphical mutual information maximization. In Proceedings of the WWW ’20: Proceedings of The Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 259–270. [Google Scholar]
- You, Y.; Chen, T.; Sui, Y.; Chen, T.; Wang, Z.; Shen, Y. Graph contrastive learning with augmentations. Adv. Neural Inf. Process. Syst. 2020, 33, 5812–5823. [Google Scholar]
- He, X.; Liao, L.; Zhang, H.; Nie, L.; Hu, X.; Chua, T.-S. Neural Collaborative Filtering. In Proceedings of the WWW ’17: Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 173–182. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).