Abstract
This paper introduces a new method for compressing images in energy-starved systems, like satellites, unmanned aerial vehicles, and Internet of Things nodes, which is based on coordinated group signal transformation (CGST). The transformation algorithm is a type of difference coding and may be classified as a non-transform-based image-compression method. CGST simplifies the difference signal conversion scheme using a single group codec for all signals. It considers color channels as correlated signals of a multi-channel communication system. The performance of CGST was evaluated using a dataset of 128 × 128 pixel images from satellite remote sensing systems. To adapt CGST to image compression, some modifications were introduced to the algorithm, such as fixing the procedure of the difference signals calculation to prevent any “zeroing” of brightness and supplementing the group codec with a neural network to improve the quality of restored images. The following types of neural networks were considered: fully connected, recurrent, convolution, and convolution in the Fourier space. Based on the simulation results, fully connected neural networks are recommended if the goal is to minimize processing delay time. These networks have a response time of 13 ms. Conversely, suppose the priority is to improve quality in cases where delays are not critical. In that case, convolution neural networks in the Fourier space should be used, providing an image compression ratio of 4.8 with better minimum square error and Mikowsky norm values than JPEG with the same compression ratio.
1. Introduction
The amount of information generated worldwide has grown dramatically over the last few years. Wireless data traffic is a very illustrative example of this tendency. The total mobile monthly traffic, including fixed wireless networks, is predicted to reach 370 EB by the end of 2027 [1]. Satellite traffic is projected to grow to 125 EB by 2030 [2]. This traffic growth is due, among other things, to the rapid development of the Internet of Things (IoT). In 2022, the number of global active IoT connections grew by 18% to 14.3 billion, which is predicted to exceed 29.7 billion in 2027 [3]. Energy efficiency is critical for wireless networks (both terrestrial and satellite) and IoT devices, particularly in 5G and 6G systems [4,5,6,7]. General approaches to reducing energy consumption and increasing energy efficiency in wireless networks are discussed in detail in [8]. The article notes that improving algorithms and architecture devices and networks make the most significant contribution to energy savings (up to 75%), taking into account [9]. Approaches to increasing energy efficiency can be classified, in general, according to the level of their implementation as follows:
- Network level;
- System (or protocol) level;
- Radio interface (channel) level;
- Source encoding level [10,11].
A network-level solution can be demonstrated by directing intra-sector traffic in mobile networks [12] or collaborating with neighboring wireless sensor network nodes to assist data transmission [13]. The protocol level includes downlink control [14], dynamic channel access [15], and uplink control [16] protocols. Optimizing MIMO technology, switching off subcarriers in orthogonal frequency division multiplexing [17,18], and applying multidimensional constellation diagrams [19,20] are examples of the channel-level methods. Finally, the source encoding level is related to various energy-efficient coding [21,22,23,24], energy-efficient redundancy coding [25] techniques, and image compression (both lossy and lossless) [26,27]. The rapid progress in multimedia and visual Internet of Things (IoT) technologies [28,29], coupled with the growing reliance on microsatellites and unmanned aerial vehicles (UAVs) for remote sensing of the Earth [30,31,32], highlight the need for improved image compression technologies. Such advancements can significantly boost the energy efficiency of these systems.
Autonomous energy-starved systems, such as satellites, UAVs, and IoT devices, can benefit from lossy image compression algorithms because they provide better compression, reducing power consumption. There are two types of lossy methods: transform-based and non-transform-based [27,33]. However, it is noteworthy that these methods can be combined into one algorithm to improve image quality [34].
Transform-based methods convert images into another area, which allows for more efficient encoding and removal of imperceptible information. The most common transform-based methods use discrete cosine transform (DCT, JPEG compression method) and wavelet transform (JPEG2000 compression method) [35].
On the other hand, non-transform-based techniques are used to reduce the number of quantization levels [36,37] and compress the dynamic range of image brightness values. However, the authors [38] noted that the use of these techniques can result in the appearance of false contours in the compressed images, which in turn significantly impairs their quality. This is particularly evident in images where the quantization accuracy has been reduced. Additionally, quantization methods can often discard colors corresponding to low frequencies and select inappropriate colors when the image contains many colors with similar frequencies [39]. These drawbacks limit the direct application of non-transform methods [40]. Furthermore, reducing the number of bits used in encoding brightness levels can cause critical distortion at high compression ratios, making it impossible to restore the original image. An alternative approach to reduce the dynamic range of signals is to determine a signal’s deviation function from a specific basis function.
Coordinated group signal transformation (CGST) is a non-transform-based approach that reduces the average power of source signals through signal prediction. It has already been proven to be effective for processing low-speed data [41,42]. Unlike existing difference coding methods that predict separate signals [43,44], CGST predicts multiple correlated signals together, simplifying the coding scheme in a multi-channel system, such as the codec structure. The hypothesis behind CGST for image compression is that an image’s color channels can be considered a correlated data source since they describe a single object. In this study, we evaluate the performance of the CGST codec in image compression using the Earth remote sensing color images dataset as an example. Using CGST combined with transform-based methods significantly reduces a transmitted signal’s dynamic range, leading to lower energy consumption at the transmitter and extra image compression. To ensure the maximum image quality of the reconstructed image, we apply additional image processing techniques, including a modified dynamic range reduction algorithm to prevent unwanted brightness “zeroing” and postprocessing using a neural network to combat image blurring.
This paper is organized as follows. In the second section, the basics of CGST are explained, and a block diagram of the CGST-based image compression algorithm is provided. The third section discusses the results of the proposed algorithm simulation for PNG images, including an analysis of resulting distortions and ways to reduce them. This section also presents the results of the joint use of our proposed algorithm and the JPEG method. Finally, in the “Discussion” section, the developed algorithm’s key features and development prospects are examined.
2. Coordinated Group Signal Transformation Basics
The main idea of the CGST method is to increase the performance of multi-channel systems by joint signal analysis. One way to achieve this is to combine the principles of differential pulse-code modulation (DPCM) with CGST, as shown in Figure 1.
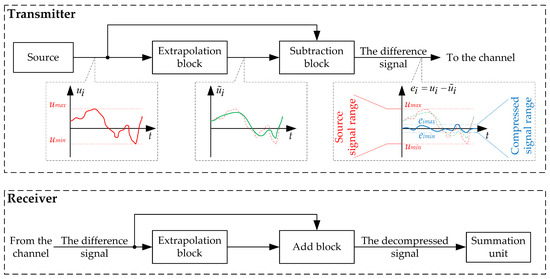
Figure 1.
Theconcept of differential coordinated group transformation (illustration for a single channel of a multichannel system). Red—source signal, green—the extrapolated one, blue—the compressed (difference) signal.
Following this approach, original signals are first processed through the coordinated extrapolation block to obtain their estimates. Then, the difference signals between the original signals and their estimates are calculated and used for further processing and transmission. At the receiver end, the original signals are restored using the known parameters of the extrapolation block. However, the main challenge is to synthesize the transfer function of the coordinated extrapolation block. One way to solve this problem is by treating it as an optimization problem using methods such as Wiener or Kalman filtering [41,45,46]. Nevertheless, this approach may be challenging due to its computational complexity. Another suggested method in [47] uses a group codec scheme for a multi-channel system with semi-type channels (Figure 2).
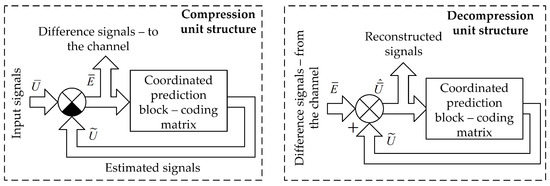
Figure 2.
The structure of the transceiver channel using coordinated codec with a coding matrix.
The input vector, (where T is the transpose operator), excites the system. The signals, (where i is the channel number), that are passed through the coding matrix are applied at the second input of the comparison elements. The vector of difference signals, , whose elements are determined by the expression , is the output for the system.
The coordinated prediction block, known as the coordinating matrix , is described as follows:
where the elements are transmission coefficients in the direct branch located on the main diagonal. The elements (correlation coefficients) are determined by the following equation:
where is the root mean square error of the channel signal, and N is the number of signal’s samples when calculating the correlation in a discrete form.
The problem of coordinated system synthesis can be solved by adjusting the coefficients k of the main diagonal, considering them to be constant for all of the channels [47]. This adjustment ensures a system’s stability while reducing the average signal amplitude at the coder output. The roots of the characteristic equation are determined outside the circumference, which completely encompasses the system hodograph, substantially simplifying the calculation. When defining the roots, the system’s hodograph is replaced by a circle circumscribed around this hodograph.
3. CGST Codec Simulation for Processing Images
As the number of color channels is limited, the dimension of the CGST system also decreases. The correlation matrix, in this case, has a size of 3 × 3 and is determined as follows:
3.1. PNG Image Compression
The field of effective image compression is a current area of research, especially in satellite remote sensing systems [48]. These systems face the challenge of providing energy efficiency. Therefore, we tested the effectiveness of the CGST performance on images from the satellite remote sensing system. For this, we obtained data using the free navigation program SASGIS. This program enables the download of satellite images of the Earth’s surface from various online mapping services. We chose Yandex Maps, which acquires images from Ikonos, QuickBird, and WorldView2 satellites. We compiled a dataset of 200 PNG images each with a resolution of 128 × 128 pixels that covered Ufa city (Russia, Republic of Bashkortostan) [49].
In CGST image compression, the input signals can be formed using the color channels to ensure their correlation. The group codec processes the original images to reduce the signal’s dynamic range, and the receiver restores the images using the inverse transformation. In our simulation, we chose a coefficient value of k to reduce the dynamic range of signals by two times, or by 3 dB. This reduces the number of bits required for coding each image pixel from 8 bits to 7 bits, providing an additional compression of about 14%. Figure 3 illustrates the image compression results at each step for this case.

Figure 3.
Low-resolution images of satellite remote sensing during some steps of the CGST-based compression.
According to the results, when using the CGST method to reduce the dynamic range of RGB channels by 3 dB or more, distortions were introduced in the transmitted information, mainly affecting the brightness. During compression, some pixels experienced a reduction in brightness level to zero, which led to a loss of information after the inverse transformation in the receiver, and the resulting image was not identical to the original. Furthermore, the extrapolation process resulted in undesirable image smoothing, which can be observed in Figure 3 in the output of the extrapolation block. As a consequence, the image produced by the codec demonstrated distorted color rendering due to the loss of brightness and blurring in the object’s contours. This happened because the brightness values of the RGB channels were restored based on the signal passed through the extrapolation block.
3.2. CGST Algorithm Modification to Reduce Distortions
As stated earlier, reducing the brightness level of darker parts of an image to zero (“zeroing”) during compression of RGB channels in the correlation matrix by 3 dB or more can make it impossible for the decoder to restore the original information with the appropriate quality. When the compressed image contains completely dark areas in all three channels that do not appear in the original image, it is crucial to retain information about the level ratio of the original signal and the signal from the matrix output. This can be achieved by fixing their positive difference value. Therefore, we made modifications to the original CGST algorithm. Before the modifications, the difference signal for the random channel at the coder output was determined using the following function:
To avoid errors caused by “zeroing”, according to Equation (5), we modified the CSGT algorithm in the simulation as follows:
where is the required coefficient of dynamic range compression, assumed to be 0.5 in the simulation. This modification to CGST ensures that the pixel brightness is not negative.
After passing through the extrapolation block and having a transformation (5) applied to it, the brightness of the areas near an object’s edges in encoded images significantly increases. On the other hand, the areas far from the borders remain at a lower brightness level. These signs indicate an increase in the image’s spatial frequency. To test this assumption, we calculated the channel-averaged spatial frequency for the original image and one that passed through the codec, which turned out to be higher for the latter. Section 3.2 offers a more detailed analysis of this issue.
3.3. CGST-Compressed Image Restoration Using the Frequency Method
The problem of image blurring from the output of an extrapolation block can be leveled by applying image restoration methods after the codec operation. However, the increased spatial frequency of processed images complicates analyzing the distorting function. It makes the use of classical approaches challenging due to the issues in determining object boundaries and the simultaneous blurring of close-in-tone areas [50].
We utilized a frequency image restoration technique called a Gaussian low-pass filter to minimize edge effects. In our simulation, we employed the standard deviation of the Gaussian distribution, which ensured that the spatial frequency graphs of the original and processed images from the codec output were almost identical, as shown in Figure 4. As a result, we obtained the following processed images that are provided in Figure 5.
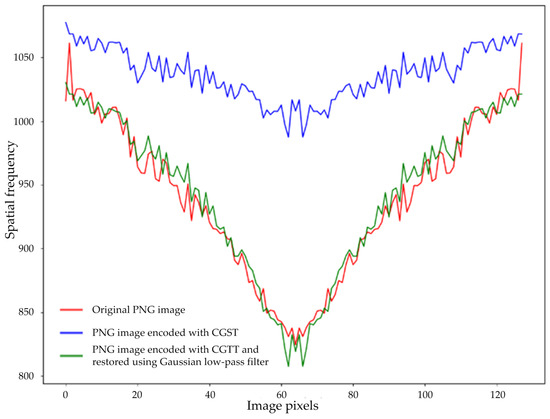
Figure 4.
Spatial frequencies of the original (red), compressed by modified CGST (blue), and restored images with a Gaussian low-pass filter technique (green).

Figure 5.
Image processing: (a) original PNG image, (b) PNG image encoded with modified CGST, (c) PNG image encoded with modified CGTT and restored using a Gaussian low-pass filter.
The quality of the recovered images was evaluated based on the following criteria: the mean square error (MSE) and the Minkowski norm (MN) to check the proximity of the RGB channels’ brightness levels and structural similarity (SSIM) [51] to assess the structural distortions’ impact. However, the SSIM algorithm in the spatial domain is highly sensitive to scaling and image shifting when processing RGB channels with an extrapolation block. To overcome this limitation, a new criterion called the complex wavelet SSIM (CW-SSIM) was introduced, which extends the SSIM algorithm to the region of the complex wavelet transform and is insensitive to non-structural distortions [52]. The averaged results obtained by applying these criteria to the entire dataset of restored images after the Gaussian filter are presented in Table 1.

Table 1.
Imagequality before and after filtering.
The results indicate that there is only a slight improvement in image quality after filtering. While the effect of increased spatial frequency was reduced, the decrease in the CW-SSIM indicates that a processed image’s blurring worsened.
Thus, using the CGST codec for image processing led to several distortions. Applying conventional methods to eliminate these distortions turns into neutralizing each other’s effects. For instance, applying a Wiener filter to a restored image after Gaussian low-pass filtering will reduce the blurring impact but increase the spatial frequency. As part of our study, we aimed to evaluate whether restoring images compressed by a CGST codec using neural network (NN) methods is possible. These methods can theoretically adapt the mapping of input data to a given output space for any distortion model.
3.4. CGST-Compressed Image Postprocessing Using Neural Networks
To solve the problem of distorted images, one option is to use a priori knowledge about the image that is being recovered. This can be achieved using supervised machine learning methods. With enough visual data, an intelligent algorithm can restore the distorted information due to its generalizing ability. Such an approach showed excellent performance for restoring medical images that had distortions in local areas, such as noise and artifacts caused by a reduction in the sampling rate or a decrease in the patient’s radiation dose [53,54,55,56].
The operation time of an NN can be reduced by processing RGB channels instead of the entire image, which simplifies the data to a vector of pixel brightness values. To meet the video broadcast encoding delay requirements [57], the minimum decode delay is 133 ms at 30 fps or 160 ms at 25 fps; however, these values can be reduced to 33 ms and 40 ms with the group-of-pictures setting. In simulations, the average operating time of the extrapolation block and the encoding matrix on the receiver is 20 ms. Therefore, the NN response time should be at most 113 ms at 30 fps and 140 ms at 25 fps (13 ms at 30 fps and 20 ms at 25 fps with the group-of-pictures setting).
The most commonly used NN types in image quality upgrade applications are fully connected, convolution, and recurrent. One of the most popular and effective intelligent methods for improving image quality nowadays is the application of deep convolution neural networks (CNNs) [58,59,60,61]. However, even if the structure is optimized, the response time of an NN is usually too long for its implementation in real-time systems [62]. Another promising method is a CNN, which parametrizes the hyperplane in the Fourier space and has shown less estimated time and greater accuracy than traditional CNNs [63]. Each NN type works effectively with various free parameters and, therefore, with various response times. Thus, the performance of different NN types strongly depends on their settings and the number of frames per second they process.
In our research, the NN structure was designed to process the RGB channel values of a CGST-compressed image in parallel and then concatenate them (Figure 6). We compared the RGB channels of an image postprocessed by a NN with those of the original image to calculate the error function and fix the total error. The performance of the NN was evaluated using the same image quality assessment metrics, which we applied after the Gaussian low-pass filter.
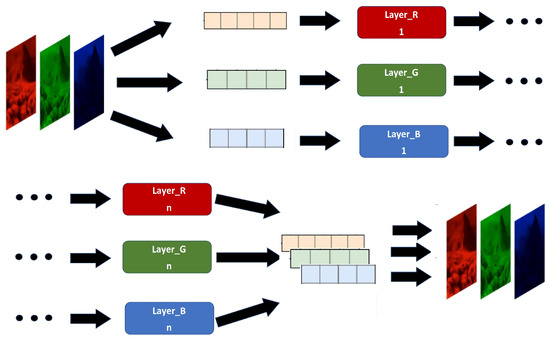
Figure 6.
Neural network structure to restore the CGST-compressed image.
Considering the allowable image processing time, we used fully connected NNs with three hidden layers operating simultaneously on the RGB channels, a four-layer convolutional NN, and a long-term short-term memory (LSTM) NN with three repeating layers. Additionally, we included fully connected layers in the input and output of the NNs for concatenation and decatenation, respectively.
The dataset used for NN training was created from 200 images obtained through SASGIS. Out of these, 150 images were assigned to the training set, while the remaining 50 were used as the testing set. We used the Adam optimization algorithm and the StepLR learning rate control function during the training process. This function reduces the number of free parameters by a gamma with each epoch, depending on the set image processing time (with or without the group-of-pictures setting). We used a set number of 100 epochs in training for all simulations. The different NNs’ results are shown in Table 2.

Table 2.
NN performance in restoring PNG images compressed by modified CGST method.
To visually evaluate the performance of the applied NNs, the examples of the restored image with varying values of CW-SSIM are shown in Figure 7.

Figure 7.
Compressed image restoring using NNs: (a) image compressed by modified CGST; (b) recurrent NN (CW-SSIM = 0.6553); (c) CNN (CW-SSIM = 0.7716); (d) CNN in Fourier space (CW-SSIM = 0.8082).
Based on the results presented in Table 1, we have concluded that using an NN helped address the two issues of blurred images and changing spatial frequency. The most significant improvement was observed in the CW-SSIM indicator, which is responsible for the visual correspondence between the restored image and the original one. We found that using a fully connected NN did not lead to any improvements. However, the recurrent NN and CNN helped increase the CW-SSIM by 0.15 and 0.27, respectively, at the maximum response time (140 ms). This led to a significant improvement in the MSE and MN criteria. The CNN in Fourier space demonstrated the best results with a CW-SSIM increase of 0.3. However, there was no significant improvement in the MSE and MN values compared to traditional NNs. At the same time, even the least efficient NN (recurrent one), with a relatively simple architecture and NN response time as low as 20 ms, provided more effective image quality restoration than traditional filtering.
At the same time, traditional JPEG compression of the source images provided an average image compression of 2.55 with SSIM equal to 0.975, an MSE of 0.140, and an MN of 12.423, which are higher than our result. It is worth noting that we previously mentioned that JPEG compression and most existing lossy image compression methods belong to the transform-based approach. In contrast, our proposed method is not transform-based and operates on several quantization levels. These two approaches can be combined for better results.
3.5. Combining CGST with JPEG Compression
To test the compatibility of our proposed method with traditional lossy compression methods, we converted the collected dataset of images into the JPEG format at 100% quality. Then, we applied the modified CGST algorithm to compress the images and restored the compressed data using the previously described sequence of actions. We used the convolution in Fourier space NN, as it showed the best restorative ability. The compression ratio obtained was approximately 4.8.
Table 3 illustrates the restored images’ quality characteristics compared to ordinary JPEG compression with an image quality of 89, which provided the same compression ratio. NN-assisted CGST showed significantly better results according to MN and MSE and was only slightly inferior to JPEG in CW-SSIM. This difference can be explained by the JPEG algorithm selectively removing high-frequency information from an image, resulting in a loss of pixel-level precision [64]. These losses may be insignificant to human vision but can reduce information for computer vision algorithms.

Table 3.
NN-assisted CGST image compression vs. traditional JPEG for the same compression ratio.
The quality metrics of the compressed and restored images prove their suitability for computer vision systems as training data for machine learning models [65]. Classical machine learning models, particularly those that perform low-level image processing functions, require a better MSE value to be trained successfully [66].
4. Discussion
This paper introduces the application of the CGST codec for image compression in energy-starved systems. To adapt the CGST algorithm for this purpose, we added some modifications. Firstly, we suggested modifying the method of generating the difference signal to eliminate data loss by “zeroing” the brightness of pixels. Secondly, we improved the quality of the restored images and reduced the distortions introduced by CGST by supplementing the output signal of the CGST decoder with a neural network. We formed a dataset of 200 remote sensing images available in open sources to train the NN (available online at [49]). Our study focused on simple geometric figures that displayed the shapes of buildings, roads, and natural objects. When training the NN for more specific details, a larger dataset may be necessary, similar to the datasets for medical image analysis, with the extracted parameters’ complex nature. Our research has substantiated that the CGST-based algorithm is compatible with transform compression methods such as PNG and JPEG to achieve energy efficiency. This substantial result indicates that the proposed method can be effectively used in conjunction with other transform-based methods, thereby ensuring extra compression. By doing so, the system’s energy efficiency can be further extended, thus making it a valuable tool in energy-starved systems.
The contribution to energy efficiency can be assessed, for example, using the Shannon–Hartley theorem.
where C is the channel throughput, is the channel bandwidth, and is the signal-to-noise ratio. By reducing the dynamic range of the encoded image by 3 dB, the number of bits in the code package can be decreased from 8 to 7, in turn reducing the required transmission speed by 1.14 times. If the channel bandwidth is maintained, the typical signal-to-noise ratio of 10 dB for CubeSat communication systems [67] can be decreased by about 1.5 dB, enabling less powerful final amplifiers in the communication system.
The test data results have shown that our proposed methods are a feasible and efficient approach to restoring images in a satellite image transmission system. This promising development could significantly impact future studies in the field. Figure 8 illustrates the possible application of CGST for image compression in such a scenario. An energy-starved system, like an Earth remote sensing satellite, compresses an image it captures using basic matrix operations. All of the resource-intensive tasks are handled by devices such as satellite earth stations or image processing servers, which have a guaranteed power supply and are not as battery-dependent. A comparable situation can be presented for technical computer vision systems in multimedia and visual IoT. In this scenario, the resource-intensive process of postprocessing a compressed image with neural networks will be executed on IoT servers. Additional compression can improve the energy efficiency of IoT sensor nodes. The joint use of CGST and neural network methods has shown a reduction of 3 dB in the dynamic range of original signals. If the most significant improvement in image restoration quality is needed, a convolutional NN should be used. On the other hand, if the priority is to increase the speed of the postprocessing system, a recurrent NN can be applied. The NN-assisted CGST-based algorithm can provide a total compression ratio of approximately 4.8 for additional compression of JPEG images. This algorithm also offers better MSE and MN values than JPEG-compressed images of the same size. This advantage could be significant in acquiring images for training machine learning algorithms. However, the CW-SSIM value still requires improvement, which is our primary goal for future research.
Figure 8.
The possible scenario of applying the CGST-based compression algorithm in the satellite image transmission system.
Author Contributions
Conceptualization, G.V. and E.L.; methodology, I.K.; software, E.L.; validation, G.V., E.G. and R.K.; formal analysis, G.V., E.G. and R.K.; investigation, G.V., V.I. and E.L.; resources, R.K.; data curation, E.L.; writing—original draft preparation, G.V. and E.L.; writing—review and editing, E.G. and R.K.; visualization, G.V.; supervision, E.G.; project administration, G.V.; funding acquisition, E.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded under the grant of the Russian Science Foundation (Project #21-79-10407).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
A dataset for training the ML algorithm is available online at https://github.com/Ekaterina-Lopukhova/A-Novel-Image-Compression-Method-Based-on-Coordinated-Group-Signal-Transformation (accessed on 8 May 2024).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ericsson Mobility Report November 2021. Available online: https://www.ericsson.com/4ad7e9/assets/local/reports-papers/mobility-report/documents/2021/ericsson-mobility-report-november-2021.pdf (accessed on 26 March 2024).
- Halpin, S. Space Traffic Data Volumes Increase 14x Over the Next Ten Years. Available online: https://www.nsr.com/space-traffic-data-volumes-increase-14x-over-the-next-ten-years/ (accessed on 26 March 2024).
- State of IoT 2023: Number of Connected IoT Devices Growing 16% to 16.7 Billion Globally. Available online: https://iot-analytics.com/number-connected-iot-devices/ (accessed on 26 March 2024).
- Alliance, B.N.; Hattachi, R.E.; Erfanian, J. NGMN 5G White Paper; NGMN: Düsseldorf, Germany, 2015. [Google Scholar]
- Tong, P.Z.W. (Ed.) 6G: The Next Horizon: From Connected People and Things to Connected Intelligence; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Plastras, S.; Tsoumatidis, D.; Skoutas, D.N.; Rouskas, A.; Kormentzas, G.; Skianis, C. Non-Terrestrial Networks for Energy-Efficient Connectivity of Remote IoT Devices in the 6G Era: A Survey. Sensors 2024, 24, 1227. [Google Scholar] [CrossRef] [PubMed]
- Ledesma, O.; Lamo, P.; Fraire, J.A. Trends in LPWAN Technologies for LEO Satellite Constellations in the NewSpace Context. Electronics 2024, 13, 579. [Google Scholar] [CrossRef]
- Alagoz, F.; Gur, G. Energy efficiency and satellite networking: A holistic overview. Proc. IEEE 2011, 99, 1954–1979. [Google Scholar] [CrossRef]
- Nekoogar, F.; Nekoogar, F. From ASICs to SOCs: A Practical Approach; Prentice Hall Professional: Hoboken, NJ, USA, 2003. [Google Scholar]
- Rathore, R.S.; Sangwan, S.; Kaiwartya, O.; Aggarwal, G. Green communication for next-generation wireless systems: Optimization strategies, challenges, solutions, and future aspects. Wirel. Commun. Mob. Comput. 2021, 2021, 5528584. [Google Scholar] [CrossRef]
- Kaur, P.; Garg, R.; Kukreja, V. Energy-efficiency schemes for base stations in 5G heterogeneous networks: A systematic literature review. Telecommun. Syst. 2023, 84, 115–151. [Google Scholar] [CrossRef]
- Sabella, D.; Rapone, D.; Fodrini, M.; Cavdar, C.; Olsson, M.; Frenger, P.; Tombaz, S. Energy management in mobile networks towards 5G. Stud. Syst. Decis. Control 2016, 50, 397–427. [Google Scholar] [CrossRef] [PubMed]
- Elhawary, M.; Haas, Z.J. Energy-Efficient Protocol for Cooperative Networks. IEEE/ACM Trans. Netw. 2011, 19, 561–574. [Google Scholar] [CrossRef]
- Herrería-Alonso, S.; Rodríguez-Pérez, M.; Fernández-Veiga, M.; Lopez-Garcia, C. Adaptive DRX Scheme to Improve Energy Efficiency in LTE Networks with Bounded Delay. IEEE J. Sel. Areas Commun. 2015, 33, 2963–2973. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, Y.; Zhang, N.; Zhang, D.; Shen, X. Dynamic Channel Access to Improve Energy Efficiency in Cognitive Radio Sensor Networks. IEEE Trans. Wirel. Commun. 2016, 15, 3143–3156. [Google Scholar] [CrossRef]
- Jong, C.; Kim, Y.C.; So, J.H.; Ri, K.C. QoS and energy-efficiency aware scheduling and resource allocation scheme in LTE—A uplink systems. Telecommun. Syst. 2023, 82, 175–191. [Google Scholar] [CrossRef]
- Dong, Z.; Wei, J.; Chen, X.; Zheng, P. Energy Efficiency Optimization and Resource Allocation of Cross-Layer Broadband Wireless Communication System. IEEE Access 2020, 8, 50740–50754. [Google Scholar] [CrossRef]
- Xiong, C.; Li, G.Y.; Zhang, S.; Chen, Y.; Xu, S. Energy-Efficient Resource Allocation in OFDMA Networks. IEEE Trans. Commun. 2012, 60, 3767–3778. [Google Scholar] [CrossRef]
- Markiewicz, T.G. An Energy Efficient QAM Modulation with Multidimensional Signal Constellation. Int. J. Electron. Telecommun. 2016, 62, 159–165. [Google Scholar] [CrossRef]
- Li, W.; Ghogho, M.; Zhang, J.; McLernon, D.; Lei, J.; Zaidi, S.A.R. Design of an energy-efficient multidimensional secure constellation for 5G communications. In Proceedings of the 2019 IEEE International Conference on Communications Workshops, ICC Workshops 2019, Shanghai, China, 20–24 May 2019. [Google Scholar] [CrossRef]
- Turcza, P.; Duplaga, M. Energy-efficient image compression algorithm for high-frame rate multi-view wireless capsule endoscopy. J. Real-Time Image Process. 2019, 16, 1425–1437. [Google Scholar] [CrossRef]
- Resmi, N.; Chouhan, S. Energy Efficient Communication with Interdependent Source-Channel Coding: An Enhanced Methodology. In Proceedings of the 2018 IEEE SENSORS, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Peng, Y.; Andrieux, G.; Diouris, J.F. Minimization of Energy Consumption for OOK Transmitter Through Minimum Energy Coding. Wirel. Pers. Commun. 2022, 122, 2219–2233. [Google Scholar] [CrossRef]
- Khammassi, M.; Kammoun, A.; Alouini, M.S. Precoding for high throughput satellite communication systems: A survey. IEEE Commun. Surv. Tutor. 2023, 26, 80–118. [Google Scholar] [CrossRef]
- Hyla, J.; Sułek, W. Energy-Efficient Raptor-like LDPC Coding Scheme Design and Implementation for IoT Communication Systems. Energies 2023, 16, 4697. [Google Scholar] [CrossRef]
- Rahman, M.A.; Hamada, M. Lossless image compression techniques: A state-of-the-art survey. Symmetry 2019, 11, 1274. [Google Scholar] [CrossRef]
- ZainEldin, H.; Elhosseini, M.A.; Ali, H.A. Image compression algorithms in wireless multimedia sensor networks: A survey. Ain Shams Eng. J. 2015, 6, 481–490. [Google Scholar] [CrossRef]
- Nauman, A.; Qadri, Y.A.; Amjad, M.; Zikria, Y.B.; Afzal, M.K.; Kim, S.W. Multimedia Internet of Things: A Comprehensive Survey. IEEE Access 2020, 8, 8202–8250. [Google Scholar] [CrossRef]
- Budati, A.K.; Islam, S.; Hasan, M.K.; Safie, N.; Bahar, N.; Ghazal, T.M. Optimized visual internet of things for video streaming enhancement in 5G sensor network devices. Sensors 2023, 23, 5072. [Google Scholar] [CrossRef] [PubMed]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Achim, A.; Mulverhill, C. Framework for near real-time forest inventory using multi source remote sensing data. Forestry 2023, 96, 1–19. [Google Scholar] [CrossRef]
- Phang, S.K.; Chiang, T.H.A.; Happonen, A.; Chang, M.M.L. From Satellite to UAV-based Remote Sensing: A Review on Precision Agriculture. IEEE Access 2023, 11, 127057–127076. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, L. A review on unmanned aerial vehicle remote sensing: Platforms, sensors, data processing methods, and applications. Drones 2023, 7, 398. [Google Scholar] [CrossRef]
- Jayasankar, U.; Thirumal, V.; Ponnurangam, D. A survey on data compression techniques: From the perspective of data quality, coding schemes, data type and applications. J. King Saud Univ.-Comput. Inf. Sci. 2021, 33, 119–140. [Google Scholar] [CrossRef]
- Zhang, C.; Ugur, K.; Lainema, J.; Gabbouj, M. Video Coding Using Spatially Varying Transform. In Advances in Image and Video Technology; Series Title: Lecture Notes in Computer Science; Wada, T., Huang, F., Lin, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5414, pp. 796–806. [Google Scholar] [CrossRef]
- Li, Z.N.; Drew, M.S.; Liu, J. Fundamentals of Multimedia; Texts in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Puzicha, J.; Held, M.; Ketterer, J.; Buhmann, J.; Fellner, D. On spatial quantization of color images. IEEE Trans. Image Process. 2000, 9, 666–682. [Google Scholar] [CrossRef] [PubMed]
- Ponti, M.; Nazaré, T.S.; Thumé, G.S. Image quantization as a dimensionality reduction procedure in color and texture feature extraction. Neurocomputing 2016, 173, 385–396. [Google Scholar] [CrossRef]
- Afonso, M.; Sole, J.; Krasula, L.; Li, Z.; Tandon, P. CAMBI: Introduction and latest advances. In Proceedings of the 1st Mile-High Video Conference, Denver, CO, USA, 1–3 March 2022; pp. 105–106. [Google Scholar]
- Pérez-Delgado, M.L.; Román Gallego, J.Á. A two-stage method to improve the quality of quantized images. J. Real-Time Image Process. 2020, 17, 581–605. [Google Scholar] [CrossRef]
- Huang, Q.; Kim, H.Y.; Tsai, W.J.; Jeong, S.Y.; Choi, J.S.; Kuo, C.C.J. Understanding and Removal of False Contour in HEVC Compressed Images. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 378–391. [Google Scholar] [CrossRef]
- Voronkov, G.S.; Smirnova, E.A.; Kuznetsov, I.V. The method for synthesis of the coordinated group DPCM codec for unmanned aerial vehicles communication systems. In Proceedings of the ICOECS 2019: 2019 International Conference on Electrotechnical Complexes and Systems, Ufa, Russia, 22–25 October 2019. [Google Scholar] [CrossRef]
- Ivanov, V.V.; Lopukhova, E.A.; Voronkov, G.S.; Kuznetsov, I.V.; Grakhova, E.P. Efficiency Evaluation of Group Signals Transformation for Wireless Communication in V2X Systems. In Proceedings of the 2022 Ural-Siberian Conference on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT), Yekaterinburg, Russia, 19–21 September 2022; pp. 167–170. [Google Scholar] [CrossRef]
- Sheferaw, G.K.; Mwangi, W.; Kimwele, M.; Mamuye, A. Waveform based speech coding using nonlinear predictive techniques: A systematic review. Int. J. Speech Technol. 2023, 26, 1–29. [Google Scholar] [CrossRef]
- Anees, M. Speech coding techniques and challenges: A comprehensive literature survey. Multimed. Tools Appl. 2023, 83, 29859–29879. [Google Scholar]
- Voronkov, G.S.; Filatov, P.E.; Sultanov, A.K.; Voronkova, A.V.; Vinogradova, I.L.; Kuznetsov, I.V. Signals and messages differential transformation research for increasing multichannel systems efficiency. J. Phys. Conf. Ser. 2018, 1096, 012175. [Google Scholar] [CrossRef]
- Voronkov, G.S.; Voronkova, A.V.; Kutluyarov, R.V.; Kuznetsov, I.V. Decreasing the dynamic range of OFDM signals based on extrapolation for information security increasing. In Proceedings of the 2018 Ural Symposium on Biomedical Engineering, Radioelectronics and Information Technology, USBEREIT 2018, Yekaterinburg, Russia, 7–8 May 2018; pp. 271–274. [Google Scholar] [CrossRef]
- Voronkov, G.S.; Filatov, P.E.; Sultanov, A.K.; Kutluyarov, R.V.; Vinogradova, I.L.; Kuznetsov, I.V. Improving the efficiency of multichannel systems based on the coordination of channel signals. J. Phys. Conf. Ser. 2019, 1368, 042047. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, Y.; Zhao, B.; Chanussot, J.; Hong, D.; Yao, J.; Gao, L. Progress and Challenges in Intelligent Remote Sensing Satellite Systems. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1814–1822. [Google Scholar] [CrossRef]
- Ekaterina-Lopukhova. The Dataset for Compression Method Based on Coordinated Group Signal Transformation. Available online: https://github.com/Ekaterina-Lopukhova/A-Novel-Image-Compression-Method-Based-on-Coordinated-Group-Signal-Transformation (accessed on 8 May 2024).
- Gonzalez, R.C. Digital Image Processing; Pearson Education India: Noida, India, 2009. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Simoncelli, E.P. Translation insensitive image similarity in complex wavelet domain. In Proceedings of the ICASSP’05: IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 18–23 March 2005; Volume 2, pp. ii/573–ii/576. [Google Scholar]
- Pelt, D.M.; Batenburg, K.J. Fast tomographic reconstruction from limited data using artificial neural networks. IEEE Trans. Image Process. 2013, 22, 5238–5251. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhang, Y.; Zhang, W.; Liao, P.; Li, K.; Zhou, J.; Wang, G. Low-dose CT via convolutional neural network. Biomed. Opt. Express 2017, 8, 679. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Su, Z.; Ying, L.; Peng, X.; Zhu, S.; Liang, F.; Feng, D.; Liang, D. Accelerating magnetic resonance imaging via deep learning. In Proceedings of the 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), Prague, Czech Republic, 13–16 April 2016; pp. 514–517. [Google Scholar]
- Schlemper, J.; Caballero, J.; Hajnal, J.V.; Price, A.; Rueckert, D. A deep cascade of convolutional neural networks for MR image reconstruction. In Proceedings of the Information Processing in Medical Imaging: 25th International Conference, IPMI 2017, Boone, NC, USA, 25–30 June 2017; Proceedings 25. pp. 647–658. [Google Scholar]
- Technical Report ITU-R BT.2044-0 (2004) Tolerable Round-Trip Time Delay for Sound-Programme and Television Broadcast Programme Inserts—Context and Rationale. Available online: https://www.itu.int/dms_pub/itu-r/opb/rep/R-REP-BT.2044-2004-PDF-E.pdf (accessed on 8 May 2024).
- Gatys, L.A.; Ecker, A.S.; Bethge, M. Image Style Transfer Using Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2414–2423. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef]
- Ignatov, A.; Kobyshev, N.; Timofte, R.; Vanhoey, K.; Gool, L.V. DSLR-Quality Photos on Mobile Devices with Deep Convolutional Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3297–3305. [Google Scholar] [CrossRef]
- Savvin, S.; Sirota, A. An Algorithm for Multi-Fame Image Super-Resolution under Applicative Noise Based on a Convolutional Neural Network. In Proceedings of the 2020 2nd International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency, SUMMA 2020, Lipetsk, Russia, 11–13 November 2020; pp. 422–424. [Google Scholar] [CrossRef]
- Vu, T.; Van Nguyen, C.; Pham, T.X.; Luu, T.M.; Yoo, C.D. Fast and efficient image quality enhancement via desubpixel convolutional neural networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier Neural Operator for Parametric Partial Differential Equations. arXiv 2020, arXiv:2010.08895. [Google Scholar]
- Gardella, M.; Nikoukhah, T.; Li, Y.; Bammey, Q. The impact of jpeg compression on prior image noise. In Proceedings of the ICASSP 2022: 2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 2689–2693. [Google Scholar]
- Ehrlich, M.; Davis, L.; Lim, S.N.; Shrivastava, A. Analyzing and mitigating jpeg compression defects in deep learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2357–2367. [Google Scholar]
- Ferianc, M.; Bohdal, O.; Hospedales, T.; Rodrigues, M. Impact of Noise on Calibration and Generalisation of Neural Networks. arXiv 2023, arXiv:2306.17630. [Google Scholar]
- Cappiello, A.G.; Popescu, D.C.; Harris, J.S.; Popescu, O. Radio link design for CubeSat-to-ground station communications using an experimental license. In Proceedings of the 2019 International Symposium on Signals, Circuits and Systems (ISSCS), Iasi, Romania, 11–12 July 2019; pp. 1–4. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).