Geometrical and Mechanical Modeling of Polymeric Multi-Ply Yarns
Abstract
:1. Introduction
2. Materials and Methods
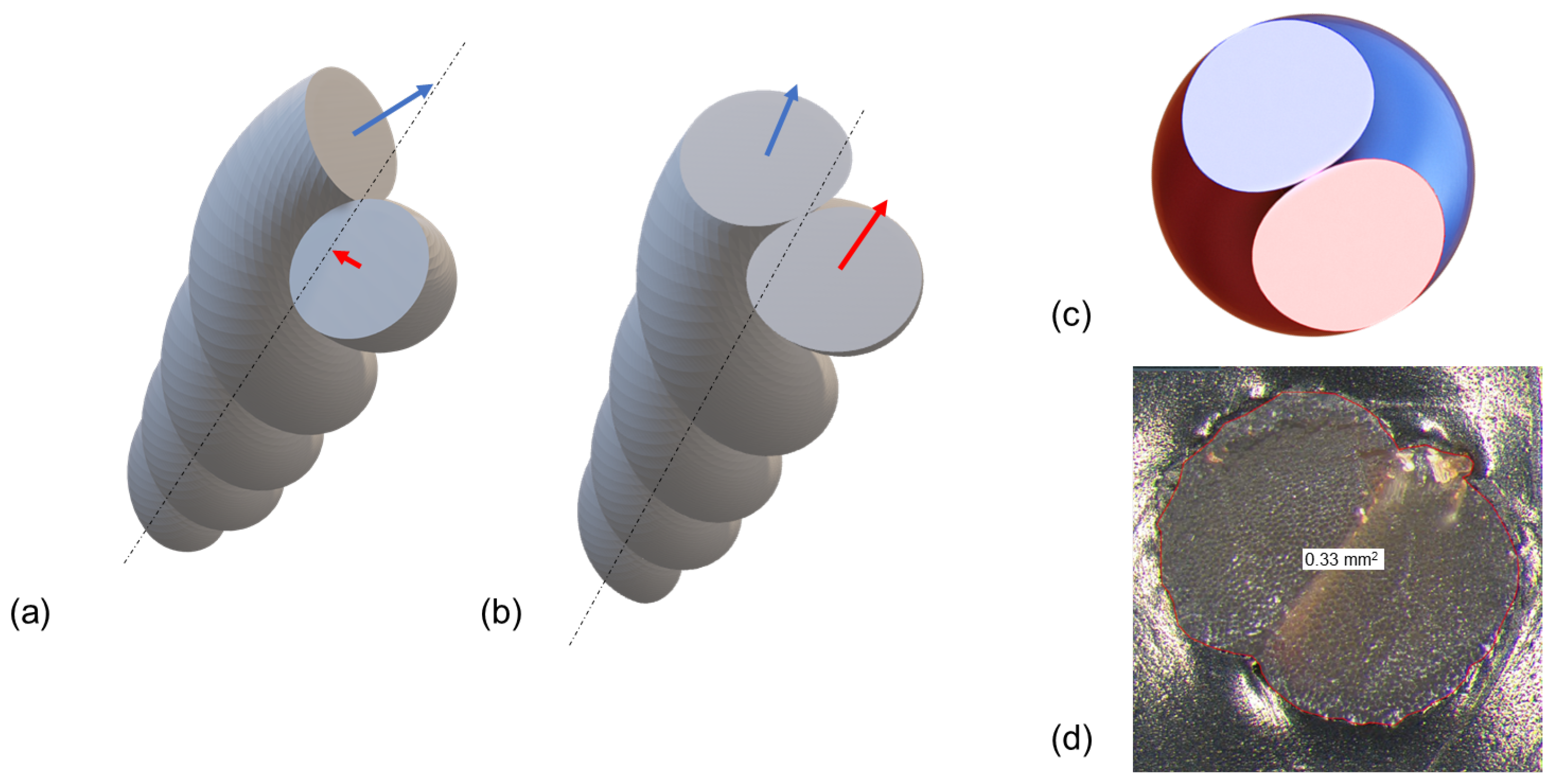
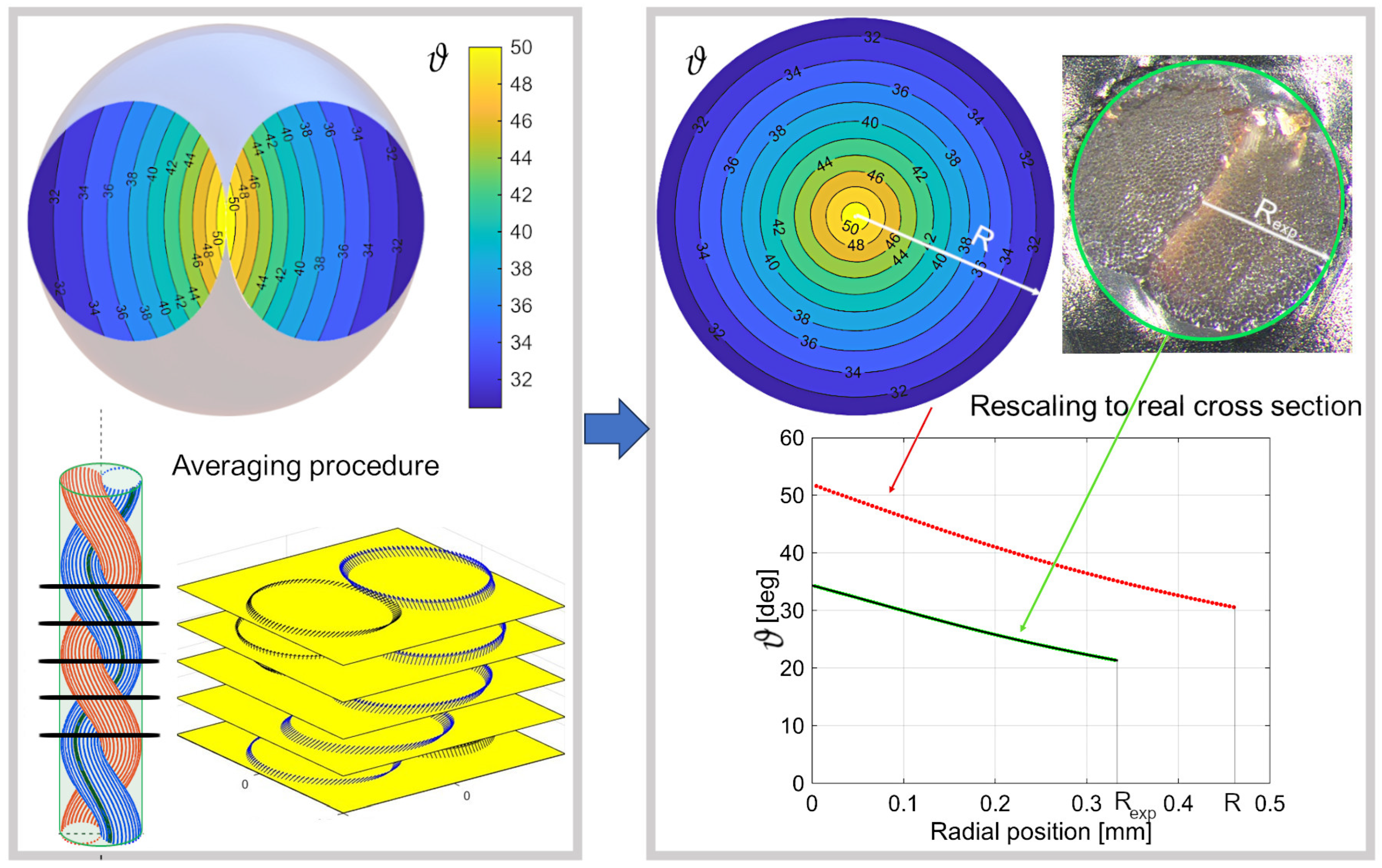
2.1. Geometrical Model of Multi-Ply Yarns
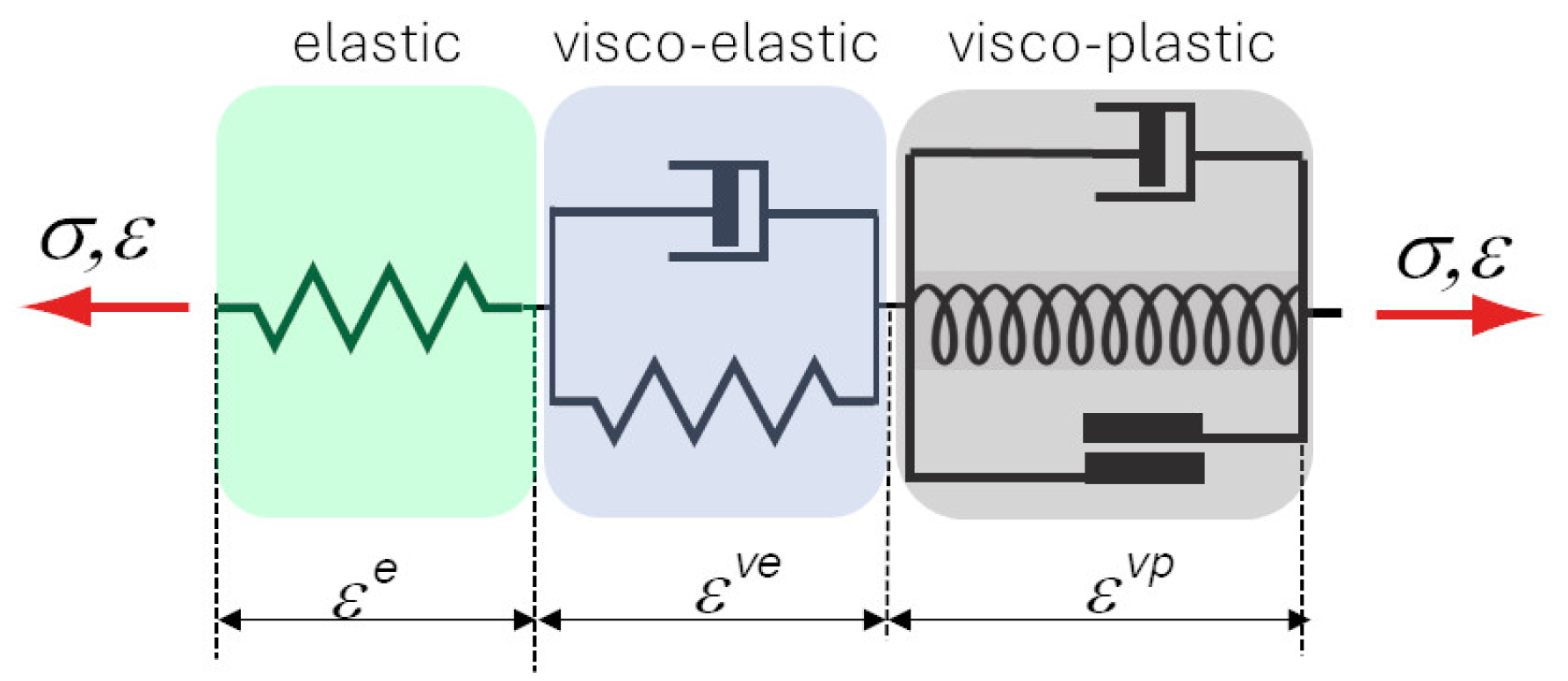
2.2. Anisotropic Viscoelastic–Viscoplastic Model
3. Results
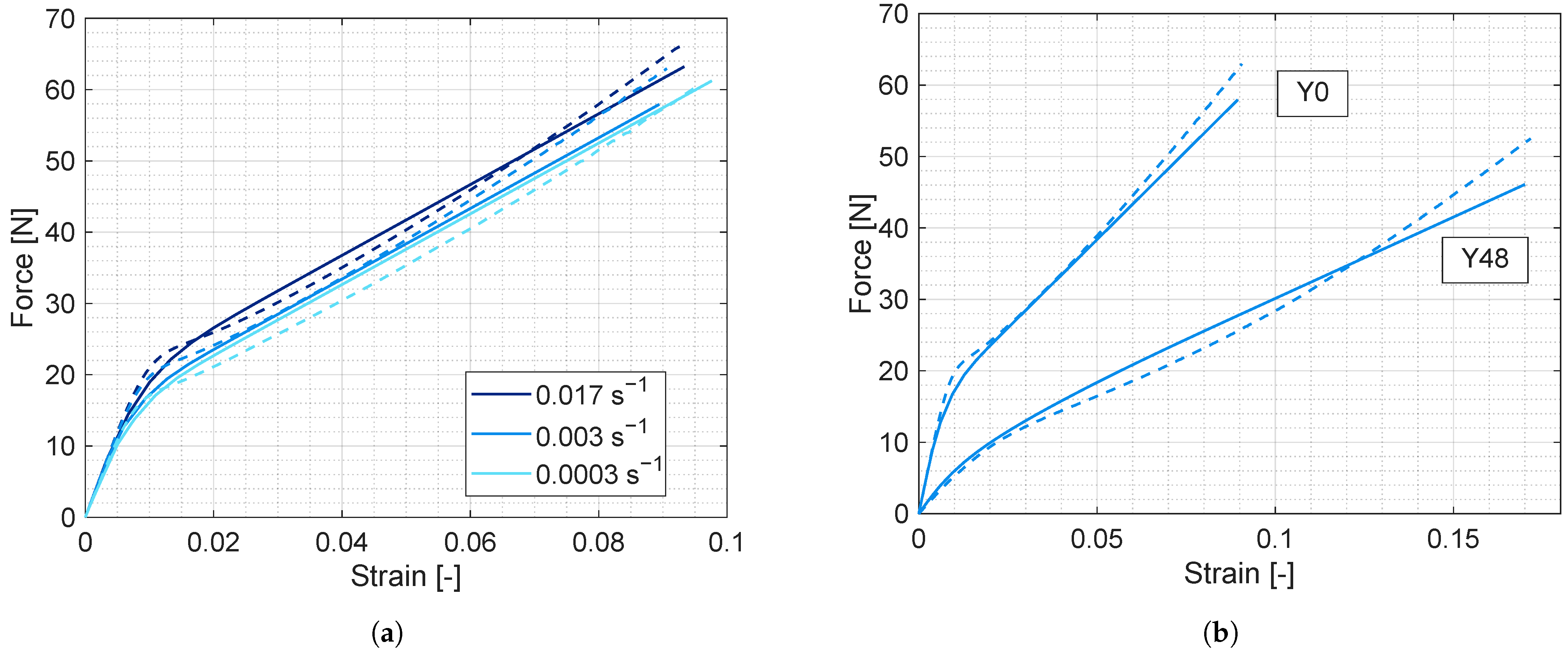
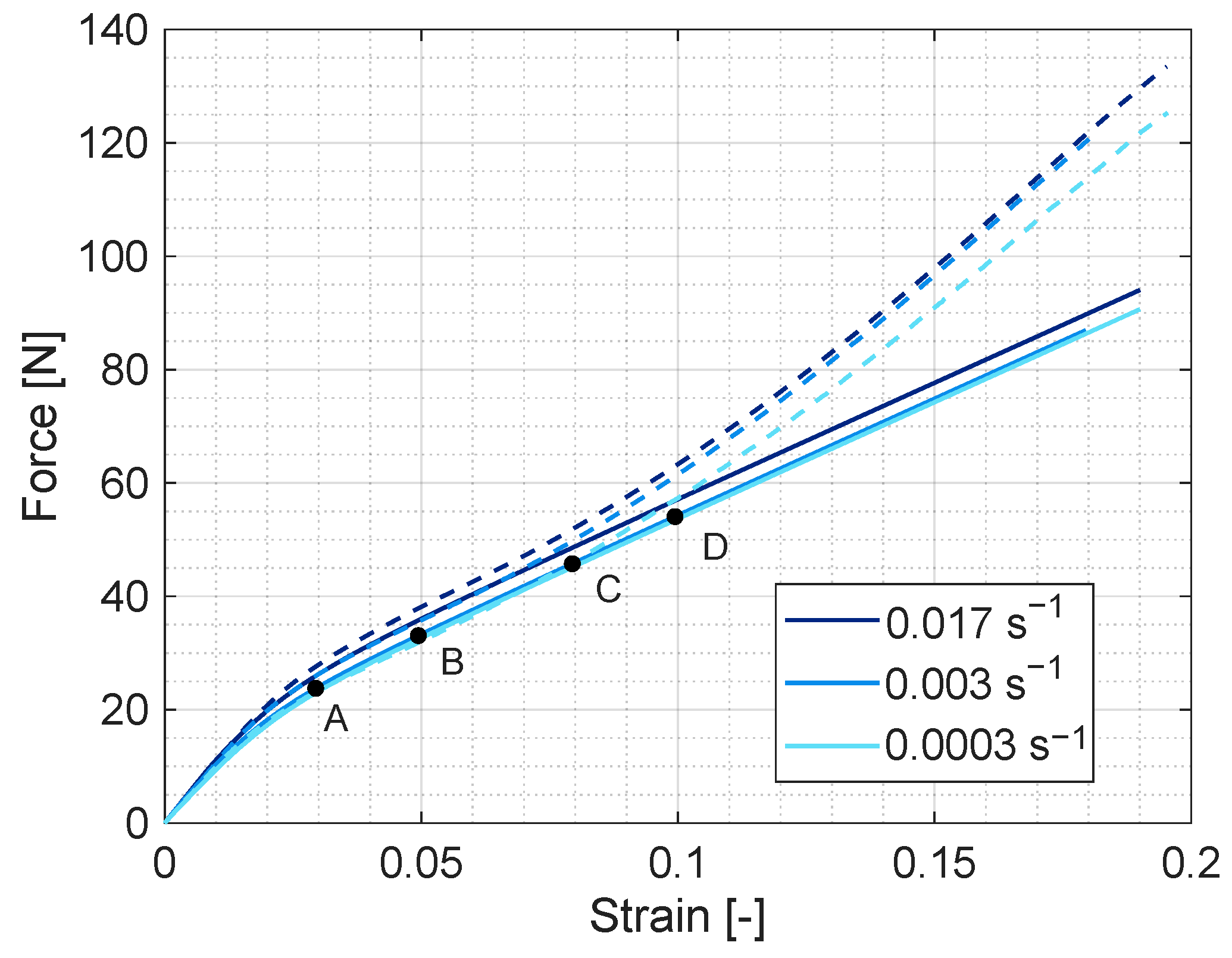
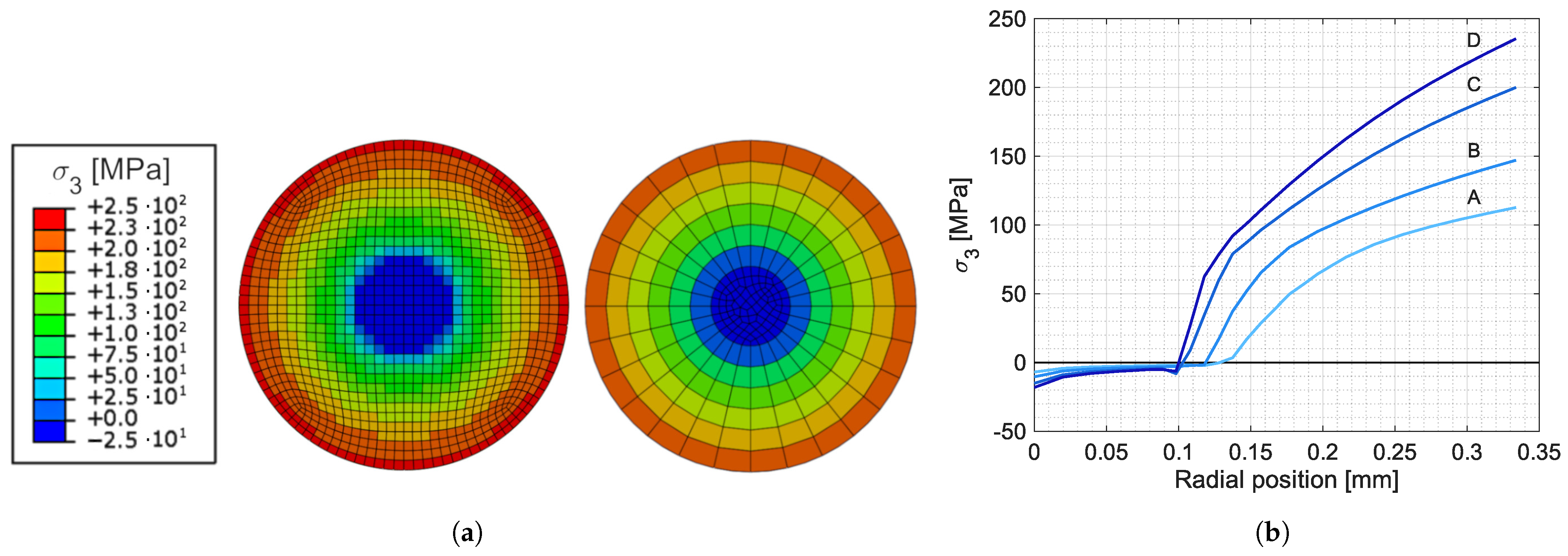
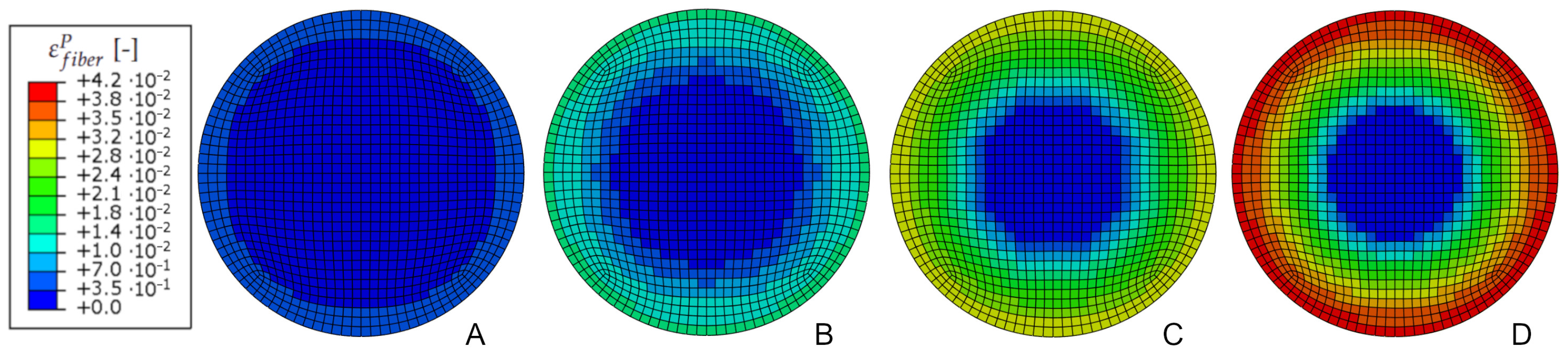
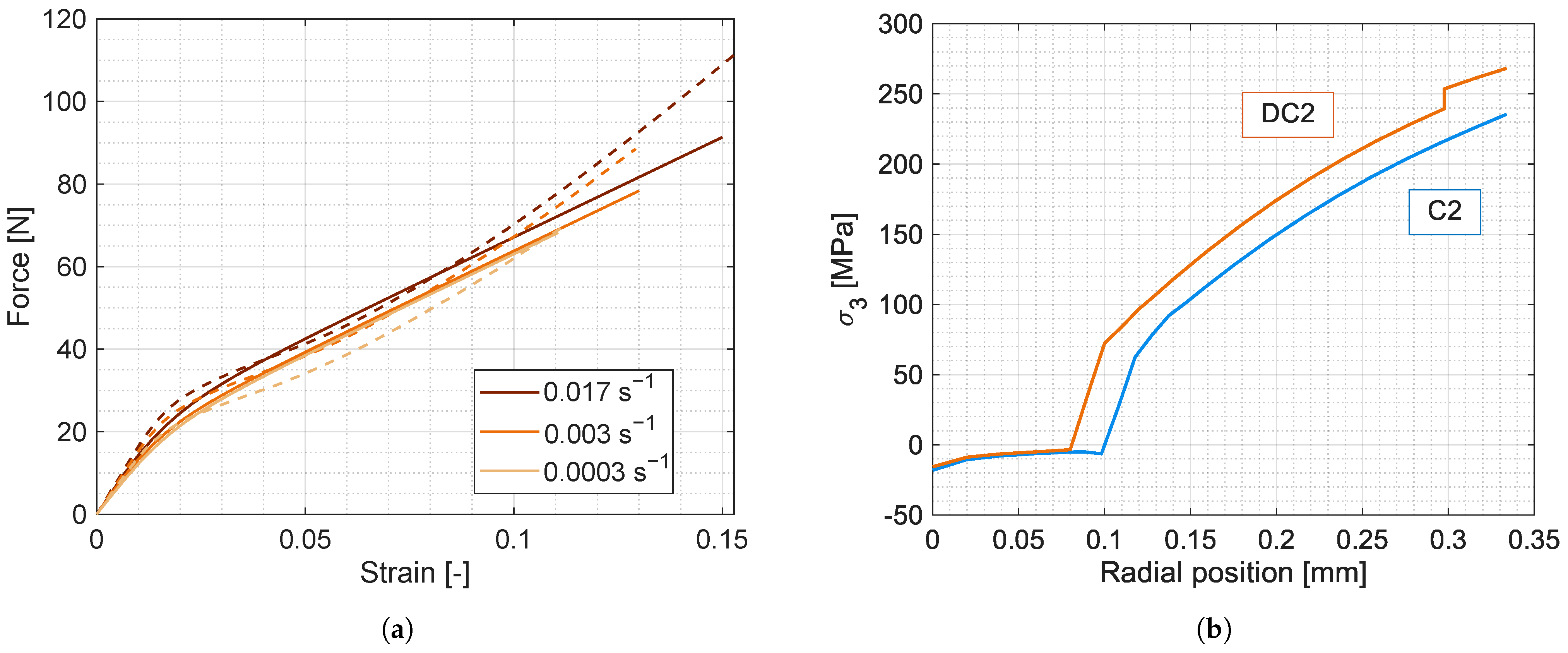
3.1. Model Calibration on Uniaxial Tensile Tests on Yarns
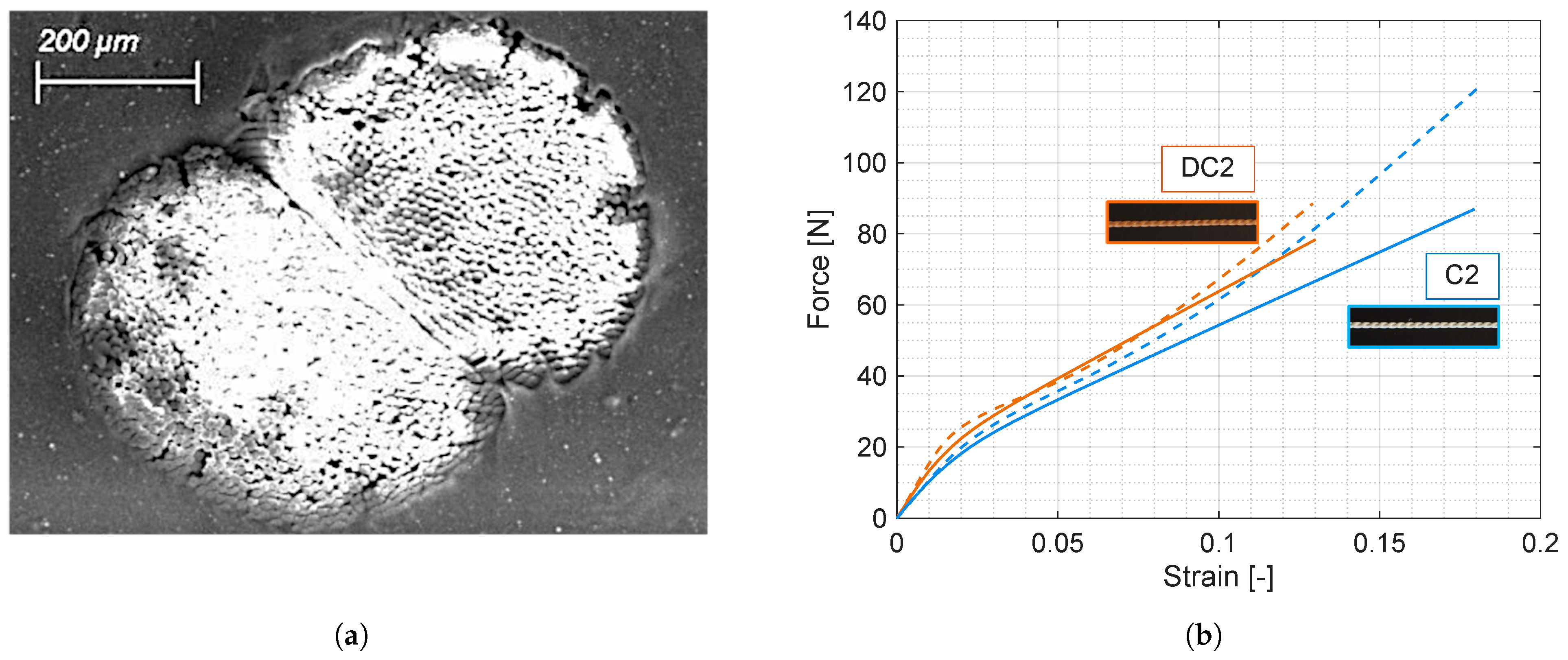
3.2. Tensile Tests on Two-Ply Greige and Dipped Cords
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Y0 | Untwisted yarn |
| Y48 | Yarn with 480 turns per meter |
| C2 | Cord made of two yarns Y48 |
| DC2 | Dipped cord C2 |
References
- Rodgers, B. Tire Engineering: An Introduction, 1st ed.; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Willett, P.R. Viscoelastic Properties of Tire Cords. J. Appl. Polym. Sci. 1975, 19, 2005–2014. [Google Scholar] [CrossRef]
- Aytaç, A.; Yilmaz, B.; Deniz, V. Nylon 66/Polyester Hybrid Cords: 1. Design and Investigation of Properties. Fibers Polym. 2011, 12, 252–257. [Google Scholar] [CrossRef]
- Yilmaz, B. Aramid-nylon 6.6 hybrid cords and investigation of their properties. Rubber Chem. Technol. 2012, 85, 180–194. [Google Scholar] [CrossRef]
- Bogusz, P.; Miedzińska, D.; Wieczorek, M. Experimental Investigation of the Tensile Behavior of Selected Tire Cords Using Novel Testing Equipment. Materials 2022, 15, 4163. [Google Scholar] [CrossRef] [PubMed]
- Krmela, J.; Michna, M.; Růžička, Z.; Krmelová, V.; Artyukhov, A. Cyclic Testing of Polymer Composites and Textile Cords for Tires. Polymers 2023, 15, 2358. [Google Scholar] [CrossRef] [PubMed]
- Caracino, P.; Agresti, S.; Pires da Costa, L.; Novati, G.; Comi, C. The nonlinear behaviour of cords to be used in rayon-rubber composites. In Constitutive Models for Rubber XII; Marano, C., Briatico Vangosa, F., Andena, L., Frassine, R., Eds.; CRC Press: London, UK, 2022; pp. 472–476. [Google Scholar] [CrossRef]
- Pires da Costa, L.; Novati, G.; Caracino, P.; Comi, C.; Agresti, S. Tensile behaviour of rayon cords in different conditions. Mater. Res. Proc. 2023, 26, 133–1388. [Google Scholar] [CrossRef]
- Meschke, G.; Helnwein, P. Computational Mechanics Large-strain 3D-analysis of fibre-reinforced composites using rebar elements: Hyperelastic formulations for cords. Comput. Mech. 1994, 13, 241–254. [Google Scholar] [CrossRef]
- Korunović, N.; Fragassa, C.; Marinković, D.; Vitković, N.; Trajanović, M. Performance evaluation of cord material models applied to structural analysis of tires. Compos. Struct. 2019, 224, 111006. [Google Scholar] [CrossRef]
- Weiser, S.; Lehmann, T.; Landgraf, R.; Goldberg, N.; Donner, H.; Ihlemann, J. Experimental and numerical analysis of cord–elastomer composites. J. Rubber Res. 2021, 24, 211–225. [Google Scholar] [CrossRef]
- Bedzra, R.; Reese, S.; Simon, J.W. Hierarchical multi-scale modelling of flax fibre/epoxy composite by means of general anisotropic viscoelastic-viscoplastic constitutive models: Part I—Micromechanical model. Int. J. Solids Struct. 2020, 202, 58–74. [Google Scholar] [CrossRef]
- Moscatelli, M.; Pires da Costa, L.; Caracino, P.; Agresti, S.; Novati, G.; Comi, C. Elasto-viscoplastic model for rayon yarns. Meccanica 2024, 1–18. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990; Volume 1, pp. 1–462. [Google Scholar] [CrossRef]
- Yeoh, O.H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Marlow, R.; Busfield, J.; Muhr, A. A general first-invariant hyperelastic constitutive model. In Proceedings of the 3rd European Conference on Constitutive Models for Rubber, London, UK, 15–17 September 2003; pp. 157–160. [Google Scholar]
- Sibellas, A.; Adrien, J.; Durville, D.; Maire, E. Experimental study of the fiber orientations in single and multi-ply continuous filament yarns. J. Text. Inst. 2020, 111, 646–659. [Google Scholar] [CrossRef]
- Treloar, L. The geometry of multi-ply yarns. J. Text. Inst. Trans. 1956, 47, T348–T368. [Google Scholar] [CrossRef]
- Jeon, B.S.; Kim, Y.J. Orientation Density Function of Ply yarn. Text. Res. J. 2010, 80, 1550–1556. [Google Scholar] [CrossRef]
- Curnier, A.; He, Q.C.; Zysset, P. Conewise linear elastic materials. J. Elast. 1995, 37, 1–38. [Google Scholar] [CrossRef]
- Bert, C.W. Models for Fibrous Composites with Different Properties in Tension and Compression. J. Eng. Mater. Technol. 1977, 99, 344–349. [Google Scholar] [CrossRef]


| [MPa] | [MPa] | [MPa] | [-] | [-] | [MPa] | [-] |
| 170 | 14,500 | 48.3 | 0 | 0 | 10 | 4.00 |
| [s] | [MPa] | [MPa] | [MPa] | h [MPa] | B [-] | [s MPa] |
| 2.50 | 60 | 2700 | 40,000 | 1200 | 1000 | 2000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pires da Costa, L.; Moscatelli, M.; Caracino, P.; Novati, G.; Comi, C. Geometrical and Mechanical Modeling of Polymeric Multi-Ply Yarns. Appl. Sci. 2024, 14, 4597. https://doi.org/10.3390/app14114597
Pires da Costa L, Moscatelli M, Caracino P, Novati G, Comi C. Geometrical and Mechanical Modeling of Polymeric Multi-Ply Yarns. Applied Sciences. 2024; 14(11):4597. https://doi.org/10.3390/app14114597
Chicago/Turabian StylePires da Costa, Lucas, Marco Moscatelli, Paola Caracino, Giorgio Novati, and Claudia Comi. 2024. "Geometrical and Mechanical Modeling of Polymeric Multi-Ply Yarns" Applied Sciences 14, no. 11: 4597. https://doi.org/10.3390/app14114597
APA StylePires da Costa, L., Moscatelli, M., Caracino, P., Novati, G., & Comi, C. (2024). Geometrical and Mechanical Modeling of Polymeric Multi-Ply Yarns. Applied Sciences, 14(11), 4597. https://doi.org/10.3390/app14114597







