Experimental Study on the Mechanical Properties of Deep Granite under Gradient-Confining Pressure
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen Preparation
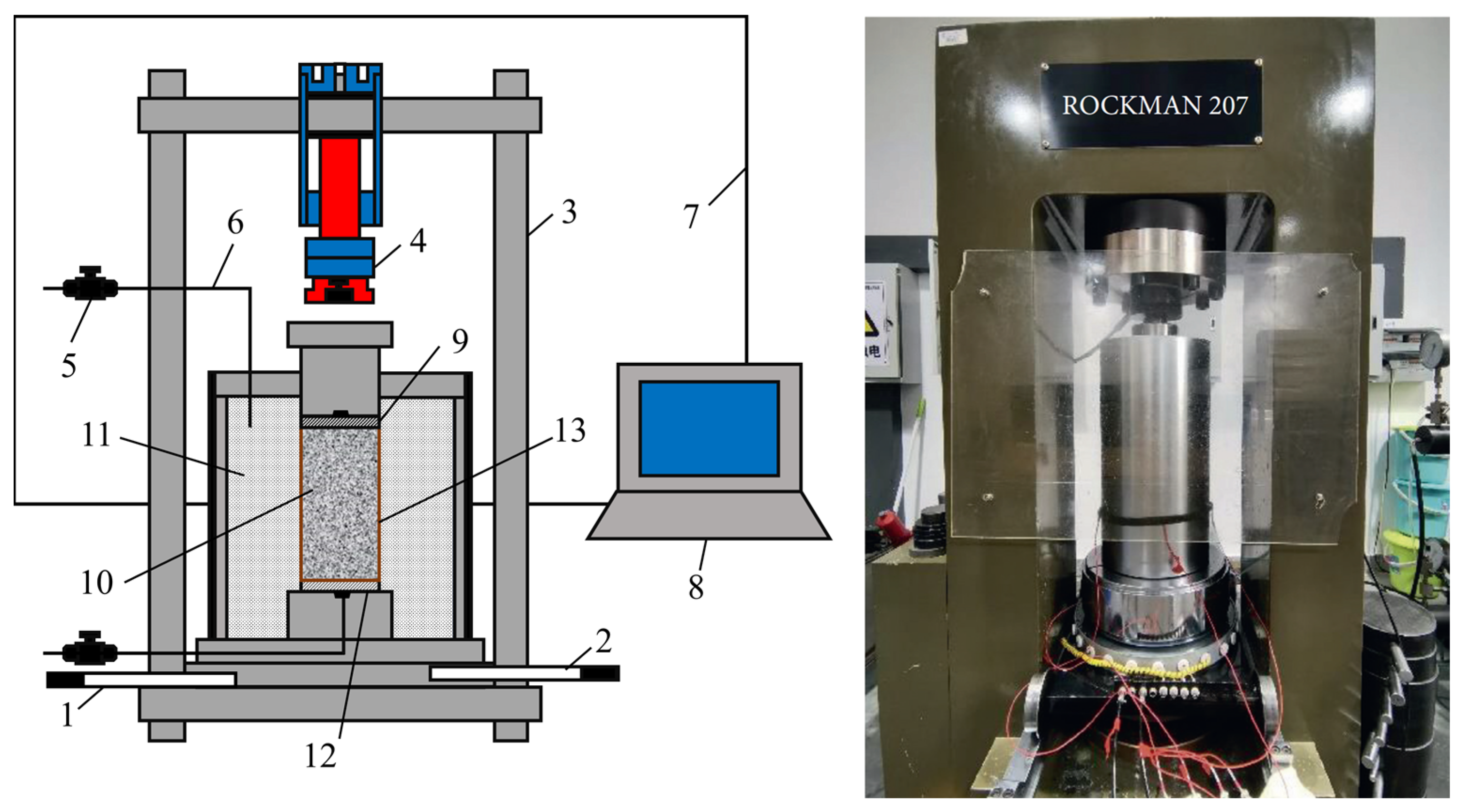
2.2. Testing Equipment
2.3. Test Scheme
3. Results and Discussion
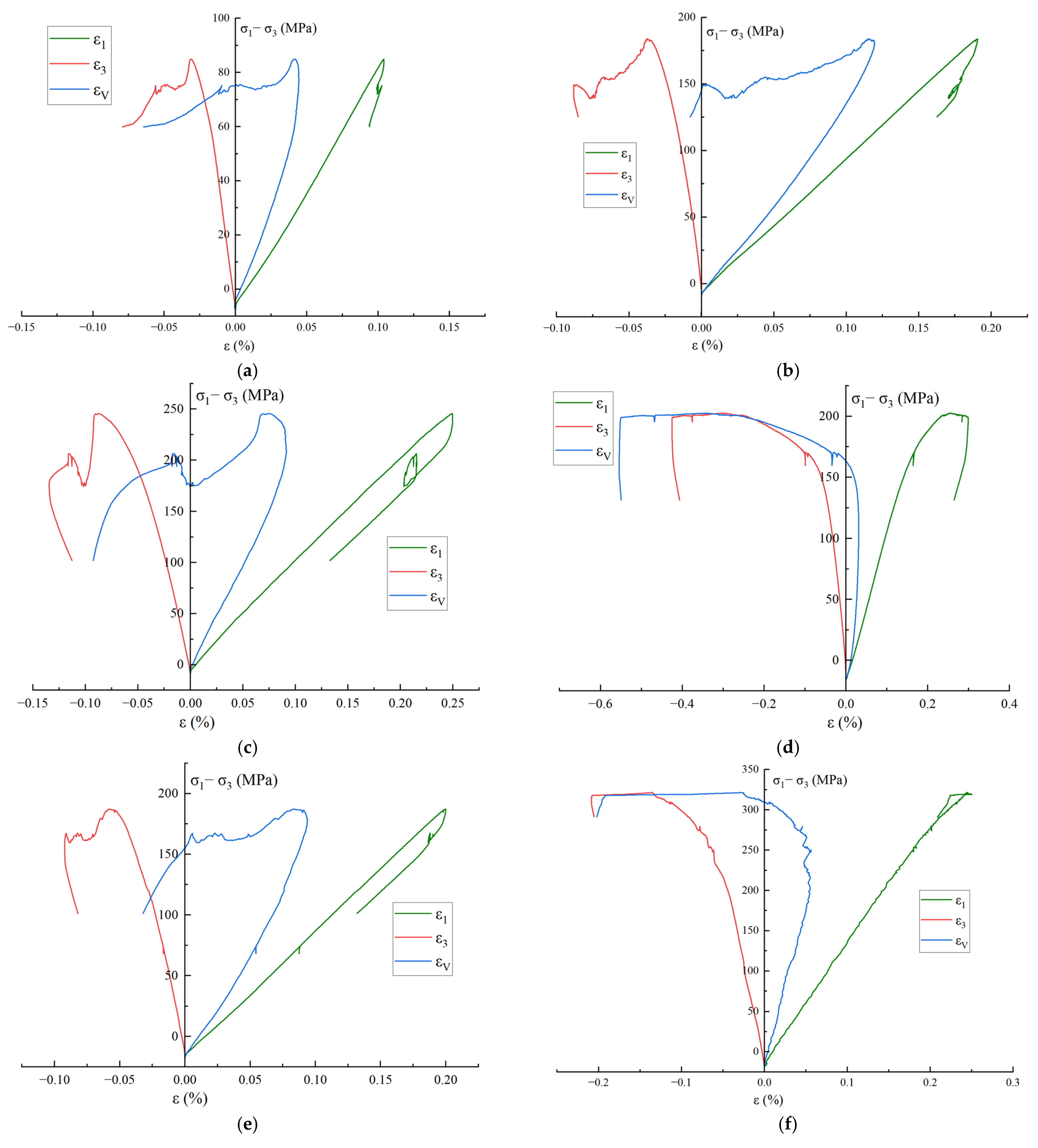
3.1. Rock Mechanical Properties and Failure Morphology
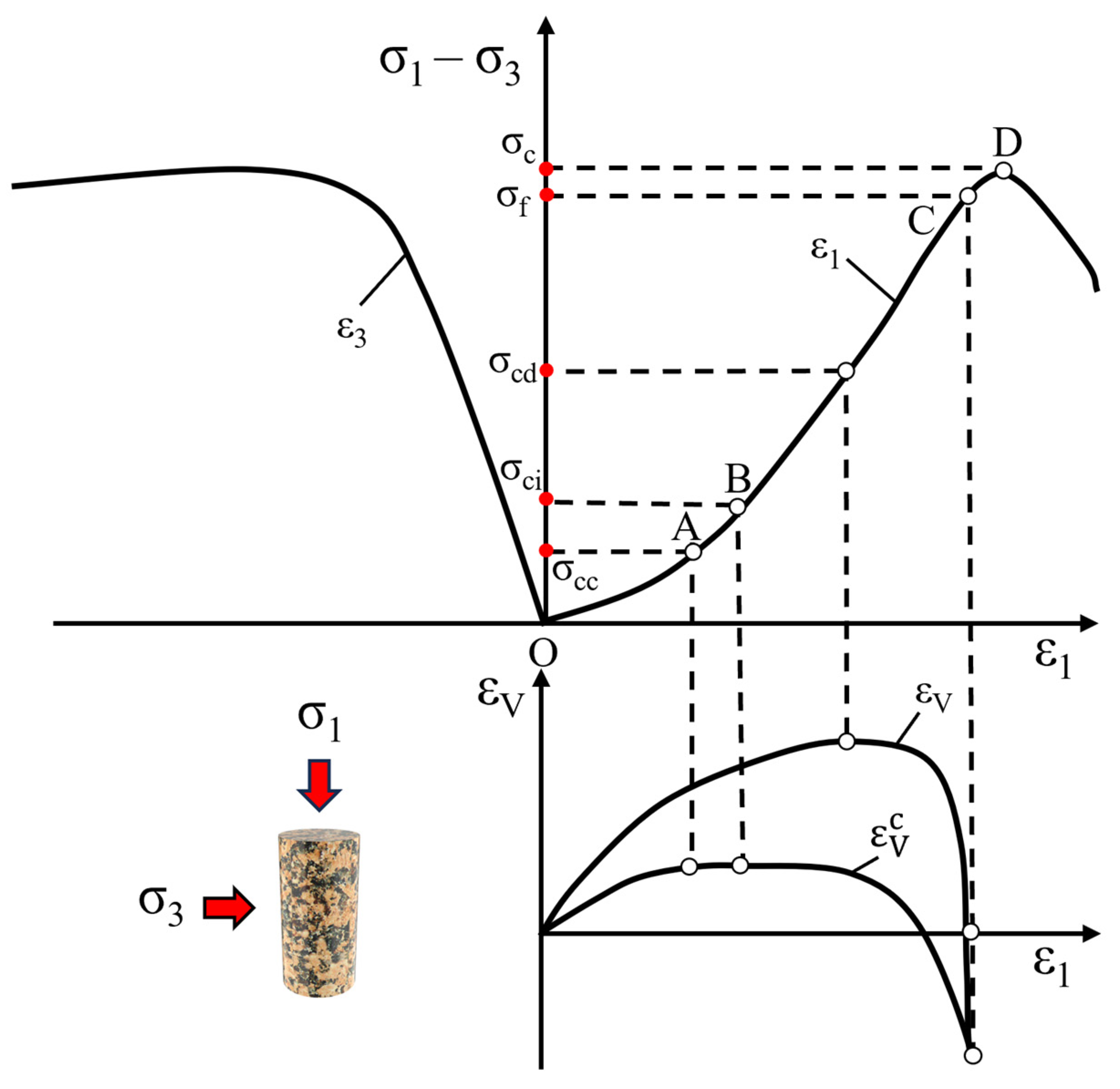
3.2. Stress-Strain Curves and Characteristic Stresses
- Restrict the fracture of the rock: the increase in the confining pressure enables the rock to receive more lateral constraints, reducing the potential for crack expansion and fracture within the rock.
- The increase in the integrity of the rock contributes to enhancing the overall strength of the rock.
- Alter the internal stress state of the rock: the stress distribution within the rock becomes more uniform, thereby enhancing the bearing capacity of the rock.
- Suppressing the brittle failure of the rock: this approach enables the rock to exhibit more plastic properties and reduces its tendency towards brittle failure.
- Augment the stability of the rock: Enhance the stability of the rock under the condition of being under force.
- The microstructure of the rock may change due to changes in the microstructure within the rock, thereby influencing its mechanical properties.
4. FEM Numerical Simulation Analysis
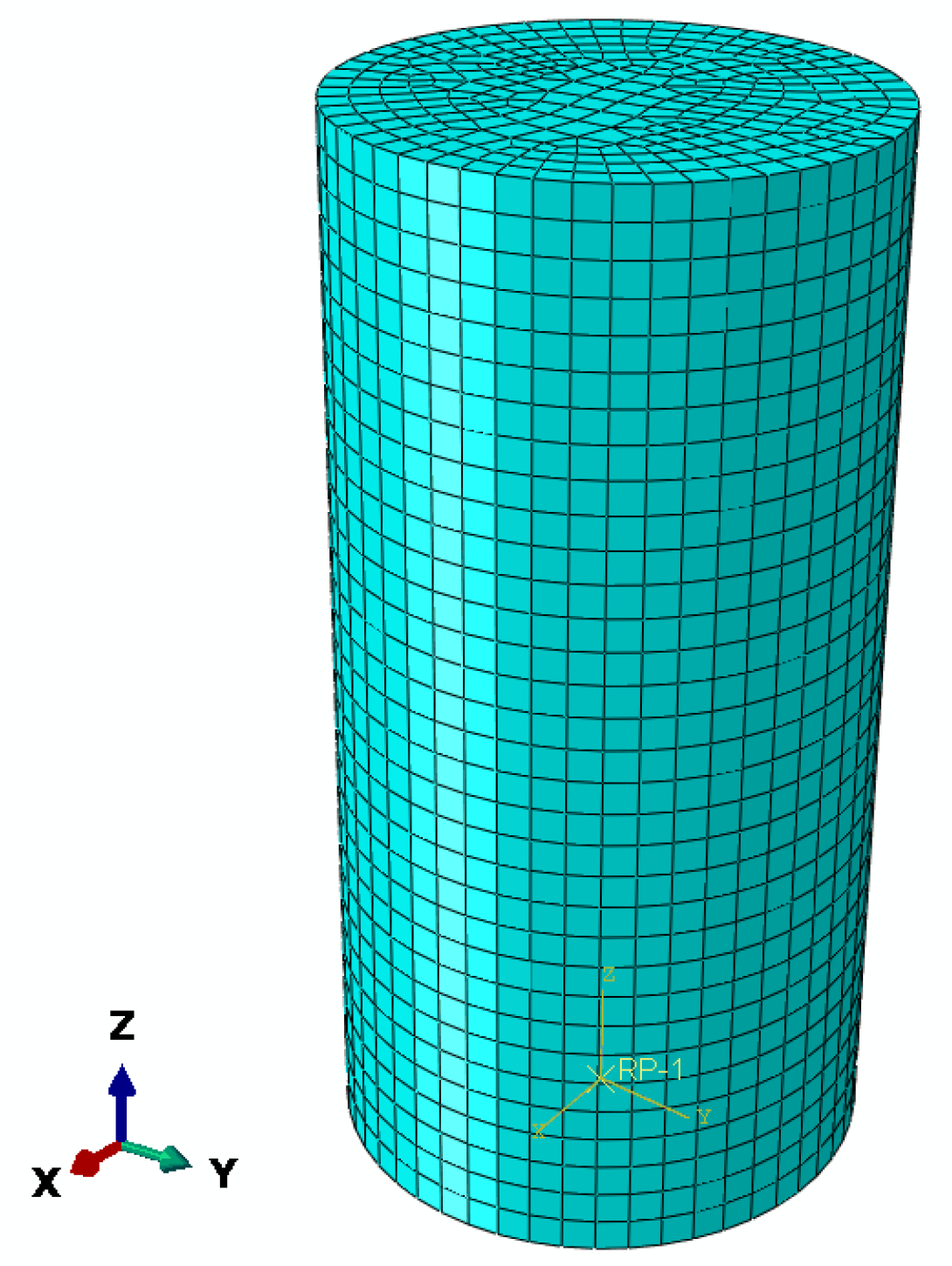
4.1. Model Establishment
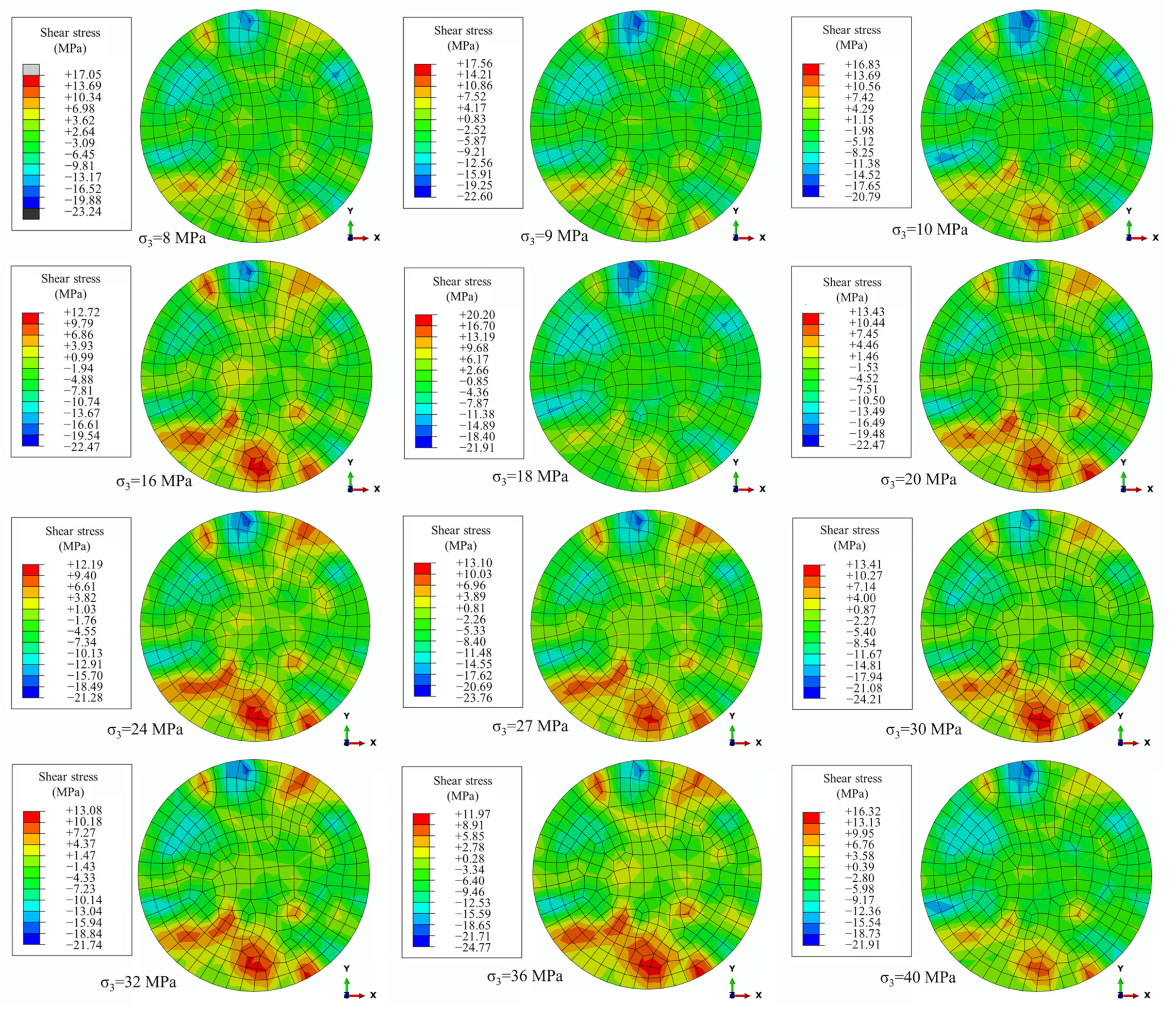
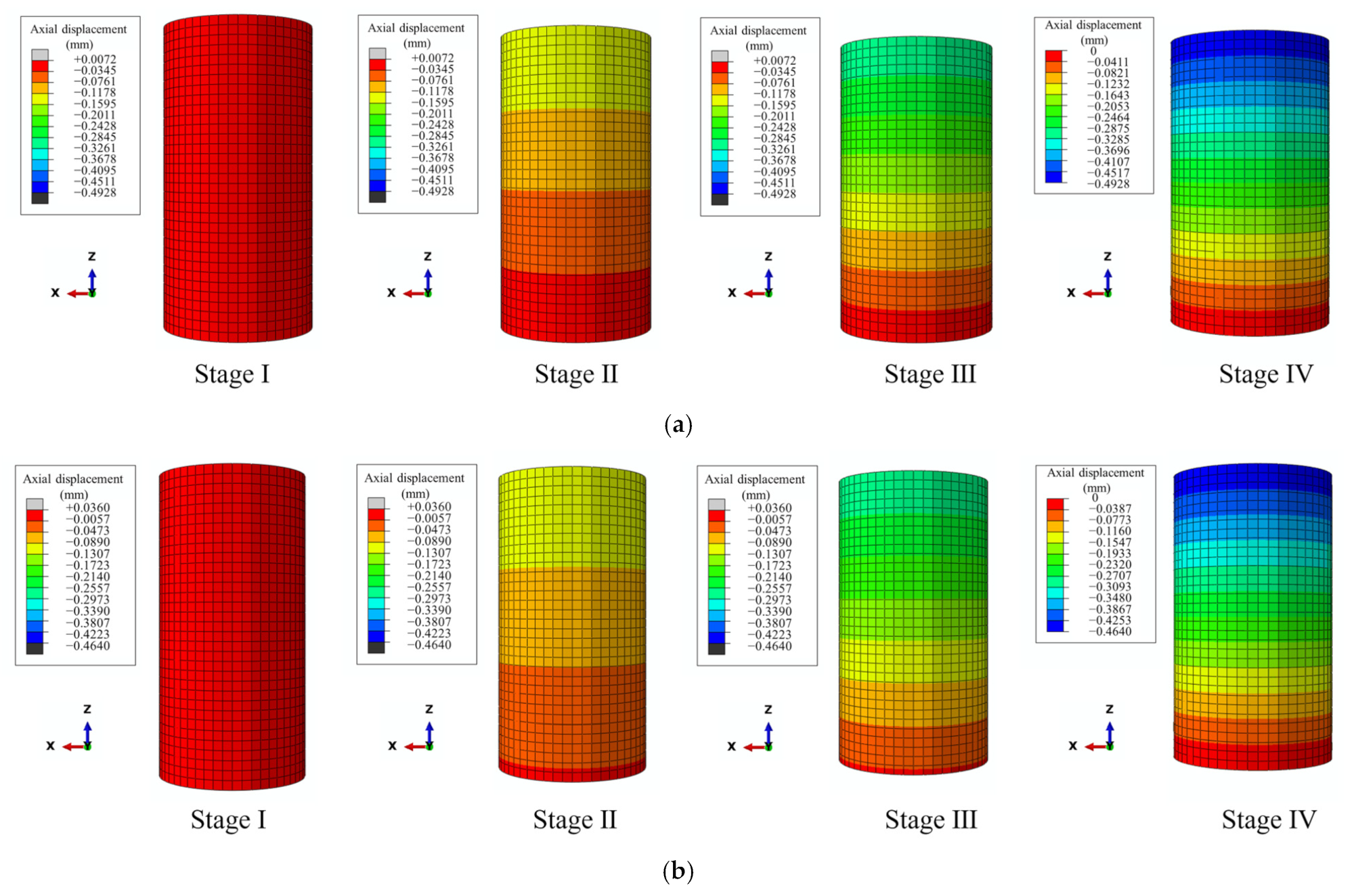
4.2. Analysis of Simulation Outcomes
5. Conclusions
- Owing to its peculiar and complex geological environment, under gradient-confining pressure, the elastic modulus, Poisson’s ratio, and peak strength of the deep granite present a greater degree of dispersion than those of the shallow granite.
- The characteristic stress of the deep granite exhibits an evident exponential function distribution under the gradient-confining pressure, which indicates that the greater the confining pressure is, the greater the characteristic stress and the faster the growth rate.
- The results of the numerical simulation indicate that in the conventional triaxial compression test, there is a marked shear stress concentration in the radial direction of the specimen, and with increasing confining pressure, the range of the shear stress concentration correspondingly expands. The axial deformation of the specimen decreases from both ends to the middle, there is a distinct layered distribution, and the layered distribution effect becomes weaker with increasing confining pressure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, R.H.; Cao, P.; Lin, H.; Fan, X.; Zhang, C.Y.; Liu, T.Y. Crack Initiation, Propagation, and Failure Characteristics of Jointed Rock or Rock-Like Specimens: A Review. Adv. Civ. Eng. 2019, 2019, 6975751. [Google Scholar] [CrossRef]
- Crampin, S.; Yuan, G. A review of the New Geophysics: A new understanding of pre-fracturing deformation in the crack-critical crust with implications for hydrocarbon production. Pet. Sci. 2008, 5, 1–12. [Google Scholar] [CrossRef]
- Brantut, N.; Heap, M.J.; Meredith, P.G.; Baud, P. Time-dependent cracking and brittle creep in crustal rocks: A review. J. Struct. Geol. 2013, 52, 17–43. [Google Scholar] [CrossRef]
- Zha, E.S.; Zhang, R.; Zhang, Z.T.; Ren, L.; Zhang, W.J.; Jia, Z.Q.; Liu, Y. Long-term creep behavior of deep-buried marble under different confining pressures. Therm. Sci. 2019, 23, S653–S660. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Ge, S.; Malekian, R.; Li, Z. Numerical simulation of rock fragmentation during cutting by conical picks under confining pressure. Comptes Rendus Mec. 2017, 345, 890–902. [Google Scholar] [CrossRef]
- Xie, H.; Lu, J.; Li, C.; Li, M.; Gao, M. Experimental study on the mechanical and failure behaviors of deep rock subjected to true triaxial stress: A review. Int. J. Min. Sci. Technol. 2022, 32, 915–950. [Google Scholar] [CrossRef]
- Diering, D.H. Ultra-deep level mining—Future requirements. J. S. Afr. Inst. Min. Metall. 1997, 97, 249–255. [Google Scholar]
- Schweitzer, J.K.; Johnson, R.A. Geotechnical classification of deep and ultra-deep Witwatersrand mining areas, South Africa. Miner. Depos. 1997, 32, 335–348. [Google Scholar] [CrossRef]
- Robb, L.J.; Meyer, F.M.; Hawkesworth, C.J.; Gardiner, N.J. Petrogenesis of Archaean granites in the Barberton region of South Africa as a guide to early crustal evolution. S. Afr. J. Geol. 2021, 124, 111–140. [Google Scholar] [CrossRef]
- Witt, W.K.; Davy, R. Geology and geochemistry of Archaean granites in the Kalgoorlie region of the eastern goldfields, Western Australia: A syn-collisional tectonic setting? Precambrian Res. 1997, 83, 133–183. [Google Scholar] [CrossRef]
- Zhao, K.D.; Jiang, S.Y.; Nakamura, E.; Moriguti, T.; Palmer, M.R.; Yang, S.Y.; Dai, B.Z.; Jiang, Y.H. Fluid-rock interaction in the Qitianling granite and associated tin deposits, South China: Evidence from boron and oxygen isotopes. Ore Geol. Rev. 2011, 43, 243–248. [Google Scholar] [CrossRef]
- Min, M.Z.; Luo, X.Z.; Du, G.S.; He, B.A.; Campbell, A.R. Mineralogical and geochemical constraints on the genesis of the granite-hosted Huangao uranium deposit, SE China. Ore Geol. Rev. 1999, 14, 105–127. [Google Scholar] [CrossRef]
- Zhang, S.S.; Yang, X.Y.; Liu, L. Evolution, Magmatic Source and Metallogenesis of A-Type Granites in the Fanchang Volcanic Basin, Middle and Lower Yangtze Metallogenic Belt: A Review. Minerals 2023, 13, 571. [Google Scholar] [CrossRef]
- Phelps, P.R.; Lee, C.-T.A.; Morton, D.M. Episodes of fast crystal growth in pegmatites. Nat. Commun. 2020, 11, 4986. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Kemeny, J.; Tan, Y.; Song, W.; Huang, K. Mechanical properties and fracturing of rock-backfill composite specimens under triaxial compression. Constr. Build. Mater. 2021, 304, 124577. [Google Scholar] [CrossRef]
- Tian, Y.K.; Weijermars, R.; Zhou, F.J.; Hu, L.Q.; Liu, T.Y.; Liu, H.T. Advances in stress-strain constitutive models for rock failure: Review and new dynamic constitutive failure (DCF) model using core data from the Tarim Basin (China). Earth-Sci. Rev. 2023, 243, 104473. [Google Scholar] [CrossRef]
- Guo, X.F.; Zhao, Z.Q.; Gao, X.; Wu, X.Y.; Ma, N.J. Analytical solutions for characteristic radii of circular roadway surrounding rock plastic zone and their application. Int. J. Min. Sci. Technol. 2019, 29, 263–272. [Google Scholar] [CrossRef]
- Hu, X.D.; Song, X.Z.; Liu, Y.; Cheng, Z.; Ji, J.Y.; Shen, Z.H. Experiment investigation of granite damage under the high-temperature and high-pressure supercritical water condition. J. Pet. Sci. Eng. 2019, 180, 289–297. [Google Scholar] [CrossRef]
- Yin, W.T.; Feng, Z.J.; Zhao, Y.S. Effect of Grain Size on the Mechanical Behaviour of Granite Under High Temperature and Triaxial Stresses. Rock Mech. Rock Eng. 2021, 54, 745–758. [Google Scholar] [CrossRef]
- Sun, Q.; Hu, J.J. The effect of rapid cooling on the thermal diffusivity of granite. J. Appl. Geophys. 2019, 168, 71–78. [Google Scholar] [CrossRef]
- Nara, Y. Effect of Anisotropy on the Long-Term Strength of Granite. Rock Mech. Rock Eng. 2015, 48, 959–969. [Google Scholar] [CrossRef]
- Zhao, F.; Shi, Z.M.; Sun, Q. Fracture Mechanics Behavior of Jointed Granite Exposed to High Temperatures. Rock Mech. Rock Eng. 2021, 54, 2183–2196. [Google Scholar] [CrossRef]
- Zhu, Z.N.; Tian, H.; Mei, G.; Jiang, G.S.; Dou, B.; Xiao, P. Experimental investigation on mechanical behaviors of Nanan granite after thermal treatment under conventional triaxial compression. Environ. Earth Sci. 2021, 80, 46. [Google Scholar] [CrossRef]
- Dongjie, Y.; Jianhua, H.; Shaowei, M.; Pingping, Z. Analysis of dynamic fracture of granite after uniaxial recompression predamaged by high confining pressure cyclic loading based on acoustic emission. Eng. Fract. Mech. 2022, 266, 108414. [Google Scholar] [CrossRef]
- Peng, K.; Lv, H.; Zou, Q.L.; Wen, Z.J.; Zhang, Y.J. Evolutionary characteristics of mode-I fracture toughness and fracture energy in granite from different burial depths under high-temperature effect. Eng. Fract. Mech. 2020, 239, 107306. [Google Scholar] [CrossRef]
- Li, X.F.; Wu, D.; Wu, M.X. Creep characteristics and fractional rheological model of granite under temperature and disturbance load coupling. Mech. Time-Depend. Mater. 2023, 28, 81–98. [Google Scholar] [CrossRef]
- Luo, Y.; Gong, H.L.; Huang, J.H.; Wang, G.; Li, X.P.; Wan, S. Dynamic cumulative damage characteristics of deep-buried granite from Shuangjiangkou hydropower station under true triaxial constraint. Int. J. Impact Eng. 2022, 165, 104215. [Google Scholar] [CrossRef]
- Du, R.F.; Pei, X.J.; Jia, J.; Zhang, X.C.; Gao, M.B.; Li, T.T.; Zhang, G.H. A novel observation method for determining the crack stress thresholds of rock based on Hooke’s law. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 3050–3062. [Google Scholar] [CrossRef]


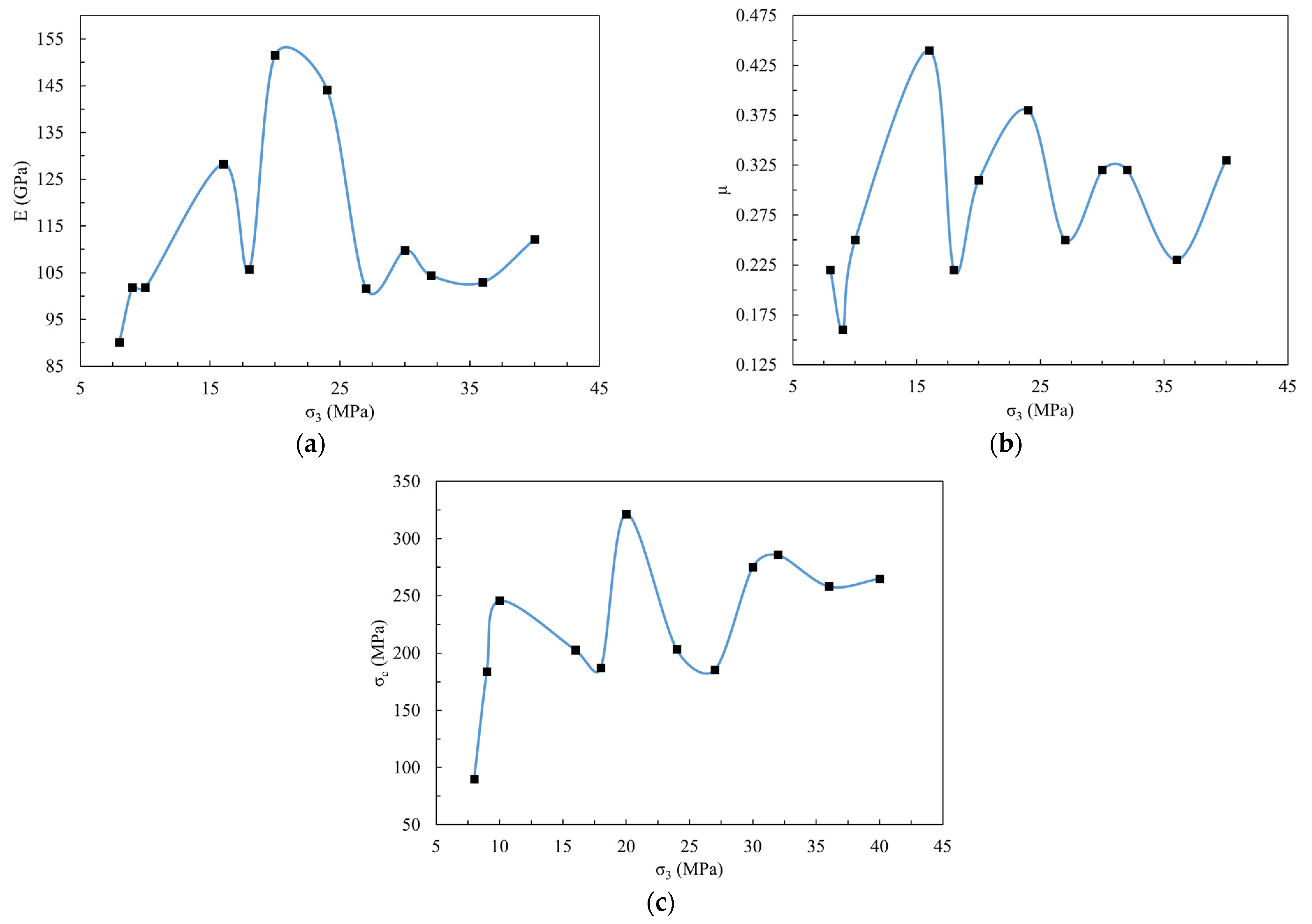

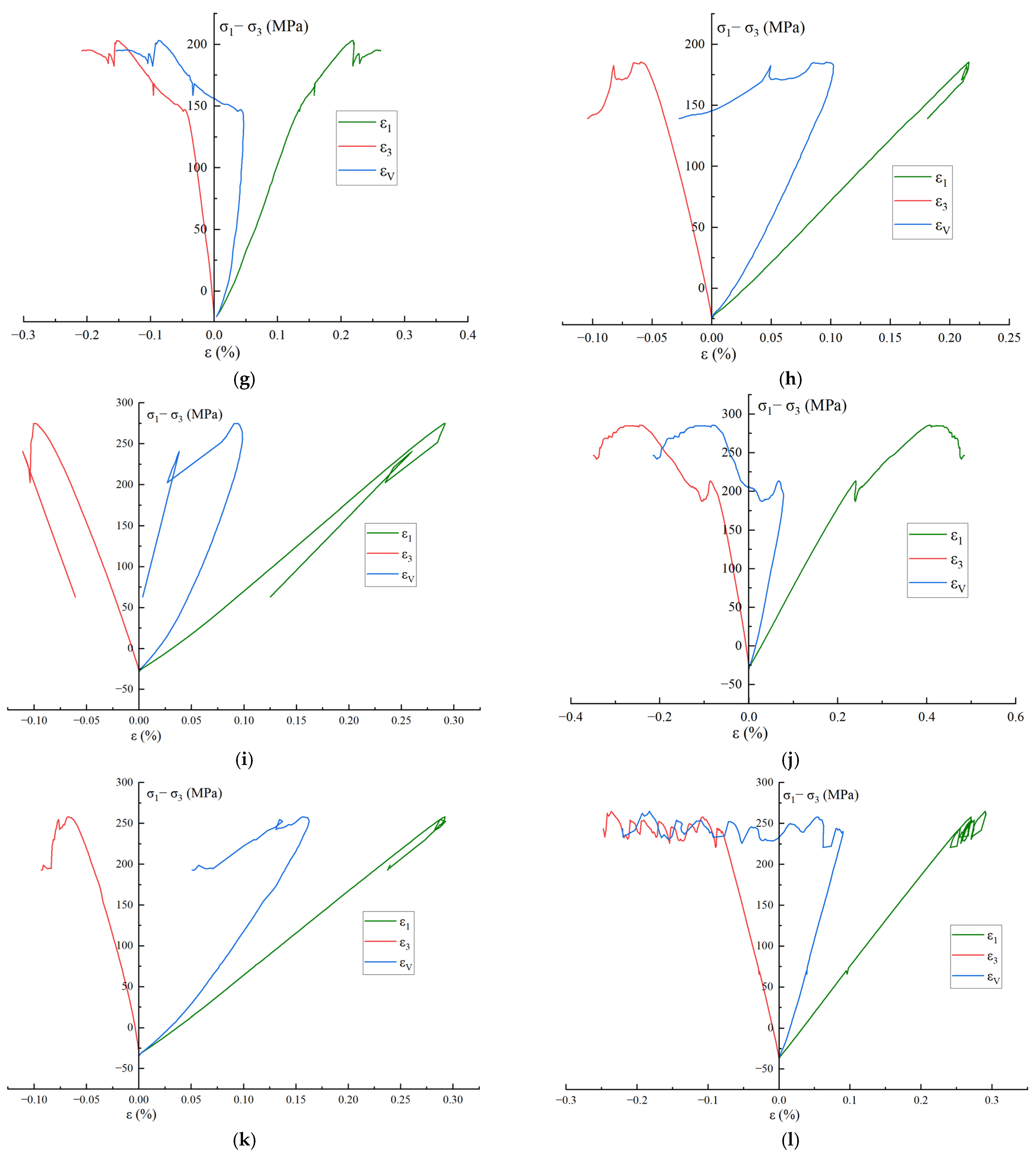
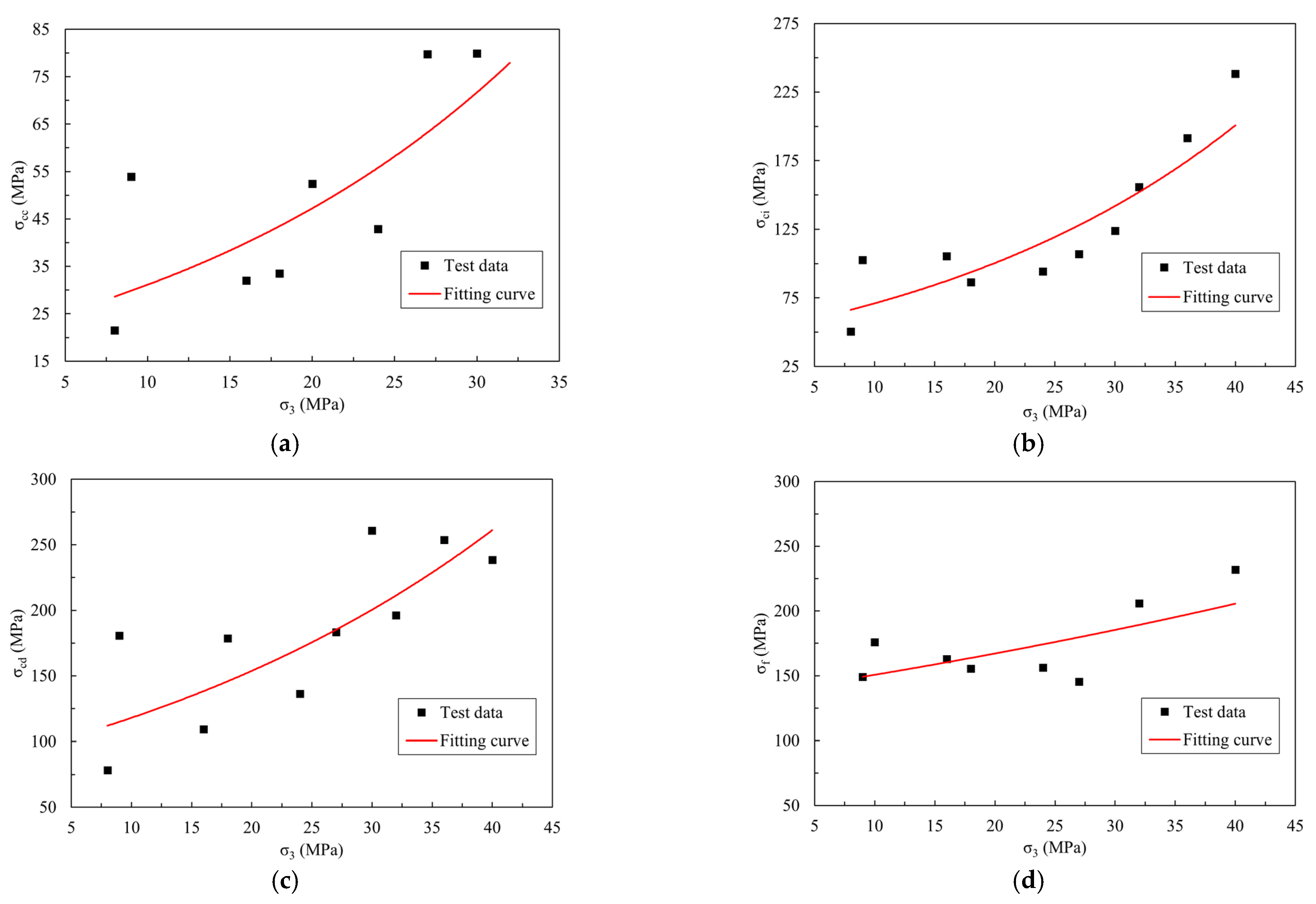
| σ3 (MPa) | E (GPa) | μ | σc (MPa) |
|---|---|---|---|
| 8 | 90.08 | 0.22 | 89.71 |
| 9 | 101.77 | 0.16 | 183.77 |
| 10 | 101.79 | 0.25 | 245.59 |
| 16 | 128.25 | 0.44 | 202.62 |
| 18 | 105.70 | 0.22 | 187.31 |
| 20 | 151.48 | 0.31 | 321.54 |
| 24 | 144.09 | 0.38 | 203.23 |
| 27 | 101.63 | 0.25 | 185.41 |
| 30 | 109.72 | 0.32 | 274.95 |
| 32 | 104.39 | 0.32 | 285.64 |
| 36 | 102.91 | 0.23 | 258.18 |
| 40 | 112.17 | 0.33 | 264.93 |
| σ3 (MPa) | σcc (MPa) | σci (MPa) | σcd (MPa) | σf (MPa) |
|---|---|---|---|---|
| 8 | 21.51 | 50.36 | 78.31 | 75.50 |
| 9 | 53.88 | 102.70 | 180.78 | 149.09 |
| 10 | 64.85 | 137.63 | 209.90 | 175.82 |
| 16 | 32.01 | 105.33 | 109.31 | 162.98 |
| 18 | 33.49 | 86.37 | 178.47 | 155.40 |
| 20 | 115.69 | 194.05 | 250.10 | 309.61 |
| 24 | 52.40 | 94.25 | 136.32 | 156.14 |
| 27 | 42.85 | 106.87 | 183.31 | 145.30 |
| 30 | 79.71 | 123.79 | 260.85 | 63.14 |
| 32 | 15.37 | 155.85 | 196.09 | 206.00 |
| 36 | 79.92 | 191.43 | 253.80 | — |
| 40 | 47.58 | 238.32 | 238.46 | 231.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, S.; Zhao, X.; Yu, W.; Song, J.; Wu, T. Experimental Study on the Mechanical Properties of Deep Granite under Gradient-Confining Pressure. Appl. Sci. 2024, 14, 4598. https://doi.org/10.3390/app14114598
Qin S, Zhao X, Yu W, Song J, Wu T. Experimental Study on the Mechanical Properties of Deep Granite under Gradient-Confining Pressure. Applied Sciences. 2024; 14(11):4598. https://doi.org/10.3390/app14114598
Chicago/Turabian StyleQin, Shaolong, Xingdong Zhao, Wenlong Yu, Jingyi Song, and Tong Wu. 2024. "Experimental Study on the Mechanical Properties of Deep Granite under Gradient-Confining Pressure" Applied Sciences 14, no. 11: 4598. https://doi.org/10.3390/app14114598
APA StyleQin, S., Zhao, X., Yu, W., Song, J., & Wu, T. (2024). Experimental Study on the Mechanical Properties of Deep Granite under Gradient-Confining Pressure. Applied Sciences, 14(11), 4598. https://doi.org/10.3390/app14114598





