Period-1 Motions and Bifurcations of a 3D Brushless DC Motor System with Voltage Disturbance

Abstract

In this paper, the nonlinear dynamic system of a brushless DC motor with voltage disturbance is studied analytically via a generalized harmonic balance method. A truncated Fourier series with time-varying coefficients is utilized to represent the analytical variations of nonlinear currents and voltages within this dynamic system. Bifurcations of periodic currents and voltages are obtained, and their stability is discussed through eigenvalue analysis. The frequency–amplitude characteristics of periodic currents and voltages exhibit complexity in the frequency domain. Comparative illustrations are provided to contrast the analytical solutions with numerical outcomes for periodic currents and voltages. These analytical findings can be effectively employed for controlling the brushless DC motors experiencing voltage disturbances.

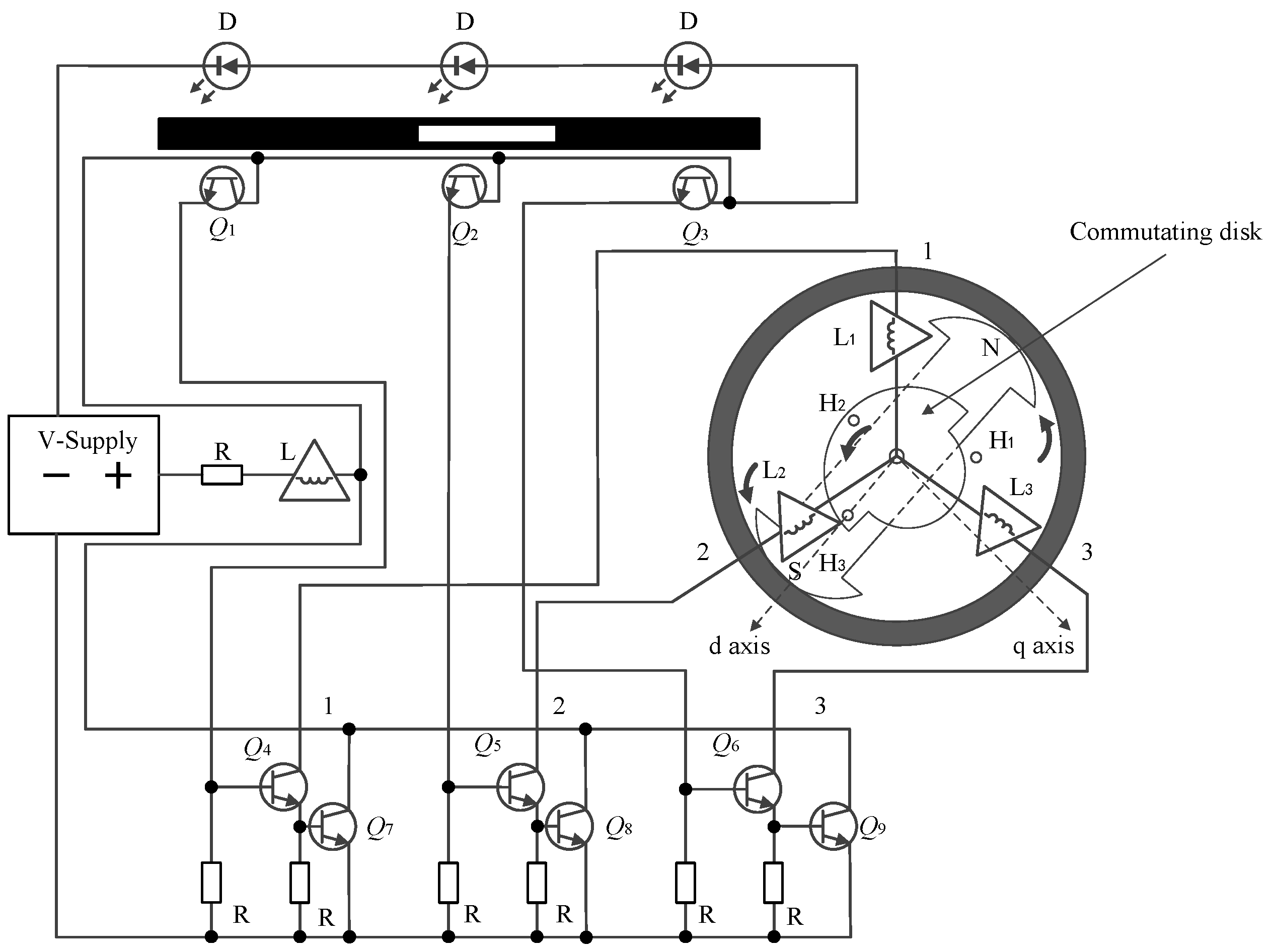
1. Introduction

Brushless DC motors are extensively utilized in rapidly developing fields, such as electric vehicles, intelligent robots, medical equipment, aerospace, and other precision industries. However, the control system of brushless DC motors is relatively intricate and lacks excitation control. Additionally, their mechanical characteristics are rigid, particularly when the inverter output waveform is suboptimal. This can result in significant torque ripple, which adversely affects low-speed performance while increasing current loss and noise levels. Consequently, scholars have conducted extensive research on the precise control of brushless DC motors from both physical modeling and control strategy perspectives.

In 1993, Hemati [1] proposed an approach for formulating concise representations of the nonlinear equations governing brushless DC motors, resulting in a significant reduction in the number of system control variables. Rubaai et al. [2] established a mathematical model of brushless DC motors and proposed a model based adaptive control method. The performance of BLDC motors was analyzed and controlled through mathematical modeling by A. Prakash et al. [3]. The terminal voltage and input current were then utilized to compute the speed, torque, and flux of the sensorless BLDC motor. In addition, Lee and Ehsani [4] proposed a Matlab-based simulation model for BLDC motor drives. This model enables the effective monitoring and analysis of the dynamic characteristics of speed, torque, voltage, and current in PWM inverter components. Jabbar et al. [5] used finite element technology to model and numerically simulate brushless permanent magnet DC motors. The aforementioned research indicates that voltage and current are crucial factors influencing the output torque, speed control, and other performance parameters of brushless DC motors.

The torque control method proposed by Kang and Sul [6] in 1995 was based on the back electromotive force waveform used to calculate applied output voltage, with the aim of addressing the torque ripple issue of non-ideal trapezoidal brushless DC motors. Ilhwan Kim et al. [7] addressed the torque pulsation problem of high-performance brushless direct current motors by adjusting the phase current excitation waveform to counteract the torque pulsation. Piotr Niemczyk et al. [8] used two currents in the BLDCM phase to estimate rotor angle and velocity. N. Hemalatha et al. [9] proposed an adaptive Neuro-fuzzy Interference System controller based on Particle Swarm Optimization. The method was able to accurately estimate the back electromotive force at the zero-crossing point of PMBLDC motors via the terminal voltages. Murali Dasari et al. [10] discussed the value of reducing torque fluctuations in brushless DC motor drive systems by studying speed, current, and commutation problems. Through the aforementioned research, it has been determined that establishing a mapping relationship between the mechanical characteristics of brushless DC motors and input parameters, such as voltage and current, can provide an enhanced technical approach for various control strategies. This holds significant importance in improving the performance and expanding the application range of brushless DC motors. However, it should be noted that brushless DC motors not only present intricate control challenges but also exhibit strong nonlinear dynamic responses under specific parameter conditions, which adversely affect their precise control.

Therefore, focusing on the control model of brushless DC motors containing nonlinear terms, Zebin Li et al. [11] proposed a method based on Lyapunov stability theory to suppress and control chaotic motion according to the chaotic phenomenon of brushless DC motors under certain specific parameters. The utilization of the differential geometric control theory by Chun-Lai Li et al. [12] facilitated the proposition of a nonlinear control approach based on current delay feedback, effectively inducing the BLDCM system to enter into a chaotic regime. The research focus of Zheng-Ming Ge et al. [13] lies in the investigation of chaotic phenomena exhibited by brushless direct current motors and the exploration of strategies for achieving chaos counter control through the implementation of external controls. Philippe Faradja et al. [14] explored the dynamics and stability of chaos in brushless direct current motor systems.

The aforementioned studies primarily address the periodic solution and stability of the brushless DC motor control model using numerical integration methods and Lyapunov stability theory. However, it is often challenging for numerical integration methods, such as the Euler method and the Runge–Kutta method, to converge at unstable solutions, thereby hindering the acquisition of complete periodic solutions. Luo and Huang [15,16] used the generalized harmonic balance method to obtain analytic solutions of periodic motions in the Duffing oscillator. The asymmetric period-1 motion was obtained and bifurcation trees of period-1 motion to chaos were discussed by Luo and Huang [17]. Luo and Yu [18] presented analytical solutions for period-1 motions of a periodically forced, quadratic nonlinear oscillator. Ying et al. [19] obtained symmetric period-1 motion to asymmetric period-2 motion, the independent period-2 and period-4 motions, and the corresponding bifurcation trees. Xu and Luo [20] investigated a one-dimensional nonlinear dynamical system. Analytical solutions of periodic motions in such 1D nonlinear dynamical systems were obtained. The frequency–amplitude characteristics of periodic motions were analyzed. Huang et al. [21,22] analyzed the same brushless DC motor model using a discrete mapping method and obtained semi-analytical periodic currents and voltages. The stability and bifurcations of the semi-analytical currents and voltages were analyzed through the eigenvalues. The feedback control of the unstable periodic motion of brushless motors with unsteady external torque was also conducted. The aforementioned methods can be taken advantage of to solve the magnetohydrodynamic [23] system and to control brushless DC motors with voltage disturbance. Chen et al. [24] focused on the analytical solution of the independent periodic potentials of a 3D brushless DC motor using the generalized harmonic balance method. Their research focused more on the higher-order nonlinear potentials, but in local and solitary frequency ranges, while this study completed the research. This study obtained the complete stable and unstable nonlinear potentials of period-1. It is more important since such nonlinear potentials happen more in industrial contexts. The stable and unstable potentials and currents were obtained and the boundaries between such potentials and currents were determined.

In this paper, the analytical variations of the nonlinear currents and voltages of a brushless DC motor will be studied, as well as its stability and bifurcations. The analytical solutions of the quadrature-axis voltage disturbance will be developed using the generalized harmonic balance method. The bifurcations of independent period-1 motions will be presented. Furthermore, numerical illustrations will be given to verify the analytical solutions.

2. Analytical Solutions

A typical electronically commutated motor is illustrated in Figure 1. Consider such a brushless DC motor in electrical dynamics [1] as

$$\frac{\mathrm{d}\mathit{I}(t)}{\mathrm{d}t}={\mathit{L}}^{-1}(\theta )[\mathit{V}(t)-\mathit{R}\mathit{I}(t)-(\frac{\partial L(\theta )}{\partial \theta }\mathit{I}(t)+\frac{\partial {\mathit{\Lambda }}_M}{\partial \theta })\frac{d\theta }{dt}]$$

(1)

where $\mathit{L}(\theta )$ is the matrix of inductance; $\mathit{V}(t)$ is the vector of voltages over the phase windings; $\mathit{I}(t)$ is the vector of phase current; $\mathit{R}$ is the matrix of resistance; ${\mathit{\Lambda }}_M$ is the flux linkage vector due to the permanent magnets, and $\theta$ is the angular displacement. The mechanical dynamics of the motor can be expressed as

$$\frac{\mathrm{d}\omega }{\mathrm{d}t}=\frac{T(\mathit{I},\theta )-T_l(t)}{J}$$

(2)

where $\omega$ is the angular velocity of the rotor; $J$ is the inertia; $T(\mathit{I},\theta )$ is the electromagnetic torque, and $T_l(t)$ stands for the external torques imposed by friction, cogging, etc.

Consider that a damping coefficient b, $T_l(t)$ has the following form

$$T_l(t)=b\omega +T_L$$

(3)

where $T_L$ is the external torque excluding the one caused by damping. Assuming such an ideal smooth-air-gap brushless DC motor is subjected to sinusoidally distributed windings, the electromagnetic torque $T(\mathit{I},\theta )$ [21] is expressed in the following form

$$T(\mathit{I},\theta )=n{k}_e{\displaystyle \sum _{k=1}^3{i}_k\cos [n\theta -\frac{2(k-1)\pi }{3}]}$$

(4)

where n is the number of permanent pole pairs; $k_e$ is the permanent-magnet flux constant, and $i_k$($k=1,2$ and 3) is the current.

To better solve Equations (1) and (2), Park’s transformation is adopted and the equations are transformed into the rotating frame [13] as

$$\begin{array}{l}\frac{\mathrm{d}{i}_q}{\mathrm{d}t}=\frac{1}{L_q}\left[-R{i}_q-n\omega (L_d{i}_d+k_t)+u_q\right],\\ \frac{\mathrm{d}{i}_d}{\mathrm{d}t}=\frac{1}{L_d}\left[-R{i}_d+n\omega L_q{i}_q+u_d\right].\end{array}$$

(5)

where $k_t=\sqrt{1.5}{k}_e$. The electromagnetic torque is

$$T(i_q,i_d)=n[k_t{i}_q+(L_d-L_q)i_d{i}_q]$$

(6)

where $i_q$ and $i_d$ are quadrature-axis and direct-axis currents; $u_q$ and $u_d$ are quadrature-axis and direct-axis voltages; and $L_q$ and $L_d$ are the quadrature-axis and direct-axis fictitious inductance. Based on Equation (5), the mechanical dynamics in Equation (2) can be rewritten as [1]

$$\frac{\mathrm{d}\omega }{\mathrm{d}t}=\frac{n}{J}\left[k_t{i}_q+(L_d-L_q)i_q{i}_d\right]-\frac{1}{J}(b\omega +T_L),$$

(7)

Define new variables as

$$x_1=\frac{i_q}{{\alpha }_1},x_2=\frac{i_d}{{\alpha }_2}+\frac{k_t}{L_d{\alpha }_2}+\rho ,x_3=\frac{i_q}{{\alpha }_1},\tau =\frac{tR}{L_q}$$

(8)

where

$${\alpha }_1=\frac{-\delta k_t\pm \sqrt{{\delta }^2{k}_t^2-4\rho \delta \zeta L_{q}b{\alpha }_3^2/R}}{2\rho \delta \zeta },{\alpha }_2=\delta {\alpha }_1,{\alpha }_3=\frac{R}{n{L}_q},\zeta =L_d-L_q,\delta =\frac{L_q}{L_d}$$

(9)

and

$$v_q=\frac{1}{{\alpha }_{1}R}{u}_q,v_d=\frac{L_q}{{\alpha }_{2}R{L}_d}[u_d+R(\rho {\alpha }_2+\frac{k_t}{L_d})],{\overline{T}}_L=\frac{L_q}{J{\alpha }_{3}R}{T}_L,\sigma =\frac{L_{q}b}{JR},\eta =\frac{\zeta {\alpha }_1{\alpha }_2}{J{\alpha }_3^2}$$

(10)

where $\rho$ is a free parameter. Combining Equations (8)–(10), Equation (1) becomes

$$\begin{array}{l}\frac{\mathrm{d}{x}_1}{\mathrm{d}\tau }=v_q-x_1-x_2{x}_3+\rho x_3,\\ \frac{\mathrm{d}{x}_2}{\mathrm{d}\tau }=v_d-\delta x_2+x_1{x}_3,\\ \frac{\mathrm{d}{x}_3}{\mathrm{d}\tau }=\sigma (x_1-x_3)+\eta x_1{x}_2-{\overline{T}}_L.\end{array}$$

(11)

Considering the quadrature-axis voltage $v_q$ varying with time as $v_q+Q_0\cos \Omega t$, where $Q_0$ and $\Omega$ are the dimensionless excitation amplitude and frequency, the corresponding dynamical system becomes

$$\begin{array}{l}{\dot{x}}_1=v_q-x_1-x_2{x}_3+\rho x_3+Q_0\cos \Omega t\\ {\dot{x}}_2=v_d-\delta x_2+x_1{x}_3\\ {\dot{x}}_3=\sigma (x_1-x_3)+\eta x_1{x}_2-{\overline{T}}_L\end{array}.$$

(12)

Define the following vectors:

$$F(x,t)=\left(\begin{array}{c}{v}_q-x_1-x_2{x}_3+\rho x_3+Q_0\cos \Omega t\\ v_d-\delta x_2+x_1{x}_3\\ \sigma (x_1-x_3)+\eta x_1{x}_2-{\overline{T}}_L\end{array}\right).$$

(13)

From Equation (13), Equation (12) becomes

$$\dot{x}=F(x,t).$$

(14)

From [11,12,13], the appropriate solution for period-m motion from Equation (14) is

$$\begin{array}{l}{x}_1^{\ast }=a_{01}^{(m)}(t)+{\displaystyle \sum _{k=1}^N{b}_{k/m1}(t)\cos \frac{k}{m}\Omega t+}{c}_{k/m1}(t)\sin \frac{k}{m}\Omega t\\ x_2^{\ast }=a_{02}^{(m)}(t)+{\displaystyle \sum _{k=1}^N{b}_{k/m2}(t)\cos \frac{k}{m}\Omega t+}{c}_{k/m2}(t)\sin \frac{k}{m}\Omega t\\ x_3^{\ast }=a_{03}^{(m)}(t)+{\displaystyle \sum _{k=1}^N{b}_{k/m3}(t)\cos \frac{k}{m}\Omega t+}{c}_{k/m3}(t)\sin \frac{k}{m}\Omega t\end{array}$$

(15)

where $a_{0i}^{(m)}(t),b_{k/mi}(t),c_{k/mi}(t)$ are the Fourier-alike coefficients. Taking the derivative of Equation (15) with respect to time gives

$$\begin{array}{l}{\dot{x}}_1^{\ast }={\dot{a}}_{01}^{(m)}+{\displaystyle \sum _{k=1}^N({\dot{b}}_{k/m1}+\frac{k}{m}\Omega c_{k/m1})\cos \frac{k}{m}\Omega t+}({\dot{c}}_{k/m1}-\frac{k}{m}\Omega b_{k/m1})\sin \frac{k}{m}\Omega t\\ {\dot{x}}_2^{\ast }={\dot{a}}_{02}^{(m)}+{\displaystyle \sum _{k=1}^N({\dot{b}}_{k/m2}+\frac{k}{m}\Omega c_{k/m2})\cos \frac{k}{m}\Omega t+}({\dot{c}}_{k/m2}-\frac{k}{m}\Omega b_{k/m2})\sin \frac{k}{m}\Omega t\\ {\dot{x}}_3^{\ast }={\dot{a}}_{03}^{(m)}+{\displaystyle \sum _{k=1}^N({\dot{b}}_{k/m3}+\frac{k}{m}\Omega c_{k/m3})\cos \frac{k}{m}\Omega t+({\dot{c}}_{k/m3}-\frac{k}{m}\Omega b_{k/m3})}\sin \frac{k}{m}\Omega t\end{array}.$$

(16)

With the substitution of Equations (15) and (16) into Equation (14), and averaging all terms of constants, $\cos (k\Omega t/m)$ and $\sin (k\Omega t/m)$ yield

$$\begin{array}{l}{\dot{a}}_{01}^{(m)}=F_{01}^{(m)},{\dot{a}}_{02}^{(m)}=F_{02}^{(m)},{\dot{a}}_{03}^{(m)}=F_{03}^{(m)};\\ {\dot{b}}_{k/m1}=-\frac{k}{m}\Omega c_{k/m1}+F_{01}^{(m)},{\dot{b}}_{k/m2}=-\frac{k}{m}\Omega c_{k/m2}+F_{02}^{(m)},{\dot{b}}_{k/m3}=-\frac{k}{m}\Omega c_{k/m3}+F_{03}^{(m)};\\ {\dot{c}}_{k/m1}=\frac{k}{m}\Omega b_{k/m1}+F_{21}^{(m)},{\dot{c}}_{k/m2}=\frac{k}{m}\Omega b_{k/m2}+F_{22}^{(m)},{\dot{c}}_{k/m3}=\frac{k}{m}\Omega b_{k/m3}+F_{23}^{(m)}.\end{array}$$

(17)

Let

$$\begin{array}{l}{a}_0^{(m)}=(a_{01}^{(m)},a_{02}^{(m)},a_{03}^{(m)}{)}^{\mathrm{T}},\\ {b^{(m)}{=(\mathrm{b}}_{1/m}^{},b_{2/m}^{},\cdots ,b_{N/m}^{})}^{\mathrm{T}},b_{k/m}^{}=(b_{k/m1}^{},b_{k/m2}^{},b_{k/m3}^{}{)}^{\mathrm{T}}\\ c^{(m)}=(c_{1/m}^{},c_{2/m}^{},\cdots ,c_{N/m}^{}{)}^{\mathrm{T}},c_{k/m}^{}=(c_{k/m1}^{},c_{k/m2}^{},c_{k/m3}^{}{)}^{\mathrm{T}}\\ {\dot{a}}_0^{(m)}=({\dot{a}}_{01}^{(m)},{\dot{a}}_{02}^{(m)},{\dot{a}}_{03}^{(m)}{)}^{\mathrm{T}}\\ {\dot{b}}^{(m)}=({\dot{b}}_{1/m}^{},{\dot{b}}_{2/m}^{},\cdots ,{\dot{b}}_{N/m}^{}{)}^{\mathrm{T}},{\dot{b}}_{k/m}^{}=({\dot{b}}_{k/m1}^{},{\dot{b}}_{k/m2}^{},{\dot{b}}_{k/m3}^{}{)}^{\mathrm{T}}\\ {\dot{c}}^{(m)}=({\dot{c}}_{1/m}^{},{\dot{c}}_{2/m}^{},\cdots ,{\dot{c}}_{N/m}^{}{)}^{\mathrm{T}},{\dot{c}}_{k/m}^{}=({\dot{c}}_{k/m1}^{},{\dot{c}}_{k/m2}^{},{\dot{c}}_{k/m3}^{}{)}^{\mathrm{T}}\\ k_1=diag\left[{\mathbf{I}}_{3\times 3},2{\mathbf{I}}_{3\times 3},\cdots ,N{\mathbf{I}}_{3\times 3}\right]\end{array}$$

(18)

and for k = 1, 2, …, N

$$\begin{array}{l}{F}_0^{(m)}(a_0^{(m)},{\mathbf{b}}_{}^{(m)},{\mathbf{c}}_{}^{(m)})=\frac{1}{mT}{\displaystyle {\int }_0^{mT}F(x_{}^{\ast },t)dt},\\ {\mathbf{F}}_{1k}^{(m)}(a_0^{(m)},{\mathbf{b}}_{}^{(m)},{\mathbf{c}}_{}^{(m)})=\frac{2}{mT}{\displaystyle {\int }_0^{mT}F(x_{}^{\ast },t)\cos (\frac{k}{m}\Omega t)dt},\\ {\mathbf{F}}_{2k}^{(m)}(a_0^{(m)},{\mathbf{b}}_{}^{(m)},{\mathbf{c}}_{}^{(m)})=\frac{2}{mT}{\displaystyle {\int }_0^{mT}F(x_{}^{\ast },t)\sin (\frac{k}{m}\Omega t)dt},\end{array}$$

(19)

where

$$\begin{array}{l}{F}_0^{(m)}=(F_{01}^{(m)},F_{02}^{(m)},F_{03}^{(m)}{)}^{\mathrm{T}}\\ F_1^{(m)}={(F_{11}^{(m)},F_{12}^{(m)},\cdots ,F_{1N}^{(m)})}^{\mathrm{T}}\\ F_2^{(m)}={(F_{21}^{(m)},F_{22}^{(m)},\cdots ,F_{2N}^{(m)})}^{\mathrm{T}}\\ F_{1k}^{(m)}={(F_{1k1}^{(m)},F_{1k2}^{(m)},F_{1k3}^{(m)})}^{\mathrm{T}}\\ F_{2k}^{(m)}={(F_{2k1}^{(m)},F_{2k2}^{(m)},F_{2k3}^{(m)})}^{\mathrm{T}}\end{array}$$

(20)

and $F_{01}^{(m)}$, $F_{02}^{(m)}$, $F_{03}^{(m)}$, $F_{1k1}^{(m)}$, $F_{1k2}^{(m)}$, $F_{1k3}^{(m)}$, $F_{2k1}^{(m)}$, $F_{2k2}^{(m)}$, and $F_{2k3}^{(m)}$ are presented in Appendix A.

From Equations (18)–(20), Equation (17) becomes

$$\begin{array}{l}{\dot{a}}_0^{(m)}=F_0^{(m)}(a_0^{(m)},{\mathbf{b}}_{}^{(m)},{\mathbf{c}}_{}^{(m)}),\\ {\dot{\mathbf{b}}}_{}^{(m)}=-\Omega \frac{k_1}{m}{\mathbf{c}}_{}^{(m)}+{\mathbf{F}}_1^{(m)}(a_0^{(m)},{\mathbf{b}}_{}^{(m)},{\mathbf{c}}_{}^{(m)}),\\ {\dot{\mathbf{c}}}_{}^{(m)}=\Omega \frac{k_1}{m}{\mathbf{b}}_{}^{(m)}+{\mathbf{F}}_2^{(m)}(a_0^{(m)},{\mathbf{b}}_{}^{(m)},{\mathbf{c}}_{}^{(m)}).\end{array}$$

(21)

Introduce

$$z_{}^{(m)}={(a_0^{(m)},b^{(m)},c^{(m)})}^{\mathrm{T}},f_{}^{(m)}={(F_0^{(m)},-\Omega \frac{k_1}{m}{\mathbf{c}}_{}^{(m)}+{\mathbf{F}}_1^{(m)},\Omega \frac{k_1}{m}{\mathbf{b}}_{}^{(m)}+{\mathbf{F}}_2^{(m)})}^{\mathrm{T}}.$$

(22)

The standard form of Equation (22) is

$${\dot{z}}_{}^{(m)}=f_{}^{(m)}(z_{}^{(m)}).$$

(23)

The periodic motion of Equation (12) can be obtained by Equation (23) with ${\dot{z}}^{(m)}=0$. The equilibrium $z^{(m)\ast }$ is obtained by solving the nonlinear algebraic equation of $f_{}^{(m)}(z^{(m)\ast })=0$. In the neighborhood of $z^{(m)\ast }$, $z^{(m)}=z^{(m)\ast }+\Delta z^{(m)}$, the linearized equation of Equation (23) is

$$\Delta {\dot{z}}_{}^{(m)}=D{f}_{}^{(m)}(z_{}^{(m)\ast })\Delta z_{}^{(m)}$$

(24)

and the Jacobian matrix is

$$D{f}_{}^{(m)}(z_{}^{(m)\ast })={\frac{\partial f_{}^{(m)}}{\partial z_{}^{(m)}}|}_{z_{}^{(m)\ast }}$$

(25)

And

$$\frac{\partial f_{}^{(m)}}{\partial z_{}^{(m)}}=\left[\begin{array}{ccc}\frac{\partial F_0^{(m)}}{\partial a_0^{(m)}}& \frac{\partial F_0^{(m)}}{\partial b^{(m)}}& \frac{\partial F_0^{(m)}}{\partial c^{(m)}}\\ \frac{\partial F_1^{(m)}}{\partial a_0^{(m)}}& \frac{\partial F_1^{(m)}}{\partial b^{(m)}}& -\Omega \frac{k_1}{m}+\frac{\partial F_1^{(m)}}{\partial c^{(m)}}\\ \frac{\partial F_2^{(m)}}{\partial a_0^{(m)}}& \Omega \frac{k_1}{m}+\frac{\partial F_2^{(m)}}{\partial b^{(m)}}& \frac{\partial F_2^{(m)}}{\partial c^{(m)}}\end{array}\right]=\left[\begin{array}{c}{G}_{0(3\times (6N+3))}\\ G_{1(3N\times (6N+3))}\\ G_{2(3N\times (6N+3))}\end{array}\right]$$

(26)

where

$$\begin{array}{l}{G}_0={(G_{01},G_{02},G_{03})}^{\mathrm{T}},G_1={(G_{11},G_{12},\cdots ,G_{1N})}^{\mathrm{T}},G_{1k}={(G_{1k1},G_{1k2},G_{1k3})}^{\mathrm{T}}\\ G_2={(G_{21},G_{22},\cdots ,G_{2N})}^{\mathrm{T}},G_{2k}={(G_{2k1},G_{2k2},G_{2k3})}^{\mathrm{T}}\\ G_{01}=\frac{\partial F_{01}^{(m)}}{\partial z_{}^{(m)}},G_{02}=\frac{\partial F_{02}^{(m)}}{\partial z_{}^{(m)}},G_{03}=\frac{\partial F_{03}^{(m)}}{\partial z_{}^{(m)}}\\ G_{1k1}=-\Omega \frac{k}{m}\frac{\partial c_{k/m1}^{}}{\partial z_{}^{(m)}}+\frac{\partial F_{1k1}^{(m)}}{\partial z_{}^{(m)}},G_{1k2}=-\Omega \frac{k}{m}\frac{\partial c_{k/m2}^{}}{\partial z_{}^{(m)}}+\frac{\partial F_{1k2}^{(m)}}{\partial z_{}^{(m)}},G_{1k3}=-\Omega \frac{k}{m}\frac{\partial c_{k/m3}^{}}{\partial z_{}^{(m)}}+\frac{\partial F_{1k3}^{(m)}}{\partial z_{}^{(m)}}\\ G_{2k1}=\Omega \frac{k}{m}\frac{\partial b_{k/m1}^{}+F_{2k1}^{(m)}}{\partial z_{}^{(m)}}+\frac{\partial F_{2k1}^{(m)}}{\partial z_{}^{(m)}},G_{2k2}=\Omega \frac{k}{m}\frac{\partial b_{k/m2}^{}}{\partial z_{}^{(m)}}+\frac{\partial F_{2k2}^{(m)}}{\partial z_{}^{(m)}},G_{2k3}=\Omega \frac{k}{m}\frac{\partial b_{k/m3}^{}}{\partial z_{}^{(m)}}+\frac{\partial F_{2k3}^{(m)}}{\partial z_{}^{(m)}}\end{array}$$

(27)

and $G_{01}$, $G_{02}$, $G_{03}$, $G_{1k1}$, $G_{1k2}$, $G_{1k3}$, $G_{2k1}$, $G_{2k2}$, and $G_{2k3}$ are listed in Appendix A.

The local stability of the equilibrium point is determined by the eigenvalues, i.e.,

$$\left|D{f}_{}^{(m)}(z_{}^{(m)\ast })-\lambda {\mathbf{I}}_{3(2N+1)\times 3(2N+1)}\right|=0.$$

(28)

In Luo [15], the eigenvalues $D{f}^{(m)}(z^{\ast (m)})$ are grouped as

$$(n_1,n_2,n_3|n_4,n_5,n_6)$$

(29)

where $n_1$ is the number of negative real eigenvalues, $n_2$ is the number of positive real eigenvalues, $n_3$ is the number of zero eigenvalues, $n_4$ is the number of the pairs of complex eigenvalues with negative real parts, $n_5$ is the number of the pairs of complex eigenvalues with positive real parts, and $n_6$ is the number of the pairs of complex eigenvalues with zero real parts.

3. Frequency–Amplitude Characteristics

The bifurcations of periodic motions leading to chaos are illustrated by the frequency–amplitude curves. Consequently, the harmonic amplitude and phase of the periodic motion in a brushless DC motor can be precisely defined as

$$A_{k/m}=\sqrt{b_{k/m}^2+c_{k/m}^2},\begin{array}{c}\end{array}\begin{array}{c}\end{array}{\phi }_{k/m}=\arctan \frac{c_{k/m}}{b_{k/m}}.$$

(30)

The analytical solutions in Equation (15) are

$$x_i^{\ast }(t)=a_{0i}^{(m)}+{\displaystyle \sum _{k=1}^N{A}_{k/mi}\cos (\frac{k}{m}\Omega t-{\phi }_{k/mi})}$$

(31)

Without losing generality, the physical coefficients of the brushless DC motor are considered as [13]

$$v_q=0.168,\rho =60,Q_0=10,\delta =0.875,v_d=20.66,\sigma =4.15,\eta =0.26,{\overline{T}}_L=0.53,\Omega \in [0,8].$$

(32)

The solid and dashed curves represent stable and unstable motions, respectively. “SN” represents stable saddle-node bifurcation. “HB” is for stable Hopf bifurcation.

Period-1 Motion

The analytical variations of currents and voltages can be obtained based on the aforementioned analysis. The analytical results are computed using C++. An overview of period-1 motions for $\Omega \in (0,8]$ is presented in Figure 2. The figure depicted in Figure 2 illustrates a multitude of independent period-1 motions and one unstable period-1 motion. The focus of this investigation lies primarily on the significant independent period-1 motions. It can be deduced from Figure 2 that these independent period-1 motions are concentrated within five disturbance frequency ranges, which are also listed in

Table 1. Disturbance frequency ranges of independent P-1 motion. Parameters: ($v_q=0.168$, $\rho =60$, $Q_0=10$, $\delta =0.875$, $v_d=20.66$, $\sigma =4.15$, $\eta =0.26$, ${\overline{T}}_L=0.53$).

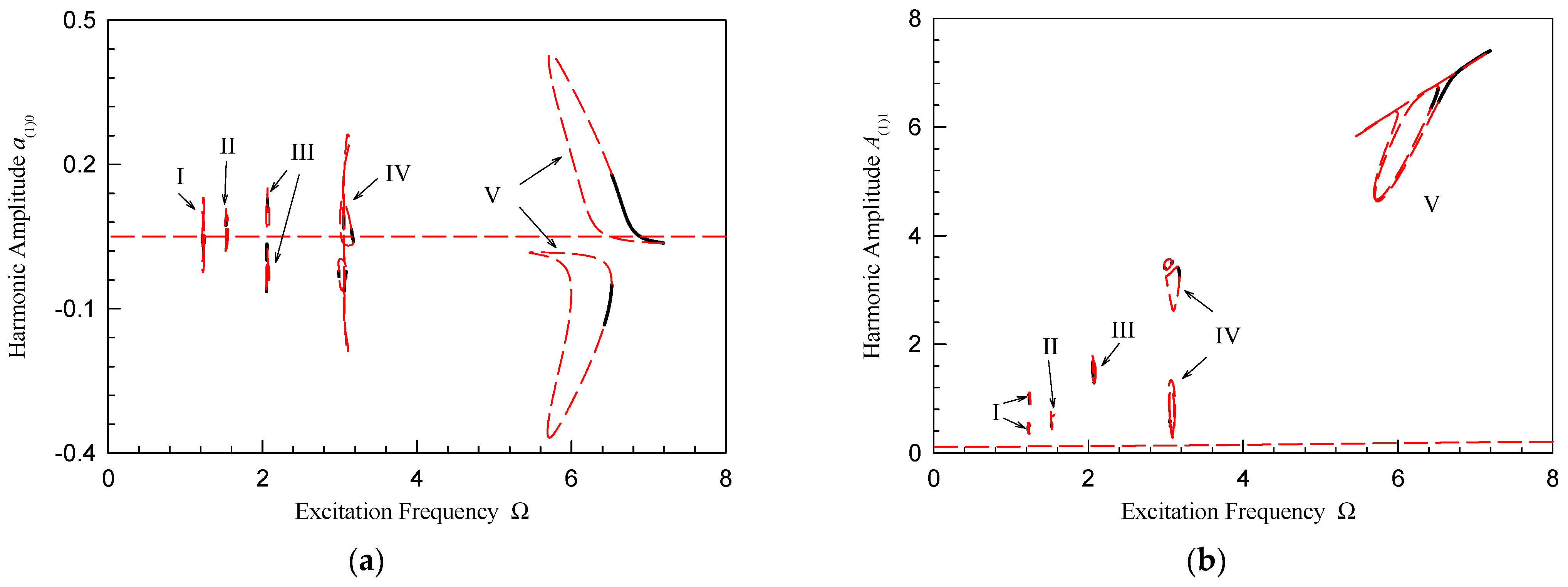
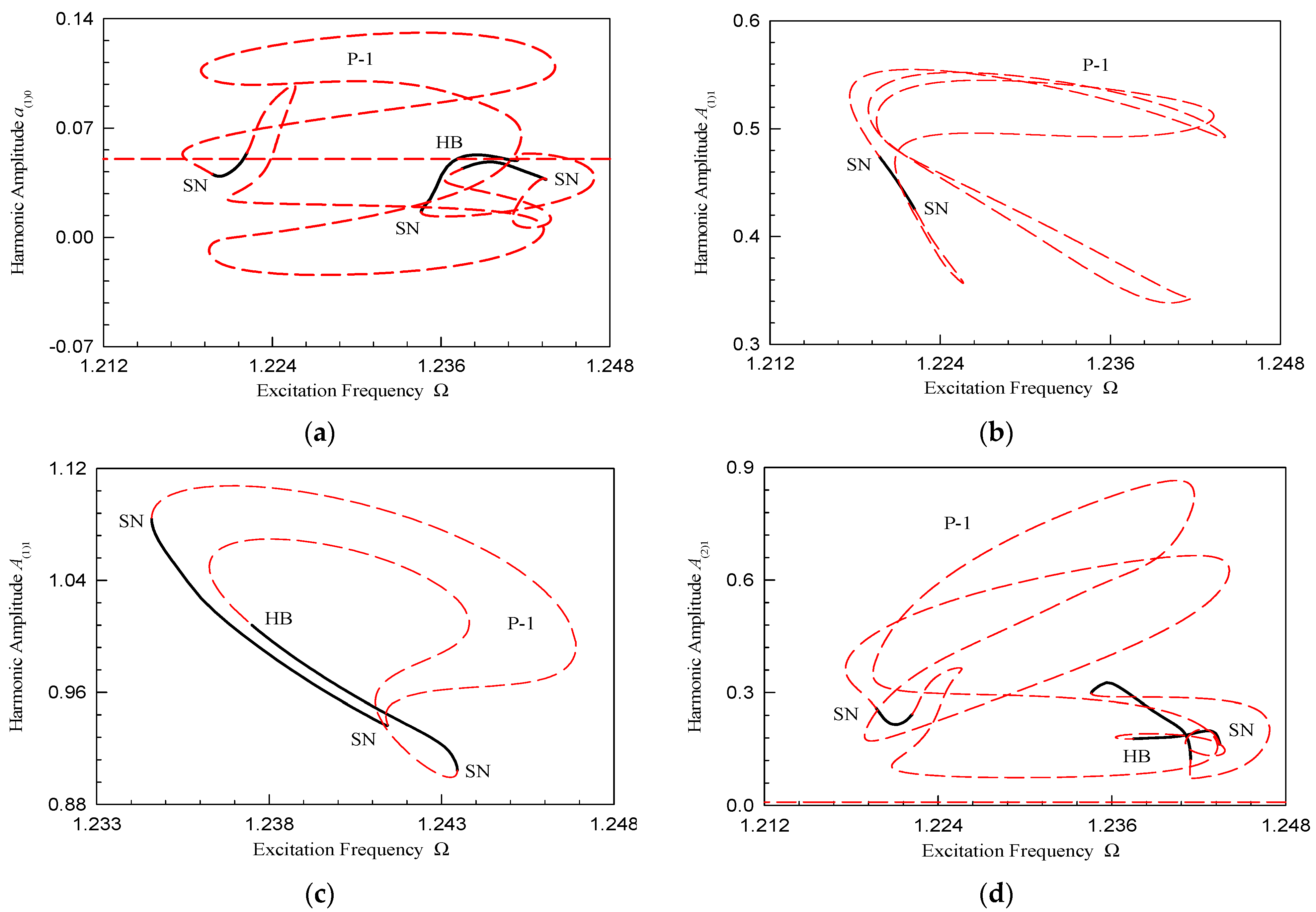
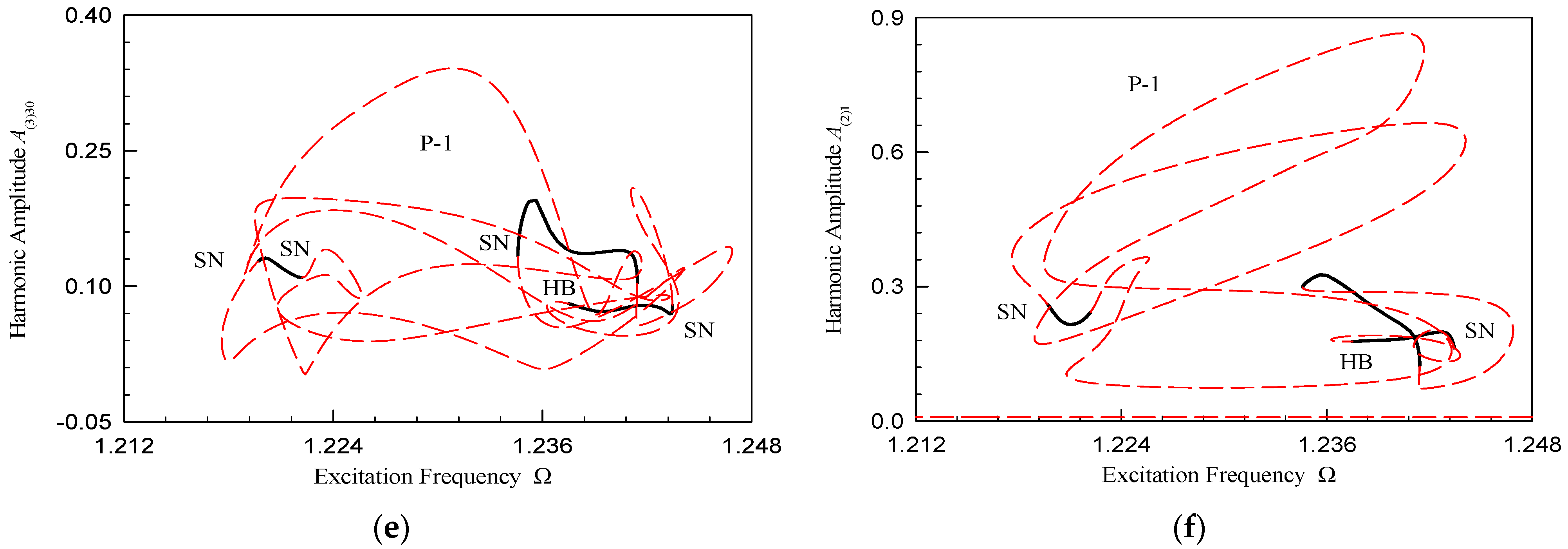
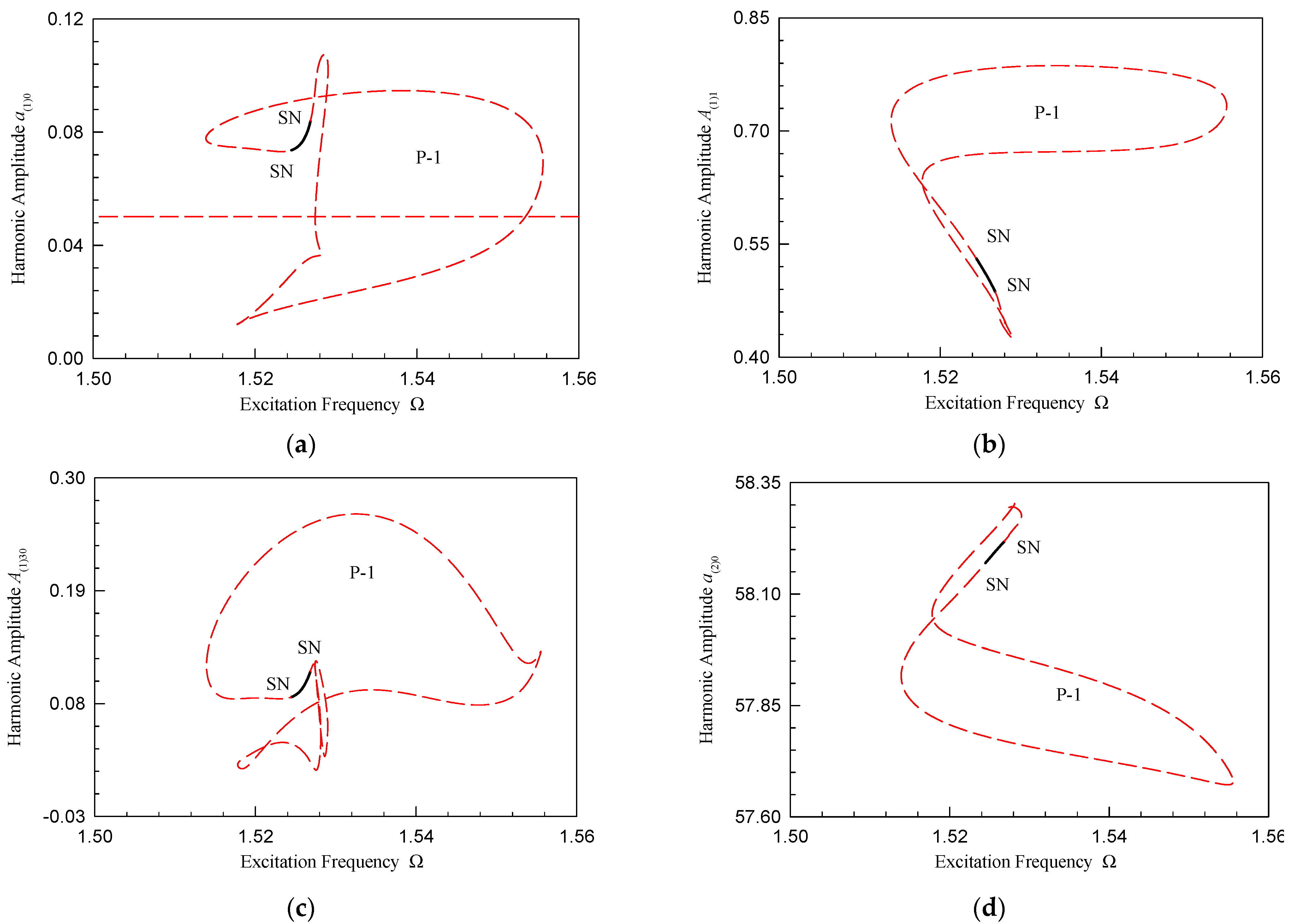
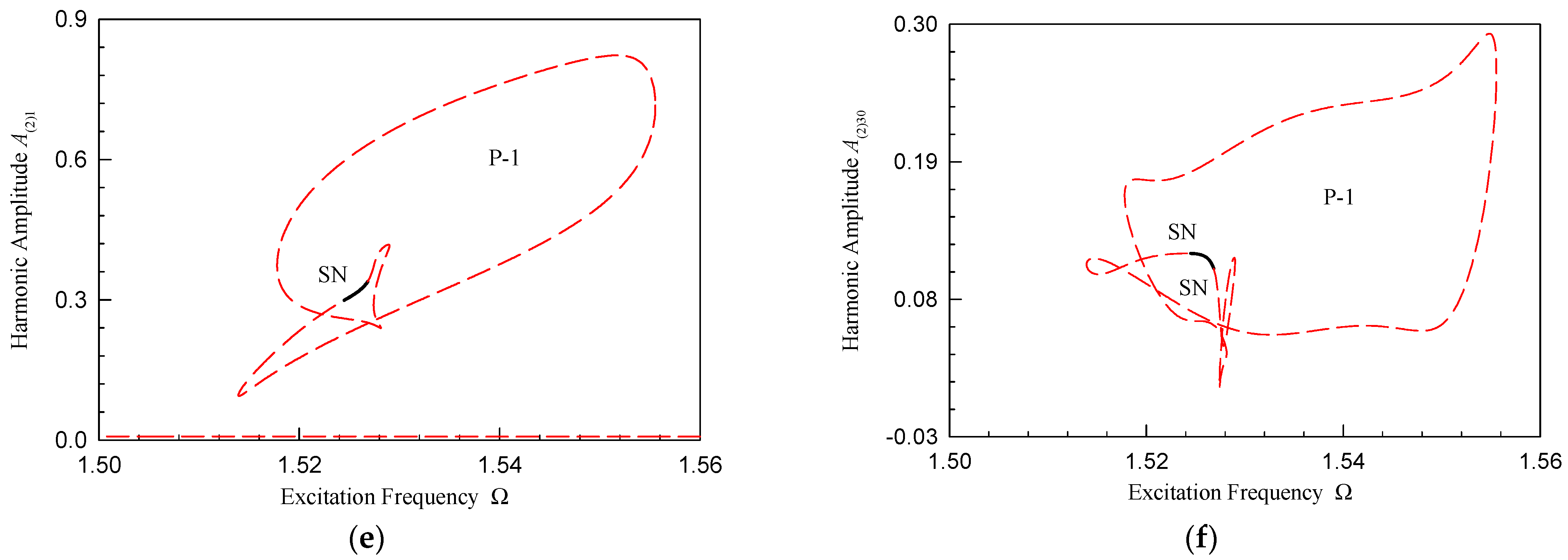
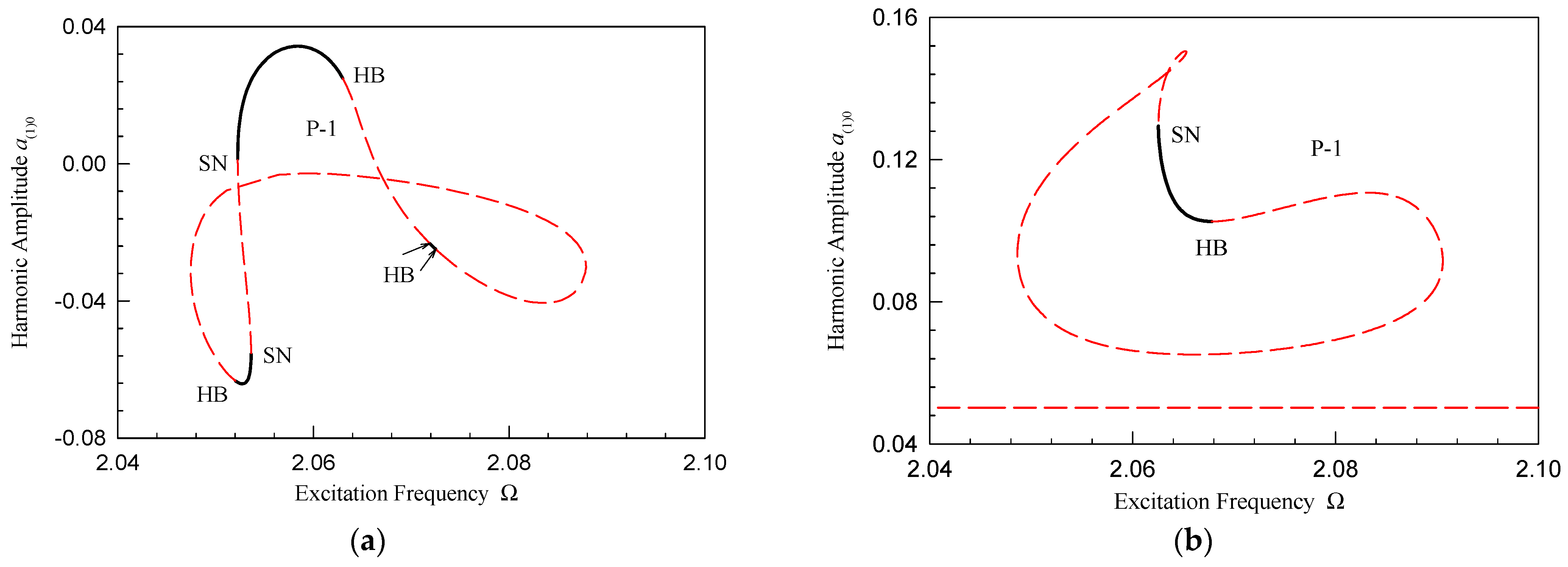
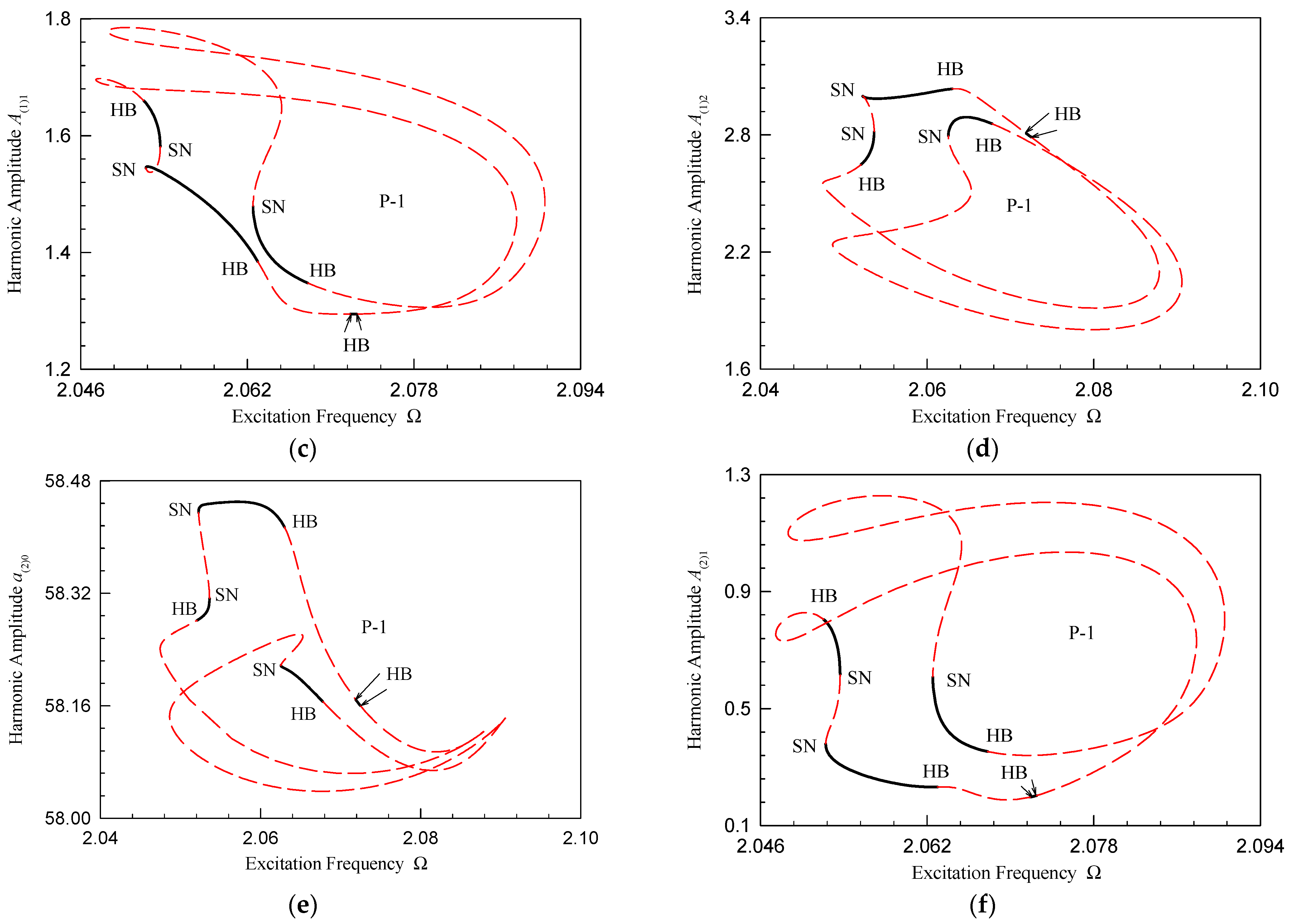
P-1 Motion Part	Disturbance Frequency Range
I	(1.211, 1.244), (1.235, 1.247)
II	(2.0474, 2.0876), (2.0487, 2.0904)
III	(5.457, 6.517), (5.698, 7.193)
IV	(2.98, 3.083), (3.038, 3.121), (3.004, 3.178)
V	(5.457, 6.517), (5.698, 7.193)

.

The bifurcations of period-1 motions, as the disturbance frequency varies within the range of Ω (1.218, 1.247), are depicted in Figure 3. In generalized harmonic balance theory, when the disturbance frequency is close to zero, the analytical solution requires infinite harmonic terms to approximate the motion. The presence of a low disturbance frequency necessitates a larger number of harmonic terms. Therefore, analytic solutions with 80 harmonic terms are applied when analyzing the bifurcation plots in this disturbance frequency range. There are three independent period-1 motions in this range. For the first independent motion in the range of Ω ∈ (1.218,1.244), the critical frequencies of saddle-node bifurcations are Ω = 1.2196 and 1.2222, and no Hopf bifurcation is observed. The stable frequency range of period-1 motion is Ω ∈ (1.2196, 1.2222). When Ω ∈ (1.234, 1.247), saddle-node bifurcations occur at Ω = 1.2345 and 1.2414, and no Hopf bifurcation is achieved in this second independent period-1 motion. The stable frequency range of period-1 motion is Ω ∈ (1.2345, 1.2414). The third independent period-1 motion occurs when Ω ∈ (1.236, 1.243). During this disturbance frequency range, Hopf bifurcation is attained at Ω = 1.2375, while saddle-node bifurcation is obtained at Ω = 1.2434. The stable frequency range of period-1 motion is Ω ∈ (1.2375, 1.2434).

The harmonic coefficients presented in Figure 4 illustrate the bifurcations of independent period-1 motions in the frequency range of Ω ∈ (1.514, 1.555). Analytic solutions with 80 harmonic terms are applied in this case of the disturbance frequency range. Only one independent period-1 motion is observed during Ω ∈ (1.514, 1.555). Hopf bifurcations are achieved when Ω = 1.5244 and 1.5267, and no saddle-node bifurcation is attained. The stable frequency range of period-1 motion is Ω ∈ (1.5244, 1.5267).

Figure 5 presents detailed bifurcations varying with disturbance frequency when Ω ∈ (2.0474, 2.0904). In order to save calculation time, analytic solutions with 50 harmonic terms are applied when analyzing the bifurcation plots during this disturbance frequency range. Two independent closed loops, Ω ∈ (2.0474, 2.0876) and Ω ∈ (2.0487, 2.0904)) for period-1 motions, are found in this range. For the independent motion in the range of Ω ∈ (2.0474, 2.0876), the critical frequencies of Hopf bifurcations are Ω = 2.052, 2.0632, 2.0719, and 2.0725; the critical frequencies of saddle-node bifurcations are Ω = 2.0523 and 2.0536. The stable frequency ranges of period-1 motions are Ω ∈ (2.052, 2.0536), (2.0523, 2.0632), and (2.0719, 2.0725). During disturbance frequency ranges of Ω ∈ (2.0487, 2.0904), Hopf bifurcations are obtained when Ω = 2.0678; saddle-node bifurcation is observed when Ω = 2.0625. The stable frequency ranges of period-1 motions are Ω ∈ (2.0625, 2.0678).

4. Numerical Illustrations

A commonly used methodology for analyzing nonlinear differential equations is numerical integration, which is both straightforward to implement and efficient in computation. The analytical solution is validated through the application of numerical integration in this section. Three-dimensional displacement and frequency spectrums are utilized to depict the dynamic characteristics of the previously discussed brushless DC motor under a specific disturbance frequency. The initial condition is provided by the analytical solution. The black lines and blue circles in the figures refer to numerical solutions and analytical solutions, respectively. In the frequency spectrum, k = 0 presents the constant term $a_{01}$, while k ≠ 0 describes the harmonic amplitude A_k/m. When the motion is unstable, the frequency spectrum based on a numerical solution is unreliable, so the analytical solutions are applied to plot the frequency spectrum. The value of each harmonic term is presented selectively. In the following figures, the time-history and frequency spectrum of x₁ are presented, and 3D displacement is also illustrated. The input data for numerical illustrations are listed in

Table 2. Input data for numerical illustrations. Parameters: ($v_q=0.168$, $\rho =60$, $Q_0=10$, $\delta =0.875$, $v_d=20.66$, $\sigma =4.15$, $\eta =0.26$, ${\overline{T}}_L=0.53$).

Figure No.	Ω	Initial Condition	Types
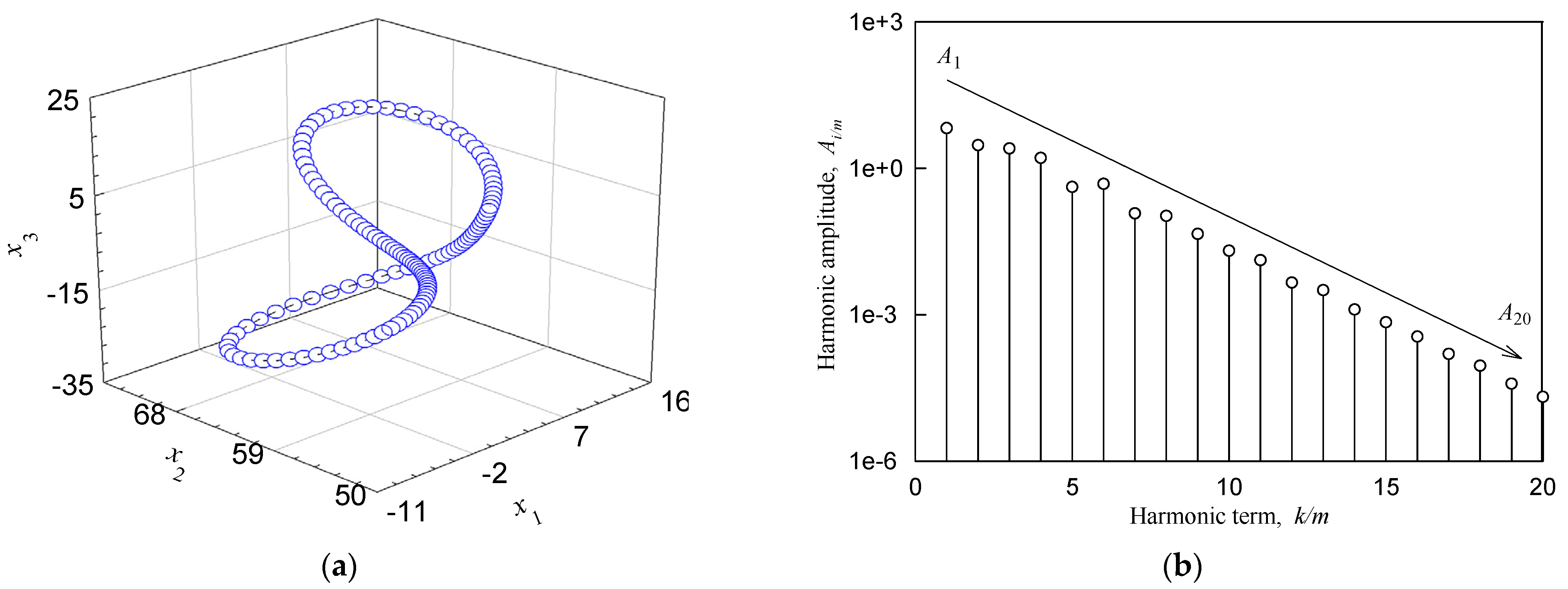
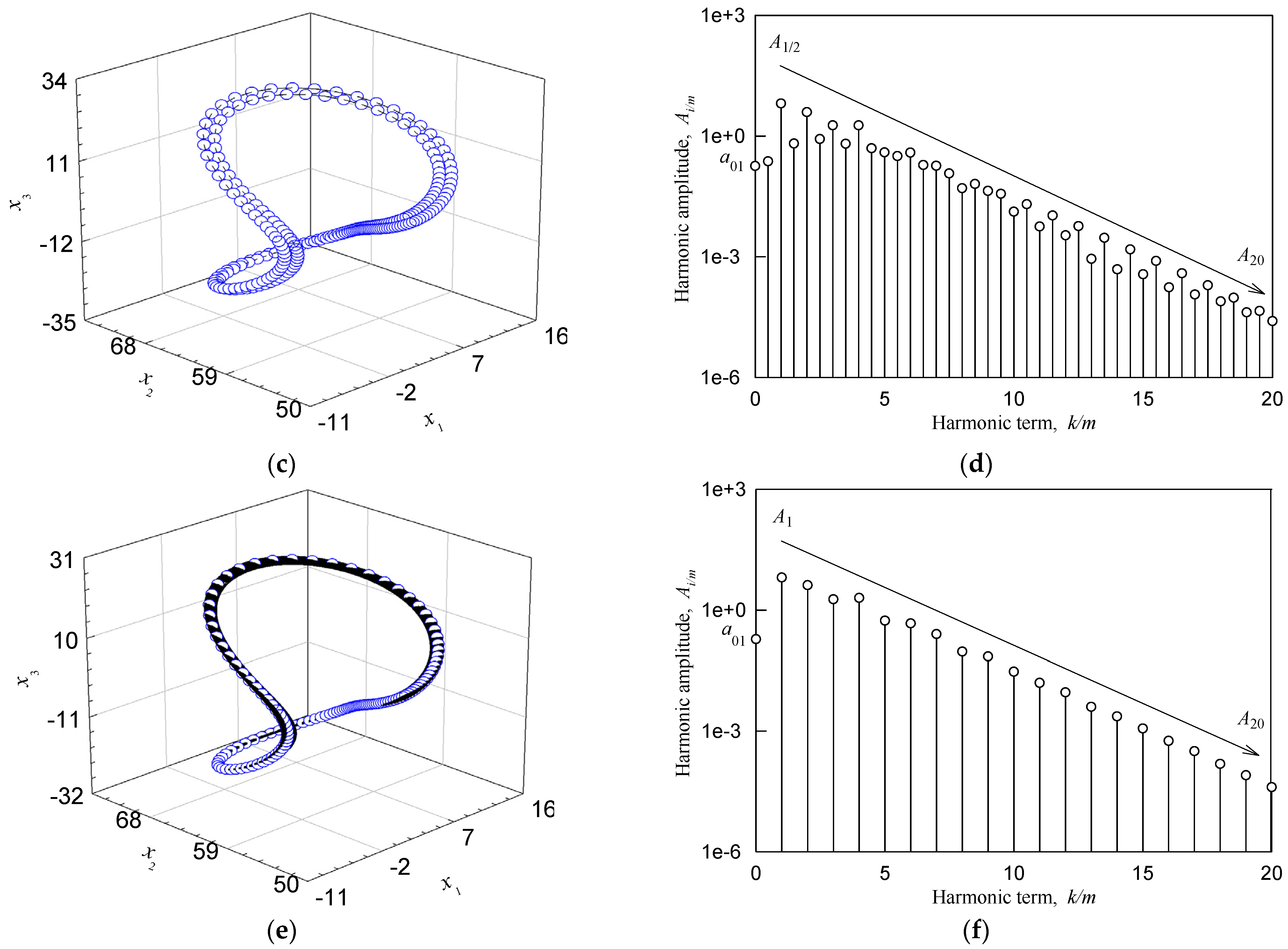
Figure 6a,b	6.5	(5.3227832, 65.525293, 19.302422)	stable P-1
Figure 6c,d	6.5	(9.7357535, 55.891501, 13.299756)	stable P-2
Figure 6e,f	6.5	(7.5583327, 63.739675, 18.706304)	unstable P-1
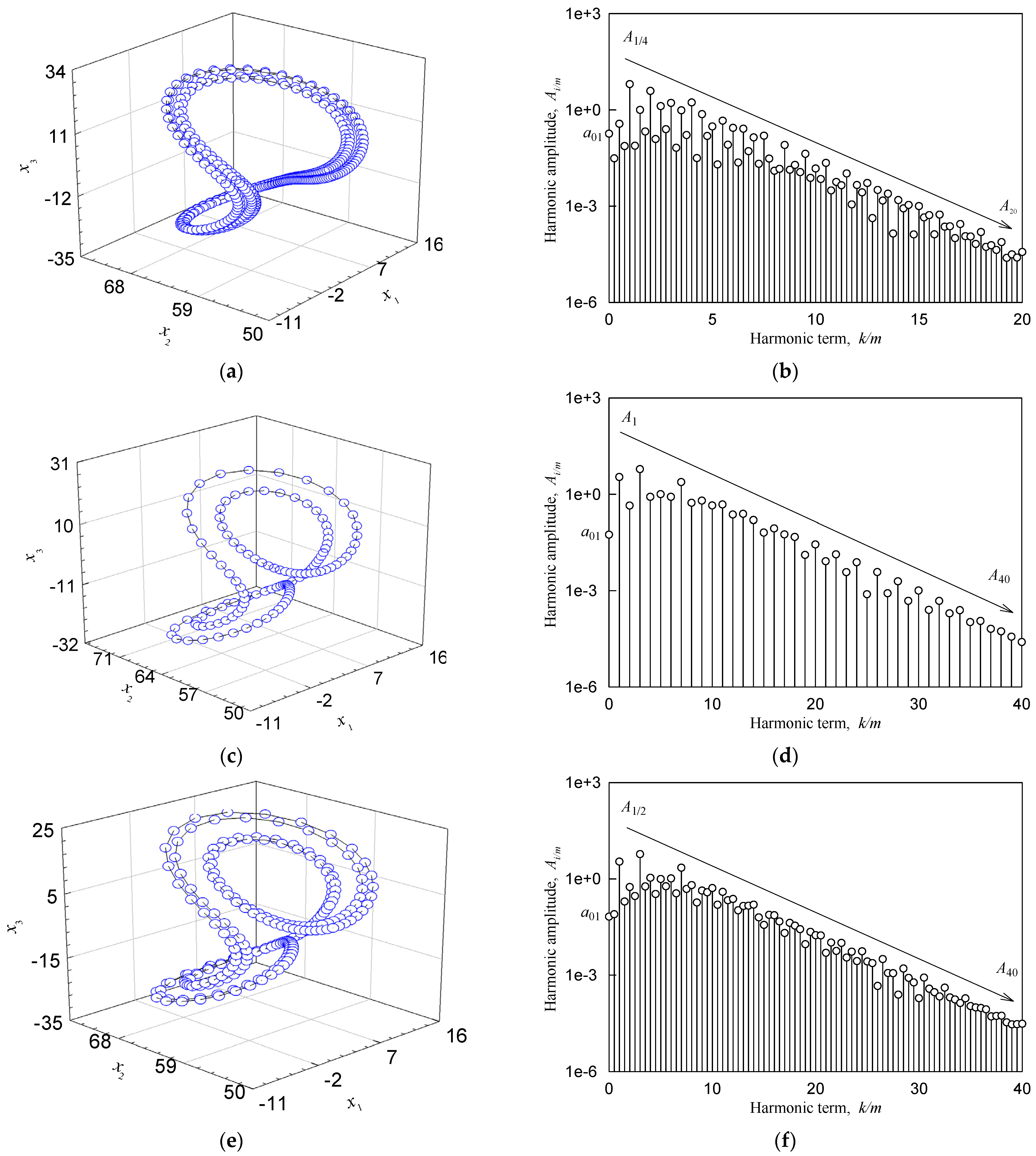
Figure 7a,b	6.46	(10.279434, 58.625938, 15.979369)	stable P-4
Figure 7c,d	3.16	(0.8259358, 53.755447, 2.0334629)	stable P-1
Figure 7e,f	3.14	(1.2720598, 52.714859, 1.8667075)	stable P-2

.

Figure 6a,b depicts the dynamic characteristics of stable period-1 motion when Ω = 6.5. The initial conditions for numerical integration are x₁ = 5.3227832, x₂ = 65.525293, and x₃= 19.302422. The analytical solution is based on 20 harmonic terms. In 3D displacement, the analytical and numerical solutions match very well. There is one obvious loop in 3D displacement, which verifies the motion is period-1. Since the value of the constant term a₀₁ is negative and the logarithmic coordinate is applied in the frequency spectrum, a₀₁ is omitted while presenting the frequency spectrum. The harmonic amplitudes in frequency spectrum are a₀₁ ≈ −0.0845, A₁ ≈ 6.6017, A₂ ≈ 2.9657, A₃ ≈ 2.5348, A₄ ≈ 1.6159, A₅ ≈ 0.4102, A₆ ≈ 0.4759, A₇ ≈ 0.1188, A₈ ≈ 0.1054, A₉ ≈ 0.0204, A₁₀ ≈ 0.0131, A₁₁ ≈ 4.5316 × 10⁻³, A₁₂ ≈ 3.1564 × 10⁻³, A₁₃ ≈ 1.2706 × 10⁻³, and A_k/m < 1 × 10⁻³ (k = 14~20; m = 1). The dynamic characteristics of stable period-2 motion are depicted in Figure 5c,d when Ω = 6.5. The initial conditions obtained from the analytical solution are x₁ = 9.7357535, x₂ = 55.891501, and x₃ = 13.299756. The analytical solution for this period-2 motion is based on 40 harmonic terms. It can be inferred from Figure 6c,d that the analytical and numerical solutions match very well. The motion repeats every two excitation periods. There are two loops in 3D displacement, which verifies the period-2 motion. The harmonic amplitudes for the analytical solution are a₀₁ ≈ 0.1796, A_1/2 ≈ 0.2342, A₁ ≈ 6.4068, A_3/2 ≈ 0.6465, A₂ ≈ 3.9061, A_5/2 ≈ 0.8423, A₃ ≈ 1.8311, A_7/2 ≈ 0.6390, A₄ ≈ 1.8305, A_9/2 ≈ 0.4933, A₅ ≈ 0.3914, A_11/2 ≈ 0.3164, A₆ ≈ 0.3853, A_13/2 ≈ 0.1888, A₇ ≈ 0.1820, A_15/2 ≈ 0.1173, and A_k < 0.05 (k = 16~40, m = 2). The dynamic characteristics of unstable period-1 motion are illustrated in Figure 6e,f when the disturbance frequency is 6.5. The initial conditions obtained from the analytical solution are x₁ = 7.5583327, x₂= 63.739675, and x₃= 18.706304. In the first several periods, the numerical and analytical solutions match well. But the complex curves shown in 3D displacement indicate that the period-1 motion is unstable. The harmonic amplitudes expressed in the frequency spectrum are a₀₁ =, A₁ ≈ 2.35206, A₃ ≈ 0.35233, A₅ ≈ 0.04062, A₇ ≈ 4.88 × 10⁻³, A₉ ≈ 5.89e × 10⁻⁴, A₁₁ ≈ 7.1 × 10⁻⁵, A₁₃ ≈ 8.6 × 10⁻⁶, and A₁₅ ≈ 1.03 × 10⁻⁶.

Figure 7a,b represents the dynamic characteristics of stable period-4 motion when Ω = 6.45. The initial conditions for numerical integration are x₁ = 10.279434, x₂ = 58.625938, and x₃ = 15.979369. The analytical solution for this period-4 motion is based on 80 harmonic terms. In 3D displacement, the analytical and numerical solutions match very well. The motion repeats every four excitation periods, which indicates that the motion of the system is period-4 motion. The harmonic amplitudes are a₀₁ ≈ 0.1808, A_1/4 ≈ 0.0306, A_1/2 ≈ 0.3646, A_3/4 ≈ 0.0738, A₁ ≈ 6.3280, A_5/4 ≈ 0.0758, A_3/2 ≈ 0.9903, A_7/4 ≈ 0.2108, A₂ ≈ 3.8709, A_9/4 ≈ 0.1220, A_5/2 ≈ 1.3008, A_11/4 ≈ 0.2486, A₃ ≈ 1.6423, A_13/4 ≈ 0.0653, A_7/2 ≈ 0.9600, A_15/4 ≈ 0.1633, A₄ ≈ 1.6915, A_17/4 ≈ 0.0312, A_9/2 ≈ 0.7286, A_19/4 ≈ 0.1521, A₅ ≈ 0.3028, and A_k/m < 1 × 10⁻¹ (k = 21~80; m = 4). The dynamic characteristics of stable period-1 motion are represented in Figure 7c,d when the disturbance frequency is 3.16. The initial conditions for a numerical solution are x₁ = 0.8259358, x₂ = 53.755447, and x₃ = 2.0334629. The number of harmonic terms increases with a lower disturbance frequency. Therefore, the analytical solution for this period-1 motion is based on 40 harmonic terms. It can be inferred from the 3D displacement that the numerical solution is almost the same as the analytical solution. There is one clear loop in 3D displacement, which indicates that the motion is stable period-1 motion. The harmonic amplitudes are a₀₁ ≈ 0.0557, A₁ ≈ 3.4044, A₂ ≈ 0.4410, A₃ ≈ 6.0229, A₅ ≈ 0.9966, A₆ ≈ 0.8270, A₇ ≈ 2.3835, A₈ ≈ 0.5349, A₉ ≈ 0.6293, A₁₀ ≈ 0.4421, A₁₁ ≈ 0.4750, A₁₂ ≈ 0.2319, A₁₃ ≈ 0.2430, A₁₄ ≈ 1570, and A_k/m < 1 × 10⁻¹ (k = 15~40; m = 1). Figure 7e,f describes the dynamic characteristics of stable period-2 motion when Ω = 3.14. The initial conditions for numerical integration are x₁ = 1.2720598, x₂ = 52.714859, and x₃ = 1.8667075. The analytical solution is based on 80 harmonic terms when analyzing asymmetric period-2 motion when Ω = 3.14. The analytical and numerical solutions match very well in the 3D displacement. The motion repeats every two excitation periods. The harmonic amplitudes in frequency spectrum are a₀₁ ≈ 0.0659, A_1/2 ≈ 0783, A₁ ≈ 3.4174, A_3/2 ≈ 0.1954, A₂ ≈ 0.5515, A_5/2 ≈ 0.2890, A₃ ≈ 5.8348, A_7/2 ≈ 0.5760, A₄ ≈ 1.0731, A_9/2 ≈ 0.3334, A₅ ≈ 0.9797, A_11/2 ≈ 0.5831, A₆ ≈ 1.0233, A_13/2 ≈ 0.3495, A₇ ≈ 2.2083, A_15/2 ≈ 0.4824, A₈ ≈ 0.6315, and A_k/m < 4 × 10⁻⁴(k = 17~80, m = 2).

5. Conclusions

The analytical variations of nonlinear currents and voltages for brushless DC motors were obtained in this paper through the application of the generalized harmonic balance method. The nonlinear model of the brushless DC model was transformed into a Fourier series system with coefficients varying with time slowly. The main conclusion can be summarized as follows:

(1) The process from period-1 motion evolutions is achieved analytically. The independent period-1 motions and their bifurcations were observed. With the analytical solution, the initial condition for numerical integration can be easily determined and the characteristics of the dynamic system for such brushless DC motors can also be investigated. With the application of the generalized harmonic method, detailed bifurcations revealing the relationship among the independent period motions can be depicted, which is unattainable with numerical integration.

(2) For the independent period-1 motions, the closed curves in harmonic amplitude are joined up by non-sequence stable and unstable routes. The continuous curves indicate that the unstable motions are connected with cyclic stable motions.

(3) The harmonic amplitude results depicted that the closer the disturbance frequency is to zero, the more complex the motions are. The numerical illustrations directly show that the analytical and numerical results match very well.

Applying the generalized harmonic method to other nonlinear differential equations and dynamic systems will be an appropriate subject for future investigations.