A Trajectory Optimisation-Based Incremental Learning Strategy for Learning from Demonstration
Abstract
:1. Introduction
- A straightforward idea is to create a new demonstration for the new situation. However, redemonstration is time consuming as the experimental environment needs to be set up again [3]. To mitigate the problem, it will be beneficial to reuse part of the originally created demonstration to adaptively generate a new trajectory (namely, an extended demonstration) for the new target;
- DMP is a one-shot learning model, which means that when the extended demonstration is learned, the knowledge gained from the previous demonstration is forgotten. Therefore, it is imperative to develop an incremental learning mechanism for the DMP model to improve its generalisation capability for various situations.
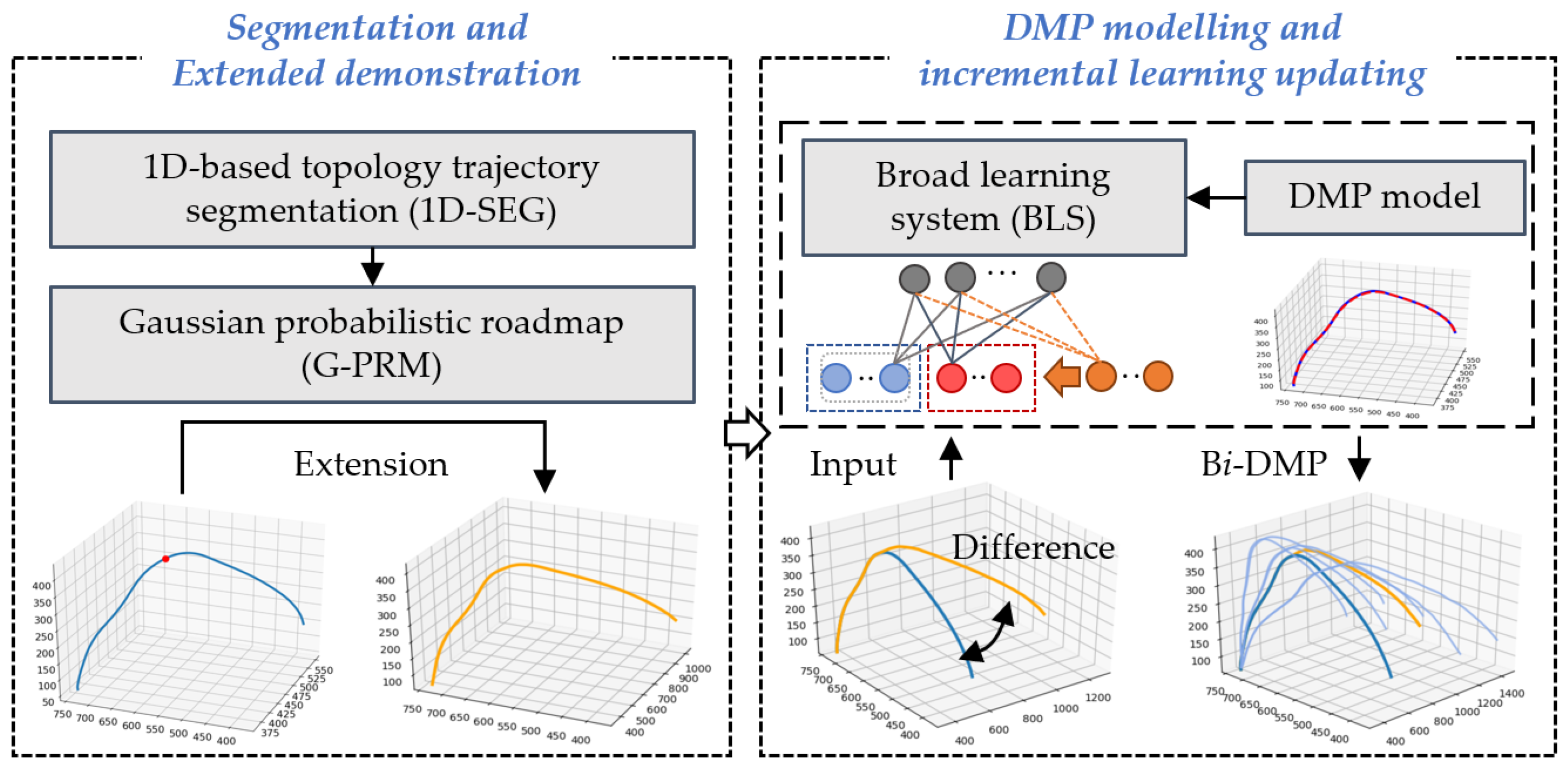
- Segmentation and extended demonstration: 1D-SEG is combined with G-PRM to generate an extended demonstration by incorporating the features of the original demonstration, so that fewer demonstrations are required to minimise the cost of data collection;
- DMP modelling and incremental learning update: The BLS learns the difference between the extended demonstration and the original demonstration by incrementally increasing the number of network nodes (hereafter referred to as additional enhancement nodes). The force item of the previously constructed DMP model is updated with the results generated by the BLS.
- Electric vehicle (EV) battery disassembly cases and an experimental platform were used to verify the effectiveness of the developed approach. Based on the approach, the successful disassembly of nuts and battery cells were achieved.
2. Review of Related Work
2.1. Trajectory Generation
2.2. DMP-Based Optimisation
- Mimicking the geometric features of the original demonstration proves challenging. There is a lack of research in designing an efficient sampling strategy and similarity measurement to avoid sharp turns in generated trajectories and enhance their resemblance to the demonstrations.
- These approaches neglect integrating the incremental learning function within DMP. When presented with a new demonstration, the DMP model has to be retrained. Meanwhile, there is a shortage of industrial applications leveraging incremental learning.
3. Research Methodology
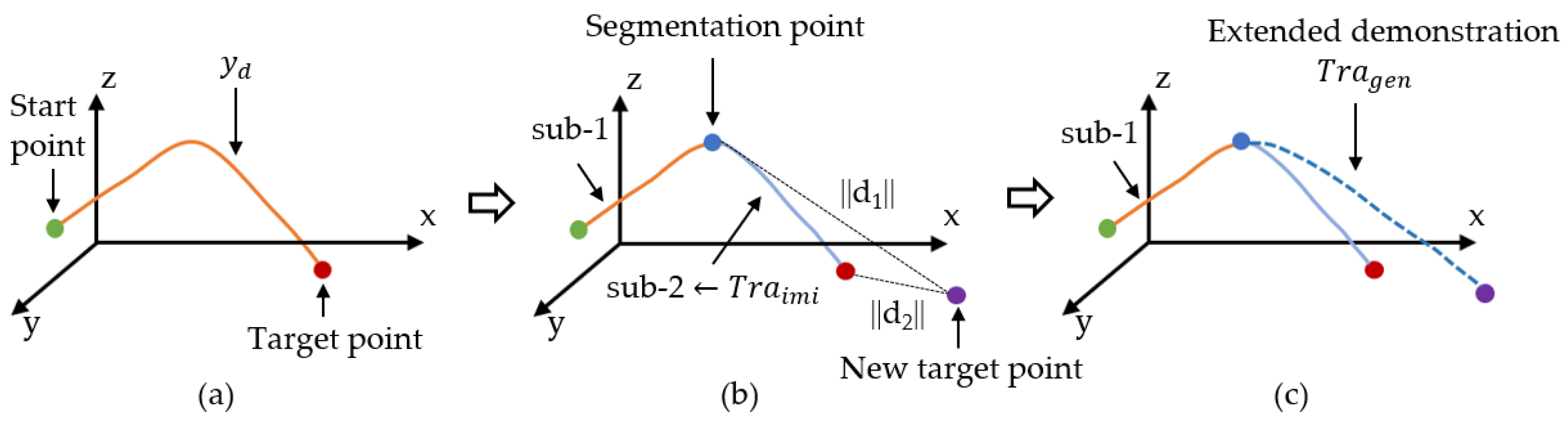
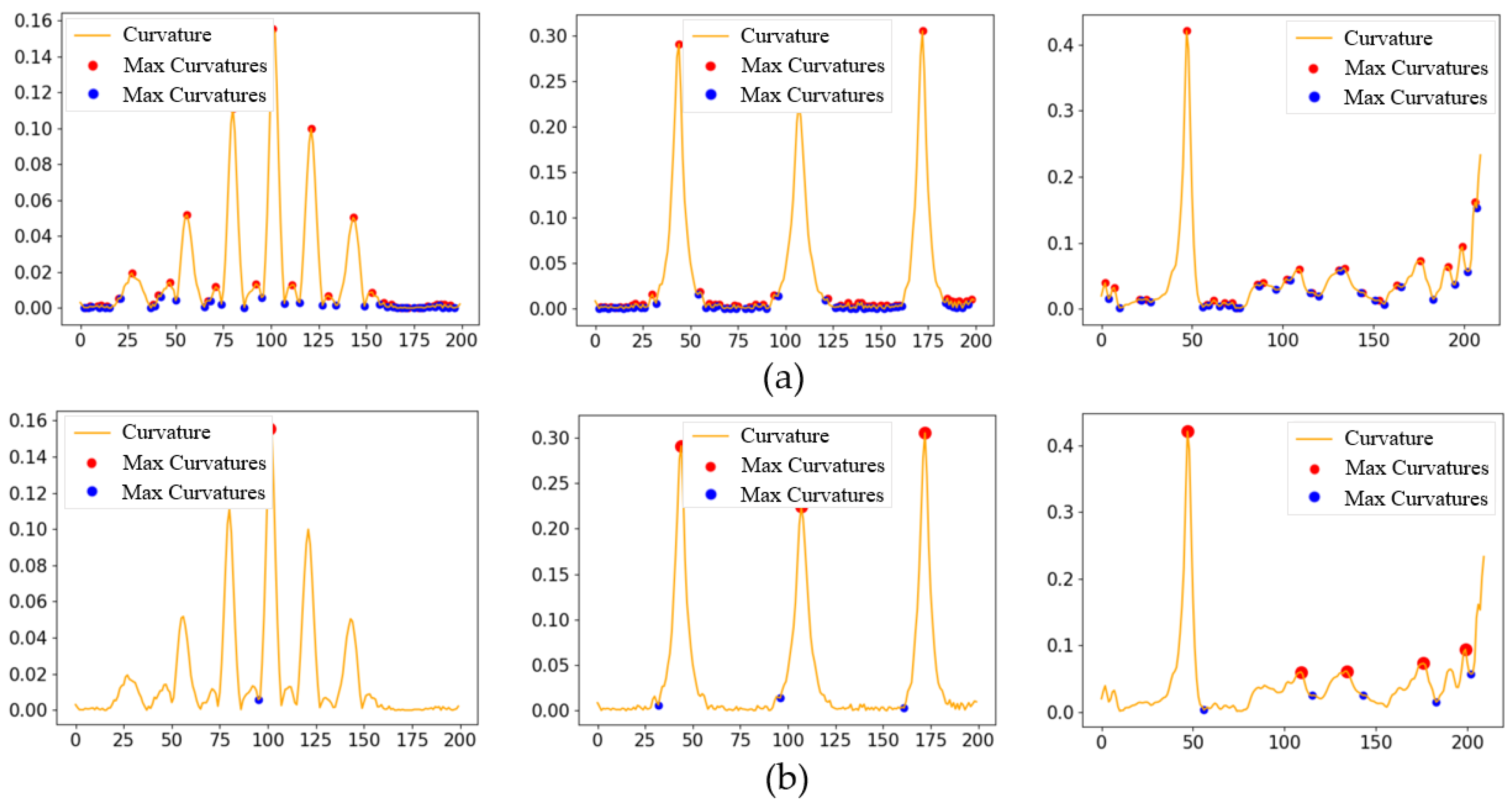
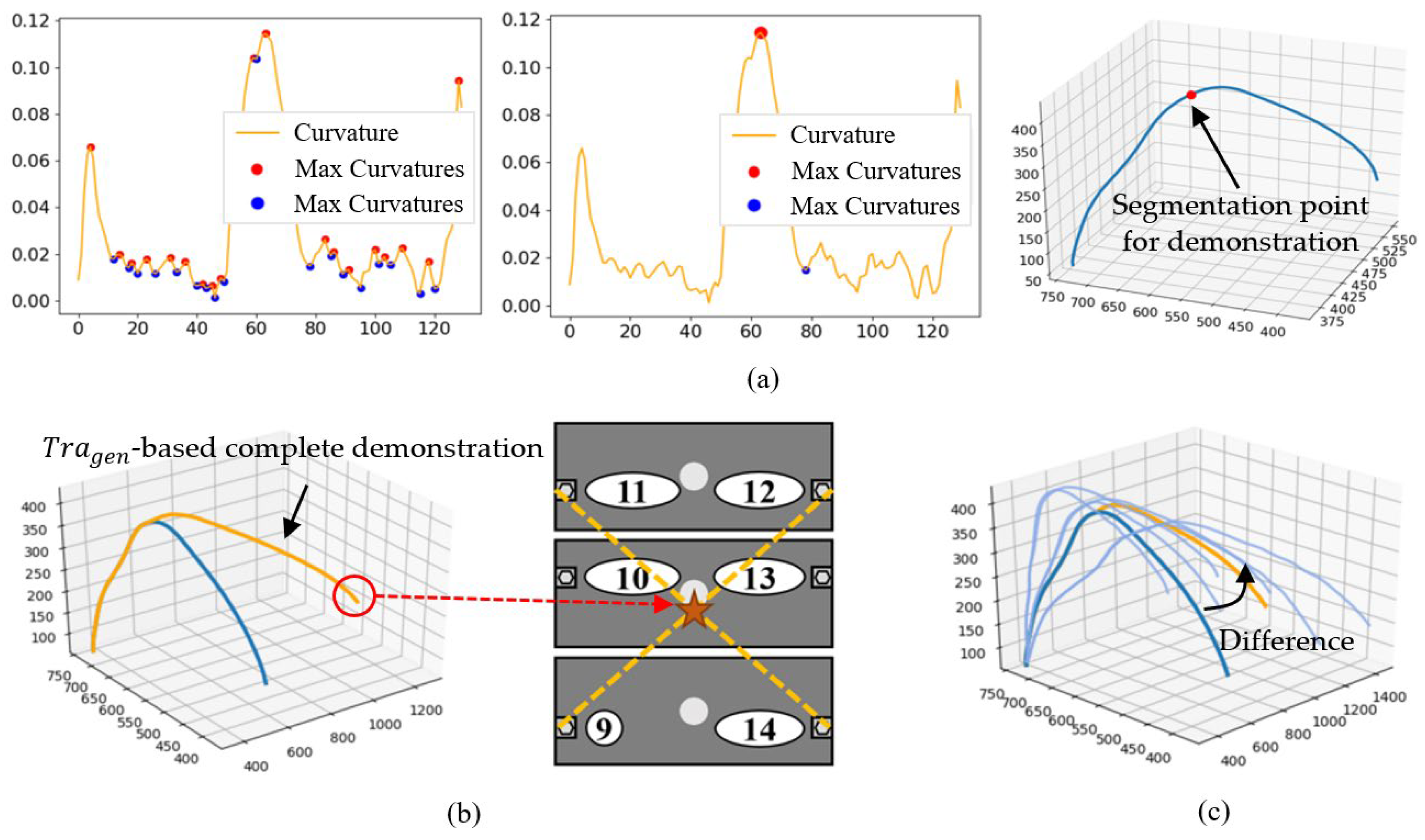
3.1. Segmentation of Demonstration
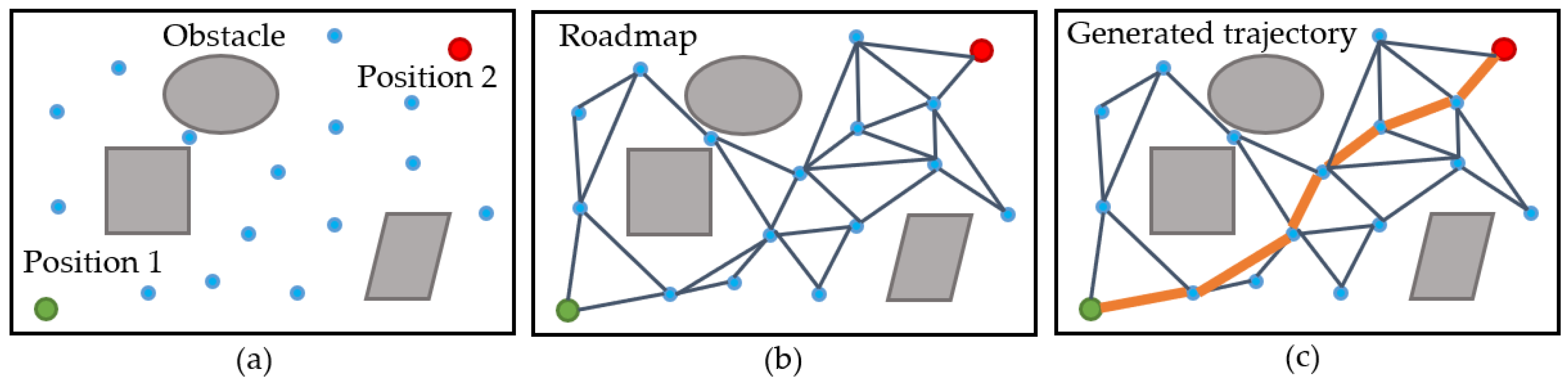
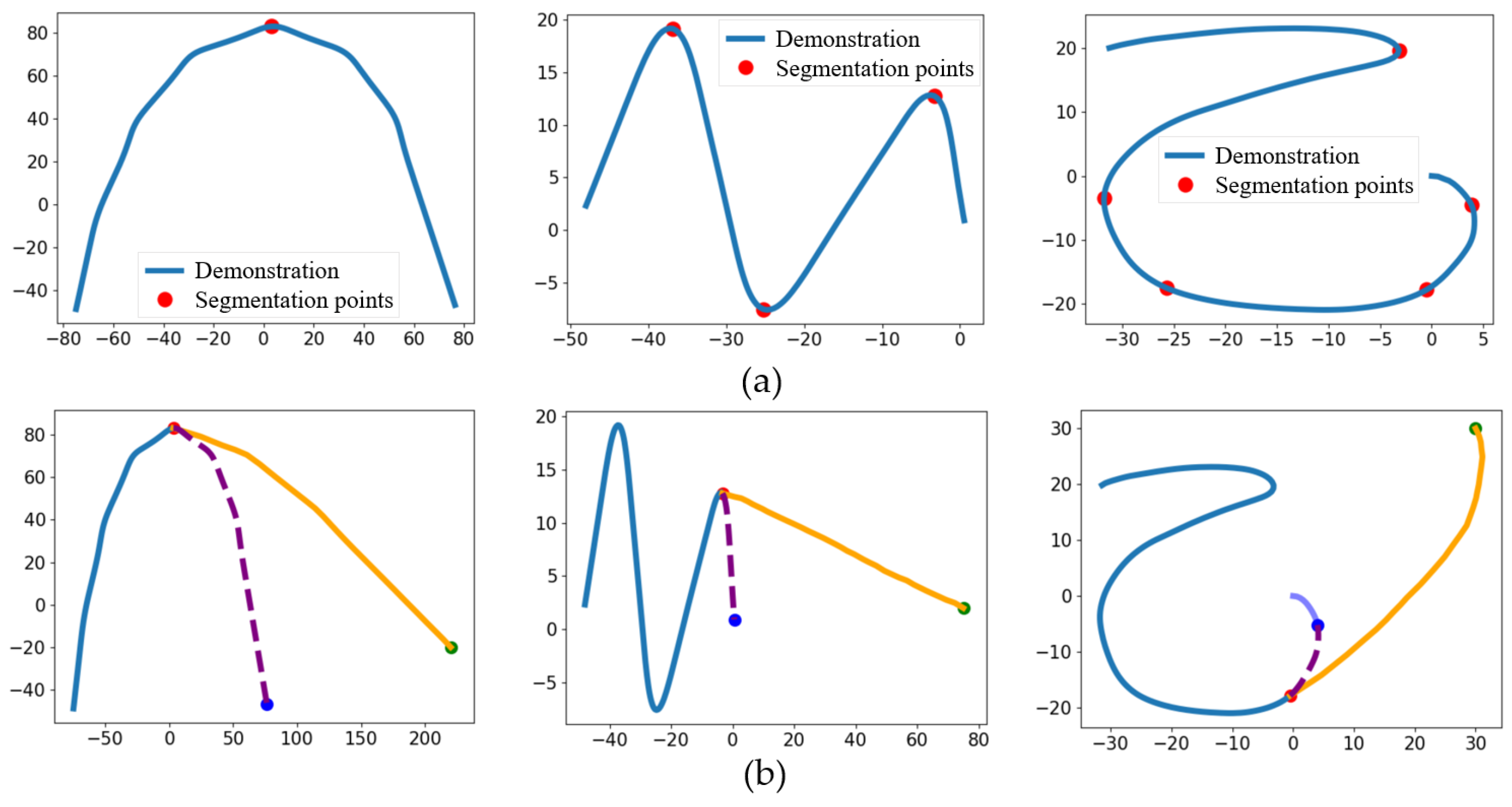
3.2. Extended Demonstration via G-PRM
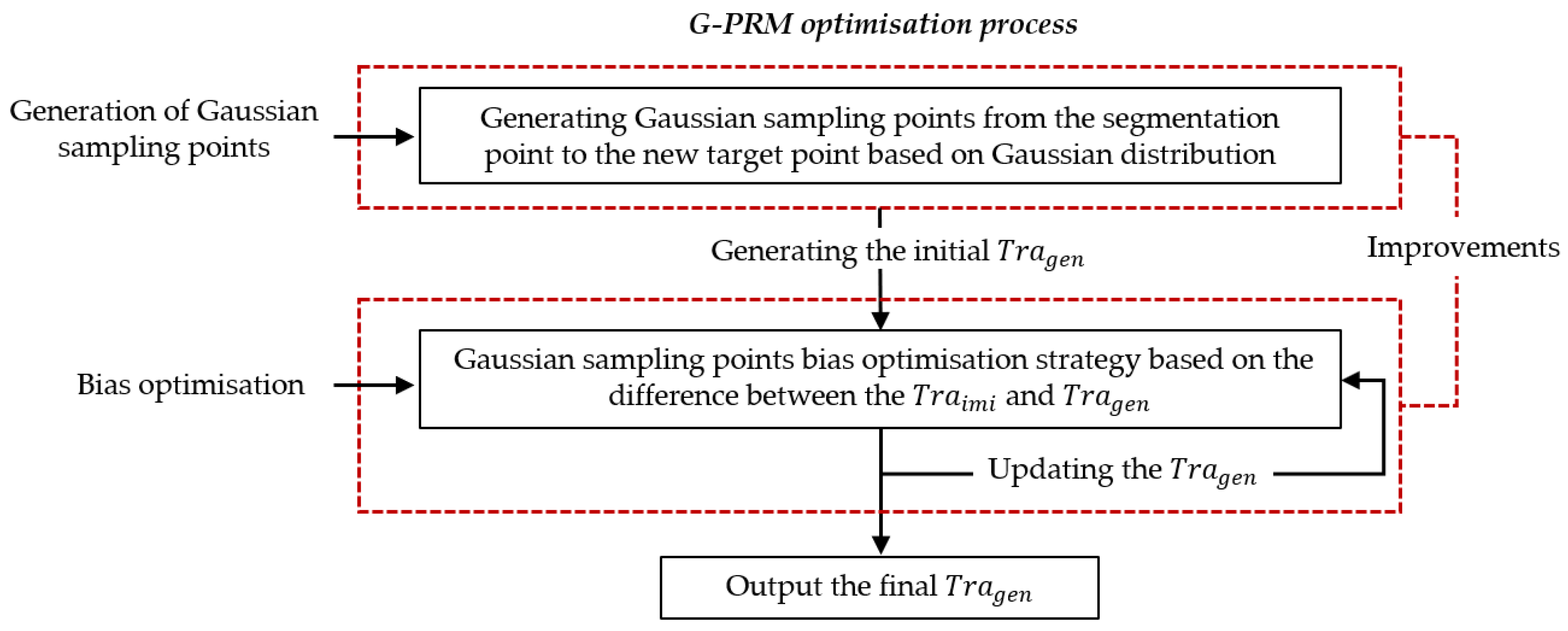
3.2.1. Generation of Sampling Points
3.2.2. Bias Optimisation
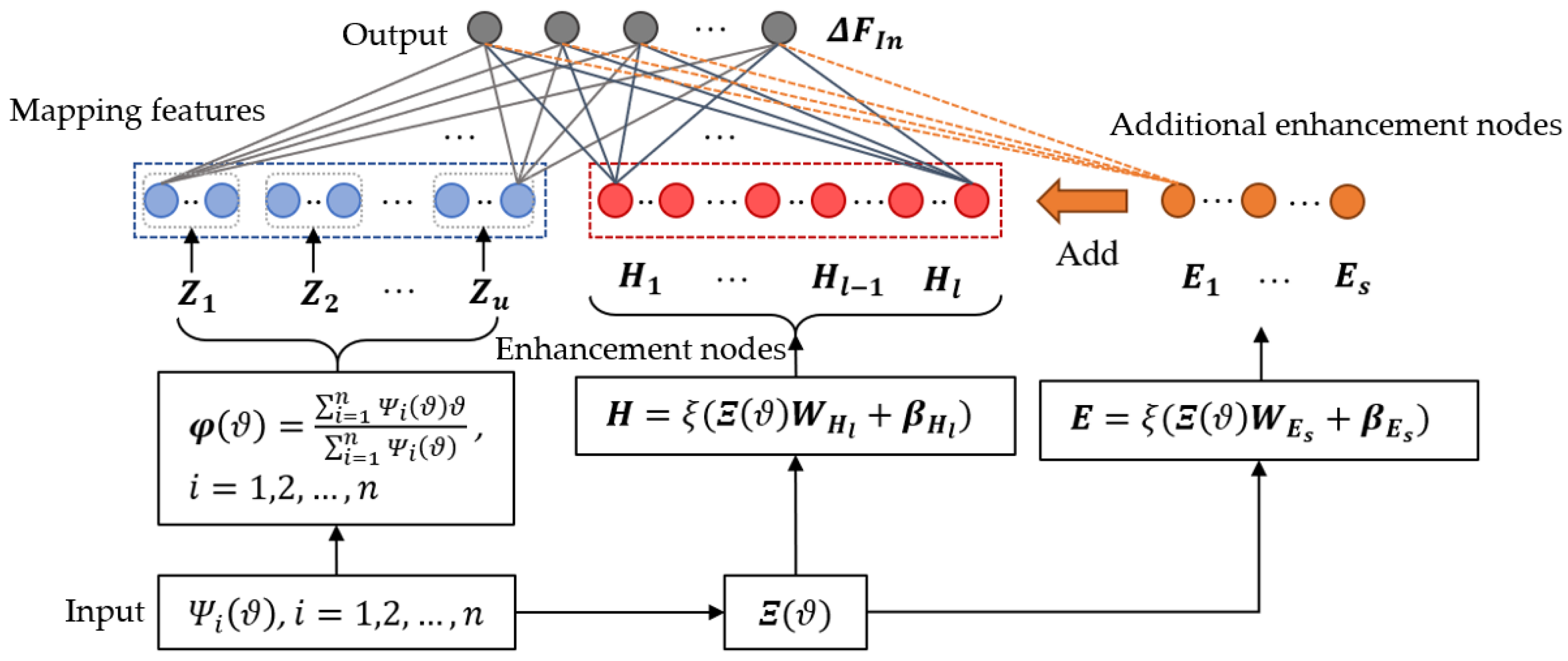
3.3. DMP Modelling and Incremental Learning Updating
3.3.1. Modelling of DMP
3.3.2. Bi-DMP for Incremental Learning Updating
3.3.3. Iterative Update of Force Item under Multi-Demonstrations
4. Experiments and Case Studies
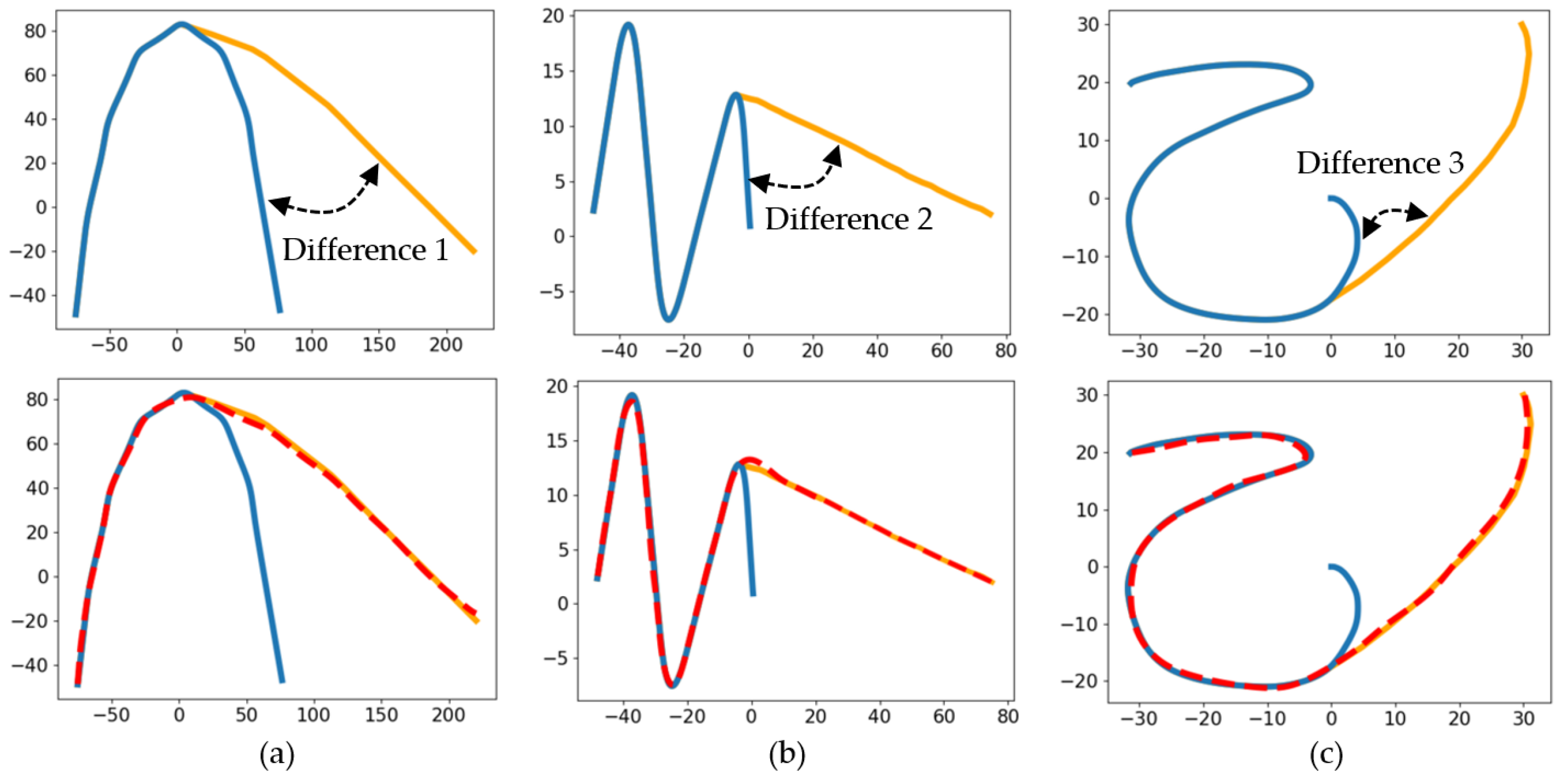
4.1. Extended Demonstration Based on 1D-SEG and G-PRM
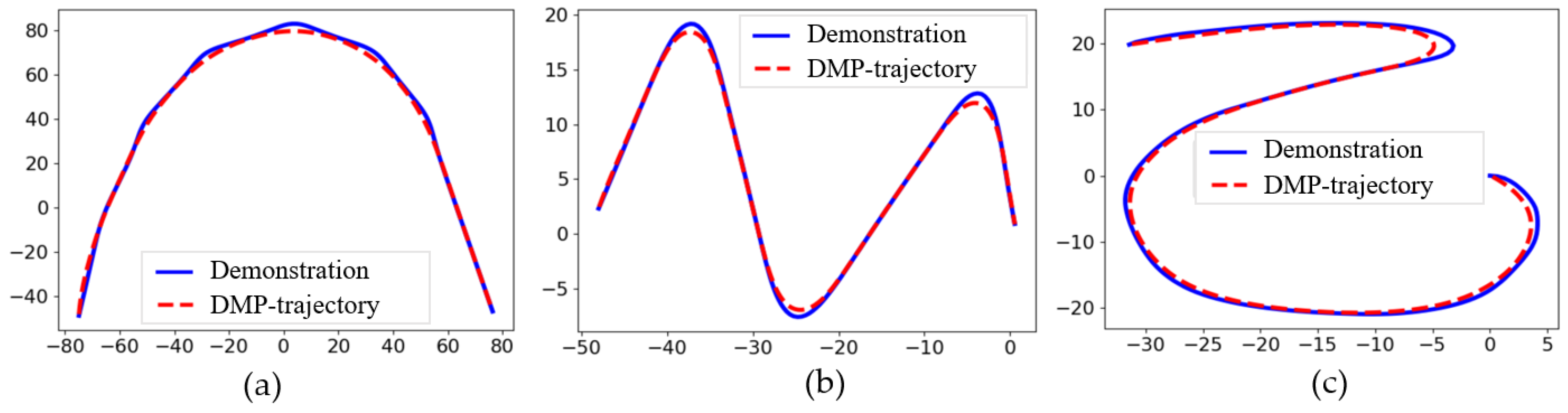
4.2. Modelling of DMP
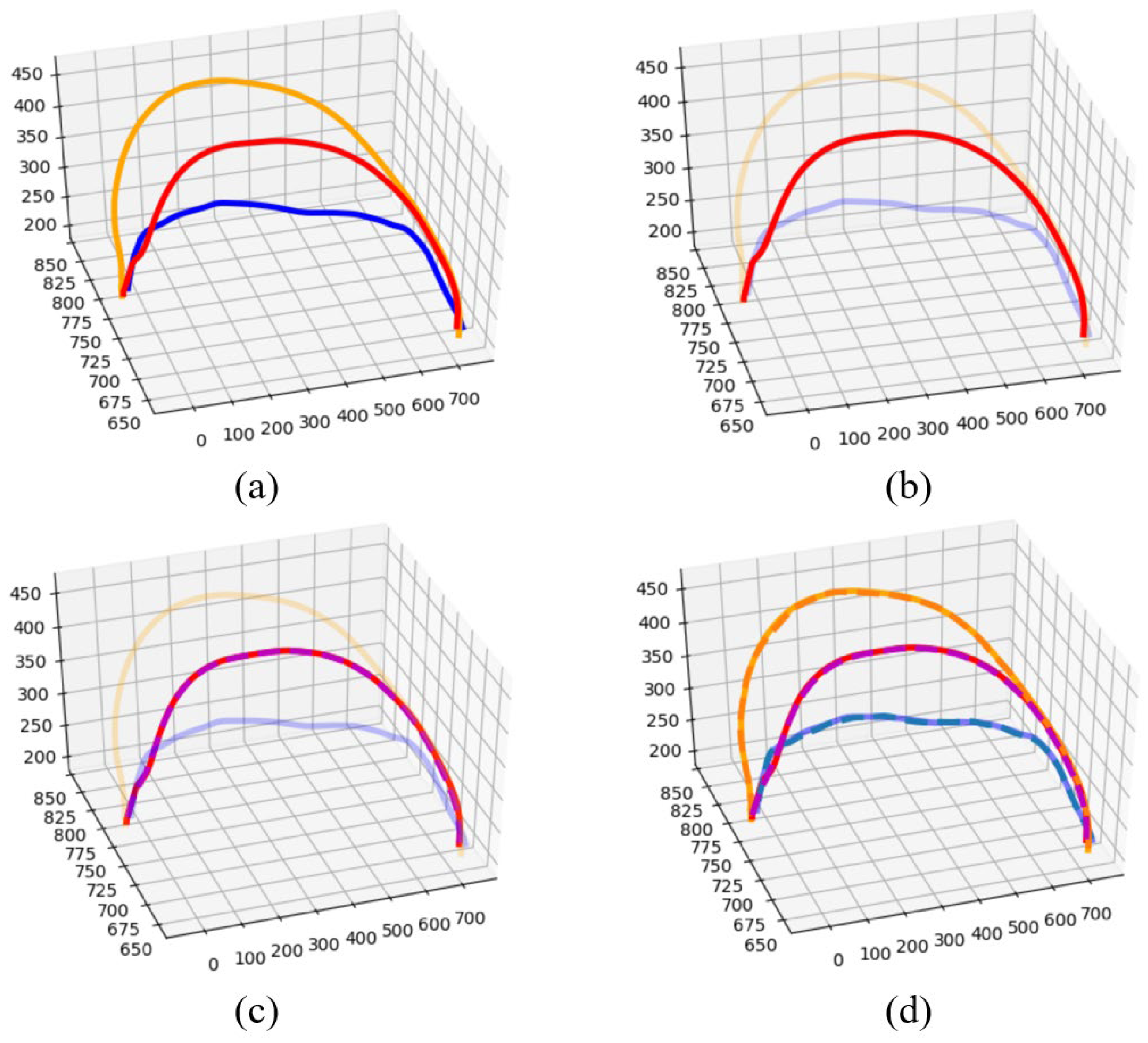
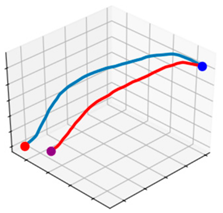
4.3. Bi-DMP for Extended Demonstration
4.4. Case Study 1—Pick-and-Place-Based Bi-DMP
4.5. Case Study 2—Unscrewing Nuts and Battery Cell Disassembly
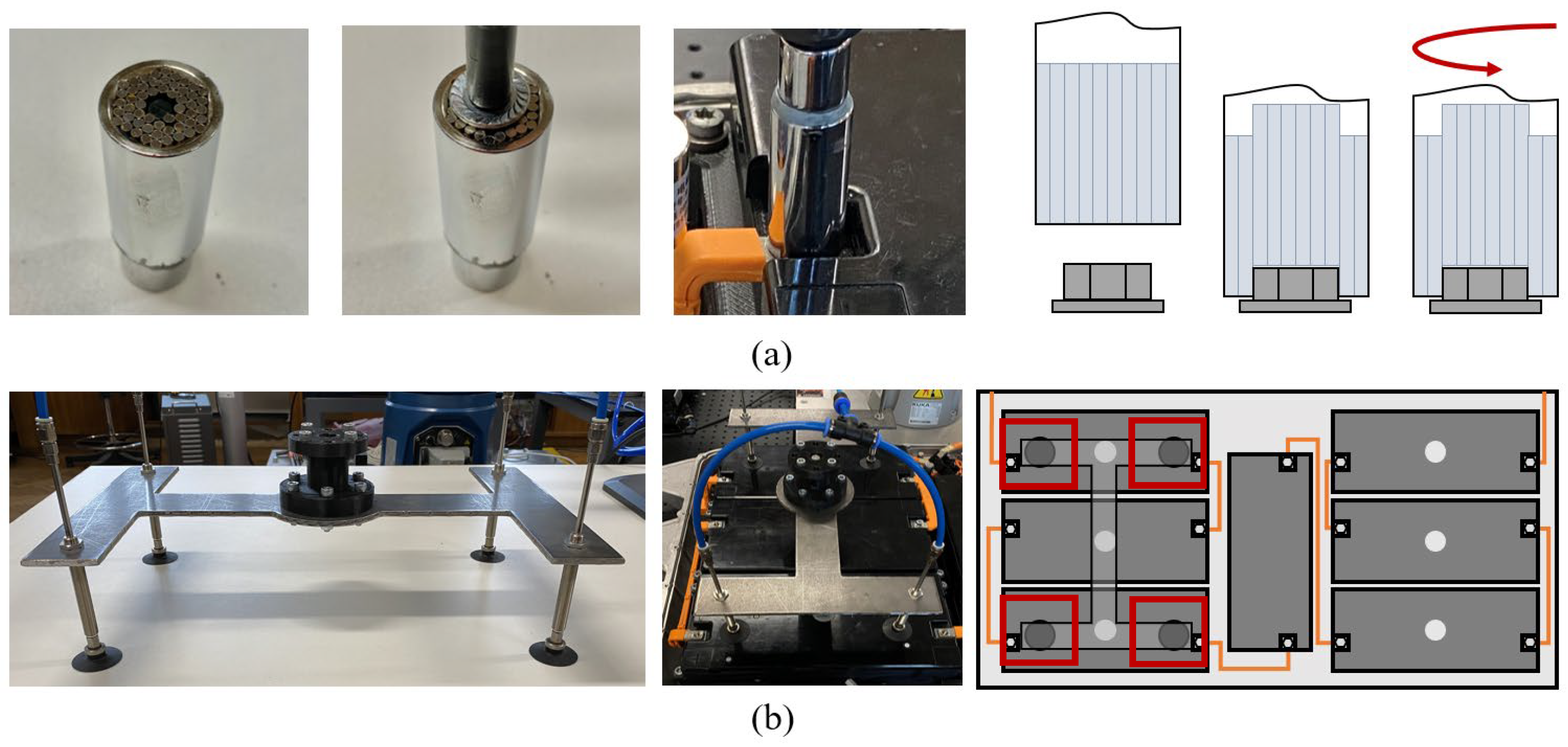
4.5.1. Experiment Platform and Problem Descriptions
4.5.2. Design and Use of End-Effectors
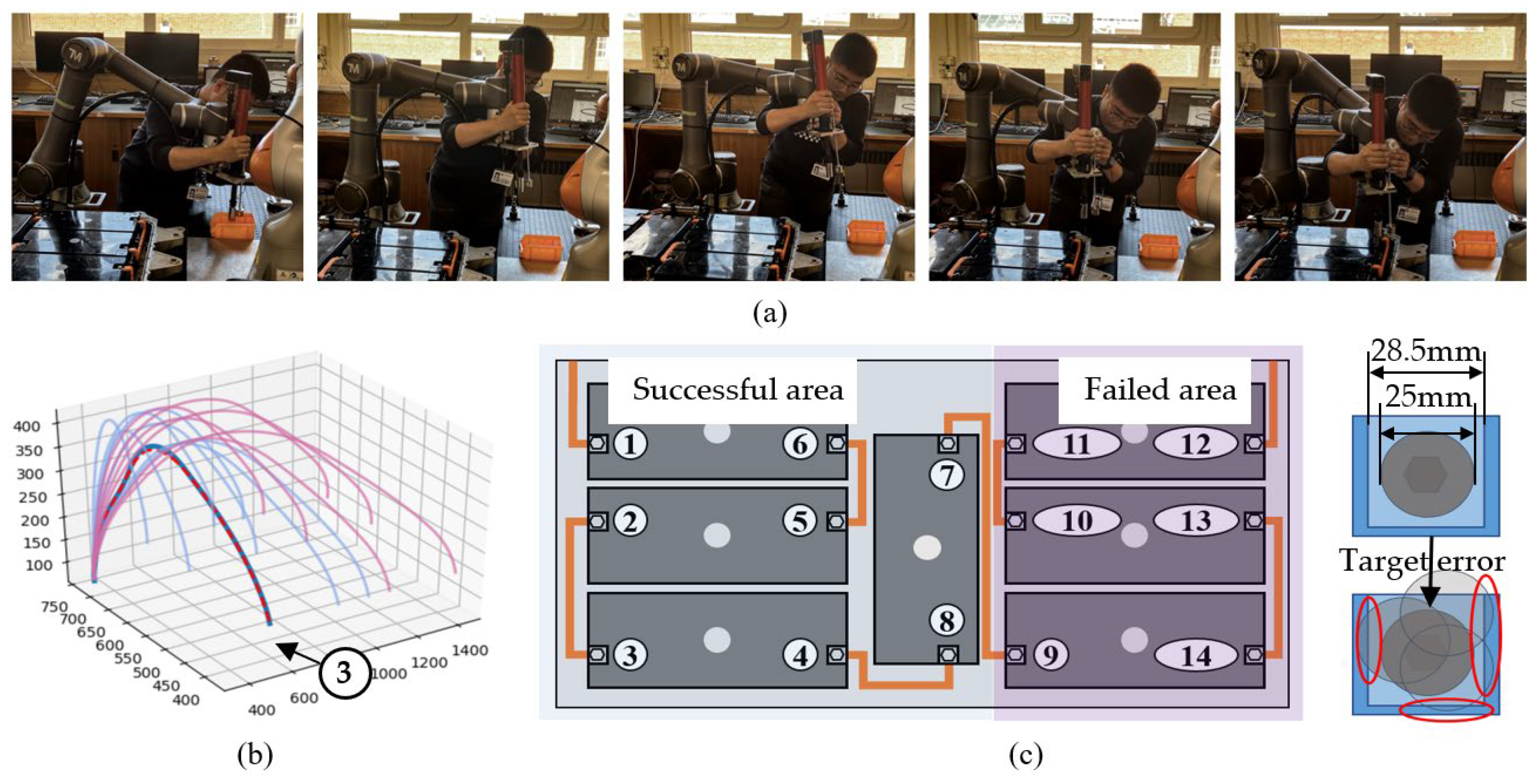
4.5.3. Demonstration and Implementation
5. Discussion
5.1. Time Complexity Analysis
5.2. Trajectory Generation Analysis among Different Algorithms
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zaatari, S.E.; Wang, Y.; Li, W.; Peng, Y. iTP-LfD: Improved task parametrised learning from demonstration for adaptive path generation of cobot. Robot. Cim-Int. Manuf. 2021, 69, 102109. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Hu, Y.D.; Zaatari, S.E.; Li, W.D.; Zhou, Y. Optimised Learning from Demonstrations for Collaborative Robots. Robot. Cim-Int. Manuf. 2021, 71, 102169. [Google Scholar] [CrossRef]
- Zhu, J.; Gienger, M.; Kober, J. Learning Task-Parameterized Skills From Few Demonstrations. IEEE Robot. Autom. Lett. 2022, 7, 4063–4070. [Google Scholar] [CrossRef]
- Chi, M.; Yao, Y.; Liu, Y.; Zhong, M. Learning, Generalization, and Obstacle Avoidance with Dynamic Movement Primitives and Dynamic Potential Fields. Appl. Sci. 2019, 9, 1535. [Google Scholar] [CrossRef]
- Zhai, D.-H.; Xia, Z.; Wu, H.; Xia, Y. A Motion Planning Method for Robots Based on DMPs and Modified Obstacle-Avoiding Algorithm. IEEE Trans. Automat. Sci. Eng. 2022, 20, 2678–2688. [Google Scholar] [CrossRef]
- Davchev, T.; Luck, K.S.; Burke, M.; Meier, F.; Schaal, S.; Ramamoorthy, S. Residual Learning from Demonstration: Adapting DMPs for Contact-Rich Manipulation. IEEE Robot. Autom. Lett. 2022, 7, 4488–4495. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, N.; Shi, D. DMPs-based skill learning for redundant dual-arm robotic synchronized cooperative manipulation. Complex Intell. Syst. 2022, 8, 2873–2882. [Google Scholar] [CrossRef]
- Yang, C.; Chen, C.; He, W.; Cui, R.; Li, Z. Robot Learning System Based on Adaptive Neural Control and Dynamic Movement Primitives. IEEE Trans. Neural Netw. Learning Syst. 2019, 30, 777–787. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.; Jiang, G.; Zhao, F.; Wu, Y.; Yue, Y.; Mei, X. Dynamic Skill Learning from Human Demonstration Based on the Human Arm Stiffness Estimation Model and Riemannian DMP. IEEE/ASME Trans. Mechatron. 2023, 28, 1149–1160. [Google Scholar] [CrossRef]
- Arguz, S.H.; Ertugrul, S.; Altun, K. Experimental Evaluation of the Success of Peg-in-Hole Tasks Learned from Demonstration. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022; pp. 861–866. [Google Scholar] [CrossRef]
- Peng, J.-W.; Hu, M.-C.; Chu, W.-T. An imitation learning framework for generating multi-modal trajectories from unstructured demonstrations. Neurocomputing 2022, 500, 712–723. [Google Scholar] [CrossRef]
- Li, X.; Gao, X.; Zhang, W.; Hao, L. Smooth and collision-free trajectory generation in cluttered environments using cubic B-spline form. Mech. Mach. Theory. 2022, 169, 104606. [Google Scholar] [CrossRef]
- Hüppi, M.; Bartolomei, L.; Mascaro, R.; Chli, M. T-PRM: Temporal Probabilistic Roadmap for Path Planning in Dynamic Environments. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 10320–10327. [Google Scholar] [CrossRef]
- Saveriano, M.; Abu-Dakka, F.J.; Kramberger, A.; Peternel, L. Dynamic movement primitives in robotics: A tutorial survey. Int. J. Robot. Res. 2023, 42, 1133–1184. [Google Scholar] [CrossRef]
- Si, W.; Wang, N.; Yang, C. Composite dynamic movement primitives based on neural networks for human–robot skill transfer. Neural Comput. Appl. 2023, 35, 23283–23293. [Google Scholar] [CrossRef]
- Noohian, A.; Raisi, M.; Khodaygan, S. A Framework for Learning Dynamic Movement Primitives with Deep Reinforcement Learning. In Proceedings of the 2022 10th RSI International Conference on Robotics and Mechatronics (ICRoM), Tehran, Islamic Republic of Iran, 15–18 November 2022; pp. 329–334. [Google Scholar] [CrossRef]
- Kim, W.; Lee, C.; Kim, H.J. Learning and Generalization of Dynamic Movement Primitives by Hierarchical Deep Reinforcement Learning from Demonstration. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 3117–3123. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, N.; Li, M.; Yang, C. Incremental Motor Skill Learning and Generalization From Human Dynamic Reactions Based on Dynamic Movement Primitives and Fuzzy Logic System. IEEE Trans. Fuzzy Syst. 2022, 30, 1506–1515. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, N.; Li, Q.; Yang, C. A trajectory and force dual-incremental robot skill learning and generalization framework using improved dynamical movement primitives and adaptive neural network control. Neurocomputing 2023, 521, 146–159. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Liu, Z. Broad Learning System: An Effective and Efficient Incremental Learning System without the Need for Deep Architecture. IEEE Trans. Neur. Net. Lear. Syst. 2018, 29, 10–24. [Google Scholar] [CrossRef]
- Hu, J.; Xiong, R. Trajectory generation with multi-stage cost functions learned from demonstrations. Robot. Auton. Syst. 2019, 117, 57–67. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, X.; Xie, Z.; Li, F.; Gu, X. Online obstacle avoidance path planning and application for arc welding robot. Robot. Cim-Int. Manuf. 2022, 78, 102413. [Google Scholar] [CrossRef]
- Park, D.H.; Hoffmann, H.; Pastor, P.; Schaal, S. Movement reproduction and obstacle avoidance with dynamic movement primitives and potential fields. In Proceedings of the 2008 8th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2008), Daejeon, Republic of Korea, 3 December 2008; pp. 91–98. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Nakanishi, J.; Hoffmann, H.; Pastor, P.; Schaal, S. Dynamical Movement Primitives: Learning Attractor Models for Motor Behaviors. Neural Comput. 2013, 25, 328–373. [Google Scholar] [CrossRef]
- Teng, T.; Gatti, M.; Poni, S.; Caldwell, D.; Chen, F. Fuzzy dynamical system for robot learning motion skills from human demonstration. Robot Auton. Syst. 2023, 164, 104406. [Google Scholar] [CrossRef]
- Ding, G.; Liu, Y.; Zang, X.; Zhang, X.; Liu, G.; Zhao, J. A Task-Learning Strategy for Robotic Assembly Tasks from Human Demonstrations. Sensors 2020, 20, 5505. [Google Scholar] [CrossRef] [PubMed]
- Si, W.; Yue, T.; Guan, Y.; Wang, N.; Yang, C. A Novel Robot Skill Learning Framework Based on Bilateral Teleoperation. In Proceedings of the 2022 IEEE 18th International Conference on Automation Science and Engineering (CASE), Mexico City, Mexico, 20–24 August 2022; pp. 758–763. [Google Scholar] [CrossRef]
- Iturrate, I.; Roberge, E.; Ostergaard, E.H.; Duchaine, V.; Savarimuthu, T.R. Improving the Generalizability of Robot Assembly Tasks Learned from Demonstration via CNN-based Segmentation. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019; pp. 553–560. [Google Scholar] [CrossRef]
- Fan, J.; Chen, X.; Liang, X. UAV trajectory planning based on bi-directional APF-RRT* algorithm with goal-biased. Expert Syst. Appl. 2023, 213, 119137. [Google Scholar] [CrossRef]
- Weinkauf, T.; Gingold, Y.; Sorkine, O. Topology-based Smoothing of 2D Scalar Fields with C1-Continuity. Comput Graph Forum. 2010, 29, 1221–1230. [Google Scholar] [CrossRef]
- Ichter, B.; Schmerling, E.; Lee, T.-W.E.; Faust, A. Learned Critical Probabilistic Roadmaps for Robotic Motion Planning. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–15 August 2020; pp. 9535–9541. [Google Scholar] [CrossRef]
- Eiter, T.; Mannila, H. Computing Discrete Fréchet Distance. 1994. Available online: https://www.researchgate.net/profile/Thomas-Eiter-2/publication/228723178_Computing_Discrete_Frechet_Distance/links/5714d93908aebda86c0d1a7b/Computing-Discrete-Frechet-Distance.pdf (accessed on 2 June 2024).
- Wang, R.; Wu, Y.; Chan, W.L.; Tee, K.P. Dynamic Movement Primitives Plus: For enhanced reproduction quality and efficient trajectory modification using truncated kernels and Local Biases. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 3765–3771. [Google Scholar] [CrossRef]
- Khansari, Billard, TRO 2011, LASA Handwriting Dataset, Stable Estimator of Dynamical Systems (SEDS). 24 March 2015. Available online: https://cs.stanford.edu/people/khansari/download.html#LearningLyapunovFunctions (accessed on 2 June 2024).
- Avaei, A.; Van Der Spaa, L.; Peternel, L.; Kober, J. An Incremental Inverse Reinforcement Learning Approach for Motion Planning with Separated Path and Velocity Preferences. Robotics 2023, 12, 61. [Google Scholar] [CrossRef]
- Xing, H.; Torabi, A.; Ding, L.; Gao, H.; Li, W.; Mushahwar, V.K.; Tavakoli, M. Human-Robot Collaboration for Heavy Object Manipulation: Kinesthetic Teaching of the Role of Wheeled Mobile Manipulator. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 2962–2969. [Google Scholar] [CrossRef]
- Liang, Y.C.; Li, W.D.; Lu, X.; Wang, S. Fog computing and convolutional neural network enabled prognosis for machining process optimization. J. Manuf. Syst. 2019, 52, 32–42. [Google Scholar] [CrossRef]
- Curry, D.; Dagli, C. Computational complexity measures for multi-objective optimization problems. Procedia Comput. Sci. 2014, 36, 185–191. [Google Scholar] [CrossRef]
- Bianchini, M.; Scarselli, F. On the complexity of neural network classifiers: A comparison between shallow and deep architectures. IEEE Trans. Neural Netw. Learn Syst. 2014, 25, 1553–1565. [Google Scholar] [CrossRef]







| 1 | |||||||
|---|---|---|---|---|---|---|---|
| Error (mm) | No. 1 | No. 2 | No. 3 | No. 4 | No. 5 | No. 6 | No. 7 |
| 0.404 | 0.260 | 0 | 0.989 | 1.023 | 1.069 | 1.487 | |
| 2 | |||||||
| Error (mm) | No. 8 | No. 9 | No. 10 | No. 11 | No. 12 | No. 13 | No. 14 |
| 1.431 | 1.751 | 1.760 | 1.787 | 2.760 | 2.743 | 2.730 | |
| Error (mm) | No. 9 | No. 10 | No. 11 | No. 12 | No. 13 | No. 14 |
|---|---|---|---|---|---|---|
| 1.477 | 1.248 | 1.477 | 1.477 | 1.248 | 1.477 |
| Algorithms | Time Complexity | Notes |
|---|---|---|
| CNN-based | : the number of samples, : the dimension of input data (feature number), : the size of convolution kernel, : the number of convolution kernels, : the number of layers, : the number of iterations of expectation–maximisation (EM) algorithm, : the number of Gaussian clusters, : the number of sampling knots, : the number of sampling points, : the number of BLS nodes | |
| TP-GMM | ||
| GMM | ||
| BLS | ||
| DMP | ||
| RRT | ||
| PRM |
| Algorithms | Success Rate | Running Time | Maximum Error (mm) | Difference Range (mm) |
|---|---|---|---|---|
| GMM | 7.14% | 0.97s | 11.21 | 132.15–180.41 |
| TP-GMM | 14.29% | 1.36s | 105.34 | 201.96–970.53 |
| DMP | 57.14% | 0.16s | 2.76 | 128.65–147.88 |
| Bi-DMP | 100% | 0.67s | 1.48 | 133.74–165.79 |
| Algorithms | Changes in Similarity (%) | |||
|---|---|---|---|---|
 | 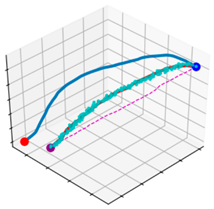 |  |  | |
| G-PRM | 79.61% | 88.41% | 92.00% | 93.39% |
| PRM | 59.35% | No change | No change | No change |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, W.; Liang, Y. A Trajectory Optimisation-Based Incremental Learning Strategy for Learning from Demonstration. Appl. Sci. 2024, 14, 4943. https://doi.org/10.3390/app14114943
Wang Y, Li W, Liang Y. A Trajectory Optimisation-Based Incremental Learning Strategy for Learning from Demonstration. Applied Sciences. 2024; 14(11):4943. https://doi.org/10.3390/app14114943
Chicago/Turabian StyleWang, Yuqi, Weidong Li, and Yuchen Liang. 2024. "A Trajectory Optimisation-Based Incremental Learning Strategy for Learning from Demonstration" Applied Sciences 14, no. 11: 4943. https://doi.org/10.3390/app14114943
APA StyleWang, Y., Li, W., & Liang, Y. (2024). A Trajectory Optimisation-Based Incremental Learning Strategy for Learning from Demonstration. Applied Sciences, 14(11), 4943. https://doi.org/10.3390/app14114943







