Linear Contact Load Law of an Elastic–Perfectly Plastic Half-Space vs. Sphere under Low Velocity Impact
Abstract
1. Introduction
2. Linear Contact Law and Finite Element Model
2.1. Linear Contact Law
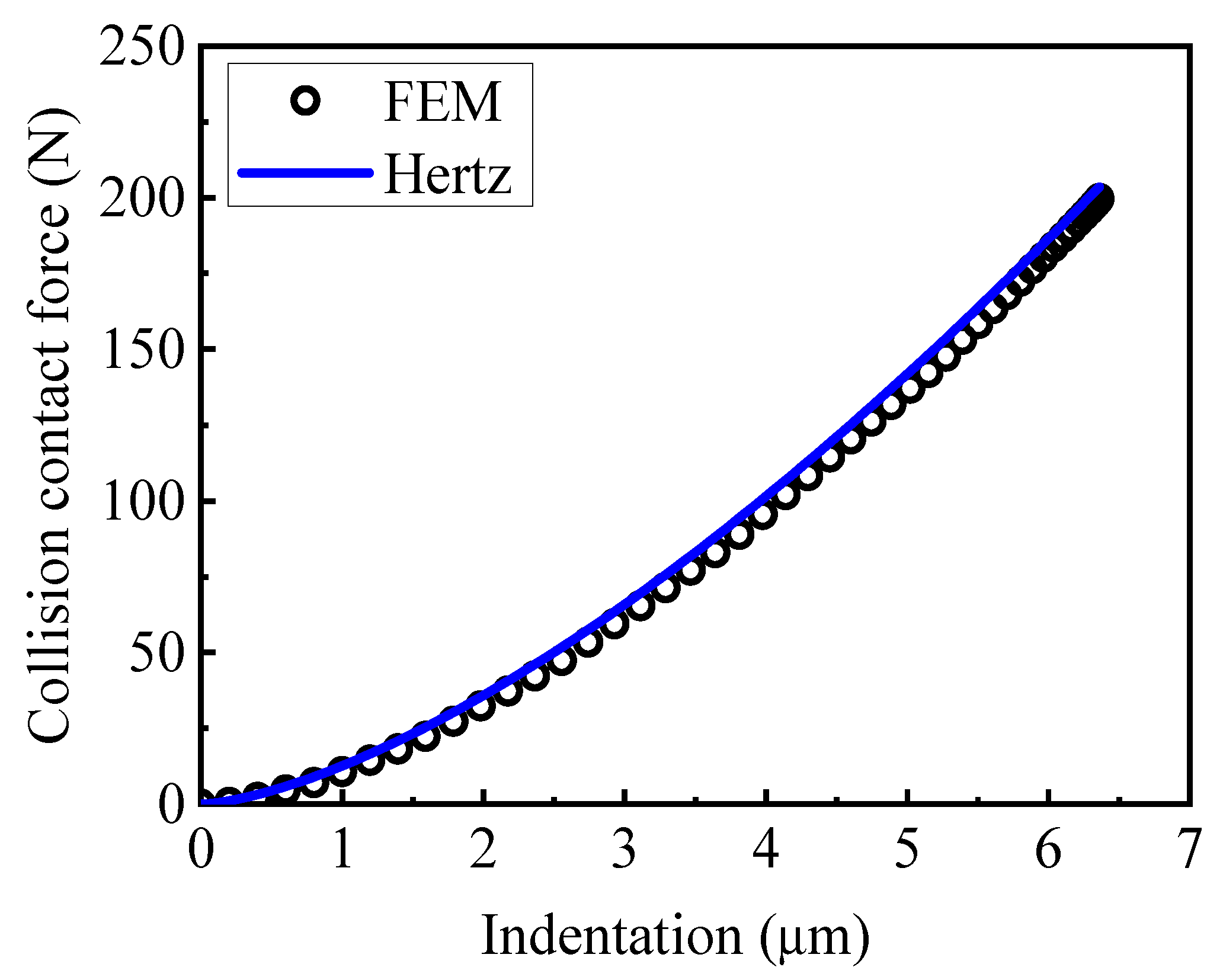
2.2. Finite Element Model
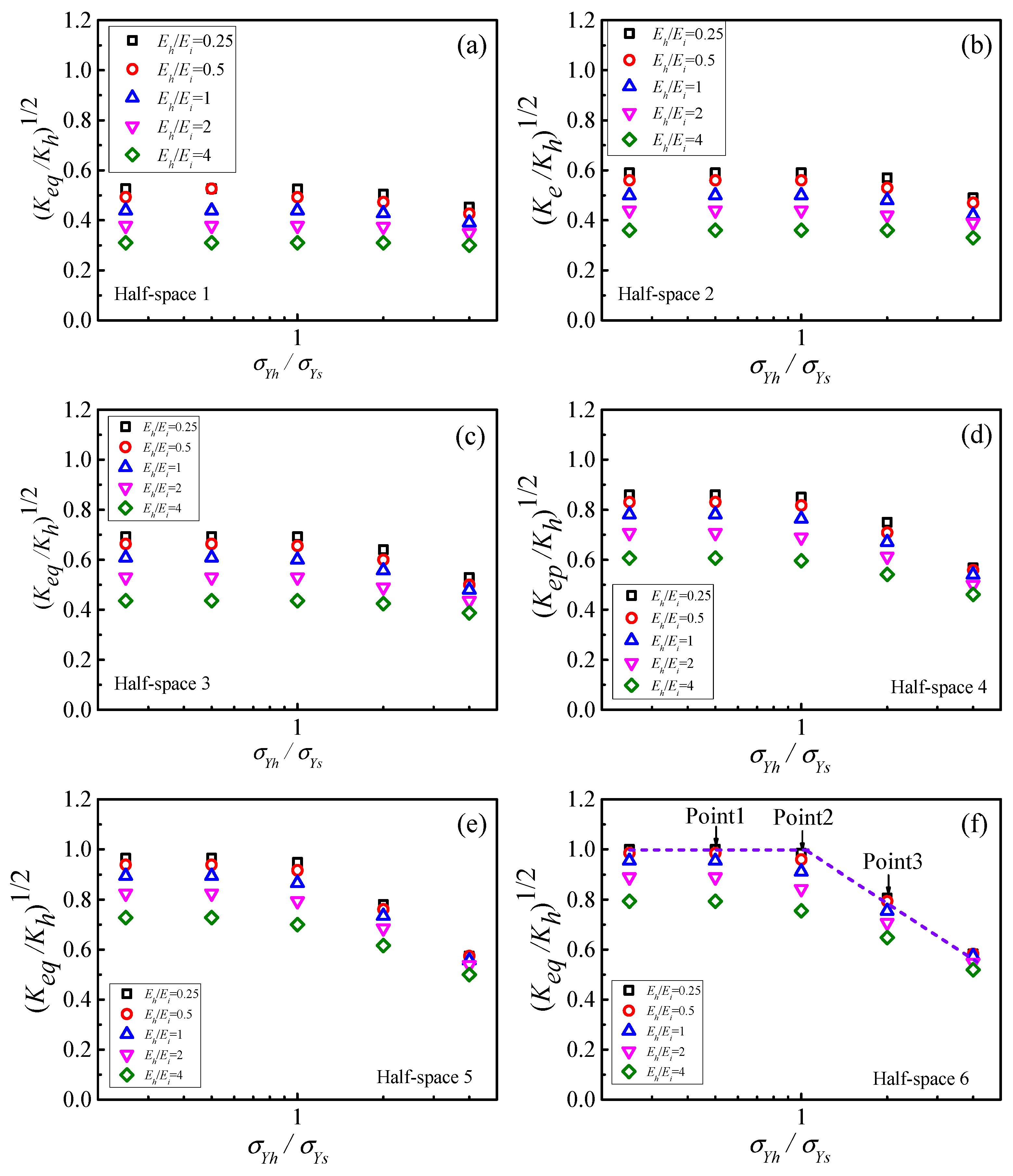
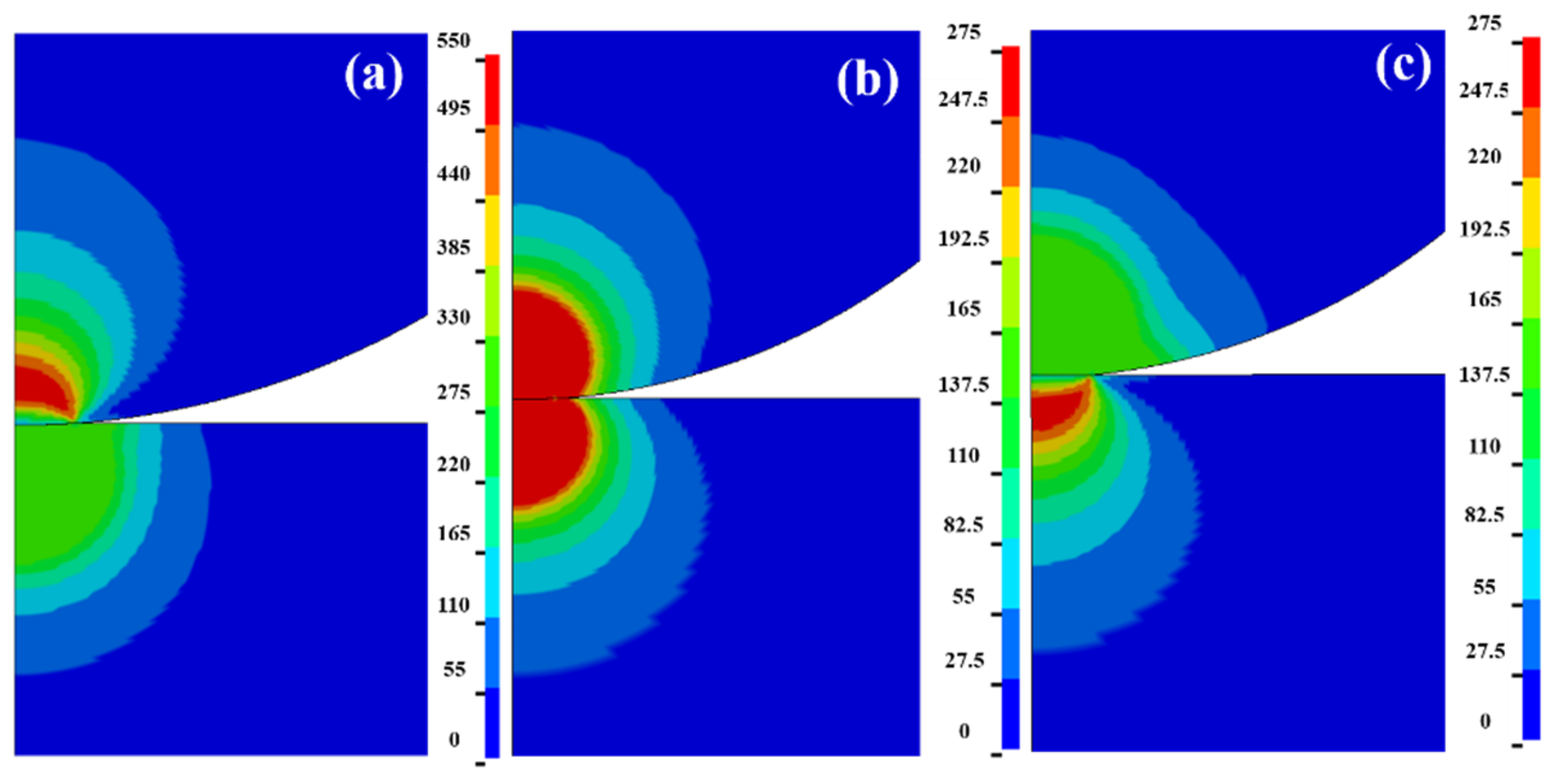
3. Influence of Spherical Elastic–Plastic Contact Deformation
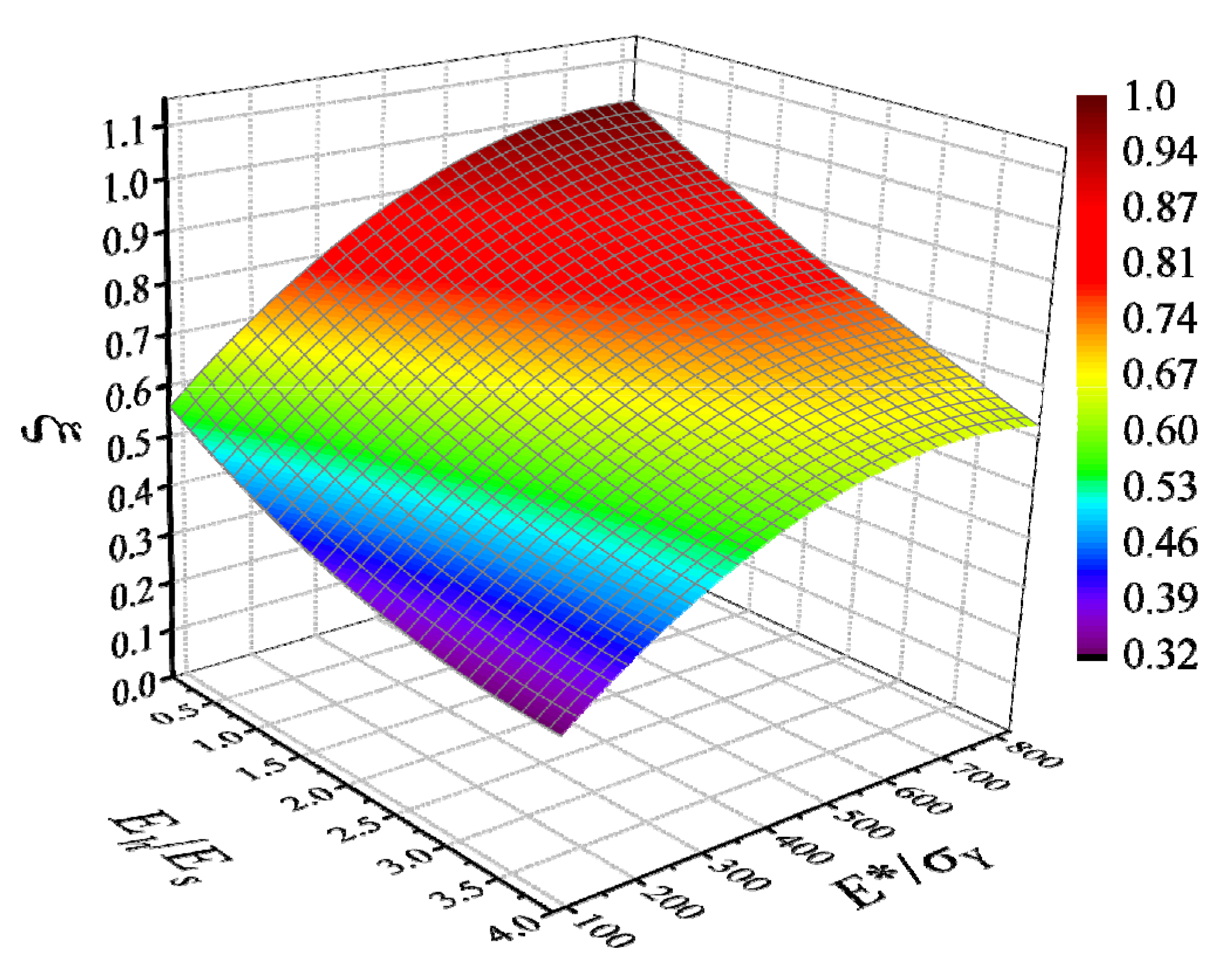
3.1. Influence of Spherical Elastic Modulus
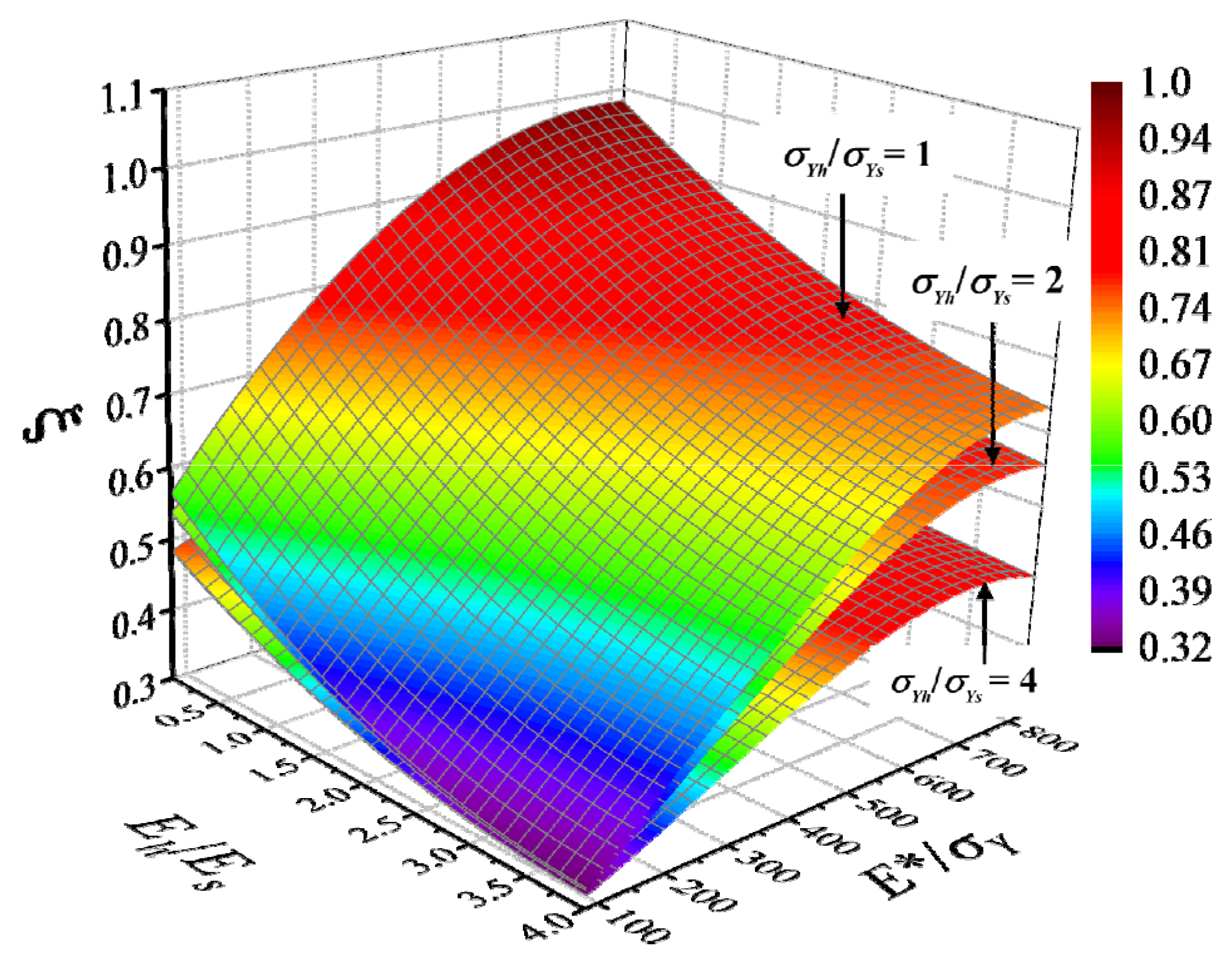
3.2. Influence of Sphere Yield Strength
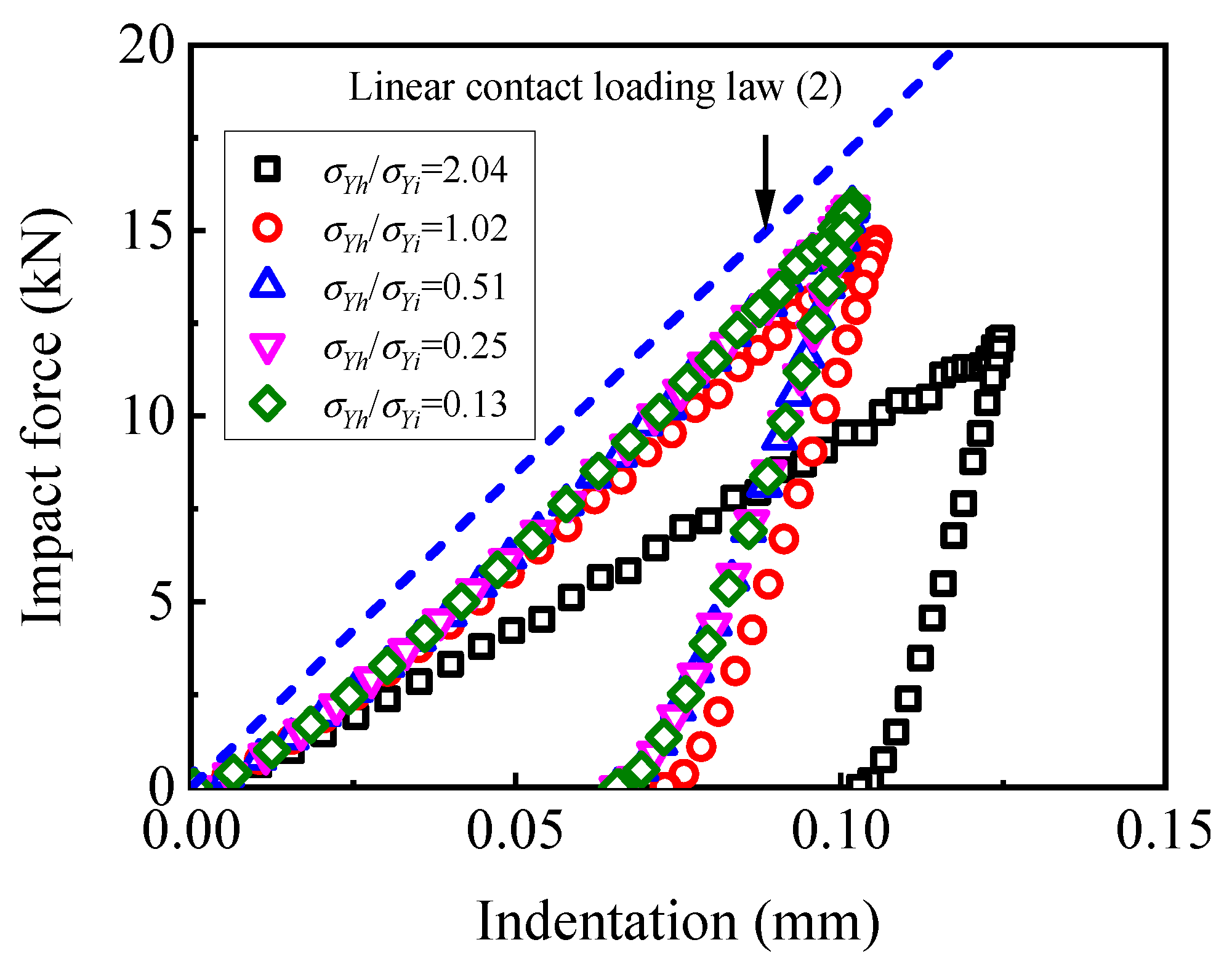
4. New Linear Contact Loading Law
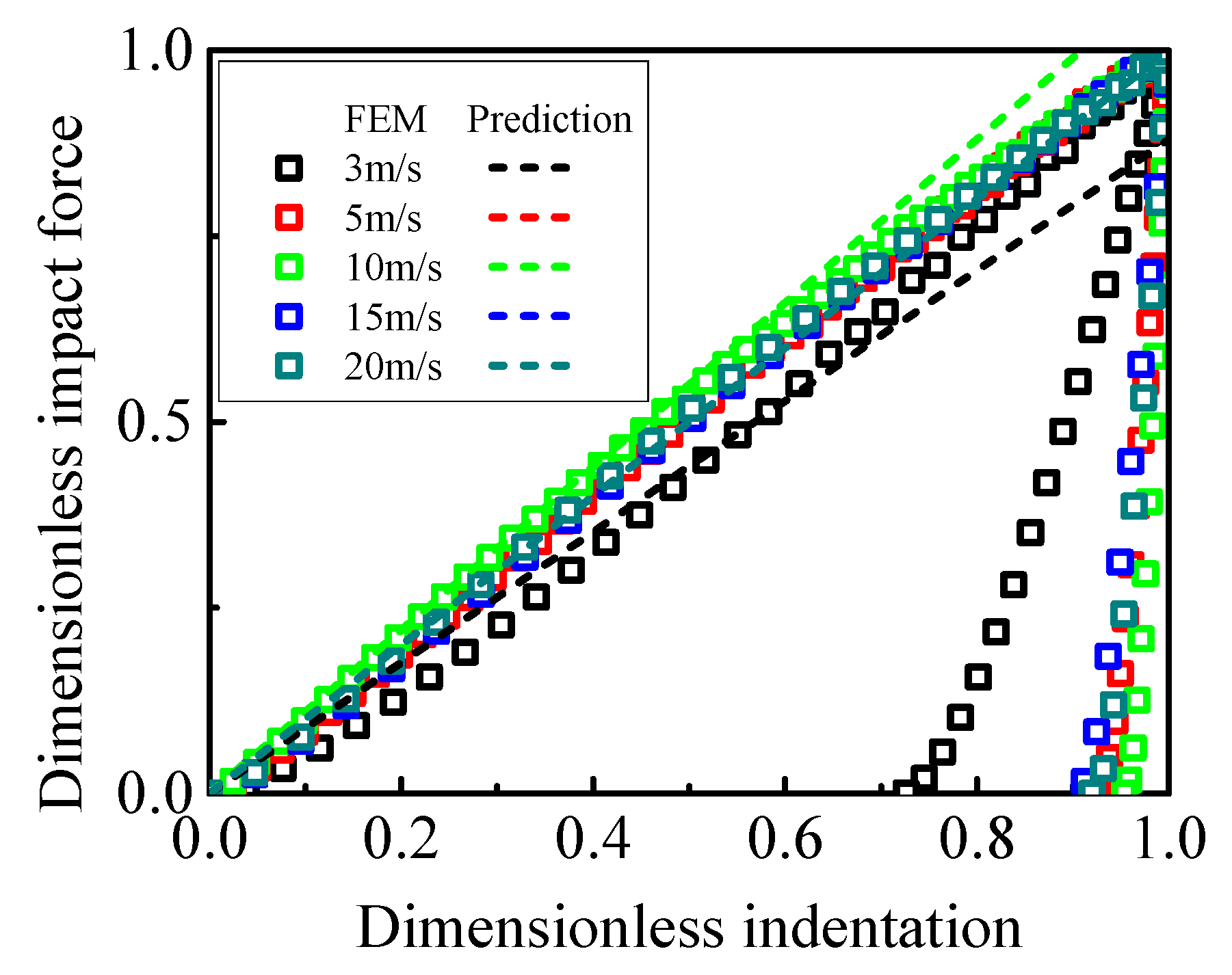
4.1. Impact Conditions
4.2. Piecewise Linear Feature
4.3. Combined New Linear Contact Loading Law
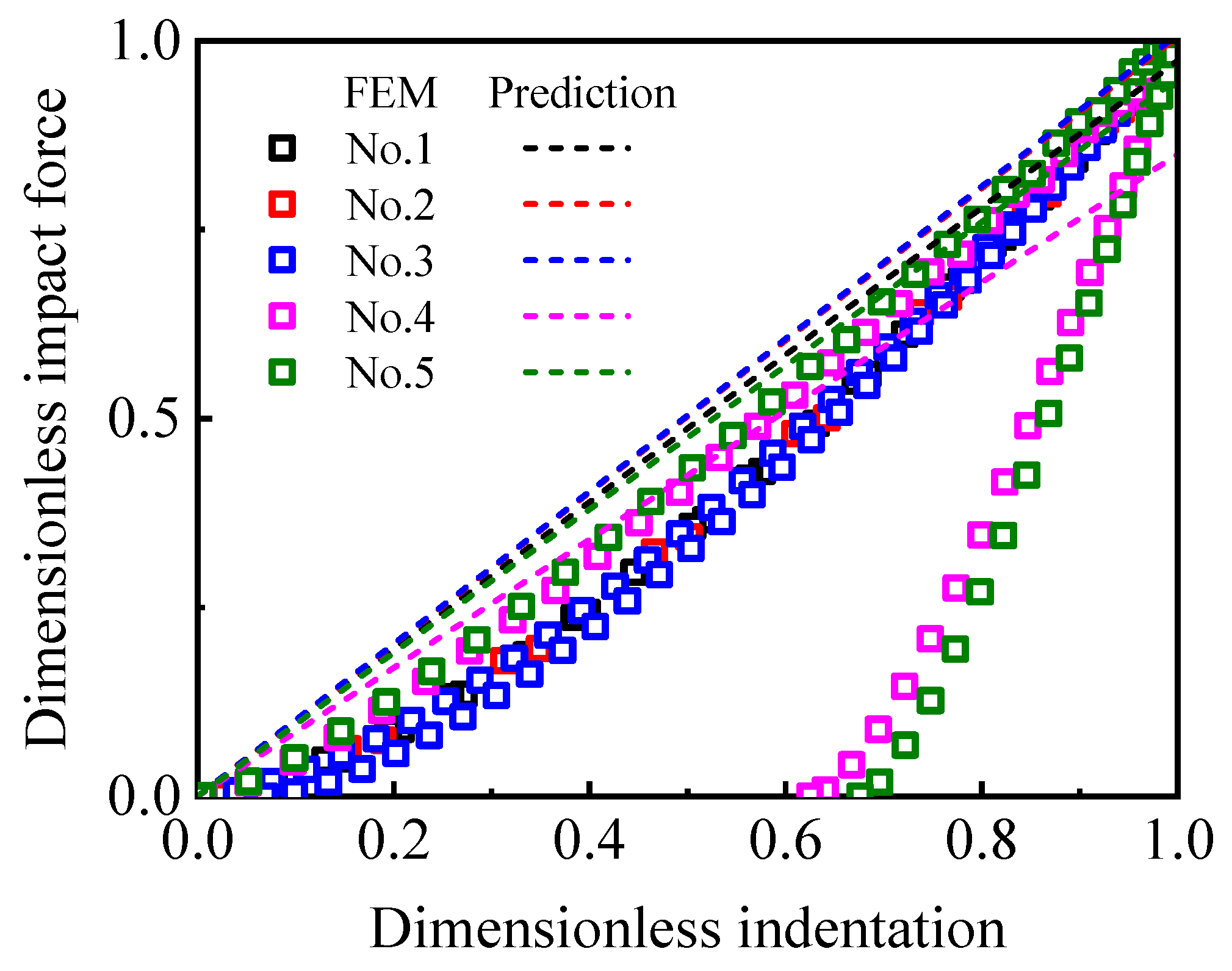
4.4. Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goldsmit, W. The Theory and Physical Behavior of Colliding Solids; Arnold: London, UK, 1960. [Google Scholar]
- Johnson, K. The correlation of indentation experiments. J. Mech. Phys. Solids 1970, 18, 115–126. [Google Scholar] [CrossRef]
- Amdahl, J. Impact from ice floes and icebergs on ships and offshore structures in Polar Regions. In IOP Conference Series: Materials Science and Engineering, 2019; IOP Publishing: Bristol, UK, 2019; p. 012039. [Google Scholar]
- Krag, H.; Serrano, M.; Braun, V.; Kuchynka, P.; Catania, M.; Siminski, J.; Schimmerohn, M.; Marc, X.; Kuijper, D.; Shurmer, I. A 1 cm space debris impact onto the sentinel-1a solar array. Acta Astronaut. 2017, 137, 434–443. [Google Scholar] [CrossRef]
- Nishikawa, M.; Hemmi, K.; Park, S.; Nadabe, T.; Takeda, N. Finite element analysis on the impact-induced damage of composite fan blades subjected to a bird strike. Trans. Jpn. Soc. Aeronaut. Space Sci. 2011, 54, 238–245. [Google Scholar] [CrossRef]
- Lu, X.; Liu, X.; Li, Y.; Zhang, Y.; Zuo, H. Simulations of airborne collisions between drones and an aircraft windshield. Aerosp. Sci. Technol. 2020, 98, 105713. [Google Scholar] [CrossRef]
- Han, M.-G.; Chang, S.-H. Evaluation of structural integrity of Type-III hydrogen pressure vessel under low-velocity car-to-car collision using finite element analysis. Compos. Struct. 2016, 148, 198–206. [Google Scholar] [CrossRef]
- Yang, B.; Chen, K.; Wang, D.-M.; Elchalakani, M. Experimental study on composite beam with various connections under midspan impact scenarios. J. Struct. Eng. 2022, 148, 04022158. [Google Scholar] [CrossRef]
- Zhang, W.; Qin, Q.; Li, J.; Li, K.; Poh, L.; Li, Y.; Zhang, J.; Xie, S.; Chen, H.; Zhao, J. Deformation and failure of hybrid composite sandwich beams with a metal foam core under quasi-static load and low-velocity impact. Compos. Struct. 2020, 242, 112175. [Google Scholar] [CrossRef]
- Caliskan, U.; Apalak, M.K. Flexural impact response and damage detection of composite sandwich beam with various PVC foam cores. Mech. Adv. Mater. Struct. 2022, 29, 1276–1293. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, L. Plastic Bending: Theory and Applications; World Scientific: London, UK, 1996; Volume 2. [Google Scholar]
- Zyczkowski, M. Combined Loadings in the Theory of Plasticity; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Iandiorio, C.; Salvini, P. Elastic-plastic analysis with pre-integrated beam finite element based on state diagrams: Elastic-perfectly plastic flow. Eur. J. Mech. -A/Solids 2023, 97, 104837. [Google Scholar] [CrossRef]
- Yi, G.; Liang, Y.; Wang, C.; Xu, J. Evolution of Residual Stress Based on Curvature Coupling in Multi-Roll Levelling. Appl. Sci. 2019, 9, 4975. [Google Scholar] [CrossRef]
- Stronge, W.J. Impact Mechanics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Minamoto, H.; Seifried, R.; Eberhard, P.; Kawamura, S. Analysis of repeated impacts on a steel rod with visco-plastic material behavior. Eur. J. Mech. -A/Solids 2011, 30, 336–344.
- Zhang, L.; Yin, X.; Yang, J.; Wang, H.; Deng, Q.; Yu, B.; Hao, Q.; Ding, H.; Qi, X.; Jin, T. Transient impact response analysis of an elastic–plastic beam. Appl. Math. Model. 2018, 55, 616–636. [Google Scholar] [CrossRef]
- Du, Y.; Wang, S. Energy dissipation in normal elastoplastic impact between two spheres. J. Appl. Mech. 2009, 76, 061010. [Google Scholar] [CrossRef]
- Patil, D.; Higgs, C.F. A coefficient of restitution model for sphere–plate elastoplastic impact with flexural vibrations. Nonlinear Dyn. 2017, 88, 1817–1832. [Google Scholar] [CrossRef]
- Thornton, C.; Cummins, S.J.; Cleary, P.W. On elastic-plastic normal contact force models, with and without adhesion. Powder Technol. 2017, 315, 339–346. [Google Scholar] [CrossRef]
- Brake, M. An analytical elastic-perfectly plastic contact model. Int. J. Solids Struct. 2012, 49, 3129–3141. [Google Scholar] [CrossRef]
- Larsson, P.-L.; Olsson, E. A numerical study of the mechanical behavior at contact between particles of dissimilar elastic–ideally plastic materials. J. Phys. Chem. Solids 2015, 77, 92–100. [Google Scholar] [CrossRef]
- Martin, C.; Bouvard, D. Isostatic compaction of bimodal powder mixtures and composites. Int. J. Mech. Sci. 2004, 46, 907–927. [Google Scholar] [CrossRef]
- Hertz, H. Ueber die Berührung fester elastischer Körper. 1882. [Google Scholar]
- Dong, X.; Yin, X.; Deng, Q.; Yu, B.; Wang, H.; Weng, P.; Chen, C.; Yuan, H. Local contact behavior between elastic and elastic–plastic bodies. Int. J. Solids Struct. 2018, 150, 22–39. [Google Scholar] [CrossRef]
- Kogut, L.; Komvopoulos, K. Analysis of the spherical indentation cycle for elastic–perfectly plastic solids. J. Mater. Res. 2004, 19, 3641–3653. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, W.; Liu, D.; Wang, C.; Zhu, L. Loading–Unloading Behavior of a Spherical Contact for Varying Tangent Modulus and Yield Strength. J. Appl. Mech. 2023, 90, 021002. [Google Scholar] [CrossRef]
- Jackson, R.L.; Green, I. A finite element study of elasto-plastic hemispherical contact against a rigid flat. J. Trib. 2005, 127, 343–354. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Becker, V.; Kamlah, M. A theoretical model for the normal contact force of two elastoplastic ellipsoidal bodies. J. Appl. Mech. 2021, 88, 031006. [Google Scholar] [CrossRef]
- Ghaednia, H.; Pope, S.A.; Jackson, R.L.; Marghitu, D.B. A comprehensive study of the elasto-plastic contact of a sphere and a flat. Tribol. Int. 2016, 93, 78–90. [Google Scholar] [CrossRef]
- Taljat, B.; Zacharia, T.; Haggag, F. Analysis of ball-indentation load-depth data: Part I. Determining elastic modulus. J. Mater. Res. 1997, 12, 965–974. [Google Scholar]
- Taljat, B.; Zacharia, T.; Kosel, F. New analytical procedure to determine stress-strain curve from spherical indentation data. Int. J. Solids Struct. 1998, 35, 4411–4426. [Google Scholar] [CrossRef]
- Knapp, J.; Follstaedt, D.; Myers, S.; Barbour, J.; Friedmann, T. Finite-element modeling of nanoindentation. J. Appl. Phys. 1999, 85, 1460–1474. [Google Scholar] [CrossRef]
- Ghaednia, H.; Mifflin, G.; Lunia, P.; O‘Neill, E.O.; Brake, M.R. Strain hardening from elastic-perfectly plastic to perfectly elastic indentation single asperity contact. Front. Mech. Eng. 2020, 6, 60. [Google Scholar] [CrossRef]
- Weng, P.; Yin, X.; Hu, W.; Yuan, H.; Chen, C.; Ding, H.; Yu, B.; Xie, W.; Jiang, L.; Wang, H. Piecewise linear deformation characteristics and a contact model for elastic-plastic indentation considering indenter elasticity. Tribol. Int. 2021, 162, 107114. [Google Scholar] [CrossRef]
- Majeed, M.A.; Yigit, A.S.; Christoforou, A.P. Modeling and analysis of elastoplastic impacts on supported composites. Key Eng. Mater. 2011, 471, 367–372. [Google Scholar] [CrossRef]


| Half-Space | Sphere | ||
|---|---|---|---|
| 800 × 800 | 35 | ||
| 1.4 | |||
| 206 | 206 | ||
| 275 | 275 | ||
| 0.3 | 0.3 | ||
| 7800 | 7800 | ||
| Half-Space | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 60 | 123 | 210 | 207 | 206 | 206 | |
| 800 | 1070 | 1079 | 540 | 345 | 275 | |
| 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | |
| 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | |
| 7800 | 7800 | 7800 | 7800 | 7800 | 7800 | |
| 7800 | 7800 | 7800 | 7800 | 7800 | 7800 | |
| 82.42 | 126.32 | 213.87 | 421.25 | 656.16 | 823.18 | |
| 0.25–4 | 0.25–4 | 0.25–4 | 0.25–4 | 0.25–4 | 0.25–4 | |
| 0.25–4 | 0.25–4 | 0.25–4 | 0.25–4 | 0.25–4 | 0.25–4 |
| Case | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 200 | 200 | 800 | 1000 | 800 | |
| 206 | 207 | 206 | 207 | 206 | |
| 275 | 540 | 345 | 540 | 345 | |
| 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | |
| 7800 | 7800 | 7800 | 7800 | 7800 | |
| R | 10 | 5 | 40 | 35 | 35 |
| 824 | 207 | 412 | 414 | 206 | |
| 1100 | 1080 | 345 | 1080 | 345 | |
| 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | |
| 7800 | 7800 | 7800 | 7800 | 7800 | |
| 0.6 | 0.5 | 0.7 | 2 | 1.5 | |
| 0.032 | 1.625 × 10−4 | 0.512 | 2.802 | 1.576 |
| Num | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 0.027 | 0.013 | 0.107 | 0.154 | 0.143 | |
| FEM | 1327.1 | 370.5 | 21,709.5 | 41,521.3 | 24,335.3 |
| prediction | 1292.4 | 372.6 | 21,895.2 | 35,208.6 | 23,174.9 |
| error | 2.6 | 0.6 | 0.8 | 15.2 | 4.8 |
| Num | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 800 | 800 | 800 | 800 | 800 | |
| 120 | 206 | 206 | 206 | 206 | |
| 320 | 345 | 345 | 345 | 345 | |
| 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | |
| 5200 | 7800 | 7800 | 7800 | 7800 | |
| R | 10 | 10 | 10 | 10 | 10 |
| 410 | 102 | 102 | 70 | 70 | |
| 690 | 100 | 100 | 140 | 140 | |
| 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | |
| 7800 | 7800 | 7800 | 2700 | 2700 | |
| 3 | 5 | 10 | 15 | 20 | |
| E(J) | 0.147 | 0.408 | 1.634 | 1.272 | 2.262 |
| Num | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 3 | 5 | 10 | 15 | 20 | |
| 0.078 | 0.200 | 0.405 | 0.314 | 0.420 | |
| FEM | 4139.2 | 4041.8 | 7724.3 | 8068.0 | 10,616.3 |
| prediction | 4236.0 | 4302.0 | 8687.7 | 7886.6 | 10,523.7 |
| error | 2.3% | 6% | 11% | 2.2% | 0.09% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Yin, X.; Wang, H.; Guo, Y.; Wang, C.; Zhou, H.; Gao, C.; Ding, H.; Deng, X. Linear Contact Load Law of an Elastic–Perfectly Plastic Half-Space vs. Sphere under Low Velocity Impact. Appl. Sci. 2024, 14, 5018. https://doi.org/10.3390/app14125018
Yuan H, Yin X, Wang H, Guo Y, Wang C, Zhou H, Gao C, Ding H, Deng X. Linear Contact Load Law of an Elastic–Perfectly Plastic Half-Space vs. Sphere under Low Velocity Impact. Applied Sciences. 2024; 14(12):5018. https://doi.org/10.3390/app14125018
Chicago/Turabian StyleYuan, Hao, Xiaochun Yin, Hui Wang, Yuanyuan Guo, Changliang Wang, Hao Zhou, Cheng Gao, Huaiping Ding, and Xiaokai Deng. 2024. "Linear Contact Load Law of an Elastic–Perfectly Plastic Half-Space vs. Sphere under Low Velocity Impact" Applied Sciences 14, no. 12: 5018. https://doi.org/10.3390/app14125018
APA StyleYuan, H., Yin, X., Wang, H., Guo, Y., Wang, C., Zhou, H., Gao, C., Ding, H., & Deng, X. (2024). Linear Contact Load Law of an Elastic–Perfectly Plastic Half-Space vs. Sphere under Low Velocity Impact. Applied Sciences, 14(12), 5018. https://doi.org/10.3390/app14125018






