Solving a Multi-Objective Optimization Problem of a Two-Stage Helical Gearbox with Second-Stage Double Gear Sets Using the MAIRCA Method
Abstract
1. Introduction
2. Optimization Problem
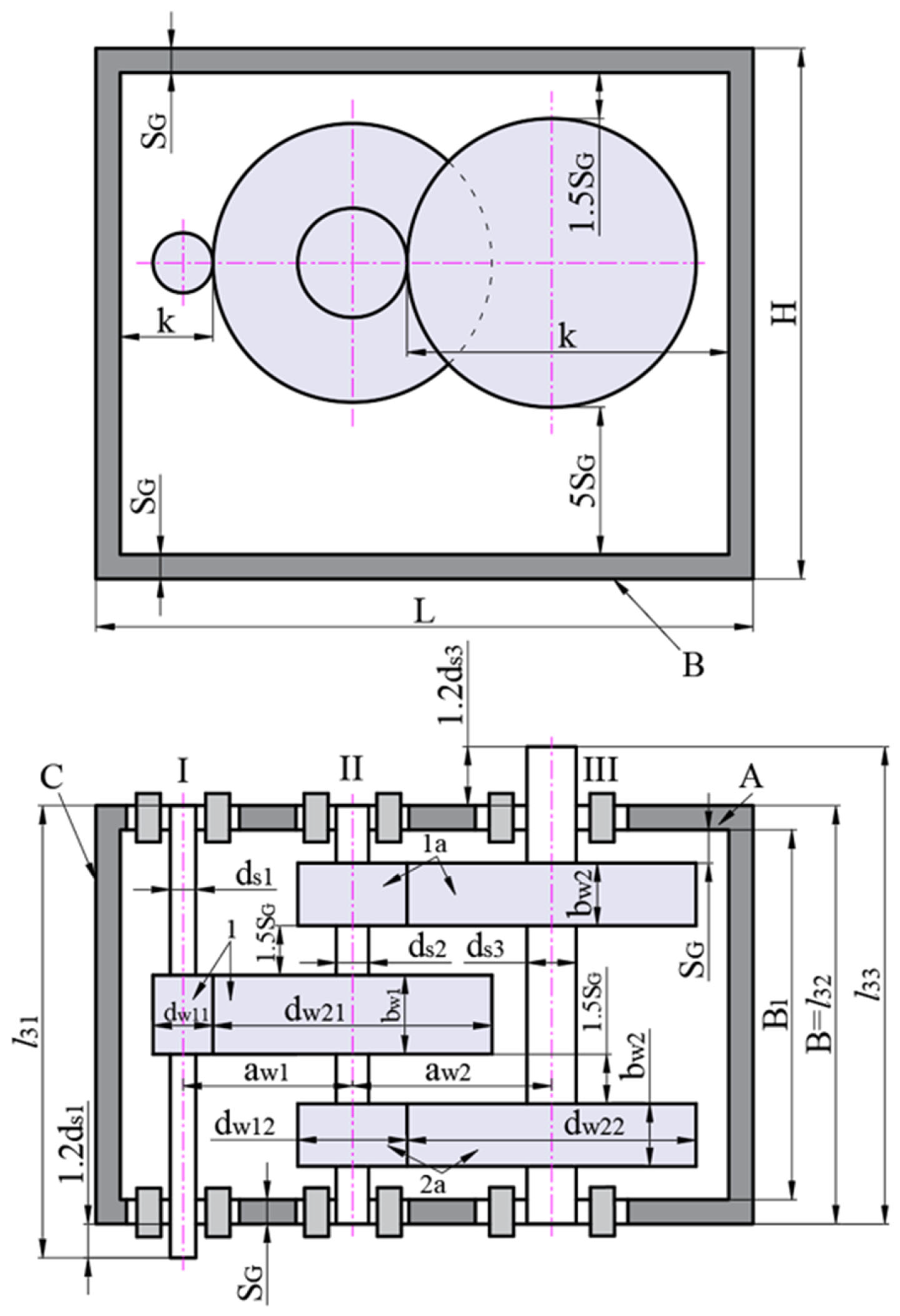
2.1. Determination of Gearbox Volume
2.2. Determination of Gearbox Efficiency
- -
- if v ≤ 0.424 (m/s):
- -
- if v > 0.424 (m/s):
2.3. Objective Functions and Constrains
2.3.1. Objectives Functions
- -
- Minimizing the gearbox volume:
- -
- Maximizing the gearbox efficiency:
2.3.2. Constrains
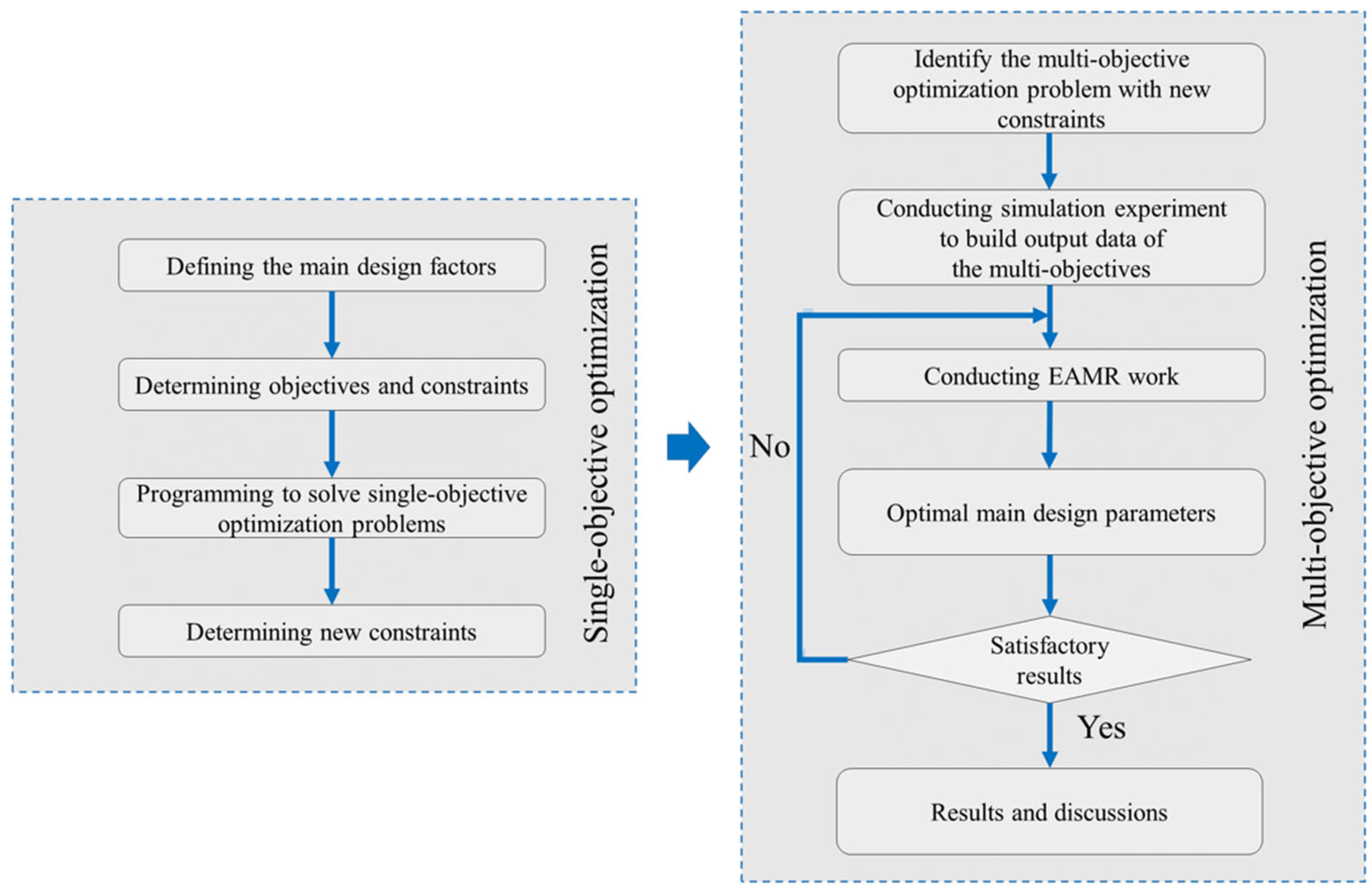
3. Methodology
3.1. Method to Solve the Multi-Objective Optimization
3.2. Method to Solve MCDM Problem
- -
- Step 1: Building the initial matrix:
- -
- Step 2: Determining options based on various selections through:
- -
- Step 3: Calculating the elements using:
- -
- Step 4: Finding by:
- (+)
- For the gearbox efficiency objective:
- (+)
- For the gearbox volume objective:
- -
- Step 5: Calculating the complete gap matrix gij by:
- -
- Step 6: Determining the final values of the criteria functions, Qi:
3.3. Method to Find the Weight of Criteria
- -
- Finding the indicator normalized values:
- -
- Calculating the entropy of each indicator:
- -
- Determining each indicator’s weight:
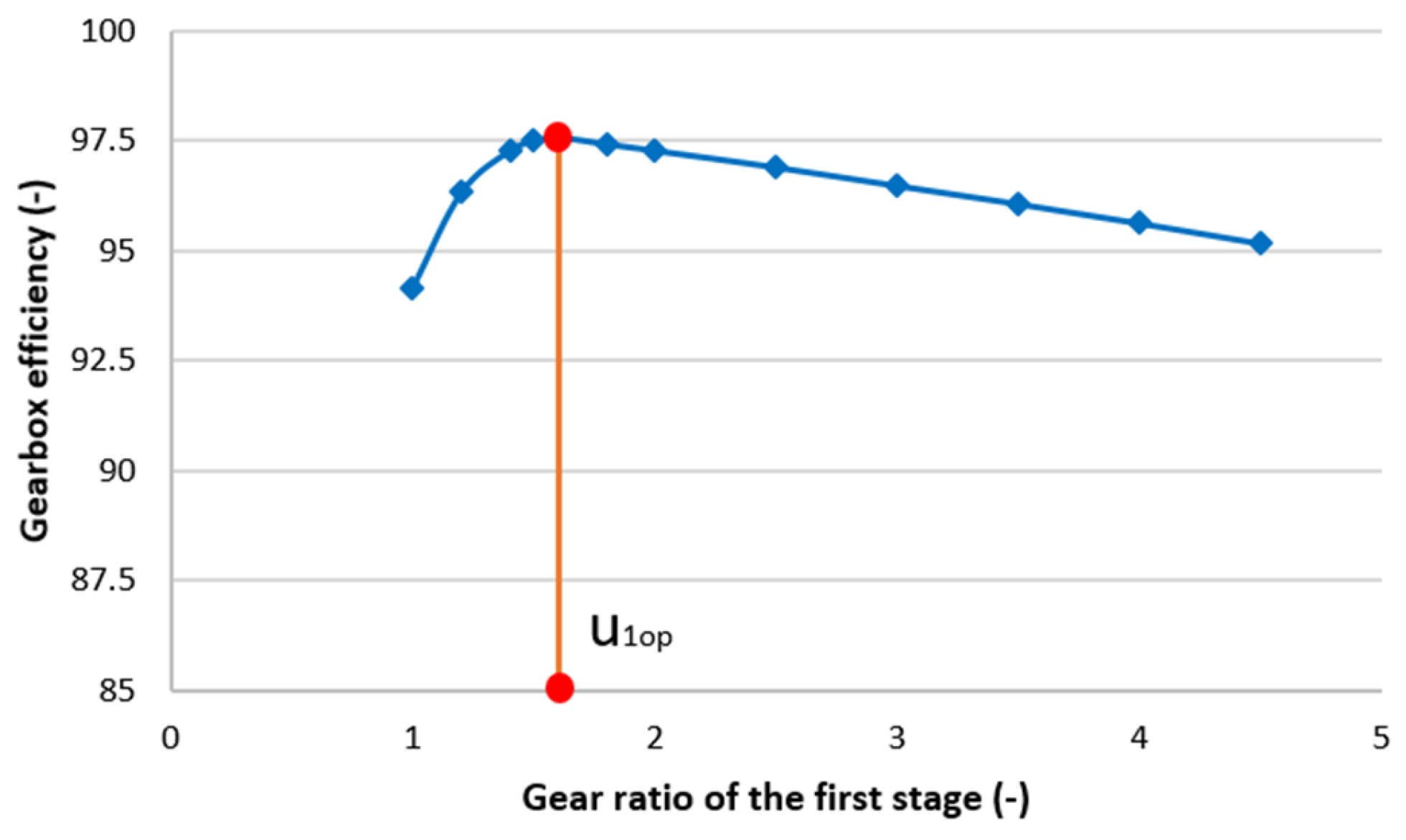
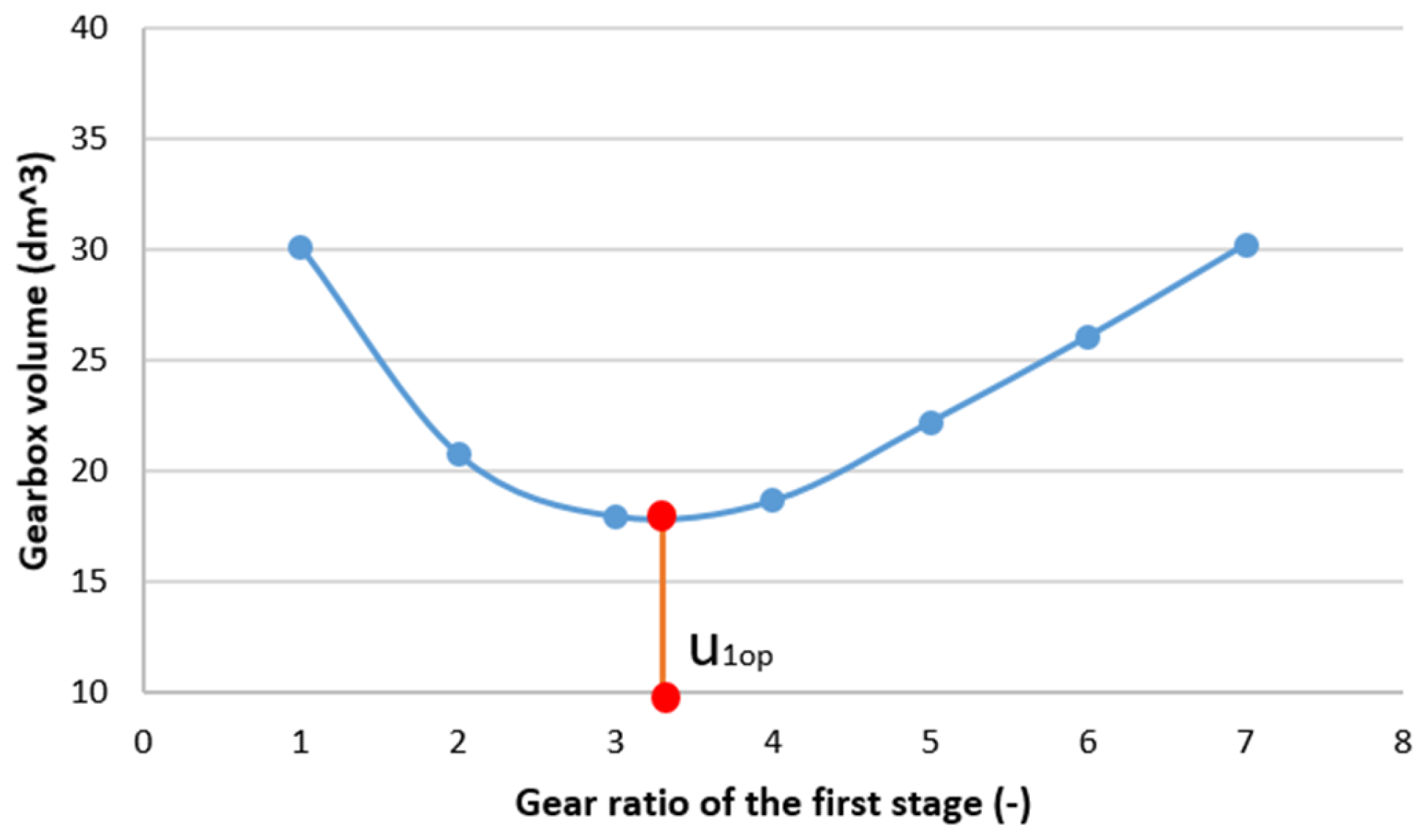
4. Single-Objective Optimization
5. Multi-Objective Optimization
6. Conclusions
- -
- Based on the study’s findings, the best values for the three primary design parameters of a two-stage helical gear gearbox with an SDGS = 0.2, = 0.4 and u1 determined according to (47).
- -
- Two individual targets are evaluated in relation to the main design parameters.
- -
- The remarkable degree of agreement between the experimental data and the u1 model suggests that the data are reliable.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Collins, J.A.; Busby, H.R.; Staab, G.H. Mechanical Design of Machine Elements and Machines: A Failure Prevention Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Höhn, B.-R.; Michaelis, K.; Hinterstoißer, M. Optimization of gearbox efficiency. Goriva I Maz. Časopis Za Tribol. Teh. Podmazivanja I Primjen. Tekućih I Plinovitih Goriva I Inžinjerstvo Izgaranja 2009, 48, 441–461. [Google Scholar]
- Kaya, İ.; Baykara, C. The investigation of the effect of operating conditions in gearboxes on efficiency. Adv. Mech. Eng. 2024, 16, 16878132241248072. [Google Scholar] [CrossRef]
- Son, G.-H.; Kim, B.-S.; Cho, S.-J.; Park, Y.-J. Optimization of the housing shape design for radiated noise reduction of an agricultural electric vehicle gearbox. Appl. Sci. 2020, 10, 8414. [Google Scholar] [CrossRef]
- Wang, J.P.; Liu, G.; Chang, S.; Wu, L.Y. Topology optimization of gearbox to reduce radiated noise. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 2–5 August 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Inoue, K.; Yamanaka, M.; Kihara, M. Optimum stiffener layout for the reduction of vibration and noise of gearbox housing. J. Mech. Des. 2002, 124, 518–523. [Google Scholar] [CrossRef]
- Pi, V.N.; Cam, N.T.H.; Hong, T.T.; Hung, L.X.; Tung, L.A.; Tuan, N.K.; Tham, H.T. Determination of optimum gear ratios of a two-stage helical gearbox with second stage double gear sets. IOP Conf. Ser. Mater. Sci. Eng. 2019, 635, 012012. [Google Scholar] [CrossRef]
- Van Cuong, N.; Le Hong, K.; Tran, T. Splitting total gear ratio of two-stage helical reducer with first-stage double gearsets for minimal reducer length. Int. J. Mech. Prod. Eng. Res. Dev. (IJMPERD) 2019, 9, 595–608. [Google Scholar]
- Pi, V.N. Optimal calculation of partial transmission ratios for four-step helical gearboxes with first and third step double gear-sets for minimal gearbox length. In Proceedings of the American Conference on Applied Mathematics, Cambridge, MA, USA, 29–32 March 2008. [Google Scholar]
- Marjanovic, N.; Kostic, N.; Petrovic, N.; Blagojevic, M.; Matejic, M.; Isailovic, B. Comparative Analysis of Analytical Calculation and Optimization on Gearbox Dimensions and Volume. Mach. Des. 2014, 6, 127–130. [Google Scholar]
- Golabi, S.; Fesharaki, J.J.; Yazdipoor, M. Gear train optimization based on minimum volume/weight design. Mech. Mach. Theory 2014, 73, 197–217. [Google Scholar] [CrossRef]
- Danh, T.H.; Huy, T.Q.; Danh, B.T.; Van Trang, N.; Hung, L.X. Optimization of Main Design Parameters for a Two-Stage Helical Gearbox Based on Gearbox Volume Function. In Proceedings of the International Conference on Engineering Research and Applications, Thai Nguyen, Vietnam, 1–2 December 2022; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Milou, G.; Dobre, G.; Visa, F.; Vitila, H. Optimal design of two step gear units, regarding the main parameters. VDI Berichte 1996, 1230, 227. [Google Scholar]
- Cam, N.T.H.; Pi, V.N.; Tuan, N.K.; Hung, L.X.; Thao, T.T.P. A study on determination of optimum partial transmission ratios of mechanical driven systems using a chain drive and a three-step helical reducer. In Advances in Engineering Research and Application: Proceedings of the International Conference, ICERA 2018; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Tuan, N.K.; Pi, V.N.; Cam NT, H.; Thao TT, P.; Thanh, H.K.; Hung, L.X.; Tham, H.T. Determining optimal gear ratios of a two-stage helical reducer for getting minimal acreage of cross section. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018. [Google Scholar]
- Pi, V.N.; Tuan, N.K.; Hung, L.X.; Tung, L.A. A new study on determination of optimum gear ratios of a two-stage helical gearbox. In Advances in Material Sciences and Engineering; Springer: Singapore, 2020. [Google Scholar]
- Tu, N.T.; Ky, L.H.; Hong, T.T.; Van Cuong, N.; Tung, L.A.; Hien, B.T.; Hung, L.X. Determining optimal gear ratios of mechanical drive systems using two-stage helical gearbox with second-stage double gear sets and chain drive for minimal system cross section area. In Advances in Engineering Research and Application: Proceedings of the International Conference on Engineering Research and Applications, ICERA 2019, Thai Nguyen, Vietnam, 1–2 December 2020; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Pi, V.N.; Tuan, N.K. Optimum determination of partial transmission ratios of three-step helical gearboxes for getting minimum cross section dimension. J. Environ. Sci. Eng. A 2016, 5, 570–573. [Google Scholar]
- Pi, V.N.; Ngoc, N.D.; Hong, T.T.; Linh, N.H. Cost optimization study of two-step helical gearboxes with first stage double gear sets. Int. J. Mech. Prod. Eng. Res. Dev. (Ijmperd) 2020, 10, 573–584. [Google Scholar]
- Danh, T.H.; Huy, T.Q.; Danh, B.T.; Tan, T.M.; Van Trang, N.; Tung, L.A. Determining Partial Gear Ratios of a Two-Stage Helical Gearbox with First Stage Double Gear Sets for Minimizing Total Gearbox Cost. In Proceedings of the International Conference on Engineering Research and Applications, Thai Nguyen, Vietnam, 1–2 December 2022; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Quang, N.H.; Tu, N.T.; Linh, N.H.; Luan, N.H.; Anh, L.H.; Tuan, N.A.; Giang, T.N.; Pi, V.N. Determining Optimum Gear Ratios for a Four-Stage Helical Gearbox for Getting Minimum Gearbox Cost. In Proceedings of the International Conference on Engineering Research and Applications, Thai Nguyen, Vietnam, 1–2 December 2021; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Pi, V.N.; Hong, T.T.; Ky, L.H.; Hung, L.X.; Tung, L.A.; Tuan, N.K. A study on calculating optimum gear ratios of a three-stage helical gearbox. Int. J. Mech. Eng. Technol. 2018, 9, 1392–1400. [Google Scholar]
- Wang, Y.; Qian, Q.; Chen, G.; Jin, S.; Chen, Y. Multi-objective optimization design of cycloid pin gear planetary reducer. Adv. Mech. Eng. 2017, 9, 1687814017720053. [Google Scholar] [CrossRef]
- Chong, T.H.; Bae, I.; Kubo, A. Multiobjective optimal design of cylindrical gear pairs for the reduction of gear size and meshing vibration. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2001, 44, 291–298. [Google Scholar] [CrossRef][Green Version]
- Park, C.I. Multi-objective optimization of the tooth surface in helical gears using design of experiment and the response surface method. J. Mech. Sci. Technol. 2010, 24, 823–829. [Google Scholar] [CrossRef]
- Terán, C.V.; Martínez-Gómez, J.; Milla, J.C.L. Material selection through of multi-criteria decisions methods applied to a helical gearbox. Int. J. Math. Oper. Res. 2020, 17, 90–109. [Google Scholar] [CrossRef]
- Alam, J.; Panda, S. comprehensive study on multi-objective design optimization of spur gear. Mech. Based Des. Struct. Mach. 2023, 51, 5272–5298. [Google Scholar] [CrossRef]
- Patil, M.; Ramkumar, P.; Shankar, K. Multi-objective optimization of spur gearbox with inclusion of tribological aspects. J. Frict. Wear 2017, 38, 430–436. [Google Scholar] [CrossRef]
- Parmar, A.; Ramkumar, P.; Shankar, K. Optimization of Planetary Gearbox Using NSGA-II. In Recent Advances in Mechanical Engineering: Select Proceedings of ICRAME 2020; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Miler, D.; Žeželj, D.; Lončar, A.; Vučković, K. Multi-objective spur gear pair optimization focused on volume and efficiency. Mech. Mach. Theory 2018, 125, 185–195. [Google Scholar] [CrossRef]
- Tudose, L.; Buiga, O.; Jucan, D.; Stefanache, C. Multi-objective optimization in helical gears design. In Proceedings of the Fifth International Symposium about Design in Mechanical Engineering-KOD, Novi Sad, Serbia, 15–16 April 2008. [Google Scholar]
- Deb, K.; Jain, S. Multi-speed gearbox design using multi-objective evolutionary algorithms. J. Mech. Des. 2003, 125, 609–619. [Google Scholar] [CrossRef]
- Maputi, E.S.; Arora, R. Multi-objective optimization of a 2-stage spur gearbox using NSGA-II and decision-making methods. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–22. [Google Scholar] [CrossRef]
- Sanghvi, R.C.; Vashi, A.S.; Patolia, H.P.; Jivani, R.G. Multi-objective optimization of two-stage helical gear train using NSGA-II. J. Optim. 2014, 2014, 670297. [Google Scholar] [CrossRef]
- Sabarinath, P.; Thansekhar, M.; Jeganathan, R.; Saravanan, R. Multi objective Design Optimization of Helical gear pair using Adaptive parameter Harmony search Algorithm. Appl. Mech. Mater. 2015, 813–814, 1032–1036. [Google Scholar] [CrossRef]
- Lagresle, C.; Guingand, M.; de Vaujany, J.-P.; Fulleringer, B. Optimization of tooth modifications for spur and helical gears using an adaptive multi-objective swarm algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 7292–7308. [Google Scholar] [CrossRef]
- Korta, J.A.; Mundo, D. Multi-objective micro-geometry optimization of gear tooth supported by response surface methodology. Mech. Mach. Theory 2017, 109, 278–295. [Google Scholar] [CrossRef]
- Wang, H.; Chen, D.; Pan, F.; Yu, D. Multi-objective Optimization Design of Helical Gear in Centrifugal Compressor Based on Response Surface Method. IOP Conf. Series Mater. Sci. Eng. 2018, 423, 012040. [Google Scholar] [CrossRef]
- Liu, S.; Li, B.; Gan, R.; Xu, Y.; Yang, G. Multi-Objective Optimization of Two-Stage Helical Pairs in Helical Hydraulic Rotary Actuator Using Ensemble of Metamodels and NSGA-II. Actuators 2023, 12, 385. [Google Scholar] [CrossRef]
- Wu, K.; Wei, D.; Lu, R.; Huang, Q.; Xie, J.; Tang, W. Multi-objective optimization of a 2-stage helical gear transmission system using NSGA-III. In Proceedings of the 2022 IEEE 6th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 4–6 March 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Le, X.-H.; Vu, N.-P. Multi-objective optimization of a two-stage helical gearbox using taguchi method and grey relational analysis. Appl. Sci. 2023, 13, 7601. [Google Scholar] [CrossRef]
- Tran, H.-D.; Le, X.-H.; Nguyen, T.-T.; Hoang, X.-T.; Trieu, Q.-H.; Vu, N.-P. Application of the Taguchi Method and Grey Relational Analysis for Multi-Objective Optimization of a Two-Stage Bevel Helical Gearbox. Machines 2023, 11, 716. [Google Scholar] [CrossRef]
- Huy, T.Q.; Van Binh, N.; Van Thanh, D.; Danh, T.H.; Van Trang, N. Optimization of a Two-stage Helical Gearbox with Second Stage Double Gear Sets to Reduce Gearbox Mass and Increase Gearbox Efficiency. WSEAS Trans. Appl. Theor. Mech. 2023, 18, 287–298. [Google Scholar] [CrossRef]
- Hung, T.Q.; Huong, T.T.T. Multi-objective Optimization of a Two-Stage Helical Gearbox to Improve Efficiency and Reduce Height. J. Environ. Sci. Eng. B 2023, 12, 236–247. [Google Scholar]
- Hung, T.Q.; Tung, L.A. Application of Taguchi Technique and Grey Relational Analysis for Multi-Target Optimization of Two Stage Helical Gearboxes. Eur. J. Appl. Sci. 2023, 11, 236–247. [Google Scholar]
- Dinh, V.-T.; Tran, H.-D.; Bui, T.-D.; Vu, D.-B.; Vu, D.; Vu, N.-P.; Truong, T.-T. Multi-Objective Optimization of a Two-Stage Helical Gearbox with Second Stage Double Gear-Sets Using TOPSIS Method. Processes 2024, 12, 1160. [Google Scholar] [CrossRef]
- Pamučar, D.; Vasin, L.; Lukovac, L. Selection of railway level crossings for investing in security equipment using hybrid DEMATEL-MARICA model. In Proceedings of the XVI International Scientific-Expert Conference on Railway, Railcon, Niš, Serbia, 13–14 October 2014. [Google Scholar]
- Pamucar, D.S.; Tarle, S.P.; Parezanovic, T. New hybrid multi-criteria decision-making DEMATELMAIRCA model: Sustainable selection of a location for the development of multimodal logistics centre. Econ. Res. Istraz. 2018, 31, 1641–1665. [Google Scholar]
- Gigović, L.; Pamučar, D.; Bajić, Z.; Milićević, M. The combination of expert judgment and GIS-MAIRCA analysis for the selection of sites for ammunition depots. Sustainability 2016, 8, 372. [Google Scholar] [CrossRef]
- Römhild, I.; Linke, H. Gezielte Auslegung Von Zahnradgetrieben mit minimaler Masse auf der Basis neuer Berechnungsverfahren. Konstruktion 1992, 44, 229–236. [Google Scholar]
- Chat, T.; Van Uyen, L. Design and Calculation of Mechanical Transmissions Systems, vol. 1; Educational Republishing House: Hanoi, Vietnam, 2007. [Google Scholar]
- Jelaska, D.T. Gears and Gear Drives; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Buckingham, E. Analytical Mechanics of Gears; Courier Corporation: North Chelmsford, MA, USA, 1988. [Google Scholar]
- Hieu, T.T.; Thao, N.X.; Thuy, L. Application of MOORA and COPRAS models to select materials for mushroom cultivation. Vietnam. J. Agric. Sci. 2019, 17, 322–331. [Google Scholar]
- Kudreavtev, V.N.; Gierzaves, I.A.; Glukharev, E.G. Design and Calculus of Gearboxes; Mashinostroenie Publishing: St. Petersburg, Russia, 1971. (In Russian) [Google Scholar]

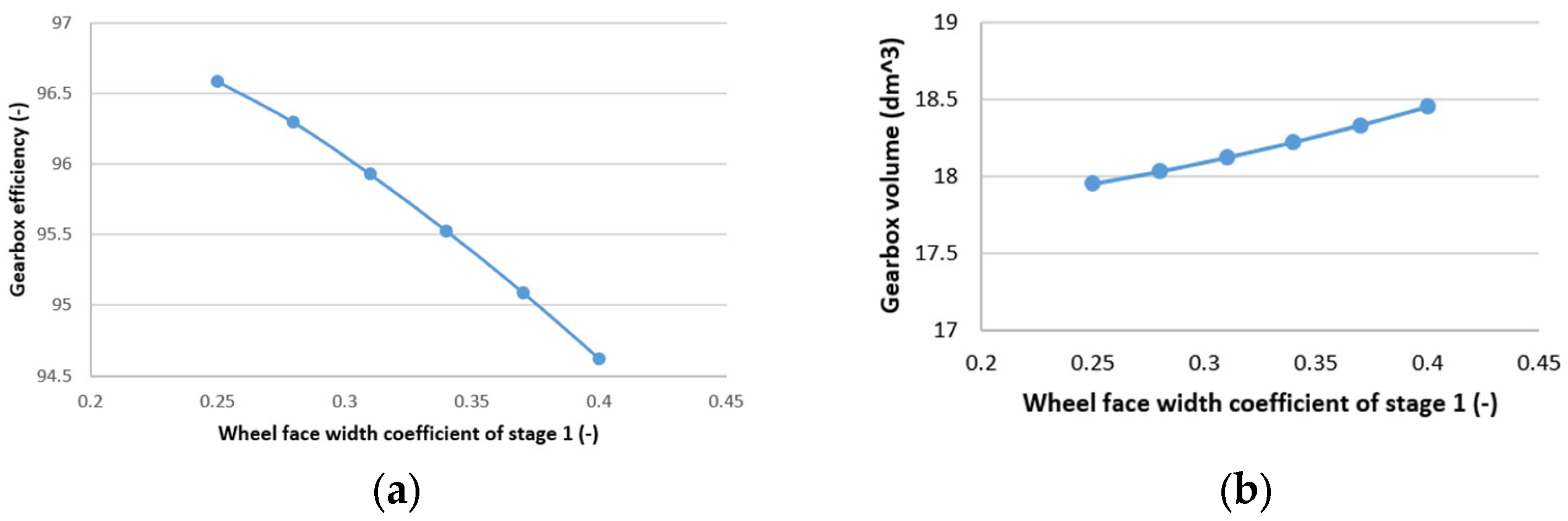

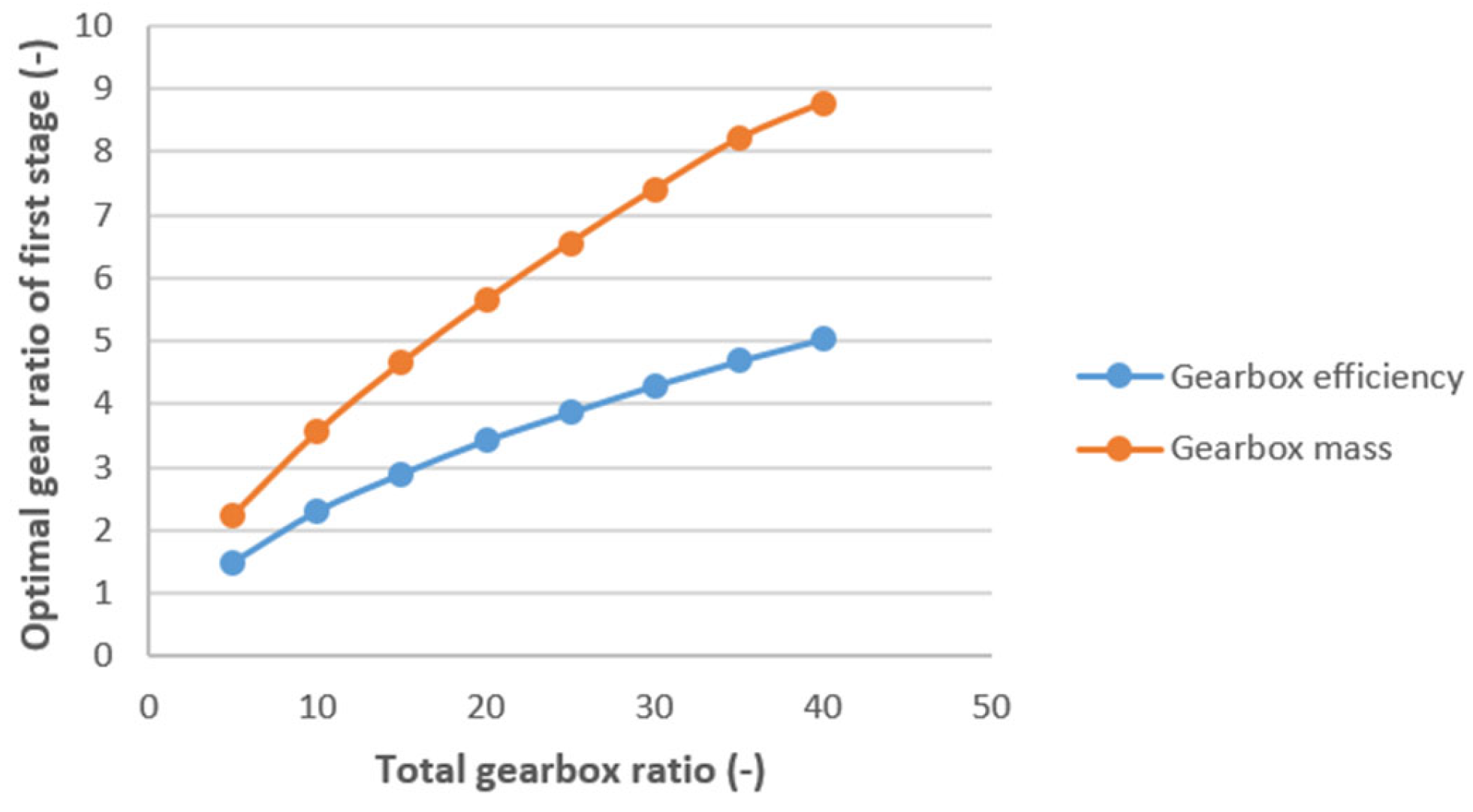

| Parameter | Symbol | Lower Limit | Upper Limit |
|---|---|---|---|
| Gearbox ratio of stage 1 | u1 | 1 | 9 |
| CWFW of stage 1 | 0.25 | 0.4 | |
| CWFW of stage 2 | 0.25 | 0.4 |
| ut | u1 | |
|---|---|---|
| Lower Limit | Upper Limit | |
| 10 | 2.2 | 2.36 |
| 15 | 2.79 | 4.76 |
| 20 | 3.32 | 5.75 |
| 25 | 3.76 | 6.66 |
| 30 | 4.19 | 7.51 |
| 35 | 4.58 | 8.31 |
| 40 | 4.93 | 8.88 |
| Trial. | u1 | Vgb (dm3) | ηgb (%) | ||
|---|---|---|---|---|---|
| 1 | 6.99 | 0.25 | 0.25 | 21.23 | 93.44 |
| 2 | 6.99 | 0.25 | 0.29 | 20.82 | 93.38 |
| 3 | 6.99 | 0.25 | 0.33 | 20.52 | 93.32 |
| 4 | 6.99 | 0.25 | 0.36 | 20.30 | 93.26 |
| 5 | 6.99 | 0.25 | 0.40 | 20.12 | 93.21 |
| 6 | 6.99 | 0.29 | 0.25 | 21.37 | 92.26 |
| 7 | 6.99 | 0.29 | 0.29 | 20.93 | 92.21 |
| 26 | 7.01 | 0.25 | 0.25 | 21.21 | 93.42 |
| 27 | 7.01 | 0.25 | 0.29 | 20.81 | 93.36 |
| 28 | 7.01 | 0.25 | 0.33 | 20.51 | 93.30 |
| 54 | 7.02 | 0.25 | 0.36 | 20.27 | 93.23 |
| 55 | 7.02 | 0.25 | 0.40 | 20.10 | 93.18 |
| 56 | 7.02 | 0.29 | 0.25 | 21.35 | 92.22 |
| 71 | 7.02 | 0.40 | 0.25 | 21.87 | 87.72 |
| 72 | 7.02 | 0.40 | 0.29 | 21.34 | 87.66 |
| 73 | 7.02 | 0.40 | 0.33 | 20.94 | 87.60 |
| 101 | 7.05 | 0.25 | 0.25 | 21.17 | 93.33 |
| 102 | 7.05 | 0.25 | 0.29 | 20.77 | 93.27 |
| 103 | 7.05 | 0.25 | 0.33 | 20.47 | 93.21 |
| 123 | 7.05 | 0.40 | 0.33 | 20.92 | 87.53 |
| 124 | 7.05 | 0.40 | 0.36 | 20.60 | 87.48 |
| 125 | 7.05 | 0.40 | 0.40 | 20.35 | 87.42 |
| Trial. | trij | gij | Qi | Rank | ||
|---|---|---|---|---|---|---|
| Vgb | ηgb | Vgb | ηgb | |||
| 1 | 0.0016 | 0.0036 | 0.0028 | 0.0000 | 0.0028 | 54 |
| 2 | 0.0026 | 0.0036 | 0.0018 | 0.0000 | 0.0018 | 30 |
| 3 | 0.0034 | 0.0035 | 0.0010 | 0.0001 | 0.0011 | 20 |
| 4 | 0.0039 | 0.0035 | 0.0005 | 0.0001 | 0.0006 | 10 |
| 5 | 0.0043 | 0.0035 | 0.0000 | 0.0001 | 0.0002 | 3 |
| 6 | 0.0013 | 0.0029 | 0.0031 | 0.0007 | 0.0038 | 75 |
| 7 | 0.0024 | 0.0029 | 0.0020 | 0.0007 | 0.0028 | 55 |
| … | ||||||
| 26 | 0.0017 | 0.0036 | 0.0027 | 0.0000 | 0.0027 | 51 |
| 27 | 0.0027 | 0.0036 | 0.0017 | 0.0000 | 0.0018 | 29 |
| 28 | 0.0034 | 0.0035 | 0.0010 | 0.0001 | 0.0011 | 19 |
| … | ||||||
| 54 | 0.0040 | 0.0035 | 0.0004 | 0.0001 | 0.0005 | 7 |
| 55 | 0.0044 | 0.0035 | 0.0000 | 0.0002 | 0.0002 | 1 |
| 56 | 0.0013 | 0.0029 | 0.0031 | 0.0007 | 0.0038 | 73 |
| … | ||||||
| 71 | 0.0001 | 0.0002 | 0.0043 | 0.0034 | 0.0077 | 123 |
| 72 | 0.0014 | 0.0001 | 0.0030 | 0.0035 | 0.0065 | 118 |
| 73 | 0.0023 | 0.0001 | 0.0021 | 0.0035 | 0.0055 | 108 |
| … | ||||||
| 101 | 0.0018 | 0.0035 | 0.0026 | 0.0001 | 0.0027 | 46 |
| 102 | 0.0028 | 0.0035 | 0.0016 | 0.0001 | 0.0017 | 26 |
| 103 | 0.0035 | 0.0035 | 0.0009 | 0.0001 | 0.0010 | 16 |
| … | ||||||
| 123 | 0.0024 | 0.0001 | 0.0020 | 0.0035 | 0.0055 | 106 |
| 124 | 0.0032 | 0.0000 | 0.0012 | 0.0036 | 0.0048 | 91 |
| 125 | 0.0038 | 0 | 0.0006 | 0.0036 | 0.00422 | 83 |
| Ranking | |||
|---|---|---|---|
| Trial. | MAIRCA | EAMR | MARCOS |
| 1 | 54 | 55 | 65 |
| 2 | 30 | 35 | 38 |
| 3 | 20 | 20 | 20 |
| 4 | 10 | 10 | 10 |
| 5 | 3 | 3 | 3 |
| 6 | 75 | 77 | 85 |
| 7 | 55 | 52 | 55 |
| … | |||
| 26 | 51 | 54 | 64 |
| 27 | 29 | 33 | 36 |
| 28 | 19 | 19 | 19 |
| … | |||
| 54 | 7 | 7 | 7 |
| 55 | 1 | 1 | 1 |
| 56 | 73 | 74 | 83 |
| … | |||
| 71 | 123 | 123 | 123 |
| 72 | 118 | 118 | 115 |
| 73 | 108 | 108 | 108 |
| … | |||
| 101 | 46 | 48 | 59 |
| 102 | 26 | 27 | 31 |
| 103 | 16 | 16 | 16 |
| … | |||
| 123 | 106 | 106 | 106 |
| 124 | 91 | 91 | 91 |
| 125 | 83 | 81 | 71 |
| No. | ut | ||||||
|---|---|---|---|---|---|---|---|
| 10 | 15 | 20 | 25 | 30 | 35 | 40 | |
| u1 | 2.4 | 4.12 | 5.02 | 5.79 | 6.63 | 7.02 | 7.66 |
| 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | |
| 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, D.-B.; Tran, H.-D.; Dinh, V.-T.; Vu, D.; Vu, N.-P.; Nguyen, V.-T. Solving a Multi-Objective Optimization Problem of a Two-Stage Helical Gearbox with Second-Stage Double Gear Sets Using the MAIRCA Method. Appl. Sci. 2024, 14, 5274. https://doi.org/10.3390/app14125274
Vu D-B, Tran H-D, Dinh V-T, Vu D, Vu N-P, Nguyen V-T. Solving a Multi-Objective Optimization Problem of a Two-Stage Helical Gearbox with Second-Stage Double Gear Sets Using the MAIRCA Method. Applied Sciences. 2024; 14(12):5274. https://doi.org/10.3390/app14125274
Chicago/Turabian StyleVu, Duc-Binh, Huu-Danh Tran, Van-Thanh Dinh, Duong Vu, Ngoc-Pi Vu, and Van-Trang Nguyen. 2024. "Solving a Multi-Objective Optimization Problem of a Two-Stage Helical Gearbox with Second-Stage Double Gear Sets Using the MAIRCA Method" Applied Sciences 14, no. 12: 5274. https://doi.org/10.3390/app14125274
APA StyleVu, D.-B., Tran, H.-D., Dinh, V.-T., Vu, D., Vu, N.-P., & Nguyen, V.-T. (2024). Solving a Multi-Objective Optimization Problem of a Two-Stage Helical Gearbox with Second-Stage Double Gear Sets Using the MAIRCA Method. Applied Sciences, 14(12), 5274. https://doi.org/10.3390/app14125274






