Novel Ordinary Differential Equation for State-of-Charge Simulation of Rechargeable Lithium-Ion Battery
Abstract
:1. Introduction
2. Some Existing Methods of Estimating the Lithium-Ion Battery State of Charge
2.1. Experimental Methods
2.2. Data-Driven Method
2.3. Model-Based Methods
- Electrolyte lithium-ion diffusion equations in the positive electrode, negative electrode, and separator according to Fick’s second law.
- Solid-phase lithium-ion diffusion equations in the electrodes due to Fick’s second law.
- Electrolyte ohm equations in the electrodes and separator.
- Solid-phase ohm equations in the positive electrode and negative electrode.
- Charge conservation equations, including a positive electrode and a negative electrode, and a separator.
- Butler–Volmer (BV) kinetic equations at the surface of the particles in the electrodes.
3. Model Configuration of a Rechargeable Lithium-Ion Battery
4. Methods
4.1. Mathematical Modeling of Rechargeable Lithium-Ion Battery State of Charge
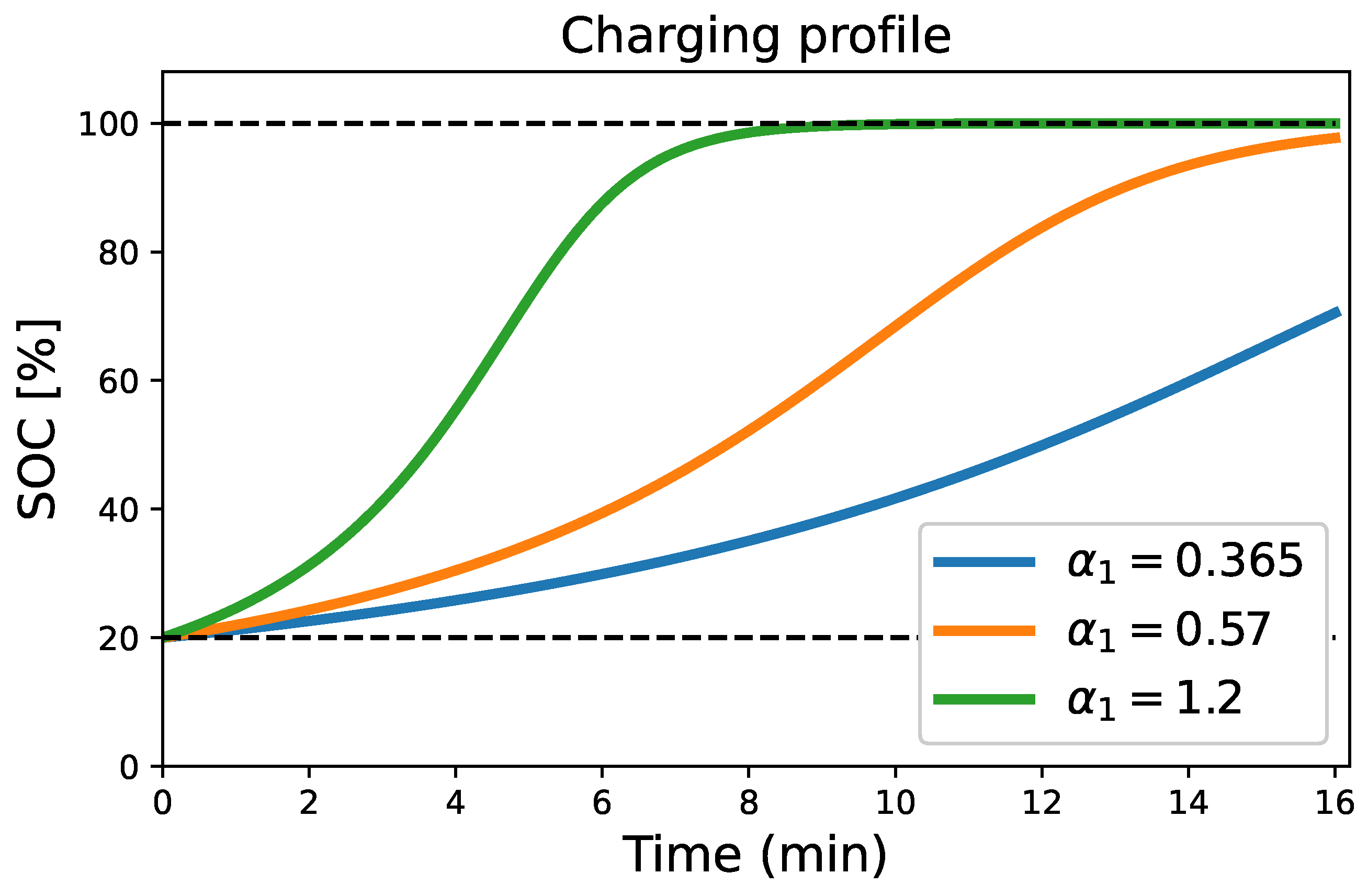
4.2. Charging Process Condition
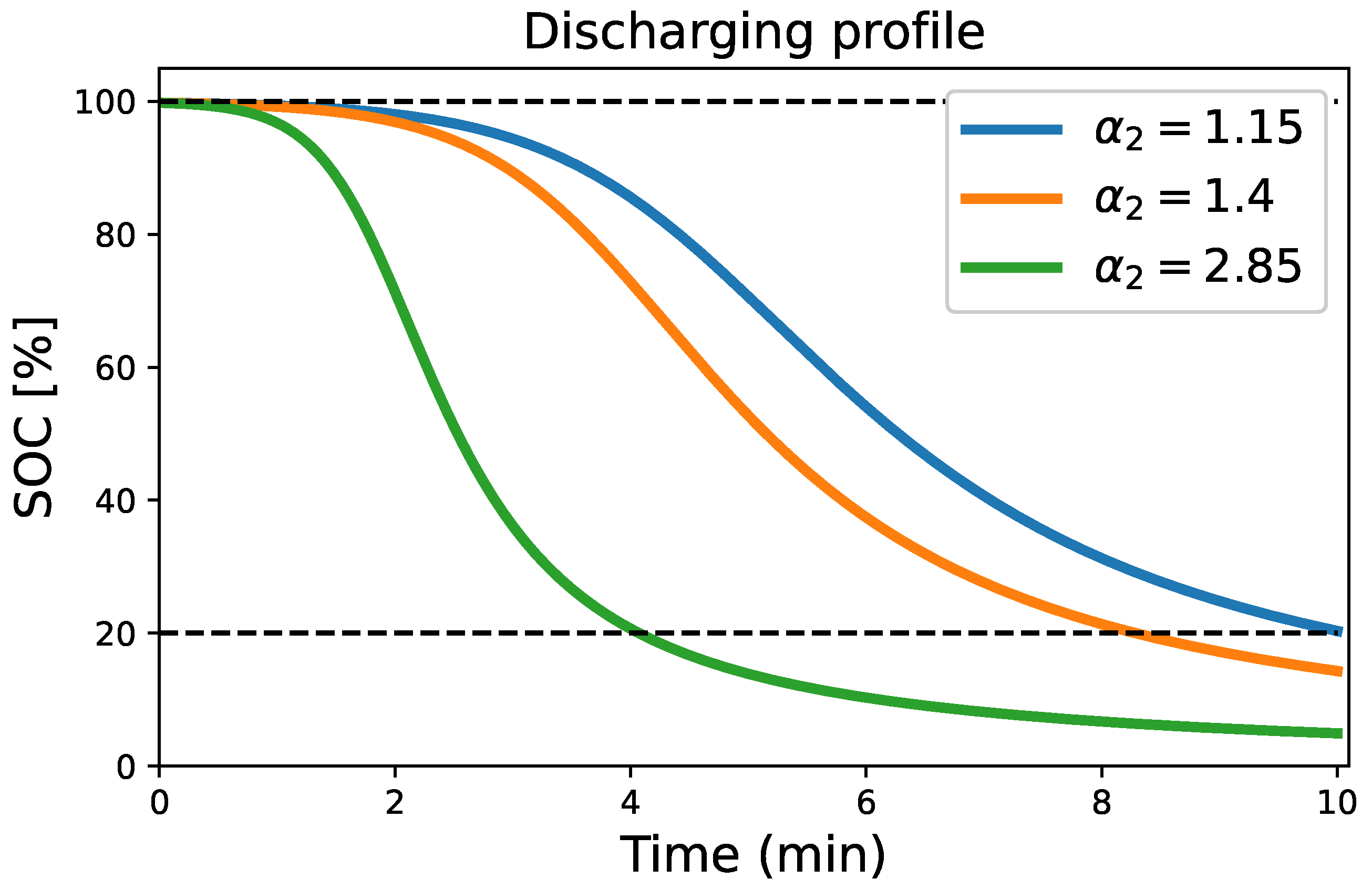
4.3. Discharging Process Condition
4.4. Comparison of Developed Model with Old Model
5. Case Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, X.; Zheng, Y.; Lin, X.; Xie, Y. Optimal Multistage Charging of NCA/Graphite Lithium-Ion Batteries Based on Electrothermal-Aging Dynamics. IEEE Trans. Transp. Electrif. 2020, 6, 427–438. [Google Scholar] [CrossRef]
- Rosewater, D.M.; Copp, D.A.; Nguyen, T.A.; Byrne, R.H.; Santoso, S. Battery Energy Storage Models for Optimal Control. IEEE Access 2019, 7, 178357–178391. [Google Scholar] [CrossRef]
- Breyer, C.; Khalili, S.; Bogdanov, D.; Ram, M.; Oyewo, A.S.; Aghahosseini, A.; Gulagi, A.; Solomon, A.A.; Keiner, D.; Lopez, G.; et al. On the History and Future of 100% Renewable Energy Systems Research. IEEE Access 2022, 10, 78176–78218. [Google Scholar] [CrossRef]
- Shaqsi, A.L.A.Z.; Kamaruzzaman, S.; Al-Hinai, A. Review of energy storage services, applications, limitations, and benefits. Energy Rep. 2020, 6, 288–306. [Google Scholar] [CrossRef]
- Chen, T.; Jin, Y.; Lv, H.; Yang, A.; Liu, M.; Chen, B.; Xie, Y.; Chen, Q. Applications of Lithium-Ion Batteries in Grid-Scale Energy Storage Systems. Trans. Tianjin Univ. 2020, 26, 208–217. [Google Scholar] [CrossRef]
- Opiyo, N. Energy storage systems for PV-based communal grids. J. Energy Storage 2016, 7, 1–12. [Google Scholar] [CrossRef]
- Das, U.K.; Shrivastava, P.; Tey, K.S.; Idris, M.Y.I.B.; Mekhilef, S.; Jamei, E.; Seyedmahmoudian, M.; Stojcevski, A. Advancement of lithium-ion battery cells voltage equalization techniques: A review. Renew. Sustain. Energy Rev. 2020, 134, 110227. [Google Scholar] [CrossRef]
- Hu, X.; Liu, W.; Lin, X.; Xie, Y. A comparative study of control-oriented thermal models for cylindrical li-ion batteries. IEEE Trans. Transp. Electrif. 2019, 5, 1237–1253. [Google Scholar] [CrossRef]
- Zhang, S.S.; Xu, K.; Jow, T.R. Study of the charging process of a LiCoO2-based Li-ion battery. J. Power Sources 2006, 160, 1349–1354. [Google Scholar] [CrossRef]
- Zhao, X.W.; Zhang, G.Y.; Yang, L.; Qiang, J.X.; Chen, Z.Q. A new charging mode of Li-ion batteries with LiFePO4/C composites under low temperature. J. Therm. Anal. Calorim. 2010, 104, 561–567. [Google Scholar] [CrossRef]
- Zhao, J.; Song, C.; Li, G. Fast-Charging Strategies for Lithium-Ion Batteries: Advances and Perspectives. ChemPlusChem 2022, 87, e202200155. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S. The effect of the charging protocol on the cycle life of a Li-ion battery. J. Power Sources 2006, 161, 1385–1391. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Liu, K.; Zou, C.; Li, K.; Wik, T. Charging Pattern Optimization for Lithium-Ion Batteries With an Electrothermal-Aging Model. IEEE Trans. Ind. Inform. 2018, 14, 5463–5474. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical Review on the Battery State of Charge Estimation Methods for Electric Vehicles. IEEE Access 2018, 6, 1832–1843. [Google Scholar] [CrossRef]
- Zhai, S.; Li, W.; Wang, C.; Chu, Y. A Novel Data-Driven Estimation Method for State-ofCharge Estimation of Li-Ion Batteries. Energies 2022, 15, 3115. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Lipu, M.S.H.; Ker, P.J. State of Charge Estimation for Lithium-Ion Batteries Using Model-Based and Data-Driven Methods: A Review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Saad, M.H.M.; Ayob, A.; Blaabjerg, F. State of Charge Estimation for Lithium-Ion Battery Using Recurrent NARX Neural Network Model Based Lighting Search Algorithm. IEEE Access 2018, 6, 28150–28161. [Google Scholar] [CrossRef]
- Murnane, M.; Ghazel, A. A Closer Look at State of Charge (SOC) and State of Health (SOH) Estimation Techniques for Batteries. Analog. Devices 2017, 2, 426–436. [Google Scholar]
- Chaowanan, J. The effect of SoC management on economic performance for battery energy storage system in providing voltage regulation in distribution networks. Electr. Power Syst. Res. 2022, 211, 108340. [Google Scholar] [CrossRef]
- Liu, T.; Tan, W.; Tang, X.; Zhang, J.; Xing, Y.; Cao, D. Driving conditions-driven energy management strategies for hybrid electric vehicles: A review. Renew. Sustain. Energy Rev. 2021, 151, 111521. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Zhao, Q.C. Efects of overcharge cycling on the aging and safety of lithium ion batteries. High Volt. Eng. 2020, 46, 3390–3397. [Google Scholar]
- Zhou, Y. Analysis of causes of fire and explosion of lithium battery and analysis of control measure. Fire Prot. Eng. 2020, 5, 126–127. [Google Scholar]
- Sun, L.; Zheng, Y.J.; Zhou, L.; Li, X.J.; Zhou, P. Experimental study on overdischarge induced internal short circuit of NCM batteries. Chin. J. Power Sources 2018, 42, 1454–1457. [Google Scholar]
- Zhang, X.; Han, Y.; Zhang, W. A Review of Factors Affecting the Lifespan of Lithium-ion Battery and its Health Estimation Methods. Trans. Electr. Electron. Mater. 2021, 22, 567–574. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, G.; Zhen, D.; Gu, F.; Ball, A. A review on online state of charge and state of health estimation for lithium-ion batteries in electric vehicles. Energy Rep. 2021, 7, 5141–5161. [Google Scholar] [CrossRef]
- Stroe, A.I.; Meng, J.; Stroe, D.I.; Świerczyński, M.; Teodorescu, R.; Kær, S.K. Influence of Battery Parametric Uncertainties on the State-of-Charge Estimation of Lithium Titanate Oxide-Based Batteries. Renew. Sustain. Energy 2018, 11, 795. [Google Scholar] [CrossRef]
- Espedal, I.B.; Jinasena, A.; Burheim, O.S.; Lamb, J.J. Current Trends for State-of-Charge (SoC) Estimation in Lithium-Ion Battery Electric Vehicles. Energy 2021, 14, 3284. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Raihan, S.A.; Balasingam, B. A scaling approach for improved state of charge representation in rechargeable batteries. Appl. Energy 2020, 267, 114880. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, J.; Gao, T.; Ren, S. State of Charge Estimation of Li-Ion Battery Based on Adaptive Sliding Mode Observer. Sensors 2022, 22, 7678. [Google Scholar] [CrossRef]
- Xuan, D.; Shi, Z.; Chen, J.; Zhang, C.; Wang, Y.X. Real-time estimation of state-of-charge in lithium-ion batteries using improved central difference transform method. J. Clean. Prod. 2020, 252, 119787. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, Z.; Gan, C.; Karlsen, H. State-of-Charge Estimation of Lithium Battery Based on Transfer Learning. In Proceedings of the 2021 International Conference on Artificial Intelligence, Big Data and Algorithms (CAIBDA), Xi’an, China, 28–30 May 2021; pp. 50–53. [Google Scholar] [CrossRef]
- Karlsen, H.; Dong, T.; Yang, Z.; Carvalho, R. Temperature-Dependence in Battery Management Systems for Electric Vehicles: Challenges, Criteria, and Solutions. IEEE Access 2019, 7, 142203–142213. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Dou, X.; Zhang, X. A data-driven coulomb counting method for state of charge calibration and estimation of lithium-ion battery. Sustain. Energy Technol. Assess. 2020, 40, 100752. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Sun, B.; Jiang, J.; Wang, Z. SOC Estimation of Ni-MH Battery Pack based on Approved HPPC Test and EKF Algorithm for HEV. Adv. Mater. Res. 2012, 403, 4398–4402. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Wimmer, C.; Soczka-Guth, T.; Sauer, D. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. I. Experimental investigation. J. Power Sources 2011, 196, 5334–5341. [Google Scholar] [CrossRef]
- ISO 12405–4:2018; Electrically Propelled Road Vehicles—Test Specification for Lithium-Ion Traction Battery Packs and Systems—Part 4: Performance Testing. Internationational Organization for Standardization (ISO): Geneva, Switzerland, 2018.
- Ciucci, F. Modeling electrochemical impedance spectroscopy. Curr. Opin. Electrochem. 2019, 13, 132–139. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, J.; Wang, X.; Mei, X. The Adaptive Fading Extended Kalman Filter SOC Estimation Method for Lithium-ion Batteries. Energy Procedia 2018, 145, 357–362. [Google Scholar] [CrossRef]
- Lin, C.; Tang, A.; Xing, J. Evaluation of electrochemical models based battery state-of-charge estimation approaches for electric vehicles. Appl. Energy 2017, 207, 394–404. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Zhao, S.; Duncan, S.R.; Howey, D.A. Observability Analysis and State Estimation of Lithium-Ion Batteries in the Presence of Sensor Biases. IEEE Trans. Control Syst. Technol. 2017, 25, 326–333. [Google Scholar] [CrossRef]
- Moura, S.J.; Chaturvedi, N.A.; Krstic, M. Adaptive partial differential equation observer for battery state-of-charge/state-of-health estimation via an electrochemical model. J. Dyn. Syst. Meas. Control 2013, 136, 011015. [Google Scholar] [CrossRef]
- Domenico, D.D.; Stefanopoulou, A.; Fiengo, G. Lithium-ion battery state of charge and critical surface charge estimation using an electrochemical model-based extended Kalman filter. J. Dyn. Syst. Meas. Control 2010, 132, 061302. [Google Scholar] [CrossRef]
- Bartlett, A.; Marcicki, J.; Onori, S.; Rizzoni, G.; Yang, X.G.; Miller, T. Electrochemical model-based state of charge and capacity estimation for a composite electrode lithium-ion battery. IEEE Trans. Control Syst. Technol. 2016, 24, 384–399. [Google Scholar] [CrossRef]
- Bizeray, A.M.; Zhao, S.; Duncan, S.R.; Howey, D.A. Lithium-ion battery thermal-electrochemical model-based state estimation using orthogonal collocation and a modified extended Kalman filter. J. Power Sources 2015, 296, 400–412. [Google Scholar] [CrossRef]
- Zou, C.; Klintberg, A.; Wei, Z.; Fridholm, B.; Wik, T.; Egardt, B. Power capability prediction for lithium-ion batteries using economic nonlinear model predictive control. J. Power Sources 2018, 396, 580–589. [Google Scholar] [CrossRef]
- Zhang, C.; Li, L.; Zhao, D. Estimation and simulation of power battery SOC based on BP neural network. Chin. J. Power Sources 2017, 41, 1356–1357. [Google Scholar]
- Luo, X.; Zhang, B.; Huang, X.; Huo, C. Estimation of lithium battery SOC based on SVM. J. Telecom Power Technol. 2016, 40, 287–290. [Google Scholar]
- Dang, X.; Yan, L.; Jiang, H.; Wu, X.; Zhang, X. Study on estimation based on online LS-SVM for state of charge of power battery. J. Telecom Power Technol. 2017, 041, 752–756. [Google Scholar]
- Yuqing, C.; Yuqiong, K.; Yun, Z.; Li, W.; Jilei, L.; Yanxi, L.; Zheng, L.; Xiangming, H.; Xing, L.; Naser, T.; et al. A review of lithium-ion battery safety concerns: The issues, strategies, and testing standards. J. Energy Chem. 2021, 59, 83–99. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods-Fundamentals and Applications, 3rd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Lagraoui, M.; Nejmi, A.; Rayhane, H.; Taouni, A. Estimation of lithium-ion battery state-of-charge using an extended kalman filter. Bull. Electr. Eng. Inform. 2021, 10, 1759–1768. [Google Scholar] [CrossRef]
- Wang, J.; Meng, J.; Peng, Q.; Liu, T.; Zeng, X.; Chen, G.; Li, Y. Lithium-ion battery state-of-charge estimation using electrochemical model with sensitive parameters adjustment. Batteries 2023, 9, 180. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Li, Z.; Yu, Q.; Mu, H. An electrochemical model based degradation state identification method of Lithium-ion battery for all-climate electric vehicles application. Appl. Energy 2018, 219, 264–275. [Google Scholar] [CrossRef]
- Moura, S.J.; Argomedo, F.B.; Klein, R.; Mirtabatabaei, A.; Krstic, M. Battery State Estimation for a Single Particle Model with Electrolyte Dynamics. IEEE Trans. Control Syst. Technol. 2016, 25, 453–468. [Google Scholar] [CrossRef]
- Hussein, H.M.; Aghmadi, A.; Abdelrahman, M.S.; Rafin, S.S.H.; Mohammed, O. A review of battery state of charge estimation and management systems: Models and future prospective. Wiley Interdiscip. Rev. Energy Environ. 2024, 13, e507. [Google Scholar] [CrossRef]
- Di Luca, G.; Di Blasio, G.; Gimelli, A.; Misul, D.A. Review on Battery State Estimation and Management Solutions for Next-Generation Connected Vehicles. Energies 2024, 17, 202. [Google Scholar] [CrossRef]
- Hwang, J.H.; Lee, J.H.; Lee, I.S. Analysis and Diagnosis of the Effect of Voltage and Current Sensor Faults on the State of Charge Estimation of Lithium-ion Batteries Based on Neural Networks. Int. J. Control Autom. Syst. 2024, 22, 1691–1706. [Google Scholar] [CrossRef]

| Symbol | Quantity | Unit |
|---|---|---|
| Energy capacity | Watt-minutes (W min) | |
| q | Inlet/outlet state of charge | % |
| Initial charging/discharging state of charge | % | |
| Maximum capacity of battery | Ampere-minutes (A min) | |
| Charging/discharging efficiency | % | |
| Terminal charging/discharging voltage | Volt (V) | |
| Battery charging voltage | Volt (V) | |
| Battery discharging voltage | Volt (V) | |
| L | Length of the energy reservoir box | m |
| H | Energy reservoir box base area | m2 |
| Charging/discharging energy transfer coefficients | Minutes (min−1) | |
| Charging/discharging state of charge | % | |
| t | Charging/discharging time | Minutes (min) |
| Item | Specification |
|---|---|
| Charging cut-off voltage | 14.6 V |
| Nominal voltage | 12.8 V |
| Discharging cut-off voltage | 12 V |
| Charging efficiency | 80% |
| Discharging efficiency | 95% |
| Different Charging Terminal Voltage [V] | Charging Terminal Voltage-Sensitive Coefficient, A [V/%] | Charging Energy Transfer Coefficient, [] | Charging Rate [] | Charging Time (min) | Corresponding State of Charge, SOC [%] |
|---|---|---|---|---|---|
| 13.2 V | 16 min | ||||
| 13.4 V | 16 min | ||||
| 14.4 V | 8 min |
| Different Discharging Terminal Voltage [V] | Discharging Terminal Voltage-Sensitive Coefficient, B [V/%] | Discharging Energy Transfer Coefficient, [] | Discharging Rate [] | Discharging Time (min) | Corresponding State of Charge, SOC [%] |
|---|---|---|---|---|---|
| 12.9 V | 10 min | ||||
| 12.8 V | 10 min | ||||
| 12 V | 10 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nteutse, P.K.; Mugenga, I.R.; Geletu, A.; Li, P. Novel Ordinary Differential Equation for State-of-Charge Simulation of Rechargeable Lithium-Ion Battery. Appl. Sci. 2024, 14, 5284. https://doi.org/10.3390/app14125284
Nteutse PK, Mugenga IR, Geletu A, Li P. Novel Ordinary Differential Equation for State-of-Charge Simulation of Rechargeable Lithium-Ion Battery. Applied Sciences. 2024; 14(12):5284. https://doi.org/10.3390/app14125284
Chicago/Turabian StyleNteutse, Peguy Kameni, Ineza Remy Mugenga, Abebe Geletu, and Pu Li. 2024. "Novel Ordinary Differential Equation for State-of-Charge Simulation of Rechargeable Lithium-Ion Battery" Applied Sciences 14, no. 12: 5284. https://doi.org/10.3390/app14125284





