An Improved Deviation Coupling Control Method for Speed Synchronization of Multi-Motor Systems
Abstract
:1. Introduction
2. Research Methods
2.1. Deviation Coupling Control Strategy

2.2. Improved Deviation Coupling Control Strategy

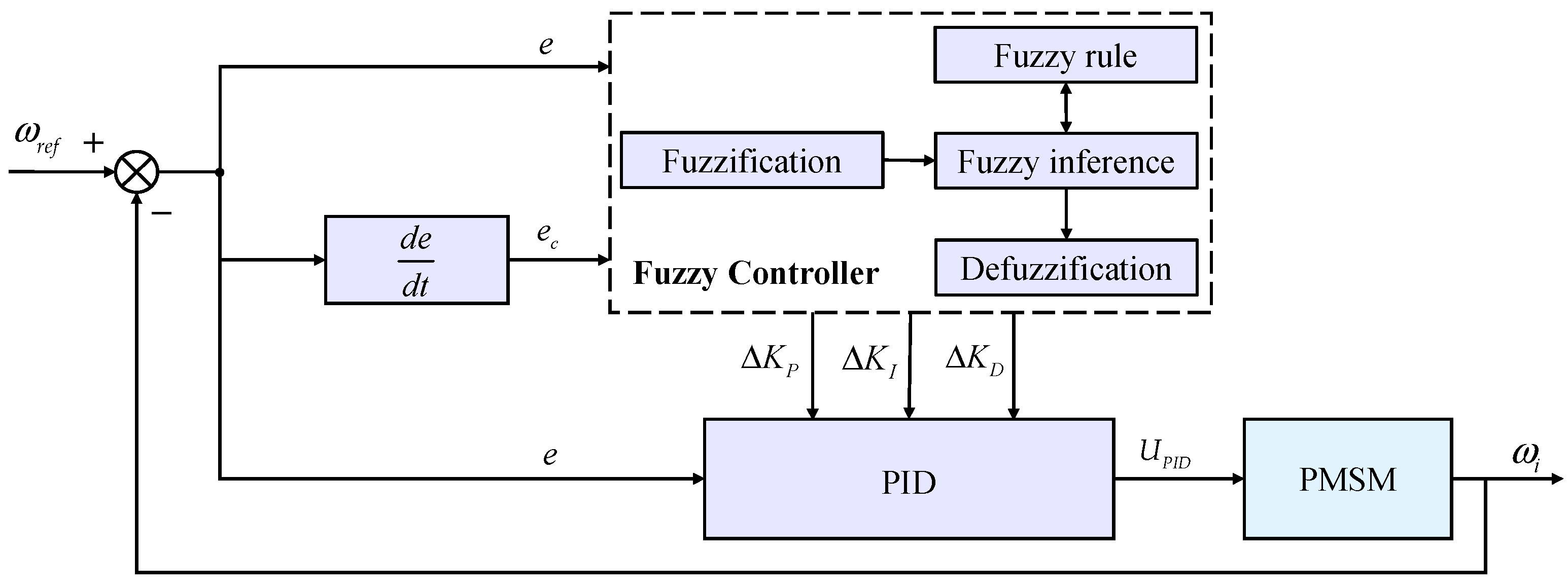
2.3. Controller Based on Fuzzy Control Algorithm
3. Simulation Experiment and Result Analysis
3.1. Model Construction
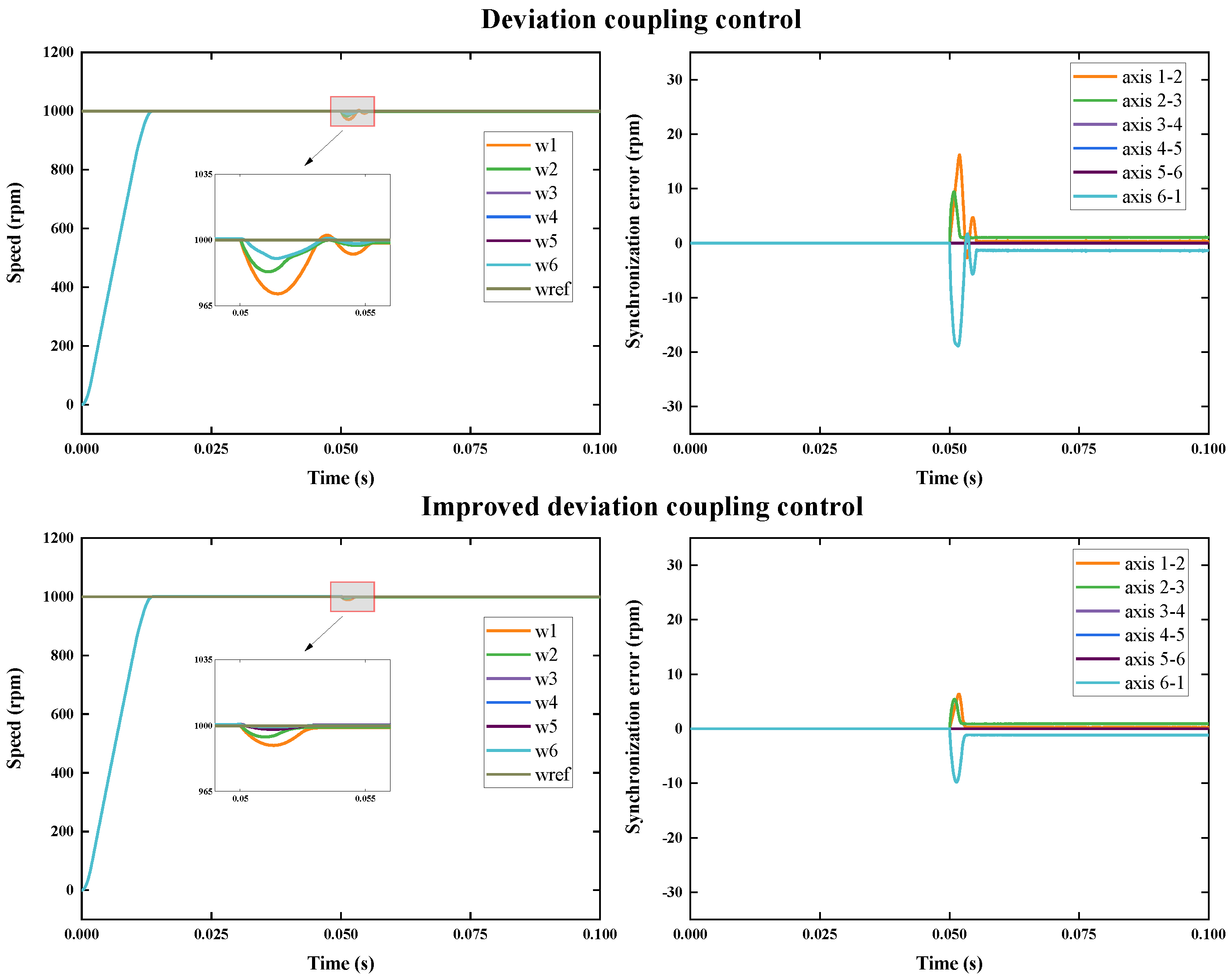
3.2. Analysis of Simulation Results
4. System Testing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Licardo, J.T.; Domjan, M.; Orehovački, T. Intelligent Robotics—A Systematic Review of Emerging Technologies and Trends. Electronics 2024, 13, 542. [Google Scholar] [CrossRef]
- Wahidi, S.I.; Oterkus, S.; Oterkus, E. Robotic Welding Techniques in Marine Structures and Production Processes: A Systematic Literature Review. Mar. Struct. 2024, 95, 103608. [Google Scholar] [CrossRef]
- Tsuzuki, R. Development of Automation and Artificial Intelligence Technology for Welding and Inspection Process in Aircraft Industry. Weld. World 2022, 66, 105–116. [Google Scholar] [CrossRef]
- Guo, Q.; Yang, Z.; Xu, J.; Jiang, Y.; Wang, W.; Liu, Z.; Zhao, W.; Sun, Y. Progress, Challenges and Trends on Vision Sensing Technologies in Automatic/Intelligent Robotic Welding: State-of-the-Art Review. Robot. Comput.-Integr. Manuf. 2024, 89, 102767. [Google Scholar] [CrossRef]
- Wang, B.; Hu, S.J.; Sun, L.; Freiheit, T. Intelligent Welding System Technologies: State-of-the-Art Review and Perspectives. J. Manuf. Syst. 2020, 56, 373–391. [Google Scholar] [CrossRef]
- Niu, F.; Sun, K.; Huang, S.; Hu, Y.; Liang, D.; Fang, Y. A Review on Multimotor Synchronous Control Methods. IEEE Trans. Transp. Electrif. 2023, 9, 22–33. [Google Scholar] [CrossRef]
- Jerković Štil, V.; Varga, T.; Benšić, T.; Barukčić, M. A Survey of Fuzzy Algorithms Used in Multi-Motor Systems Control. Electronics 2020, 9, 1788. [Google Scholar] [CrossRef]
- Li, R.; Yuan, W.; Ding, X.; Xu, J.; Sun, Q.; Zhang, Y. Review of Research and Development of Hydraulic Synchronous Control System. Processes 2023, 11, 981. [Google Scholar] [CrossRef]
- Ismail, K.; Sabar, M. Speed Synchronization Technique for a Multi DC Motor System Using Serial Synchronization. In Proceedings of the 2020 International Conference on Sustainable Energy Engineering and Application (ICSEEA), Tangerang, Indonesia, 18–20 November 2020; pp. 1–5. [Google Scholar]
- Koren, Y. Cross-Coupled Biaxial Computer Control for Manufacturing Systems. J. Dyn. Syst. Meas. Control 1980, 102, 265–272. [Google Scholar] [CrossRef]
- Gao, L. Friction Compensation-Based Cross-Coupled Synchronous Control Method for Multiple Servo Motors. In Proceedings of the 2022 4th International Conference on Robotics, Intelligent Control and Artificial Intelligence, Dongguan, China, 16–18 December 2022; pp. 408–412. [Google Scholar]
- Payette, K. The Virtual Shaft Control Algorithm for Synchronized Motion Control. In Proceedings of the 1998 American Control Conference. ACC (IEEE Cat. No.98CH36207), Philadelphia, PA, USA, 26 June 1998; pp. 3008–3012. [Google Scholar]
- Han, G.; Hong, J.; Chen, B.; Zhu, H.; Zhu, B.; Yu, D. An Improved Virtual-Shaft Control Strategy for Speed Synchronization of Dual-SRM Drive. IEEE Trans. Ind. Electron. 2024, 71, 5485–5495. [Google Scholar] [CrossRef]
- Shih, Y.-T.; Chen, C.-S.; Lee, A.-C. A Novel Cross-Coupling Control Design for Bi-Axis Motion. Int. J. Mach. Tool. Manu. 2002, 42, 1539–1548. [Google Scholar] [CrossRef]
- Fang, P.; Wang, Y.; Zou, M.; Zhang, Z. Combined Control Strategy for Synchronization Control in Multi-Motor-Pendulum Vibration System. J. Vib. Control 2022, 28, 2254–2267. [Google Scholar] [CrossRef]
- Perez-Pinal, F.J.; Calderon, G.; Araujo-Vargas, I. Relative Coupling Strategy. In Proceedings of the IEEE International Electric Machines and Drives Conference, 2003. IEMDC’03., Madison, WI, USA, 1–4 June 2003; pp. 1162–1166. [Google Scholar]
- Chen, Q.; Dong, F.; Tao, L.; Nan, Y. Multiple Motors Synchronization Based on Active Disturbance Rejection Control with Improved Adjacent Coupling. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 4510–4516. [Google Scholar]
- Zhao, M.; Wang, Q.; Wang, Y.; Dong, Q. Multi-Motor Cooperative Control Strategy for Speed Synchronous Control of Construction Platform. Electronics 2022, 11, 4162. [Google Scholar] [CrossRef]
- Jiang, J.; Ren, J.; Gao, X.; Bian, H.; Wu, Y.; Lou, Z. Modeling and Simulation of Multi-Motor Synchronous Control System Based on Slide Mode Controller. In Proceedings of the International Conference on Smart Transportation and City Engineering (STCE 2022), Chongqing, China, 22 December 2022; p. 1246028. [Google Scholar]
- Lan, C.; Wang, H.; Deng, X.; Zhang, X.; Song, H. Multi-Motor Position Synchronization Control Method Based on Non-Singular Fast Terminal Sliding Mode Control. PLoS ONE 2023, 18, e0281721. [Google Scholar] [CrossRef]
- Zhang, P.; Li, Z. Multi-Motor Speed Synchronization Control System Based on Improved ADRC. In Proceedings of the 2023 8th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 21–23 April 2023; pp. 542–546. [Google Scholar]
- Hao, Y.; Zhao, Y. Research on Coupling Control of Multiple Permanent Magnet Synchronous Motors Based on NAISMC and SMDO. PLoS ONE 2023, 18, e0292913. [Google Scholar] [CrossRef]
- Zou, S.; Zhao, W.; Wang, C. Tracking and Synchronization Control Strategy of Vehicle Dual-Motor Steer-by-Wire System via Super-Twisting SOSMC and MDCS. Mech. Syst. Signal Proc. 2023, 183, 109638. [Google Scholar] [CrossRef]
- Wu, X.; Wei, S.; You, J.; Sun, J. Research on Multi-Motor Speed Synchronous Control Based on Mean Coupling Control. In Proceedings of the 9th International Symposium on Sensors, Mechatronics, and Automation (ISSMAS 2023), Nanjing, China, 12 August 2023; p. 1298161. [Google Scholar]
- Li, L.; Sun, L.; Zhang, S. Mean Deviation Coupling Synchronous Control for Multiple Motors via Second-Order Adaptive Sliding Mode Control. ISA Trans. 2016, 62, 222–235. [Google Scholar] [CrossRef]
- Jin, F.; Wan, H.; Huang, Z.; Gu, M. PMSM Vector Control Based on Fuzzy PID Controller. In Proceedings of the Journal of Physics: Conference Series, 2nd International Conference on Electronic Engineering and Informatics, Lanzhou, China, 17–19 July 2020; p. 012016. [Google Scholar]
- Zhao, M.; Xu, X.; Yang, H.; Pan, Z. Design of a Predictive RBF Compensation Fuzzy PID Controller for 3D Laser Scanning System. Appl. Sci. 2020, 10, 4662. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, J.; Gu, J.; Du, Y.; Li, Z.; Zhu, Z.; Mao, E. Pressure Control Algorithm Based on Adaptive Fuzzy PID with Compensation Correction for the Tractor Electronic Hydraulic Hitch. Appl. Sci. 2020, 10, 3179. [Google Scholar] [CrossRef]
- Deng, L.; Liu, T.; Jiang, P.; Xie, F.; Zhou, J.; Yang, W.; Qi, A. Design of an Adaptive Algorithm for Feeding Volume–Traveling Speed Coupling Systems of Rice Harvesters in Southern China. Appl. Sci. 2023, 13, 4876. [Google Scholar] [CrossRef]






| Parameters | Values |
|---|---|
| Rated torque T | 15 Nm |
| Rated speed v | 3000 rpm |
| Pole logarithm Pn | 4 |
| Moment of inertia J | 0.003 kg·m2 |
| Stator resistance R | 0.958 Ω |
| Magnetic chain amplitude ψf | 0.1827 Wb |
| Friction coefficient B | 0.003 N·m·s |
| Cross-axis inductance Ld | 0.00525 H |
| Straight-axis inductance Lq | 0.012 H |
| Without | Deviation Coupling | Improved | Compare | |
|---|---|---|---|---|
| Maximum synchronization error | 28.82 rpm | 19.19 rpm | 11.71 rpm | −59% |
| Synchronization error adjustment time | 5.94 ms | 8.92 ms | 4.74 ms | −20% |
| Deviation Coupling | Improved | Compare | |
|---|---|---|---|
| Maximum synchronization error | 18.88 rpm | 9.81 rpm | −48% |
| Synchronization error adjustment time | 5.59 ms | 3.78 ms | −32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, Y.; Qi, L.; Sun, M.; Han, W. An Improved Deviation Coupling Control Method for Speed Synchronization of Multi-Motor Systems. Appl. Sci. 2024, 14, 5300. https://doi.org/10.3390/app14125300
Mu Y, Qi L, Sun M, Han W. An Improved Deviation Coupling Control Method for Speed Synchronization of Multi-Motor Systems. Applied Sciences. 2024; 14(12):5300. https://doi.org/10.3390/app14125300
Chicago/Turabian StyleMu, Ying, Liqun Qi, Mingyuan Sun, and Wenbo Han. 2024. "An Improved Deviation Coupling Control Method for Speed Synchronization of Multi-Motor Systems" Applied Sciences 14, no. 12: 5300. https://doi.org/10.3390/app14125300
APA StyleMu, Y., Qi, L., Sun, M., & Han, W. (2024). An Improved Deviation Coupling Control Method for Speed Synchronization of Multi-Motor Systems. Applied Sciences, 14(12), 5300. https://doi.org/10.3390/app14125300






