Design and Control of a Pneumatic Muscle Servo Drive Applied to a 6-DoF Parallel Manipulator
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Methodology
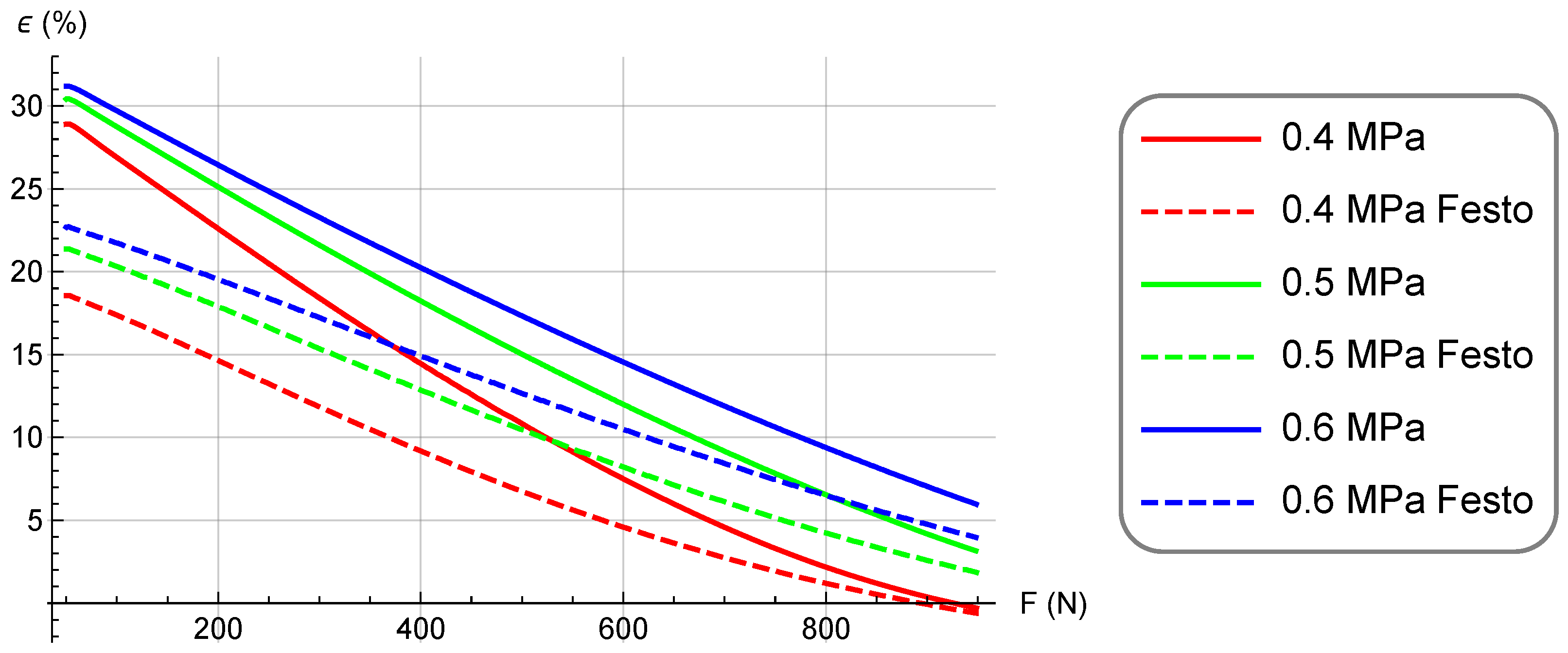
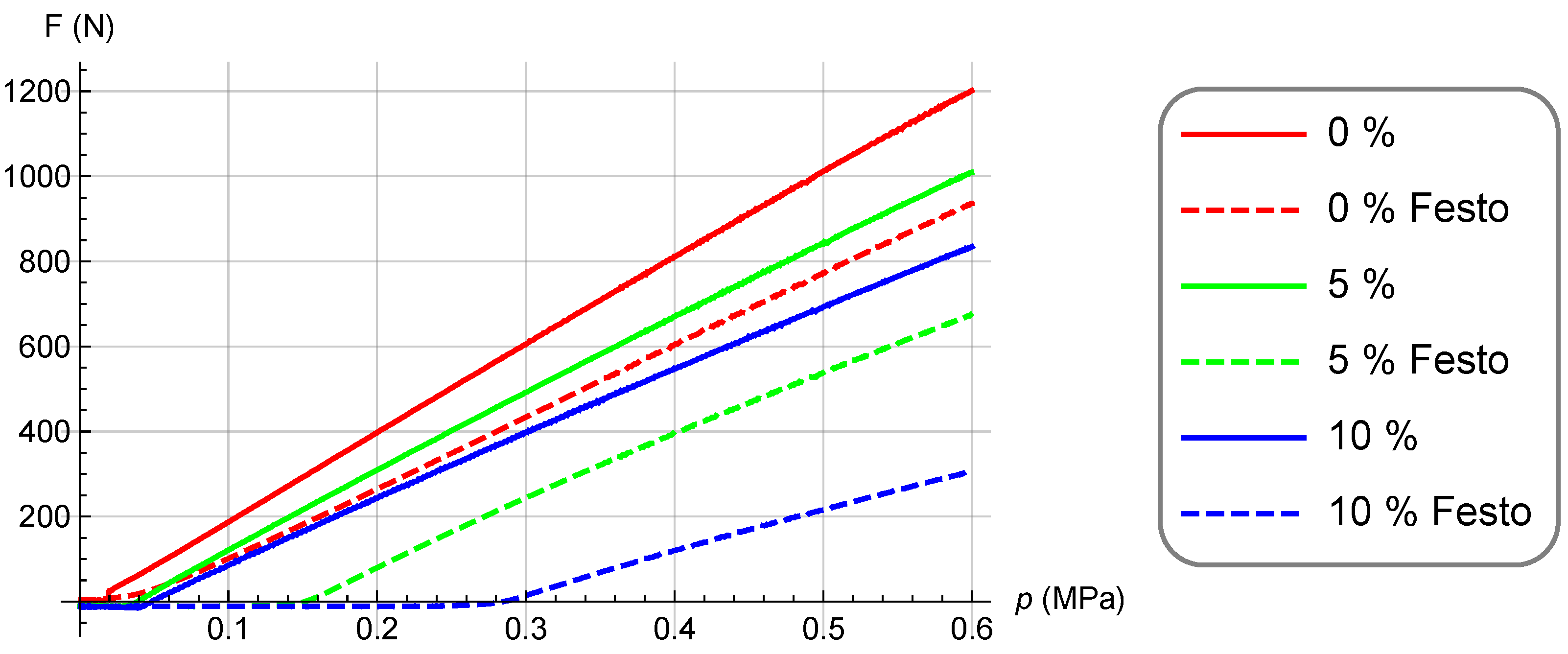
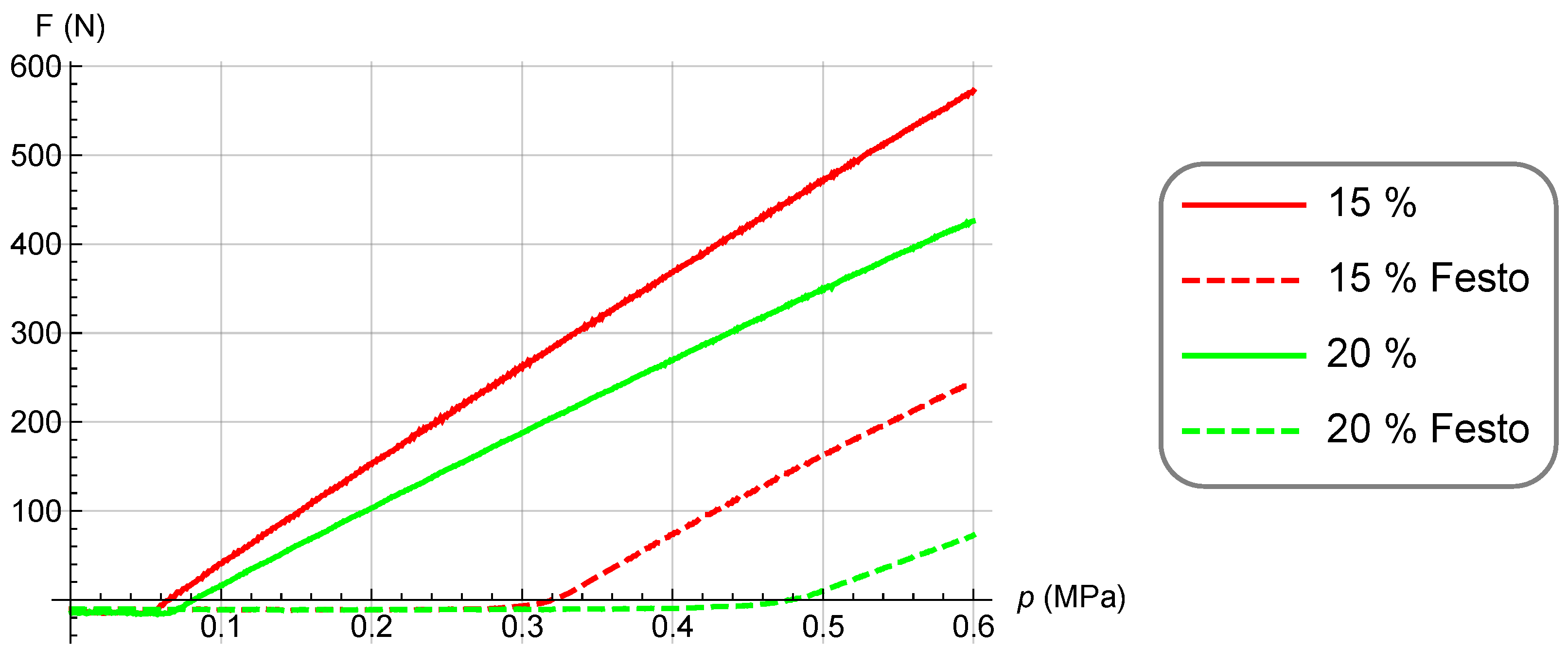
2.2. Comparison with Commercial Muscles
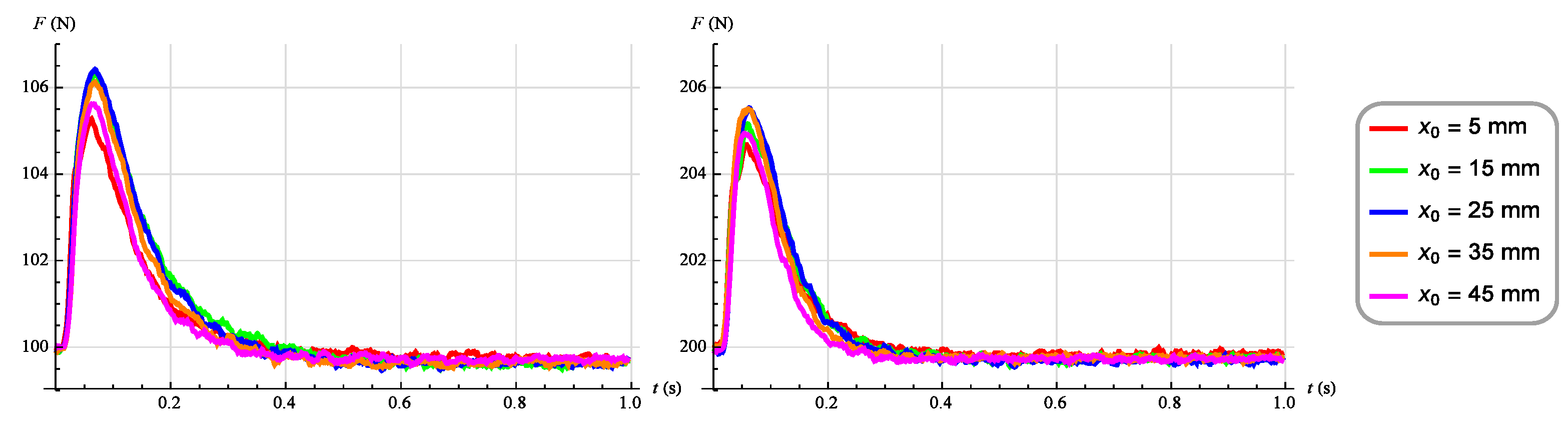
2.3. Dynamic Characteristics
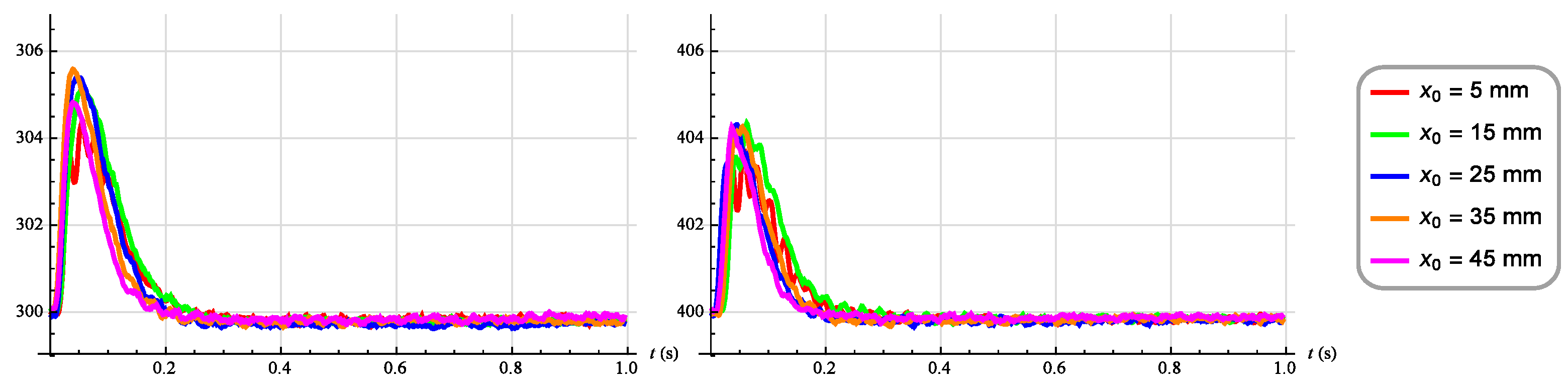
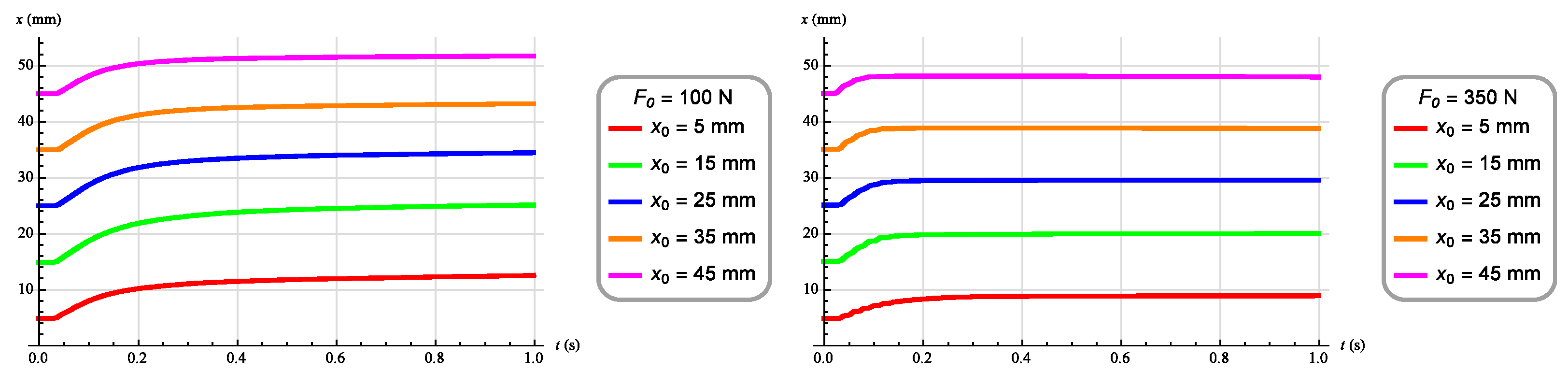
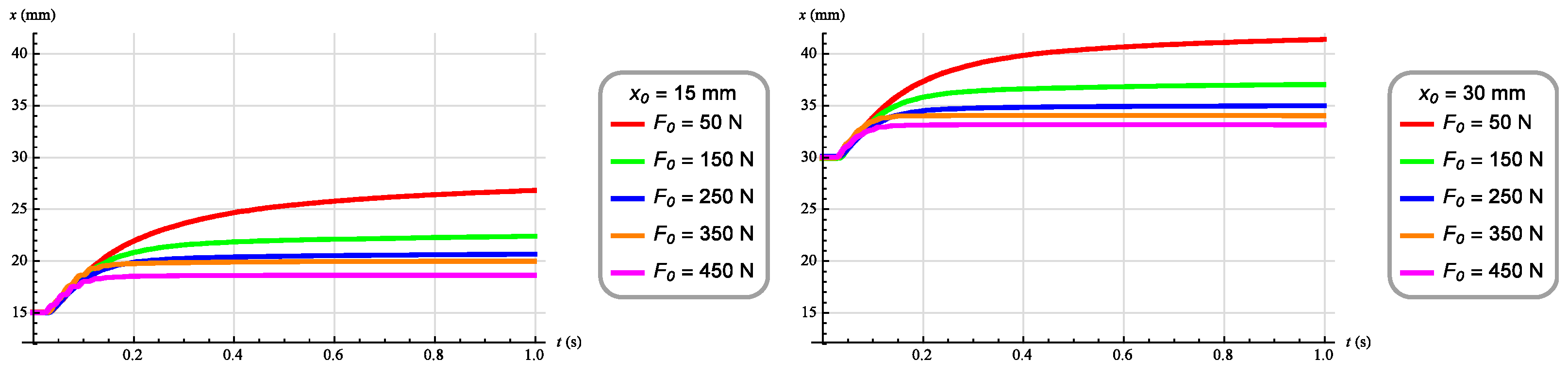
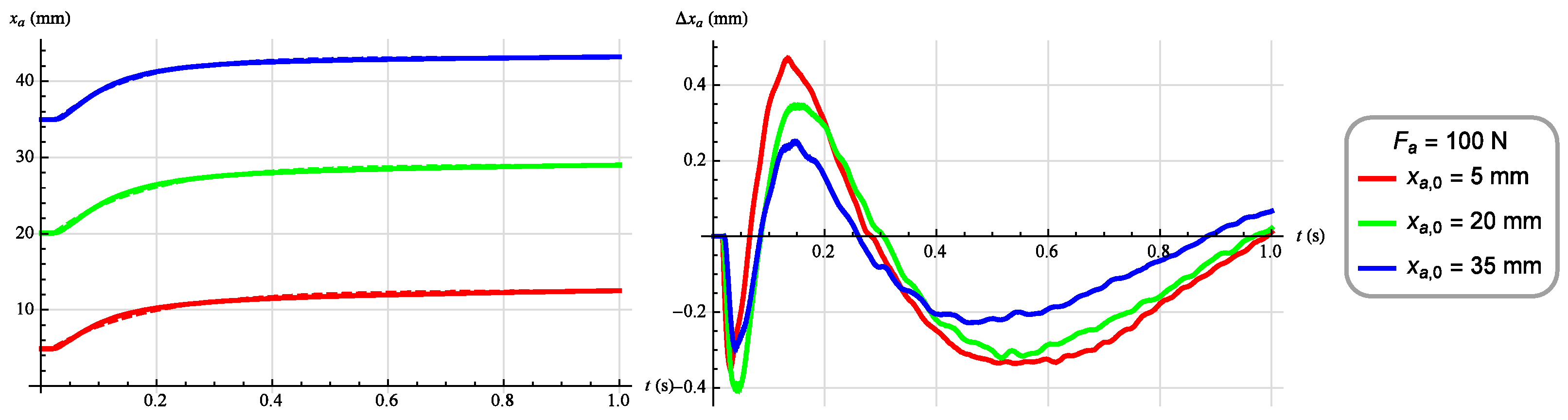
3. Results
3.1. Functional Model of the Pneumatic Muscle
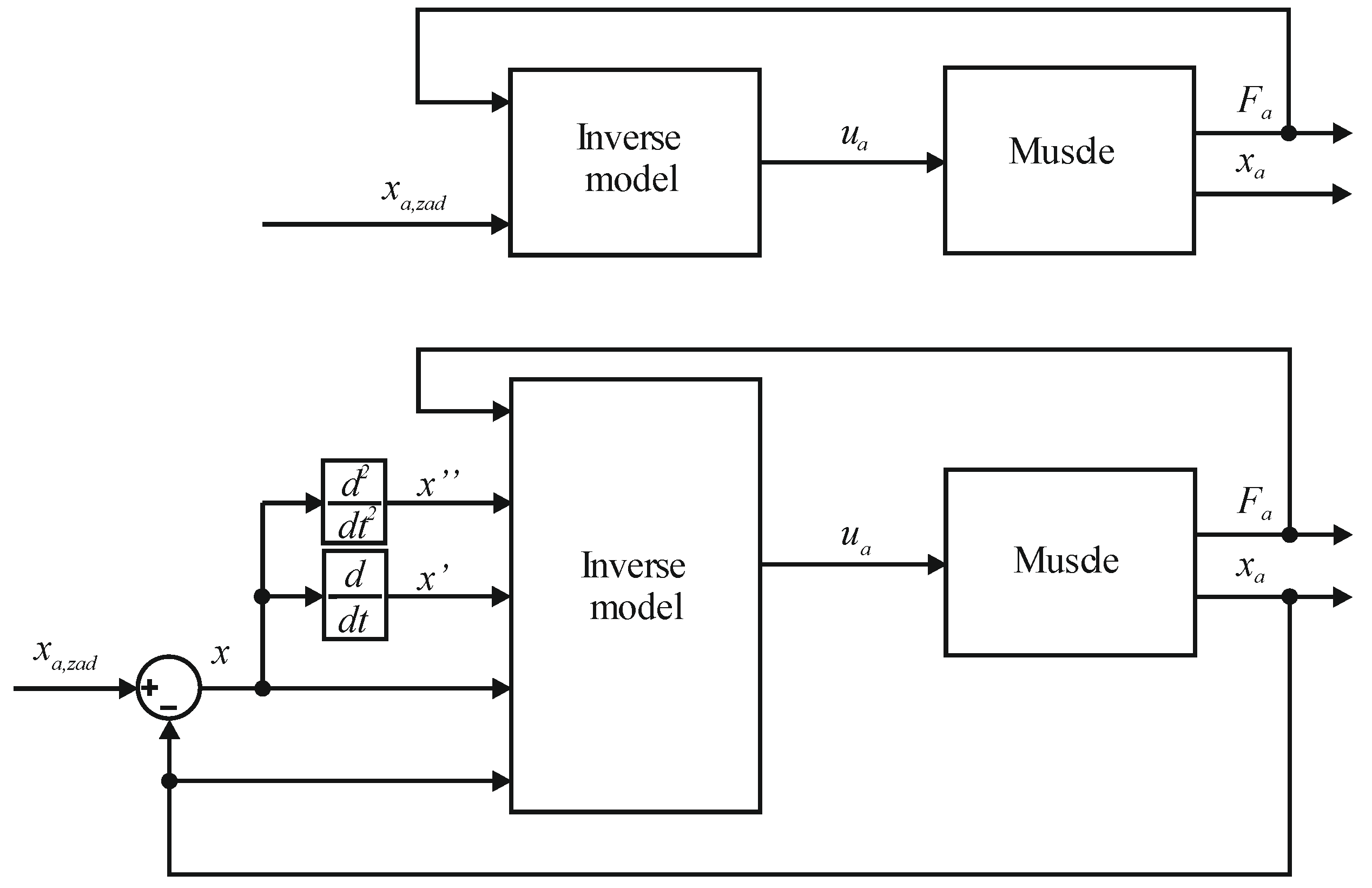
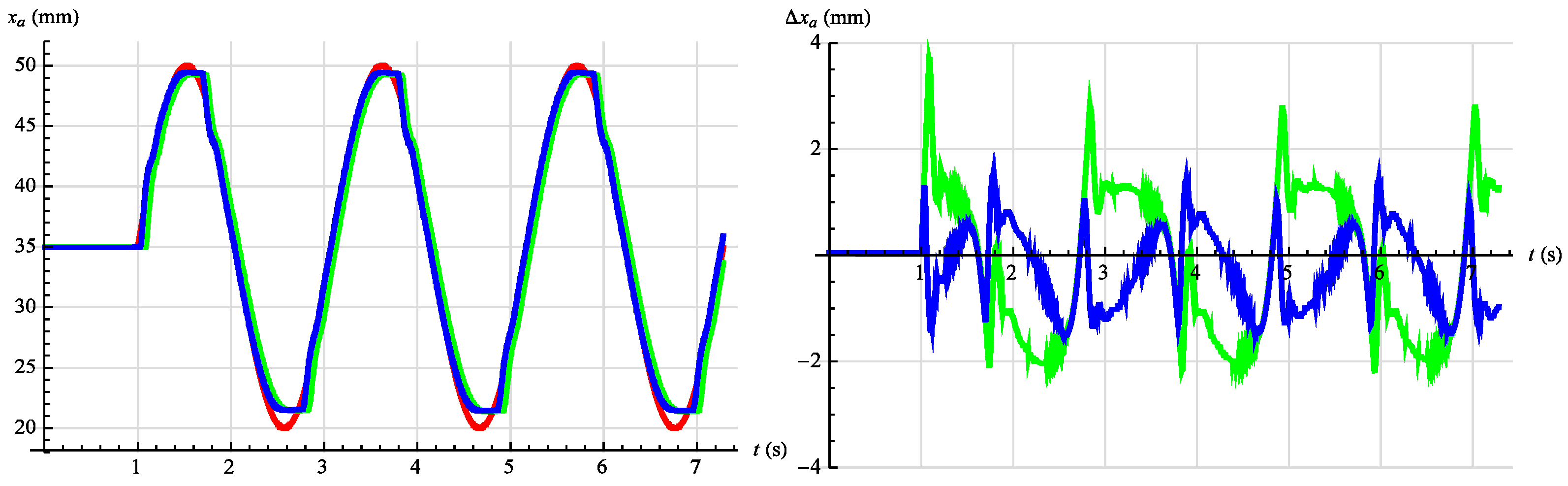
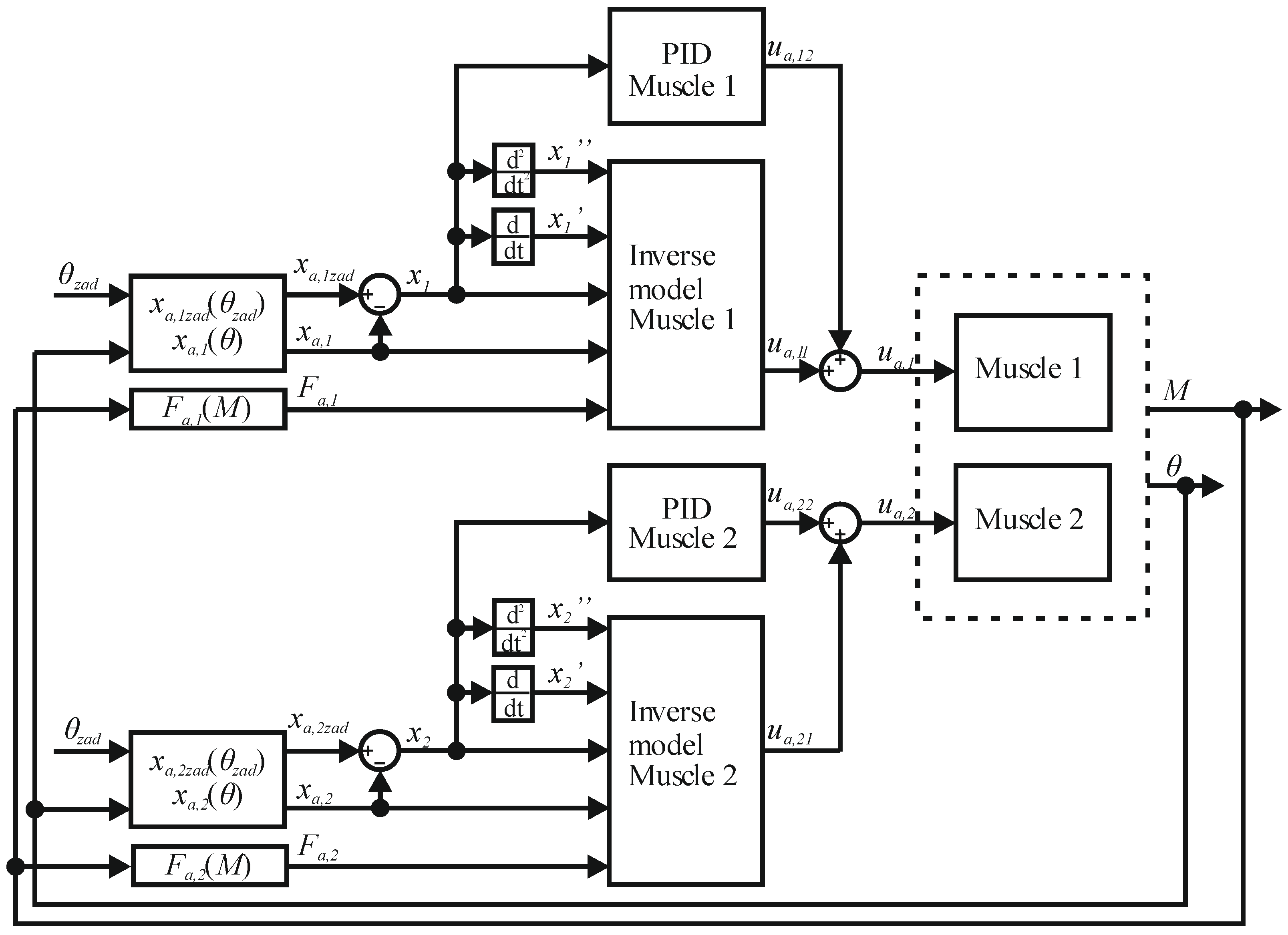
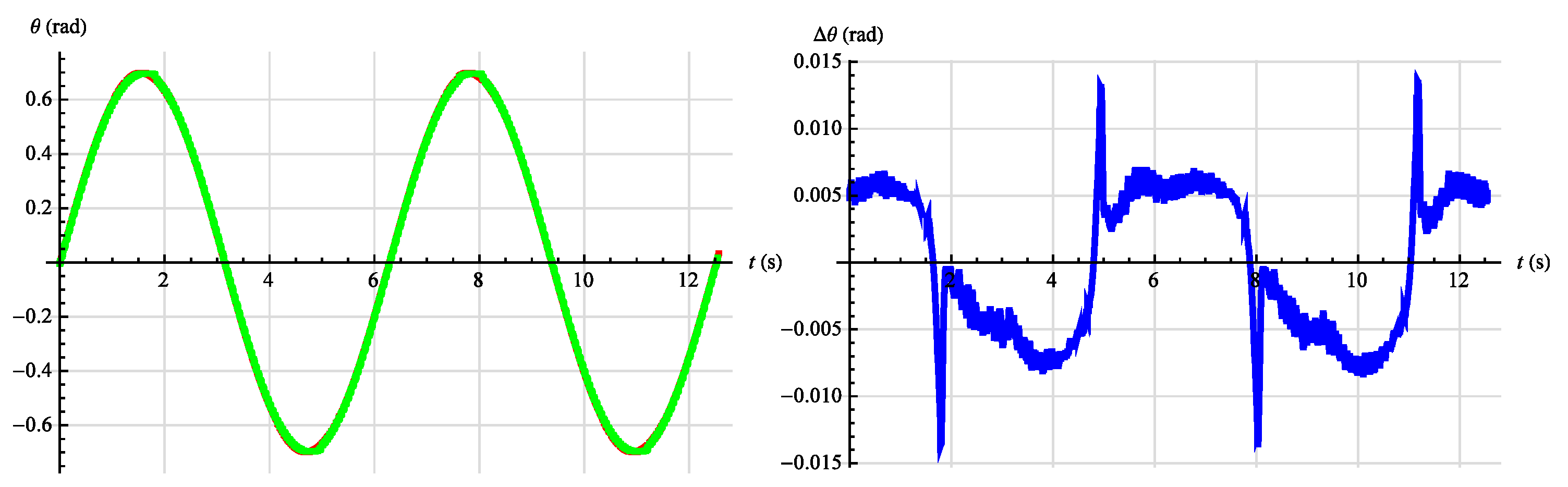
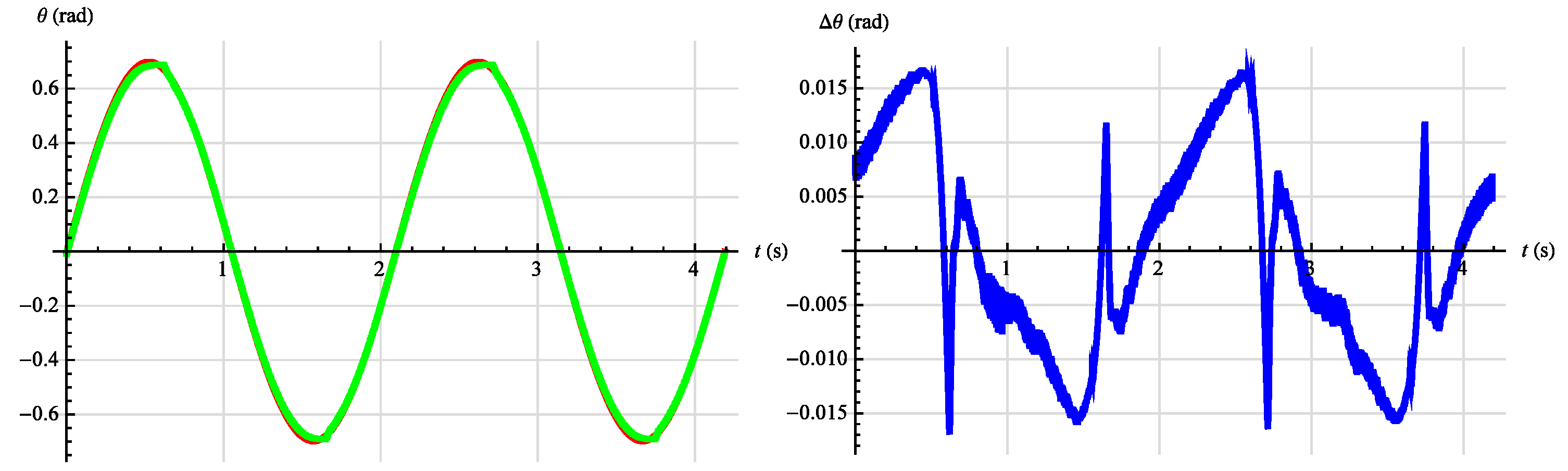
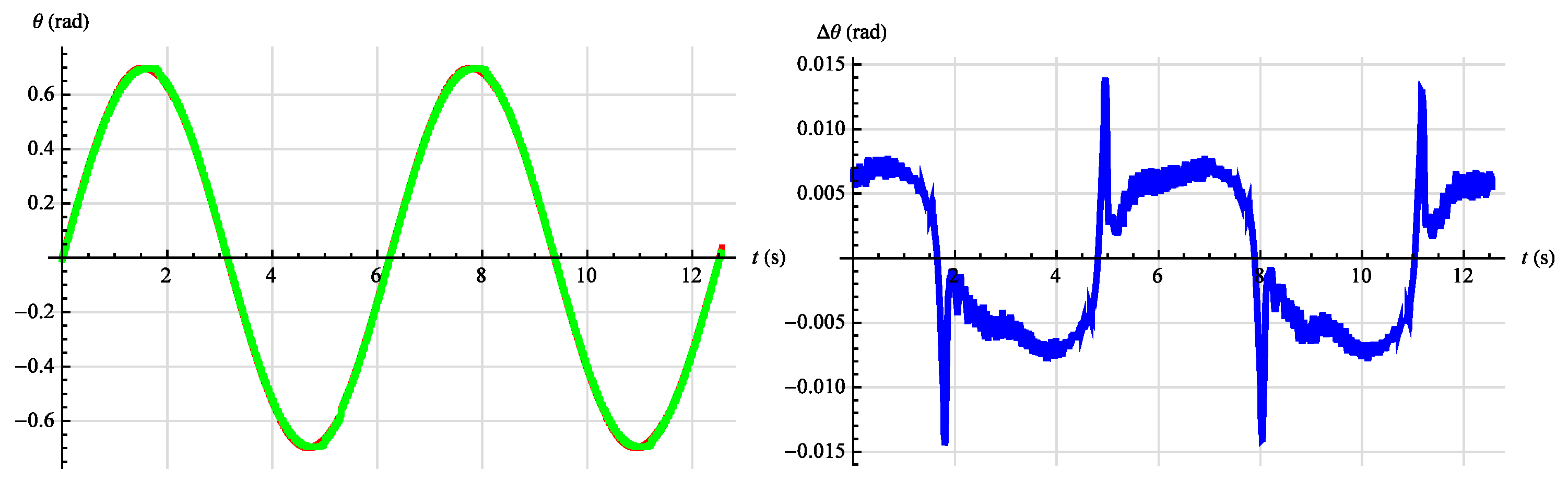
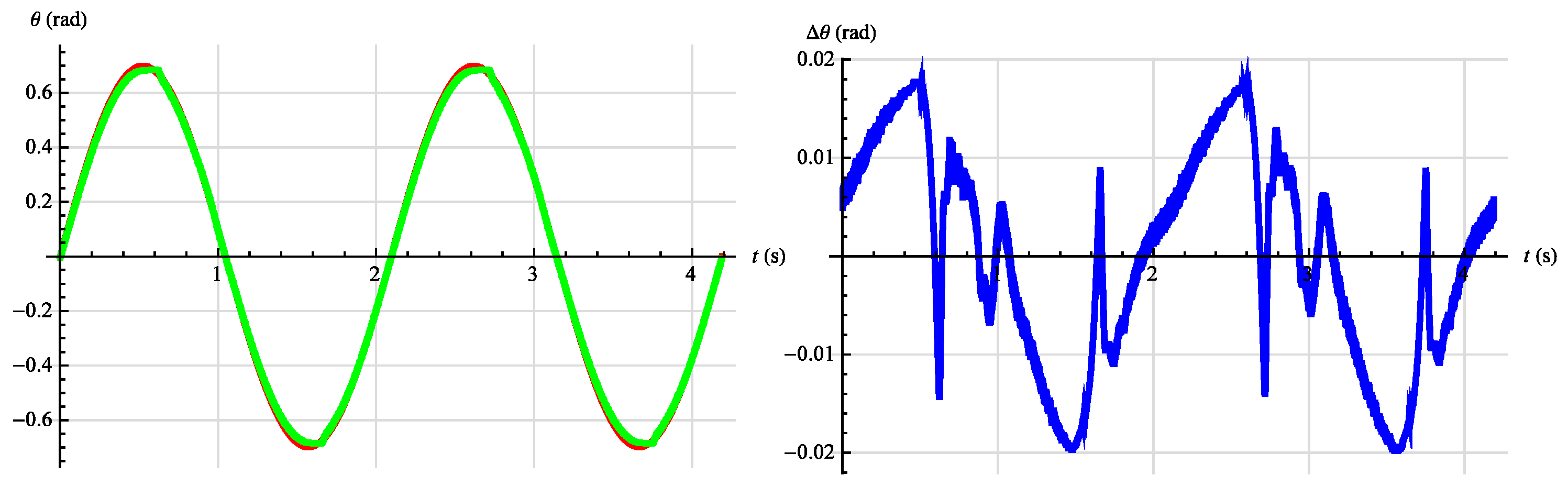
3.2. Synthesis of Angular Position Control System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pietrala, D.S.; Łaski, P.A. Design and Control of a Pneumatic Muscle Servo Drive Containing Its Own Pneumatic Muscles. Appl. Sci. 2022, 12, 11024. [Google Scholar] [CrossRef]
- Nazarczuk, K. Niektóre Zagadnienia Analizy i Syntezy Sztucznego Mięśnia Pneumatycznego; Archiwum Budowy Maszyn: Warszawa, Poland, 1967. [Google Scholar]
- Chou, C.P.; Hannaford, B. Static and Dynamic Characteristics of McKibben Pneumatic Artificial Muscles. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; Volume 1–4, pp. 281–286. [Google Scholar]
- Chou, C.P.; Hannaford, B. Measurement and modeling of McKibben pneumatic artificial muscles. IEEE Trans. Robot. Autom. 1996, 12, 90–102. [Google Scholar] [CrossRef]
- Doumit, M.; Fahim, A.; Munro, M. Analytical Modeling and Experimental Validation of the Braided Pneumatic Muscle. IEEE Trans. Robot. 2009, 25, 1282–1291. [Google Scholar] [CrossRef]
- Takosoglu, J.E.; Łaski, P.A.; Blasiak, S.; Bracha, G.; Pietrala, D. Determining the Static Characteristics of Pneumatic Muscles. Meas. Control 2016, 49, 62–71. [Google Scholar] [CrossRef]
- Tondu, B.; Lopez, B. Modeling and control of McKibben artificial muscle robot actuators. IEEE Control. Syst. Mag. 2000, 20, 15–38. [Google Scholar]
- Pietrala, D. The characteristics of a pneumatic muscle. EPJ Web Conf. 2017, 143, 02093. [Google Scholar] [CrossRef]
- Pietrala, D.S. Analiza i Synteza Pneumatycznego Serwonapędu Mięśniowego w Zastosowaniu do Manipulatora Równoległego o Sześciu Stopniach Swobody. Ph.D. Thesis, Politechnika Świętokrzyska, Kielce, Poland, 2020. [Google Scholar]
- Carvalho, A.D.D.R.; Karanth, P.N.; Desai, V. Characterization of pneumatic muscle actuators and their implementation on an elbow exoskeleton with a novel hinge design. Sens. Actuators Rep. 2022, 4, 100109. [Google Scholar] [CrossRef]
- Dyrr, F.; Dvorak, L.; Fojtasek, K.; Brzezina, P.; Hruzik, L.; Burecek, A. Experimental analysis of fluidic muscles. MM Sci. J. 2022, 2022, 5759–5763. [Google Scholar] [CrossRef]
- Xavier, M.S.; Tawk, C.D.; Zolfagharian, A.; Pinskier, J.; Howard, D.; Young, T.; Lai, J.; Harrison, S.M.; Yong, Y.K.; Bodaghi, M.; et al. Soft Pneumatic Actuators: A Review of Design, Fabrication, Modeling, Sensing, Control and Applications. IEEE Access 2022, 10, 59442–59485. [Google Scholar] [CrossRef]
- Kalita, B.; Leonessa, A.; Dwivedy, S.K. A Review on the Development of Pneumatic Artificial Muscle Actuators: Force Model and Application. Actuators 2022, 11, 288. [Google Scholar] [CrossRef]
- Ganguly, S.; Garg, A.; Pasricha, A.; Dwivedy, S.K. Control of pneumatic artificial muscle system through experimental modelling. Mechatronics 2012, 22, 1135–1147. [Google Scholar] [CrossRef]
- Godage, I.S.; Branson, D.T.; Guglielmino, E.; Caldwell, D.G. Pneumatic Muscle Actuated Continuum Arms: Modelling and Experimental Assessment. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 4980–4985. [Google Scholar]
- Kang, B.-S.; Kothera, C.S.; Woods, B.K.S.; Wereley, N.M. Dynamic Modeling of McKibben Pneumatic Artificial Muscles for Antagonistic Actuation. In Proceedings of the ICRA 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 17 May 2009; Volume 1–7, p. 643. [Google Scholar]
- Shen, X. Nonlinear model-based control of pneumatic artificial muscle servo systems. Control Eng. Pract. 2010, 18, 311–317. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, X.; Han, J. Active Model-Based Control for Pneumatic Artificial Muscle. IEEE Trans. Ind. Electron. 2017, 64, 1686–1695. [Google Scholar] [CrossRef]
- Dai, Z.; Rao, J.; Xu, Z.; Lei, J. Design and Joint Position Control of Bionic Jumping Leg Driven by Pneumatic Artificial Muscles. Micromachines 2022, 13, 827. [Google Scholar] [CrossRef]
- Andrikopoulos, G.; Nikolakopoulos, G.; Manesis, S. Advanced Nonlinear PID-Based Antagonistic Control for Pneumatic Muscle Actuators. IEEE Trans. Ind. Electron. 2014, 61, 6926–6937. [Google Scholar] [CrossRef]
- Minh, T.V.; Tjahjowidodo, T.; Ramon, H.; Brussel, H.V. Control of a Pneumatic Artificial Muscle (PAM) with Model-Based Hysteresis Compensation. In Proceedings of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Suntec Convention and Exhibition Center, Singapore, 14–17 July 2009; Volume 1–3, p. 1086. [Google Scholar]
- Minh, T.V.; Tjahjowidodo, T.; Ramon, H.; Brussel, H.V. Cascade position control of a single pneumatic artificial muscle-mass system with hysteresis compensation. Mechatronics 2010, 20, 402–414. [Google Scholar] [CrossRef]
- Minh, T.V.; Kamers, B.; Ramon, H.; Brussel, H.V. Modeling Torque-Angle Hysteresis in a Pneumatic Muscle Manipulator. In Proceedings of the 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Montreal, QC, Canada, 6–9 July 2010. [Google Scholar]
- Minh, T.V.; Kamers, B.; Ramon, H.; Brussel, H.V. Modeling and control of a pneumatic artificial muscle manipulator joint—Part I: Modeling of a pneumatic artificial muscle manipulator joint with accounting for creep effect. Mechatronics 2012, 22, 923–933. [Google Scholar] [CrossRef]
- Yeh, T.-J.; Wu, M.-J.; Lu, T.-J.; Wu, F.-K.; Huang, C.-R. Control of McKibben pneumatic muscles for a power-assist, lower-limb orthosis. Mechatronics 2010, 20, 686–697. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, H.; Wang, X.; Han, J. Active Model-Based Hysteresis Compensation and Tracking Control of Pneumatic Artificial Muscle. Sensors 2022, 22, 364. [Google Scholar] [CrossRef] [PubMed]



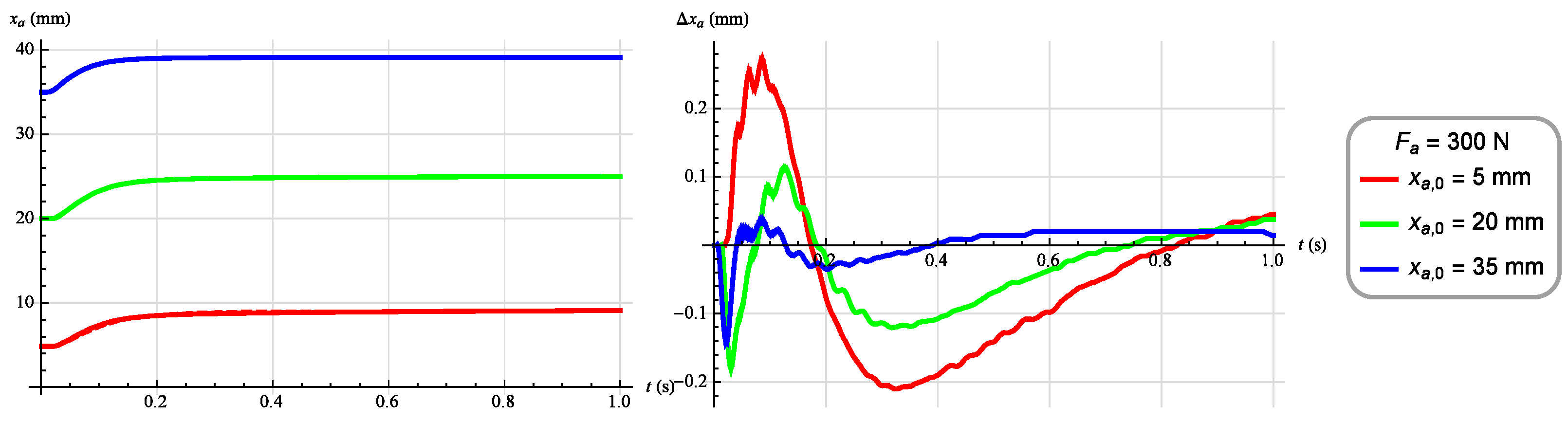

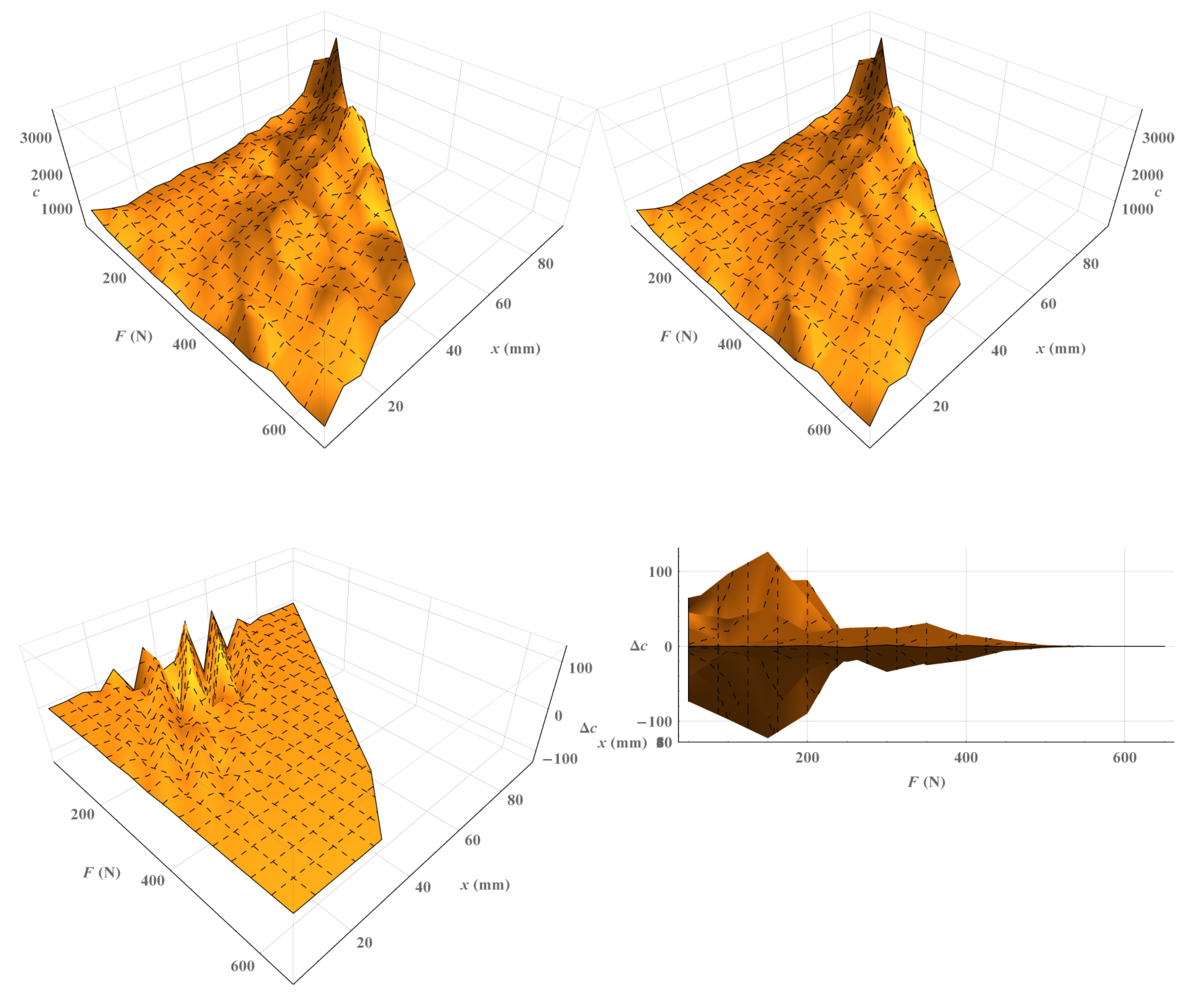
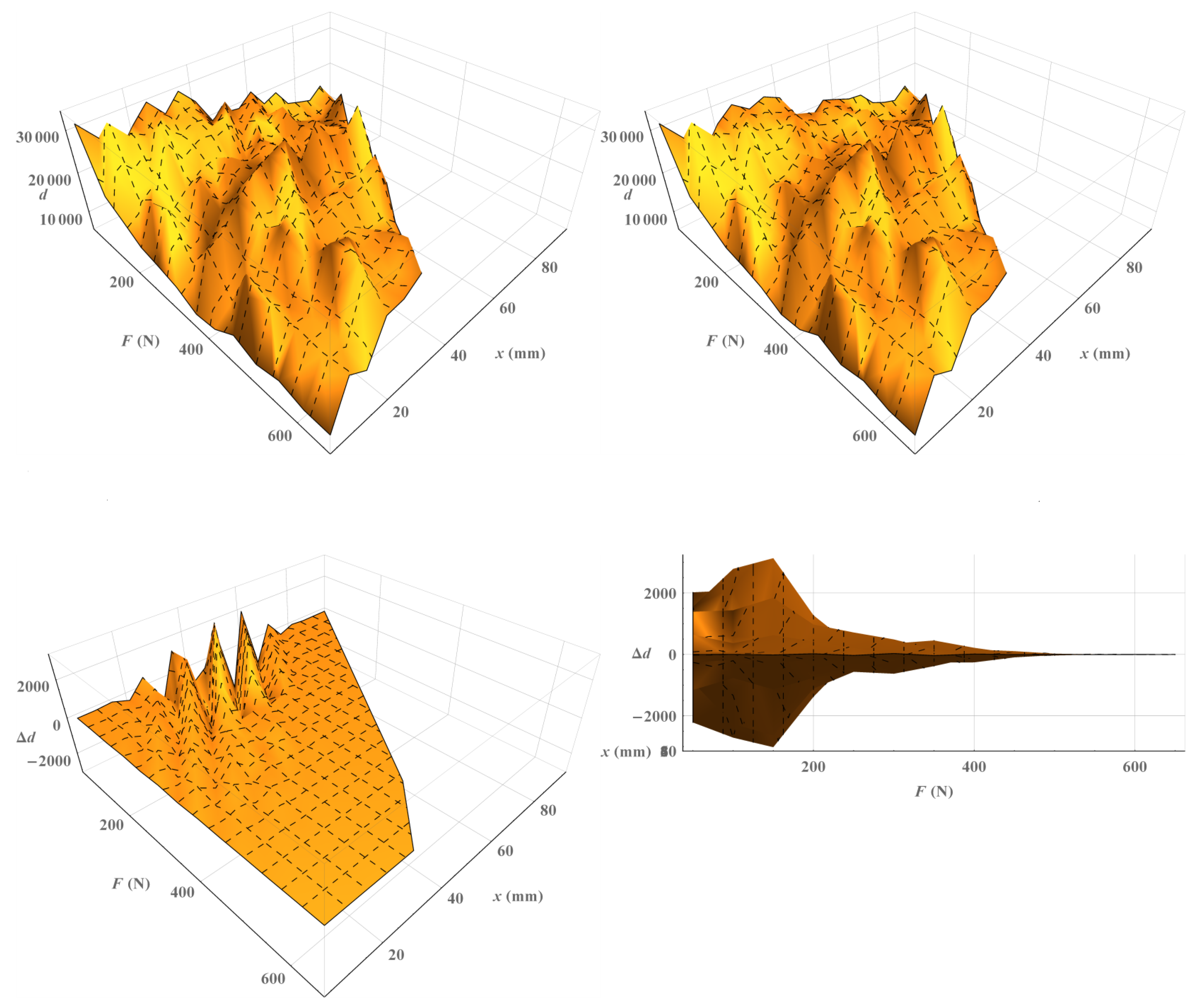
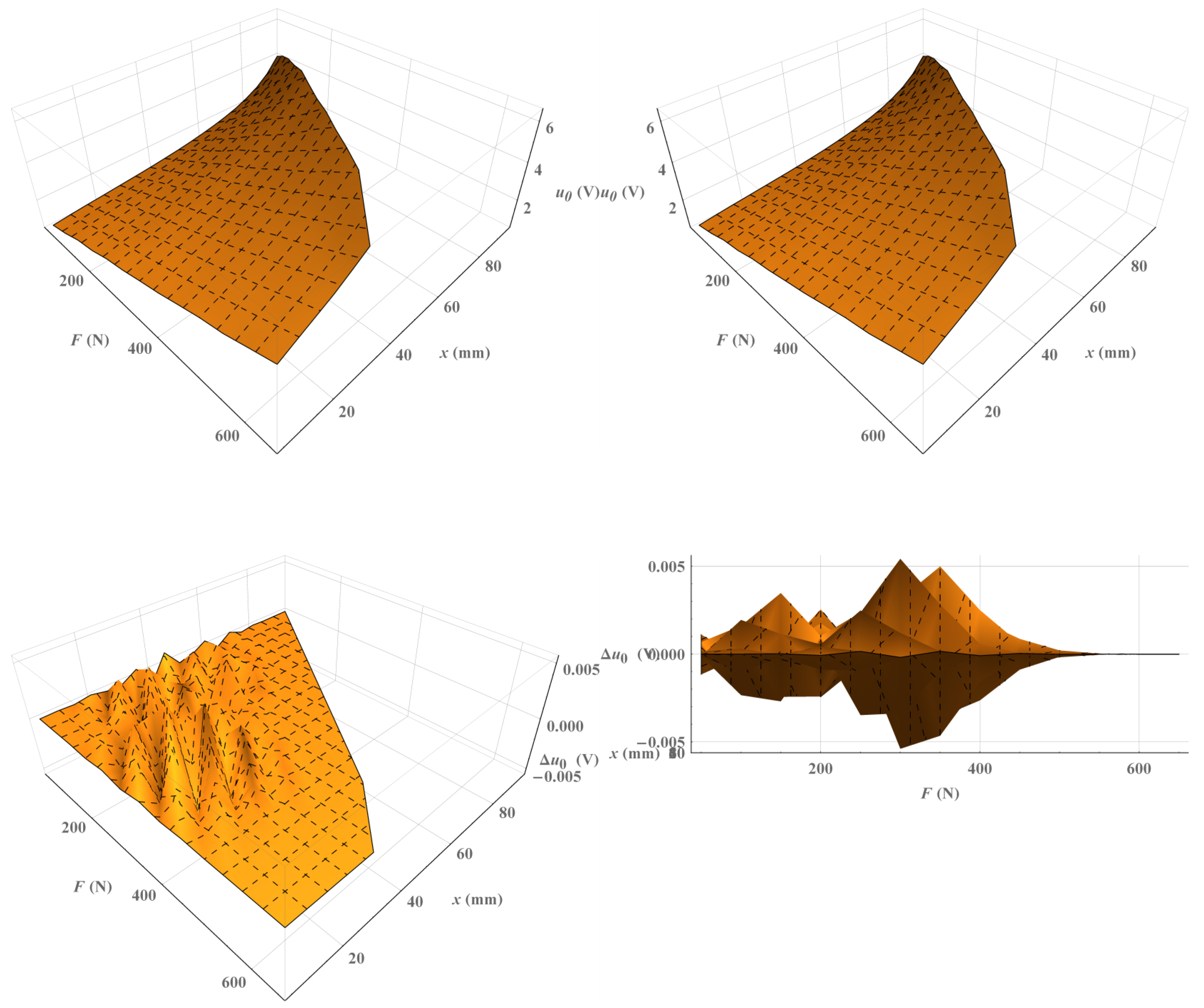



| (mm) | b | c | d | (V) |
|---|---|---|---|---|
| 5 | 122.62 | 957.41 | 33,330.0 | 0.84 |
| 10 | 112.76 | 775.59 | 31,335.3 | 0.95 |
| 15 | 94.08 | 662.68 | 31,716,3 | 1.06 |
| 20 | 69.14 | 524.55 | 21,838.9 | 1.12 |
| 25 | 73.56 | 577.66 | 25,709.5 | 1.22 |
| 30 | 67.61 | 560.13 | 23,357.6 | 1.31 |
| 35 | 72.27 | 624.12 | 24,316.4 | 1.40 |
| 40 | 64.26 | 576.44 | 20,535.6 | 1.51 |
| 45 | 77.82 | 750.06 | 24,096.8 | 1.63 |
| 50 | 65.02 | 654.24 | 18,675.3 | 1,76 |
| 55 | 81.97 | 887.24 | 21,933.3 | 1.92 |
| 60 | 69.79 | 793.37 | 17,452.7 | 2.10 |
| 65 | 62.50 | 748.39 | 13,045.2 | 2.30 |
| 70 | 66.51 | 848.06 | 12,567.3 | 2.58 |
| 75 | 71.27 | 1056.75 | 13,055.3 | 2.90 |
| 80 | 68.15 | 1089.00 | 10,214.1 | 3.32 |
| 85 | 88.18 | 1539.92 | 10,914.0 | 3.89 |
| 90 | 122.07 | 2545.10 | 13,172.4 | 4.69 |
| (mm) | b | c | d | (V) |
|---|---|---|---|---|
| 5 | 97.61 | 953.89 | 25,126.8 | 1.42 |
| 10 | 79.22 | 742.11 | 24,444.6 | 1.58 |
| 15 | 68.20 | 682.04 | 19,716.6 | 1.68 |
| 20 | 57.16 | 573.95 | 17,407.9 | 1.82 |
| 25 | 62.43 | 665.15 | 19,953.9 | 1.97 |
| 30 | 64.07 | 752.55 | 21,483.4 | 2.11 |
| 35 | 58.90 | 708.48 | 19,054.1 | 2.27 |
| 40 | 57.11 | 725.15 | 17,903.7 | 2.44 |
| 45 | 72.61 | 982.46 | 21,409.4 | 2.64 |
| 50 | 44.88 | 576.91 | 10,872.4 | 2.86 |
| 55 | 61.77 | 935.85 | 15,833.9 | 3.12 |
| 60 | 82.39 | 1387.44 | 19,843.6 | 3.42 |
| 65 | 94.31 | 1712.43 | 20,007.5 | 3.78 |
| 70 | 81.78 | 1636.40 | 15,931.9 | 4.23 |
| 75 | 91.88 | 2123.36 | 16,771.0 | 4.79 |
| 80 | 103.93 | 2570.42 | 15,668.4 | 5.54 |
| (mm) | b | c | d | (V) |
|---|---|---|---|---|
| 5 | 87.87 | 1071.91 | 21,538.4 | 2.00 |
| 10 | 60.36 | 690.15 | 15,207.9 | 2.20 |
| 15 | 60.37 | 732.23 | 18,077.5 | 2.38 |
| 20 | 61.67 | 794.31 | 19,306.4 | 2.55 |
| 25 | 64.50 | 908.30 | 21,698.3 | 2.74 |
| 30 | 71.17 | 1065.53 | 23,788.4 | 2.94 |
| 35 | 70.42 | 1138.32 | 23,425.3 | 3.15 |
| 40 | 69.60 | 1095.38 | 19,684.4 | 3.40 |
| 45 | 67.53 | 1187.75 | 19,249.2 | 3.67 |
| 50 | 73.07 | 1319.48 | 18,167.5 | 3.99 |
| 55 | 87.03 | 1695.44 | 19,666.4 | 4.36 |
| 60 | 78.60 | 1748.91 | 17,782.4 | 4.79 |
| 65 | 110.72 | 2804.38 | 23,168.6 | 5.33 |
| 70 | 90.49 | 2365.22 | 16,692.0 | 6.01 |
| (mm) | b | c | d | (V) |
|---|---|---|---|---|
| 5 | 83.92 | 1079.55 | 16,687.1 | 2.58 |
| 10 | 67.30 | 835.22 | 13,068.6 | 2.81 |
| 15 | 75.73 | 1002.05 | 18,387.3 | 3.05 |
| 20 | 80.71 | 1174.23 | 21,503.9 | 3.28 |
| 25 | 77.49 | 1350.28 | 20,937.3 | 3.48 |
| 30 | 84.94 | 1613.87 | 27,991.7 | 3.78 |
| 35 | 70.51 | 1229.30 | 18,264.0 | 4.06 |
| 40 | 78.05 | 1549.41 | 21,158.5 | 4.39 |
| 45 | 87.73 | 1861.74 | 22,103.3 | 4.75 |
| 50 | 80.10 | 1918.73 | 19,903.4 | 5.17 |
| 55 | 75.60 | 1853.75 | 17,117.1 | 5.68 |
| 60 | 86.73 | 2307.93 | 18,940.3 | 6.29 |
| Static Model (mm) | Dynamic Model (mm) | |
|---|---|---|
| mm N | 2.21 | 1.71 |
| mm N | 1.14 | 0.60 |
| (rad) | (rad) | |
|---|---|---|
| rad Nm | 0.0051 | 0.013 |
| rad Nm | 0.008 | 0.016 |
| rad Nm | 0.005 | 0.013 |
| rad Nm | 0.009 | 0.018 |
| rad Nm | 0.028 | 1.047 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pietrala, D.S.; Laski, P.A.; Zwierzchowski, J. Design and Control of a Pneumatic Muscle Servo Drive Applied to a 6-DoF Parallel Manipulator. Appl. Sci. 2024, 14, 5329. https://doi.org/10.3390/app14125329
Pietrala DS, Laski PA, Zwierzchowski J. Design and Control of a Pneumatic Muscle Servo Drive Applied to a 6-DoF Parallel Manipulator. Applied Sciences. 2024; 14(12):5329. https://doi.org/10.3390/app14125329
Chicago/Turabian StylePietrala, Dawid Sebastian, Pawel Andrzej Laski, and Jaroslaw Zwierzchowski. 2024. "Design and Control of a Pneumatic Muscle Servo Drive Applied to a 6-DoF Parallel Manipulator" Applied Sciences 14, no. 12: 5329. https://doi.org/10.3390/app14125329
APA StylePietrala, D. S., Laski, P. A., & Zwierzchowski, J. (2024). Design and Control of a Pneumatic Muscle Servo Drive Applied to a 6-DoF Parallel Manipulator. Applied Sciences, 14(12), 5329. https://doi.org/10.3390/app14125329






