Next Article in Journal
A Deep Learning Approach for Intrusion Detection Systems in Cloud Computing Environments
Previous Article in Journal
Semantic Hierarchical Classification Applied to Anomaly Detection Using System Logs with a BERT Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 14
Issue 13
10.3390/app14135389
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Grout Diffusion Mechanism along the Pile Shaft during the Process of Pile Tip Post-Grouting in Sand

by
Yue Wu
1,2,3,4,
Yating Deng
2,*,
Xuefu Zhang
2,
Lang Liu
2,
Chunfeng Zhao
5 and
Jiaqi Zhang
5
1
Chongqing Jianzhu College, Chongqing 400072, China
2
School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China
3
State Key Laboratory of Mountain Bridge and Tunnel Engineering, Chongqing Jiaotong University, Chongqing 400074, China
4
Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China
5
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
*
Author to whom correspondence should be addressed.
Appl. Sci. 2024, 14(13), 5389; https://doi.org/10.3390/app14135389
Submission received: 1 June 2024 / Revised: 18 June 2024 / Accepted: 19 June 2024 / Published: 21 June 2024
Browse Figures
Versions Notes

Abstract

:

Featured Application

The research results will improve the understanding of the diffusion process, the shape of grout bulbs, and the grouting mode of cement along the pile body during the process of pile tip post-grouting in sand.

Abstract

Pile tip post-grouting technology has been widely adopted in pile foundations to improve its bearing characteristics. Grouting in the pile tip leads to the grouting cement spreading along the pile body to a certain extent. To better understand the grout diffusion mechanism along the pile body returned, a total of 45 groups of laboratory model tests were carried out on sand, with different grouting pressures, grout volumes, and soil stress histories taken into account. By comparing the characteristics of the grouted bulbs, the grout diffusion mechanism along the pile body returned was revealed. Combined with the test results, a simplified model to describe the grout diffusion pattern and the corresponding grouting mode of grouting cement along the pile body returned during the process of pile tip post-grouting was proposed. This model can comprehensively reflect the grout diffusion characteristics along the pile body, with different grouting conditions and soil stress histories taken into account.

1. Introduction

The post-grouting pile bearing capacity could be improved mainly due to the diffusion of grouting cement in the soil [1]. At present, research on the grouting cement diffusion mechanism during the process of pile tip post-grouting is mainly focused on the cement diffusion in the soil below the pile tip. The grouting diffusion patterns could be divided into three types, including penetration grouting, compaction grouting, and fracture grouting, respectively, according to the grouting cement diffusion forms. Yin, X. L [2] developed a combined finite-discrete-element method-based grouting simulator, and results indicated that the developed simulator could accurately capture the effect of time-dependent rheological characteristics caused by grout hydration on the grouting penetration process. Sha, F [3] designed a visual simulation test device for fixed pressure penetration grouting for sandy soil and studied the influence of grout type, sand gradation, and grouting pressure on the reinforcement result. Wu, Y [4] derived and verified the theoretical relationship model between the soil unloading degree and the soil deformation modulus and proposed a compaction grouting diffusion model considering the soil unloading effect. Shrivastana, N [5] analyzed the injection pressure, spacing of injection points, overburden pressure, and initial relative density of ground based on the elasto-plastic theory of strain hardening. Brown, D. R [6] studied the applicability of compaction grouting via laboratory and field tests. El-Kelesh, A. M [7] analyzed the reinforcement of compaction grouting on the soil by field tests and studied the effects of initial soil properties, the injection depth, the replacement ratio, and the injection sequence on the compaction grouting effectiveness. Seo, H. J [8] conducted a series of pilot-scale chamber tests performed on four different granite residual soils to study the compaction grouting effectiveness, and the experimental results were compared with a closed-form solution derived from the cavity expansion theory. Nichols, S. C [9] found that the compaction grouting grout bulbs tended to develop in either a cylindrical or teardrop shape through indoor model tests. Wang, Q [10] studied the grout diffusion process upon pressure grouting injection in the sand through laboratory-scale tests, with different grout water/cement (w/c) ratios and soil degrees of saturation taken into account. Zhang, Z. M [11] deduced the formulas for calculating the flow velocity, grouting flow, grouting pressure difference, and penetration radius in fracture grouting based on the assumption of exponential fluid and narrow plate model. Zou, J. F [12] deduced the attenuation law of pressure and the fracture pervasion along the penetrating radius direction based on the assumption that the grouting flow in soil fracture accords with Darcy’s law and the fracture widths in soil formed by fracturing grouting is evenly distributed. Liang, J. S [13] designed an easily assembled/disassembled test apparatus for polymer fracture grouting and investigated the influences of the fracture characteristic parameters and grouting volume on the grouting effect. Zhang, L. Z [14] developed a one-dimensional visual fracture grouting experimental system and proposed a new characterization method of slurry concentration based on the image gray level to characterize the variation law of the slurry-water mixing region during the grouting process. Xiao, F [15] used the data from individual grout holes to construct the regional geological conditions via inverse analysis and found that grouting of fractured rock masses is accompanied by great uncertainty. Yan, C. Z [16] presented a three-dimensional grouting model based on the combined finite-discrete element method and researched the influence of several key parameters on grout penetration in fractured rock masses.
Different from the diffusion of the grouting cement in the soil below the pile tip, the research on the grout diffusion mechanism along the pile shaft during the process of pile tip post-grouting is rarely reported. For the shape of the grout bulbs below the pile tip, when the grouting mode is compaction grouting, it is generally assumed to be either a spherical shape or columnar shape, and the rationality of this assumption has been confirmed through extensive research. At the same time, there is no clear definition for the dimension and shape of the grout bulbs that the grouting cement along the pile body returned. The determination of the returned height of the grouting cement along the pile body is mainly dependent on empirical methods; even the different standards give different suggestion values of the grout returned height for the same situation [17,18]. The shape of grout bulbs and the corresponding grouting mode along the pile body are affected by various parameters such as the grouting conditions, including the grouting pressure and grout volume [19,20], the stress history of soil, etc. In this paper, self-developed grouting devices and an improved large-scale multi-functional interface shear apparatus that can be used to simulate the diffusion process of grouting cement along the pile body are adopted to conduct a series of indoor model tests, with three types of grouting pressure and grout volume, two types of soil stress history taken into account. By comparing the characteristics of the grouted bulbs, including the returned height along the pile shaft, the radial expansion distance, and the shape of grout bulbs, the grouting mode with different conditions was revealed. Finally, combined with the test results, a simplified model to describe the grout diffusion pattern and the corresponding grouting mode during the process of grouting cement along the pile body was proposed. The research results will improve the understanding of the diffusion process, the shape of grout bulbs, and the grouting mode of cement along the pile body during the process of pile tip post-grouting in sand.

2. Experimental Materials

2.1. Sand

The soil specimen was gray silt obtained from a project in Shanghai [21]. The characteristics of this layer of soil are as follows: Holocene Q42 coastal to shallow stacked soil; the thickness of this soil layer distribution range from about 3.00–4.30 m, an average thickness of 3.55 m; bottom elevation −1.35–−3.20 m, the average bottom elevation of −2.46 m; containing mica, quartz, feldspar, etc., the clay content Pc is about 4.3%; The distribution range is distributed throughout the site. The main properties of the soil are listed in Table 1; the grain-size distribution of the soil is shown in Figure 1.

2.2. Cement

The cement used in this study was ordinary Portland cement, with the reference P.O 42.5. In addition to the type of cement, the water/cement ratio is also an important factor affecting the properties of the grouting cement. According to the recommended water/cement ratio given in the standard [17], pre-experiments of three kinds of grouting cement with water/cement ratios of 0.5, 0.6, and 0.7 were carried out, respectively. A comprehensive comparison focus on the injectability and properties of the grouting cement was conducted and found that when the w/c = 0.5, it is difficult to inject the grouting cement into the sand/concrete interface at the set grouting pressure and grouting volume; when the w/c = 0.7, there is a good injectability, but the grouting cement is easy to segregate, and the early strength of grout bulb is very low and cannot meet the test requirements; when the w/c = 0.6, it can meet the above three requirements. Hence, the value of the water-cement ratio in this paper is 0.6.
The objectives of this paper involve studying the grout diffusion mechanism along the pile body during the process of pile tip post-grouting, which necessitates consideration of different grouting pressures, grout volumes, and soil stress history. The number of test groups reached a total of 45 groups; the early strength of the grout bulb will be improved by adding an early strength agent in the grouting cement.

2.3. Concrete Plate

For the field pile, the pile/soil interface can be simplified as the interface between the concrete and soil. Hence, a concrete plate is used to simulate the pile body in this paper to conduct the simulation model test. The concrete plate is made of C25 concrete, and bidirectional bars with a diameter of Φ 8 @ 100 are added into it, with a net size of 590 mm × 390 mm × 50 mm (length × width × height). This paper mainly studied the effect of different grouting pressures, grout volume, and soil stress history on the grout diffusion mechanism along the pile body during the process of pile tip post-grouting. Hence, the effect of the surface roughness of the concrete plate is not taken into account. The concrete plate is shown in Figure 2.

3. Experimental Methods

3.1. Test Apparatus

The test apparatus used in this paper is shown in Figure 3 and Figure 4. The entire test apparatus includes test components and grouting components. The test components include an interface shear apparatus and a grouted shear box that is composed of a top shear box and a bottom shear box. The grouting components include an air compressor and a pressure grouting cement tank. The air compressor named Anjieshun (Qingdao, China) can provide a pressure range of 0–0.8 MPa. The pressure grouting cement tank with a 120 mm inner diameter and 200 mm height was designed for the grout cement contained. The pressure grouting cement tank is a sealed transparent Polymethyl Methacrylate (PMMA) cylinder, with the top three being the grouting inflow, air pressure relief, and air pressure supply, and the bottom side being the grouting pipe that connects the pressure grouting cement tank and the grouting pipeline of the top shear box.
The test apparatus was improved on the large-scale multi-function direct shear test apparatus SJW-200 (Shanghai, China), which was independently researched and developed by Tongji University. The test apparatus has a large size shear box with a net size of 600 mm × 400 mm × 200 mm (length × width × height) and a wall thickness of 40 mm. Grouting holes are present at the bottom of the left side plate of the top shear box. The grouting hole with a 10 mm inner diameter and a threaded structure that can be connected to the Polycarbonate (PC) thread adapter for the grouting test. The position of the grouting hole on the top shear box satisfies the following: The central axis of the grouting hole is parallel to the horizontal relative movement direction between the bottom shear box and the top shear box. The position needs to be tangent to the bottom surface of the short side plate of the top shear box, and the gap space between the concrete plate and the bottom shear box wall, as well as between the top shear box and the bottom shear box, are sewed with hot melt glue, to ensure that the grouting cement only flows into the soil/concrete interface during the grouting process.

3.2. Test Program and Methods

Via pre-experiment results and considering the injectability of the grouting cement, the grouting pressure set in this paper is three levels of 500 kPa, 600 kPa, and 700 kPa, respectively; the grout volume set in this paper is also three levels of 200 mL, 300 mL, and 400 mL, respectively. The normal loading and unloading program is as follows: (1) the initial normal stress of 100 kPa and then unload to 25 kPa, 50 kPa, and 75 kPa, respectively, to conduct the grouting process and (2) the initial normal stress of 25 kPa, 50 kPa, 75 kPa, and 100 kPa and do not perform normal unloading and grouting directly. The specific test program is shown in Table 2 and Table 3.
The steps of the experiment are as follows:
First, install a PC thread adapter, fill and compact the soil specimen with layers into the top shear box. Next, connect air compressors and grouting cement tank, prepare the cement to the designed volume, and proceed with grouting at a predetermined pressure. Finally, release the pressure, clean the apparatus, and conduct tests to evaluate the mechanical properties of the grouting soil/concrete interface and analyze the characteristics of the grouted bulbs and the grout diffusion mode.

3.3. Grout Diffusion Range and Mode

The grout diffusion range includes horizontal diffusion distance and vertical diffusion distance, which can be measured by the steel rule. The horizontal diffusion is the diffusion along the surface of the concrete plate. The distance is the farthest distance from the grouting hole to the grout bulb edge along with the concrete plate, corresponding to the height of the grouting cement returned along the pile body during the process of pile tip post-grouting. Vertical diffusion is the diffusion along the direction perpendicular to the surface of the concrete plate. The distance is measured as the vertical maximum distance of the grout bulb with the concrete plate surface as the base plane, corresponding to the radial expansion of the grouting cement returned along the pile body during the process of pile tip post-grouting.
The grout bulb shapes are reported in this paper using digital photos. By comparing the chosen bulbs at various conditions, the grout diffusion mode can be distinguished qualitatively by considering the effects of grouting pressure, grout volume, and soil stress history.

4. Experimental Results

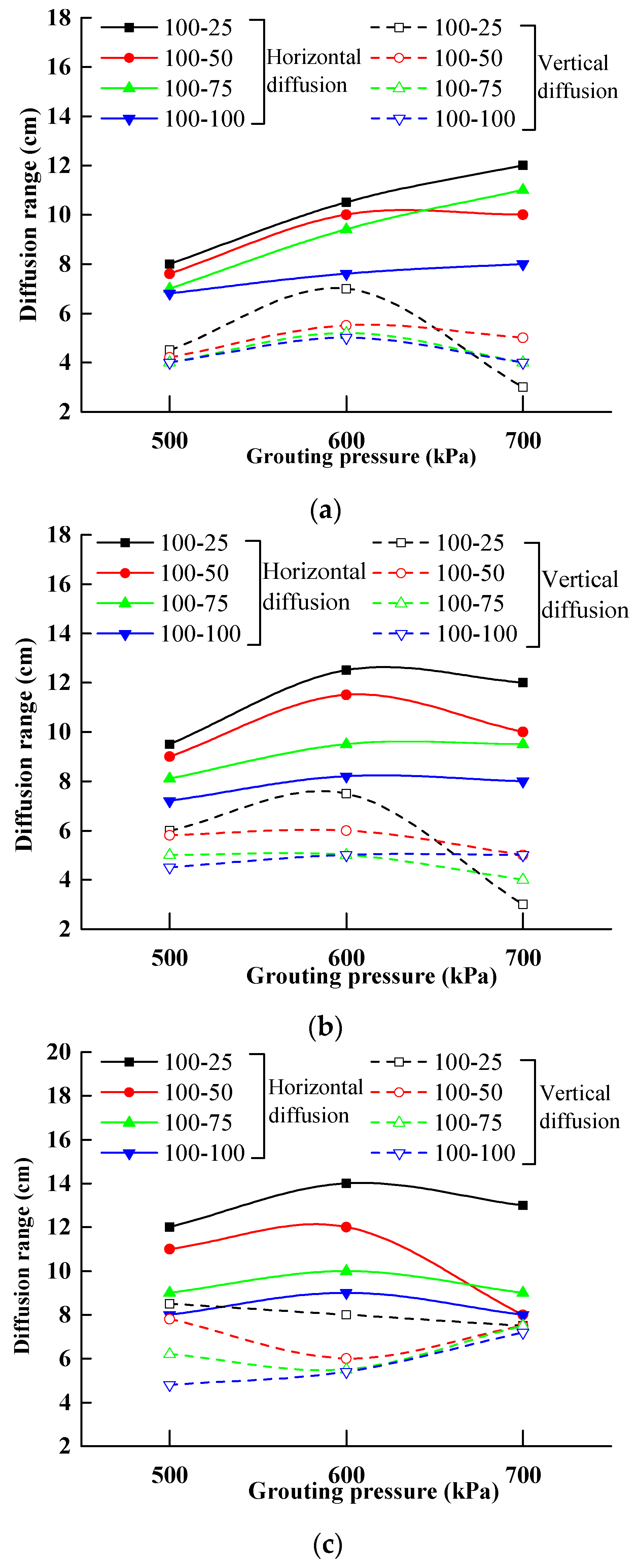
4.1. Effect of Grouting Pressure on the Grouting Diffusion Range

Figure 5a–c present the horizontal and vertical grout diffusion distance-grouting pressure curves for the grout volume at 200 mL, 300 mL, and 400 mL, respectively, with different normal load conditions. For the sake of simplicity, the legend is expressed as initial normal stress σc-applied normal stress σs. For example, the legend showing 100-25 means the soil is consolidated at the initial normal stress of 100 kPa and is grouted at the applied normal stress of 25 kPa. Figure 5 shows that the returned height of the grouting cement along the pile body increases non-linear with the increase of the grouting pressure under different loading and unloading conditions when the grout volume is 200 mL. When the grout volume is 400 mL, the returned height reaches the maximum value when the grouting pressure is 600 kPa. When the grout volume is 300 mL, the variation laws of the returned height of the grouting cement with grouting pressure under different loading and unloading conditions are between the grout volume at 200 mL and 400 mL.
The vertical grout diffusion distance-grouting pressure curves in Figure 5 present that the changes of the radial expansion distance of the grouting cement returned along the pile body with increasing grouting pressure are not monotonic under different load conditions and grout volumes. When the grouting pressure is 600 kPa, the corresponding radial expansion distance reaches the maximum at the grout volume of 200 mL and 300 mL. The returned height of the grouting cement is greater than the radial expansion distance under the same work conditions. The reason for this phenomenon is explained later in the Section 5.
Table 4 shows the distance difference between the returned height and the radial expansion distance between the maximum and minimum grouting pressures. Table 4 presents that with the increase in grout volume, the contribution of the grouting pressure on the returned height increased and gradually weakened. When there exists an unloading condition in the soil, with the increase of grout volume, the increase of grouting pressure has an obstructive effect on the returned height increase. When there were no unloading conditions in the soil, with the increase of grout volume, the increase of grouting pressure would gradually strengthen the contribution on the radial expansion distance increased.

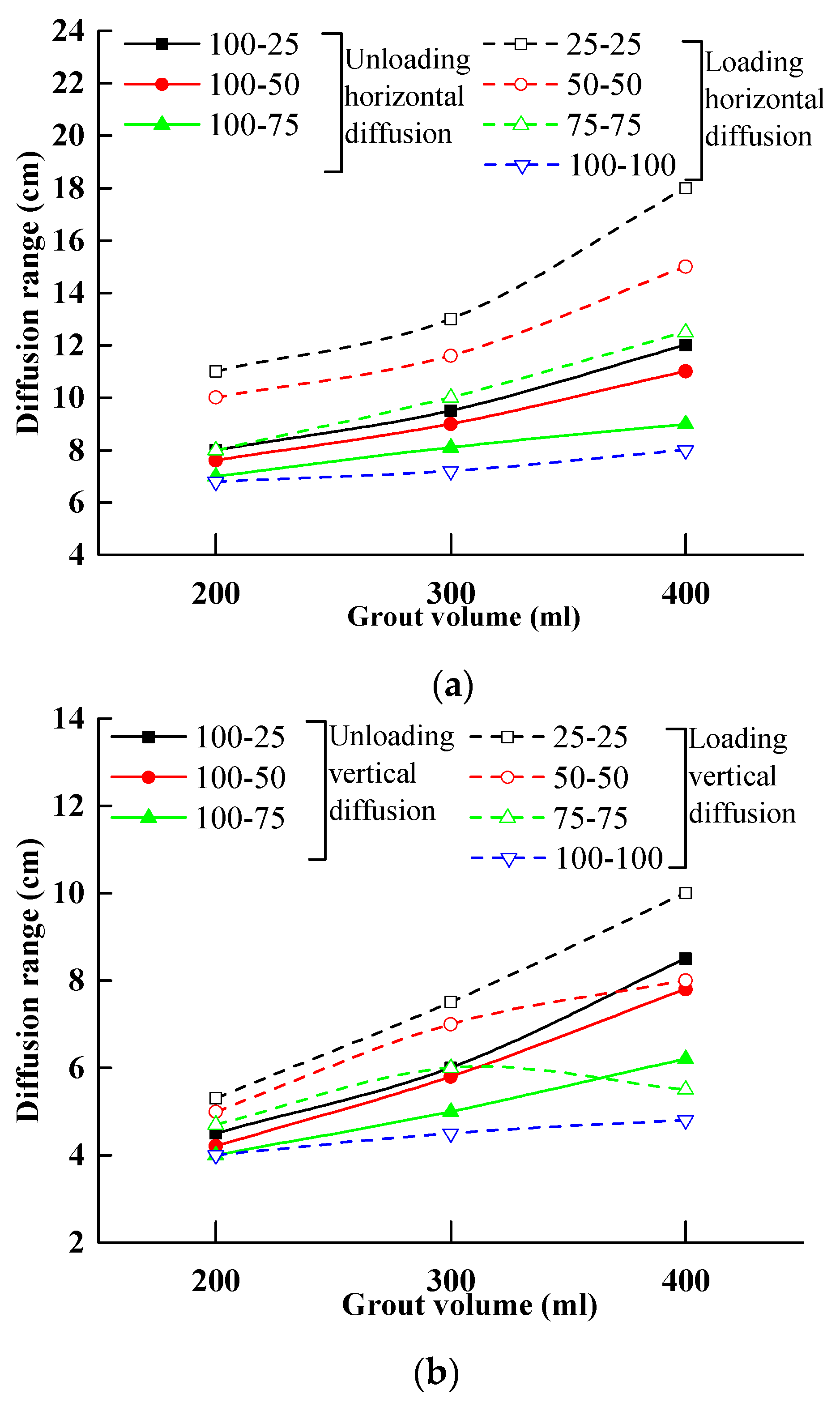
4.2. Effect of Grout Volume on the Grouting Diffusion Range

Figure 6a–c present the horizontal and vertical grout diffusion distance-grout volume curves for the grouting pressure at 500 kPa, 600 kPa, and 700 kPa, respectively, with different normal load conditions. Figure 6 shows that the returned height increases with the grout volume increased for the grouting pressure at 500 kPa and 600 kPa. When the grouting pressure is 700 kPa, the relationship between the returned height and grout volume is affected by the degree of unloading. Defined the unloading degree as the ratio of the difference of initial normal stress and applied normal stress to the initial normal stress [21]. As the unloading degree decreases, the variation laws between the returned height and grout volume transferred from a positive correlation to a negative correlation. When the unloading degree is 0, the returned height remains unchanged with the increase of the grout volume.
The radial expansion distance is maintained within the range of 5–8 cm with different grout volume and load conditions for the grouting pressure at 500 kPa and 600 kPa. The radial expansion distance fluctuates little with the grout volume under the same load conditions. When the grouting pressure is 700 kPa, the radial expansion distance fluctuates little when the grout volume is less than 300 mL, whereas its value increases significantly with the increase of grout volume when the grout volume is greater than 300 mL.
Table 5 shows the distance difference between the returned height and the radial expansion distance between the maximum and minimum grout volume. Table 5 presents that with the increase of grouting pressure, the increase of grout volume gradually weakens the contribution on the returned height increased, and may even have an obstructive effect, whereas its contribution on the radial expansion distance is weakened first and then gradually strengthened. This may be due to the transfer of the grouting mode caused by the changes in grouting pressure and grout volume.
Figure 7a,b show the comparison of grout diffusion distance-grout volume between loading and unloading conditions for the grouting pressure at 500 kPa. As the grout volume increased, the returned height increased non-linearly for the soil stress history with loading conditions but increased linearly for the soil stress history with unloading conditions. Moreover, the parallel nature of the lines shows a similar rate of increase in the returned height with grout volume for different soil stresses history with loading conditions. The increased rate of the returned height with increasing grout volume under the unloading condition is lower than that under the loading condition for the same applied normal stress condition.
Figure 7b shows that the variation laws of the radial expansion distance with the grout volume under loading and unloading conditions are consistent with what Figure 7a shows, except for the result of the group experiment that under the normal stress at 75 kPa, no unloading condition and grout volume at 400 mL. The grouting cement formed grout veins in the soil through subsequent excavation, as shown in Figure 8. The diffusion of the grouting cement in different directions inside the soil may be the cause of the small measurement of the radial expansion distance.

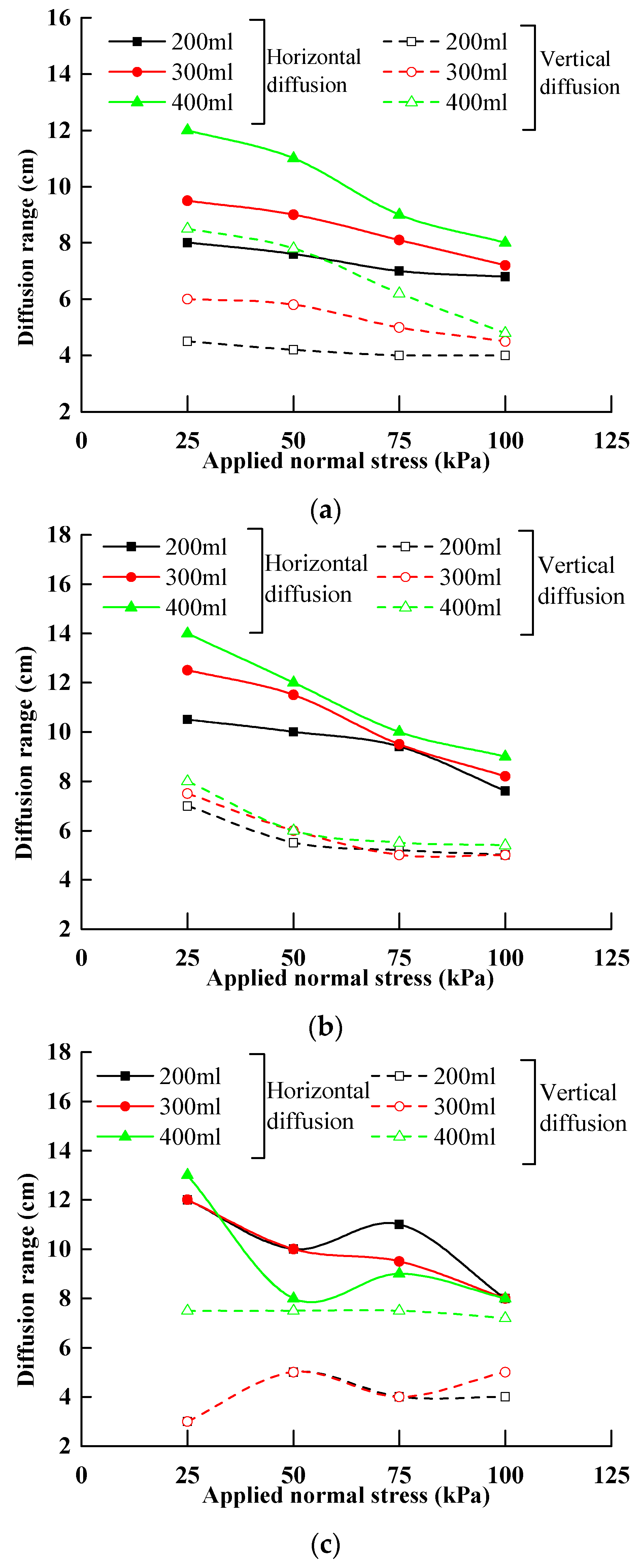
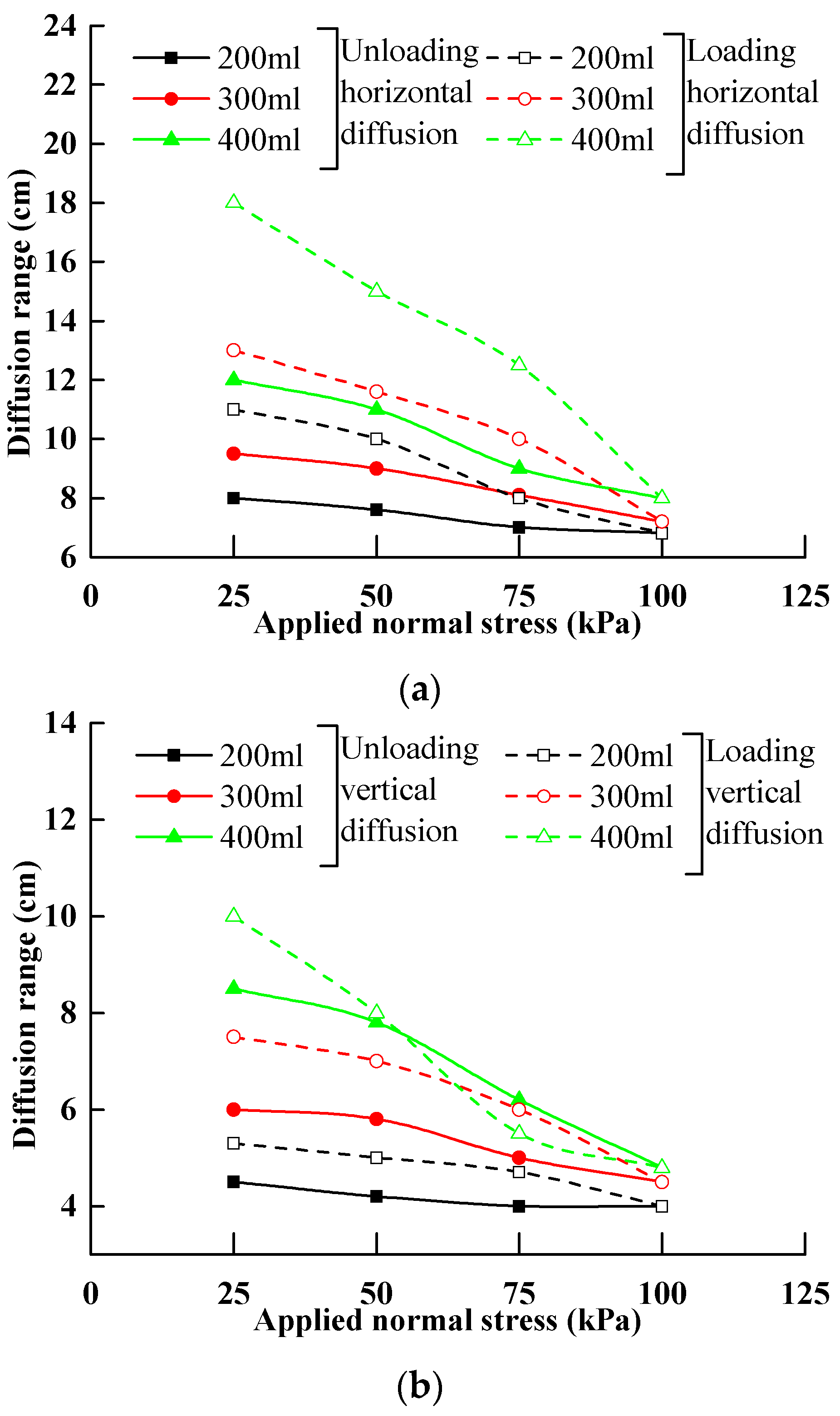
4.3. Effect of Soil Stress History on the Grouting Diffusion Range

Figure 9a–c present the horizontal and vertical grout diffusion distance-applied normal stress curves for the grouting pressure at 500 kPa, 600 kPa, and 700 kPa, respectively. Figure 9 illustrates that as the grouting pressure increases from 500 kPa to 600 kPa, the height of grout return and the radial expansion distance of the cement along the pile shaft both decrease with a reduction in the unloading degree for varying grout volumes, ultimately stabilizing. The decreased rate of the returned height and radial expansion distance with the unloading degree increases with the grout volume increased. When the grouting pressure is 700 kPa, there is a certain degree of fluctuation in the process of the returned height decreases with decreasing unloading degree for different grout volumes, whereas the overall variation laws are still consistent with the grouting pressure at 500 kPa and 600 kPa. However, the variation of the radial expansion distance with the unloading degree is maintained at a constant value, and this constant value depends on the grout volume. The constant value is about 5 cm for the grout volume at 200 mL and 300 mL but rising to 7.5 cm for the grout volume at 400 mL.
Figure 10a,b present the comparison of grout diffusion distance-applied normal stress between loading and unloading conditions for the grouting pressure at 500 kPa. Figure 10 shows that under the same grouting pressure, the returned height and radial expansion distance both decrease nonlinearly with increasing applied normal stress whether or not there exist unloading conditions in soils, and finally, the grout diffusion distance tends to be constant. For the same grout volume and applied normal stress, the returned height and radial expansion distance under the unloading conditions is less than that of the loading conditions. That is, the soil stress history has a significant effect on the grout diffusion range for the grouting cement returned along the pile body during the process of pile tip post-grouting.

4.4. Grout Diffusion Characteristics

The characteristics of the grout bulbs obtained at increasing grouting pressure for different grout volumes are compared in Table 6 in terms of digital photos, dimensions, and description of the main features (at the same unloading condition of 100-25 kPa). Table 6 shows that the grouting pressure and grout volume affect both the grout bulb shapes and the grout diffusion patterns. When the grout volume is 200 mL, the grout bulb shape gradually transitions from a half-droplet shape to a long and narrow strip shape with increasing grouting pressure, indicating that the grout diffusion mode transitions from perfect compaction grouting to compaction dominant. When the grout volume is 300 mL, the grout bulb shape gradually transitions from a half-droplet shape to a flat shape and exists thick and short grout veins in the horizontal and lateral directions with increasing grouting pressure, indicating that the grout diffusion mode transitions from a perfectly compaction grouting to compaction dominant and thick and short pulp veins in the horizontal and lateral directions. When the grout volume is 400 mL, the grout bulb shape gradually transitions from a combination of a semi-cylindrical body and a semi-cone body to an obvious grout bulb shell and a cracked surface morphology existed with increasing grouting pressure, indicating that the grout diffusion mode transitions from compaction grouting to fracture grouting dominant.
Table 7 exhibits the compared characteristics of the grout bulbs obtained at increasing grouting pressure for different grout volumes and the soil stress history with loading conditions at 100-100 kPa in terms of digital photos, dimensions, and description of the main features. Table 7 shows when the grout volume is 200 mL, the grout bulb shape gradually transitions from a half-droplet shape to a long and narrow half-ellipsoidal shape with increasing grouting pressure, indicating that the grout diffusion mode is perfectly compaction grouting. When the grout volume is 300 mL, the grout bulb shape gradually transitions from a wide and short half-ellipsoidal shape to the half-spherical shape closing to the grouting hole, and thick and short grout veins away from the grouting hole with increasing grouting pressure, indicating that the grout diffusion mode transitions from a perfectly compaction grouting to compaction grouting dominant and fracture grouting coexistence grout diffusion mode. When the grouting volume is 400 mL, the grout bulb shape gradually transitions from the initial grout bulb gathered on the grouting hole liked ancient bell and sheet shape away from the grouting hole to the shape of the “ball snout” at the bottom of the ship and obvious grout bulb shell and cracked surface morphology existed with increasing grouting pressure, indicating that the grout diffusion mode transitions from a compaction grouting dominant to fracture grouting dominant.

5. Discussion and Interpretation

Analysis of Table 6 and Table 7 reveals that the main factors influencing the characteristics of the grouting cement returned during the process of the pile tip post-grouting, under both loading and unloading conditions in the soil, are grouting pressure and grout volume, with the grouting mode transition primarily affected by the grouting pressure. The lower grout volume and grouting pressure corresponding to the grout diffusion shape is mainly half-ellipsoidal or half-droplet-shaped, and the grouting mode is compaction grouting. With the increase of grout volume and grouting pressure, other irregular shapes of the grout bulb and grout veins and shells will appear, and the grouting mode will change to fracture grouting. However, there is no sharp distinction between the compaction and fracture grouting phases. In other words, for the process that is governed by the compaction effect, some fracturing also exists [14]. For example, the grouting pressures at 600 kPa and 700 kPa and the grout volume at 300 mL and 400 mL in Table 6, where thick and short grout veins in the horizontal and lateral directions were also formed. The fracture grouting mode is generally produced by continuing grouting cement after the compaction grouting mode is maintained for some time.
The soil/grout interactions during pressure injection have been noted in previous studies [22], and a simplified model is given to describe the process of compaction grouting and fracture grouting during pressure injection [23,24]. This paper is based on the grouting cement returned along the pile body during the process of pile tip post-grouting as the background to study the grout diffusion characteristics on the shaft of the pile. Combined with test results in this paper, a simplified model to describe the grouting cement diffusion pattern and the corresponding grouting mode of the grouting cement returned along the pile body during the process of pile tip post-grouting was proposed, as shown in Figure 11a–d, they are modes of compaction grouting, compaction grouting, compaction grouting dominant and some fracture grouting and some fracture grouting also exists, and fracture compaction grouting dominant and some compaction grouting also exists, respectively. Through the four types of grout diffusion patterns and grouting modes in Figure 11, it is possible to generalize all test results and explain the aforementioned test variation laws.
The pile/soil interface is weaker than the soil particles interface generally [25], and the grouting cement is easier to return along the weak surface. Hence, the returned height is greater than the radial expansion distance of the grouting cement returned along the pile body under the same work conditions (Figure 5, Figure 6 and Figure 9). When the grout volume is low, the grouting mode is generally compact according to the model proposed above in this paper. Therefore, grouting cement is mainly used for compacting the soil and returned along with the pile/soil interface.
The effect of soil stress history on the grout diffusion characteristics in the soil is mainly reflected in its influence on the compactness and strength characteristics of the soil’s initial mechanical properties. The grout injection will lead to a compacting effect on the soil. Using the cavity expansion theory [22], the soil particles will generate motion, and the density of the soil will be increased. For the soil under the unloading condition in this paper, the initial state density of the soil is higher than that under the loading condition for the same applied normal stress to conduct the grouting process due to the effect of the initial normal stress. Hence, soil particles inside the loading soil are easier to generate motion than in unloading soil, and the compaction grout diffusion range in the loading soil is higher than that in the unloading soil under the same grouting pressure and grout volume (Figure 10). As there is no tensile strength between the sand grains, the fracture pressure must overcome the tangential shear strength in the soil and push the grains apart to instigate a fracture [22,26,27]. According to previous studies, the soil shear strength under unloading conditions is higher than that under loading conditions for the same applied normal stress [28]. In this case, the soil under the unloading condition is equivalent to over-consolidated soil (the initial normal pressure is greater than the applied normal pressure). Hence, the fracture grout diffusion range in the loading soil is higher than that in the unloading soil under the same grouting pressure, grout volume, and the existing stress (the applied normal stress in this paper) of the soil.
Considering there are many factors that influence the grouting diffusion process, such as aggregate size, cement type, water/cement ratio, grouting pressure, etc. Hence, the simplified grouting model proposed by this paper can be used as a guideline for similar conditions and may require adjustments if applied to different conditions.

6. Conclusions

In this study, a series of indoor model tests were conducted to analyze the characteristics of the grouting cement returned along the pile body, and the grouting mode with different conditions was revealed. These findings benefit the understanding of the process of grouting diffusion along the pile body for the pile tip post-grouting under different load conditions and grouting conditions and could be useful for potential engineering applications, such as post-grouting piles, tunnels, and the metro train construction process.
  • The returned height increases non-linearly with increasing grouting pressure when the grout volume is low. With the increase of the grout volume, the returned height with increasing grouting pressure is not monotonic, and the threshold value is approximately 600 kPa. The radial expansion distance with increasing grouting pressure is also not monotonic, and the threshold value is also approximately 600 kPa.
  • The returned height increases with the grout volume increased, but the radial expansion distance is maintained within the range of 5–8 cm for the grouting pressure at 500 kPa and 600 kPa. When the grouting pressure is 700 kPa, the relationship between the returned height and the grout volume is affected by the degree of unloading, but the radial expansion distance is affected by the grout volume.
  • The grout diffusion range in the loading soil is higher than that in the unloading soil and the returned height is greater than the radial expansion distance under the same grouting pressure, grout volume, and the applied normal stress of the soil.
  • Regardless of loading and unloading conditions in the soil stress history, the characteristic of the grouting cement returned along the pile body during the process of the pile tip post-grouting is mainly affected by the grouting pressure and the grout volume, whereas the transition of grouting mode is mainly affected by the grouting pressure.
  • A simplified model to describe the grouting cement diffusion pattern and the corresponding grouting mode of grouting cement returned along the pile body during the process of pile tip post-grouting was proposed. This model can comprehensively reflect the grouting cement diffusion characteristics along the pile body, with different grouting and load conditions taken into account.

Author Contributions

Conceptualization, Y.W. and Y.D.; methodology, Y.W.; software, Y.D.; validation, Y.W., Y.D. and X.Z.; formal analysis, Y.W.; investigation, L.L.; resources, C.Z.; data curation, J.Z.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W.; visualization, Y.D.; supervision, X.Z.; project administration, Y.W.; funding acquisition, Y.W., X.Z. and C.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of Chongqing (CSTB2023NSCQ-BHX0149), the China Postdoctoral Science Foundation (2023MD734112), the Special Funding of Chongqing Postdoctoral Research Project (2022CQBSHTB3051), the Science and Technology Research Program of Chongqing Municipal Education Commission (KJQN202100705), the Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education Tongji University (KLE-TJGE-G2201), the National Natural Science Foundation of China (42377151 and 41672265), and the Cooperation Projects between Undergraduate University in Chongqing and Affiliated Institutes of the Chinese Academy of Sciences (HZ2021009).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Zhang, Q.Q.; Li, H.T.; Cui, W.; Zhao, Y.H.; Wang, S.L.; Xu, F. Analysis of grout diffusion of postgrouting pile considering the time-dependent behavior of grout viscosity. Int. J. Geomech. 2021, 21, 04021201. [Google Scholar] [CrossRef]
  2. Yin, X.L.; Wu, Z.J.; Xu, X.Y.; Weng, L.; Liu, Q.S. Numerical investigation on the grouting penetration process of quick-setting grout in discrete fractured rock mass based on the combined finite-discrete-element method. Int. J. Geomech. 2023, 24, 04023298. [Google Scholar] [CrossRef]
  3. Sha, F.; Zhang, L.Y.; Zhang, M.l.; Zuo, Y.H.; Niu, H.Y. Penetration grouting diffusion and strengthening mechanism of sand layer with crucial grout. J. Build. 2024, 91, 109585. [Google Scholar] [CrossRef]
  4. Wu, Y.; Zhao, C.; Zhao, C.F.; Liu, F.M.; Zhang, Z.Q. Modeling of compaction grouting considering the soil unloading effect. Int. J. Geomech. 2022, 22, 04022061. [Google Scholar] [CrossRef]
  5. Shrivastava, N.; Zen, K. Finite element modeling of compaction grouting on its densification and confining aspects. Geotech. Geol. Eng. 2018, 36, 2235–2378. [Google Scholar] [CrossRef]
  6. Brown, D.R.; Warner, J. Compaction grouting. J. Soil Mech. Found. 1973, 99, 589–601. [Google Scholar] [CrossRef]
  7. El-Kelesh, A.M.; Matsui, T.; Tokida, K.I. Field investigation into effectiveness of compaction grouting. J. Geotech. Geoenviron. Eng. 2012, 138, 451–460. [Google Scholar] [CrossRef]
  8. Seo, H.J.; Jeong, K.H.; Choi, H.; Lee, I.M. Pullout resistance increase of soil nailing induced by pressurized grouting. J. Geotech. Geoenviron. Eng. 2012, 138, 604–613. [Google Scholar] [CrossRef]
  9. Nichols, S.C.; Goodings, D.J. Physical model testing of compaction grouting in cohesionless soil. J. Geotech. Geoenviron. Eng. 2000, 126, 848–852. [Google Scholar] [CrossRef]
  10. Wang, Q.; Wang, S.; Sloan, S.W.; Sheng, D.; Pakzad, R. Experimental investigation of pressure grouting in sand. Soils Found. 2016, 56, 161–173. [Google Scholar] [CrossRef]
  11. Zhang, Z.M.; Jian, Z. Penetration radius and grouting pressure in fracture grouting. Chin. J. Geotech. Eng. 2008, 30, 181–184. [Google Scholar] [CrossRef]
  12. Zou, J.F.; Li, L.; Yang, X.L. Penetration radius and pressure attenuation law in fracturing grouting. J. Hydraul. Eng. 2006, 37, 314–319. [Google Scholar]
  13. Liang, J.S.; Du, X.m.; Fang, H.Y.; Li, B.; Wang, N.N.; Di, D.Y.; Xue, B.H.; Zhai, K.J.; Wang, S.Y. Intelligent prediction model of a polymer fracture grouting effect based on a genetic algorithm-optimized back propagation neural network. Tunn. Undergr. Space Technol. 2024, 148, 105781. [Google Scholar] [CrossRef]
  14. Zhang, L.Z.; Huang, C.X.; Li, Z.P.; Han, X.; Zhang, Q.S.; Gao, Y. Characteristics of slurry-water mixing region in fractured rock mass grouting process: Experimental study. Constr. Build Mater. 2024, 427, 136244. [Google Scholar] [CrossRef]
  15. Xiao, F.; Liu, Q.; Zhao, Z.Y.; Xiao, F.; Liu, Q.; Zhao, Z.Y. Information and knowledge behind data from underground rock grouting. J. Rock Mech. Geotech. Eng. 2021, 13, 1326–1339. [Google Scholar] [CrossRef]
  16. Yan, C.Z.; Wang, T.; Gao, Y.K.; Ke, W.H.; Wang, G. A three-dimensional grouting model considering hydromechanical coupling based on the combined finite-discrete element method. Int. J. Geomech. 2022, 22, 04022189. [Google Scholar] [CrossRef]
  17. JGJ 94-2008; Technical Code for Building Pile Foundations. China Architecture and Building Press: Beijing, China, 2008.
  18. JTG D63-2007; Code for Design of Ground Base and Foundation of Highway Bridges and Culverts. China Communications Press: Beijing, China, 2007.
  19. Mori, A.; Tamura, M.; Fukul, Y. Fracturing pressure of soil ground by viscous materials. Soils Found. 1990, 30, 129–136. [Google Scholar] [CrossRef]
  20. Mori, A.; Tamura, M.; Shibata, H.; Hayashi, H. Some factors related to injected shape in grouting. Grouting Soil Improv. Geosynth. 1992, 3, 313–324. [Google Scholar]
  21. Zhao, C.F.; Wu, Y.; Zhao, C.; Liu, F.M.; Liu, F. Effect of unloading on shear behavior of interface between sand and concrete. Chin. J. Rock Mech. Eng. 2018, 37, 1020–1029. [Google Scholar] [CrossRef]
  22. Bezuijen, A.; Tol, A.F.V. Compensation grouting in sand, fractures and compaction. In Proceedings of the XIV European Conference on Soil Mechanics and Geotechnical Engineering, Madrid, Spain, January 2007; pp. 1257–1262. [Google Scholar]
  23. Jafari, M.R.; Au, S.K.; Soga, K.; Bolton, M.D.; Karim, U.F.A.; Komiya, K. Experimental and numerical investigation of compensation grouting in clay. J. Appl. Microbiol. 2000, 17, 333–334. [Google Scholar]
  24. Komiya, K. Soil consolidation associated with grouting during shield tunnelling in soft clayey ground. Géotechnique 2001, 53, 447–448. [Google Scholar] [CrossRef]
  25. Zhao, C.F.; Wu, Y.; Zhao, C.; Zhang, Q.Z.; Liu, F.M.; Liu, F. Pile side resistance in sands for the unloading effect and modulus degradation. Mater. Constr. 2019, 69, 185. [Google Scholar] [CrossRef]
  26. Bezuijen, A.; Tol, A.F.V.; Sanders, M.P.M. Mechanisms that determine between fracture and compaction grouting in sand. In Aspects of Underground Construction in Soft Ground, Proceeding of the 6st International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground, Shanghai, China, 10–14 April 2008; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
  27. Gafar, K.; Soga, K.; Bezuijen, A.; Sanders, M.P.M.; Tol, A.F.V. Fracturing of sand in compensation grouting. In Geotechnical Aspects of Underground Construction in Soft Ground; CRC Press: Boca Raton, FL, USA, 2009; Volume 156, pp. 117–123. [Google Scholar]
  28. Zhao, C.; Zhao, C.F.; Gong, H. Elastoplastical analysis of the interface between clay and concrete incorporating the effect of the normal stress history. J. Appl. Math. 2013, 12, 673057. [Google Scholar] [CrossRef]
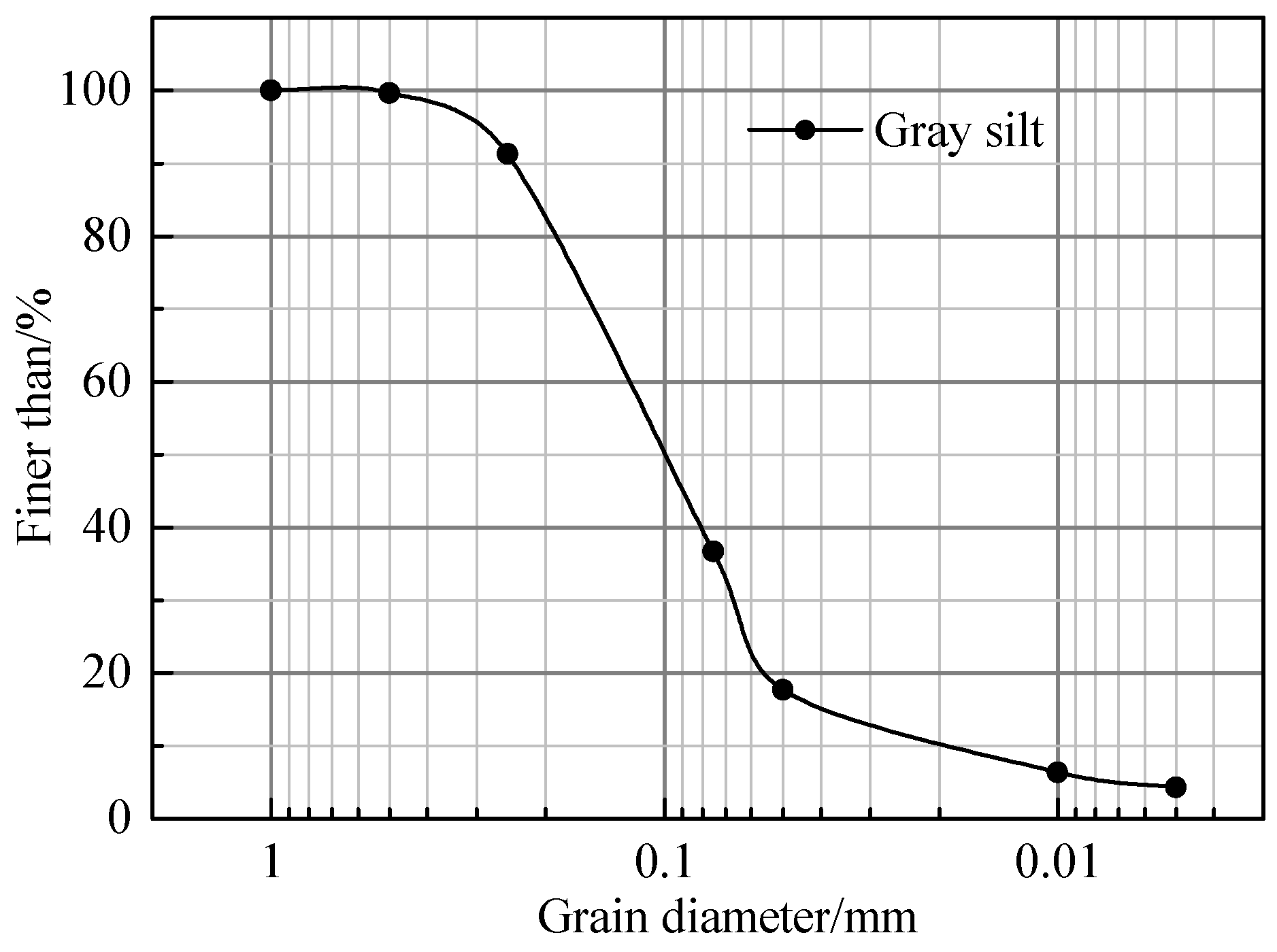
Applsci 14 05389 g001
Figure 1. Grain-size distribution of gray silt soil.
Figure 1. Grain-size distribution of gray silt soil.
Applsci 14 05389 g001
Applsci 14 05389 g002
Figure 2. Concrete plate.
Figure 2. Concrete plate.
Applsci 14 05389 g002
Applsci 14 05389 g003
Figure 3. Test apparatus. (a) Air compressor; (b) interface shear apparatus.
Figure 3. Test apparatus. (a) Air compressor; (b) interface shear apparatus.
Applsci 14 05389 g003
Applsci 14 05389 g004
Figure 4. Schematic diagram of the test apparatus.
Figure 4. Schematic diagram of the test apparatus.
Applsci 14 05389 g004
Applsci 14 05389 g005
Figure 5. Horizontal and vertical grout diffusion distance-grouting pressure curves: (a) 200 mL; (b) 300 mL; (c) 400 mL.
Figure 5. Horizontal and vertical grout diffusion distance-grouting pressure curves: (a) 200 mL; (b) 300 mL; (c) 400 mL.
Applsci 14 05389 g005
Applsci 14 05389 g006
Figure 6. Horizontal and vertical grout diffusion distance-grout volume curves: (a) 500 kPa; (b) 600 kPa; (c) 700 kPa.
Figure 6. Horizontal and vertical grout diffusion distance-grout volume curves: (a) 500 kPa; (b) 600 kPa; (c) 700 kPa.
Applsci 14 05389 g006
Applsci 14 05389 g007
Figure 7. Grout diffusion distance-grout volume curves under loading and unloading conditions: (a) horizontal grout diffusion; (b) vertical grout diffusion.
Figure 7. Grout diffusion distance-grout volume curves under loading and unloading conditions: (a) horizontal grout diffusion; (b) vertical grout diffusion.
Applsci 14 05389 g007
Applsci 14 05389 g008
Figure 8. Grout veins formed by fracture grouting.
Figure 8. Grout veins formed by fracture grouting.
Applsci 14 05389 g008
Applsci 14 05389 g009
Figure 9. Horizontal and vertical grout diffusion distance-applied normal stress curves under unloading conditions: (a) 500 kPa; (b) 600 kPa; (c) 700 kPa.
Figure 9. Horizontal and vertical grout diffusion distance-applied normal stress curves under unloading conditions: (a) 500 kPa; (b) 600 kPa; (c) 700 kPa.
Applsci 14 05389 g009
Applsci 14 05389 g010
Figure 10. Grout diffusion distance-applied normal stress curves under loading and unloading conditions: (a) horizontal grout diffusion; (b) vertical grout diffusion.
Figure 10. Grout diffusion distance-applied normal stress curves under loading and unloading conditions: (a) horizontal grout diffusion; (b) vertical grout diffusion.
Applsci 14 05389 g010
Applsci 14 05389 g011
Figure 11. Simplified model of grouting cement returned diffusion characteristics along the pile body: (a) compaction grouting; (b) compaction grouting; (c) compaction grouting dominant and some fracture grouting and some fracture grouting also exists; (d) fracture compaction grouting dominant and some compaction grouting also exists.
Figure 11. Simplified model of grouting cement returned diffusion characteristics along the pile body: (a) compaction grouting; (b) compaction grouting; (c) compaction grouting dominant and some fracture grouting and some fracture grouting also exists; (d) fracture compaction grouting dominant and some compaction grouting also exists.
Applsci 14 05389 g011
Table 1. Parameters of the silt in tests.
Table 1. Parameters of the silt in tests.
Unit Weight γ/(kN·m−3)Internal Friction Angle φ/(°)Water Content ω/%Void Ratio eCompression Modulus ES1–2/MPa
19.531.5200.75411.23
Table 2. Test program considering unloading condition.
Table 2. Test program considering unloading condition.
Grouting Pressure (kPa)Grout Volume (mL)Initial Normal Stress (kPa)Applied Normal Stress (kPa)
500200100255075
300100255075
400100255075
600200100255075
300100255075
400100255075
700200100255075
300100255075
400100255075
Table 3. Test program not considering unloading condition.
Table 3. Test program not considering unloading condition.
Grouting Pressure (kPa)Grout Volume (mL)Normal Stress (kPa)
500200255075100
300255075100
400255075100
600200×××100
300×××100
400×××100
700200×××100
300×××100
400×××100
Table 4. Difference in the grout diffusion range between the maximum and minimum grouting pressures.
Table 4. Difference in the grout diffusion range between the maximum and minimum grouting pressures.
Grout Volume (mL)Difference of the Returned Height (cm)Difference of the Radial Expansion Distance (cm)
Load Conditions (kPa)Load Conditions (kPa)
100-25100-50100-75100-100100-25100-50100-75100-100
20042.441.2−1.50.800
3002.511.40.8−3−0.8−10.5
4001−300−1−0.31.32.4
Table 5. Difference in the grout diffusion range between the maximum and minimum grout volume.
Table 5. Difference in the grout diffusion range between the maximum and minimum grout volume.
Grouting
Pressure (kPa)		Difference of the Returned Height (cm)Difference of the Radial Expansion Distance (cm)
Load Conditions (kPa)Load Conditions (kPa)
100-25100-50100-75100-100100-25100-50100-75100-100
50043.421.242.42.20.8
6003.520.61.410.50.30.4
7001−2204.52.53.53.2
Table 6. Evolution of grout bulb shape with increasing grouting pressure and grout volume at unloading condition of 100-25 kPa.
Table 6. Evolution of grout bulb shape with increasing grouting pressure and grout volume at unloading condition of 100-25 kPa.
Grout Volume (mL)Grouting Pressure (kPa)Digital PhotosHorizontal Diffusion Grout Distance (cm)Vertical Diffusion Grout Distance (cm)Main Features
200500Applsci 14 05389 i00184.5Compaction grouting; Half-droplet shape
600Applsci 14 05389 i00210.57Compaction grouting; Similar to a half-droplet shape
700Applsci 14 05389 i003123Compaction dominant; Long and narrow strip shape
300500Applsci 14 05389 i0049.56Compaction grouting; Half-droplet shape
600Applsci 14 05389 i00512.57.5Compaction dominant; Thick and short grout veins in the horizontal and lateral directions
700Applsci 14 05389 i006123Compaction dominant; Thick and short grout veins in the horizontal and lateral directions
400500Applsci 14 05389 i007128.5Compaction grouting; combination of a semi-cylindrical body and a semi-cone body
600Applsci 14 05389 i008148Compaction and fracture; Grout bulb crack tip in the horizontal direction, thick and short grout veins, and grout bulb shell in the lateral direction
700Applsci 14 05389 i009137.5Fracture dominant; Obviously, grout bulb shell and cracked surface morphology existed
Table 7. Evolution of grout bulb shape with increasing grouting pressure and grout volume at loading condition of 100-100 kPa.
Table 7. Evolution of grout bulb shape with increasing grouting pressure and grout volume at loading condition of 100-100 kPa.
Grout Volume (mL)Grouting Pressure (kPa)Digital PhotosHorizontal Diffusion Grout Distance (cm)Vertical Diffusion Grout Distance (cm)Main Features
200500Applsci 14 05389 i0106.84Compaction grouting; Half-droplet shape
600Applsci 14 05389 i0117.65Compaction grouting; Long and narrow half-droplet shape
700Applsci 14 05389 i01284Compaction grouting; Long and narrow strip shape
300500Applsci 14 05389 i0137.24.5Compaction grouting; Wide and short half-ellipsoidal shape
600Applsci 14 05389 i0148.25Compaction dominant; Irregular in shape, similar to a double half-spherical shape
700Applsci 14 05389 i01585Compaction and fracture; Half-spherical shape closing to the grouting hole and thick and short grout veins away from the grouting hole
400500Applsci 14 05389 i01684.8Compaction dominant; Grout bulb gathered on the grouting hole like ancient bell and sheet shape away from the grouting hole
600Applsci 14 05389 i01795.4Compaction and fracture; Broad and long of grout bulb with short and thick veins and grout bulb shells on the tail and sides of the grout bulb.
700Applsci 14 05389 i01887.2Fracture dominant; Similar to the “ball snout” at the bottom of the ship, an obvious grout bulb shell and cracked surface morphology existed
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wu, Y.; Deng, Y.; Zhang, X.; Liu, L.; Zhao, C.; Zhang, J. Grout Diffusion Mechanism along the Pile Shaft during the Process of Pile Tip Post-Grouting in Sand. Appl. Sci. 2024, 14, 5389. https://doi.org/10.3390/app14135389

AMA Style

Wu Y, Deng Y, Zhang X, Liu L, Zhao C, Zhang J. Grout Diffusion Mechanism along the Pile Shaft during the Process of Pile Tip Post-Grouting in Sand. Applied Sciences. 2024; 14(13):5389. https://doi.org/10.3390/app14135389

Chicago/Turabian Style

Wu, Yue, Yating Deng, Xuefu Zhang, Lang Liu, Chunfeng Zhao, and Jiaqi Zhang. 2024. "Grout Diffusion Mechanism along the Pile Shaft during the Process of Pile Tip Post-Grouting in Sand" Applied Sciences 14, no. 13: 5389. https://doi.org/10.3390/app14135389

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop