Helmholtz–Galerkin Technique in Dipole Field Scattering from Buried Zero-Thickness Perfectly Electrically Conducting Disk
Abstract
1. Introduction
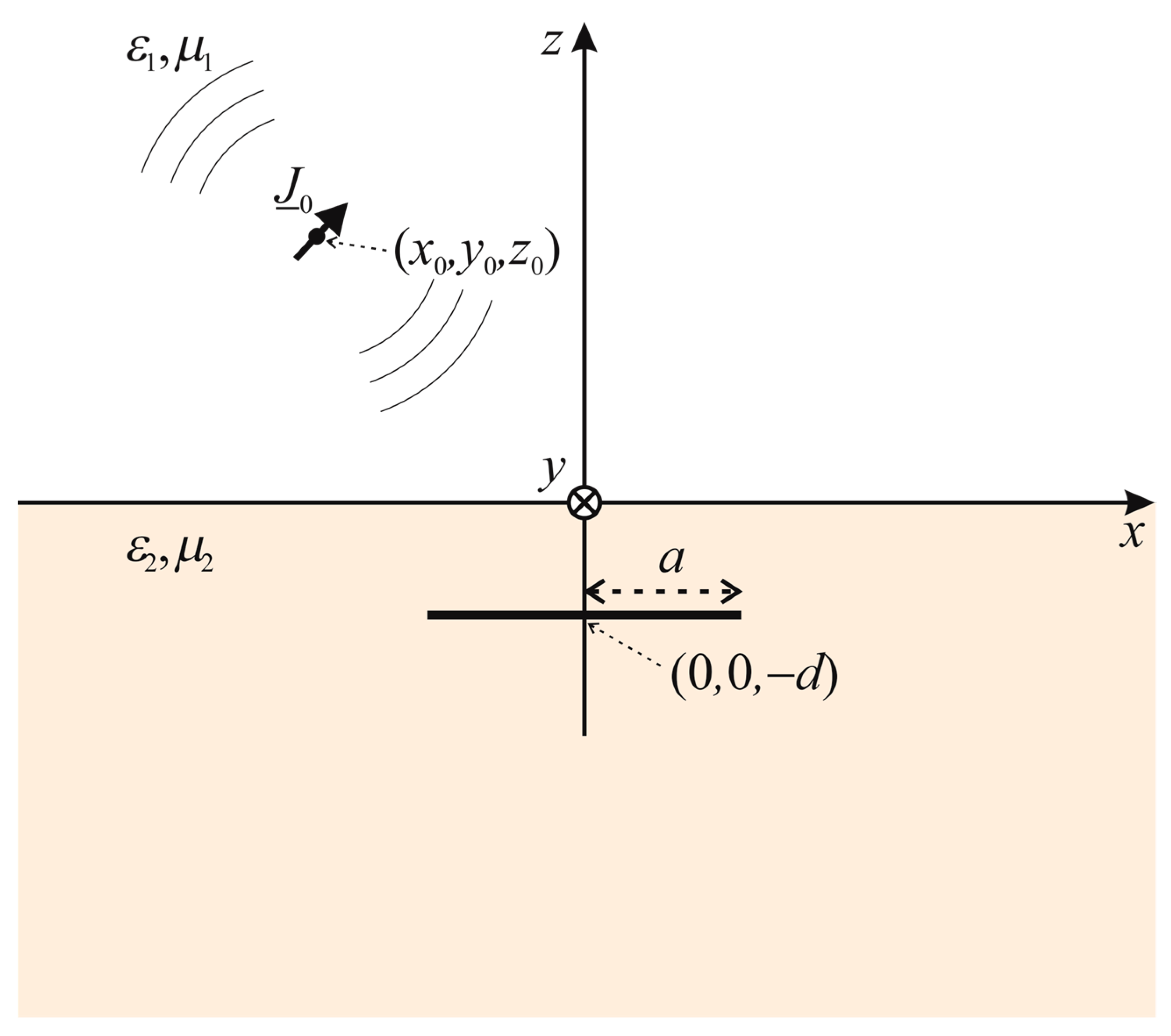
2. Formulation of the Problem and Proposed Solution
2.1. Formulation of the Problem
2.2. Proposed Solution
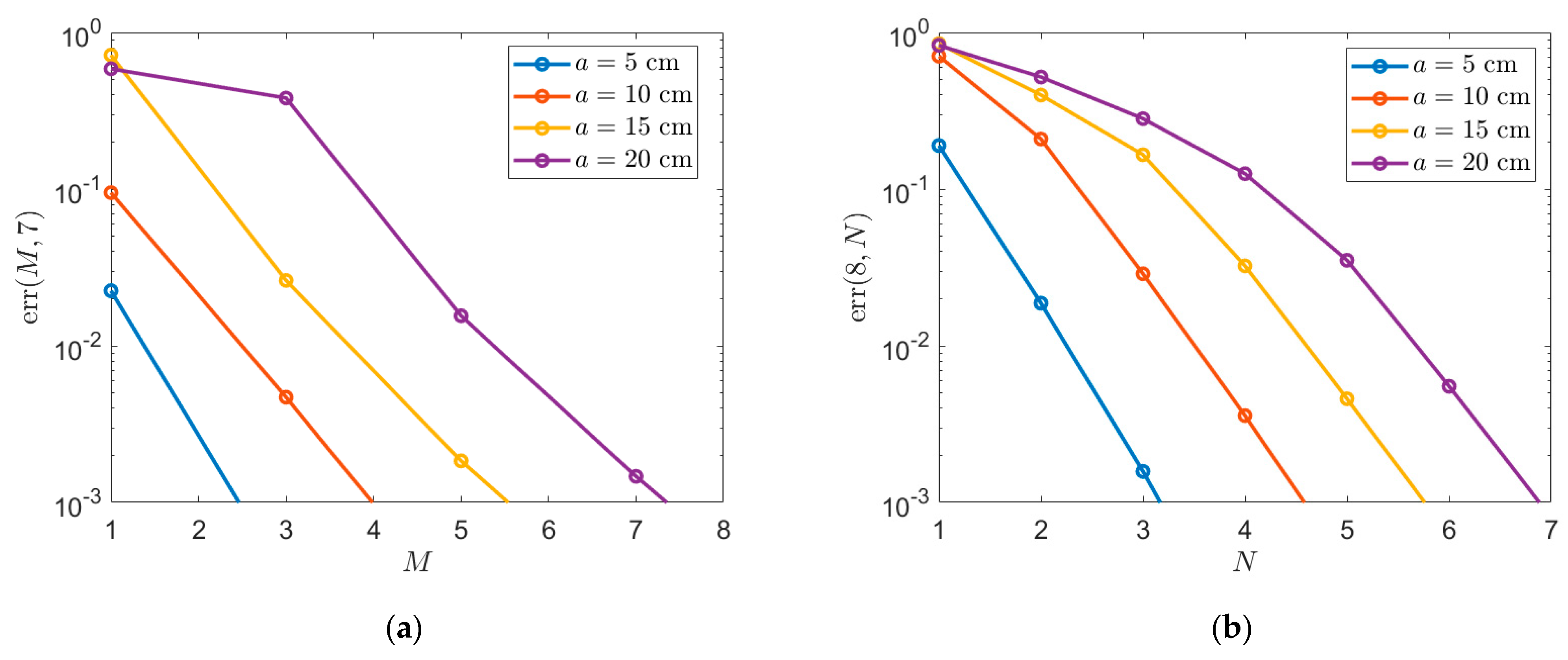
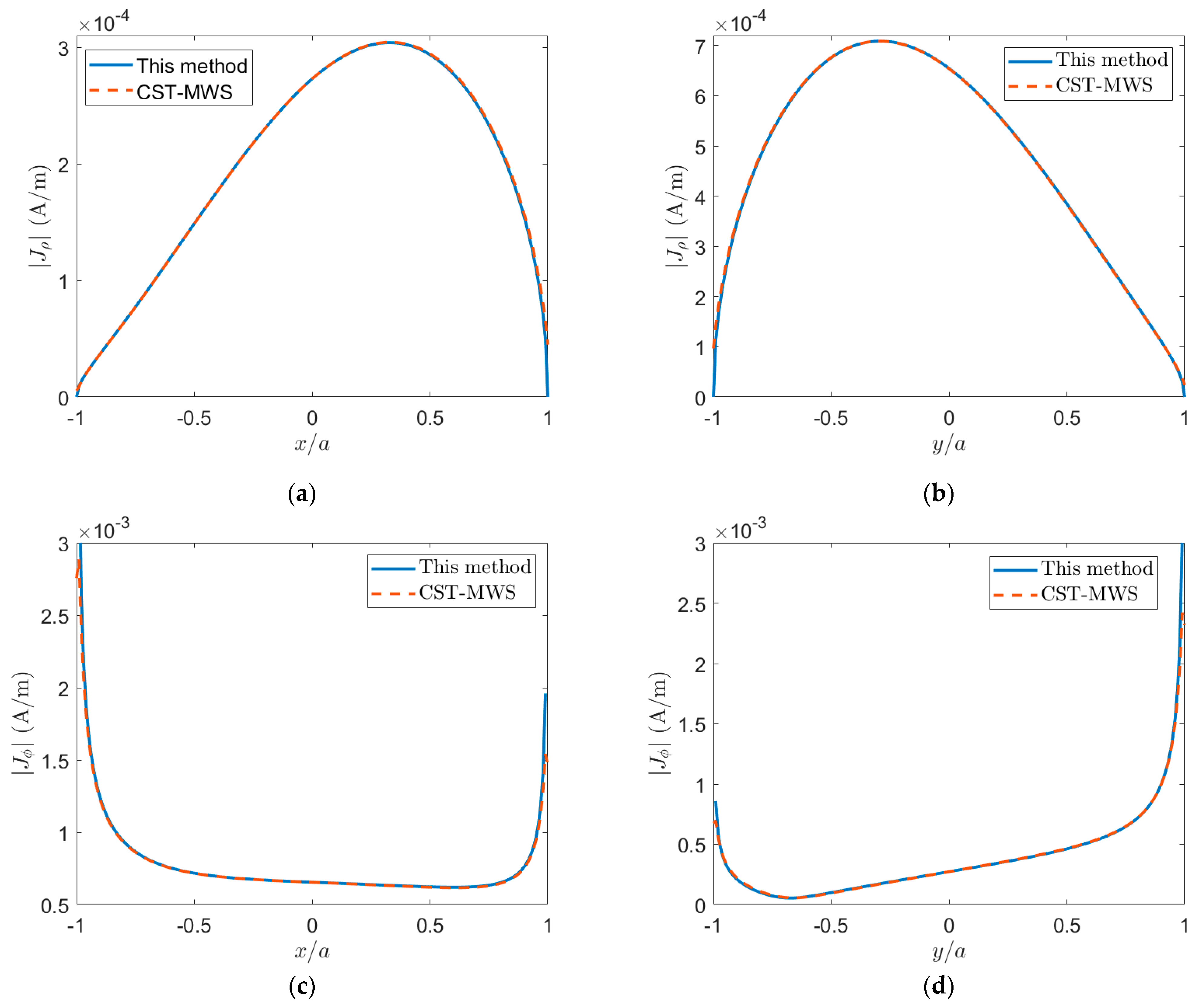
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Robledo, L.; Carrasco, M.; Mery, D. A survey of land mine detection technology. Int. J. Remote Sens. 2009, 30, 2399–2410. [Google Scholar] [CrossRef]
- Amiri, A.; Tong, K.; Chetty, K. Feasibility study of multi-frequency ground penetrating radar for rotary UAV platforms. In Proceedings of the IET International Conference on Radar Systems, Glasgow, UK, 22–25 October 2012. [Google Scholar]
- Colorado, J.; Perez, M.; Mondragon, I.; Mendez, D.; Parra, C.; Devia, C.; Martinez-Moritz, J.; Neira, L. An integrated aerial system for landmine detection: SDR-based ground penetrating radar onboard an autonomous drone. Adv. Robot. 2017, 31, 791–808. [Google Scholar] [CrossRef]
- Sipos, D.; Planinsic, P.; Gleich, D. On drone ground penetrating radar for landmine detection. In Proceedings of the IEEE 1st International Conference on Landmine, Detection, Clearance Legislations, Beirut, Lebanon, 26–28 April 2017. [Google Scholar]
- Ferrara, V.; Pietrelli, A.; Chicarella, S.; Pajewski, L. GPR/GPS/IMU system as buried objects locator. Measurements 2018, 114, 534–541. [Google Scholar] [CrossRef]
- García Fernández, M.; Álvarez López, Y.; Arboleya Arboleya, A.; González Valdés, B.; Rodríguez Vaqueiro, Y.; Las-Heras Andrés, F.; Pino García, A. Synthetic aperture radar imaging system for landmine detection using a Ground Penetrating Radar on board a Unmanned Aerial Vehicle. IEEE Access 2018, 6, 45100–45112. [Google Scholar] [CrossRef]
- Pinchera, D.; Migliore, M.D. Efficient synthesis of concentric-rings plane wave generators. IEEE Trans. Antennas Propag. 2023, 71, 4967–4975. [Google Scholar] [CrossRef]
- O’Neill, K.; Haider, S.A.; Geimer, S.D.; Paulsen, K.D. Effects of the ground surface on polarimetric features of broadband radar scattering from subsurface metallic objects. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1556–1565. [Google Scholar] [CrossRef]
- Demarest, K.; Plumb, R.; Huang, Z. FDTD modeling of scatterers in stratified media. IEEE Trans. Antennas Propag. 1995, 43, 1164–1168. [Google Scholar] [CrossRef]
- Huang, Z.; Demarest, K.R.; Plumb, R.G. An FDTD/MoM hydrid technique for modeling complex antennas in the presence of heterogeneous grounds. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2692–2698. [Google Scholar] [CrossRef]
- Cui, T.J.; Chew, W.C. Fast algorithm for electromagnetic scattering by buried conducting plates of large size. IEEE Trans. Antennas Propag. 1999, 47, 1116–1118. [Google Scholar] [CrossRef]
- Zhuang, L.; He, S.Y.; Ye, X.B.; Hu, W.D.; Yu, W.X.; Zhu, G.Q. The BCGS-FFT method combined with an improved discrete complex image method for EM scattering from electrically large objects in multilayered media. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1180–1185. [Google Scholar] [CrossRef]
- Losada, V.; Boix, R.R.; Medina, F. Fast and accurate algorithm for the short-pulse electromagnetic scattering from conducting circular plates buried inside a lossy dispersive half-space. IEEE Trans. Geosci. Remote Sens. 2003, 41, 988–997. [Google Scholar] [CrossRef]
- Alcuntu, Y.; Yapar, A.; Akduman, I. On the scattering of electromagnetic waves by bodies buried in a half-space with locally rough interface. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1435–1443. [Google Scholar]
- Hongo, K.; Jafri, A.D.U.; Naqvi, Q.A. Scattering of electromagnetic spherical wave by a perfectly conducting disk. Prog. Electromagn. Res. 2012, 129, 315–343. [Google Scholar] [CrossRef]
- Balaban, M.V.; Sauleau, R.; Garcia-Vigueras, M.; Nosich, A.I. Terahertz range elementary dipole excitation of a thin dielectric disk sandwiched between two graphene covers: Integral equation analysis. In Proceedings of the IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS), Tel-Aviv, Israel, 4–6 November 2019. [Google Scholar]
- Herasymova, D.O.; Dukhopelnykov, S.V.; Lucido, M.; Nosich, A.I. Optical sensing of electron-beam position with twin silver nanotube antenna tuned to hybrid surface plasmon resonance. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 4601008. [Google Scholar] [CrossRef]
- Kantorovich, L.V.; Akilov, G.P. Functional Analysis, 2nd ed.; Pergamon/Oxford-Elmsford: New York, NY, USA, 1982. [Google Scholar]
- Tsalamengas, J.L. Exponentially converging Nystrom’s methods for systems of singular integral equations with applications to open/closed strip- or slot-loaded 2-D structures. IEEE Antennas Propag. Mag. 2006, 54, 1549–1558. [Google Scholar] [CrossRef]
- Bulygin, V.S.; Nosich, A.I.; Gandel, Y.V. Nystrom-type method in three-dimensional electromagnetic diffraction by a finite PEC rotationally symmetric surface. IEEE Trans. Antennas Propag. 2012, 60, 4710–4718. [Google Scholar] [CrossRef]
- Bulygin, V.S.; Benson, T.M.; Gandel, Y.V.; Nosich, A.I. Full-wave analysis and optimization of a TARA-like shield-assisted paraboloidal reflector antenna using Nystrom-type method. IEEE Trans. Antennas Propag. 2013, 61, 4981–4989. [Google Scholar] [CrossRef]
- Lucido, M.; Schettino, F.; Migliore, M.D.; Pinchera, D.; Di Murro, F.; Panariello, G. Electromagnetic scattering by a zero-thickness PEC annular ring: A new highly efficient MoM solution. J. Electromagn. Waves Appl. 2017, 31, 405–416. [Google Scholar] [CrossRef]
- Lucido, M.; Balaban, M.V.; Nosich, A.I. Terahertz-range plasmon and whispering gallery mode resonances in the plane wave scattering from thin microsize dielectric disk with graphene covers. Proc. Math. Phys. Eng. Sci. 2022, 478, 2262. [Google Scholar] [CrossRef]
- Lucido, M.; Nosich, A.I. Analytical regularization approach to plane wave diffraction from circular hole in infinite resistive plane. IEEE Trans. Antennas Propag. 2023, 71, 6878–6892. [Google Scholar] [CrossRef]
- Chew, W.C.; Kong, J.A. Resonance of nonaxial symmetric modes in circular microstrip disk antenna. J. Math. Phys. 1980, 21, 2590–2598. [Google Scholar] [CrossRef]
- Lucido, M.; Di Murro, F.; Panariello, G. Electromagnetic scattering from a zero-thickness PEC disk: A note on the Helmholtz-Galerkin analytically regularizing procedure. Progr. Electromagn. Res. Lett. 2017, 71, 7–13. [Google Scholar] [CrossRef]
- Chew, W.C. Waves and Fields in Inhomogeneous Media; IEEE Press: Piscataway, NJ, USA, 1995. [Google Scholar]
- Chew, W.C.; Chen, S.Y. Response of a point source embedded in a layered medium. IEEE Antennas Wirel. Propag. Lett. 2003, 2, 254–258. [Google Scholar] [CrossRef][Green Version]
- Michalski, K.A.; Zheng, D. Rigorous analysis of open microstrip lines of arbitrary cross section in bound and leaky regimes. IEEE Trans. Microw. Theory Tech. 1989, 37, 2005–2010. [Google Scholar] [CrossRef]
- Meixner, J. The behavior of electromagnetic fields at edges. IEEE Trans. Antennas Propag. 1972, 20, 442–446. [Google Scholar] [CrossRef]
- Makarov, G.I.; Osipov, A.V. Structure of Meixner’s series. Radiophys. Quantum Electron. 1986, 29, 544–549. [Google Scholar] [CrossRef]
- Van Bladel, J. A discussion of Helmholtz’ theorem on a surface. Arch. Elektron. Ubertrag. 1993, 47, 131–136. [Google Scholar]
- Lucido, M.; Balaban, M.V.; Dukhopelnykov, S.V.; Nosich, A.I. A fast-converging scheme for the electromagnetic scattering from a thin dielectric disk. Electronics 2020, 9, 1451. [Google Scholar] [CrossRef]
- Wilkins, J.E. Neumann series of Bessel functions. Trans. Am. Math. Soc. 1948, 64, 359–385. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucido, M.; Casula, G.A.; Chirico, G.; Migliore, M.D.; Pinchera, D.; Schettino, F. Helmholtz–Galerkin Technique in Dipole Field Scattering from Buried Zero-Thickness Perfectly Electrically Conducting Disk. Appl. Sci. 2024, 14, 5544. https://doi.org/10.3390/app14135544
Lucido M, Casula GA, Chirico G, Migliore MD, Pinchera D, Schettino F. Helmholtz–Galerkin Technique in Dipole Field Scattering from Buried Zero-Thickness Perfectly Electrically Conducting Disk. Applied Sciences. 2024; 14(13):5544. https://doi.org/10.3390/app14135544
Chicago/Turabian StyleLucido, Mario, Giovanni Andrea Casula, Gaetano Chirico, Marco Donald Migliore, Daniele Pinchera, and Fulvio Schettino. 2024. "Helmholtz–Galerkin Technique in Dipole Field Scattering from Buried Zero-Thickness Perfectly Electrically Conducting Disk" Applied Sciences 14, no. 13: 5544. https://doi.org/10.3390/app14135544
APA StyleLucido, M., Casula, G. A., Chirico, G., Migliore, M. D., Pinchera, D., & Schettino, F. (2024). Helmholtz–Galerkin Technique in Dipole Field Scattering from Buried Zero-Thickness Perfectly Electrically Conducting Disk. Applied Sciences, 14(13), 5544. https://doi.org/10.3390/app14135544









