Integrated Plug High-Strength Geocell Reinforcement in Foundation Design for Square Footing
Abstract
1. Introduction
2. Methodology and Analytical Equation
2.1. Ultimate Bearing Capacity of Unreinforced Foundation under a Square Footing
2.2. Enhancement of Ultimate Bearing Capacity by the IPGC
2.2.1. The Relationship between Vertical and Horizontal Stress of Soil in a Cell
2.2.2. The Relationship between the Overburden Loading and the Vertical Stress of the Soil
2.2.3. The Relationship between Hoop Stress and Cell Wall Tearing Strength of the IPGC
3. Results and Discussion
4. Conclusions
- The calculated values from the theoretical model align well with experimental data, with a maximum error of 18%. It was observed that the reinforcement effect of IPGC may be disregarded when the top space exceeds the footing width.
- When the cell diameter surpasses 1.8 times the foundation width, the confinement effect of IPGC becomes negligible, resulting in an ultimate bearing capacity similar to that of unreinforced foundations.
- It is essential to note that additional tests and discussions on scale ratios are necessary if the results are to be applied to real projects. Meanwhile, further comparative studies involving various foundation reinforcement technologies and soils are required to fully assess the effectiveness of IPGC compared to other solutions available on the market.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| B | the width of the square footing; |
| b | the width of the short side of the rectangular; |
| c | the cohesion of soil; |
| Du | the top space of IPGC from the bottom of the footing; |
| d0 | the diameter of the cell; |
| F | the tearing force of the cell wall; |
| h | the height of the cell wall; |
| i | the ith cell; |
| K0 | empirical static earth pressure coefficient; |
| l | the width of the long side of the rectangular; |
| Nc, Nq, Nγ | the bearing capacity coefficient; |
| n | the number of cells; |
| p | the overburden loading; |
| pu | the ultimate bearing capacity of an IPGC-reinforced foundation under a square footing; |
| p0 | the ultimate bearing capacity of an unreinforced foundation; |
| Δp | the bearing capacity increased by the IPGC; |
| q | the surcharge beside two sides of the footing; |
| t | the thickness of the cell wall; |
| α | the vertical additional stress coefficient under uniformly distributed rectangular loading; |
| γ | the gravity of soil; |
| β | the influence coefficient of the top space; |
| φ | the internal friction angle of the soil; |
| σx, σy | stress in the x and y lateral directions, respectively; |
| σz | the vertical stress of soil under overburden loading p; |
| σt | the linear elastic tensile stress of the cell wall; |
| σr | the lateral confinement of the cell induced by the movement of soil particles. |
Appendix A. An Example of the Calculation Process
References
- Hegde, A.; Sitharam, T.G. 3-Dimensional numerical modelling of geocell reinforced sand beds. Geotext. Geomembr. 2015, 43, 171–181. [Google Scholar] [CrossRef]
- Hegde, A. Geocell reinforced foundation beds-past findings, present trends and future prospects: A state-of-the-art review. Constr. Build. Mater. 2017, 154, 658–674. [Google Scholar] [CrossRef]
- Dash, S.K.; Krishnaswamy, N.R.; Rajagopal, K. Bearing capacity of strip footings supported on geocell-reinforced sand. Geotext. Geomembr. 2001, 19, 235–256. [Google Scholar] [CrossRef]
- Pokharel, S.K.; Han, J.; Leshchinsky, D.; Parsons, R.; Halahmi, I. Investigation of factors influencing behavior of single geocell-reinforced bases under static loading. Geotext. Geomembr. 2010, 28, 570–578. [Google Scholar] [CrossRef]
- Tafreshi, S.M.; Dawson, A.R. Comparison of bearing capacity of a strip footing on the sand with geocell and with planar forms of geotextile reinforcement. Geotext. Geomembr. 2010, 28, 72–81. [Google Scholar] [CrossRef]
- Avesani Neto, J.O.; Bueno, B.S.; Futai, M.M. A bearing capacity calculation method for soil reinforced with a geocell. Geosynth. Int. 2013, 20, 129–142. [Google Scholar] [CrossRef]
- Tafreshi, S.N.M.; Shaghaghi, T.; Mehrjardi, G.T.; Dawson, A.R.; Ghadrdan, M. A simplified method for predicting the settlement of circular footings on multi-layered geocell-reinforced non-cohesive soils. Geotext. Geomembr. 2015, 43, 332–344. [Google Scholar] [CrossRef]
- Sireesh, S.; Sitharam, T.G.; Dash, S.K. Bearing capacity of circular footing on geocell-sand mattress overlying clay bed with void. Geotext. Geomembr. 2009, 27, 89–98. [Google Scholar] [CrossRef]
- Zhao, M.H.; Chen, B.C.; Yin, B.P.; Hu, Z. Model tests on bearing capacity characteristics of geocell gravel base and rigid pavement. Chin. J. Geotech. Eng. 2012, 34, 577–581. [Google Scholar]
- Zhao, M.H.; Long, J.; Zhang, L.; Ma, B.H.; He, L.P. Comparative analysis of model tests on different types of composite foundations. Chin. J. Geotech. Eng. 2013, 44, 611–618. [Google Scholar]
- Latha, G.M.; Somwanshi, A. Effect of reinforcement form on the bearing capacity of square footings on sand. Geotext. Geomembr. 2009, 27, 409–422. [Google Scholar] [CrossRef]
- Han, X.; Zhang, M.X.; Li, J.Y.; Jiang, S.W. Model test of IEI reinforced sand foundation. J. Yangtze River Sci. Res. Inst. 2014, 31, 27–33. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, M.X.; Han, X.; Li, R. Mechanism of a IEI using FEM. Chin. J. Geotech. Eng. 2015, 37, 26–30. [Google Scholar] [CrossRef]
- Dai, Z.H.; Zhang, M.X.; Hou, J.; Li, J.Z. Experimental comparative study of new lock enhanced integral geocell and geogrid mesh elements reinforced foundation. J. Shanghai Univ. (Nat. Sci.) 2019, 25, 796–806. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, M.X.; Jiang, S.W. Model tests on sand embankment reinforced with geocell subjected to strip loading. Chin. J. Geotech. Eng. 2015, 37, 170–175. [Google Scholar] [CrossRef]
- Hou, J.; Chu, C.X.; Lu, X.Q.; Xing, X. FEM3D analysis of interlock-enhanced integral geocell-reinforced foundation. Soil Mech. Found. Eng. 2024, in press. [Google Scholar]
- Hou, J.; Liu, S.T.; Lu, X.Q.; Karen, M. Simulation of geocell-reinforced foundation using particle flow code. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 032069. [Google Scholar] [CrossRef]
- Wang, C.H. Soil Mechanics; China Architecture & Building Press: Beijing, China, 2012. [Google Scholar]
- Michalowski, R.L.; Asce, F. Coefficient of earth pressure at rest. J. Geotech. Geoenviron. Eng. 2005, 133, 1429–1433. [Google Scholar] [CrossRef]
- Hirai, H. Settlements and stresses of multi-layered grounds and improved grounds by equivalent elastic method. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 523–557. [Google Scholar] [CrossRef]
- Vakili, J. A simplified method for evaluation of pavement layers moduli using surface deflection data. In Proceedings of the 12th International Conference of International Association for Computer Methods and Advances in Geomechanics (IACMAG), Goa, India, 1–6 October 2008; Volume 16, pp. 4314–4319. [Google Scholar]
- Fu, Z.Q.; Wang, G.Y.; Hou, D.Y.; Che, Q. Study on bearing capacity of rectangular foundations supported on geogrid reinforced sand. J. Shandong Univ. (Eng. Sci.) 2003, 60, 61–62+68. [Google Scholar]
- Dash, S.K. Influence of relative density of soil on performance of geocell-reinforced sand foundations. J. Mater. Civ. Eng. 2010, 22, 533–538. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, M.X.; Dai, Z.H.; Li, J.Z.; Zeng, F.F. Bearing capacity of strip foundations in horizontal-vertical reinforced soils. Geotext. Geomembr. 2017, 45, 29–34. [Google Scholar] [CrossRef]
- Shadmand, A.; Ghazavi, M.; Ganjian, N. Load-settlement characteristics of large-scale square footing on sand reinforced with opening geocell reinforcement. Geotext. Geomembr. 2018, 46, 319–326. [Google Scholar] [CrossRef]



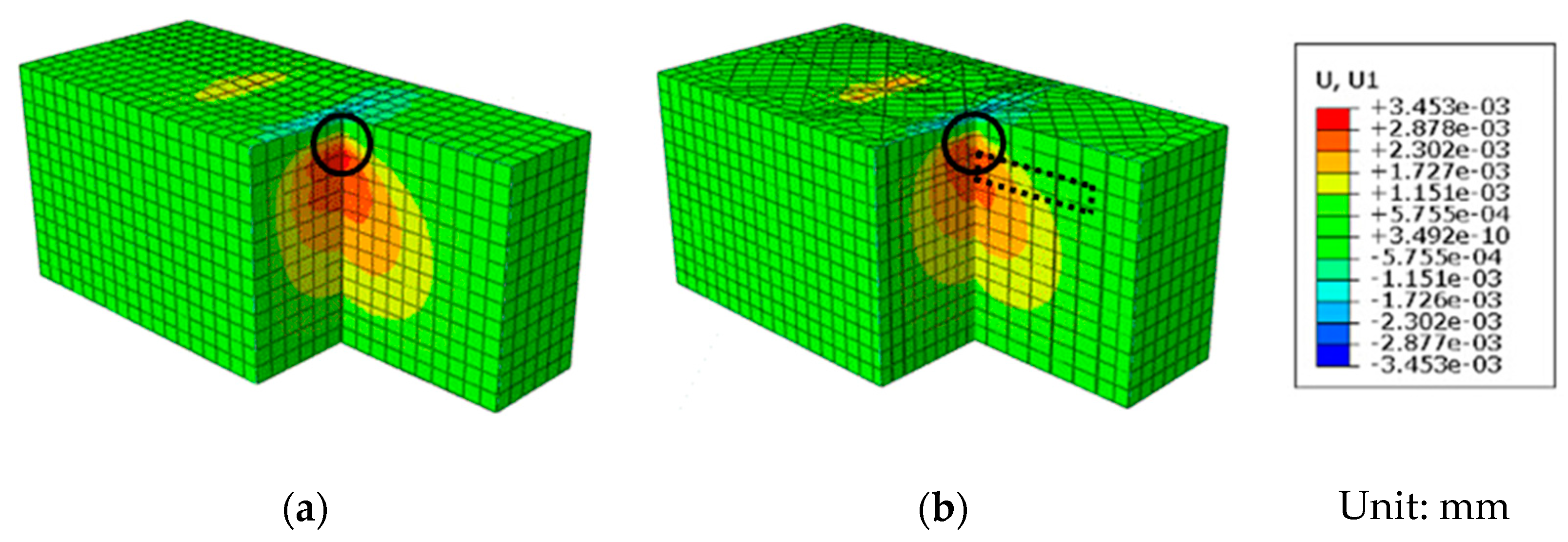


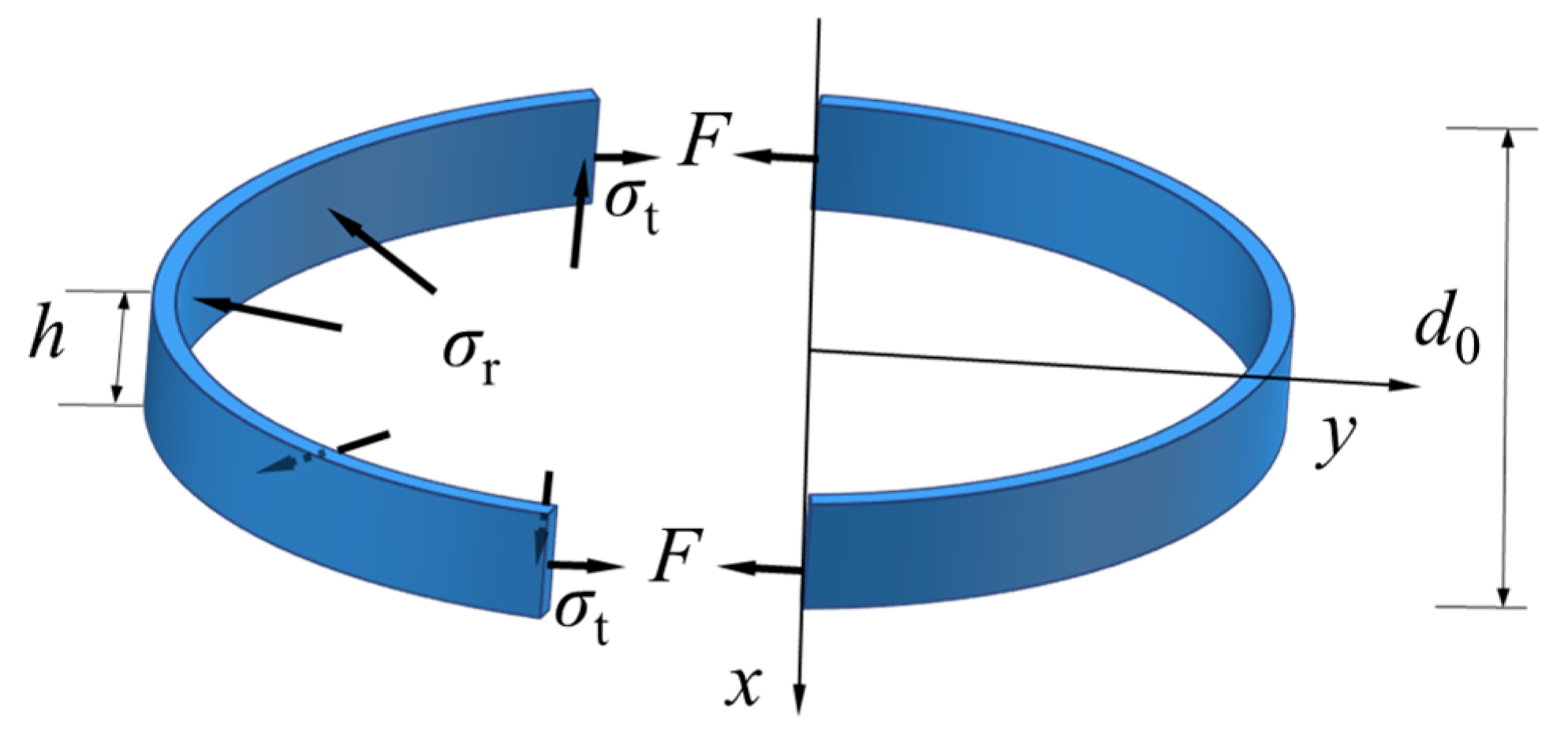
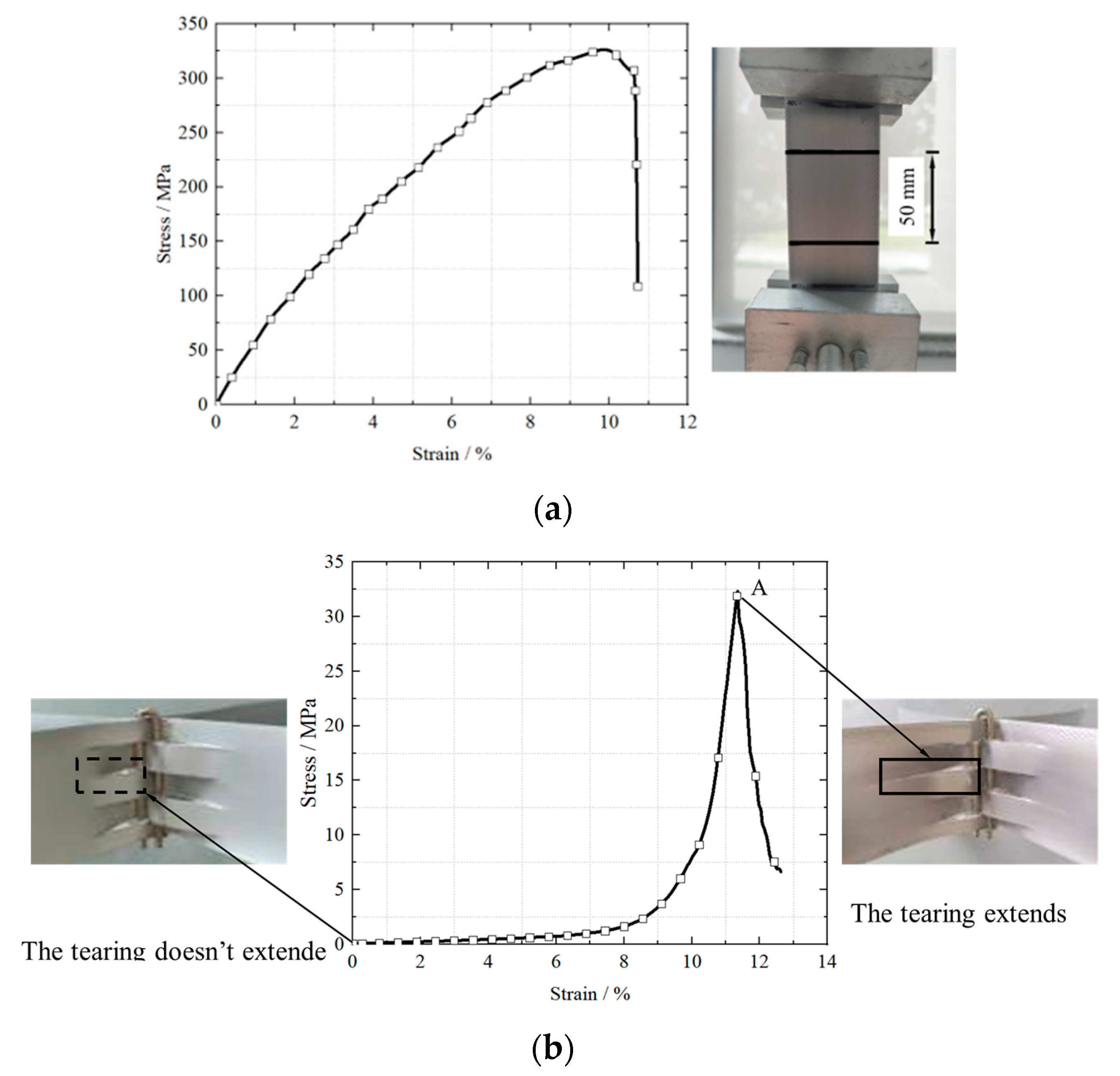


| Literature | B /m | γ /kN/m3 | φ /° | h /m | d0 /cm | Du /cm | F /kN | α | Pu /kPa | Pexp /kPa | Error /% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Han et al. (2014) [12] | 0.3 | 18.1 | 35.4 | 0.05 | 11.1 | 9.9 | 0.73 | 0.83 | 888.0 | 749.7 | 18 |
| 20.1 | 0.72 | 607.9 | 670.6 | 9 | |||||||
| 28.2 | 0.51 | 610.9 | 559.8 | 9 | |||||||
| Shadmand et al. (2018) [25] | 0.5 | 18.6 | 41.0 | 0.15 | 22.0 | 5.0 | 0.27 | 0.99 | 596.8 | 705.1 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, J.; He, X.; Lu, S.; Ma, Y. Integrated Plug High-Strength Geocell Reinforcement in Foundation Design for Square Footing. Appl. Sci. 2024, 14, 5547. https://doi.org/10.3390/app14135547
Hou J, He X, Lu S, Ma Y. Integrated Plug High-Strength Geocell Reinforcement in Foundation Design for Square Footing. Applied Sciences. 2024; 14(13):5547. https://doi.org/10.3390/app14135547
Chicago/Turabian StyleHou, Juan, Xin He, Shen Lu, and Yanxia Ma. 2024. "Integrated Plug High-Strength Geocell Reinforcement in Foundation Design for Square Footing" Applied Sciences 14, no. 13: 5547. https://doi.org/10.3390/app14135547
APA StyleHou, J., He, X., Lu, S., & Ma, Y. (2024). Integrated Plug High-Strength Geocell Reinforcement in Foundation Design for Square Footing. Applied Sciences, 14(13), 5547. https://doi.org/10.3390/app14135547







