Analysis and Experimental Study on the Stability of Large-Span Caverns’ Surrounding Rock Based on the Progressive Collapse Mechanism
Abstract
:1. Introduction
2. Basic Theory
2.1. Upper Limit Theorem
2.2. Hoek–Brown Nonlinear Failure Criterion
2.3. Calculation of Energy Consumption Based on the Upper Limit Method
3. Analysis of the Collapse Mechanism of the Surrounding Rock of Large-Span Caverns
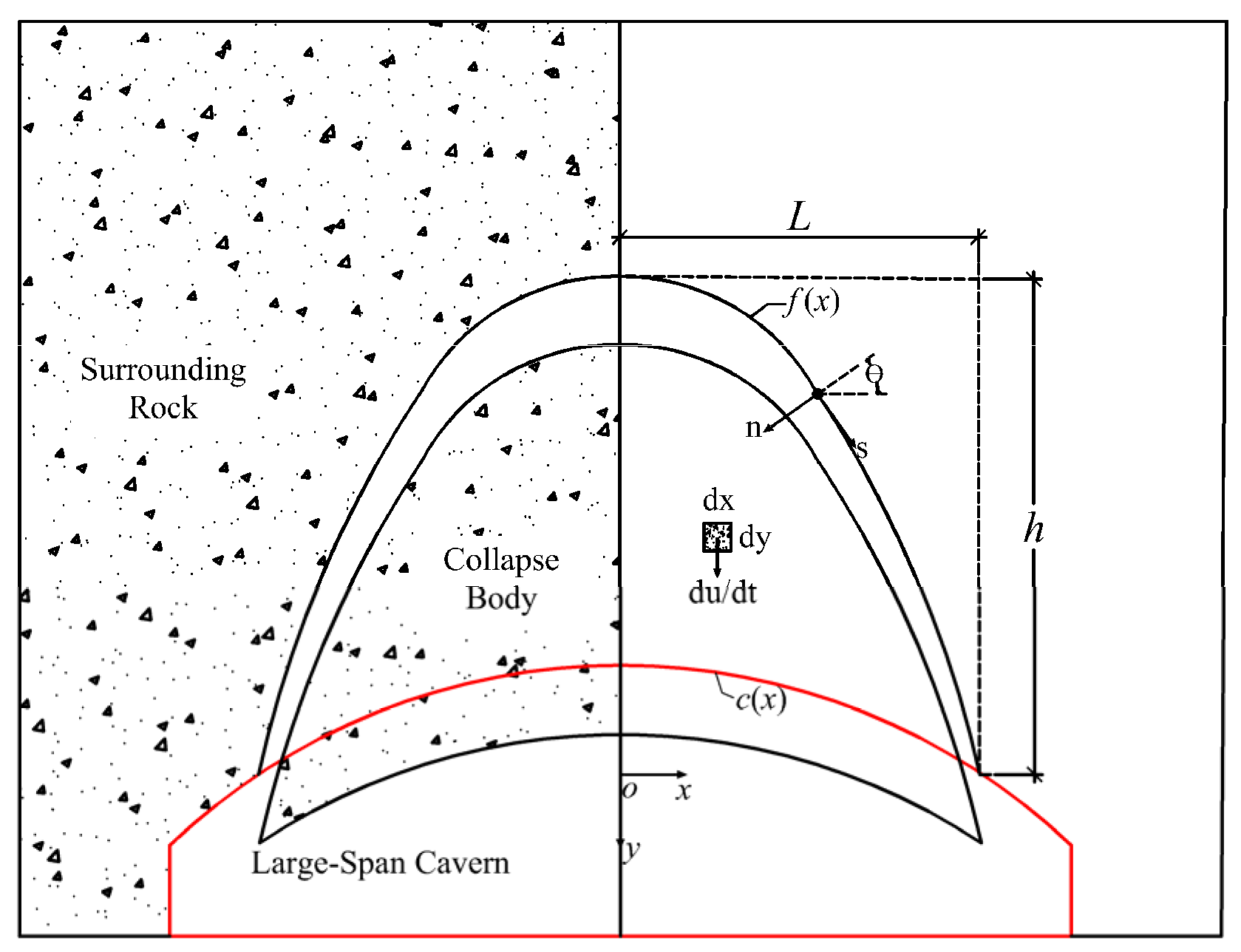
3.1. Establishment of a Computational Model
3.2. Solution to the Collapse Curve of Rock Surrounding a Large-Span Cavern Vault
4. Calculation of the Progressive Collapse Process of the Surrounding Rock of a Large-Span Cavern
4.1. Establishment of the Progressive Collapse Model
4.2. Analytical Solution of the Progressive Collapse Curve of a Large-Span Cavern’s Surrounding Rock
5. Model Test of the Progressive Collapse of the Surrounding Rock of a Large-Span Cavern
5.1. Selection of Similar Scale
5.2. Identification of Similar Materials
5.3. Test Conditions
5.4. Test Steps for the Progressive Collapse Model of Large-Span Caverns
- (1)
- Rotate the model box of the test device to the level and apply a layer of lubricating oil evenly around the model box to reduce the friction between the model box and the model material;
- (2)
- Mix the model material evenly according to the ratio, divide it into two layers, each layer 2.5 cm thick, and strictly control the weight and thickness of each layer to ensure that the density of the model material is consistent;
- (3)
- Model self-compaction and cavern excavation. After the model has been rammed and formed, the model box is rotated to 90° and left to stand for 2 h to complete the self-compaction of the model material to simulate the initial stress state of the rock mass. Then, the model box is rotated to the horizontal level and excavated according to the prefabricated cavern-shaped template;
- (4)
- Observation and recording of the whole process of the collapse and destruction of the cavern’s surrounding rock. In order to facilitate recording, an acrylic pen can be used to divide the upper glass of the model box into 2 × 2 cm squares, so that the deformation of the cavern surrounding rock can be observed more intuitively. Slowly rotate the model box with every 5° increase, and then let it stand for 10 min, observe, and record the collapse of the cavern surrounding rock until it rotates to 90°. When material is found to collapse around the cavern during the rotation process, immediately stop rotation and rest for 30 min to fully deform the surrounding rock, and then observe and record the collapse of the cavern. When the model frame rotates to 90°, let it stand for 30 min to record the final collapse of the cavern’s surrounding rock. The contents recorded during the test mainly include the rotation angle of the model frame and the shape and position of the collapsed part of the surrounding rock collapse.
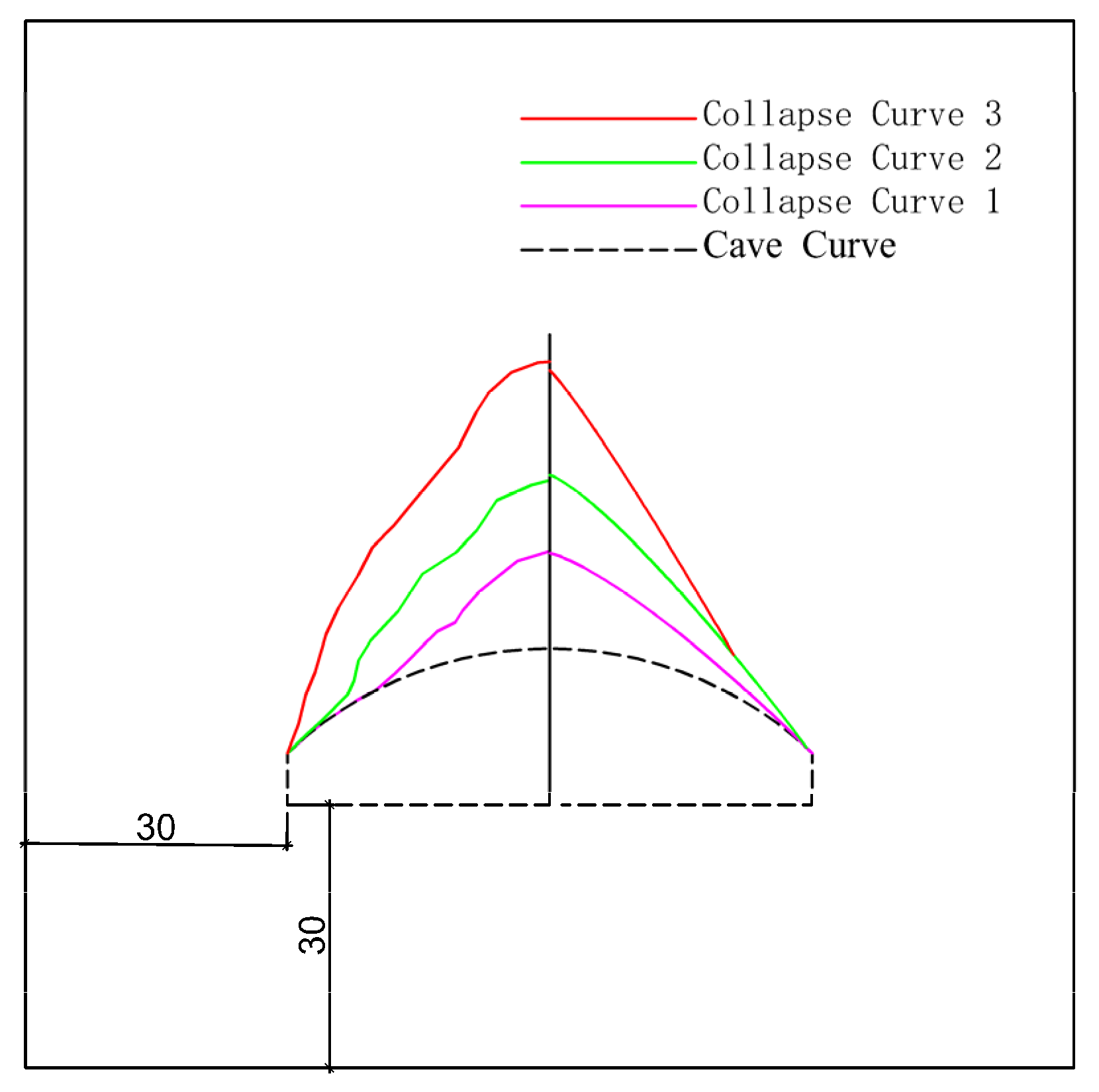
5.5. Results and Analysis of a 60 m Large-Span Cavern Model Test
5.6. Comparative Analysis of Theoretical Calculation and Experimental Results
6. Influence of Cavern Span on Stability of Surrounding Rock
6.1. Model Test of 30 m-Span Cavern
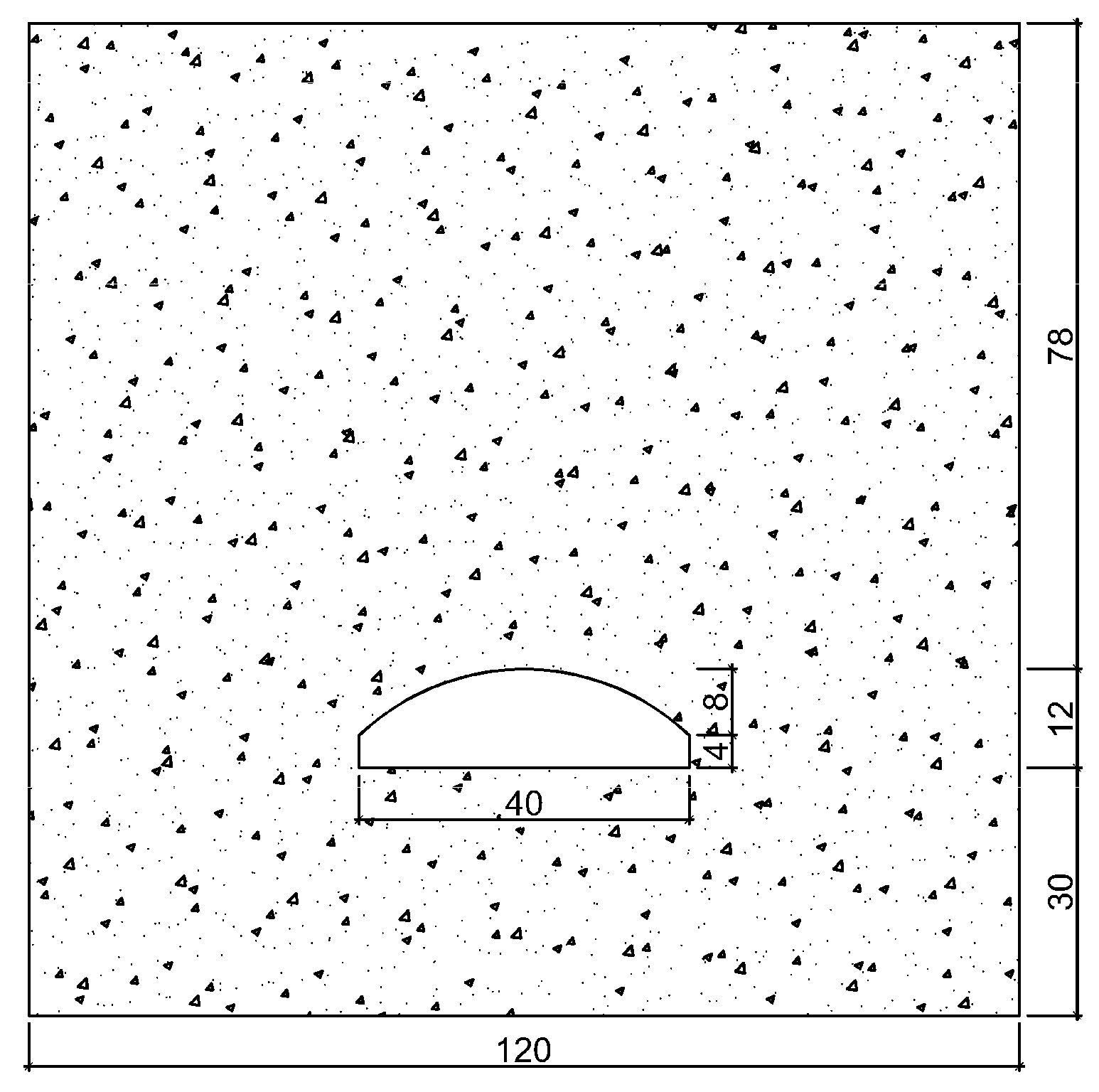
6.2. Model Test of 40 m-Span Cavern
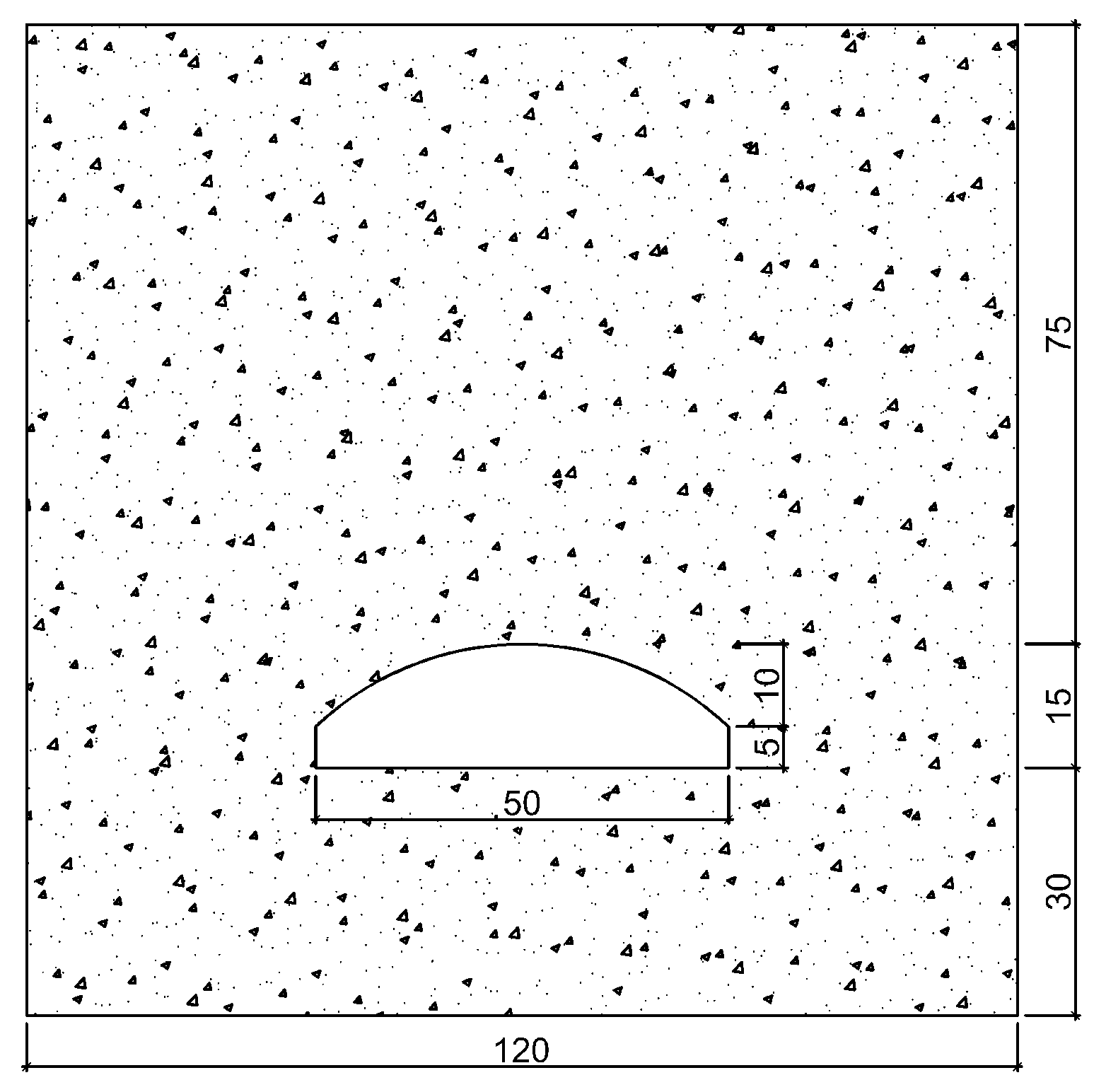
6.3. Model Test of 50 m-Span Cavern
7. Conclusions
- (1)
- The mechanism model of progressive collapse of large-span caverns is established, and the calculation method of the whole process curve of the progressive collapse of large-span caverns’ surrounding rock is deduced and compared with the model test results;
- (2)
- Using the self-developed geomechanical model device for visualizing large-span caverns with variable angles, the load on the top of the cavern is increased in a rotating manner, and the progressive collapse process of the surrounding rock of large-span caverns is revealed through the method of model tests;
- (3)
- Three collapses occurred in the 60 m large-span chamber. Due to the large span of the cavern, with an increase in surrounding rock pressure, the middle part of the vault roof will collapse first. When the overburden increases to a certain extent, the arch foot is the weakest part, and the rock mass will be found along the arch foot. Two shear failures will occur and gradually extend upward. Finally, the half-width of the collapse body will be 30 cm and the height will be 45.06 cm, which is 75.1% of the span of the cavern;
- (4)
- Through theoretical analysis and model tests, it was found that the large-span cavern model underwent collapse three times, and the collapse range calculated only once was quite different from the actual one. The theoretical calculation results in this paper are basically consistent with the model test results, verifying the rationality of the theoretical calculation and the model test for predicting the progressive collapse curve of the surrounding rock of the large-span cavern. The experimental method was used to obtain the progressive collapse characteristics and evolution processes of the surrounding rock of the large-span cavern, providing a basis for the selection of construction plans and the optimization of the supporting structure. It has certain guiding significance for the large-span cavern project;
- (5)
- Under the condition of rock mass and the shape of the cavern, the larger the span of the cavern, the more times the surrounding rock collapses. No collapse has occurred in the cavern with a span of 30 m, one collapse has occurred in the cavern with a span of 40 m, two collapses have occurred in the cavern with a span of 50 m, and three collapses have occurred in the cavern with a span of 60 m. Simultaneously, the collapse range also increases as the span increases;
- (6)
- Statement on Future Studies: The theoretical models and experimental results of this study lay the foundation for the excavation and support engineering of large-span caverns. Future work will focus on verifying these results under industrial conditions, ensuring practical applicability and enhancing the understanding of large span cavern stability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, M.; Jing, H.; Sun, X. Soft Rock Engineering Mechanics; Science Press: Beijing, China, 2002. [Google Scholar]
- Cai, M.; He, M.; Liu, D. Rock Mechanics and Engineering; Science Press: Beijing, China, 2013. [Google Scholar]
- Fraldi, M.; Guarracino, F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek-Brown failure criterion. Int. J. Rock Mech. Min. Sci. 2009, 46, 665–673. [Google Scholar] [CrossRef]
- Fraldi, M.; Guarracino, F. Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections. Int. J. Solids Struct. 2010, 47, 216–223. [Google Scholar] [CrossRef]
- Fraldi, M.; Guarracino, F. Evaluation of impending collapse in circular tunnels by analytical and numerical approaches. Tunn. Undergr. Space Technol. 2011, 26, 507–516. [Google Scholar] [CrossRef]
- Yang, X.L.; Huang, F. Collapse mechanism of shallow tunnel based on nonlinear Hoek–Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 686–691. [Google Scholar] [CrossRef]
- Yang, X.L.; Yan, R.M. Collapse mechanism for deep tunnel subjected to seepage force in layered soils. Geomech. Eng. 2015, 8, 741–756. [Google Scholar] [CrossRef]
- Yang, X.L.; Xu, J.S.; Li, Y.X.; Yan, R.M. Collapse mechanism of tunnel roof considering joined influences of nonlinearity and non-associated flow rule. Geomech. Eng. 2016, 10, 21–35. [Google Scholar] [CrossRef]
- Yang, X.L.; Zhou, T.; Li, W.T. Reliability analysis of tunnel roof in layered Hoek-Brown rock masses. Comput. Geotech. 2018, 104, 302–309. [Google Scholar] [CrossRef]
- Yu, L.; Lü, C.; Wang, M. Three-dimensional upper bound limit analysis of deep soil tunnels based on nonlinear Mohr-Coulomb criterion. Chin. J. Geotech. Eng. 2019, 41, 1023–1030. [Google Scholar]
- Sun, C.; Lan, S.; Tao, Q.; Guan, X.; Han, X. Upper bound analysis of three-dimensional progressive collapse mechanism of deep tunnel roof with weak surrounding rock. Rock Soil Mech. 2023, 44, 2471–2484. [Google Scholar]
- Skrzypkowski, K.; Korzeniowski, W.; Zagórski, K.; Zagórska, A. Adjustment of the Yielding System of Mechanical Rock Bolts for Room and Pillar Mining Method in Stratified Rock Mass. Energies 2020, 13, 2082. [Google Scholar] [CrossRef]
- Korzeniowski, W.; Poborska-Młynarska, K.; Skrzypkowski, K. The Idea of the Recovery of Municipal Solid Waste Incineration (MSWI) Residues in Klodawa Salt Mine Sa by Filling the Excavations With Self-Solidifying Mixtures. Arch. Min. Sci. 2018, 63, 553–565. [Google Scholar]
- Wang, C. Study on the Progressive Failure Mechanism of the Surrounding Rock of Tunnel Constructed in Soft Rock. Ph.D. Dissertation, Tongji University, Shanghai, China, 2007. [Google Scholar]
- Zhu, H.; Huang, F.; Xu, Q. Model test and numerical simulation for progressive failure of weak and fractured tunnel surrounding rock under different overburden depths. Chin. J. Rock Mech. Eng. 2010, 29, 1113–1122. [Google Scholar]
- Xu, Q.; Ding, W.; Zhu, H.; Tang, Z.; Li, Y. Study on progressive unloading failure characteristics of superlarge tunnel in soft and weak rock mass. China Civ. Eng. J. 2017, 50, 104–114. [Google Scholar]
- Wei, X.; Duan, Y.; Qiao, N.; Feng, J. Causes and countermeasures of accidents related to underground construction in China. J. Tsinghua Univ. (Sci. Technol.) 2019, 59, 314–325. [Google Scholar]
- Chen, W.F. Limit Analysis and Soil Plasticity; Elsevier: Amsterdam, The Netherlands, 1975; pp. 85–96. [Google Scholar]
- Hoek, E.; Brown, E.T. Practical estimate the rock mass strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek-Brown Failure Criterion; University of Toronto Press: Toronto, ON, Canada, 2002; pp. 267–273. [Google Scholar]







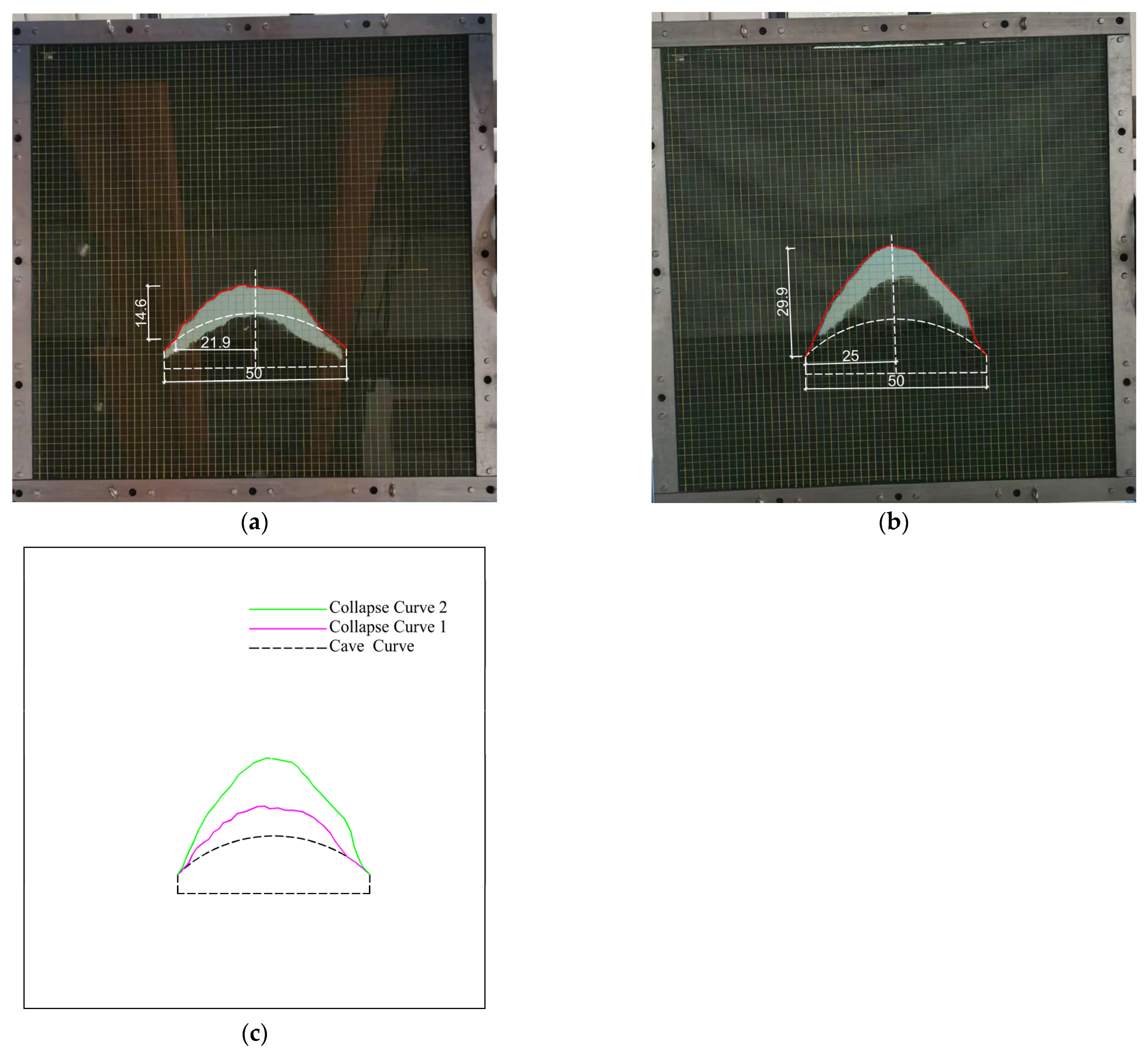
| CAVERN Span (cm) | Number of Collapses | Half Width of Falling Body (cm) | Collapse Height (cm) |
|---|---|---|---|
| 30 | 0 | 0 | 0 |
| 40 | 1 | 15 | 10.9 |
| 50 | 2 | 25 | 29.9 |
| 60 | 3 | 30 | 45.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Fan, J.; Xu, J. Analysis and Experimental Study on the Stability of Large-Span Caverns’ Surrounding Rock Based on the Progressive Collapse Mechanism. Appl. Sci. 2024, 14, 5929. https://doi.org/10.3390/app14135929
Chen H, Fan J, Xu J. Analysis and Experimental Study on the Stability of Large-Span Caverns’ Surrounding Rock Based on the Progressive Collapse Mechanism. Applied Sciences. 2024; 14(13):5929. https://doi.org/10.3390/app14135929
Chicago/Turabian StyleChen, Huanxia, Junqi Fan, and Jingmao Xu. 2024. "Analysis and Experimental Study on the Stability of Large-Span Caverns’ Surrounding Rock Based on the Progressive Collapse Mechanism" Applied Sciences 14, no. 13: 5929. https://doi.org/10.3390/app14135929




