Multicriteria Decision Model for Port Evaluation and Ranking: An Analysis of Container Terminals in Latin America and the Caribbean Using PCA-TOPSIS Methodologies
Abstract
:1. Introduction
2. Materials and Methods
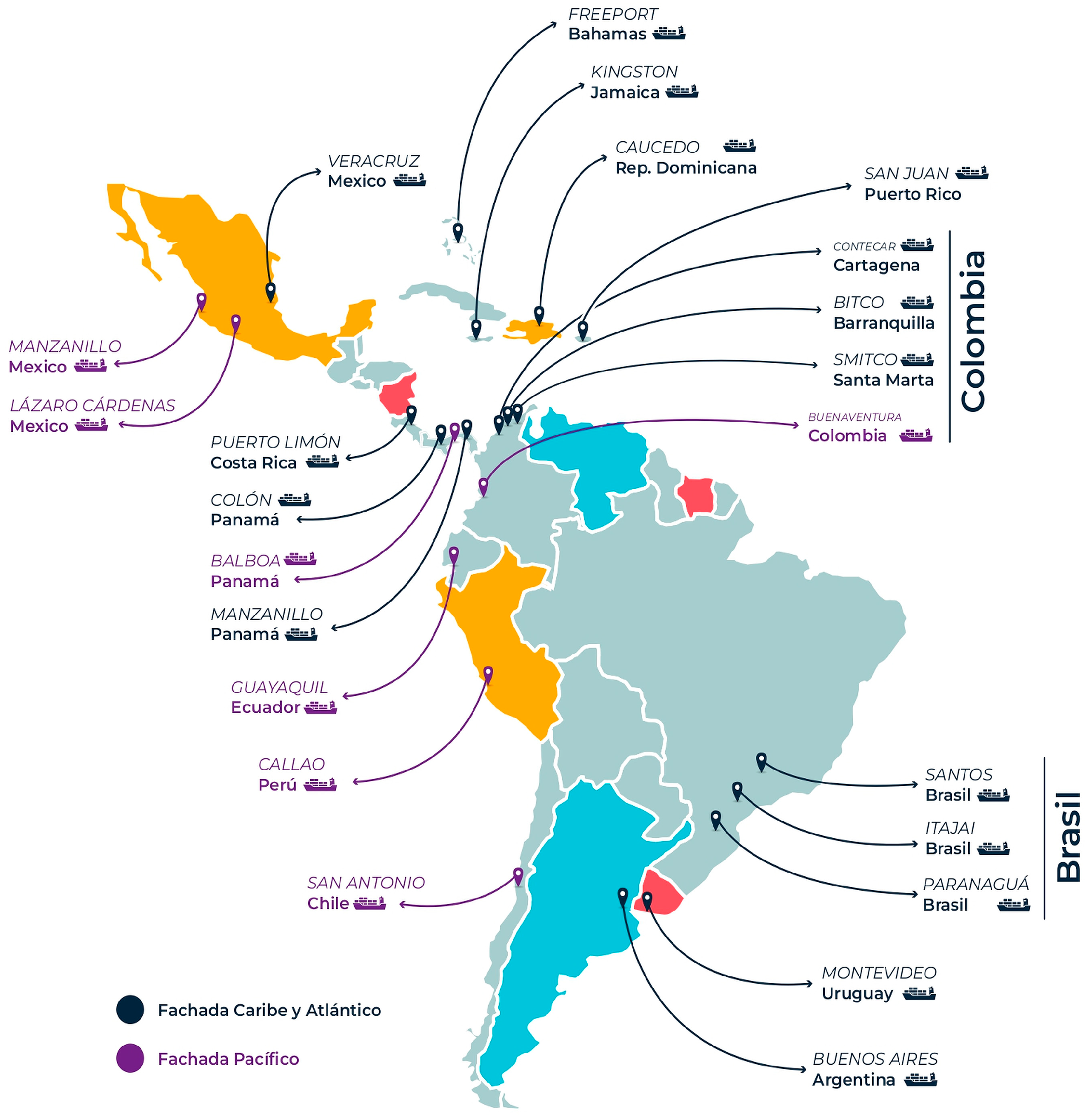
2.1. Data Description
2.2. Methodology
2.2.1. Principal Component Analysis (PCA)
2.2.2. Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)
- TOPSIS evaluates the relative closeness of each alternative to an ideal solution, making it straightforward to understand and implement [30].
- TOPSIS is compensatory, meaning that poor performance in one criterion can be compensated by good performance in another, which is often more realistic in practical decision-making scenarios [31].
- TOPSIS requires the normalization of criteria to ensure comparability. This step helps in handling criteria measured in different units and scales, allowing a fair comparison among alternatives [32].
- Criteria weights can be assigned based on their importance, reflecting the decision-maker’s priorities. This flexibility allows customization of the decision-making process according to specific needs [32].
- TOPSIS provides a clear ranking of alternatives, facilitating easy interpretation of results. The ranking helps decision-makers to understand the relative performance of each alternative quickly [33].
- Phase 1: Calculate the normalized performance ratings.
- Phase 2: Integrate weight with ratings.
- Stage 3: Find positive and negative ideal solutions.
- Stage 4: Obtain the separation values.
- Stage 5: Calculate the overall preference score.
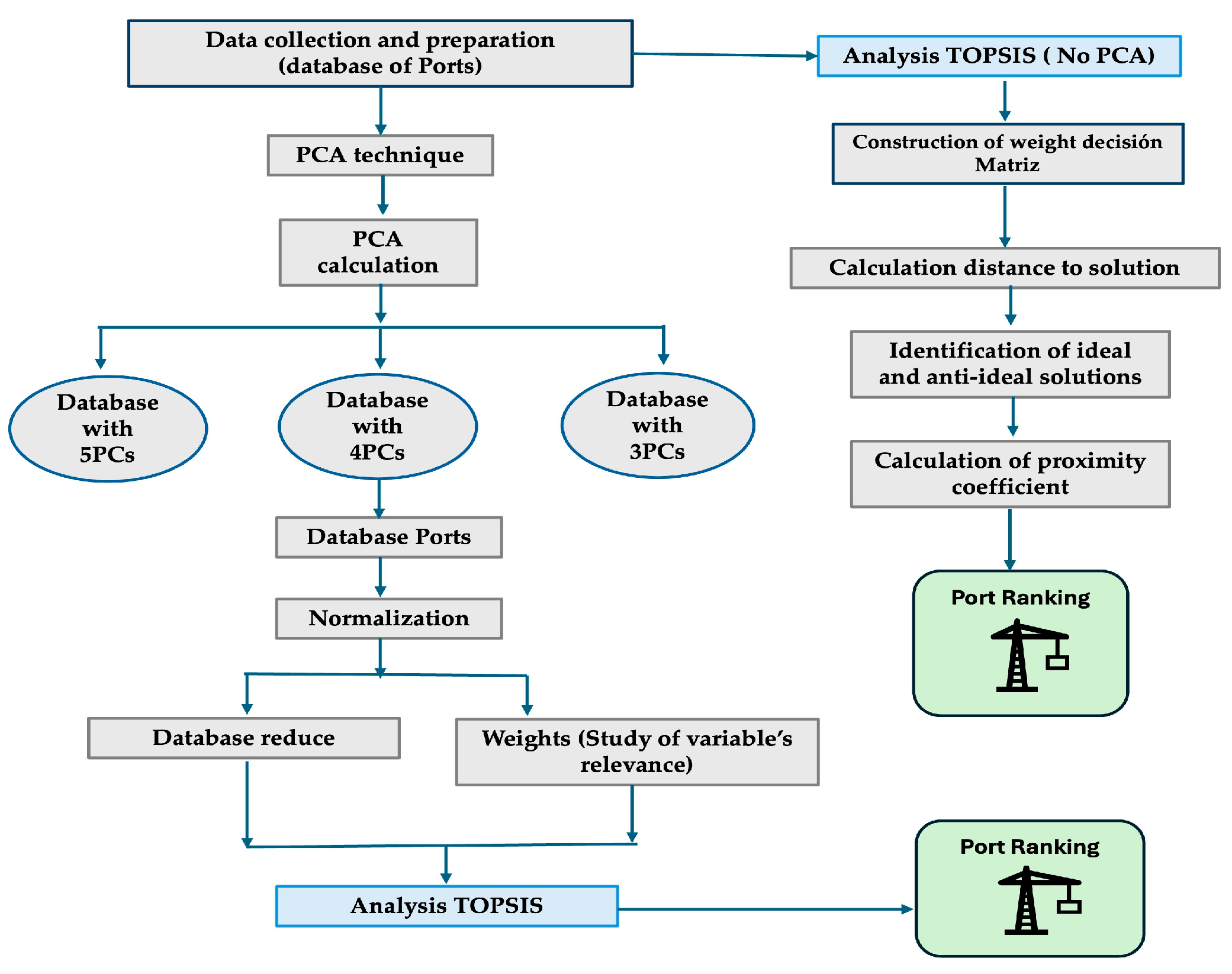
2.2.3. Experimental Procedure
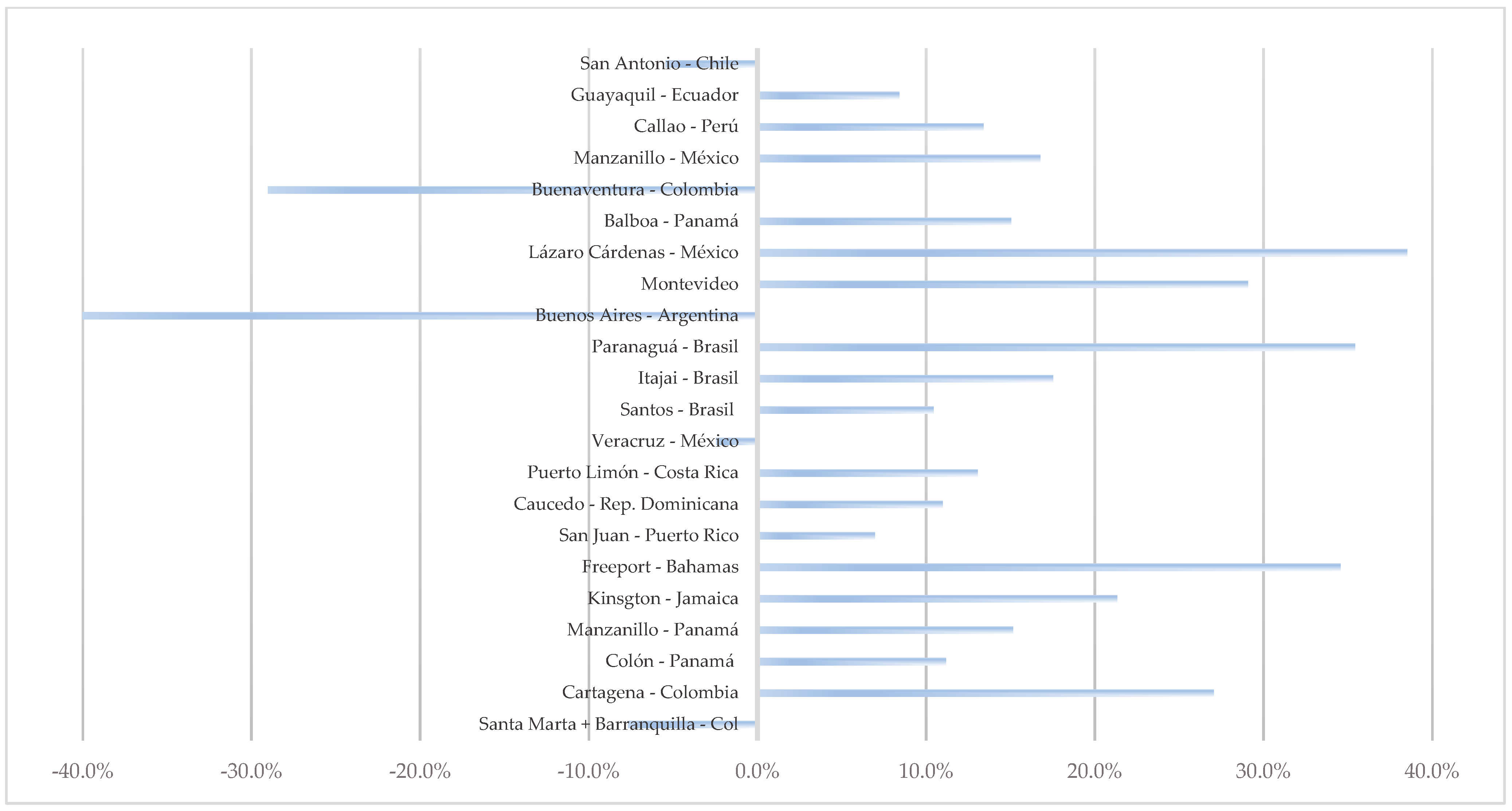
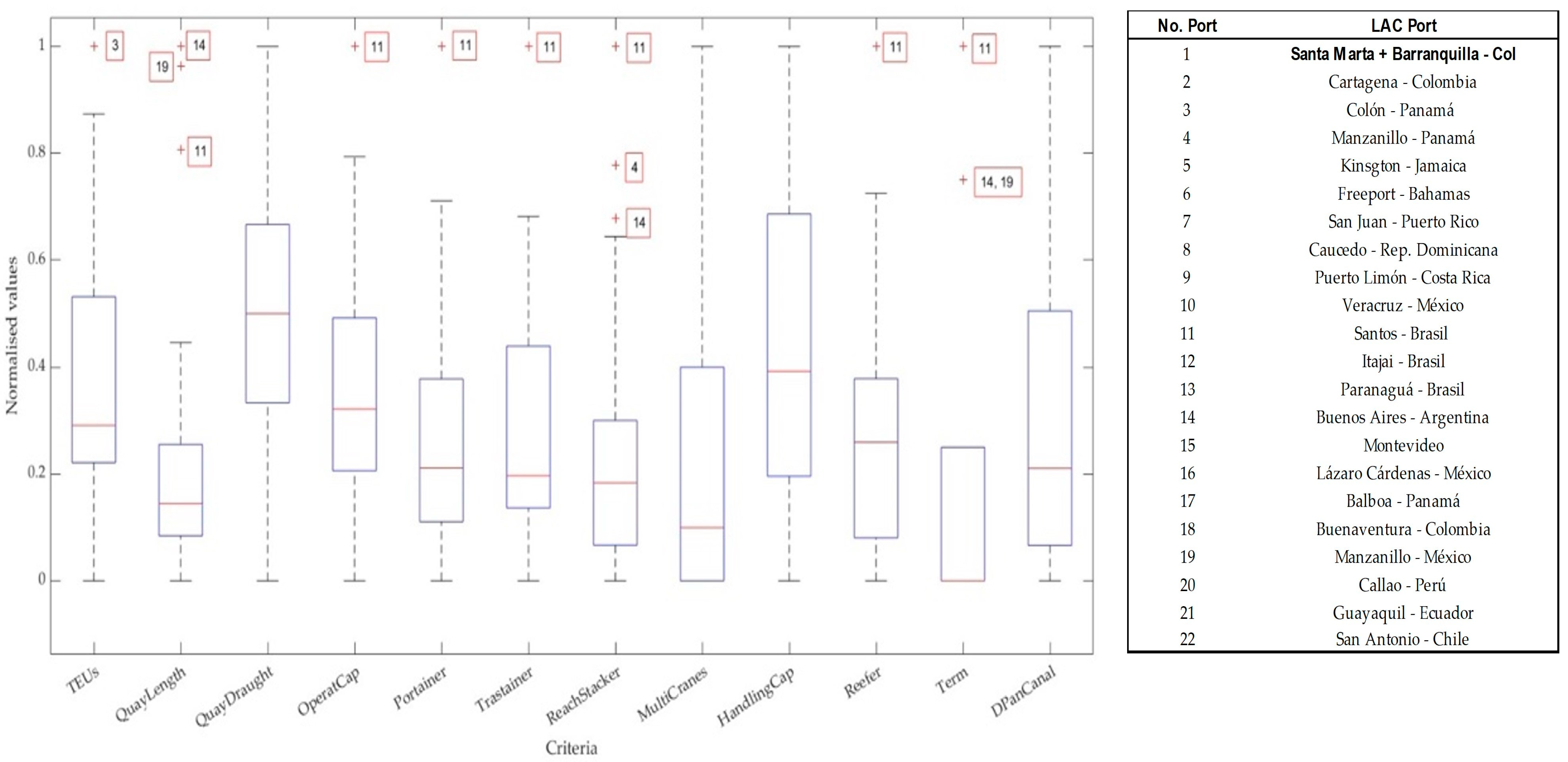
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Port | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
|---|---|---|---|---|---|---|---|---|---|---|
| Santa Marta (SMITCO) | 71,219 | 120,468 | 120,543 | 120,000 | 104,521 | 124,439 | 129,294 | 62,773 | 77,093 | 82,570 |
| Barranquilla (BITCO) | 92,346 | 136,624 | 137,683 | 125,943 | 160,104 | 160,892 | 146,563 | 172,655 | 187,534 | 163,154 |
| Santa Marta + Barranquilla-Col | 163,565 | 257,092 | 258,226 | 245,943 | 264,625 | 285,331 | 275,857 | 235,428 | 264,627 | 245,724 |
| Cartagena-Colombia | 2,037,000 | 2,135,508 | 2,245,588 | 2,094,539 | 2,406,339 | 2,932,000 | 3,127,000 | 3,344,000 | 3,145,449 | 3,299,000 |
| Colón-Panamá | 3,286,300 | 3,577,477 | 3,258,381 | 3,891,209 | 4,324,478 | 4,379,477 | 4,454,902 | 4,915,980 | 5,102,600 | 4,869,000 |
| Manzanillo-Panamá | 2,100,000 | 2,120,000 | 2,145,600 | 2,150,004 | 2,225,048 | 2,543,339 | 2,663,435 | 2,814,015 | 2,744,014 | 2,622,300 |
| Kinsgton-Jamaica | 1,638,113 | 1,653,272 | 1,567,442 | 1,560,000 | 1,833,053 | 1,647,609 | 1,611,637 | 1,975,400 | 2,137,500 | 2,329,875 |
| Freeport-Bahamas | 1,400,500 | 1,400,560 | 1,200,000 | 850,426 | 1,050,140 | 1,396,600 | 1,231,703 | 1,642,790 | 1,574,200 | 1,605,000 |
| San Juan-Puerto Rico | 1,319,961 | 1,210,000 | 1,110,000 | 1,199,157 | 1,405,348 | 1,404,602 | 1,490,218 | 1,438,740 | 1,398,600 | 1,510,488 |
| Caucedo-Rep, Dominicana | 831,375 | 826,935 | 918,542 | 1,149,079 | 1,314,798 | 1,263,991 | 950,219 | 1,265,459 | 1,406,500 | 1,476,825 |
| Puerto Limón-Costa Rica | 1,089,500 | 1,134,282 | 1,177,385 | 1,199,620 | 1,187,760 | 1,247,000 | 1,213,000 | 1,319,000 | 1,321,000 | 1,366,000 |
| Veracruz-México | 847,370 | 937,139 | 965,254 | 1,117,304 | 1,176,253 | 1,144,000 | 1,006,000 | 1,165,000 | 1,187,000 | 1,148,000 |
| Santos-Brasil | 3,569,870 | 3,265,410 | 3,393,593 | 3,578,192 | 3,836,487 | 4,165,000 | 4,232,000 | 4,442,880 | 4,451,000 | 4,284,000 |
| Itajai-Brasil | 971,358 | 963,565 | 926,926 | 999,277 | 1,045,813 | 1,235,000 | 1,273,000 | 1,610,000 | 1,493,000 | 1,268,000 |
| Paranaguá-Brasil | 757,320 | 782,346 | 635,536 | 752,250 | 765,785 | 865,000 | 925,000 | 1,044,000 | 1,114,000 | 1,186,000 |
| Buenos Aires-Argentina | 1,428,843 | 1,433,053 | 1,352,068 | 1,468,960 | 1,797,955 | 1,485,328 | 1,371,980 | 1,446,450 | 1,508,647 | 1,279,000 |
| Montevideo | 776,554 | 811,297 | 951,050 | 939,427 | 797,874 | 750,000 | 765,000 | 978,000 | 1,085,000 | 1,125,000 |
| Lázaro Cárdenas-México | 996,654 | 1,014,047 | 1,115,452 | 1,314,798 | 1,149,079 | 1,319,000 | 1,064,000 | 1,686,000 | 2,027,000 | 1,869,000 |
| Balboa-Panamá | 3,468,283 | 3,294,113 | 2,989,869 | 2,678,005 | 2,862,767 | 2,898,977 | 3,161,658 | 3,563,430 | 3,348,900 | 3,370,000 |
| Buenaventura-Colombia | 855,400 | 911,533 | 865,749 | 920,000 | 1,369,140 | 1,453,000 | 1,018,840 | 1,082,746 | 1,211,000 | 1,061,256 |
| Manzanillo-México | 2,355,150 | 2,541,140 | 2,580,900 | 2,830,370 | 3,078,513 | 3,069,185 | 2,910,000 | 3,371,438 | 3,474,000 | 3,699,000 |
| Callao-Perú | 1,992,473 | 1,900,444 | 2,054,970 | 2,250,224 | 2,340,657 | 2,313,907 | 2,250,827 | 2,486,430 | 2,461,000 | 2,703,000 |
| Guayaquil-Ecuador | 1,621,381 | 1,764,937 | 1,821,654 | 1,871,591 | 2,064,281 | 2,074,000 | 2,071,124 | 2,163,150 | 2,170,000 | 2,254,000 |
| San Antonio-Chile | 1,093,625 | 1,170,184 | 1,287,658 | 1,296,890 | 1,660,832 | 1,709,642 | 1,556,708 | 1,840,460 | 1,683,000 | 1,575,000 |
Appendix B
| Port | Berth (mt) | Draft (mt) | Yard (m2) | Quay Crane | Yard Crane | Reachstacker | Multicranes | TEUs/Day Capacity | Reefer Stations | No. Terminals | Distance to Panamá Canal (kms) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Santa Marta (SMITCO) | 325 | 15 | 87,000 | 2 | 4 | 6 | 0 | 1440 | 1300 | 1 | 790 |
| Barranquilla (BITCO) | 700 | 11 | 120,000 | 0 | 3 | 17 | 2 | 2880 | 181 | 1 | 720 |
| Santa Marta + Barranquilla-Col | 1050 | 14 | 207,000 | 2 | 7 | 23 | 2 | 1500 | 1800 | 2 | 755 |
| Cartagena-Colombia | 1670 | 16 | 580,000 | 19 | 70 | 18 | 0 | 12,000 | 1640 | 2 | 570 |
| Colón-Panamá | 2500 | 15 | 740,000 | 13 | 30 | 17 | 0 | 9360 | 1032 | 1 | 0 |
| Manzanillo-Panamá | 1300 | 14 | 520,000 | 21 | 30 | 70 | 0 | 10,900 | 1500 | 1 | 0 |
| Kinsgton-Jamaica | 2400 | 15 | 800,000 | 18 | 74 | 27 | 6 | 9500 | 172 | 1 | 920 |
| Freeport-Bahamas | 1500 | 16 | 570,000 | 10 | 35 | 0 | 0 | 7200 | 750 | 1 | 2250 |
| San Juan-Puerto Rico | 850 | 13 | 400,000 | 4 | 4 | 15 | 0 | 2500 | 280 | 1 | 1875 |
| Caucedo-Rep, Dominicana | 1000 | 14,5 | 800,000 | 10 | 32 | 11 | 3 | 7500 | 654 | 1 | 1570 |
| Puerto Limón-Moin-Costa Rica | 650 | 14.5 | 400,000 | 6 | 29 | 5 | 0 | 3500 | 3800 | 1 | 470 |
| Veracruz-México | 750 | 15 | 420,000 | 7 | 15 | 18 | 5 | 9500 | 520 | 1 | 2650 |
| Santos-Brasil | 4000 | 14 | 1,400,000 | 47 | 136 | 90 | 10 | 16,800 | 6142 | 5 | 8160 |
| Itajai-Brasil | 900 | 14 | 400,000 | 6 | 18 | 6 | 1 | 12,250 | 2430 | 1 | 8620 |
| Paranaguá-Brasil | 1000 | 13 | 420,000 | 8 | 22 | 2 | 1 | 4500 | 4500 | 1 | 8430 |
| Buenos Aires-Argentina | 4800 | 14 | 650,000 | 22 | 62 | 61 | 5 | 3800 | 2800 | 4 | 9800 |
| Montevideo | 650 | 14 | 350,000 | 7 | 28 | 2 | 0 | 4500 | 2500 | 1 | 9660 |
| Lázaro Cárdenas-México | 1650 | 16 | 760,000 | 14 | 28 | 12 | 0 | 5500 | 650 | 2 | 2890 |
| Balboa-Panamá | 1710 | 15 | 1,000,000 | 25 | 83 | 5 | 0 | 15,500 | 2184 | 2 | 0 |
| Buenaventura-Colombia | 1200 | 14 | 360,000 | 13 | 36 | 8 | 3 | 150,000 | 1320 | 1 | 650 |
| Manzanillo-México | 4650 | 14.5 | 1,140,000 | 34 | 94 | 58 | 4 | 16,300 | 2000 | 4 | 3100 |
| Callao-Perú | 1600 | 15 | 570,000 | 13 | 39 | 22 | 4 | 4500 | 2100 | 2 | 2490 |
| Guayaquil-Ecuador | 1000 | 13 | 140,000 | 6 | 23 | 16 | 3 | 3500 | 250 | 2 | 1450 |
| San Antonio-Chile | 1050 | 15 | 300,000 | 8 | 10 | 31 | 0 | 7500 | 2328 | 2 | 4950 |
References
- Cullinane, K.; Fei, W.T.; Cullinane, S. Container terminal development in mainland China and its impact on the competitiveness of the port of Hong Kong. Transp. Rev. 2004, 24, 33–56. [Google Scholar] [CrossRef]
- Kaliszewski, A.; Kozłowski, A.; Dąbrowski, J.; Klimek, H. Key factors of container port competitiveness: A global shipping lines perspective. Mar. Policy 2020, 117, 103896. [Google Scholar] [CrossRef]
- Campos, R.; Timini, J. Los vínculos comerciales de América Latina y el Caribe ante los riesgos de fragmentación geopolítica global. Boletín Económico/Banco De España 2023, 13, 2–6. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.; Hyodo, T. Assessment of port efficiency within Latin America. J. Shipp. Trade 2022, 7, 4. [Google Scholar] [CrossRef]
- Gervasi, O.; Murgante, B.; Misra, S.; Rocha, A.M.A.C.; Garau, C. (Eds.) Computational Science and Its Applications—ICCSA 2022 Workshops. In Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2022; Volume 13381. [Google Scholar] [CrossRef]
- Yannis, G.; Kopsacheili, A.; Dragomanovits, A.; Petraki, V. State-of-the-art review on multi-criteria decision-making in the transport sector. J. Traffic Transp. Eng. (Engl. Ed.) 2020, 7, 413–431. [Google Scholar] [CrossRef]
- Vega, L.; Cantillo, V.; Arellana, J. Assessing the impact of major infrastructure projects on port choice decision: The Colombian case. Transp. Res. Part A Policy Pract. 2019, 120, 132–148. [Google Scholar] [CrossRef]
- Chang, Y.-T.; Talley, W.K. Port Competitiveness, Efficiency, and Supply Chains: A Literature Review. Transp. J. 2019, 58, 1–20. [Google Scholar] [CrossRef]
- Ližbetin, J.; Stopka, O. Application of specific mathematical methods in the context of revitalization of defunct intermodal transport terminal: A case study. Sustainability 2020, 12, 2295. [Google Scholar] [CrossRef]
- Kudlac, S.; Gasparik, J.; Dedik, M.; Kurenkov, P.V. Identification of Restricting Criteria for Comprehensive Assessment of Logistics Chains in Intermodal Transport. LOGI—Sci. J. Transp. Logist. 2018, 9, 18–27. [Google Scholar] [CrossRef]
- Čarný, Š.; Šperka, A.; Zitrický, V. Multi-criteria evaluation of railway transport using evaluation method. LOGI—Sci. J. Transp. Logist. 2020, 11, 88–99. [Google Scholar] [CrossRef]
- Golnar, M.; Beškovnik, B. A Multi-Criteria Approach for Evaluating a Sustainable Intermodal Transport Chain Affected by the COVID-19 Pandemic. J. Mar. Sci. Eng. 2022, 10, 1644. [Google Scholar] [CrossRef]
- Barysienė, J. A Multi-criteria evaluation of container terminal technologies applying the COPRAS-G method. Transport 2012, 27, 364–372. [Google Scholar] [CrossRef]
- Luo, M.; Chen, F.; Zhang, J. Relationships among port competition, cooperation and competitiveness: A literature review. Transp. Policy 2022, 118, 1–9. [Google Scholar] [CrossRef]
- Parola, F.; Risitano, M.; Ferretti, M.; Panetti, E. The drivers of port competitiveness: A critical review. Transp. Rev. 2017, 37, 116–138. [Google Scholar] [CrossRef]
- Serebrisky, T.; Sarriera, J.M.; Suárez-Alemán, A.; Araya, G.; Briceño-Garmendía, C.; Schwartz, J. Exploring the drivers of port efficiency in Latin America and the Caribbean. Transp. Policy 2016, 45, 31–45. [Google Scholar] [CrossRef]
- Ilyas, M.; Jin, Z.; Ullah, I. Optimizing Logistics and Transportation Locations in the China–Pakistan Economic Corridor: A Strategic Risk Assessment. Appl. Sci. 2024, 14, 1738. [Google Scholar] [CrossRef]
- da Costa, D.S.; Carvalho, M.V.G.S.d.A.; de Figueiredo, N.M.; de Moraes, H.B.; Ferreira, R.C.B. The efficiency of container terminals in the northern region of Brazil. Util. Policy 2021, 72, 101278. [Google Scholar] [CrossRef]
- Lirn, T.C.; A Thanopoulou, H.; Beynon, M.J.; Beresford, A.K.C. An application of AHP on transhipment port selection: A global perspective. Marit. Econ. Logist. 2004, 6, 70–91. [Google Scholar] [CrossRef]
- Ghazinoory, S.; Mansour, S.; Sadeghian, A. A hybrid Fuzzy AHP-TOPSIS approach for assessing the sustainability of industrial parks. Environ. Model. Softw. 2009, 24, 730–735. [Google Scholar] [CrossRef]
- Wang, T.-C.; Lee, H.-D. Developing a fuzzy TOPSIS approach based on subjective weights and objective weights. Expert Syst. Appl. 2009, 36, 8980–8985. [Google Scholar] [CrossRef]
- Cullinane, K.P.; Wang, T.F. The efficiency of European container ports: A cross-sectional data envelopment analysis. Int. J. Logist. Res. Appl. 2006, 9, 19–31. [Google Scholar] [CrossRef]
- Kabak, M.; Burmaoglu, S.; Kazancoglu, Y. A fuzzy hybrid MCDM approach for professional selection. Expert Syst. Appl. 2012, 39, 3516–3525. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 498–520. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Król, R.; Więckowski, J.; Wątróbski, J. Accuracy of the TOPSIS Method with Different Input Data. Procedia Comput. Sci. 2022, 207, 4574–4583. [Google Scholar] [CrossRef]
- Kim, A.R. A Study on Competitiveness Analysis of Ports in Korea and China by Entropy Weight TOPSIS. Asian J. Shipp. Logist. 2016, 32, 187–194. [Google Scholar] [CrossRef]
- Sayareh, J.; Iranshahi, S.; Golfakhrabadi, N. Service Quality Evaluation and Ranking of Container terminal Operators. Asian J. Shipp. Logist. 2016, 32, 203–212. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, Z.; Xu, C.; Cai, G.; Zhan, J. Assessment of provincial waterlogging risk based on entropy weight TOPSIS–PCA method. Nat. Hazards 2021, 108, 1545–1567. [Google Scholar] [CrossRef]
- Sonawane, S.A.; Wangikar, S.S. Multi-superiority response optimization of WEDM for titanium grade-5 using PCA based TOPSIS theory. Mater. Today Proc. 2022, 62, 841–847. [Google Scholar] [CrossRef]
- Li, Y.; Wu, L.; Han, Q.; Wang, X.; Zou, T.; Fan, C. Estimation of remote sensing based ecological index along the Grand Canal based on PCA-AHP-TOPSIS methodology. Ecol. Indic. 2021, 122, 107214. [Google Scholar] [CrossRef]
- Wang, Y.; Yeo, G.-T.; Ng, A.K. Choosing optimal bunkering ports for liner shipping companies: A hybrid Fuzzy-Delphi–TOPSIS approach. Transp. Policy 2014, 35, 358–365. [Google Scholar] [CrossRef]
- Chakraborty, S. TOPSIS and Modified TOPSIS: A comparative analysis. Decis. Anal. J. 2022, 2, 100021. [Google Scholar] [CrossRef]
- Wang, T.; Wang, D.; Zeng, Z. Research on the Construction and Measurement of Digital Governance Level System of County Rural Areas in China—Empirical Analysis Based on Entropy Weight TOPSIS Model. Sustainability 2024, 16, 4374. [Google Scholar] [CrossRef]
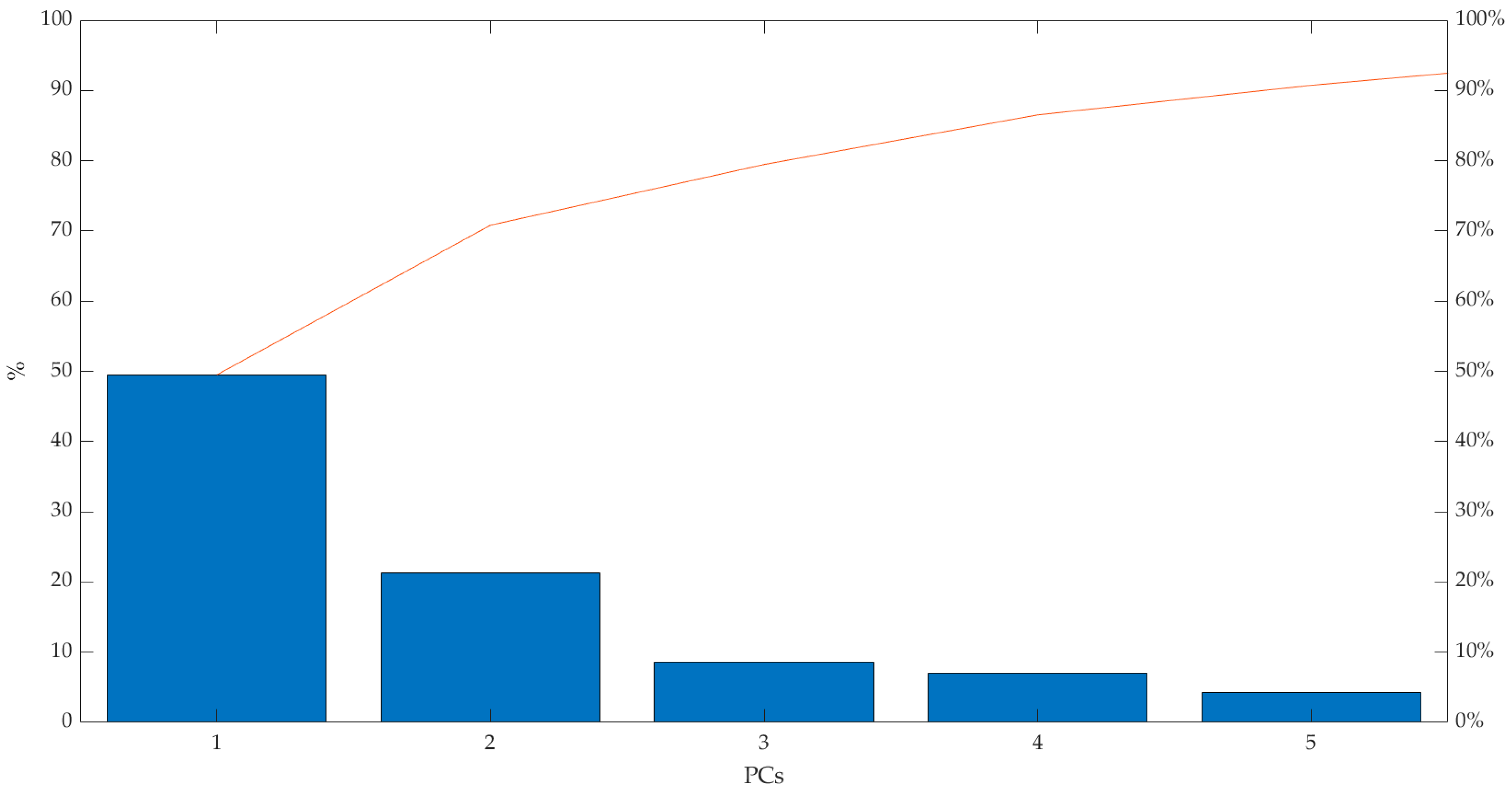
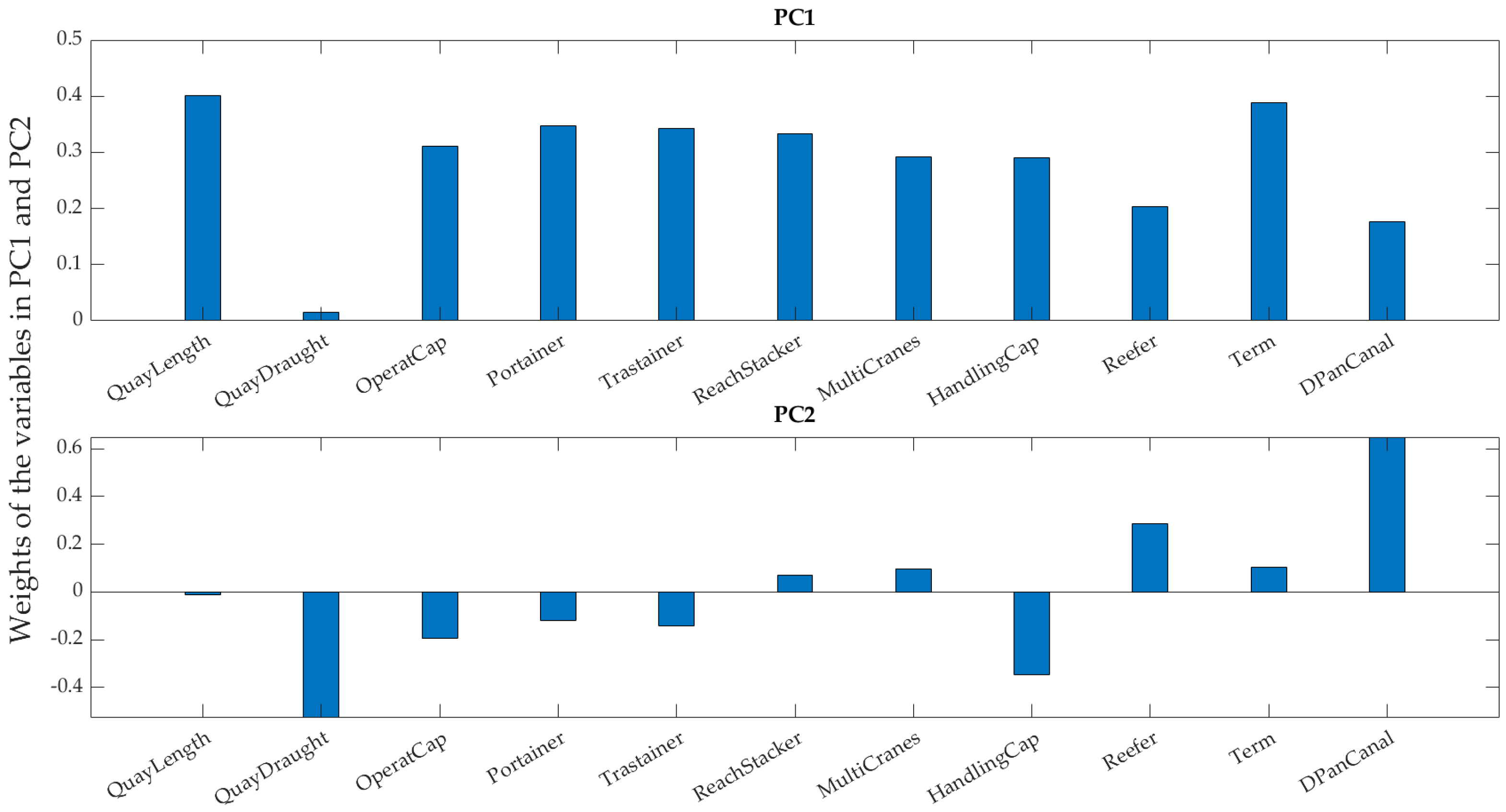

| LAC Studied Ports | World * | Europe Union | China | LAC Entire Port System | USA |
|---|---|---|---|---|---|
| 46,572,664 | 840,635,534 | 102,751,696 | 262,605,700 | 58,669,478 | 60,554,285 |
| 5.13% | 41.9% | 16.41% | 71.3% |
| Year | Geographical Zone | Methodology | Criteria | Review’s Papers |
|---|---|---|---|---|
| 1990–2000 | North American, Asia | Surveys, Univariate and multivariate analysis | Number of sailings, Freight rates, User satisfaction, Loading and unloading Facilities, Equipment available, Port congestion, Special handling ability | [14] |
| 2001–2010 | Asia, Europe | Discrete Choice Model-DCM, Analytic Hierarchy Process-AHP, Gray Decision Model-GDM, Surveys and ranking of importance, Binary Logistic Regression-BLR | Port location, Port characteristics, Number of berths, Travel time, Maritime costs, Reability, Port charges and port services, Number of routes and frequency, Hinterland and quality of connection, Feeder connection | [6,14] |
| 2011–2020 | Asia, Europe, South America | Discrete Choice Model-DCM, Analytic Hierarchy Process-AHP, Data Envelopment Analysis-DEA, Electre III, Promethee Stochastic Frontier Analysis–SFA, COPRAS–model | Port location, Port characteristics, Number of berths, Cranes, productivity, Cargo handling costs, Maritime costs, Port charges and port services, Number of routes and frequency, Hinterland and Foreland and quality of connection, Connection among ports, Maritime transit time, Proximity to import/export areas, Channel access depth, Freights | [14,15,16] |
| 2021–2024 | Asia, Europa | Discrete Choice Model, Data Envelopment Analysis-DEA, Principal Component Analysis-PCA, Clustering | Port location, Number of berths, Yard, Quay Cranes, Throughput (TEUS)/(Tons) | [5,6] |
| Ranking | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
|---|---|---|---|---|---|---|
| 1 | Colón | Colón | Colón | Colón | Colón | Colón |
| 2 | Santos | Santos | Santos | Santos | Santos | Santos |
| 3 | Manz-Mex | Manz-Mex | Balboa | Balboa | Manz-Mex | Manz-Mex |
| 4 | Balboa | Cartagena | Cartagena | Manz-Mex | Balboa | Balboa |
| 5 | Cartagena | Balboa | Manz-Mex | Cartagena | Cartagena | Cartagena |
| Ranking LAC | TOPSIS (No Throughput Considered) |
|---|---|
| 1 | Santos-Brasil |
| 2 | Manzanillo-México |
| 3 | Buenos Aires-Argentina |
| 4 | Kingston-Jamaica |
| 5 | Balboa-Panamá |
| 6 | Cartagena-Colombia |
| 7 | Manzanillo-Panamá |
| 8 | Callao-Perú |
| 9 | Buenaventura-Colombia |
| 10 | Colón-Panamá |
| 11 | Veracruz-México |
| 12 | Lázaro Cárdenas-México |
| 13 | Caucedo-Rep. Dominicana |
| 14 | Itajai-Brasil |
| 15 | San Antonio-Chile |
| 16 | Freeport-Bahamas |
| 17 | Paranaguá-Brasil |
| 18 | Montevideo-Uruguay |
| 19 | Guayaquil-Ecuador |
| 20 | Santa Marta + Barranquilla-Col |
| 21 | Puerto Limón-Moin Costa Rica |
| 22 | San Juan-Puerto Rico |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pabón-Noguera, A.; Carrasco-García, M.G.; Ruíz-Aguilar, J.J.; Rodríguez-García, M.I.; Cerbán-Jimenez, M.; Domínguez, I.J.T. Multicriteria Decision Model for Port Evaluation and Ranking: An Analysis of Container Terminals in Latin America and the Caribbean Using PCA-TOPSIS Methodologies. Appl. Sci. 2024, 14, 6174. https://doi.org/10.3390/app14146174
Pabón-Noguera A, Carrasco-García MG, Ruíz-Aguilar JJ, Rodríguez-García MI, Cerbán-Jimenez M, Domínguez IJT. Multicriteria Decision Model for Port Evaluation and Ranking: An Analysis of Container Terminals in Latin America and the Caribbean Using PCA-TOPSIS Methodologies. Applied Sciences. 2024; 14(14):6174. https://doi.org/10.3390/app14146174
Chicago/Turabian StylePabón-Noguera, Adriana, María Gema Carrasco-García, Juan Jesús Ruíz-Aguilar, María Inmaculada Rodríguez-García, María Cerbán-Jimenez, and Ignacio José Turias Domínguez. 2024. "Multicriteria Decision Model for Port Evaluation and Ranking: An Analysis of Container Terminals in Latin America and the Caribbean Using PCA-TOPSIS Methodologies" Applied Sciences 14, no. 14: 6174. https://doi.org/10.3390/app14146174
APA StylePabón-Noguera, A., Carrasco-García, M. G., Ruíz-Aguilar, J. J., Rodríguez-García, M. I., Cerbán-Jimenez, M., & Domínguez, I. J. T. (2024). Multicriteria Decision Model for Port Evaluation and Ranking: An Analysis of Container Terminals in Latin America and the Caribbean Using PCA-TOPSIS Methodologies. Applied Sciences, 14(14), 6174. https://doi.org/10.3390/app14146174







