Effect of the Inter-Ring Delay Time on Rock Fragmentation: Field Tests at the Underground Mine
Abstract
1. Introduction
2. Mine Condition
3. Theoretical Analysis of IRDT in Tunnel Excavation Blasting
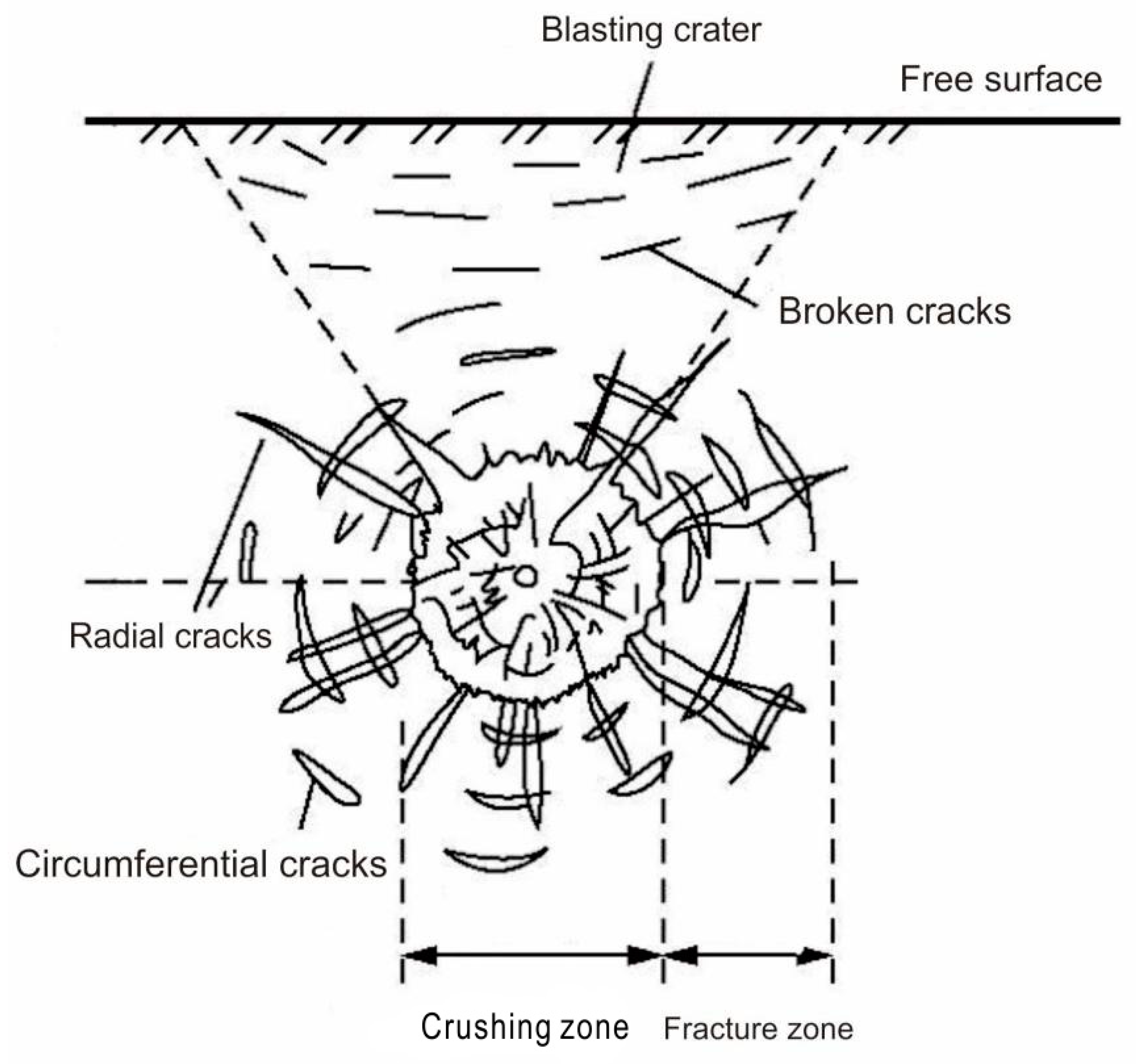
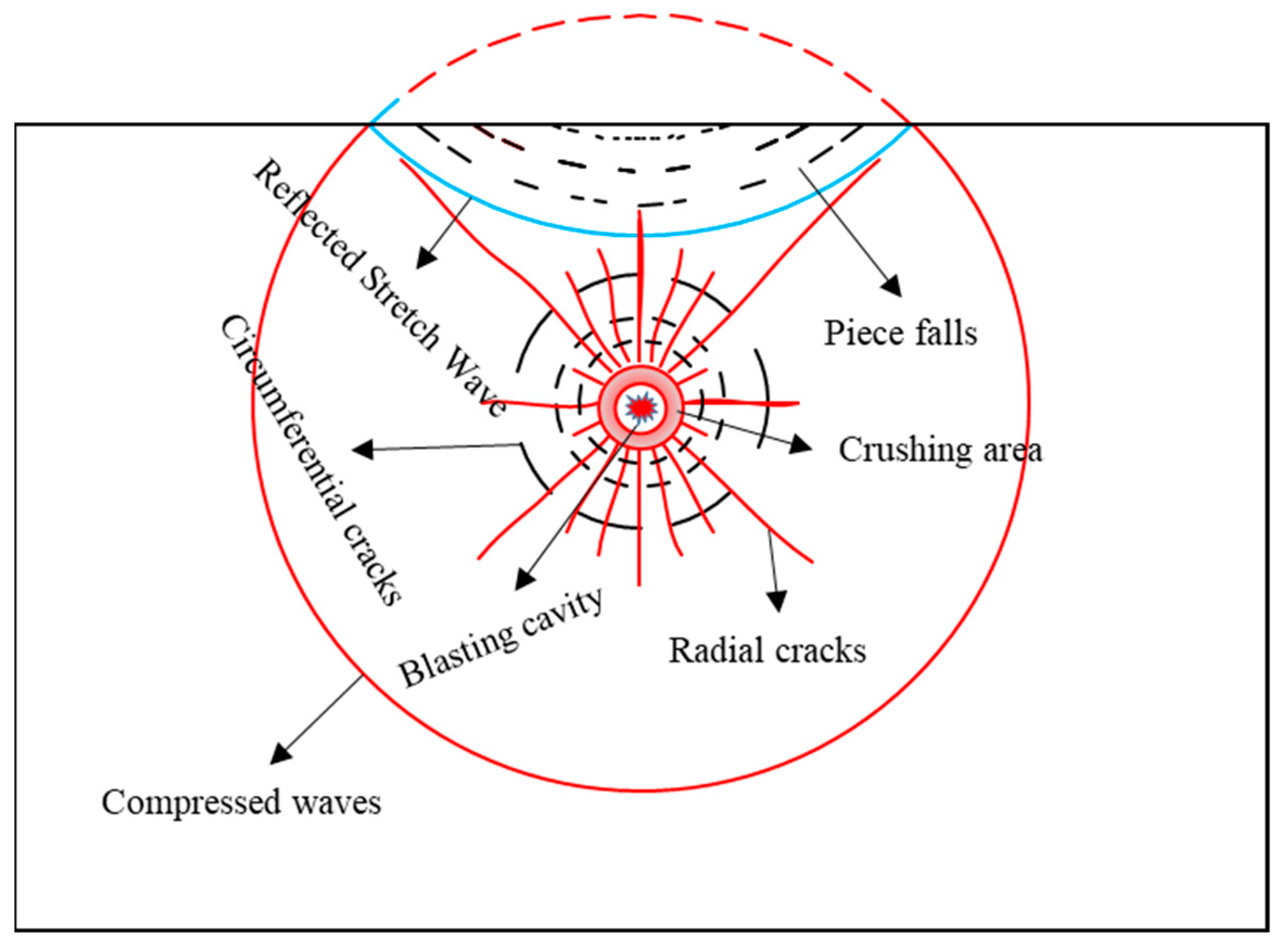
3.1. Energy of Rock Fragmentation in Tunnel Excavation Blasting
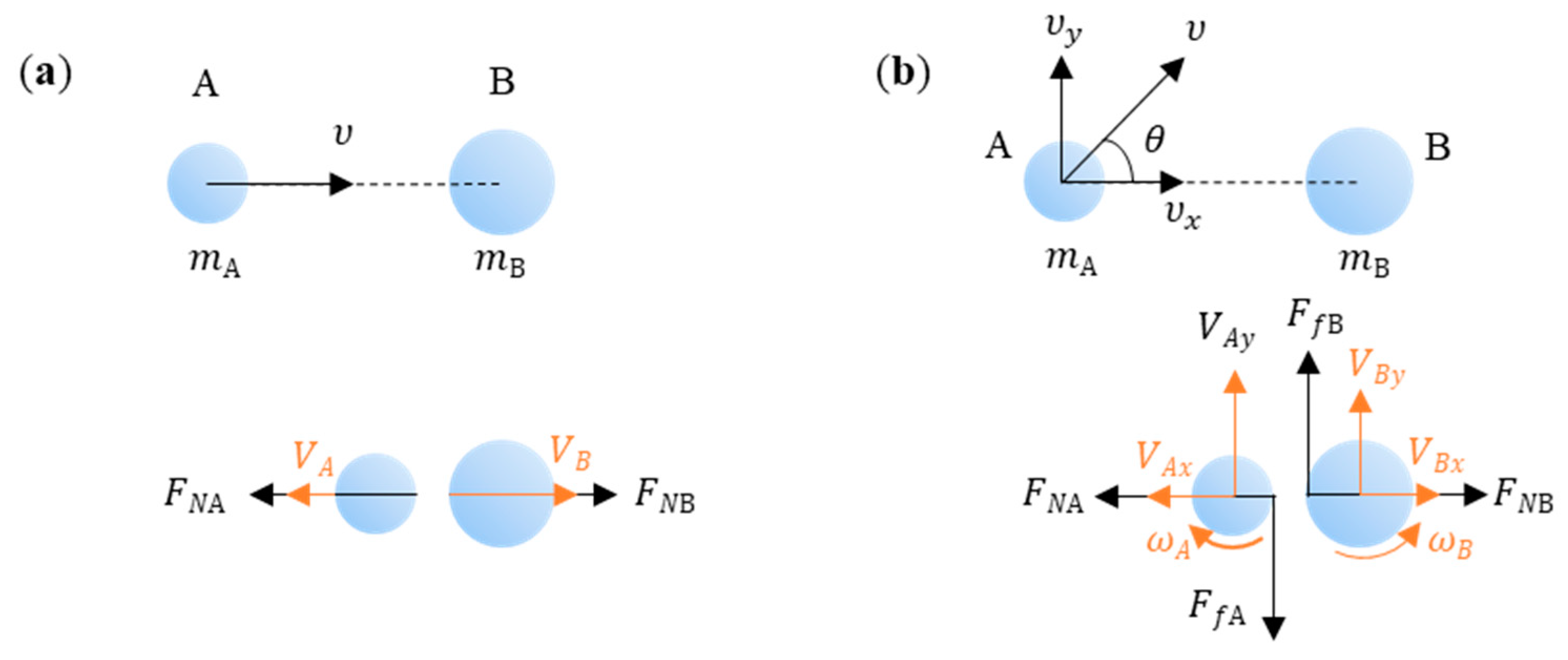
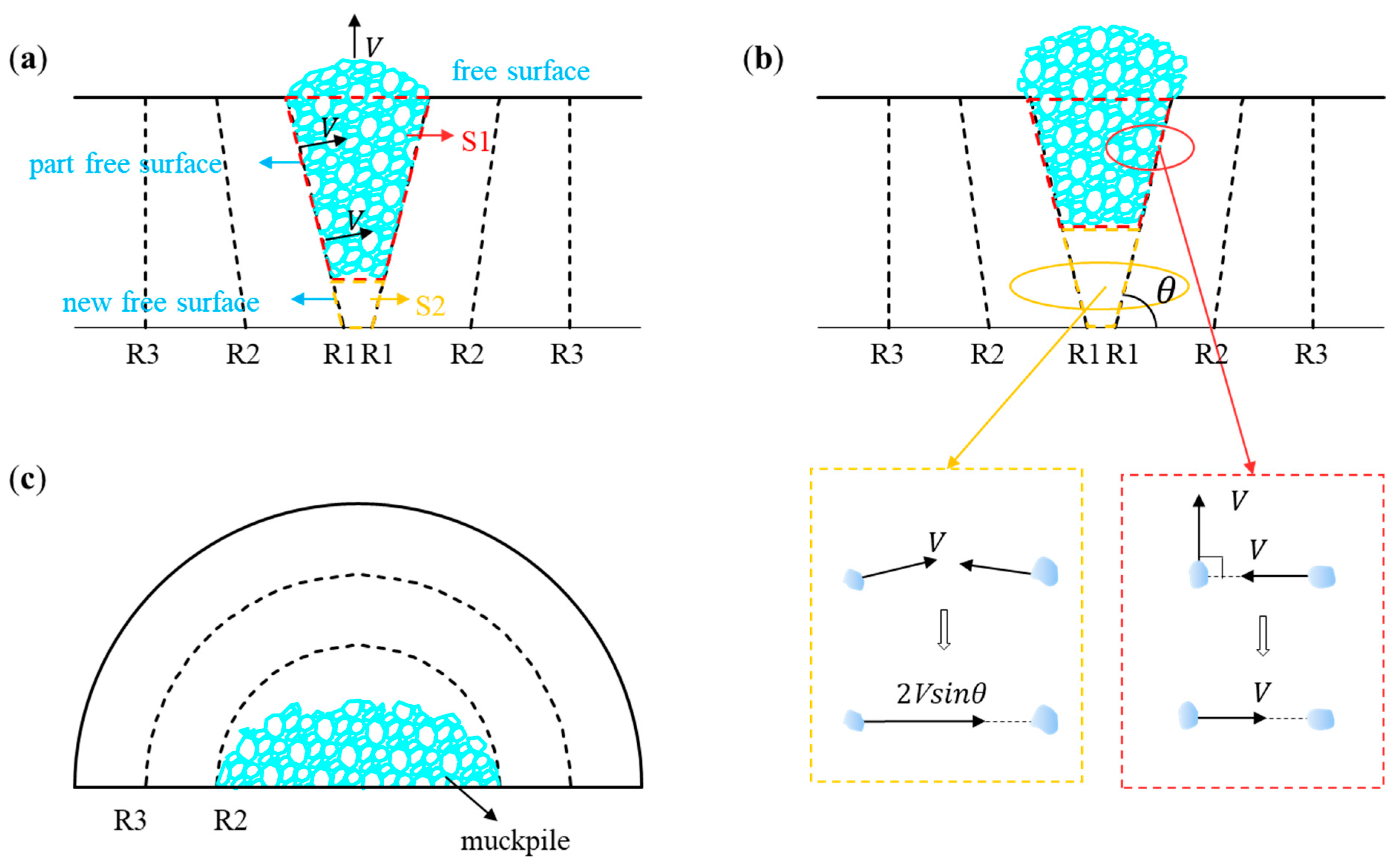
3.2. Energy Conversion in Collisions
3.3. Explosive Load and Rock Interaction Processes
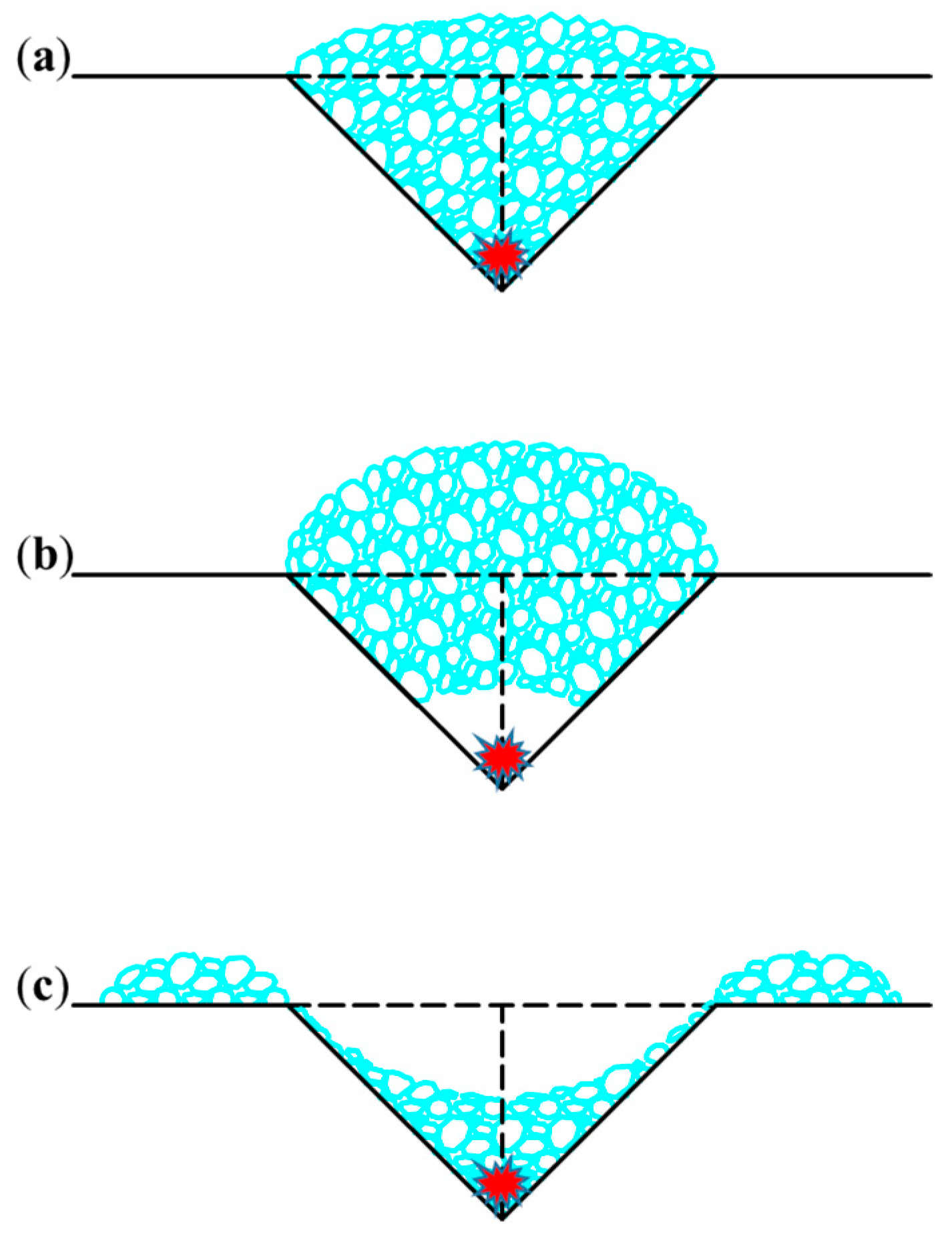
3.4. Collision of Fragment
4. Field Blasting Tests
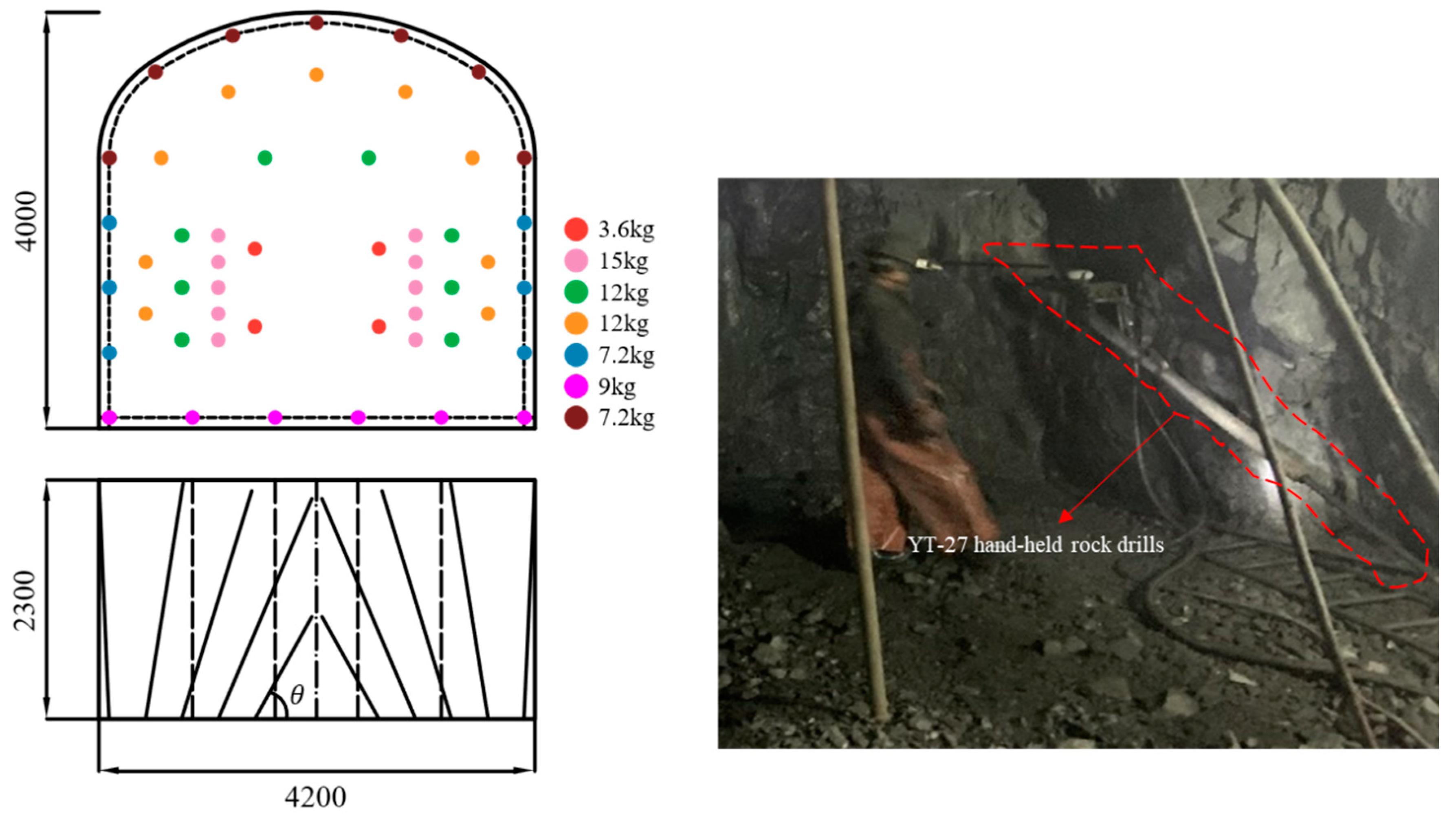
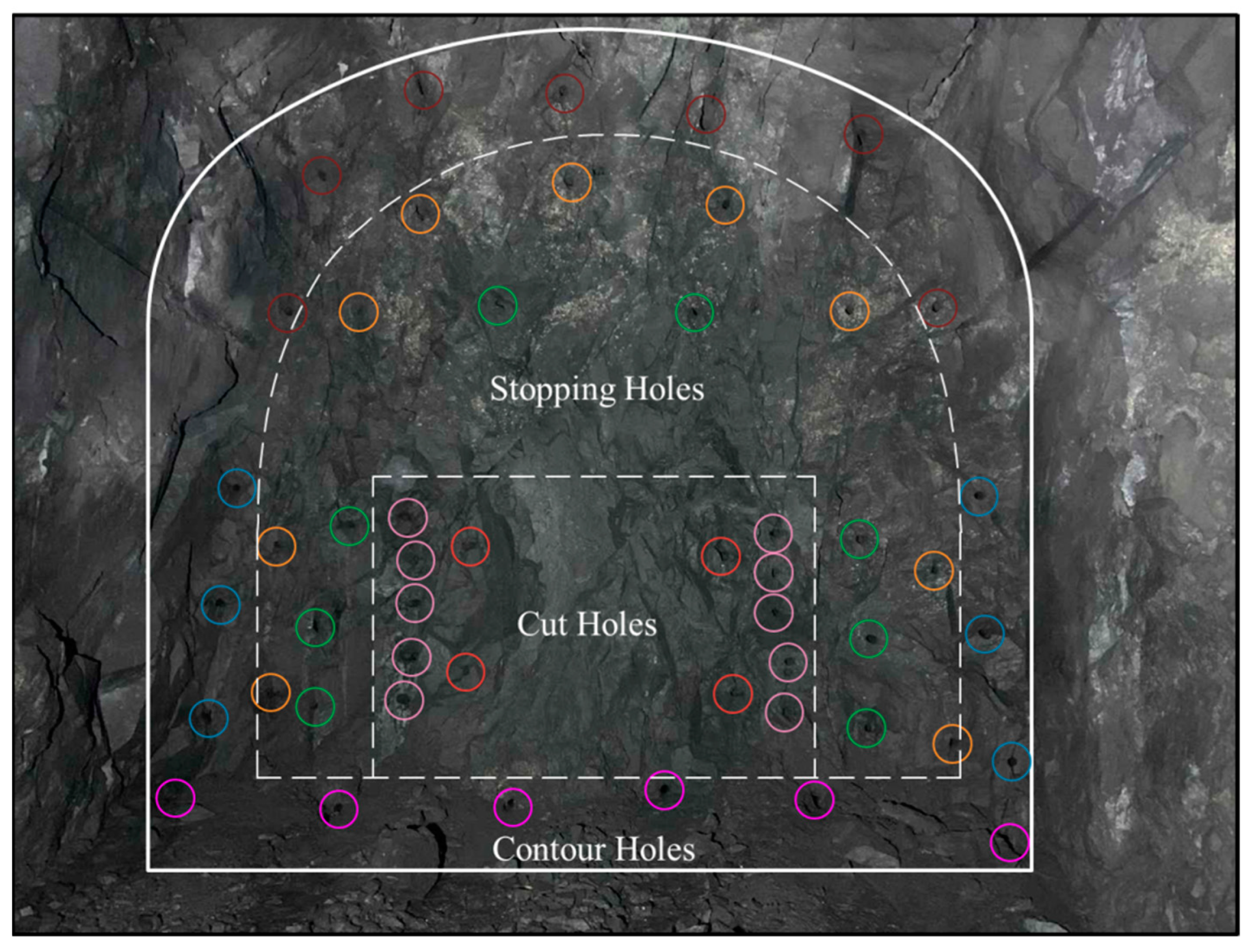
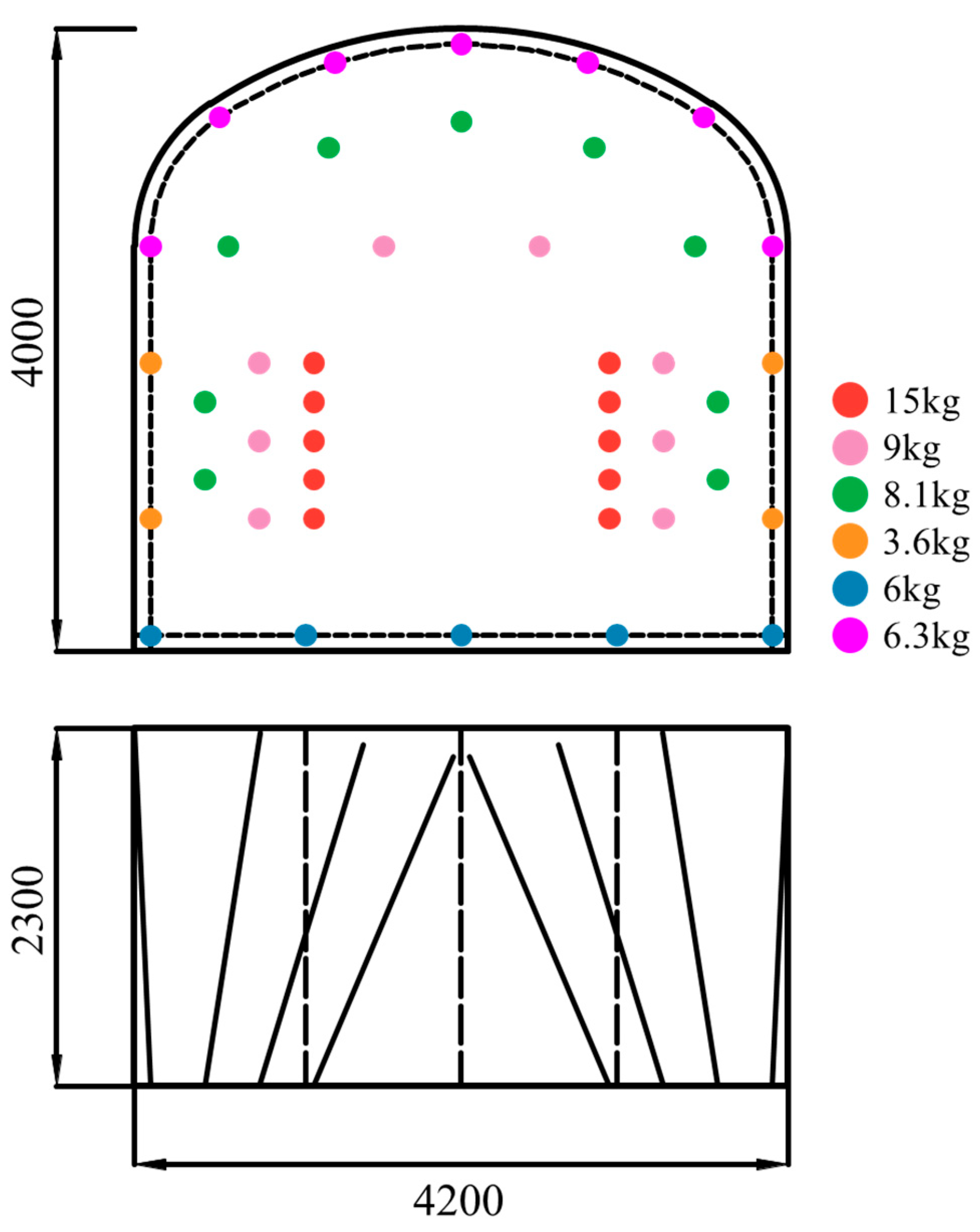
4.1. Test Blast Design
4.1.1. IRDT Blasting Tests
4.1.2. Tunnel Excavation Blasting Optimization
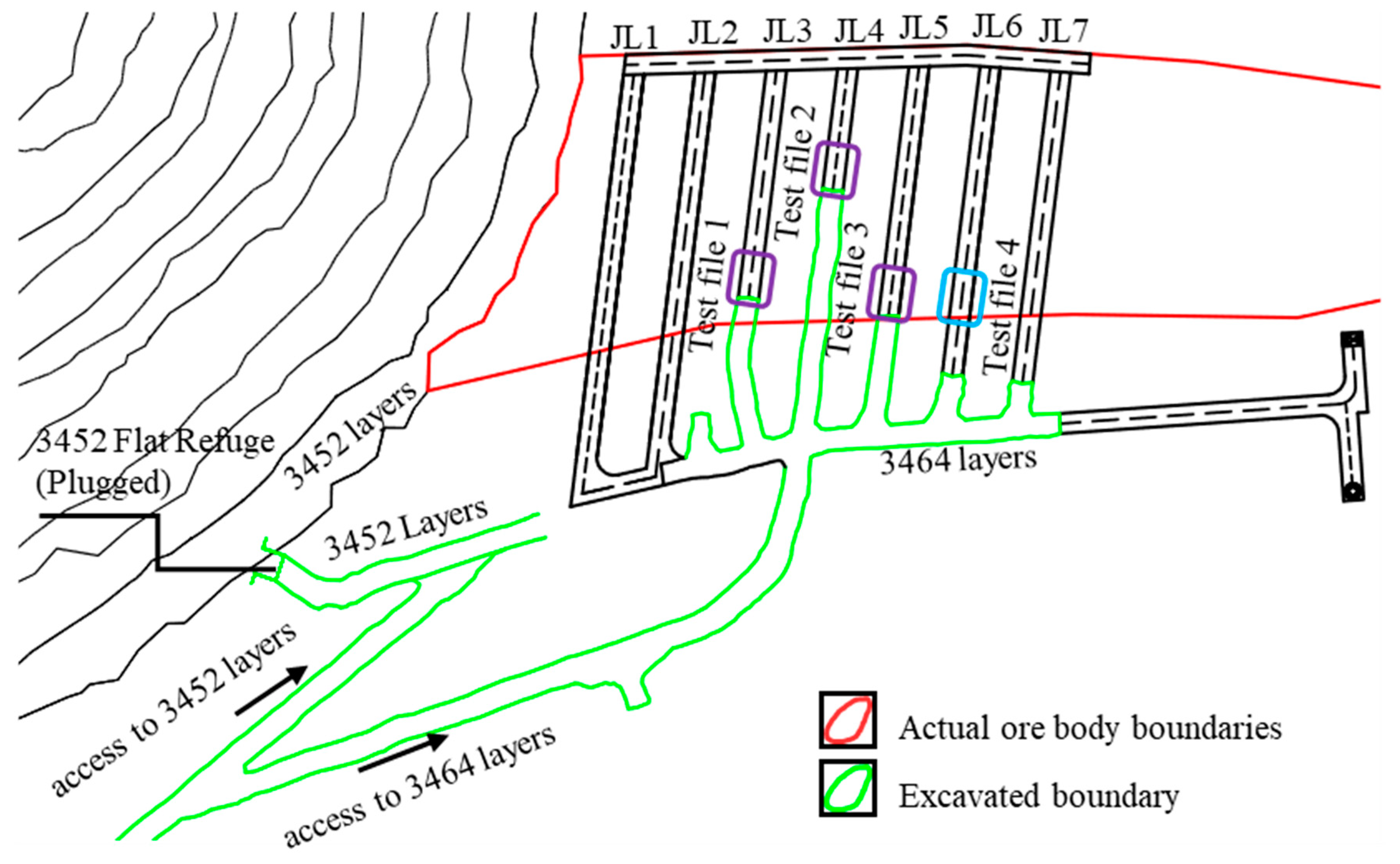
4.2. Test Fields
4.3. Assessment Method of Rock Fragments
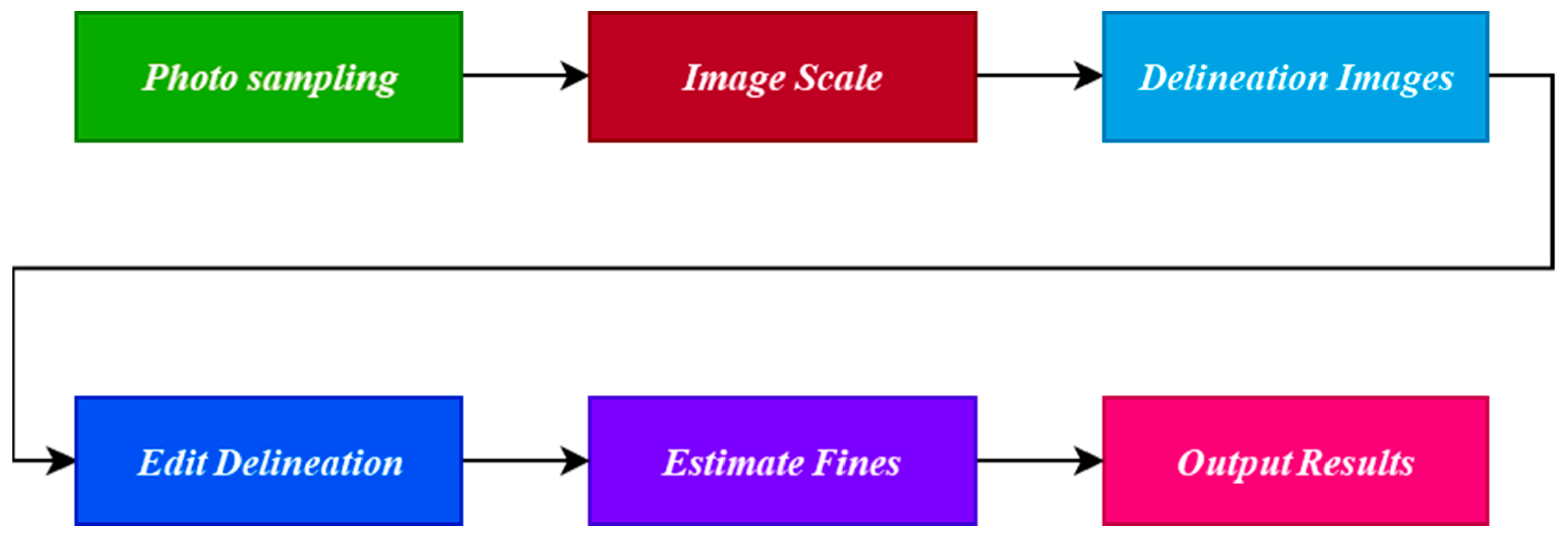
4.3.1. Photo Sampling
4.3.2. Image Scale, Delineation Images, Edit Delineation, Estimate Fines
4.3.3. Output Results
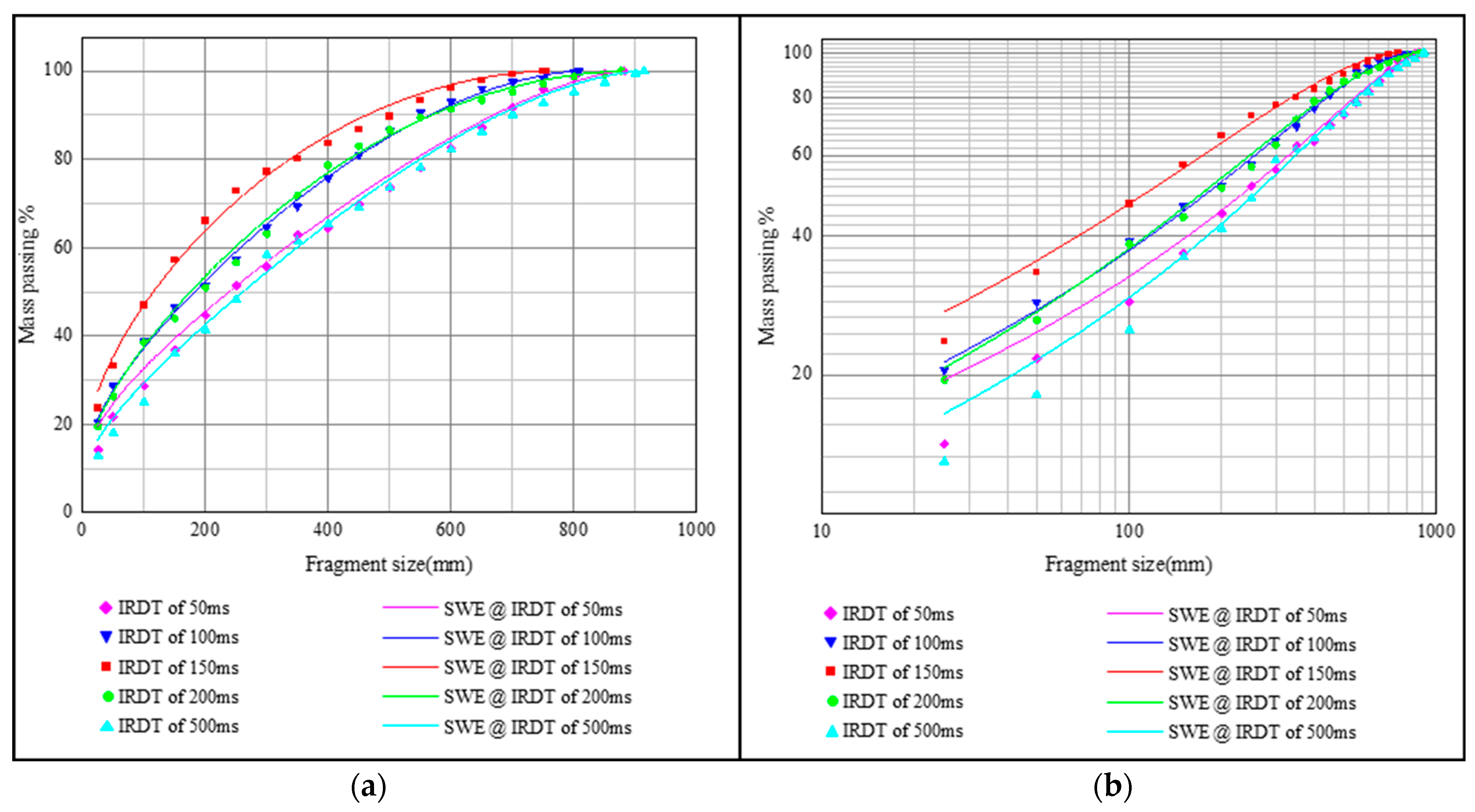
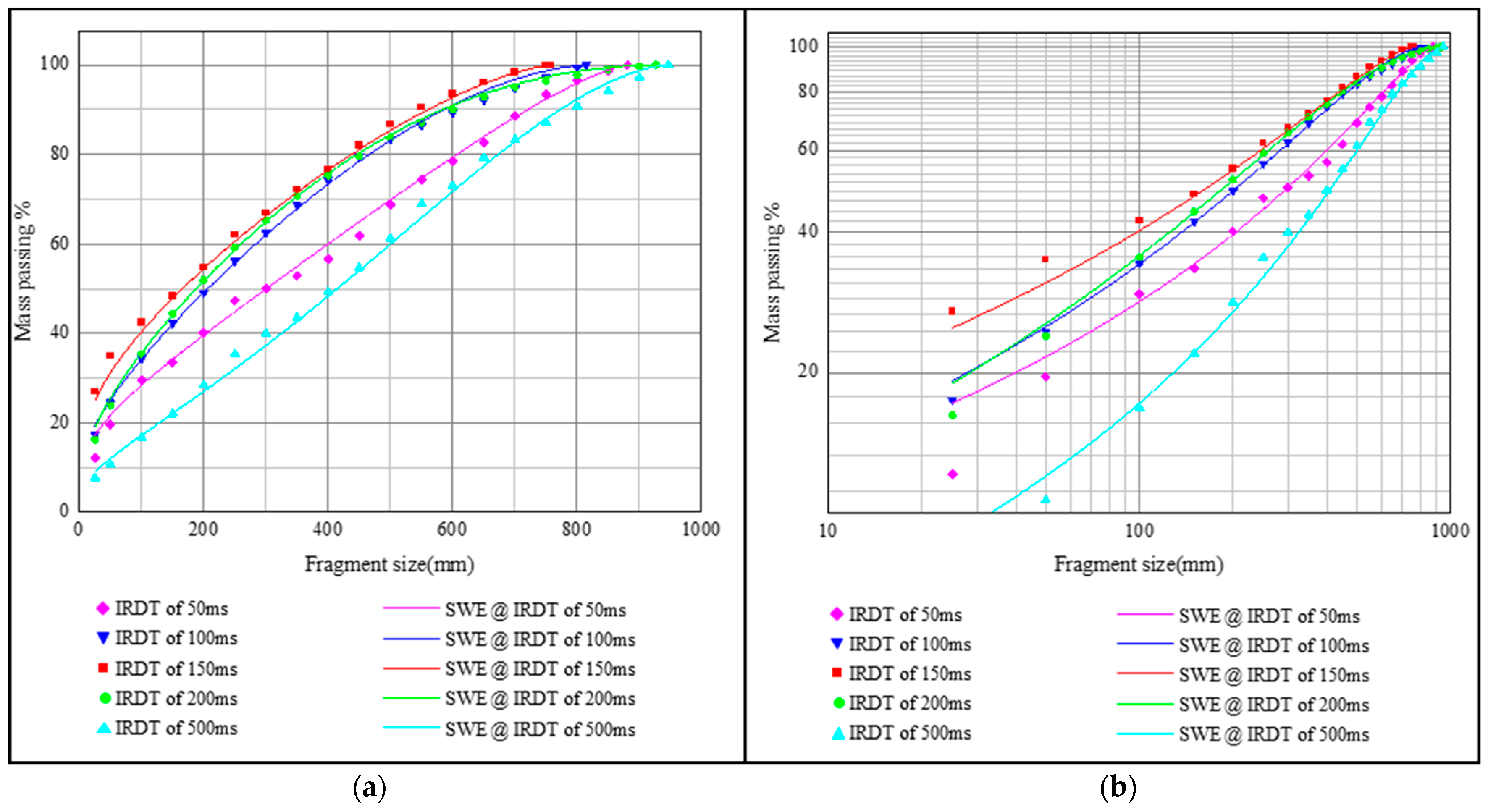
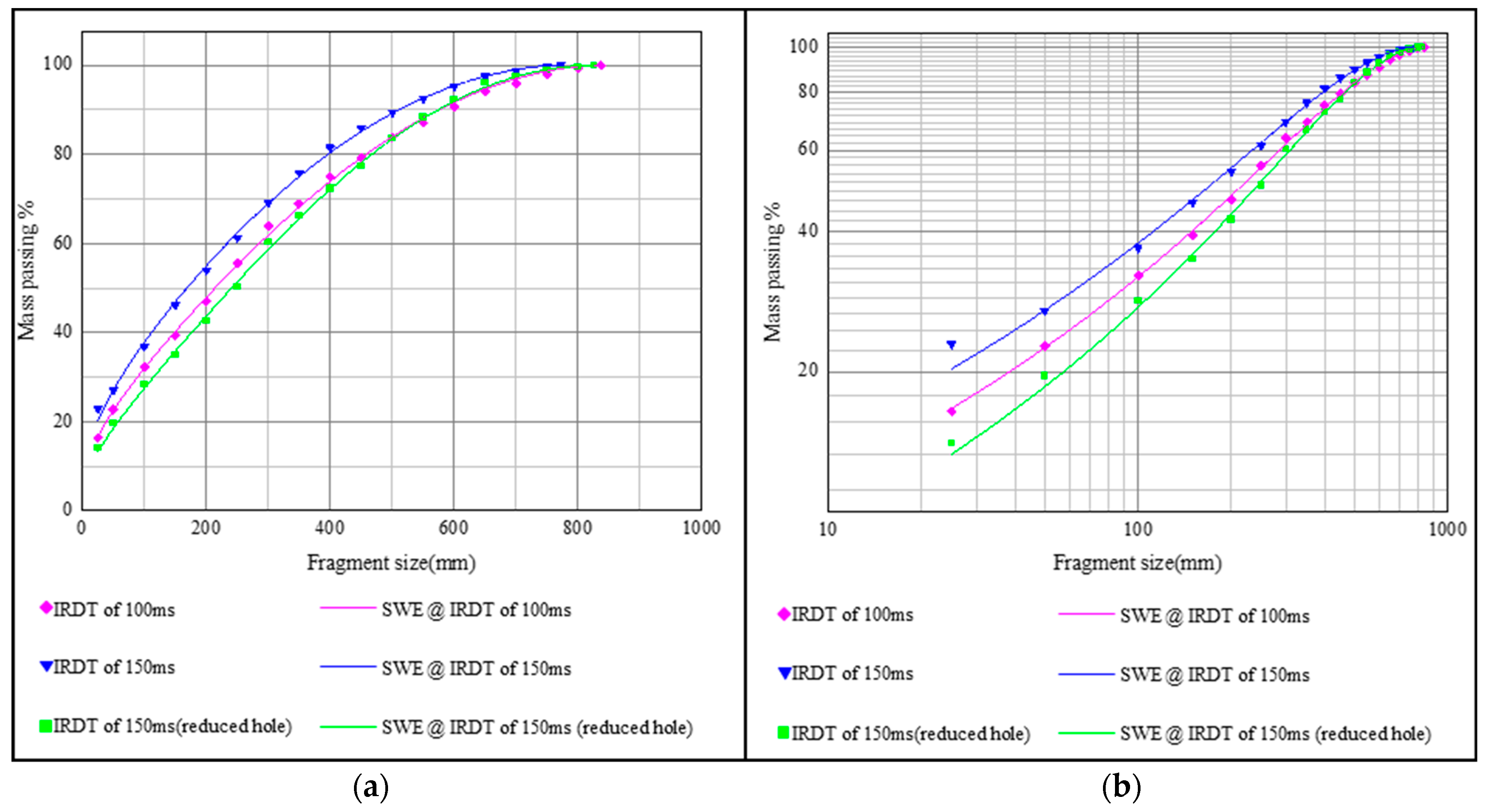
5. Results
6. Discussion
7. Conclusions
- IRDT blasting tests
- For blasting tests with IRDTs of 50, 100, 150, 200, and 500 ms, the content of the percentage of small fragments P25 and the fragment sizes X20, X50, X80, and Xmax first increased and then decreased, while the percentage of large fragments (1-P750) decreased first and then increased.
- Among the test plans, the delay timing of 150 ms resulted in the lowest percentage of large fragments (1-P750) and the highest percentage of small fragments (P25 mm), indicating better rock fragmentation.
- Optimized blasting tests
- Compared with the control test (original blasting plan), optimized plan 1 achieved better rock fragmentation without changing the blasting cost. For example, the fragment sizes X20, X50, and X80, and the percentage of large fragments (1-P750) reduced by 37.37%, 21.21%, 13.45%, and 90.37%, respectively, and the percentage of small fragments P25 increased by 21.63%.
- Furthermore, optimized plan 2 achieved a cost reduction while maintaining the degree of rock fragmentation, with the use of digital electronic detonators and explosives reduced by 14.0% and 27.27%, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sanchidrian, J.A.; Ouchterlony, F.; Segarra, P.; Moser, P. Size Distribution Functions for Rock Fragments. Int. J. Rock Mech. Min. Sci. 2014, 71, 381–394. [Google Scholar] [CrossRef]
- Sharma, A.; Mishra, A.K.; Choudhary, B.S.; Meena, R. Impact of Blast Design Parameters on Rock Fragmentation in Building Stone Quarries. Curr. Sci. 2019, 116, 1861–1867. [Google Scholar] [CrossRef]
- Zhang, Z.-X. Rock Fracture and Blasting: Theory and Applications; Butterworth-Heinemann: Oxford, UK, 2016. [Google Scholar]
- Zhang, Z.-X.; Sanchidrian, J.A.; Ouchterlony, F.; Luukkanen, S. Reduction of Fragment Size from Mining to Mineral Processing: A Review. Rock Mech. Rock Eng. 2023, 56, 747–778. [Google Scholar] [CrossRef]
- Cardu, M.; Seccatore, J.; Vaudagna, A.; Rezende, A.; Galvão, F.; Bettencourt, J.; de Tomi, G. Evidences of the Influence of the Detonation Sequence in Rock Fragmentation by Blasting—Part II. Rem Rev. Esc. Minas 2015, 68, 455–462. [Google Scholar] [CrossRef]
- Rossmanith, H.P. The Use of Lagrange Diagrams in Precise Initiation Blasting. Part I: Two Interacting Blastholes. Fragblast 2002, 6, 104–136. [Google Scholar] [CrossRef]
- Rossmanith, H.P.; Kouzniak, N. Supersonic Detonation in Rock Mass-Part 2: Particle Displacements and Velocity Fields for Single and Multiple Non-Delayed and Delayed Detonating Blastholes. Fragblast 2004, 8, 95–117. [Google Scholar] [CrossRef]
- Vanbrabant, F.; Espinosa, A. Impact of Short Delays Sequence on Fragmentation by Means of Electronic Detonators: Theoretical Concepts and Field Validation. Fragblast 2006, 8, 326–331. [Google Scholar]
- Cho, S.H.; Kaneko, K. Rock Fragmentation Control in Blasting. Mater. Trans. 2004, 45, 1722–1730. [Google Scholar] [CrossRef]
- Sjöberg, J.; Schill, M.; Hilding, D.; Yi, C.-P.; Nyberg, U.; Johansson, D. Computer Simulations of Blasting with Precise Initiation. In Proceedings of the ISRM International Symposium-EUROCK 2012, Stockholm, Sweden, 28–30 May 2012; OnePetro: Richardson, TX, USA, 2012. [Google Scholar]
- Yi, C.-P.; Johansson, D.; Nyberg, U.; Beyglou, A. Stress Wave Interaction Between Two Adjacent Blast Holes. Rock Mech. Rock Eng. 2016, 49, 1803–1812. [Google Scholar] [CrossRef]
- Yi, C.-P.; Sjöberg, J.; Johansson, D.; Petropoulos, N. A Numerical Study of the Impact of Short Delays on Rock Fragmentation. Int. J. Rock Mech. Min. Sci. 2017, 100, 250–254. [Google Scholar] [CrossRef]
- Johansson, D.; Ouchterlony, F. Shock Wave Interactions in Rock Blasting: The Use of Short Delays to Improve Fragmentation in Model-Scale. Rock Mech. Rock Eng. 2013, 46, 1–18. [Google Scholar] [CrossRef]
- Shi, X.-Z.; Qiu, X.-Y.; Zhou, J.; Wang, Y.; Nie, J.; Li, B.-H. Technology and Case Study of Ultra-Large Section and High Shaft Excavation by Short-Millisecond Spherical-like Blasting. Chin. J. Rock Mech. Eng. 2016, 35, 1659–1667. [Google Scholar]
- Gao, X.T. A Review of the Study on Energy Distribution of Explosives in Rock Fragmentation and Prospects. Constr. Eng. 2009, 41, 1–6+10. [Google Scholar] [CrossRef]
- Yan, S.L.; Chen, Y.Q. Calculation of Energy Distribution from Concentrated Explosive Charges in Rock. Blasting Equip. 1993, 1–5. [Google Scholar]
- Carroll, M.M. Mechanics of Geological Materials. Appl. Mech. Rev. 1985, 38, 1256. [Google Scholar] [CrossRef]
- Revnivtsev, V.I. We Really Need Revolution in Comminution. In Proceedings of the XVI International Mineral Processing Congress, Delhi, India, 24–28 September 2012; Elsevier Science Publishers: Amsterdam, The Netherlands, 1988; pp. 93–114. [Google Scholar]
- Stronge, W.J. Impact Mechanics; Cambridge University Press: Cambridge, UK, 2000; pp. 26–29. [Google Scholar]
- Henrych, J.; Abrahamson, G.R. The Dynamics of Explosion and Its Use. J. Appl. Mech. 1980, 47, 218. [Google Scholar] [CrossRef]
- Bamford, T.; Esmaeili, K.; Schoellig, A.P. A Deep Learning Approach for Rock Fragmentation Analysis. Int. J. Rock Mech. Min. Sci. 2021, 145, 104839. [Google Scholar] [CrossRef]
- Ylitalo, R.M. Effect of Detonator Position on Rock Fragmentation: Full-Scale Field Tests at Kevitsa Open Pit Mine. Int. J. Rock Mech. Min. Sci. 2021, 147, 104918. [Google Scholar] [CrossRef]
- Ouchterlony, F.; Sanchidrián, J.A. A Review of Development of Better Prediction Equations for Blast Fragmentation. J. Rock Mech. Geotech. Eng. 2019, 11, 1094–1109. [Google Scholar] [CrossRef]
- Ouchterlony, F. The Swebrec© Function: Linking Fragmentation by Blasting and Crushing. Min. Technol. 2005, 114, 29–44. [Google Scholar] [CrossRef]
- Zhang, Z.-X.; Hou, D.-F.; Guo, Z.; He, Z.; Zhang, Q. Experimental Study of Surface Constraint Effect on Rock Fragmentation by Blasting. Int. J. Rock Mech. Min. Sci. 2020, 128, 104278. [Google Scholar] [CrossRef]



| Ruggedness | Wave Speed (km/s) | Tensile Strength (MPa) | UCS (MPa) | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|---|
| Chloritized silica | 3.24 | 7.7 | 56.4 | 38 | 0.20 |
| Magnetized silica | 4.11 | 10.2 | 82.1 | 44 | 0.27 |
| Crystalline tuff | 3.53 | 8.3 | 59.3 | 35 | 0.20 |
| Parameter | Plans Comparison | ||
|---|---|---|---|
| Optimization Plan 1 and Original Plan | Optimization Plan 2 | Change (%) | |
| No. of blastholes (detonators) | 50 | 43 | −14.0% |
| Total Explosives | 66 | 48 | −27.27% |
| Test field 1, 3464#JL3 | Xmax (mm) | X50 (mm) | b | R2 |
| 50 ms | 881.48 | 238.4 | 1.41273 | 0.99243 |
| 100 ms | 808.71 | 181.84 | 1.54132 | 0.99819 |
| 150 ms | 756.89 | 115.07 | 1.64063 | 0.99419 |
| 200 ms | 877.39 | 175.25 | 1.70078 | 0.99591 |
| 500 ms | 913.89 | 260.88 | 1.53795 | 0.99393 |
| Test field 2, 3464#JL4 | Xmax (mm) | X50 (mm) | b | R2 |
| 50 ms | 909.05 | 259.63 | 1.67884 | 0.99723 |
| 100 ms | 811.03 | 204.53 | 1.70185 | 0.99641 |
| 150 ms | 757.16 | 128.82 | 2.10332 | 0.99244 |
| 200 ms | 880.29 | 196.6 | 1.72351 | 0.9945 |
| 500 ms | 894.38 | 264.31 | 1.84568 | 0.99672 |
| Test field 3, 3464#JL5 | Xmax (mm) | X50 (mm) | b | R2 |
| 50 ms | 881.16 | 300.55 | 1.31133 | 0.99491 |
| 100 ms | 814.74 | 206.35 | 1.54239 | 0.99824 |
| 150 ms | 758.22 | 165.72 | 1.36273 | 0.99672 |
| 200 ms | 927.16 | 187.79 | 1.77686 | 0.99882 |
| 500 ms | 946.83 | 414.58 | 1.5688 | 0.9972 |
| Test field 4, 3464#JL6 | Xmax (mm) | X50 (mm) | b | R2 |
| 100 ms | 836.66 | 213.92 | 1.70082 | 0.9991 |
| 150 ms | 772.11 | 168.54 | 1.68278 | 0.99883 |
| 150 ms (Reduced hole) | 825.73 | 240.69 | 1.79796 | 0.99931 |
| Test field 1, 3464#JL3 | 50 ms | 100 ms | 150 ms | 200 ms | 500 ms | 50 ms | 100 ms | 150 ms | 200 ms | 500 ms |
| X20 (mm) | 25.31 | 20.28 | 8.39 | 26.24 | 58.54 | 26.92 | 20.64 | 9.43 | 23.05 | 41.67 |
| X50 (mm) | 238.4 | 181.84 | 115.07 | 175.25 | 260.88 | 238.4 | 181.84 | 115.07 | 175.25 | 260.88 |
| X80 (mm) | 524.56 | 434.85 | 179.64 | 348.61 | 529.75 | 539.94 | 440.70 | 336.98 | 430.11 | 549.34 |
| P25 (%) | 14.15 | 20.47 | 23.64 | 19.48 | 12.96 | 19.53 | 21.36 | 27.41 | 20.62 | 16.50 |
| 1-P750 (%) | 4.24 | 1.71 | 0.11 | 2.99 | 7.21 | 4.95 | 0.99 | 0.02 | 1.87 | 5.51 |
| Test field 2, 3464#JL4 | 50 ms | 100 ms | 150 ms | 200 ms | 500 ms | 50 ms | 100 ms | 150 ms | 200 ms | 500 ms |
| X20 (mm) | 59.32 | 28.95 | 20.36 | 41.74 | 66.27 | 51.98 | 36.14 | 24.68 | 30.86 | 67.53 |
| X50 (mm) | 259.63 | 204.53 | 128.82 | 196.6 | 264.31 | 259.63 | 204.53 | 128.82 | 196.6 | 264.31 |
| X80 (mm) | 547.29 | 438.62 | 251.68 | 427.83 | 509.65 | 525.13 | 440.66 | 302.88 | 450.15 | 503.18 |
| P25 (%) | 10.77 | 18.58 | 23.62 | 15.29 | 9.72 | 14.57 | 17.12 | 20.13 | 18.37 | 12.06 |
| 1-P750 (%) | 5.56 | 1.08 | 0.13 | 3.27 | 5.19 | 4.12 | 0.75 | 0 | 2.07 | 2.73 |
| Test field 3, 3464#JL5 | 50 ms | 100 ms | 150 ms | 200 ms | 500 ms | 50 ms | 100 ms | 150 ms | 200 ms | 500 ms |
| X20 (mm) | 51.46 | 35.18 | 9.59 | 33.54 | 119.15 | 39.86 | 27.92 | 11.31 | 28.45 | 128.35 |
| X50 (mm) | 300.55 | 206.35 | 165.72 | 187.79 | 414.58 | 300.55 | 206.35 | 165.72 | 187.79 | 414.58 |
| X80 (mm) | 619.27 | 452.36 | 409.37 | 455.83 | 654.25 | 606.39 | 465.85 | 437.53 | 445.98 | 673.05 |
| P25 (%) | 12.11 | 17.46 | 27.03 | 16.19 | 7.75 | 17.22 | 19.22 | 24.95 | 18.98 | 8.19 |
| 1-P750 (%) | 6.57 | 2.83 | 0.17 | 3.53 | 12.91 | 7.66 | 1.3 | 0.12 | 2.69 | 12.08 |
| Test Field 4, 3464#JL3 | Image Processing Data | Swebrec Function | ||||||
|---|---|---|---|---|---|---|---|---|
| 100 ms | 150 ms | 150 ms(Reduced Hole) | 100 ms | 150 ms | 150 ms (Reduced Hole) | Change 1 | Change 2 | |
| X20 (mm) | 34.78 | 19.56 | 59.34 | 38.40 | 24.05 | 57.46 | −37.37 | +49.64 |
| X50 (mm) | 213.92 | 168.54 | 240.69 | 213.92 | 168.54 | 240.69 | −21.21 | +12.51 |
| X80 (mm) | 456.67 | 396.38 | 471.19 | 457.50 | 395.98 | 466.88 | −13.45 | +2.05 |
| P25 (%) | 16.43 | 22.93 | 14.03 | 16.69 | 20.30 | 13.30 | +21.63 | −20.31 |
| 1-P750 (%) | 2.06 | 0.39 | 1.06 | 1.35 | 0.13 | 1.01 | −90.37 | −25.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Liu, C.; Feng, Y.; Yin, H. Effect of the Inter-Ring Delay Time on Rock Fragmentation: Field Tests at the Underground Mine. Appl. Sci. 2024, 14, 6372. https://doi.org/10.3390/app14146372
Chen H, Liu C, Feng Y, Yin H. Effect of the Inter-Ring Delay Time on Rock Fragmentation: Field Tests at the Underground Mine. Applied Sciences. 2024; 14(14):6372. https://doi.org/10.3390/app14146372
Chicago/Turabian StyleChen, Hui, Chengyu Liu, Yin Feng, and Haojie Yin. 2024. "Effect of the Inter-Ring Delay Time on Rock Fragmentation: Field Tests at the Underground Mine" Applied Sciences 14, no. 14: 6372. https://doi.org/10.3390/app14146372
APA StyleChen, H., Liu, C., Feng, Y., & Yin, H. (2024). Effect of the Inter-Ring Delay Time on Rock Fragmentation: Field Tests at the Underground Mine. Applied Sciences, 14(14), 6372. https://doi.org/10.3390/app14146372





