Peak and Residual Shear Interface Measurement between Sand and Continuum Surfaces Using Ring Shear Apparatus
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
2.2. Methods
3. Results and Discussion
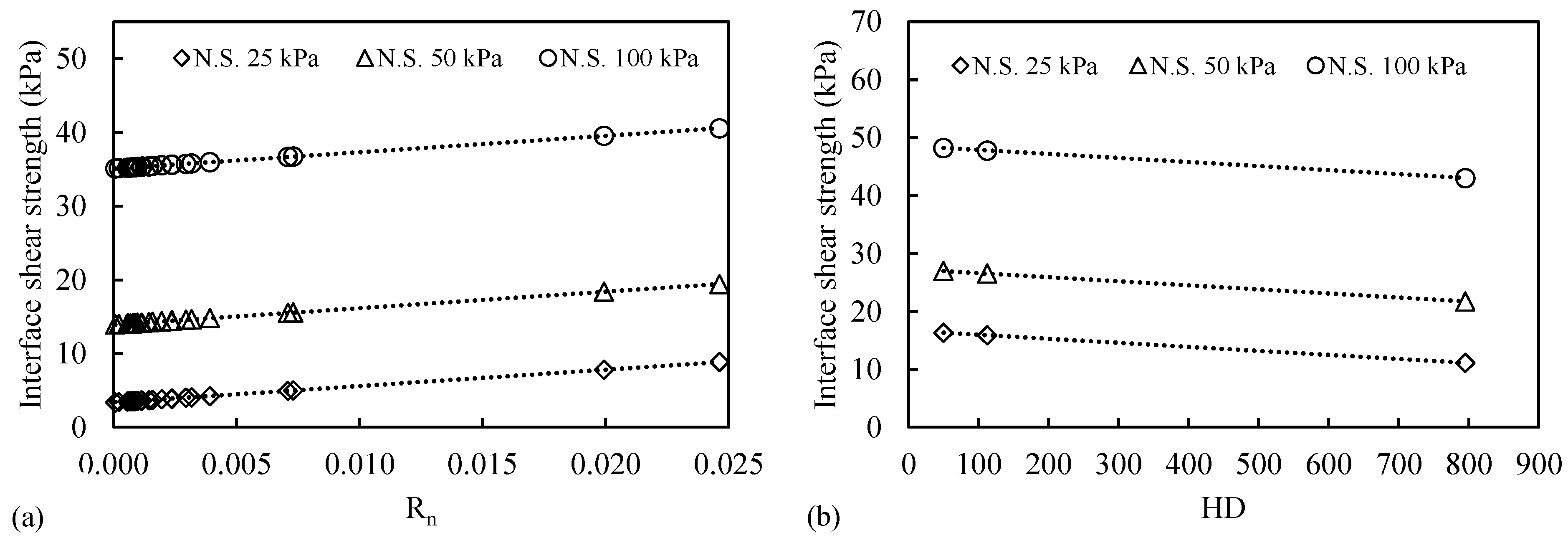
3.1. Continuum Surfaces Properties
3.2. Sand Properties
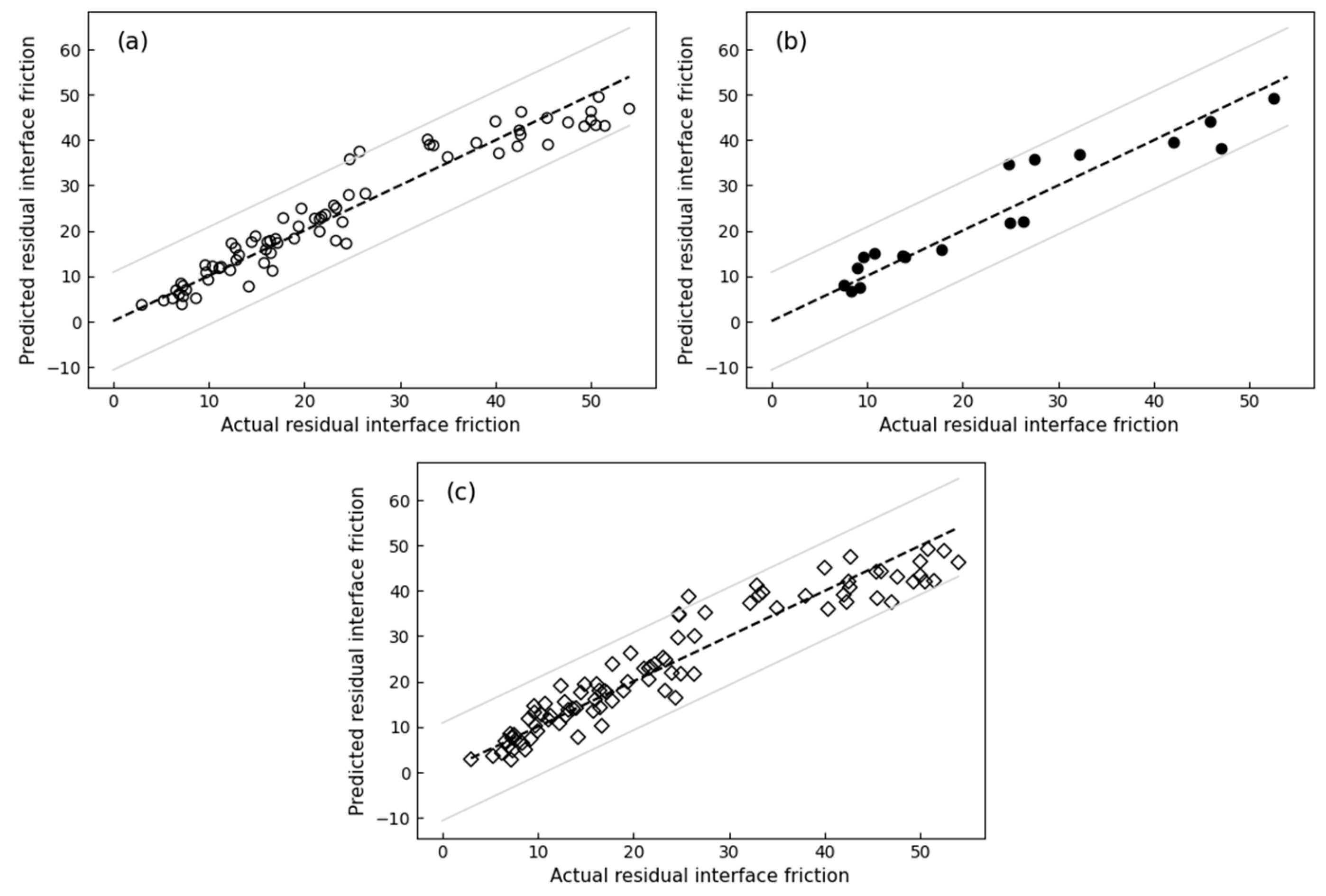
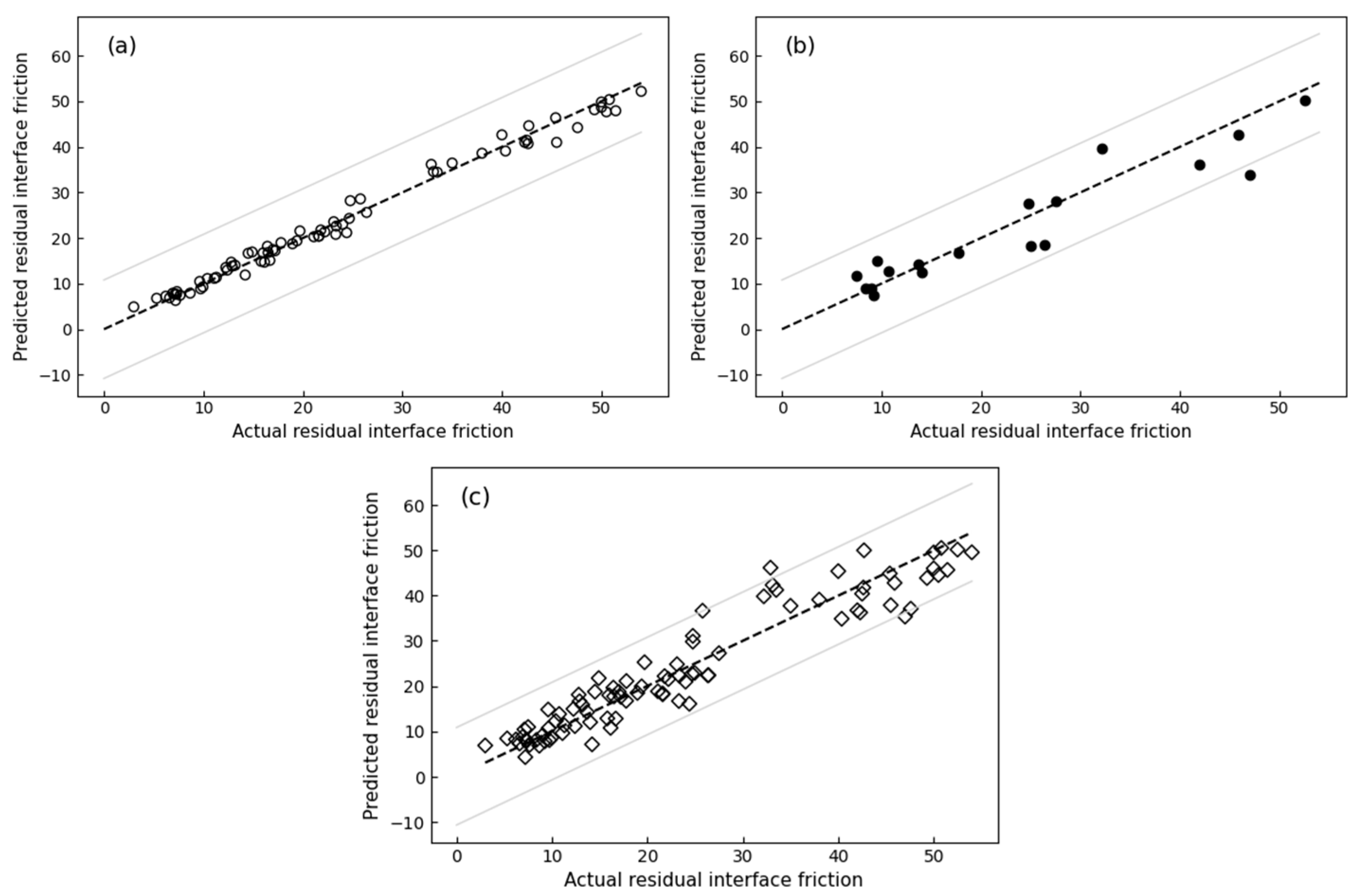
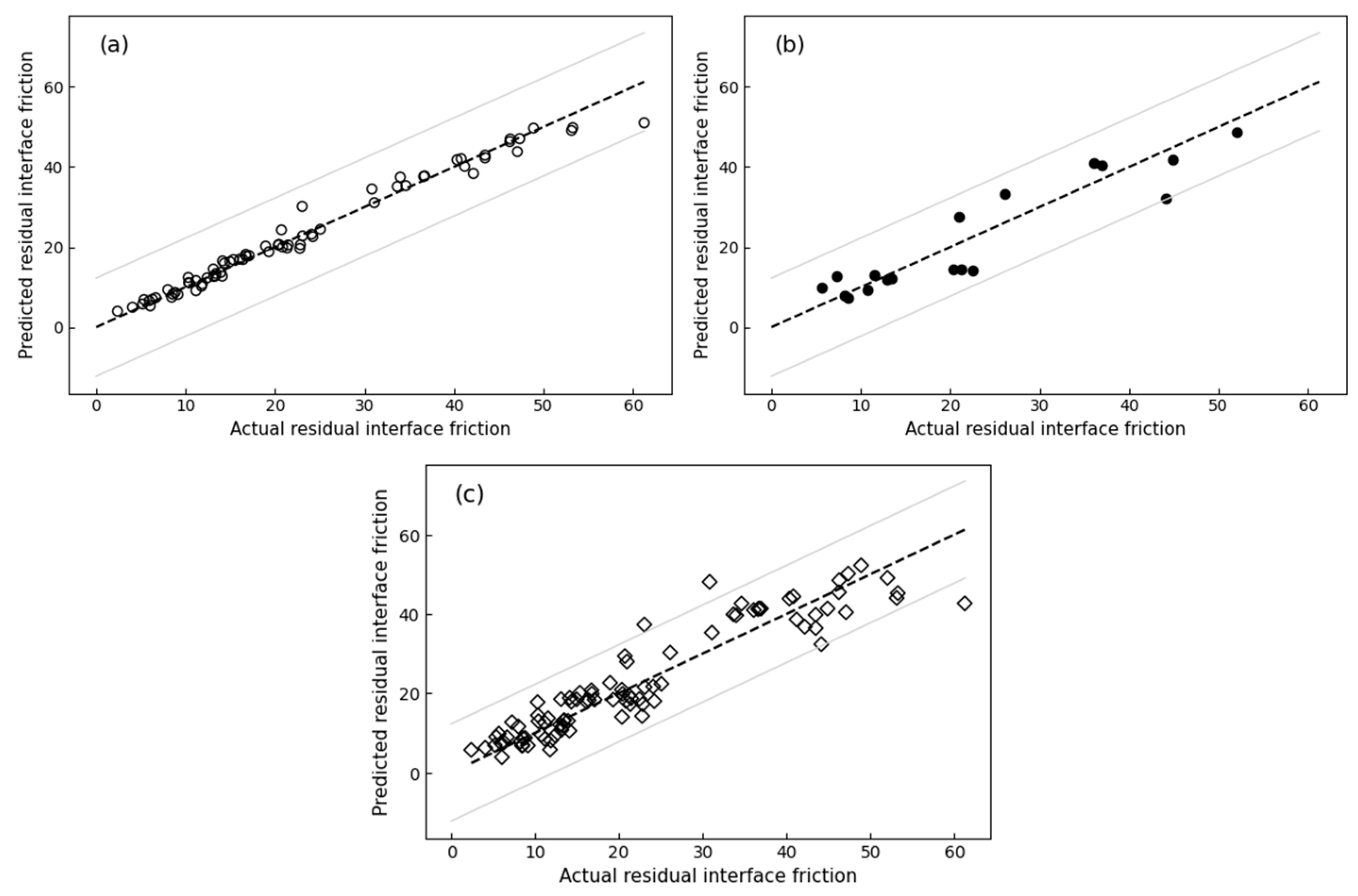
3.3. Multiple Linear Regression
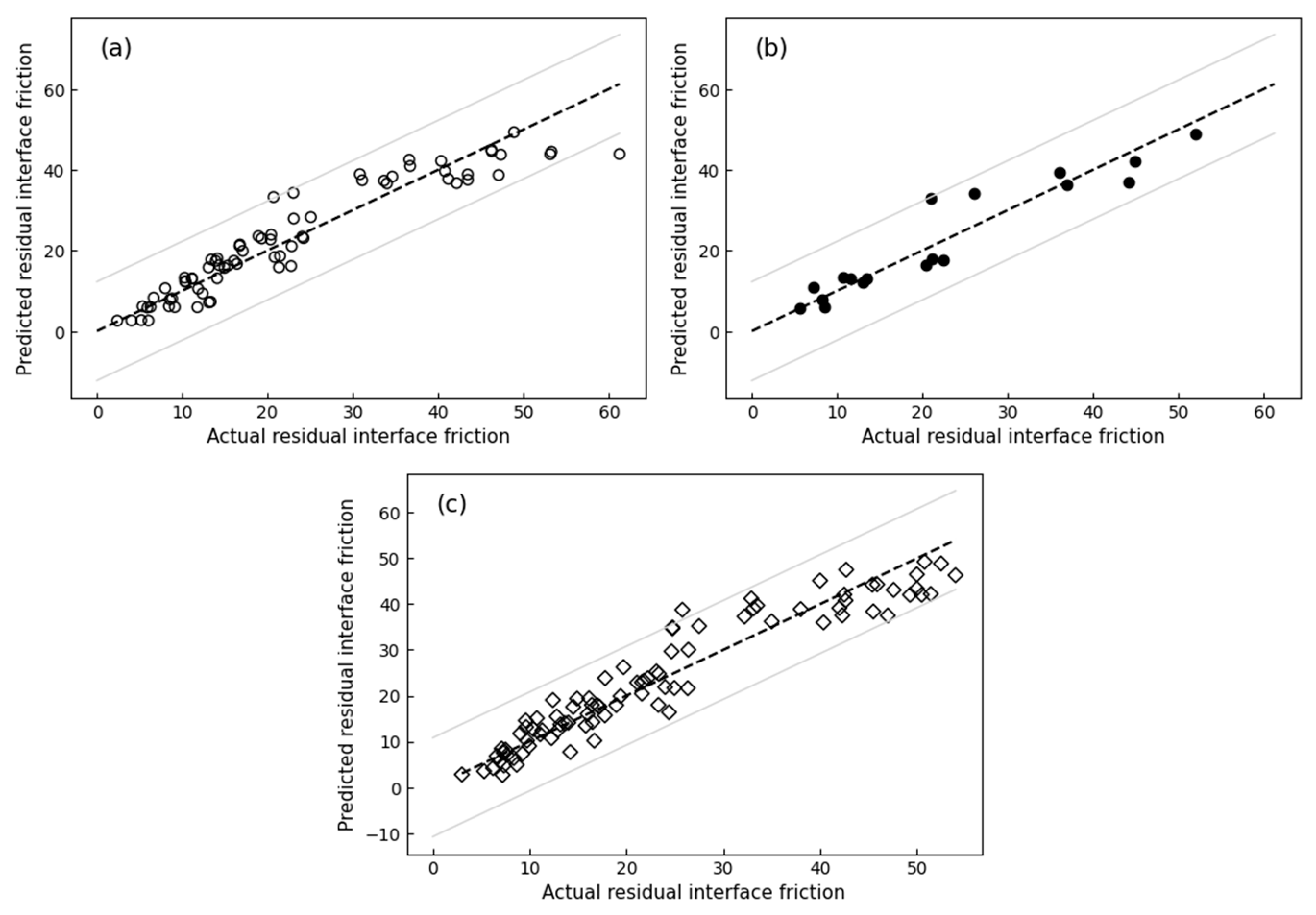
3.4. Random Forest Regression
3.5. Method Comparison
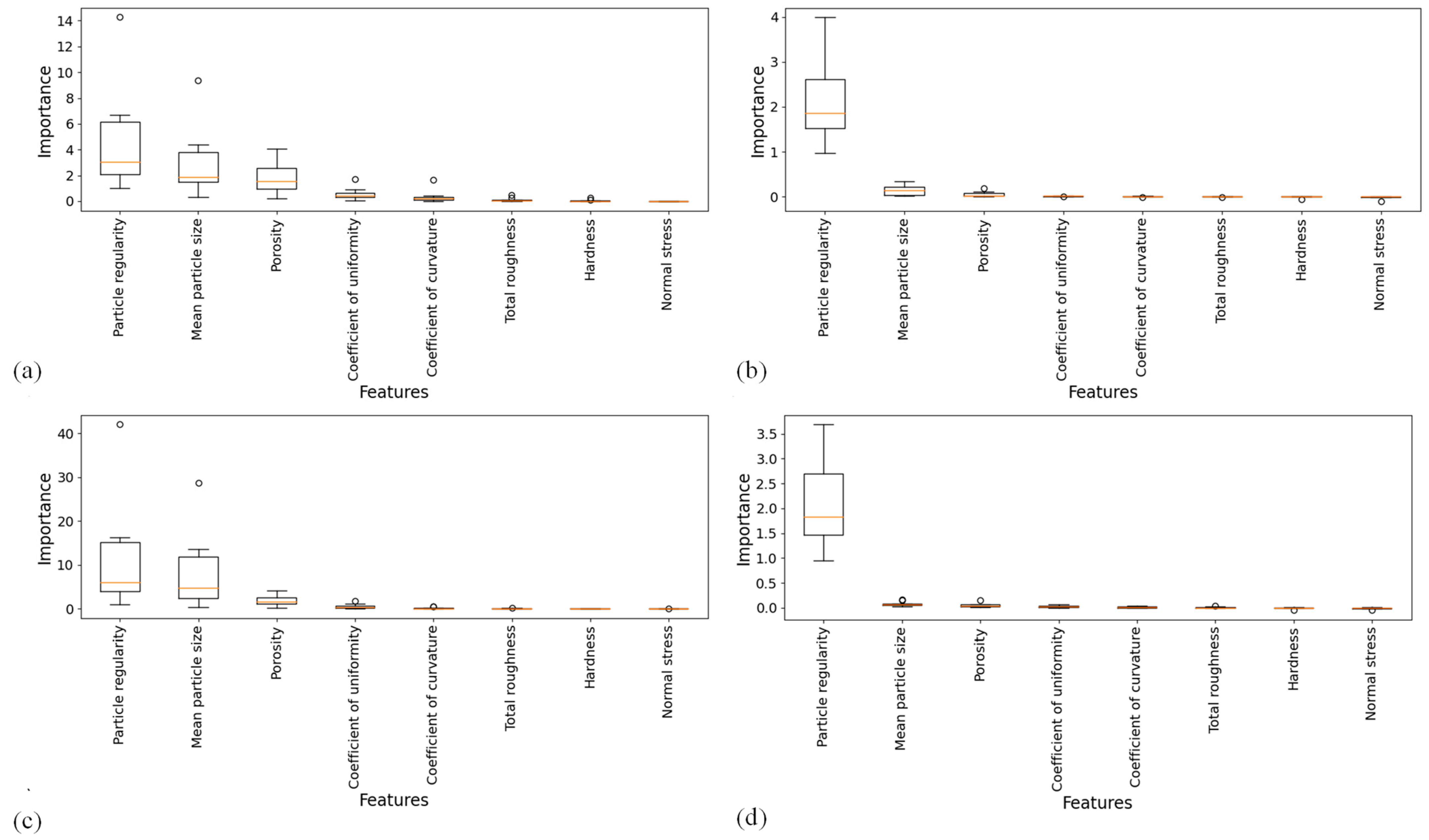
3.6. Important of Input Parameters
4. Conclusions
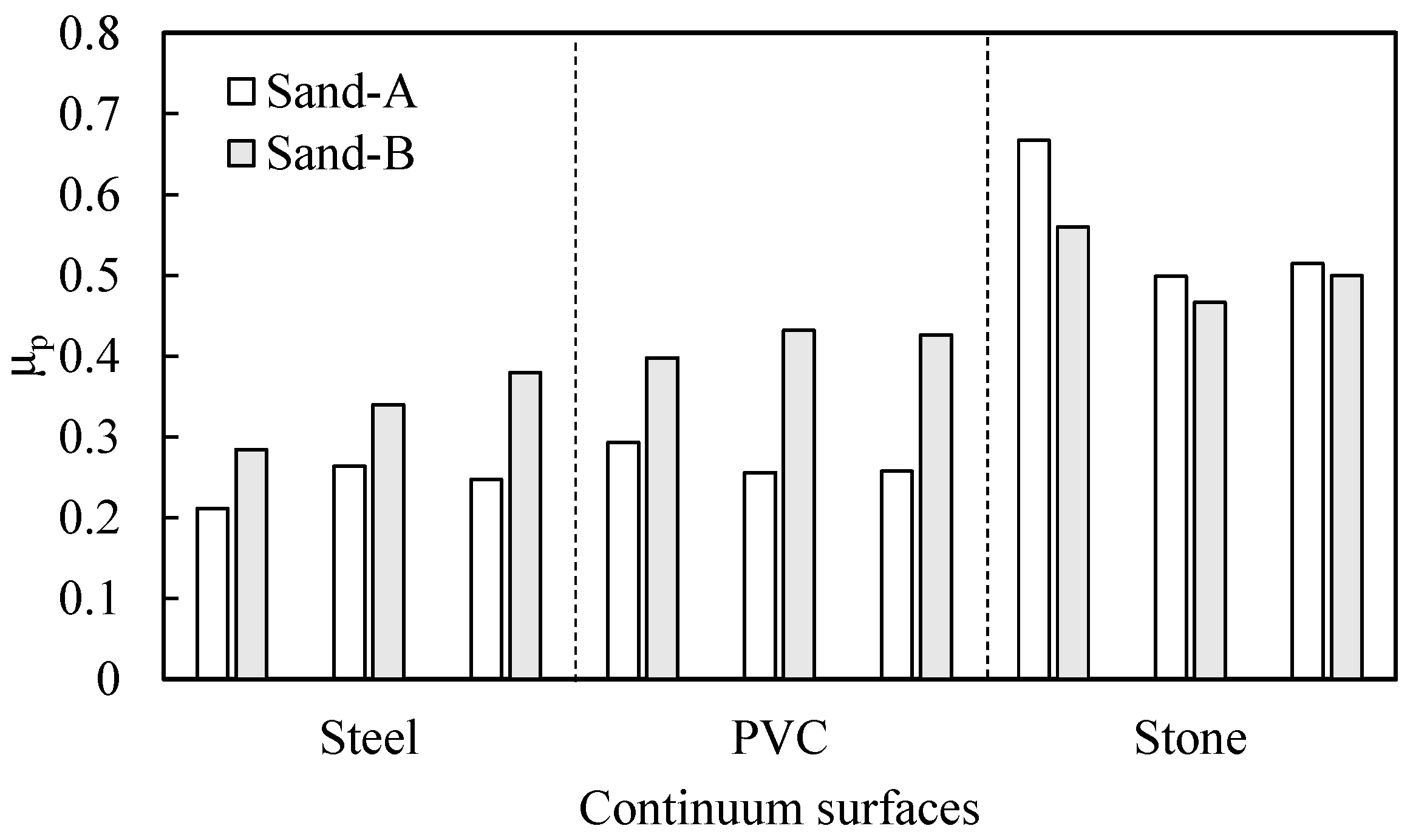
- Coarse sand exhibited higher μp with steel and PVC surfaces, while medium sand showed higher μp with stone.
- Well-graded sand showed a higher μp compared to poorly graded sand.
- As the sample density increases, the μp also increases.
- Due to its high roughness and hardness, stone consistently provided the highest interface shear strength values across different sand types, followed by PVC and then steel.
- The machine learning models (MLR and RFR) demonstrated high accuracy for both peak and residual shear strength. For peak shear strength, the MLR model achieved an R2 of 0.92 during training and 0.90 during testing, while the RFR model achieved an R2 of 0.98 during training and 0.88 during testing. For residual shear strength, the MLR model achieved an R2 of 0.89 during both training and testing, while the RFR model achieved an R2 of 0.97 during training and 0.88 during testing.
- In the 10-fold cross-validation, the models continued to demonstrate high accuracy. For peak shear strength, both models achieved an R2 of 0.90. For residual shear strength, the MLR model achieved an R2 of 0.90, while the RFR model attained an R2 of 0.87.
- Among the eight input parameters, particle regularity was identified as the most influential factor for both peak and residual shear strength, followed by mean particle size and porosity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| μp | Peak interface friction |
| δp | Peak interface friction angle |
| RI | Particle regularity |
| D50 | Median particle size |
| n | Porosity |
| Cu | Coefficient of uniformity |
| Cc | Coefficient of curvature |
| Rt | Surface roughness |
| HD | Surface hardness |
| σ | Normal stress |
| τp | Peak interface shear strength |
| τr | Residual interface shear stress |
| MLR | Multiple linear regression |
| RFR | Random Forest regression |
Appendix A
| # | RI | D50 (mm) | n | Cu | Cc | Rt (μm) | HD | σ (kPa) | τp (kPa) | τr (kPa) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.715 | 0.51 | 0.377 | 1.2 | 0.97 | 4 | 112.2 | 25 | 3 | 2.38 |
| 2 | 0.715 | 0.51 | 0.291 | 1.2 | 0.97 | 4 | 112.2 | 50 | 12.89 | 10.39 |
| 3 | 0.715 | 0.51 | 0.268 | 1.2 | 0.97 | 4 | 112.2 | 100 | 24.76 | 20.95 |
| 4 | 0.715 | 0.51 | 0.351 | 1.2 | 0.97 | 12 | 112.2 | 25 | 5.3 | 4.05 |
| 5 | 0.715 | 0.51 | 0.279 | 1.2 | 0.97 | 12 | 112.2 | 50 | 13.18 | 10.33 |
| 6 | 0.715 | 0.51 | 0.26 | 1.2 | 0.97 | 12 | 112.2 | 100 | 24.76 | 20.70 |
| 7 | 0.715 | 0.51 | 0.408 | 1.2 | 0.97 | 0.5 | 50 | 25 | 7.2 | 6.04 |
| 8 | 0.715 | 0.51 | 0.408 | 1.2 | 0.97 | 0.5 | 50 | 50 | 13.68 | 11.54 |
| 9 | 0.715 | 0.51 | 0.408 | 1.2 | 0.97 | 0.5 | 50 | 100 | 27.5 | 26.10 |
| 10 | 0.715 | 0.51 | 0.362 | 1.2 | 0.97 | 15 | 50 | 25 | 7.34 | 5.20 |
| 11 | 0.715 | 0.51 | 0.362 | 1.2 | 0.97 | 15 | 50 | 50 | 12.8 | 10.29 |
| 12 | 0.715 | 0.51 | 0.362 | 1.2 | 0.97 | 15 | 50 | 100 | 25.78 | 23.02 |
| 13 | 0.715 | 0.51 | 0.362 | 1.2 | 0.97 | 82.92 | 795 | 25 | 12.25 | 13.33 |
| 14 | 0.715 | 0.51 | 0.362 | 1.2 | 0.97 | 82.92 | 795 | 50 | 26.34 | 21.17 |
| 15 | 0.715 | 0.51 | 0.362 | 1.2 | 0.97 | 82.92 | 795 | 100 | 50.5 | 43.45 |
| 16 | 0.715 | 0.51 | 0.347 | 1.2 | 0.97 | 82.92 | 795 | 25 | 16.68 | 13.14 |
| 17 | 0.715 | 0.51 | 0.347 | 1.2 | 0.97 | 82.92 | 795 | 50 | 24.95 | 22.44 |
| 18 | 0.715 | 0.51 | 0.347 | 1.2 | 0.97 | 82.92 | 795 | 100 | 51.44 | 47.07 |
| 19 | 0.395 | 1.77 | 0.381 | 1.45 | 0.96 | 8 | 112.2 | 25 | 7.3 | 6.66 |
| 20 | 0.395 | 1.77 | 0.306 | 1.45 | 0.96 | 8 | 112.2 | 50 | 16.43 | 14.12 |
| 21 | 0.395 | 1.77 | 0.291 | 1.45 | 0.96 | 8 | 112.2 | 100 | 33.12 | 30.81 |
| 22 | 0.395 | 1.77 | 0.309 | 1.45 | 0.96 | 16 | 112.2 | 25 | 7.11 | 8.56 |
| 23 | 0.395 | 1.77 | 0.219 | 1.45 | 0.96 | 16 | 112.2 | 50 | 17 | 16.06 |
| 24 | 0.395 | 1.77 | 0.204 | 1.45 | 0.96 | 16 | 112.2 | 100 | 38 | 34.61 |
| 25 | 0.395 | 1.77 | 0.366 | 1.45 | 0.96 | 5 | 50 | 25 | 9.25 | 8.24 |
| 26 | 0.395 | 1.77 | 0.366 | 1.45 | 0.96 | 5 | 50 | 50 | 18.95 | 20.83 |
| 27 | 0.395 | 1.77 | 0.366 | 1.45 | 0.96 | 5 | 50 | 100 | 42 | 36.08 |
| 28 | 0.395 | 1.77 | 0.343 | 1.45 | 0.96 | 17 | 50 | 25 | 9.95 | 8.81 |
| 29 | 0.395 | 1.77 | 0.343 | 1.45 | 0.96 | 17 | 50 | 50 | 21.6 | 21.46 |
| 30 | 0.395 | 1.77 | 0.343 | 1.45 | 0.96 | 17 | 50 | 100 | 42.63 | 40.79 |
| 31 | 0.395 | 1.77 | 0.374 | 1.45 | 0.96 | 82.92 | 795 | 25 | 10.75 | 13.46 |
| 32 | 0.395 | 1.77 | 0.374 | 1.45 | 0.96 | 82.92 | 795 | 50 | 23.1 | 24.07 |
| 33 | 0.395 | 1.77 | 0.374 | 1.45 | 0.96 | 82.92 | 795 | 100 | 54 | 53.26 |
| 34 | 0.395 | 1.77 | 0.306 | 1.45 | 0.96 | 82.92 | 795 | 25 | 14 | 12.97 |
| 35 | 0.395 | 1.77 | 0.306 | 1.45 | 0.96 | 82.92 | 795 | 50 | 23.35 | 20.35 |
| 36 | 0.395 | 1.77 | 0.306 | 1.45 | 0.96 | 82.92 | 795 | 100 | 50 | 47.33 |
| 37 | 0.395 | 0.63 | 0.343 | 6.2 | 1.31 | 8 | 112.2 | 25 | 6.22 | 6.28 |
| 38 | 0.395 | 0.63 | 0.272 | 6.2 | 1.31 | 8 | 112.2 | 50 | 16.5 | 13.09 |
| 39 | 0.395 | 0.63 | 0.253 | 6.2 | 1.31 | 8 | 112.2 | 100 | 35 | 33.98 |
| 40 | 0.37 | 0.63 | 0.234 | 6.2 | 1.31 | 16 | 112.2 | 25 | 6.92 | 5.35 |
| 41 | 0.37 | 0.63 | 0.14 | 6.2 | 1.31 | 16 | 112.2 | 50 | 15.99 | 14.95 |
| 42 | 0.37 | 0.63 | 0.113 | 6.2 | 1.31 | 16 | 112.2 | 100 | 32.2 | 36.93 |
| 43 | 0.37 | 0.63 | 0.272 | 6.2 | 1.31 | 5 | 50 | 25 | 8.67 | 9.13 |
| 44 | 0.37 | 0.63 | 0.272 | 6.2 | 1.31 | 5 | 50 | 50 | 17.77 | 20.36 |
| 45 | 0.37 | 0.63 | 0.272 | 6.2 | 1.31 | 5 | 50 | 100 | 40.36 | 43.46 |
| 46 | 0.37 | 0.63 | 0.245 | 6.2 | 1.31 | 17 | 50 | 25 | 8.36 | 8.51 |
| 47 | 0.37 | 0.63 | 0.245 | 6.2 | 1.31 | 17 | 50 | 50 | 17.2 | 16.40 |
| 48 | 0.37 | 0.63 | 0.245 | 6.2 | 1.31 | 17 | 50 | 100 | 42.3 | 41.18 |
| 49 | 0.37 | 0.63 | 0.245 | 6.2 | 1.31 | 82.92 | 795 | 25 | 10.4 | 8.00 |
| 50 | 0.37 | 0.63 | 0.245 | 6.2 | 1.31 | 82.92 | 795 | 50 | 17.8 | 16.71 |
| 51 | 0.37 | 0.63 | 0.245 | 6.2 | 1.31 | 82.92 | 795 | 100 | 40 | 40.33 |
| 52 | 0.37 | 0.63 | 0.234 | 6.2 | 1.31 | 82.92 | 795 | 25 | 11.3 | 11.86 |
| 53 | 0.37 | 0.63 | 0.234 | 6.2 | 1.31 | 82.92 | 795 | 50 | 21.1 | 22.82 |
| 54 | 0.37 | 0.63 | 0.234 | 6.2 | 1.31 | 82.92 | 795 | 100 | 45.9 | 44.87 |
| 55 | 0.635 | 0.51 | 0.408 | 1.2 | 0.97 | 8 | 112.2 | 25 | 7.65 | 8.44 |
| 56 | 0.635 | 0.51 | 0.357 | 1.2 | 0.97 | 8 | 112.2 | 50 | 24.4 | 22.76 |
| 57 | 0.635 | 0.51 | 0.339 | 1.2 | 0.97 | 8 | 112.2 | 100 | 47 | 44.13 |
| 58 | 0.635 | 0.51 | 0.355 | 1.2 | 0.97 | 16 | 112.2 | 25 | 14.2 | 11.77 |
| 59 | 0.635 | 0.51 | 0.296 | 1.2 | 0.97 | 16 | 112.2 | 50 | 23.3 | 21.34 |
| 60 | 0.635 | 0.51 | 0.28 | 1.2 | 0.97 | 16 | 112.2 | 100 | 45.5 | 42.15 |
| 61 | 0.635 | 0.51 | 0.403 | 1.2 | 0.97 | 5 | 50 | 25 | 6.6 | 5.92 |
| 62 | 0.635 | 0.51 | 0.403 | 1.2 | 0.97 | 5 | 50 | 50 | 14.5 | 14.32 |
| 63 | 0.635 | 0.51 | 0.403 | 1.2 | 0.97 | 5 | 50 | 100 | 33.5 | 31.08 |
| 64 | 0.635 | 0.51 | 0.347 | 1.2 | 0.97 | 17 | 50 | 25 | 7.5 | 5.67 |
| 65 | 0.635 | 0.51 | 0.347 | 1.2 | 0.97 | 17 | 50 | 50 | 14.9 | 15.34 |
| 66 | 0.635 | 0.51 | 0.347 | 1.2 | 0.97 | 17 | 50 | 100 | 32.9 | 33.64 |
| 67 | 0.635 | 0.51 | 0.416 | 1.2 | 0.97 | 82.92 | 795 | 25 | 9.6 | 7.24 |
| 68 | 0.635 | 0.51 | 0.416 | 1.2 | 0.97 | 82.92 | 795 | 50 | 19.7 | 16.76 |
| 69 | 0.635 | 0.51 | 0.416 | 1.2 | 0.97 | 82.92 | 795 | 100 | 42.7 | 36.60 |
| 70 | 0.635 | 0.51 | 0.267 | 1.2 | 0.97 | 82.92 | 795 | 25 | 15.8 | 12.39 |
| 71 | 0.635 | 0.51 | 0.267 | 1.2 | 0.97 | 82.92 | 795 | 50 | 22.2 | 17.09 |
| 72 | 0.635 | 0.51 | 0.267 | 1.2 | 0.97 | 82.92 | 795 | 100 | 45.4 | 36.70 |
| 73 | 0.41 | 1.72 | 0.374 | 1.69 | 1.01 | 12 | 112.2 | 25 | 9.73 | 11.15 |
| 74 | 0.41 | 1.72 | 0.317 | 1.69 | 1.01 | 12 | 112.2 | 50 | 19.4 | 19.30 |
| 75 | 0.41 | 1.72 | 0.306 | 1.69 | 1.01 | 12 | 112.2 | 100 | 42.5 | 61.24 |
| 76 | 0.41 | 1.72 | 0.347 | 1.69 | 1.01 | 20 | 112.2 | 25 | 11.1 | 14.09 |
| 77 | 0.41 | 1.72 | 0.294 | 1.69 | 1.01 | 20 | 112.2 | 50 | 24 | 24.21 |
| 78 | 0.41 | 1.72 | 0.272 | 1.69 | 1.01 | 20 | 112.2 | 100 | 49.3 | 53.12 |
| 79 | 0.41 | 1.72 | 0.408 | 1.69 | 1.01 | 15 | 50 | 25 | 9.03 | 10.75 |
| 80 | 0.41 | 1.72 | 0.408 | 1.69 | 1.01 | 15 | 50 | 50 | 21.6 | 20.42 |
| 81 | 0.41 | 1.72 | 0.408 | 1.69 | 1.01 | 15 | 50 | 100 | 47.6 | 46.22 |
| 82 | 0.41 | 1.72 | 0.347 | 1.69 | 1.01 | 22 | 50 | 25 | 9.63 | 11.15 |
| 83 | 0.41 | 1.72 | 0.347 | 1.69 | 1.01 | 22 | 50 | 50 | 21.8 | 18.93 |
| 84 | 0.41 | 1.72 | 0.347 | 1.69 | 1.01 | 22 | 50 | 100 | 50 | 46.26 |
| 85 | 0.41 | 1.72 | 0.389 | 1.69 | 1.01 | 82.92 | 795 | 25 | 16.14 | 13.40 |
| 86 | 0.41 | 1.72 | 0.389 | 1.69 | 1.01 | 82.92 | 795 | 50 | 26.4 | 25.06 |
| 87 | 0.41 | 1.72 | 0.389 | 1.69 | 1.01 | 82.92 | 795 | 100 | 50.8 | 48.87 |
| 88 | 0.41 | 1.72 | 0.355 | 1.69 | 1.01 | 82.92 | 795 | 25 | 12.4 | 13.92 |
| 89 | 0.41 | 1.72 | 0.355 | 1.69 | 1.01 | 82.92 | 795 | 50 | 24.66 | 23.06 |
| 90 | 0.41 | 1.72 | 0.355 | 1.69 | 1.01 | 82.92 | 795 | 100 | 52.5 | 52.02 |
References
- Abuel-Naga, H.M.; Shaia, H.A.; Bouazza, A. Effect of Surface Roughness and Hardness of Continuum Materials on Interface Shear Strength of Granular Materials. J. Test. Eval. 2017, 46, 826–831. [Google Scholar] [CrossRef]
- AS1289.3.6.1; Method of Testing Soils for Engineering Purposes—Soil Classification. Australian Standard: Sydney, Australia, 2009.
- Brumund, W.; Leonards, G. Experimental study of static and dynamic friction between sand and typical constuction materials. J. Test. Eval. 1973, 1, 162–165. [Google Scholar] [CrossRef]
- Daghistani, F.; Abuel-Naga, H. Advancements in Understanding Interface Friction: A Combined Experimental and Machine Learning Approach Using Multiple Linear and Random Forest Regressions. Geotechnics 2024, 4, 109–126. [Google Scholar] [CrossRef]
- DeJong, J.T.; Westgate, Z.J. Role of initial state, material properties, and confinement condition on local and global soil-structure interface behavior. J. Geotech. Geoenviron. Eng. 2009, 135, 1646–1660. [Google Scholar] [CrossRef]
- Dove, J.; Bents, D.; Wang, J.; Gao, B. Particle-scale surface interactions of non-dilative interface systems. Geotext. Geomembr. 2006, 24, 156–168. [Google Scholar] [CrossRef]
- Dove, J.E.; Frost, J.D. Peak friction behavior of smooth geomembrane-particle interfaces. J. Geotech. Geoenviron. Eng. 1999, 125, 544–555. [Google Scholar] [CrossRef]
- Ebrahimian, B.; Bauer, E. Numerical simulation of the effect of interface friction of a bounding structure on shear deformation in a granular soil. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 1486–1506. [Google Scholar] [CrossRef]
- Frost, J.; Han, J. Behavior of interfaces between fiber-reinforced polymers and sands. J. Geotech. Geoenviron. Eng. 1999, 125, 633–640. [Google Scholar] [CrossRef]
- Frost, J.D.; DeJong, J.; Recalde, M. Shear failure behavior of granular–continuum interfaces. Eng Fract. Mech. 2002, 69, 2029–2048. [Google Scholar] [CrossRef]
- Guo, H.; Wang, S.; Guo, C.; Yang, K.; Guo, R.; Fu, J.; Nan, Y.; Tao, M. Effect of grain size distribution on the shear properties of sand. Front. Mater. 2023, 10, 1219765. [Google Scholar] [CrossRef]
- Haeri, H.; Sarfarazi, V.; Zhu, Z.; Marji, M.F.; Masoumi, A. Investigation of shear behavior of soil-concrete interface. Smart Struct. Syst. 2019, 23, 81–90. [Google Scholar]
- Karimi, M.R.; Abrinia, K.; Hamdia, K.M.; Hashemianzadeh, S.M.; Baniassadi, M. Effects of Functional Group Type and Coverage on the Interfacial Strength and Load Transfer of Graphene-Polyethylene Nanocomposites: A Molecular Dynamics Simulation. Appl. Phys. A 2022, 128, 341. [Google Scholar] [CrossRef]
- Pham, H.H.G.; Van Impe, P.; Van Impe, W.; Mengé, P.; Haegeman, W. Shear and interface shear strengths of calcareous sand. In Proceedings of the 19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Republic of Korea, 17–21 September 2017. [Google Scholar]
- Potyondy, J.G. Skin friction between various soils and construction materials. Géotechnique 1961, 11, 339–353. [Google Scholar] [CrossRef]
- Powers, M.C. A new roundness scale for sedimentary particles. SEPM J. Sediment. Res. 1953, 23, 117–119. [Google Scholar] [CrossRef]
- Rowe, P.W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1962, 269, 500–527. [Google Scholar]
- Shaia, H. Behaviour of Fibre Reinforced Polymer Composite Piles: Experimental and Numerical Study. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2013. [Google Scholar]
- Stacho, J.; Sulovska, M.; Slavik, I. Analysis of the Shear Strength of a Soil-Geosynthetic Interface. Civ. Environ. Eng. 2023, 19, 452–463. [Google Scholar] [CrossRef]
- Stachowiak, G.; Batchelor, A. Engineering Tribology; Butterworth Heinemann Team LRN: Oxford, UK, 2013. [Google Scholar]
- Uesugi, M.; Kishida, H. Frictional resistance at yield between dry sand and mild steel. Soils Found. 1986, 26, 139–149. [Google Scholar] [CrossRef] [PubMed]
- Vangla, P.; Latha, G.M. Influence of particle size on the friction and interfacial shear strength of sands of similar morphology. Int. J. Geosynth. Ground Eng. 2015, 1, 6. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, G.; Wang, Z.; Yuan, S. Research on the effect of particle size on the interface friction between geogrid reinforcement and soil. Sustainability 2022, 14, 15443. [Google Scholar] [CrossRef]
- Zhou, J.; Ban, C.; Zhou, H.; Ren, J.; Liu, Z. Experimental study on the shear strength and failure mechanism of cemented soil–concrete interface. Materials 2023, 16, 4222. [Google Scholar] [CrossRef] [PubMed]
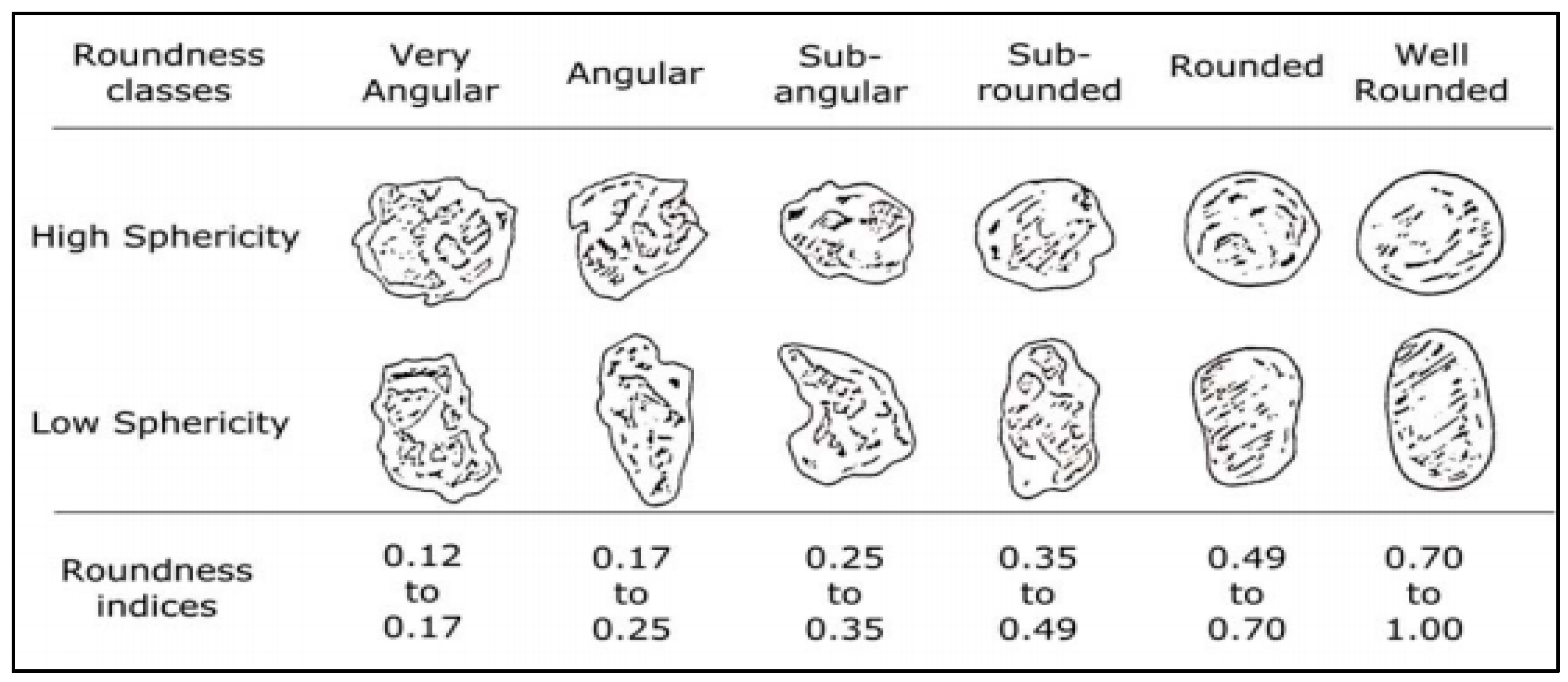



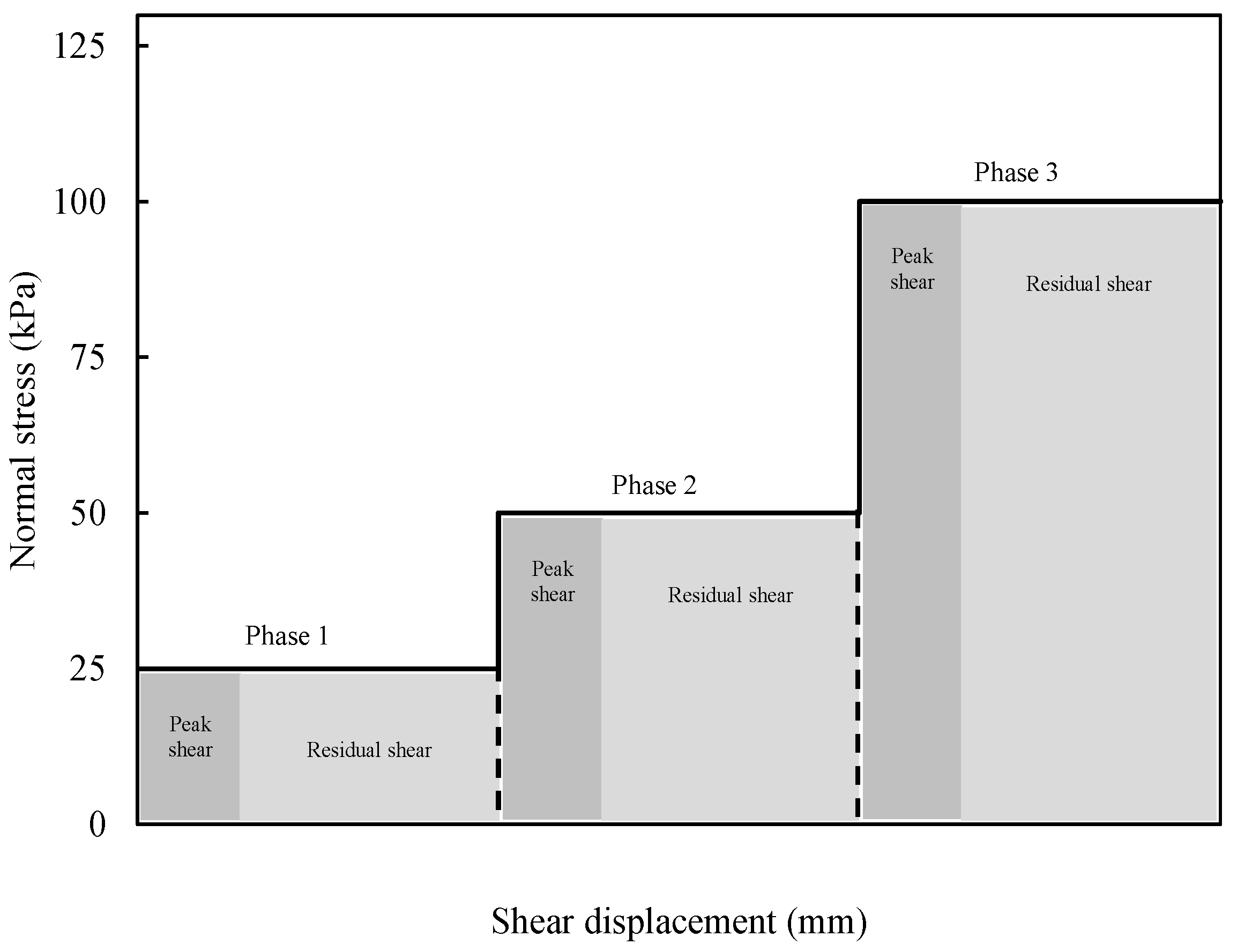
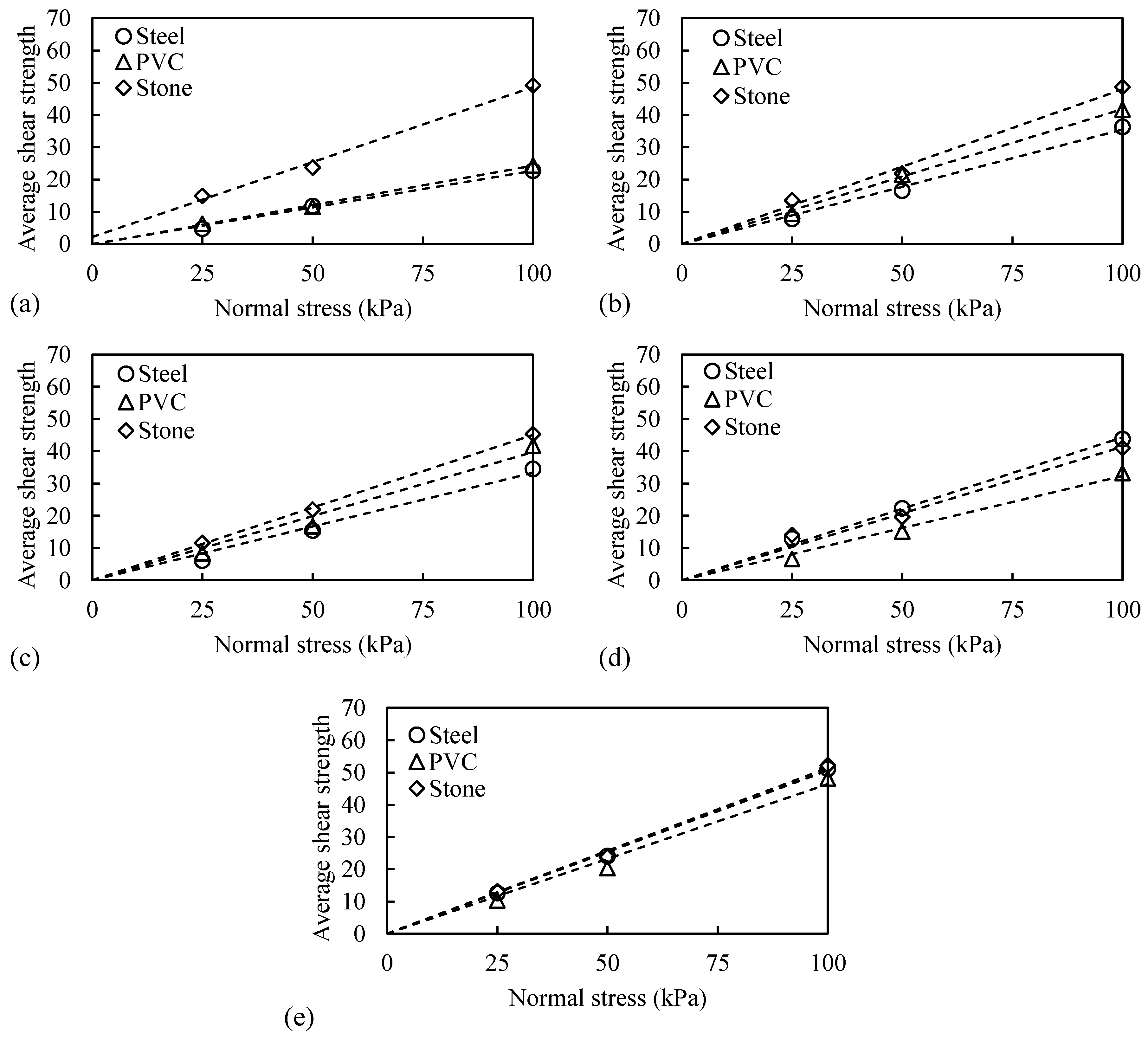
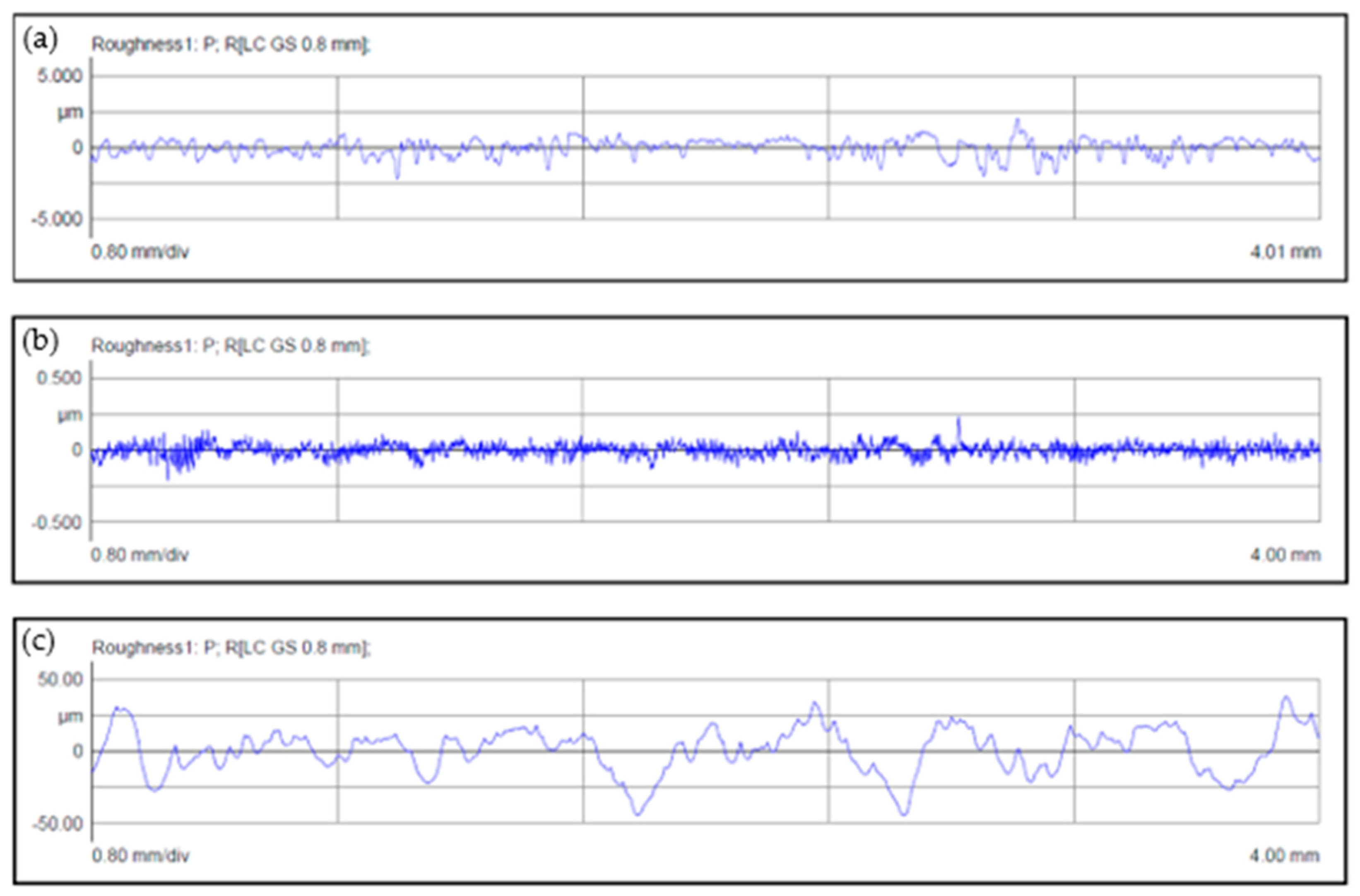


| Soil | Type | Gs | D50 (mm) | Cu | Cc | RI |
|---|---|---|---|---|---|---|
| A | Quartz Medium Sand | 2.65 | 0.51 | 0.97 | 0.72 | 0.72 |
| B | Quartz Coarse Sand | 2.65 | 1.77 | 1.45 | 0.96 | 0.40 |
| C | Quartz Well Graded Sand | 2.65 | 0.63 | 6.20 | 1.31 | 0.37 |
| D | Granite Sand | 3.75 | 0.51 | 1.20 | 0.97 | 0.64 |
| E | Quartz Fine Gravel | 2.65 | 1.72 | 1.69 | 1.01 | 0.41 |
| Material | Rt (μm) | HD |
|---|---|---|
| Steel | 4.2 | 112.2 |
| PVC | 0.45 | 50 |
| Stone | 82.92 | 795 |
| Sand Type | A | B | C | D | E |
|---|---|---|---|---|---|
| Loose state (g/cm3) | 1.65 | 1.64 | 1.74 | 2.22 | 1.66 |
| Dense state (g/cm3) | 1.72 | 1.83 | 2.03 | 2.42 | 1.73 |
| Training Database | Testing Database | 10-Fold CV | ||
|---|---|---|---|---|
| Observations | 72 | 18 | 90 | |
| Peak | MAE | 2.98 | 3.62 | 3.45 |
| RMSE | 3.93 | 4.53 | 4.47 | |
| RMSLE | 0.18 | 0.19 | 0.21 | |
| R2 | 0.92 | 0.90 | 0.90 | |
| Residual | MAE | 3.61 | 3.39 | 3.45 |
| RMSE | 4.72 | 4.52 | 4.47 | |
| RMSLE | 0.23 | 0.19 | 0.21 | |
| R2 | 0.89 | 0.89 | 0.90 |
| Training Database | Testing Database | 10-Fold CV | ||
|---|---|---|---|---|
| Observations | 72 | 18 | 90 | |
| Peak | MAE | 1.28 | 3.74 | 3.46 |
| RMSE | 1.60 | 4.99 | 4.48 | |
| RMSLE | 0.07 | 0.19 | 0.20 | |
| R2 | 0.98 | 0.88 | 0.90 | |
| Residual | MAE | 1.53 | 3.77 | 3.97 |
| RMSE | 2.13 | 4.82 | 5.16 | |
| RMSLE | 0.09 | 0.23 | 0.24 | |
| R2 | 0.97 | 0.88 | 0.87 |
| Multiple Linear Regression | Random Forest Regression | ||||||
|---|---|---|---|---|---|---|---|
| Training Data | Testing Data | 10-Fold CV | Training Data | Testing Data | 10-Fold CV | ||
| Observation | 72 | 18 | 90 | 72 | 18 | 90 | |
| Peak | MAE | 2.98 | 3.62 | 3.45 | 1.28 | 3.74 | 3.46 |
| RMSE | 3.93 | 4.53 | 4.47 | 1.60 | 4.99 | 4.48 | |
| RMSLE | 0.18 | 0.19 | 0.21 | 0.07 | 0.19 | 0.20 | |
| R2 | 0.92 | 0.90 | 0.90 | 0.98 | 0.88 | 0.90 | |
| Residual | MAE | 3.61 | 3.39 | 3.45 | 1.53 | 3.77 | 3.97 |
| RMSE | 4.72 | 4.52 | 4.47 | 2.13 | 4.82 | 5.16 | |
| RMSLE | 0.23 | 0.19 | 0.21 | 0.09 | 0.23 | 0.24 | |
| R2 | 0.89 | 0.89 | 0.90 | 0.97 | 0.88 | 0.87 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almasoudi, R.; Daghistani, F.; Abuel-Naga, H. Peak and Residual Shear Interface Measurement between Sand and Continuum Surfaces Using Ring Shear Apparatus. Appl. Sci. 2024, 14, 6373. https://doi.org/10.3390/app14146373
Almasoudi R, Daghistani F, Abuel-Naga H. Peak and Residual Shear Interface Measurement between Sand and Continuum Surfaces Using Ring Shear Apparatus. Applied Sciences. 2024; 14(14):6373. https://doi.org/10.3390/app14146373
Chicago/Turabian StyleAlmasoudi, Rayed, Firas Daghistani, and Hossam Abuel-Naga. 2024. "Peak and Residual Shear Interface Measurement between Sand and Continuum Surfaces Using Ring Shear Apparatus" Applied Sciences 14, no. 14: 6373. https://doi.org/10.3390/app14146373
APA StyleAlmasoudi, R., Daghistani, F., & Abuel-Naga, H. (2024). Peak and Residual Shear Interface Measurement between Sand and Continuum Surfaces Using Ring Shear Apparatus. Applied Sciences, 14(14), 6373. https://doi.org/10.3390/app14146373






