Analysis of Planar Double-Layer Timber Spatial Frames by Using Parametric Tools
Abstract
1. Introduction
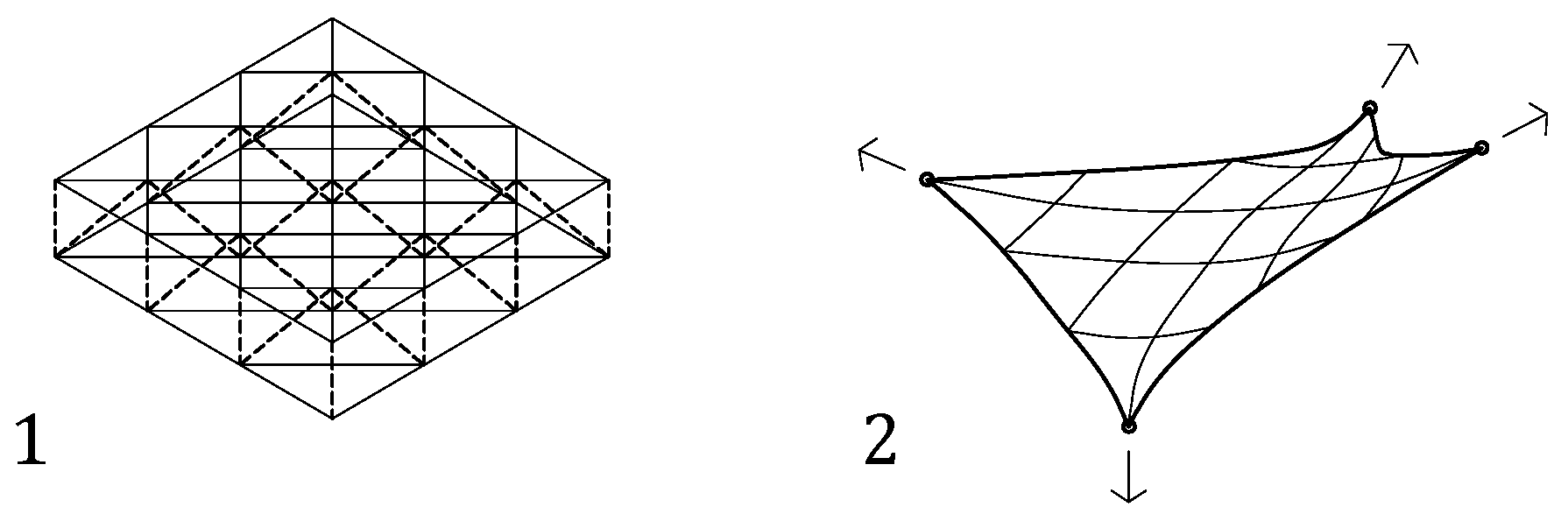
1.1. Space Frames
- lattice discrete structures: they are based on discretization to create a more or less regular frame (grid, barrel vaults, domes, towers and free forms).
- continuous structures: a single surface acting as a membrane (slabs, shell, fabric).
- biform structures: combination of both discrete and continuous parts.
- -
- Both planar and curved surfaces can be used. This research is focused on flat frames with the awareness that processes designed for a simple shape can be extrapolated to more complex ones. Parametrically, it is possible to apply any algorithmically designed process to any type of geometry.
- -
- A wide range of patented systems is available on the market. Even though most of them are aimed at metal construction, development in timber construction is also being accomplished. The main focus of the research is the node solution. It is at the joint where the stress transmission is concentrated and where the constructive requirements tend to reduce the cross-section of the timber bar. This contradiction poses a challenge in the development of the connection. It is, however, a difficulty that can be overcome, since timber construction is an option that looks very promising in the current climate crisis [3,6,7].
1.2. Construction Systems
1.2.1. Bar Elements
- -
- The hollow section equals the material’s value and offers less sensitivity to dimensional variations due to changes in environmental factors. Also, there is a reduction in risk against possible attacks of abiotic and biotic origin due to the fact that it is easier to carry out the integral treatment given its hollow character.
- -
- There is exploitation of the advantages offered by wood products in general and laminated ones in particular. It is a material that, due to its production process, has fewer imperfections and, therefore, a higher resistance performance. The same could be said of microlam (VLV).
- -
- The process of simple industrial execution consists of laminating rectangular pieces three or four times wider than the wall thickness of the hollow section so that, once the faces have been obtained by simple cutting, they can be glued against a master or guide piece and thus form the final piece. Consequently, the handling required is reduced, making the manufacturing cost competitive.
- -
- The square or rectangular hollow section is considered suitable for any type of frame, although it seems to be particularly suitable for the semi-octahedron frame.
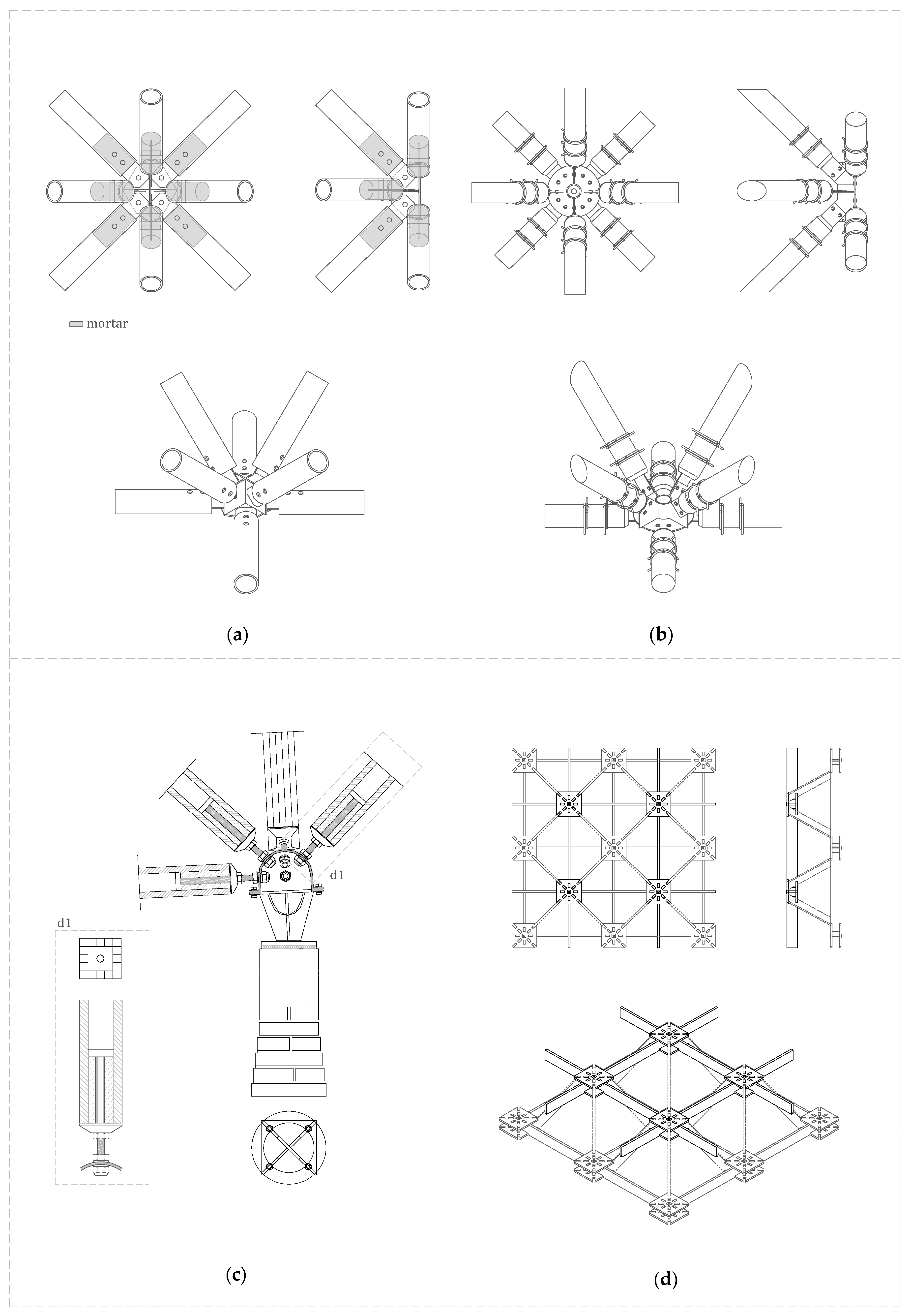
1.2.2. Joints
- -
- Bamboo connectors (Figure 4a): Ghavami and Moreira [13] developed a joint for the construction of double-layered bamboo space frames from octagonal plates welded to an octagonal base plate. During the research, the joint was tested on a double-layer bamboo space frame prototype with single supports every 4 m. The results were satisfactory. Currently, research is being continued with prototypes of larger spans.
- -
- Solid wood log connectors (Figure 4b): One of the most well-known researchers in this field is Dr. Huybers [14]. Interested in the use of small-diameter logs, which, until then, had no use and were abundant in forestry waste, he developed a simple wire-tying method for attaching galvanized steel connector plates to the previously hollowed ends of roundwood poles.
- -
- Connectors in glulam sections (Figure 4c): In the same thesis [12] in which hollow sections of glulam are developed as bars, the appropriate joint solution for them is also uncovered. A hollow sphere is proposed with a screwed cover that allows access to the interior and incorporates unthreaded holes for inserting the threaded rods and fixing them inside the sphere by means of nuts. At the opposite end, the bar is threaded into an octagonal nut. To attach the node to the wood, casting plates are fixed to the inside of the wooden element.
- -
- Connectors by CNC fabrication (Figure 4d): So far, metal-to-wood joints have been presented. The node is usually made of a high strength steel, since the stress concentration is very high at that point. Steel is a material easily shaped to the desired geometry (spherical, cylindrical, etc.) and strong enough to resist this punctual concentration of forces.
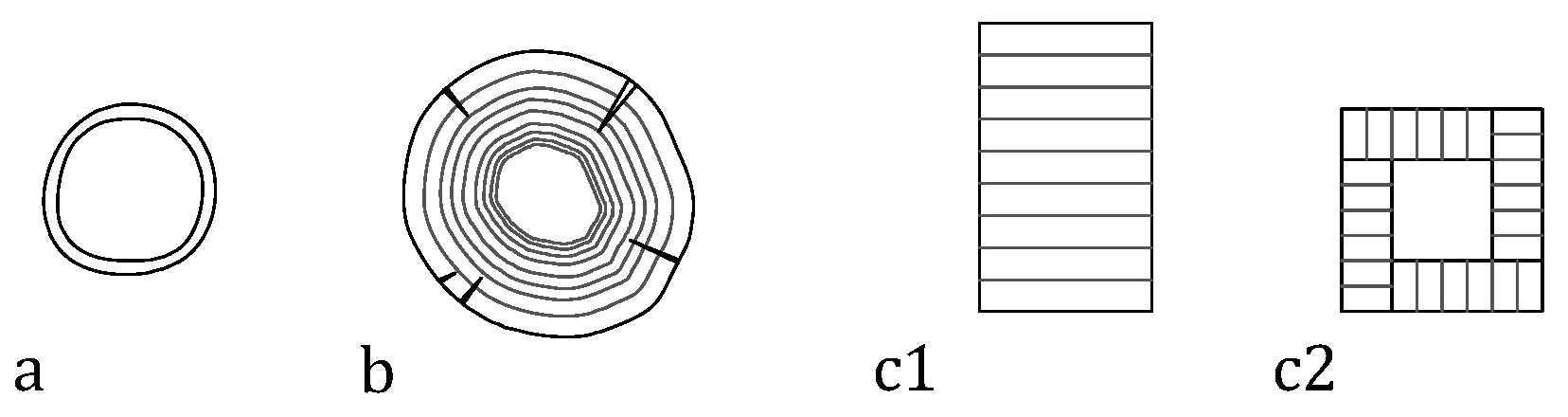
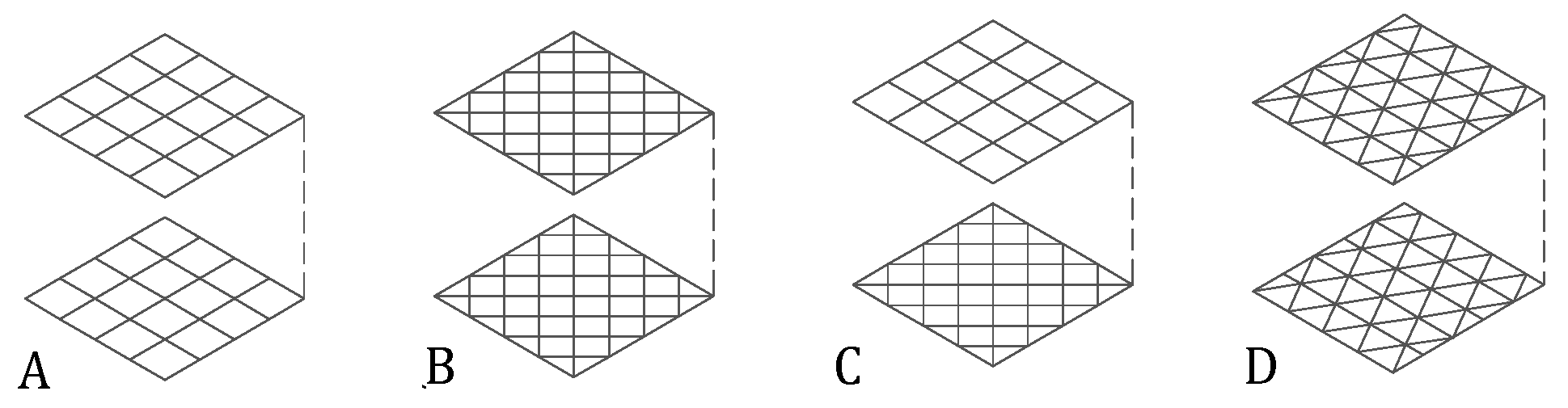
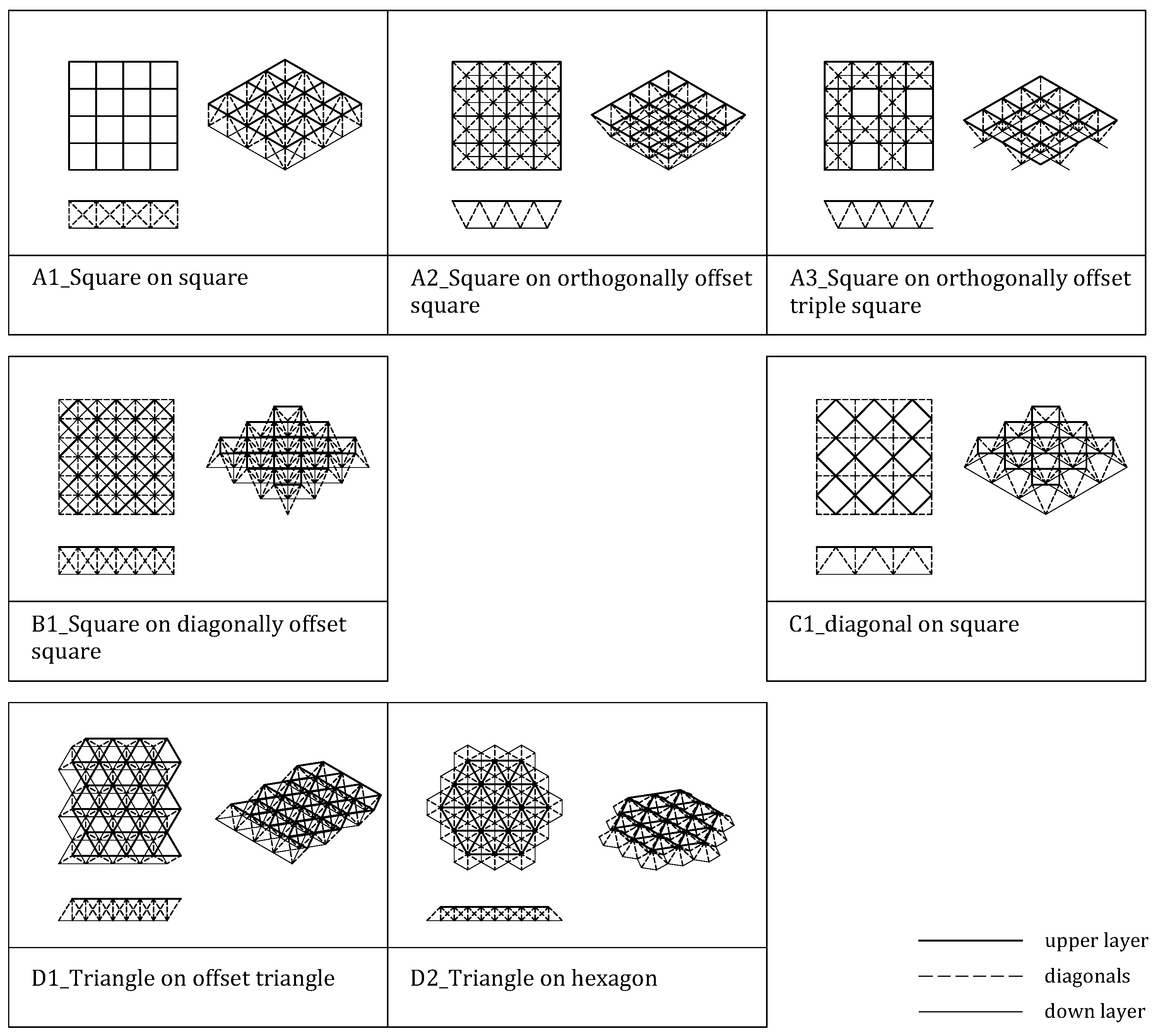
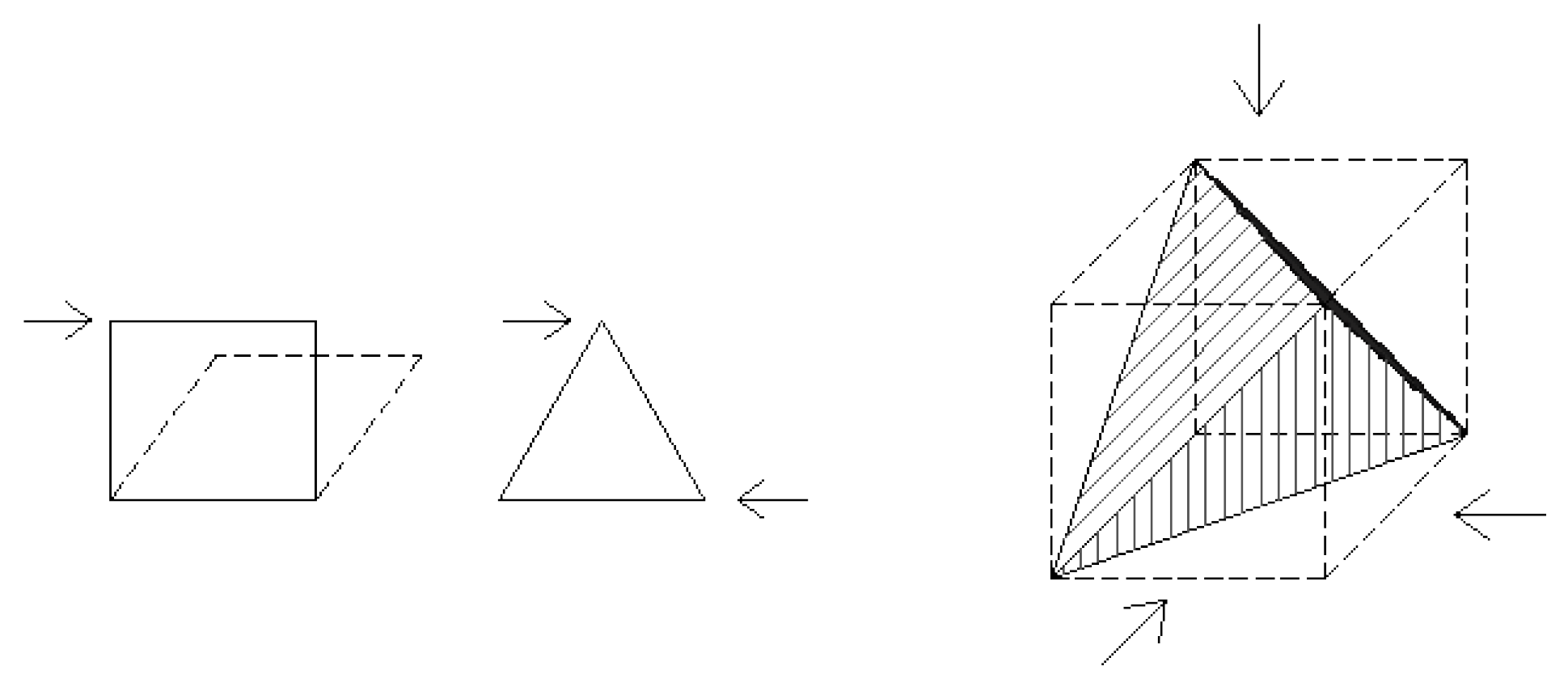
1.2.3. Topology
1.3. Computational Design
1.4. Objective
2. Materials and Methods
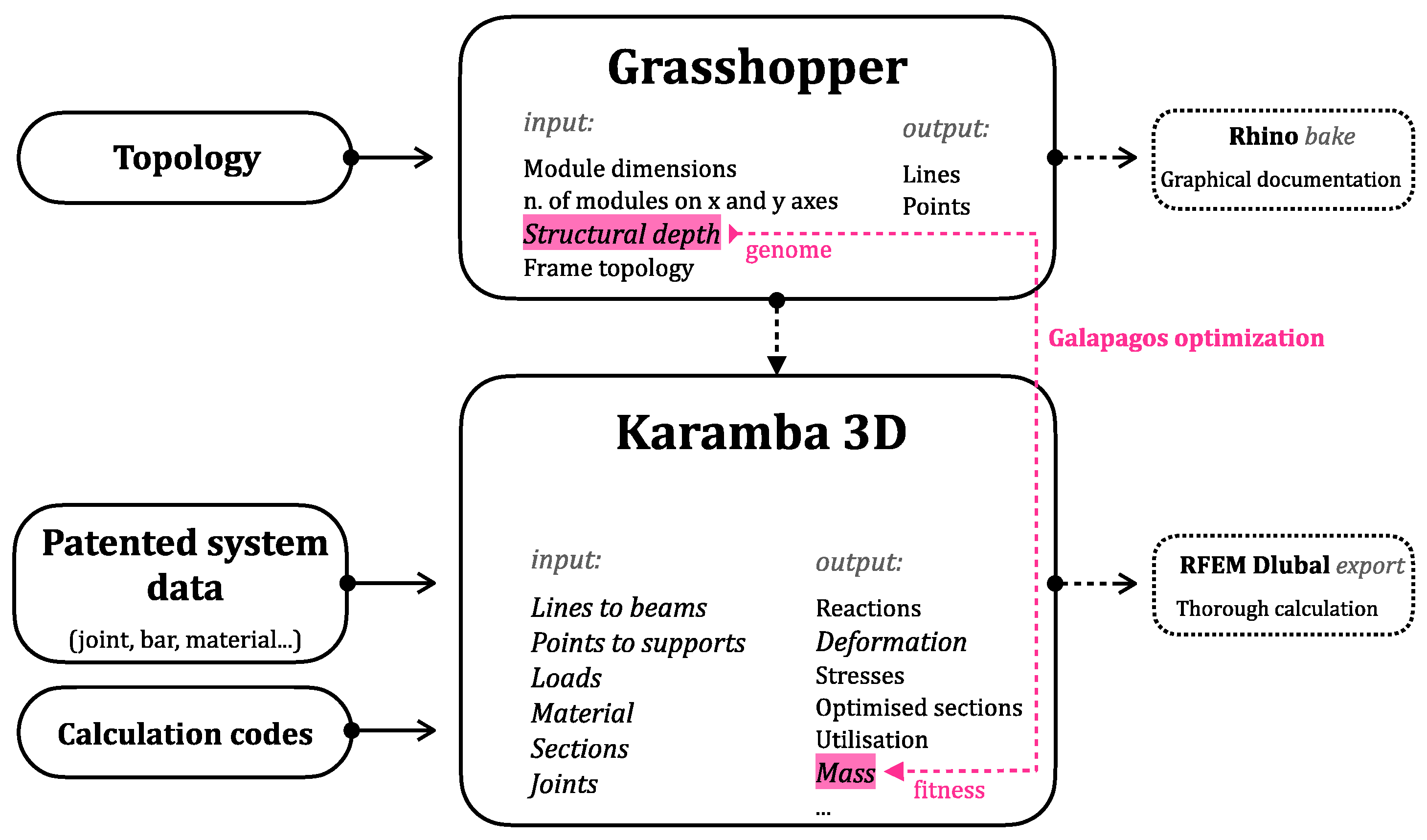
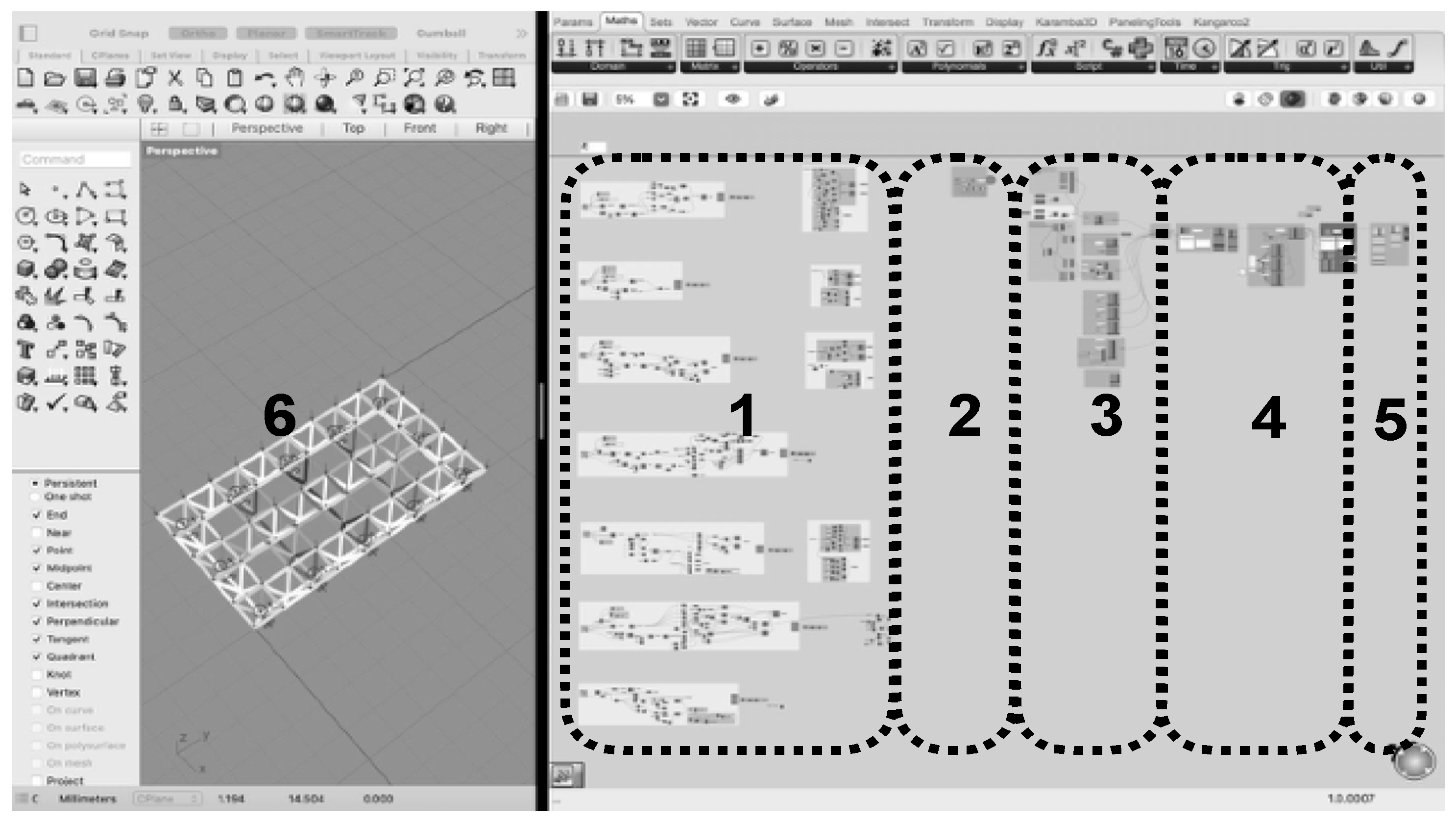
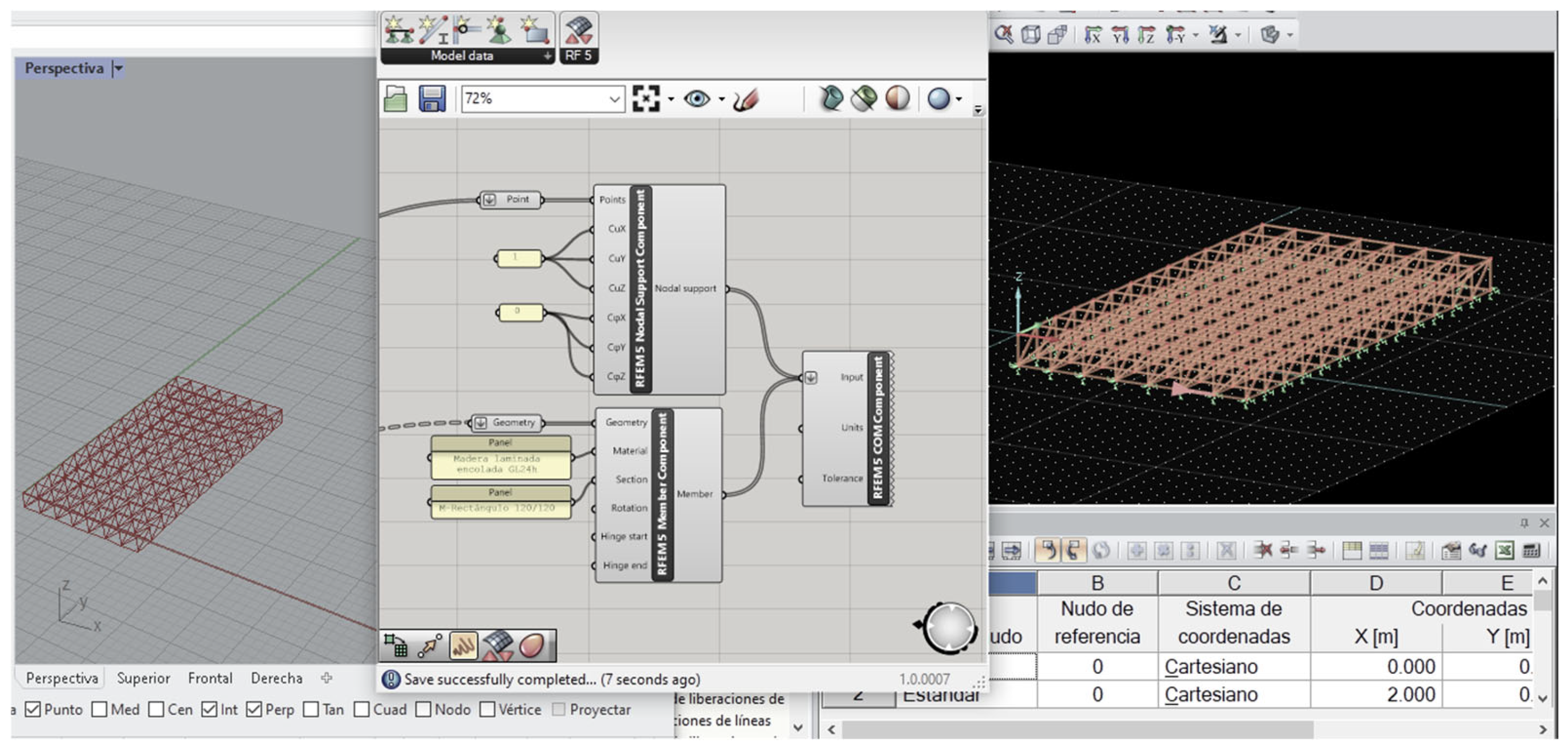
2.1. Creation of the Parametric Model
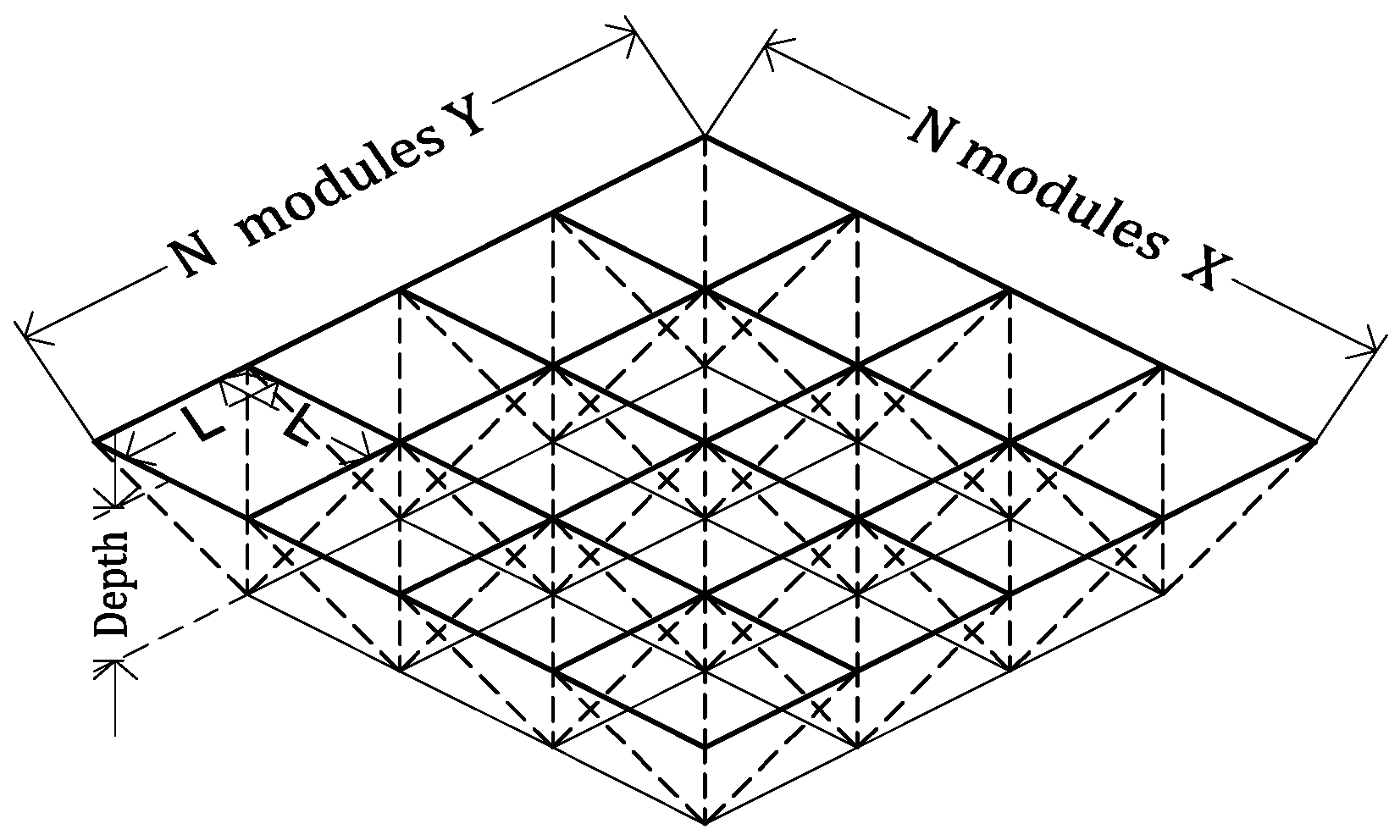
- parametric definition of the geometry of the frame: the 7 chosen frame topologies and their respective parameterized supports.
- grouping of the parameters: box grouping all the parameters to be chosen for the calculation, such as the frame topology, dimensions and number of modules and the depth.
- transformation from geometrical model to structural model: by entering data (loads, supports, material, cross-sections and joints), the chosen geometry (in the parameters grouping, 2) is translated into a finite element model.
- calculation and optimization: by means of Karamba 3D, the frame is calculated. Certain components (section optimization and genetic algorithms) are added to optimize the results.
- visualization of results: a command is given to visualize the results in the Rhino viewer (6).
2.2. Optimization Components
2.2.1. Cross-Section Optimization
2.2.2. Genetic Algorithm
2.3. Data Entry
- -
- 7 m × 12.5 m: In order to be able to analyze the behavior in relatively small spans, the 12.5 m dimension has been taken. This measure is the limit above which special transport is required. One of the advantages of space frames is that they are reduced to easily transportable bars and nodes regardless of the span they have to overcome.
- -
- 12.5 m × 25 m: medium spans, very common in light covers for semi-Olympic swimming pools, frontons, children’s playgrounds and so on.
- -
- 20 m × 40 m: As the work has developed, it has been considered necessary to add a roof of intermediate measures between 25 and 50 m, since many of the topologies do not reach 50 m but 40 m (with the following limitations: GL24h wood and maximum depth of 3 m).
- -
- 25 m × 50 m: large spans suitable for Olympic swimming pools, markets and so on.
- perimeter continuous support: The most stable of all. The situation may occur that the facade of the covered space is the supporting element, and in such cases, this is the option to go for.
- three-sided support: All the roofs analyzed are rectangular in plan, and one of the longer sides has been freed to force the structure. This case is common in roofs for frontons, recreational areas, multi-purpose halls, etc., where the entire perimeter is closed except for one of the long sides.
- four point support: The two previous options correspond to continuous supports (walls/columns in a row); this, however, is the option to analyze the performance with 4 punctual supports uniformly distributed. In order to generate numerical results [42,43], a system of hollow glulam bars and a generic articulated joint has been simulated.
3. Results and Discussion
- A first individual analysis, in which each frame is studied separately to obtain the optimal depth-to-span ratio by means of the genetic algorithm.
- A second comparative phase, where the results and data on the performance of each topology are collected for a comparative analysis. This will enable the identification of the range of use and limitation of each frame.
- -
- Wind load: To avoid the extra parameterization of the pressure/suction areas defined by the CTE, the maximum load has been applied.
- -
- Application of the loads: To calculate the point load, instead of differentiating between edge, corner and center nodes, the same area (that of the center being the largest) has been applied equally to all nodes.
- -
- The joints are modeled as simple articulations, although the reality is that moments are always produced due to the lack of complete articulation. A developed calculation would involve nuancing the stiffness of the joint.
3.1. Individual Analysis
Optimal Depth for the Lowest Weight Possible
3.2. Comparative Analysis
- -
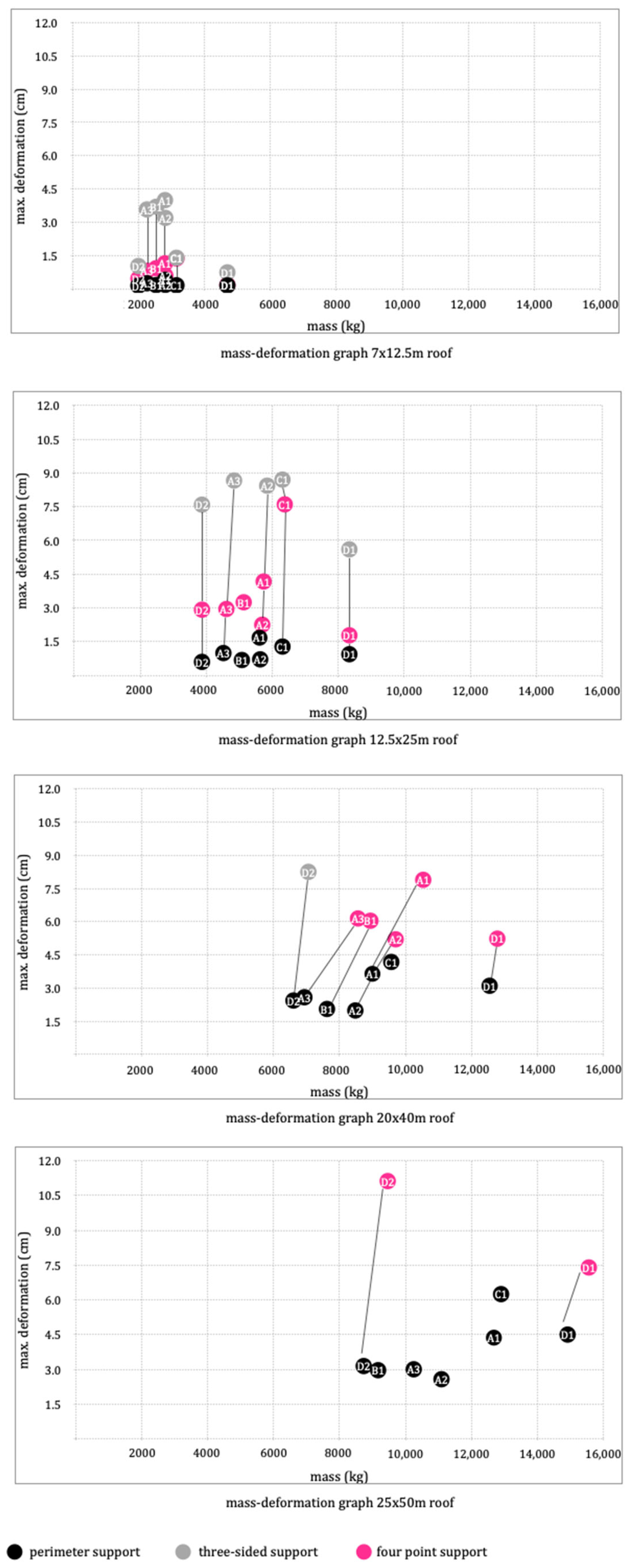
- Mass–deformation relationship: The relationship that summarizes the structural behavior of the frame. This shows how stiff the topology is and how much the section has to be increased to cover the required span (as it affects the mass).
- -
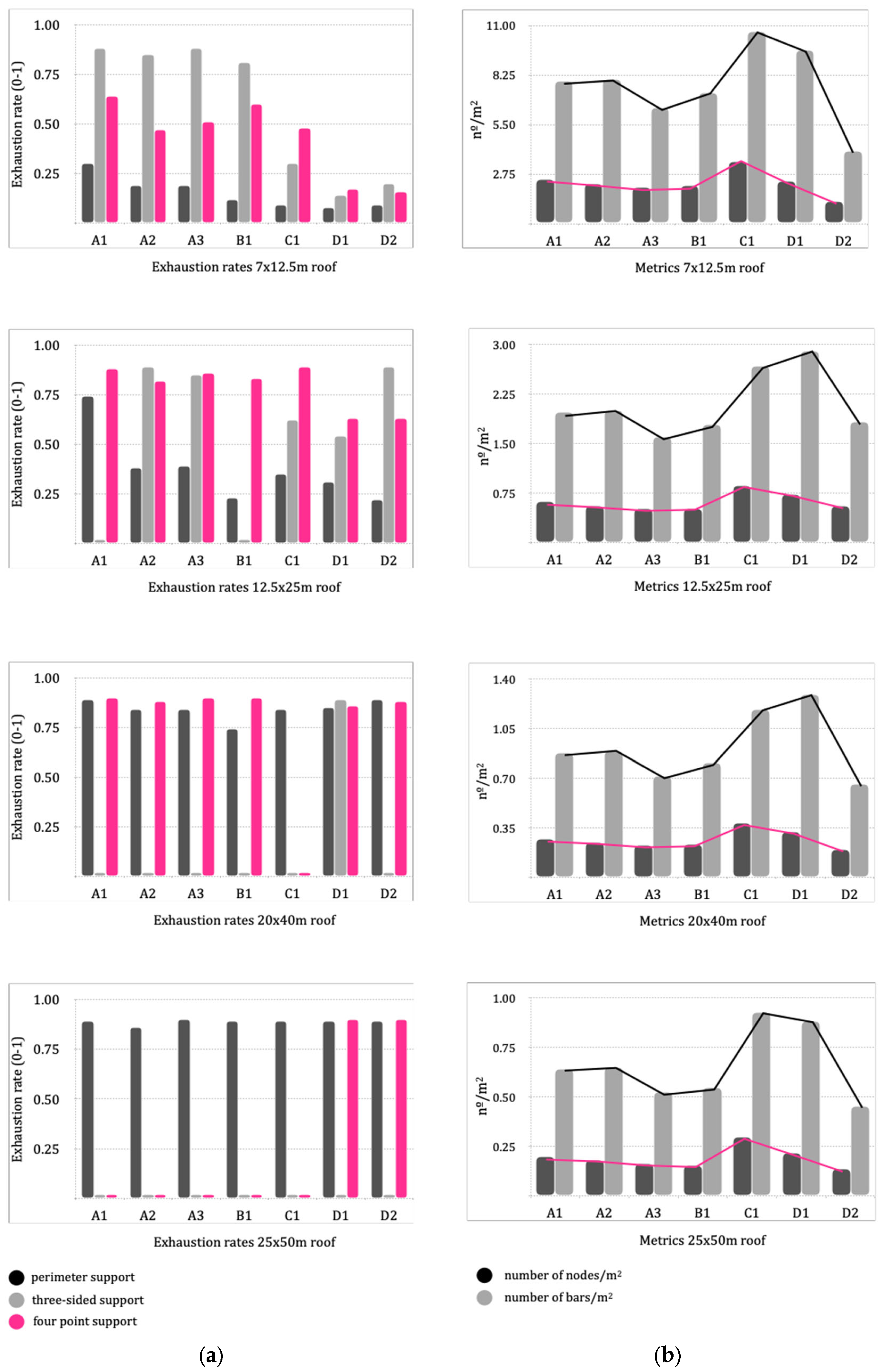
- Exhaustion rates: This indicates how close the bars are to their maximum stress capacity. In addition, it also detects when the structure is being optimally utilized and when the geometry does not allow the bars to work efficiently.
- -
- Metrics: Along with the structural behavior, the numbers of bars and nodes are collected for cost estimations.
3.2.1. Mass–Deformation Ratio
3.2.2. Exhaustion Rates
3.2.3. Metrics: Nodes and Bars
4. Conclusions
4.1. Topologies
- Group A (A1–A2–A3): These are the most balanced topologies, applicable in various situations. In this regard, it is only logical that they are the most common ones used. Of the three, A1 is the worst performer; its cubic module means that with the greatest number of nodes per square meter, it still has the greatest deformation.
- On the other hand, the semi-octahedral modulus provides A2 and A3 meshes with sufficient stiffness without affecting the mass too much. Between the last two, there is not that much difference; A3 turns out to be a good alternative to A2 when mass/economics is the determining factor, without serious detriment in deformations. In general, all three are relatively simple geometry topologies and easy to fit.
- Group D (D1–D2): their tetrahedral modulus makes them extremely rigid. Especially D1 is the preferred choice for large spans (over 40–50 m). From these spans on, the mesh starts to be competitive: the node-bar/m2 ratio decreases drastically (which makes them more cost-effective) and the depletion rates go up (which indicates that the structure is working). A future research task would be to further analyze the limits of tetrahedral meshes in larger spans (above 50 m).
- The D2 mesh is presented as a good alternative to D1. Although the lower layer detaches a significant number of bars to form hexagons, it is still a rigid mesh, competitive for its lightness (with deformations lower than those of mesh A3, also lightened). One drawback that can arise is the difficulty in handling the hexagonal geometry. If the project does not contemplate the use of these characteristic shapes from the beginning, edges and joints can become an added complication.
- B1: It can be a good alternative to A2 mesh. The metrics (number of bars and nodes) are better, and for what is saved in elements, the deformations do not increase so much.
- The only doubt that may come up is (as in the D2) the geometry itself. As the bars are not arranged parallel to the edges, bars of special lengths arise to finish off the mesh, problems that group A can avoid.
- C1: Of the seven topologies, C1 is the one that behaves the worst in general. It tends to destabilize easily, and it is comfortable up to a 20–25 m span. Beyond this limit, it becomes very limited. It is also the topology that needs more nodes and bars per square meter (slightly more than D1). In general, it seems that the geometry is not appropriate for generating a structural space frame.
4.2. Support Distributions
4.3. Using Grasshopper and Karamba
4.4. Final Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Margarit, J.; Buxadé, C.; Buxadé i Ribot, C.; Margarit, J. Las Mallas Espaciales en Arquitectura; Gustavo Gili: Barcelona, Spain, 1972. [Google Scholar]
- Xu, X.; You, J.; Wang, Y.; Luo, Y. Analysis and assessment of life-cycle carbon emissions of space frame structures. J. Clean. Prod. 2023, 385, 135521. [Google Scholar] [CrossRef]
- Robotic Manufacturing of Timber Space-Frames—DigitalFUTURES. Available online: https://digitalfutures.international/workshop/robotic-manufacturing-of-timber-space-frames/ (accessed on 12 March 2023).
- Huang, Y.; Garrett, C.R.; Ting, I.; Parascho, S.; Mueller, C.T. Robotic additive construction of bar structures: Unified sequence and motion planning. Constr. Robot. 2021, 5, 115–130. [Google Scholar] [CrossRef]
- Finch, G.; Marriage, G. Reducing Building Waste through Light Timber Frame Design. In Proceedings of the PLEA 2018 HONG KONG, Hong Kong, China, 10–12 December 2018. [Google Scholar]
- Koronaki, A.; Shepherd, P.; Evernden, M. Rationalization of freeform space-frame structures: Reducing variability in the joints. Int. J. Archit. Comput. 2020, 18, 84–99. [Google Scholar] [CrossRef]
- Finch, G.; Marriage, G.; Pelosi, A.; Gjerde, M. Applications and Opportunities for Timber Space Frames in the Circular Economy. In Proceedings of the CIB World Building Congress, Hong Kong, China, 17–21 June 2019. [Google Scholar]
- Bruun, E.P.G.; Adriaenssens, S.; Parascho, S. Structural rigidity theory applied to the scaffold-free (dis)assembly of space frames using cooperative robotics. Autom. Constr. 2022, 141, 104405. [Google Scholar] [CrossRef]
- Baverel, O. Nexorade: A Family of Interwoven Structures; University of Surrey (United Kingdom): Guildford, UK, 2000. [Google Scholar]
- Gutiérrez-Astudillo, N.C.; Flores, A.; Preciado, A. Reciprocal frame structures, a first academic approach to sustainable structures. In Proceedings of the IASS Annual Symposia, Tokyo, Japan, 26–30 September 2016; Available online: https://www.semanticscholar.org/paper/Reciprocal-frame-structures%2C-a-first-academic-to-Guti%C3%A9rrez-Astudillo-Flores/bad4f5510e8ebd89e009c3bd8d9762e3132616e5 (accessed on 25 April 2023).
- Adriaenssens, S.; Block, P.; Veenendaal, D.; Williams, C. (Eds.) Shell Structures for Architecture: Form Finding and Optimization; Routledge: London, UK, 2014; ISBN 978-1-315-84927-0. [Google Scholar]
- Vázquez, J.A. Las Barras Huecas de Madera en la Construcción de Estructuras Espaciales; Universidade da Coruña: La Coruna, Spain, 2001. [Google Scholar]
- Ghavami, K.; Moreira, L.E. 61. Double-layer bamboo space structures. In Space Structures 4; Thomas Telford Publishing: London, UK, 1993; ISBN 978-0-7277-4941-3. [Google Scholar]
- Huybers, P. Palos de madera como elementos de estructuras espaciales. Rev. Digit. Cedex 1990, 79, 99. [Google Scholar]
- Finch, G.; Marriage, G.; Gjerde, M.; Pelosi, A. Experiments in Timber Space Frame Design: Fabrication, Construction and Structural Performance. In Proceedings of the 24th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA), Hong Kong, China, 15–18 April 2019. [Google Scholar]
- Lan, T.T. Space Frame Structures; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Mupona, G.T. Development of Space Truss Systems in Timber. Master’s Thesis, Faculty of Engineering and the Built Environment, University of Cape Town, Cape Town, South Africa, 2004. Available online: https://www.semanticscholar.org/paper/Development-of-space-truss-systems-in-timber-Mupona/211102da0a241e41447b23fcb658ca3a7b9fd99b (accessed on 12 March 2023).
- Moggio, N. Glued Laminated Timber Space Truss Systems. Master’s Thesis, Università di Trento, Trento, Italky, 2012. Available online: http://lup.lub.lu.se/student-papers/record/3131142 (accessed on 12 March 2023).
- Álvarez Pablos, J. Mallas Planas y Cilíndricas de Módulos Apilables de Madera Laminada; Universidade da Coruña. Escola Técnica Superior de Arquitectura: La Coruna, Spain, 1998; ISBN 978-84-692-8073-7. Available online: https://ruc.udc.es/dspace/handle/2183/5561 (accessed on 12 March 2023).
- Chilton, J. Space Grid Structures; Architectural Press: Oxford, UK, 2000; ISBN 978-0-7506-3275-1. [Google Scholar]
- Eekhout, M. Architecture in Space Structures; Uitgeverij 010 Publishers: Rotterdam, The Netherlands, 1989; ISBN 978-90-6450-080-0. [Google Scholar]
- Aksöz, Z.; Preisinger, C. An Interactive Structural Optimization of Space Frame Structures Using Machine Learning. In Impact: Design with All Senses; Gengnagel, C., Baverel, O., Burry, J., Ramsgaard Thomsen, M., Weinzierl, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 18–31. [Google Scholar]
- Jormakka, K. Basics Design Methods; Birkhäuser: Basel, Switzerland, 2017; ISBN 978-3-0356-1147-2. [Google Scholar]
- Koronaki, A.; Shepherd, P.; Evernden, M. Layout Optimization of Space Frame Structures. In Proceedings of the IASS Annual Symposium 2017, Hamburg, Germany, 25–28 September 2017. [Google Scholar]
- Gordon, J.E. Estructuras o Por qué las Cosas no se Caen, 2nd ed.; Calamar: Madrid, Spain, 2004; ISBN 978-84-96235-06-9. [Google Scholar]
- De Moraes, M.H.; Fraga, I.; Junior, W.; Christoforo, A. Comparative analysis of the mechanical performance of timber trusses structural typologies applying computational intelligence. Rev. Árvore 2022, 46, e4604. [Google Scholar] [CrossRef]
- Apolinarska, A.A. Complex Timber Structures from Simple Elements: Computational Design of Novel Bar Structures for Robotic Fabrication and Assembly. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2018. [Google Scholar]
- Andrén Jakobsson, N.; Bohman, S. A Generative Design of Timber Structures according to Eurocode. Development of a Parametric Model in Grasshopper; KTH Royal Institute of Technology: Stockholm, Sweden, 2019; Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-255661 (accessed on 12 March 2023).
- Almaraz, A. Evolutionary Optimization of Parametric Structures: Understanding Structure and Architecture as a Whole from Early Design Stages. Master’s Thesis, University of A Coruña, La Coruna, Spain, 2015. Available online: https://ruc.udc.es/dspace/handle/2183/15965 (accessed on 12 March 2023).
- Martínez Villarroya, D. Arquitectura Fractal: Optimización Topológica. Available online: https://oa.upm.es/55874/ (accessed on 12 March 2023).
- Muñoz Ávila, D.A. Implementación de un Algoritmo de Optimización Multi—Objeto de una red de Barras Utilizando un Lenguaje de Programa-ción Visual en “Rhinoceros’ y sus Extensiones. 2021. Available online: https://repositorio.uisek.edu.ec/handle/123456789/4519 (accessed on 12 March 2023).
- Navarro Mateu, D. Procesos Naturales Aplicados a la Arquitectura Mediante Computación: Ciencia Evo-Devo y Modelado Algorítmico a Través de Grasshopper. Ph.D. Thesis, Universitat Internacional de Catalunya, Barcelona, Spain, 2017. Available online: https://www.tdx.cat/handle/10803/552427 (accessed on 12 March 2023).
- Villar Monteagudo, I. Estudio Paramétrico Sobre Mallas de Doble Capa. 2015. Available online: https://ruc.udc.es/dspace/handle/2183/16171 (accessed on 12 March 2023).
- Weldegiorgis, F.; Dhungana, A.R. Parametric Design and Optimization of Steel and Timber Truss Structures: Development of a Workflow for Design and Optimization Processes in Grasshopper 3D Environment. 2020. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-277901 (accessed on 12 March 2023).
- Yan, X.; Bao, D.; Zhou, Y.; Xie, Y.; Cui, T. Detail control strategies for topology optimization in architectural design and development. Front. Archit. Res. 2022, 11, 340–356. [Google Scholar] [CrossRef]
- Preisinger, C. Linking Structure and Parametric Geometry. Archit. Des. 2013, 83, 110–113. [Google Scholar] [CrossRef]
- Network, Scott Davidson Created This Ning Network. Grasshopper. Available online: https://www.grasshopper3d.com/ (accessed on 29 April 2023).
- Associates, Robert McNeel & Associates. Rhinoceros 3D. Available online: https://www.rhino3d.com/es/ (accessed on 29 April 2023).
- Karamba3D. Available online: https://karamba3d.com/ (accessed on 29 April 2023).
- Software Para Análisis Estructural y Dimensionado|Dlubal Software. Available online: https://www.dlubal.com/es (accessed on 29 April 2023).
- UNE-EN 1995-1-1:2016 Eurocódigo 5. Proyecto de Estructuras de Madera. Parte 1-1: Reglas Generales y Reglas para Edificación. Available online: https://www.une.org/encuentra-tu-norma/busca-tu-norma/norma?c=N0056510 (accessed on 1 May 2023).
- Muñoz-Vidal, M. Generación y Cálculo de Mallas Espaciales; Universidad, Departamento de Tecnolog’ia de la Construcción: La Coruña, Spain, 1993. [Google Scholar]
- Navarro Carrasco, S. Cálculo Estructural de Una Gran Marquesina Espacial Ejecutada Íntegramente Mediante una Malla Espacial de Doble Capa de Acuerdo con los Eurocódigos que Disponen de Anejo Nacional; Cartagena, Spain. 2015. Available online: https://repositorio.upct.es/handle/10317/4912 (accessed on 12 March 2023).
- Cavia-Sorret, P. Las mallas espaciales y su aplicación en cubiertas de grandes luces. Re. Rev. De Edif. 1993, 15, 7–15. [Google Scholar] [CrossRef]

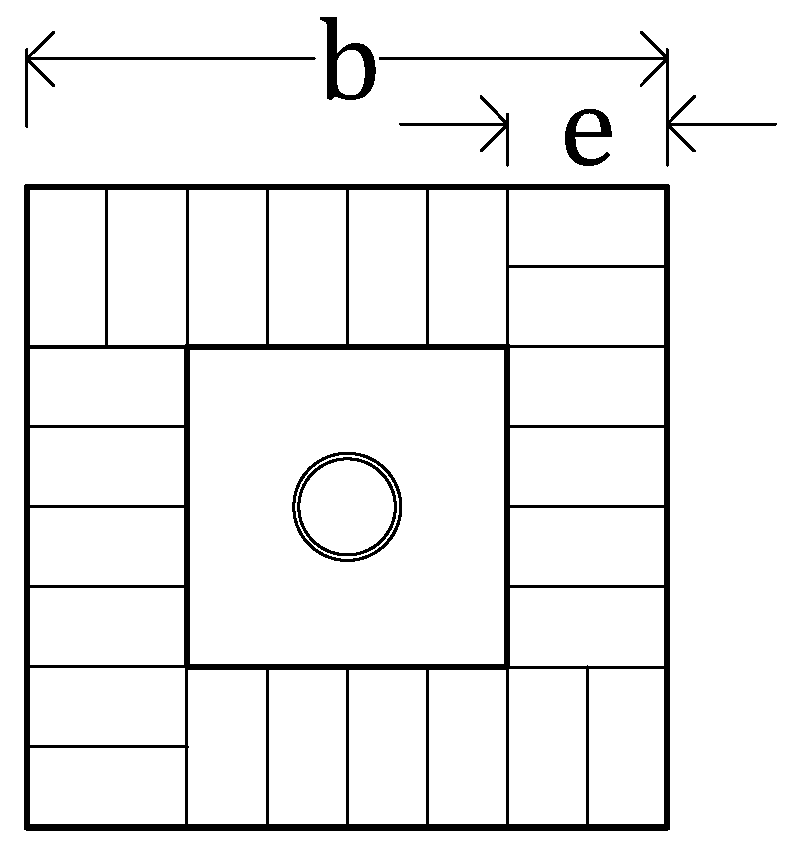
| Sections (Figure 13) | Hollow section bars with a solid wood plug at both ends where a threaded tube is screwed. Values for b (cm) = between 10 y 22; values for e(mm) = 25, 30, 35, 40 |
| Joints-Supports | Joints and supports are modeled as articulations. |
| Material | The GL24h class is chosen to see the performance of the frames with the lowest of the laminated classes (values from table E3 of the CTE-DB-SE-M). |
| from the current regulations (CTE-DB-SE, EA, M) are extracted: | |
| Loads | Dead weight, G1 overload, snow (<1000 m) and wind. |
| 5 hypothetical load combinations corresponding to light roofs (G1): H1_1.35 G + 1.5 Quse + (1.5 × 0.5 × Qsnow) H2_1.35 G + 1.5 Qsnow + (1.5 × 0.6 × Qwind pressure) H3_1.35 G + 1.5 Qwind pressure + (1.5 × 0.5 × Qsnow) H4_1.35 G + 1.5 Quse + (1.5 × 0.5 × Qsnow) + (1.5 × 0.6 × Qwind pressure) H5_1.35 G + 1.5 Qwind suction + (1.5 × 0.5 × Qsnow) | |
| Service Class | 2 (open roof) |
| Kmod | 0.8 (service class 2 y medium duration) |
| Security coef. | 1.35 (Table 4.1 -glued laminated timber) |
| Simultaneity rate | ψuse class = 0; ψsnow = 0.5; ψwind = 0.6 (Table 4.2) |
| Deflection limit | L/300 (Section “4.3.3.1 Flecha”, case c) |
| Use case | 2 (open roof) NP1 no specific requirements. All sides treated with insecticide and fungicide product. |
| of the current regulations (CTE-DB-SI) are extracted: | |
| Fire reaction | C-s2-d0 (SI 1-Table 4.1) by intumescent coating |
| Fire stability | R30 (SI 6-light roofs) by intumescent coating |
| Frame | Number of Modules | Module Dimensions * (cm) | Galapagos Depth (cm) | Depth/Module Ratio |
|---|---|---|---|---|
| A1 | x = 7, y = 13 | 200 | 100 | 0.50 |
| 300 | 210 | 0.70 | ||
| A2 | x = 7, y = 13 | 200 | 100 | 0.50 |
| 300 | 180 | 0.60 | ||
| A3 | x = 7, y = 13 | 200 | 110 | 0.55 |
| 300 | 210 | 0.70 | ||
| B1 | x = 5, y = 9 | 200 | 100 | 0.50 |
| 300 | 210 | 0.70 | ||
| C1 | x = 7, y = 13 | 200 | 140 | 0.70 |
| - | - | - | ||
| D1 | x = 14, y = 16 | 200 | 100 | 0.50 |
| 300 | 190 | 0.63 | ||
| D2 | x = 5, y = 9 | 150 | 100 | 0.67 |
| 250 | 170 | 0.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manterola-Ubillos, M.; Gonzalez-Quintial, F.; Rico-Martinez, J.M.; Benito Ayucar, J.; Begiristain-Mitxelena, J.A. Analysis of Planar Double-Layer Timber Spatial Frames by Using Parametric Tools. Appl. Sci. 2024, 14, 6400. https://doi.org/10.3390/app14156400
Manterola-Ubillos M, Gonzalez-Quintial F, Rico-Martinez JM, Benito Ayucar J, Begiristain-Mitxelena JA. Analysis of Planar Double-Layer Timber Spatial Frames by Using Parametric Tools. Applied Sciences. 2024; 14(15):6400. https://doi.org/10.3390/app14156400
Chicago/Turabian StyleManterola-Ubillos, Maddi, Francisco Gonzalez-Quintial, Jose Miguel Rico-Martinez, Josu Benito Ayucar, and Jon Andoni Begiristain-Mitxelena. 2024. "Analysis of Planar Double-Layer Timber Spatial Frames by Using Parametric Tools" Applied Sciences 14, no. 15: 6400. https://doi.org/10.3390/app14156400
APA StyleManterola-Ubillos, M., Gonzalez-Quintial, F., Rico-Martinez, J. M., Benito Ayucar, J., & Begiristain-Mitxelena, J. A. (2024). Analysis of Planar Double-Layer Timber Spatial Frames by Using Parametric Tools. Applied Sciences, 14(15), 6400. https://doi.org/10.3390/app14156400







