New Physically-Based Mathematical Model and Experiments for a Recently Invented Solar Pot
Abstract
:1. Introduction
- A new physically-based mathematical model is proposed to describe the examined, recently invented solar pot. Computer simulations are made with the model, based on which conclusions are drawn regarding the practical applicability of the solar pot.
- An experimental system of the hydraulically connected solar pot and a solar collector is physically assembled. The different variables of the system (different temperature values) are measured. Based on measured data, conclusions are drawn regarding the practical applicability of the solar pot.
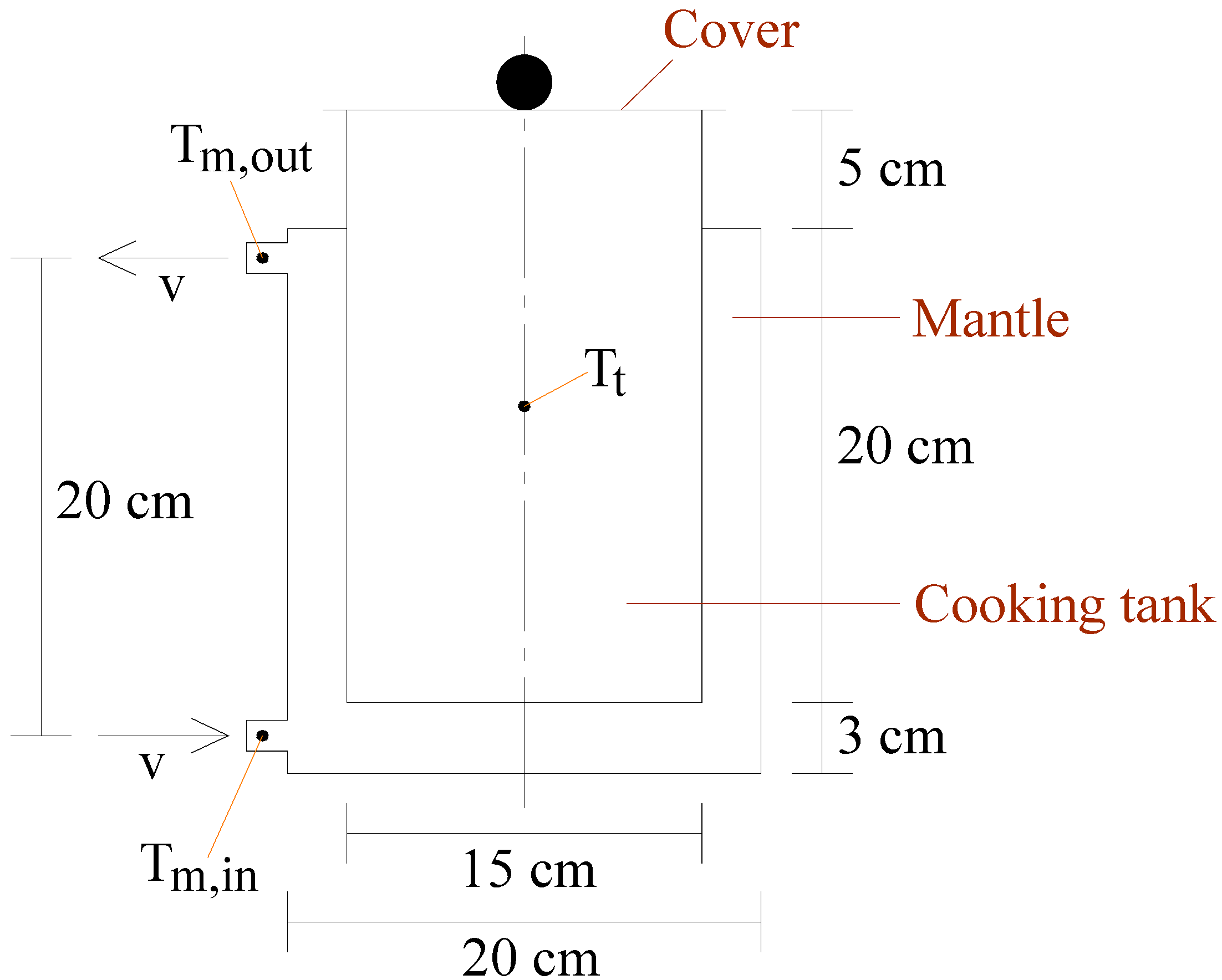
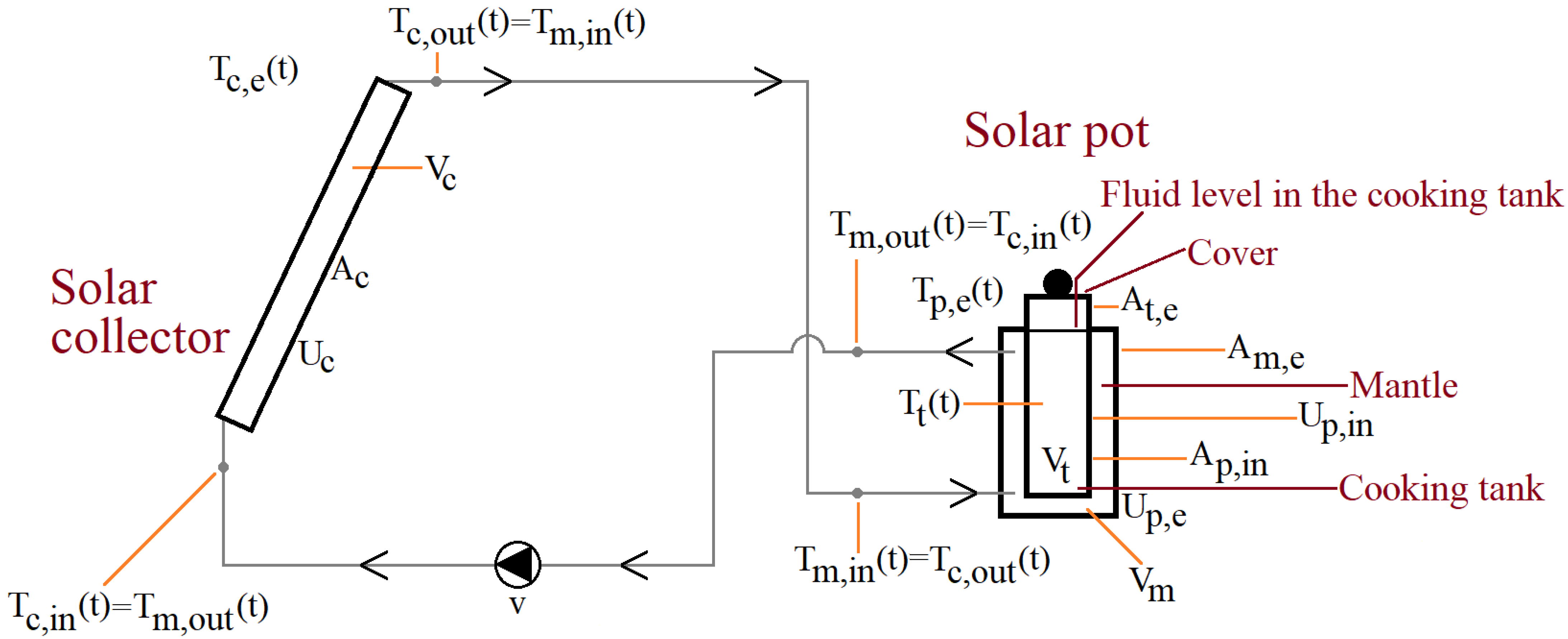
2. System Description
- : temperature of the solar collectors’s environment (outdoors), °C,
- : solar collector inlet (water) temperature, °C,
- : solar collector outlet (water) temperature, °C,
- : temperature in the cooking tank, °C,
- : temperature of the solar pot’s environment (indoors), °C,
- : mantle inlet (water) temperature, °C,
- : mantle outlet (water) temperature, °C.
- : surface area of the collector (one side), ,
- : surface area of the mantle to the environment, ,
- : surface area of the cooking tank to the environment, ,
- : surface area between the mantle and the cooking tank, ,
- : overall heat loss coefficient of the solar collector, ,
- : overall heat loss coefficient of the solar pot, ,
- : overall heat transfer coefficient between the mantle and the cooking tank, ,
- v: volumetric flow rate of the pump, ,
- : volume of the collector, ,
- : volume of the mantle, ,
- : volume of the cooking tank, .
3. Mathematical Modelling
3.1. Mathematical Model
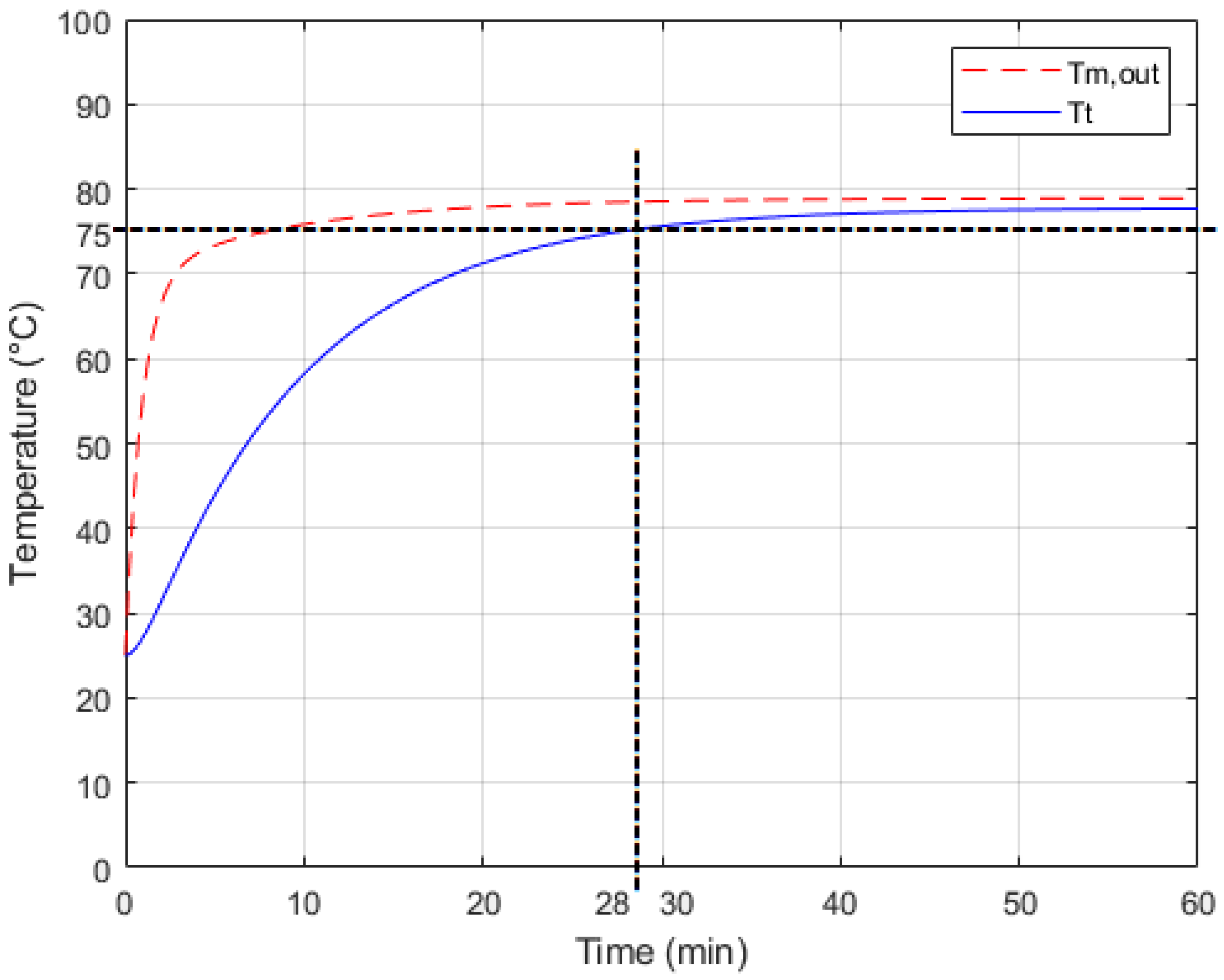
3.2. Simulation Results
- Convective heat transfer between the inside of the mantle and the inner surface of the mantle’s wall. (This wall is adjacent to the environment.) Taking into account the liquid in the mantle (water) and the material of the mantle’s wall (stainless steel), and assuming forced convective heat transfer along the inner surface of the mantle’s wall, the heat transfer coefficient is , which is an average value according to [34].
- Thermal conduction inside the mantle’s wall. Taking into account the material of the mantle’s wall, which is stainless steel (with a thickness of 0.002 m), the thermal conductivity coefficient is , which is an average value according to [34].
- Convective heat transfer between the outer surface of the mantle’s wall and the solar pot’s environment. Taking into account the material of the mantle’s wall (stainless steel) and the air surrounding the pot from outside, and assuming free convective heat transfer along the surface of the wall, the heat transfer coefficient is , which is an average value according to [34].
- Convective heat transfer between the inside of the mantle and the outer surface of the cooking tank’s wall. Taking into account the liquid in the mantle (water) and the material of the cooking tank wall (stainless steel), and assuming forced convective heat transfer along the surface of the wall, the heat transfer coefficient is , which is an average value according to [34].
- Thermal conduction inside the mantle’s wall. (For more details, see Note 2 above.)
- Convective heat transfer between the inner surface of the cooking tank’s wall and the inside of the cooking tank. Taking into account the material of the wall (stainless steel) and the liquid in the cooking tank (water), and assuming free convective heat transfer along the surface of the wall, the heat transfer coefficient is , which is an average value according to [34].
3.3. Exact Calculation of the Equilibrium
4. Experimentation
4.1. Experimental System
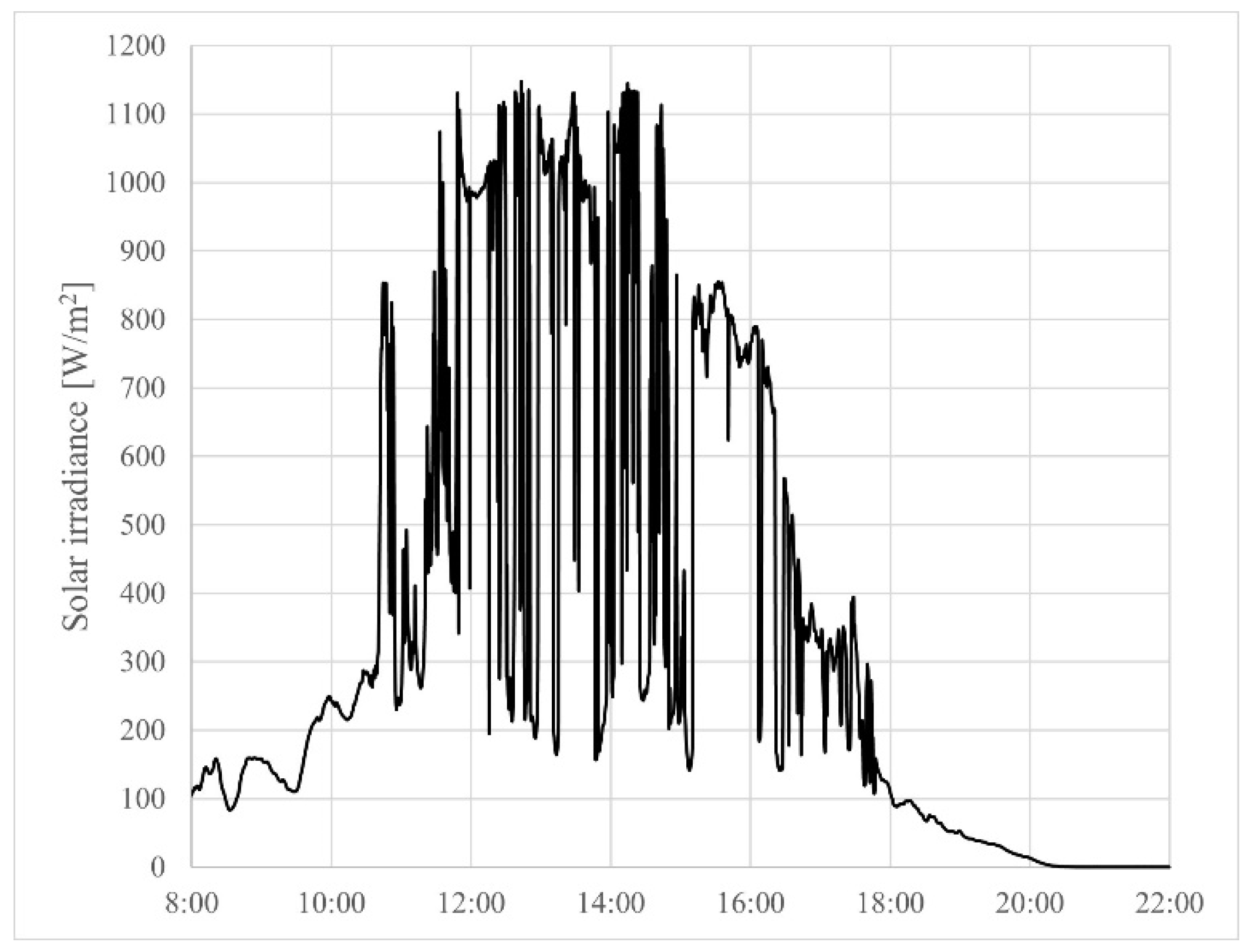
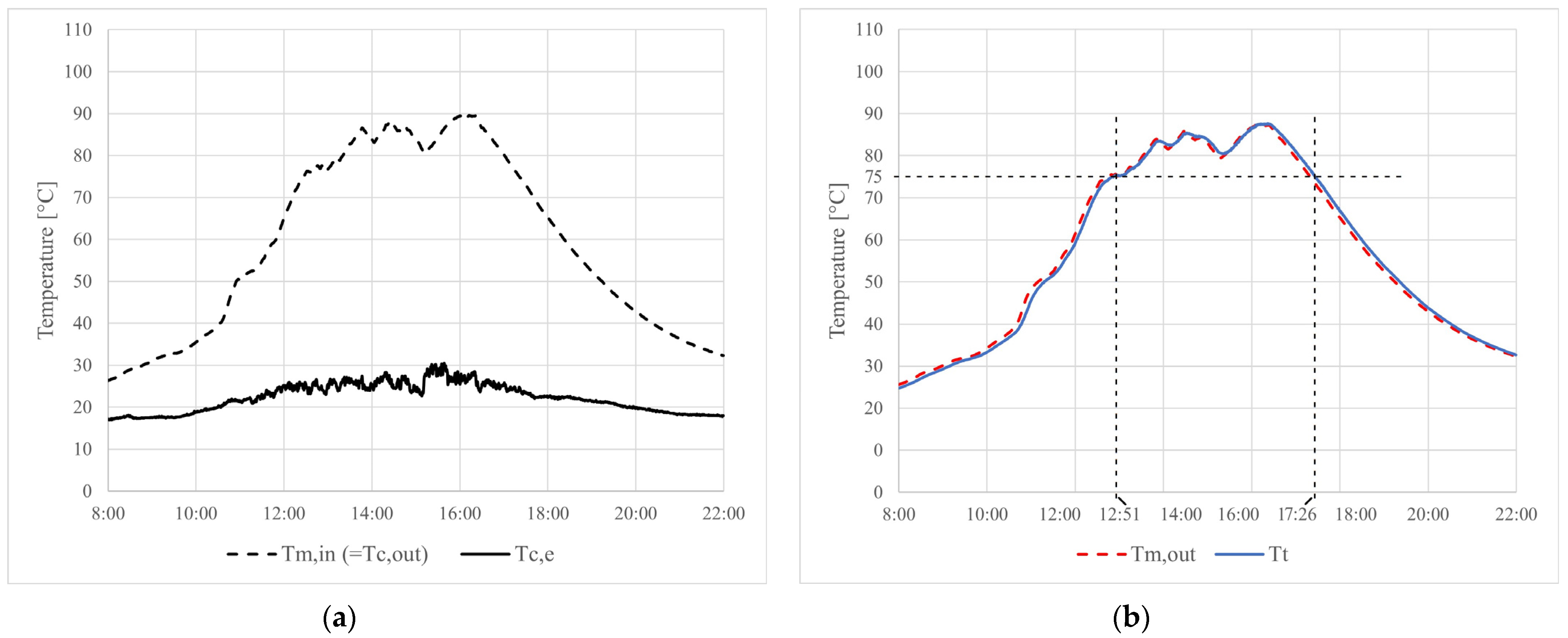
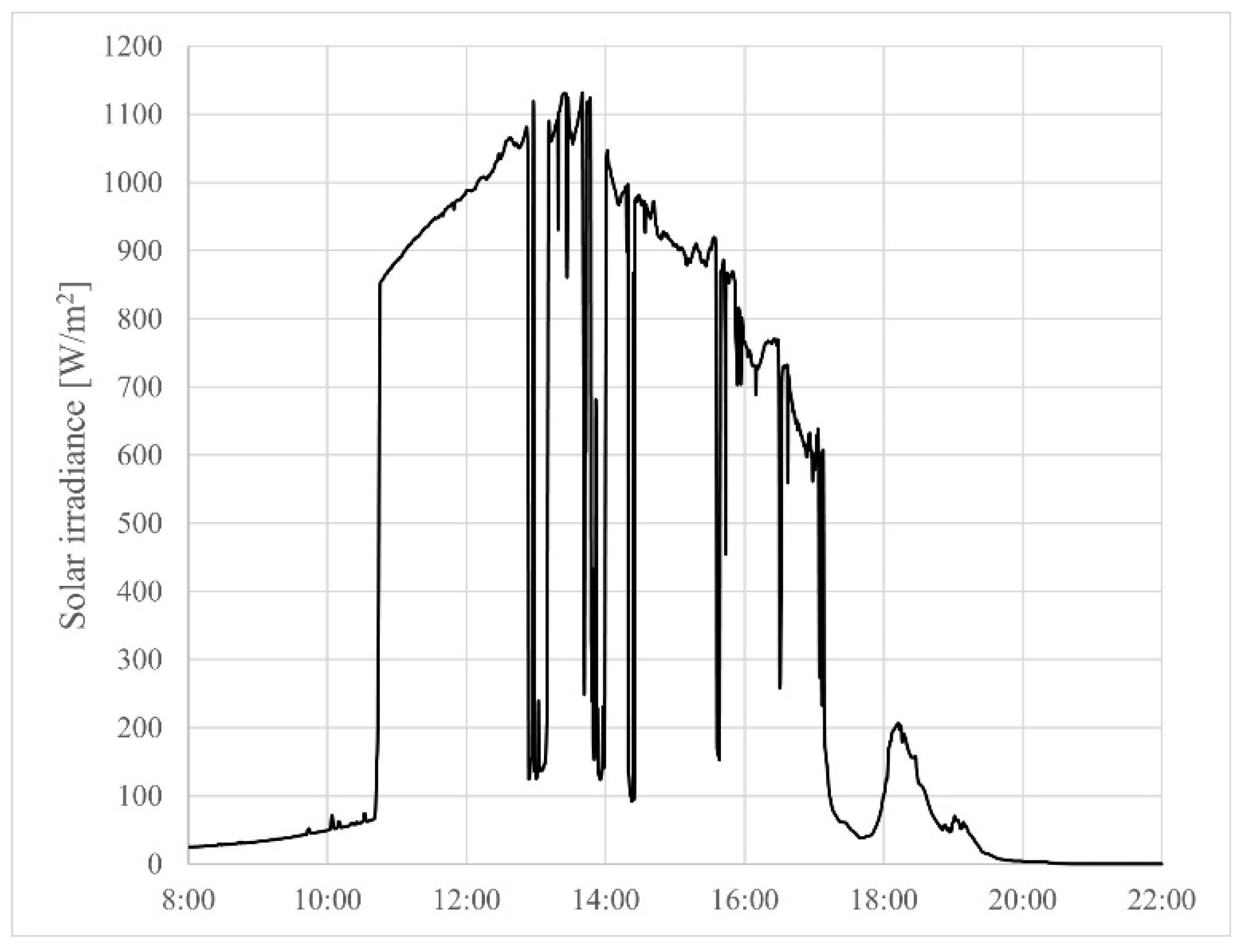
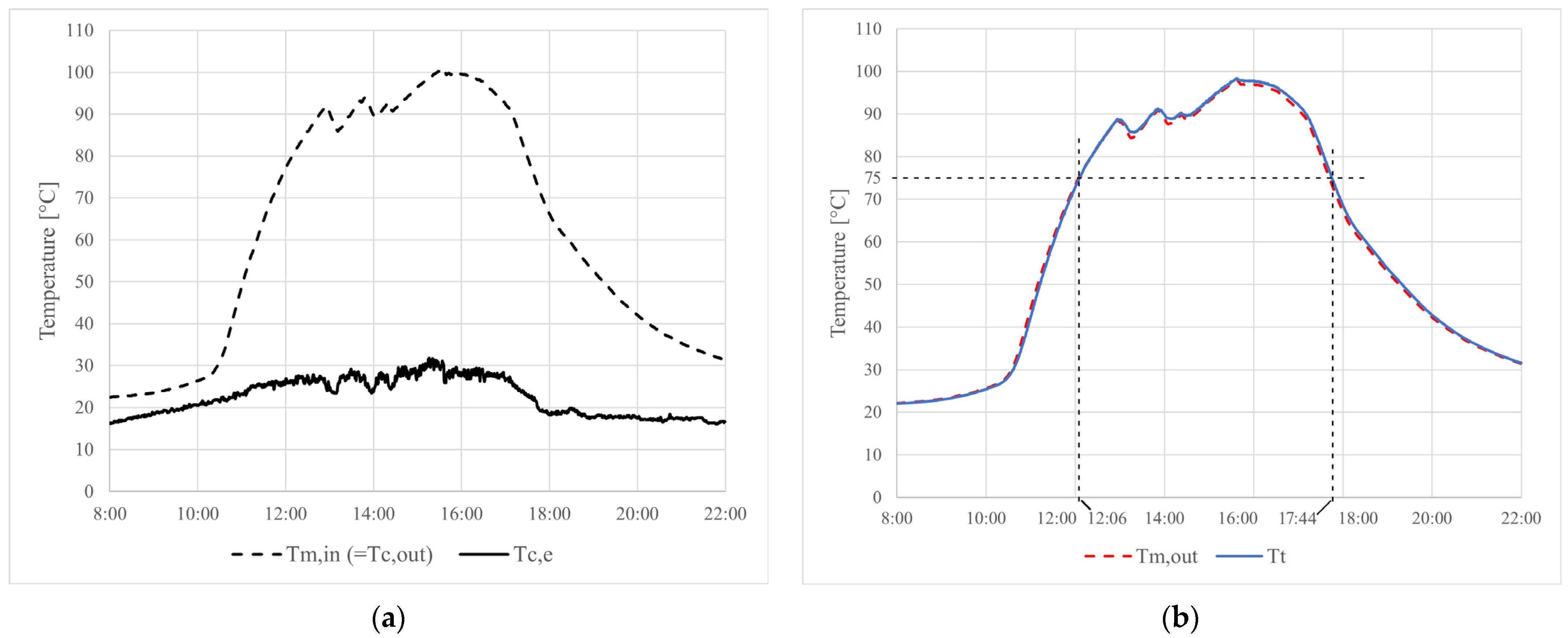
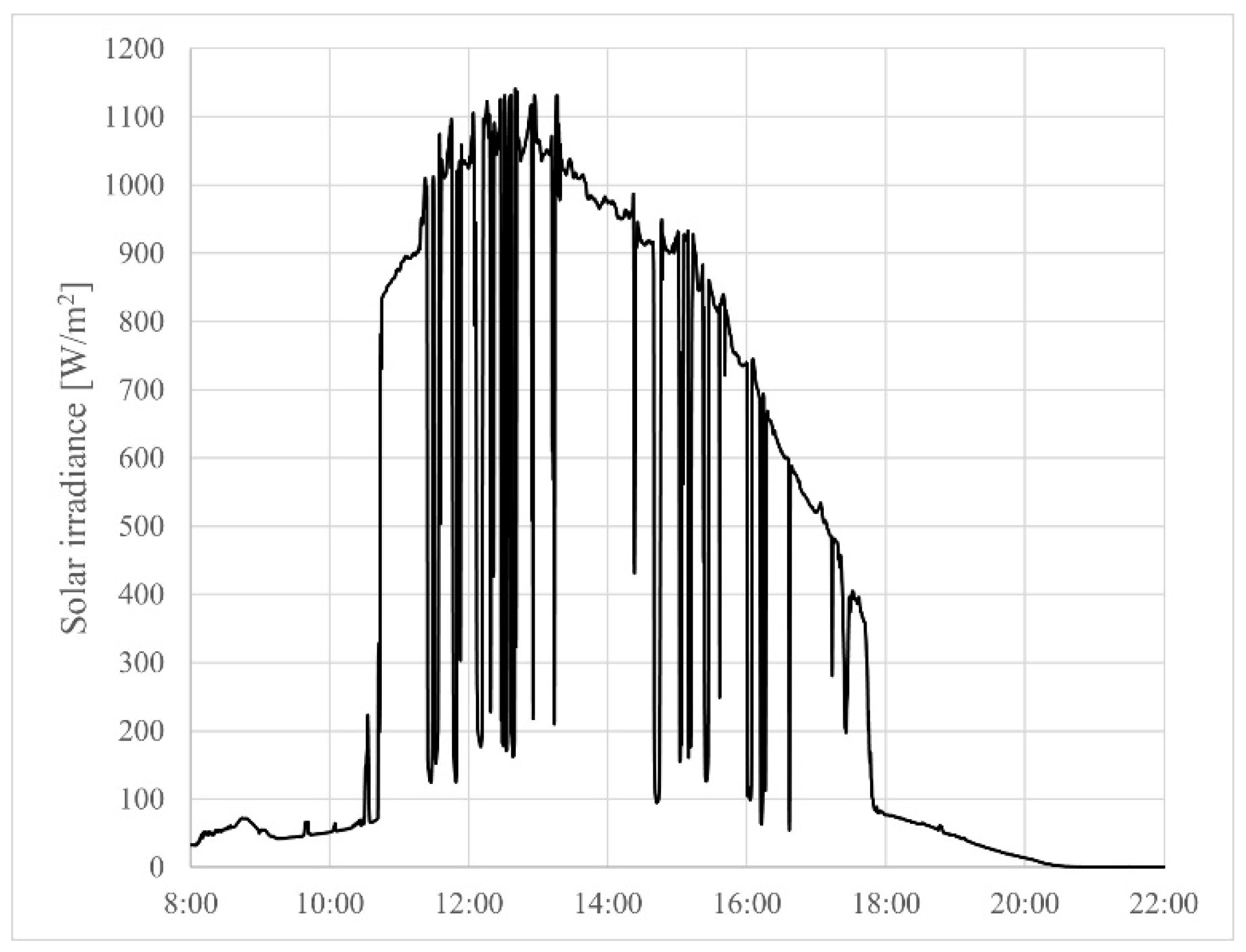
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kalita, N.; Muthukumar, P.; Dalal, A. Performance investigation of a hybrid solar dryer with electric and biogas backup air heaters for chilli drying. Therm. Sci. Eng. Prog. 2024, 52, 102646. [Google Scholar] [CrossRef]
- Mehling, H. Use of phase change materials for food applications—State of the art in 2022. Appl. Sci. 2023, 13, 3354. [Google Scholar] [CrossRef]
- Saxena, A.; Cuce, E.; Tiwari, G.N.; Kumar, A. Design and thermal performance investigation of a box cooker with flexible solar collector tubes: An experimental research. Energy 2020, 206, 118144. [Google Scholar] [CrossRef]
- Bigelow, A.W.; Tabatchnick, J.; Hughes, C. Testing Solar Cookers for Cooking Efficiency. Sol. Energy Adv. 2024, 4, 100053. [Google Scholar] [CrossRef]
- USDA (Food Safety and Inspection Service, U.S. Department of Agriculture). Safe Minimum Internal Temperature Chart. Available online: https://www.fsis.usda.gov/food-safety/safe-food-handling-and-preparation/food-safety-basics/safe-temperature-chart (accessed on 6 June 2024).
- Gupta, P.K.; Misal, A.; Agrawal, S. Development of low cost reflective panel solar cooker. Mater. Today Proc. 2021, 45, 3010–3013. [Google Scholar] [CrossRef]
- Saini, P.; Pandey, S.; Goswami, S.; Dhar, A.; Mohamed, M.E.; Powar, S. Experimental and numerical investigation of a hybrid solar thermal-electric powered cooking oven. Energy 2023, 280, 128188. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Faezian, A.; Mirzababaee, S.M. Parametric analysis and optimization of a portable evacuated tube solar cooker. Energy 2020, 194, 116816. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, Y.; Li, J.; Ma, X.; Li, Q.; Yang, M.; Zhao, X.; Zhu, Y. Simulation and economic analysis of an innovative indoor solar cooking system with energy storage. Sol. Energy 2023, 263, 111816. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Sadeghirad, R.; Zamani, H.; Kianifar, A.; Mirzababaee, S.M. The performance improvement of an indirect solar cooker using multi-walled carbon nanotube-oil nanofluid: An experimental study with thermodynamic analysis. Renew. Energy 2021, 165, 14–24. [Google Scholar] [CrossRef]
- Hussein, H.M.S.; El-Ghetany, H.H.; Nada, S.A. Experimental investigation of novel indirect solar cooker with indoor PCM thermal storage and cooking unit. Energy Convers. Manag. 2008, 49, 2237–2246. [Google Scholar] [CrossRef]
- Getnet, M.Y.; Gunjo, D.G.; Sinha, D.K. Experimental investigation of thermal storage integrated indirect solar cooker with and without reflectors. Results Eng. 2023, 18, 101022. [Google Scholar] [CrossRef]
- Kumar, R.; Adhikari, R.S.; Garg, H.P.; Kumar, A. Thermal performance of a solar pressure cooker based on evacuated tube solar collector. Appl. Therm. Eng. 2001, 21, 1699–1706. [Google Scholar] [CrossRef]
- Schwarzer, K.; Krings, T. Demonstrations-und Feldtest von Solarkochern mit Temporärem Speicher in Indien und Mali; Shaker Verlag: Aachen, Germany, 1996. (In German) [Google Scholar]
- Buzás, J.; Farkas, I. Solar domestic hot water system simulation using blockoriented software. In The 3rd ISES-europe Solar World Congress; CD-ROM Proceedings: København, Denmark, 2000; pp. 1–9. [Google Scholar]
- Castellanos, L.S.M.; Noguera, A.L.G.; Velásquez, E.I.G.; Caballero, G.E.C.; Lora, E.E.S.; Cobas, V.R.M. Mathematical modeling of a system composed of parabolic trough solar collectors integrated with a hydraulic energy storage system. Energy 2020, 208, 118255. [Google Scholar] [CrossRef]
- Kalogirou, S.A.; Panteliou, S.; Dentsoras, A. Modeling of Solar Domestic Water Heating Systems Using Artificial Neural Networks. Sol. Energy 1999, 65, 335–342. [Google Scholar] [CrossRef]
- Brus, L.; Zambrano, D. Black-box identification of solar collector dynamics with variant time delay. Control Eng. Pract. 2010, 18, 1133–1146. [Google Scholar] [CrossRef]
- Zheng, J.; Febrer, R.; Castro, J.; Kizildag, D.; Rigola, J. A new high-performance flat plate solar collector. Numerical modelling and experimental validation. Appl. Energy 2023, 355, 122221. [Google Scholar] [CrossRef]
- Hottel, H.C.; Woertz, B.B. The performance of flat plate solar heat collectors. Trans. ASME 1942, 64, 91–104. [Google Scholar] [CrossRef]
- Buzás, J.; Farkas, I.; Biró, A.; Németh, R. Modelling and simulation aspects of a solar hot water system. Math. Comput. Simul. 1998, 48, 33–46. [Google Scholar] [CrossRef]
- Hilmer, F.; Vajen, K.; Ratka, A.; Ackermann, H.; Fuhs, W.; Melsheimer, O. Numerical solution and validation of a dynamic model of solar collectors working with varying fluid flow rate. Sol. Energy 1999, 65, 305–321. [Google Scholar] [CrossRef]
- Mao, C.; Li, M.; Li, N.; Shan, M.; Yang, X. Mathematical model development and optimal design of the horizontal all-glass evacuated tube solar collectors integrated with bottom mirror reflectors for solar energy harvesting. Appl. Energy 2019, 238, 54–68. [Google Scholar] [CrossRef]
- Víg, P.G. Modelling of Solar Collector Systems with Neural Network. Ph.D. Thesis, Szent István University, Gödöllő, Hungary, 2007. (In Hungarian). [Google Scholar]
- Kicsiny, R. Multiple linear regression based model for solar collectors. Sol. Energy 2014, 110, 496–506. [Google Scholar] [CrossRef]
- Hiris, D.P.; Pop, O.G.; Balan, M.C. Analytical modeling and validation of the thermal behavior of seasonal storage tanks for solar district heating. Energy Rep. 2022, 8, 741–755. [Google Scholar] [CrossRef]
- Badescu, V. Optimal control of flow in solar collector systems with fully mixed water storage tanks. Energy Convers. Manag. 2008, 49, 169–184. [Google Scholar] [CrossRef]
- Kicsiny, R. Black-box model for solar storage tanks based on multiple linear regression. Renew. Energy 2018, 125, 857–865. [Google Scholar] [CrossRef]
- Bradley, J. Counterflow, crossflow and cocurrent flow heat transfer in heat exchangers: Analytical solution based on transfer units. Heat Mass Transf. 2010, 46, 381–394. [Google Scholar] [CrossRef]
- Zohuri, B. Compact Heat Exchangers, Selection, Application, Design and Evaluation; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Géczi, G.; Kicsiny, R.; Korzenszky, P. Modified effectiveness and linear regression based models for heat exchangers under heat gain/loss to the environment. Heat Mass Transf. 2019, 55, 1167–1179. [Google Scholar] [CrossRef]
- Zavala-Río, A.; Santiesteban-Cos, R. Reliable compartmental models for double-pipe heat exchangers: An analytical study. Appl. Math. Model. 2007, 31, 1739–1752. [Google Scholar] [CrossRef]
- Géczi, G.; Kicsiny, R. Hungarian University of Agriculture and Life Sciences. Apparatus for Preparing Food with Solar Energy and/or for Heating Liquid, Utility Model Protection, Hungarian Intellectual Property. Office. Patent 5489, 27 October 2021. (In Hungarian). [Google Scholar]
- Cao, E. Heat Transfer in Process Engineering, 1st ed.; McGraw-Hill Education: New York, NY, USA, 2010; ISBN 9780071624084. [Google Scholar]
- Engineering Toolbox. Available online: https://www.engineeringtoolbox.com/overall-heat-transfer-coefficient-d_434.html (accessed on 6 June 2024).
- Székely, L.; Kicsiny, R.; Hermanucz, P.; Géczi, G. Explicit analytical solution of a differential equation model for solar heating systems. Sol. Energy 2021, 222, 219–229. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rátkai, M.; Géczi, G.; Kicsiny, R.; Székely, L. New Physically-Based Mathematical Model and Experiments for a Recently Invented Solar Pot. Appl. Sci. 2024, 14, 6643. https://doi.org/10.3390/app14156643
Rátkai M, Géczi G, Kicsiny R, Székely L. New Physically-Based Mathematical Model and Experiments for a Recently Invented Solar Pot. Applied Sciences. 2024; 14(15):6643. https://doi.org/10.3390/app14156643
Chicago/Turabian StyleRátkai, Márton, Gábor Géczi, Richárd Kicsiny, and László Székely. 2024. "New Physically-Based Mathematical Model and Experiments for a Recently Invented Solar Pot" Applied Sciences 14, no. 15: 6643. https://doi.org/10.3390/app14156643
APA StyleRátkai, M., Géczi, G., Kicsiny, R., & Székely, L. (2024). New Physically-Based Mathematical Model and Experiments for a Recently Invented Solar Pot. Applied Sciences, 14(15), 6643. https://doi.org/10.3390/app14156643





